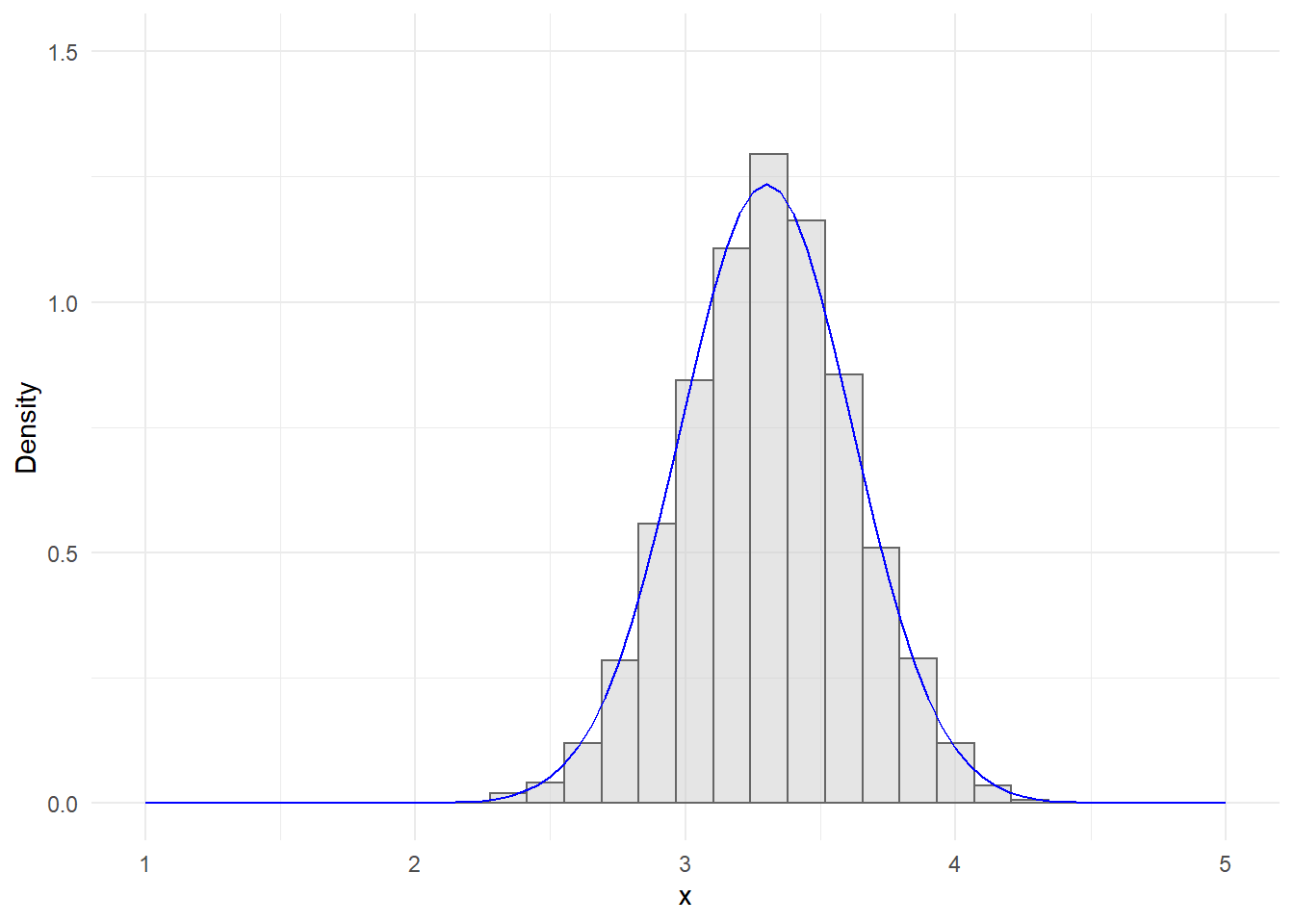
2 Προσομοίωση Τυχαίων Μεταβλητών

2.1 Ψευδοτυχαίοι Αριθμοί

Η δυνατότητα προσομοίωσης δεδομένων που παράγονται σύμφωνα με κάποιο υποτιθέμενο στοχαστικό πρότυπο επιτυγχάνεται πολύ εύκολα σήμερα με τη βοήθεια των ηλεκτρονικών υπολογιστών. Κάθε στατιστικό λογισμικό είναι εφοδιασμένο με γεννήτορες ψευδοτυχαίων αριθμών. Συγκεκριμένα, χρησιμοποιούνται κατάλληλοι αλγόριθμοι που παράγουν λιγότερο ή περισσότερο πολύπλοκες ντετερμινιστικές ακολουθίες αριθμών έτσι ώστε να φαίνονται ως ακολουθίες που έχουν παραχθεί από ανεξάρτητες και ομοιόμορφες στο \((0,1)\) τυχαίες μεταβλητές. Ο προκαθορισμένος αλγόριθμος στην R είναι ο Mersenne-Twister που βασίζεται στους πρώτους αριθμούς του Mersenne. Οι πρώτοι αριθμοί του Mersenne είναι της μορφής \(n=2^p-1\), όπου \(p\) κατάλληλος πρώτος αριθμός ώστε ο \(n\) να βγαίνει πρώτος. Η πιο διαδεδομένη μορφή του αλγορίθμου Mersenne Twister είναι η MT19337 που βασίζεται στον πρώτο \(n=2^{19337}-1\). Ο αλγόριθμος κάνει την αναδρομή με κατάλληλο γραμμικό μετασχηματισμό της μορφής \(x_{n+1}=Ax_n,\) όπου \(Α\) είναι πίνακας ειδικής μορφής, δημιουργώντας έτσι μία ακολουθία διανυσμάτων καταστάσεων μεγάλης διάστασης που μετατρέπονται πάλι σε αριθμούς στο \((0,1)\). Η μελέτη αυτού του αλγορίθμου αποτελεί αντικείμενο ενός μαθήματος προσομοίωσης.

Η σημασία προσομοίωσης τιμών από την ομοιόμορφη κατανομή βρίσκεται στο γεγονός ότι οι προσομοιώσεις άλλων κατανομών βασίζονται είτε άμεσα, είτε έμμεσα στην ομοιόμορφη. Η R έχει έτοιμη συνάρτηση για την παραγωγή τιμών από την \(Unif(0,1)\). Κάθε φορά που ζητάμε μία τιμή της, η R μας δίνει μία διαφορετική παρατήρηση, υλοποιώντας τον Mersenne-Twister. H αρχικοποίηση \(x_0\), χωρίς άλλη παρέμβαση, γίνεται αρκετά “τυχαία” καθώς υπεισέρχεται ο χρόνος που πατήσαμε την εντολή:

runif(1)
## [1] 0.1120287
runif(1)
## [1] 0.063733

Στην R μπορούμε να ορίσουμε έναν σπόρο με την εντολή set.seed(\(k\)), αρχικοποιώντας έτσι τον MT19337 σε συγκεκριμένη θέση της ακολουθίας που καθορίζεται από την επιλογή ενός θετικού ακεραίου \(k.\) Με αυτόν τον τρόπο, αν επαναλάβουμε τις προσομοιώσεις με την ίδια τιμή του \(k\), θα παίρνουμε τις ίδιες παρατηρήσεις:

set.seed(1465)
runif(1)
## [1] 0.7645799
runif(1)
## [1] 0.9772592

set.seed(1465)
runif(1)
## [1] 0.7645799
runif(1)
## [1] 0.9772592

2.2 Μέθοδος Αντιστροφής

Η μέθοδος της αντιστροφής μας επιτρέπει να προσομοιώνουμε τιμές από τυχαίες μεταβλητές που έχουν συνάρτηση κατανομής \(F\), προϋποθέτοντας ότι έχουμε γνώση της \(F\). Το μόνο που χρειάζεται να διαθέτουμε είναι μία τιμή που έχει παραχθεί από την \(Unif(0,1)\) (η οποία δίνεται από το γεννήτορα) και έναν τρόπο αντιστροφής της \(F\).

Η αιτιολόγηση είναι απλή στην περίπτωση που η \(F\) ικανοποιεί τις υποθέσεις της παρακάτω πρότασης.

Πρόταση 2.1 Έστω \(F:\mathbb{R}\rightarrow [0,1]\) συνάρτηση κατανομής που είναι συνεχής και γνησίως αύξουσα στο \(I=\{x\in \mathbb{R}:F(x)\in (0,1)\}.\) Αν \(U\thicksim Unif(0,1)\), τότε \(X=F^{-1}(U) \thicksim F\).

Απόδειξη:. Με τις υποθέσεις της Πρότασης έχουμε ότι η \(F:I\rightarrow (0,1)\) έχει συνήθη αντίστροφη. Θα δείξουμε λοιπόν ότι η \(X=F^{-1}(U)\thicksim F\) με τη βοήθεια συναρτήσεων κατανομών.

Έστω \(x \in I\). Θέτουμε \(F_X\) τη συνάρτηση κατανομής της \(X=F^{-1}(U)\) και έχουμε \[\begin{align*} F_X(x) & = \mathbf{P}(F^{-1}(U) \leq x) = \mathbf{P}(F\left(F^{-1}(U)\right) \leq F(x)) = \mathbf{P}(U \leq F(x)) = F_U\left( F(x) \right) \\ & = F(x). \end{align*}\]

Από το παραπάνω συμπεραίνουμε ότι \(F_X=F\) και άρα \(X\thicksim F\).

Ένα παράδειγμα σ.κ. που ικανοποιεί αυτές τις υποθέσεις με \(I=\mathbb{R}\) είναι η σ.κ. της τυπικής κανονικής \(\Phi\) που είναι συνεχής και γνησίως αύξουσα σε όλο το \(\mathbb{R}\). Έτσι η εξίσωση \(F(x)=u\) έχει μοναδική λύση για \(u\in (0,1)\) και καθορίζει μονοσήμαντα τα κάτω ποσοστημόρια \(q_u:=F^{-1}(u)\) της κατανομής, τα οποία ικανοποιούν τη σχέση \(F(q_u)=F\left(F^{-1}(u)\right)=u\).

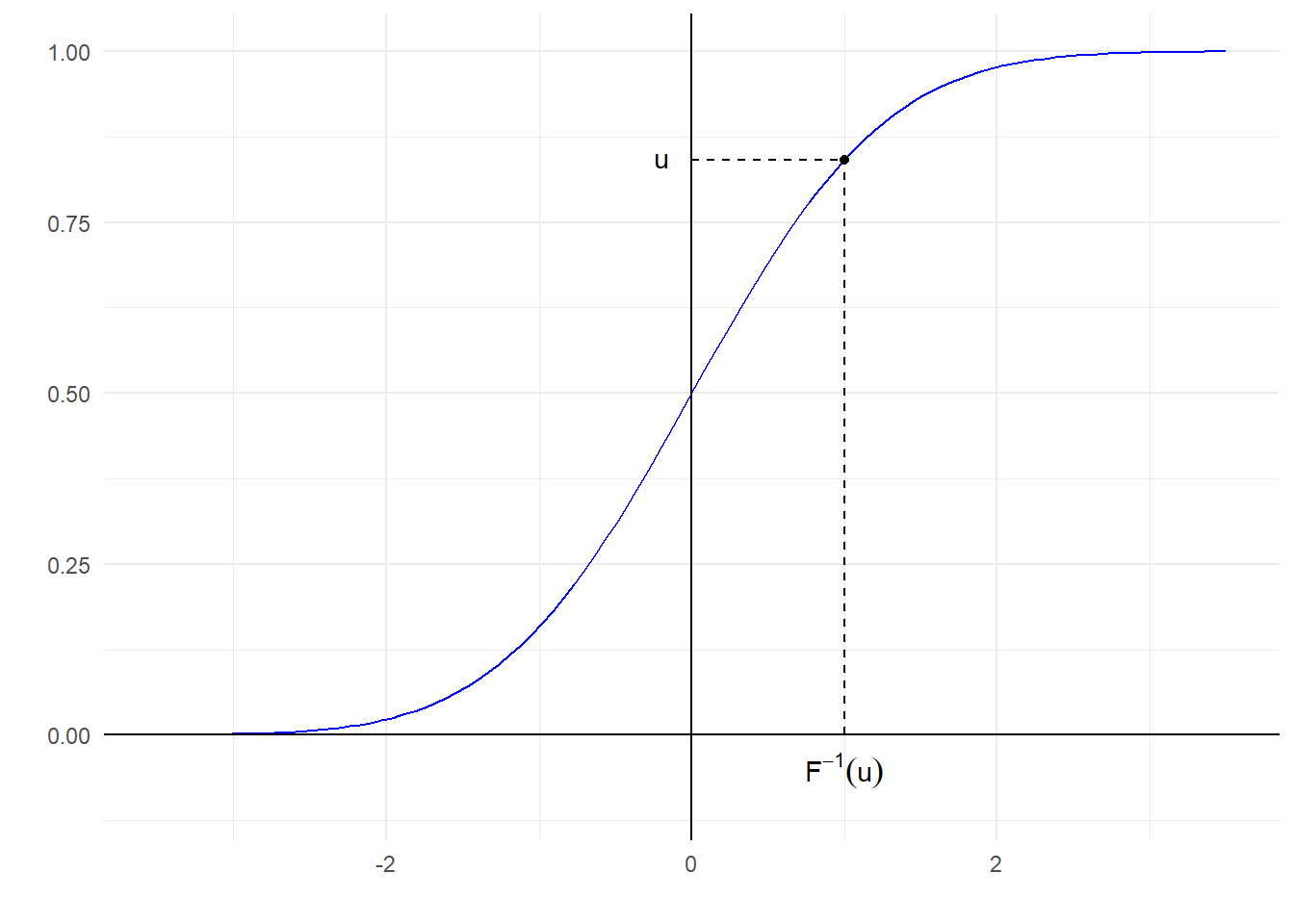
Τελικά, ο τρόπος παραγωγής ενός τυχαίου δείγματος από την \(F\) είναι πολύ απλός. Αν \(\{U_i\}_{i=1}^{n}\) είναι ένα τυχαίο δείγμα από την \(Unif(0,1)\), τότε οι \(\{X_i\}_{i=1}^{n}\) με \(X_i = F^{-1}(U_i)\) αποτελούν ένα τυχαίο δείγμα από την \(F\).

Η χρήση της γενικευμένης αντίστροφης μας δίνει τη δυνατότητα να κάνουμε αντιστροφή σ.κ. που δεν είναι αντιστρέψιμες με τη συνήθη έννοια.

Ορισμός 2.1 Έστω \(F: \mathbb{R}\rightarrow [0,1]\) μία συνάρτηση κατανομής. Γενικευμένη αντίστροφη ονομάζουμε τη συνάρτηση \(F^{-}:(0,1)\rightarrow \mathbb{R}\) με

\[\begin{equation*} F^-(u) = \inf \left\{ x \in \mathbb{R}: F(x) \geq u \right\}. \end{equation*}\]

Η παρακάτω πρόταση γενικεύει τη δυνατότητα χρήσης της μεθόδου αντιστροφής για την προσομοίωση τιμών από κατανομές με γνωστή συνάρτηση κατανομής \(F\).

Πρόταση 2.2 Έστω \(F:\mathbb{R}\rightarrow [0,1]\) συνάρτηση κατανομής. Αν \(U\thicksim Unif(0,1)\), τότε \(X=F^-(U) \thicksim F\).

Η απόδειξη της παραπάνω πρότασης γίνεται στο μάθημα της Μη-Παραμετρικής Στατιστικής.

Η γενικευμένη αντίστροφη \(F^-\) λύνει το πρόβλημα αντιστροφής σε 2 “προβληματικές” περιπτώσεις. Η μία αφορά τις περιοχές σταθεροποίησης της \(F\) και η άλλη των σημείων που παρουσιάζονται άλματα ασυνέχειας της \(F\). Ισοδύναμα, από αλγεβρική σκοπιά, οι παραπάνω περιπτώσεις αναφέρονται στις περιπτώσεις που η εξίσωση \(F(x)=u\) έχει άπειρες λύσεις ή είναι αδύνατη αντίστοιχα.

Παράδειγμα 2.1 Θεωρούμε την παρακάτω συνάρτηση κατανομής με περιοχή σταθεροποίησης το \([x_a, x_b]\):

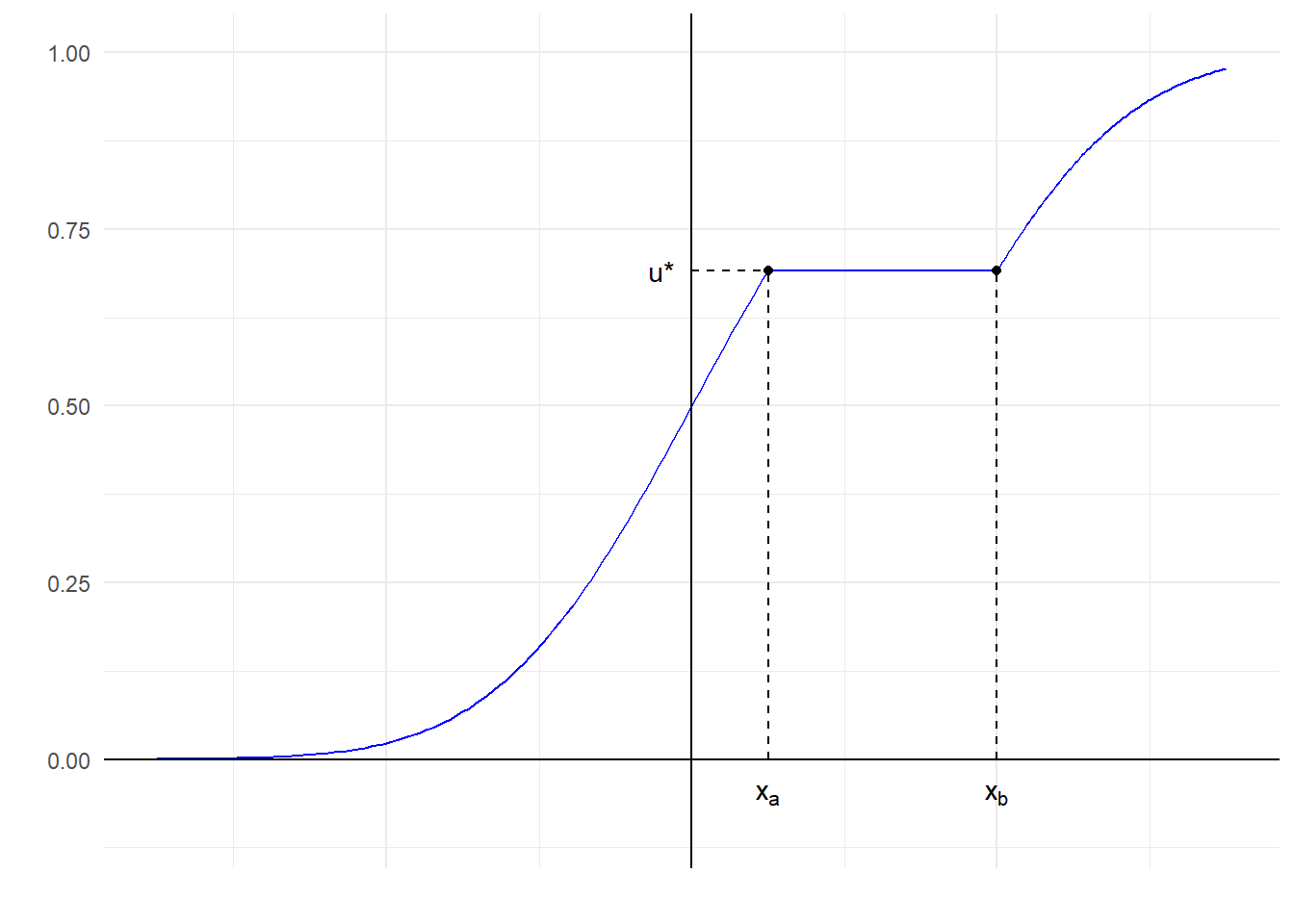
Στο παραπάνω γράφημα βλέπουμε πως για \(u^\star\) όλα τα \(x\) στο διάστημα \(I=[x_a, x_b]\) ικανοποιούν την σχέση \(F(x)=u^\star\). Επομένως, η συνάρτηση \(F\) δεν είναι 1-1, άρα ούτε και αντιστρέψιμη. Παρότι η \(F\) δεν έχει συνήθη αντίστροφη, έχει γενικευμένη αντίστροφη, σύμφωνα με τον ορισμό της οποίας:

\[\begin{equation*} F^{-}(u^\star)=\inf\{x: F(x)\geq u^\star\}=\inf\{x:F(x)=u^\star\}=x_a. \end{equation*}\]

Παράδειγμα 2.2 Θεωρούμε την παρακάτω συνάρτηση κατανομής με άλμα ασυνέχειας \([u_a, u_b)\) στο \(x_0\):

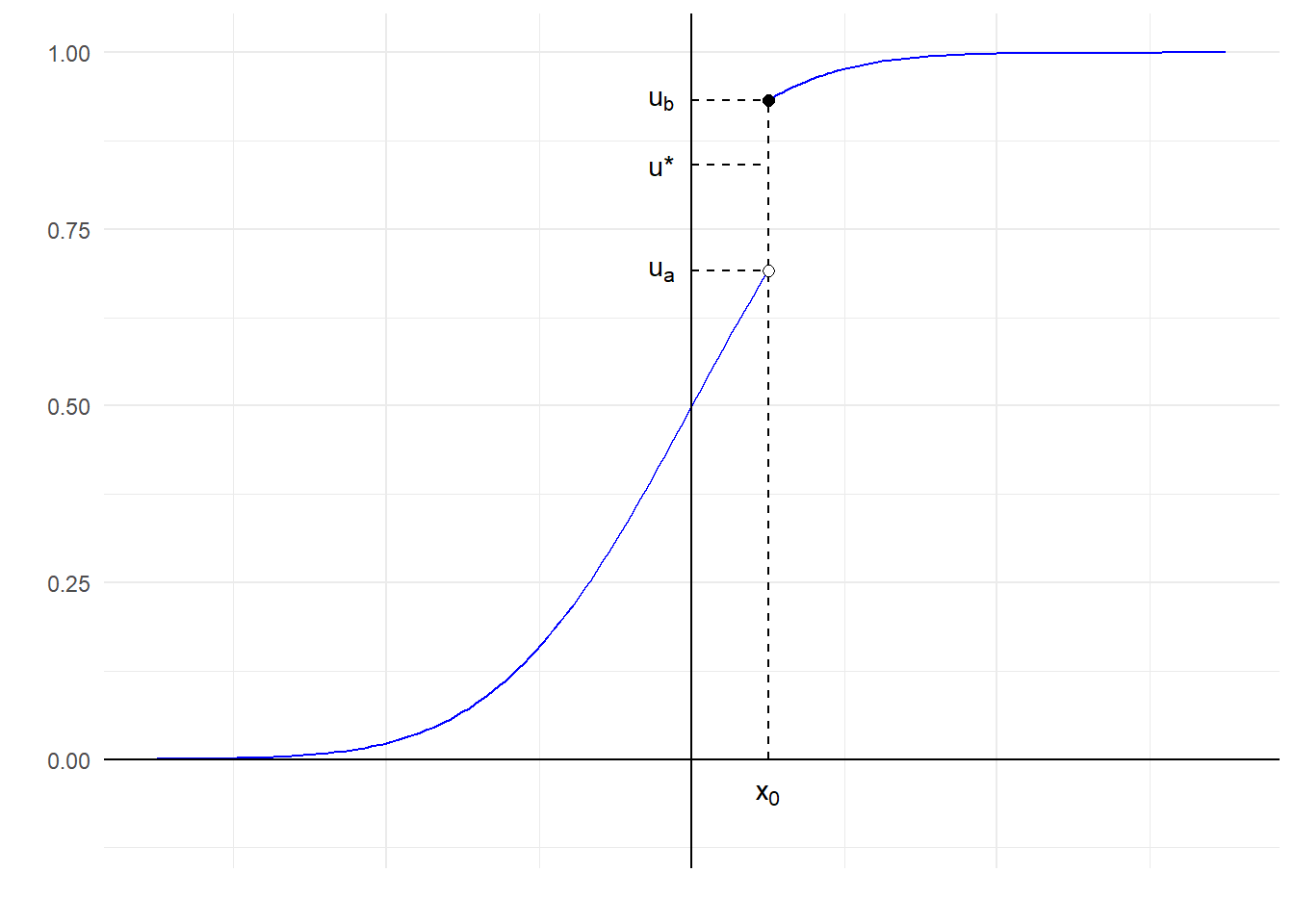
Στο παραπάνω γράφημα βλέπουμε πως για \(u^\star \in [u_a, u_b)\) δεν υπάρχει κανένα \(x \in \mathbb{R}\) που να ικανοποιεί την σχέση \(F(x)=u^\star\). Επομένως, η συνάρτηση \(F\) δεν είναι επί του \((0,1)\), άρα δεν υπάρχει αντίστροφη της \(F\) με πεδίο ορισμού το \((0,1)\). Υπάρχει όμως η γενικευμένη αντίστροφη, σύμφωνα με τον ορισμό της οποίας:

\[\begin{equation*} F^{-}(u^\star)=\inf\{x: F(x)\geq u^\star\}=\inf\{x:F(x)=u_b\}=x_0. \end{equation*}\]

2.2.1 Προσομοίωση από Εκθετική κατανομή

Παράδειγμα 2.3 Έστω ότι θέλουμε να παράγουμε παρατηρήσεις από την \(Exp(1)\). Υπενθυμίζουμε ότι:

\[\begin{equation*} F(x) = 1-e^{-x}, \ \ x>0, \end{equation*}\]

και εύκολα βλέπουμε ότι η \(F\) είναι συνεχής και γνησίως αύξουσα στο \((0,+\infty)\). Έτσι μπορούμε να ορίσουμε τη συνήθη αντίστροφη της \(F\) στο \((0,1)\). Συγκεκριμένα, έχουμε

\[\begin{equation*} u = 1-e^{-x} \Leftrightarrow e^{-x} = 1-u \Leftrightarrow -x = \log(1-u) \Leftrightarrow x=-\log(1-u). \end{equation*}\]

Συμπεραίνουμε ότι \(F^{-1}(u)=-\log(1-u)\) και από τη μέθοδο της αντιστροφής έχουμε ότι αν \(U\thicksim Unif(0,1)\), τότε η \(X=-\log(1-U) \thicksim Exp(1)\).

Στην περίπτωση της ομοιόμορφης κατανομής παρατηρούμε ότι \(U\overset{d}{=} 1-U\) και έτσι μπορούμε να απλοποιήσουμε ακόμα πιο πολύ στη μορφή \(X=-\log(U) \thicksim Exp(1)\).

Στην R το παραπάνω μπορεί να υλοποιηθεί ως εξής:

set.seed(123)

Nsim <- 10 ^ 4 
U <- runif(Nsim)
X <- - log(U) 
Y <- rexp(Nsim)

hist(X, freq = FALSE, main = "Exp from Uniform", breaks = seq(0, 12, 0.5))
curve(dexp, from = 0, to = 10, lty = 1, lwd = 1, col = "red", add = TRUE)

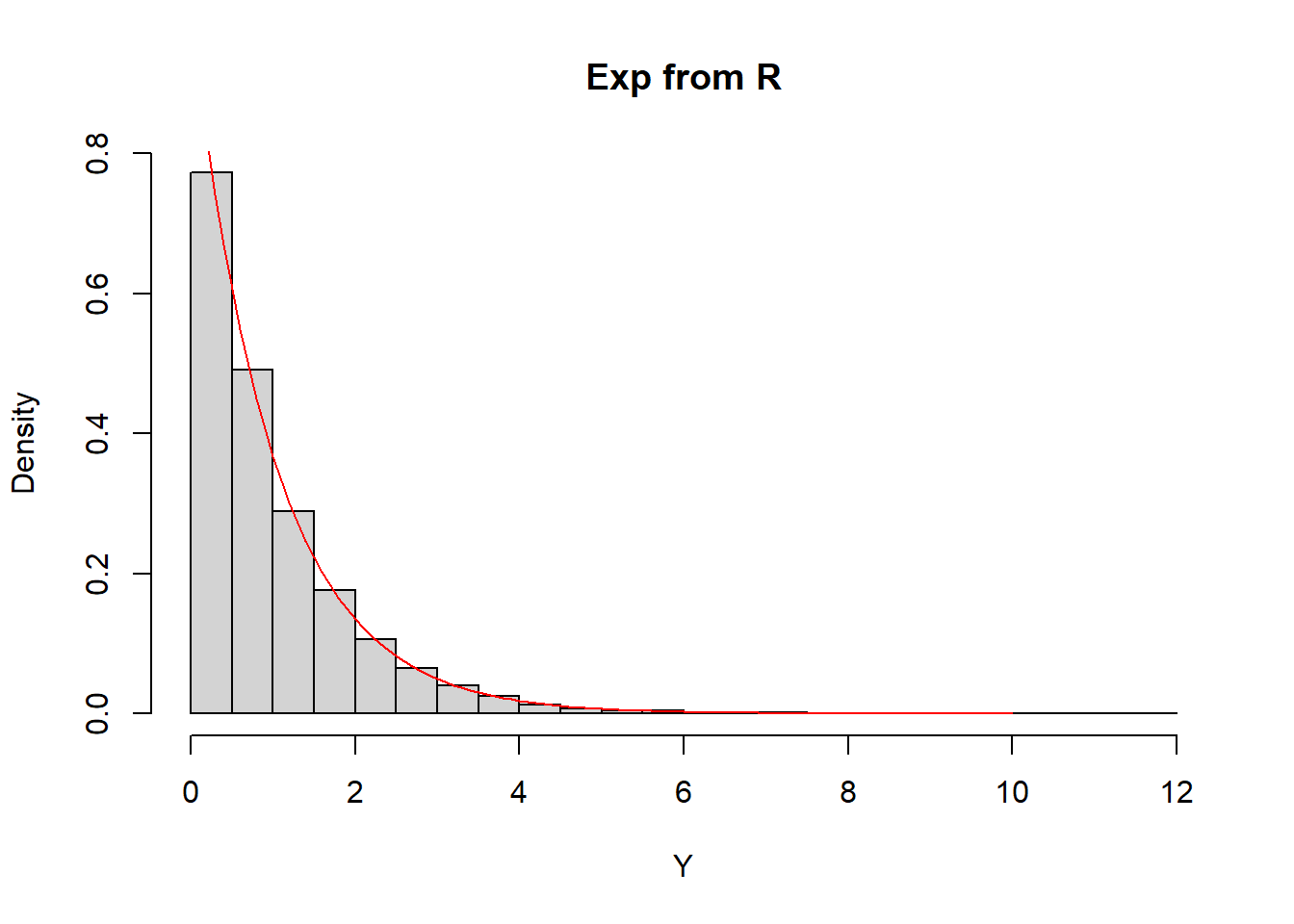
hist(Y, freq = FALSE, main = "Exp from R", breaks = seq(0, 12, 0.5))
curve(dexp, from = 0, to = 10, lty = 1, lwd = 1, col = "red", add = TRUE)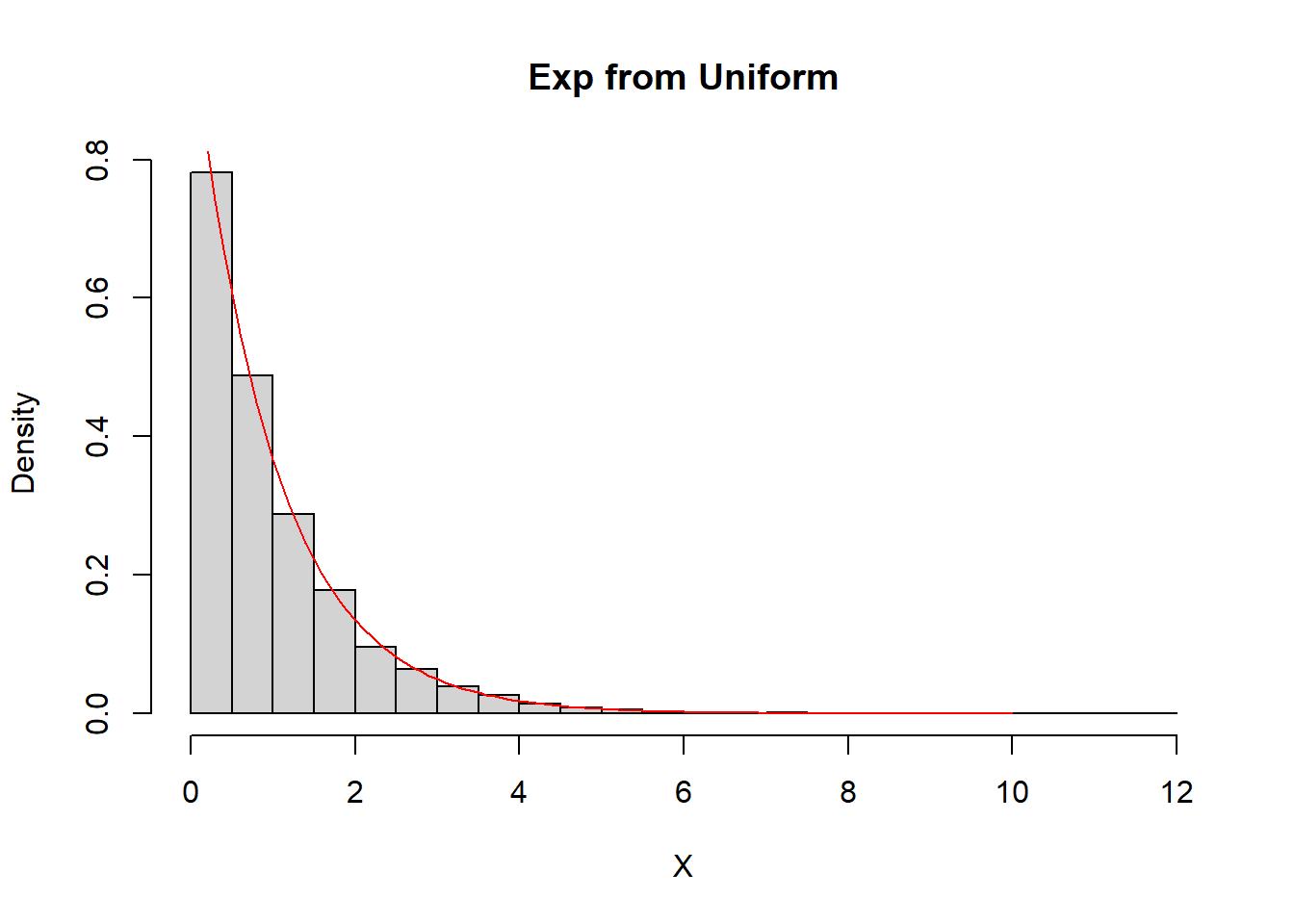

2.2.2 Παραγωγή από Λογιστική Κατανομή

Παράδειγμα 2.4 Έστω ότι θέλουμε να παράγουμε παρατηρήσεις από τη Λογιστική κατανομή \(L(0,1)\). Υπενθυμίζουμε ότι αν \(L\thicksim L(0,1)\), τότε:

\[\begin{equation*} F_L(x)=\frac{1}{1+e^{-x}}, \quad x\in \mathbb{R}. \end{equation*}\]

Θα χρησιμοποιήσουμε τη μέθοδο αντιστροφής:

\[\begin{equation*} F_L(x)=\frac{1}{1+e^{-x}} \Rightarrow u = \frac{1}{1+e^{-x}} \Leftrightarrow u+ue^{-x}=1 \Leftrightarrow e^{-x} = \frac{1-u}{u} \Leftrightarrow -x = \log \frac{1-u}{u} \Leftrightarrow x = \log \frac{u}{1-u}. \end{equation*}\]

Τελικά,

\[\begin{equation*} X_i = \log \frac{U_i}{1-U_i}. \end{equation*}\]

2.2.3 Παραγωγή Διακριτών Κατανομών

Η μέθοδος της αντιστροφής μας επιτρέπει να παράγουμε παρατηρήσεις διακριτών κατανομών χρησιμοποιώντας την ομοιόμορφη κατανομή.

Παράδειγμα 2.5 (Binomial Simulation) Ας δούμε το παρακάτω παράδειγμα στην R για την Bin(10, 0.3).

set.seed(2184)
Nsim <- 10 ;  N <- 10 ; p <- 0.3
prob <- pbinom((-1):(N - 1), N, p)
X <- rep(10, Nsim)
for (i in 1:Nsim){
  u <- runif(1)
  while(prob[X[i] + 1] >= u){
   X[i] <- X[i] - 1 
  }
}
X
##  [1] 3 3 2 3 0 3 1 0 1 3

Συγκρίνετε με τον παρακάτω τρόπο παραγωγής.

set.seed(2184)
Nsim <- 10 ;  N <- 10 ; p <- 0.3
prob <- pbinom(0:9, N, p)
X <- rep(0, Nsim)
for (i in 1:Nsim){
   u <- runif(1)
   X[i] <- sum(prob < u) 
}
X
##  [1] 3 3 2 3 0 3 1 0 1 3

Είναι φανερό ότι οδηγούμαστε στις ίδιες τιμές. Ο πρώτος τρόπος χρησιμοποιεί τον ορισμό της γενικευμένης αντίστροφης. Ο δεύτερος τρόπος είναι ισοδύναμος, αλλά αποδοτικότερος. Για να δούμε πώς προσομοιώνει και η R:

set.seed(2184)
rbinom(10, N, p)
##  [1] 3 3 2 3 0 3 1 0 1 3

Προσομοιώνει λοιπόν ακριβώς με τον ίδιο τρόπο.

Παράδειγμα 2.6 (Poisson Simulation) Ας μελετήσουμε ένα παράδειγμα από την Poisson(100).

set.seed(2544)
Nsim <- 10 ^ 4 ; lambda <- 100
lmax <- 300 
prob <- ppois(0:lmax, lambda)

X <- rep(0, Nsim)
for (i in 1:Nsim) {
  u <- runif(1)
  X[i] <- sum(prob < u) 
}
X[1:10]
##  [1] 101  84 112 108 102 105 120 107  97  98

Συγκρίνεται με τον παρακάτω τρόπο προσομοίωσης

set.seed(2544)
Nsim <- 10 ^ 4 ; lambda <- 100
spread <- 3 * sqrt(lambda)  # recall that var(Poisson(lambda)) = lambda
t <- round(seq(max(0, lambda - spread), lambda + spread, 1))
prob <- ppois(t, lambda)

Y <- rep(0,Nsim)
for (i in 1:Nsim){
  u <- runif(1)
  Y[i] <- t[1] + sum(prob < u)  # practically assuming that X[1]\geq t[1]
}
Y[1:10]
##  [1] 101  84 112 108 102 105 120 107  97  98

Ίσως φαίνεται να μην υπάρχουν διαφορές. Όμως, υπάρχουν κάποιες παρατηρήσεις που διαφέρουν στα 2 δείγματα. Μπορούμε λοιπόν να υπολογίσουμε, όπως παρακάτω, την πιθανότητα μία παρατήρηση να βρεθεί εντός του διαστήματος που καθορίσαμε \([\lambda -3*\sqrt{\lambda},\lambda+3*\sqrt{\lambda}]\) και άρα και το αναμενόμενο πλήθος των παρατηρήσεων που θα διαφέρουν. Στο συγκεκριμένο βέβαια πρόβλημα μπορούμε να το ελέγξουμε κατάλληλα.

sum(X != Y)
## [1] 15
proba.in <- ppois(lambda + spread, lambda) - ppois(lambda - spread - 1, lambda)
proba.in
## [1] 0.9976323
1 - proba.in
## [1] 0.002367724
expected.out <- Nsim * (1 - proba.in)
expected.out
## [1] 23.67724

Τέλος, ας δούμε και η R πώς παράγει από την παραπάνω Poisson.

set.seed(2544)
rpois(10, 100)
##  [1] 100 112 102 119  97  82 102  83  98  99

Φαίνεται λοιπόν η R να ακολουθεί το δικό της μονοπάτι. Διερευνήστε αυτό το θέμα…

2.3 Οικογένειες Κατανομών Θέσης - Κλίμακας

2.3.1 Μετασχηματισμοί Κατανομών

Έστω ότι έχουμε μία πραγματική τ.μ. \(X\) με συνάρτηση πυκνότητας πιθανότητας \(f_X\) και θέλουμε να κάνουμε το μετασχηματισμό \(Y=g(X)\), με \(g\) 1-1 και αμφιδιαφορίσιμη (\(g,g^{-1}\) διαφορίσιμες). Τότε:

\[\begin{equation*} f_Y(y)=f_X\left(g^{-1}(y)\right) \cdot \left| \frac{dg^{-1}(y)}{dy}\right| , \ \ \forall y\in g(S_X). \end{equation*}\]

Μας ενδιαφέρει η προσομοίωση τιμών από οικογένειες κατανομών θέσης - κλίμακας, δηλ τ.μ. της μορφής \(X=\mu +\sigma Z\), όπου \(\mu \in \mathbb{R}\) και \(\sigma >0\). Το \(\mu\) ονομάζεται παράμετρος θέσης (location) ενώ το \(\sigma\) παράμετρος κλίμακας (scale). Για να μην τα μπερδεύουμε με τη μέση τιμή και την τυπική απόκλιση μίας τυχαίας μεταβλητής, πολλές φορές θα χρησιμοποιούμε διαφορετικά σύμβολα.

Παρατήρηση:. Συνήθως το \(\theta=1/\sigma\) ονομάζεται παράμετρος ρυθμού (rate). Για παράδειγμα, η εκθετική κατανομή μπορεί να εκφραστεί είτε ως \(Exp(rate)\), είτε ως \(Exp(scale)\). Χρησιμοποιώντας τα σύμβολα \(\theta, \lambda\) αντίστοιχα, η σ.π.π. γράφεται

\[\begin{align*} f(x) &= \theta e^{-\theta x}, \quad x>0, \\ f(x) &= \frac{1}{\lambda} e^{-\frac{x}{\lambda}}, \quad x>0, \end{align*}\]

Είναι φανερό ότι οι μετασχηματισμοί θέσης - κλίμακας αποτελούν ειδική κατηγορία μετασχηματισμών, για τους οποίους έχουμε \(g(x)=\mu+\sigma x\). Επομένως:

\[\begin{equation*} F_Y(y)=\mathbf{P}(Y\leq y) = \mathbf{P}(\mu+\sigma X \leq y)= \mathbf{P}(X\leq \frac{y-\mu}{\sigma}) = F_X\left(\frac{y-\mu}{\sigma}\right), \end{equation*}\]

και

\[\begin{equation*} f_Y(y) = \frac{1}{\sigma} \cdot f_X\left( \frac{y-\mu}{\sigma} \right). \end{equation*}\]

Γενικότερα, σε μετασχηματισμούς θέσης - κλίμακας (ή μόνο θέσης αν \(\sigma=0\), ή μόνο κλίμακας αν \(\mu=0\)) αρκεί να βρούμε την αντίστροφη για την “τυπική” κατανομή αυτής της οικογένειας.

Παράδειγμα 2.7 Ας υποθέσουμε πως μπορούμε να παράγουμε από την \(Exp(1)\). Πώς μπορούμε να παράγουμε από την \(Exp(\theta)\), όπου \(θ\) παράμετρος ρυθμού;

Ισχύει ότι

\[\begin{equation*} X \thicksim Exp(1) \Rightarrow Y=\frac{1}{\theta} X \thicksim Exp(\theta). \end{equation*}\]

Επομένως, από το παράδειγμα 2.3 παίρνουμε ότι \(Y=-\frac{1}{\theta}\log U \thicksim Exp(\theta).\)

Άσκηση 2.1 (Robert and Casella 2.2 a) Έστω ότι η \(X\thicksim Logistic(\mu, \beta), \mu \in \mathbb{R}, \beta >0\). Τότε \(X=\mu +\beta L, \ L \thicksim Logistic(0,1)\) και

\[\begin{equation*} F_L(x) = \frac{1}{1+e^{-x}}, \ \ f_L(x) = \frac{e^{-x}}{\left( 1+ e^{-x} \right)^2}, \ \ \forall x\in \mathbb{R}. \end{equation*}\]

Χρησιμοποιώντας ότι έχουμε οικογένεια θέσης-κλίμακας για τη \(X\) ισχύει ότι:

\[\begin{equation*} F_X(x) = F_L\left(\frac{x-\mu}{\beta}\right) \Rightarrow f_X(x) = \frac{1}{\beta} f_L\left(\frac{x-\mu}{\beta}\right), \ \ \forall x\in \mathbb{R}. \end{equation*}\]

Ας υλοποιήσουμε το παραπάνω στην R:

mu <- 0
beta <- 1
U <- runif(10 ^ 4)
L1 <- mu + beta * log(U / (1 - U))
L2 <- rlogis(10 ^ 4)

hist(L1, freq = FALSE, main = "Logistic(0,1) from Uniform", breaks = 50, ylim = c(0, 0.3))
curve(dlogis, from = -10, to = 10, lty = 1, lwd = 1, col = "red", add = TRUE)

hist(L2, freq = FALSE, main = "Logistic(0,1) from R", breaks = 50, ylim = c(0, 0.3))
curve(dlogis,  from = -10, to = 10, lty= 1, lwd = 1, col = "red", add = TRUE)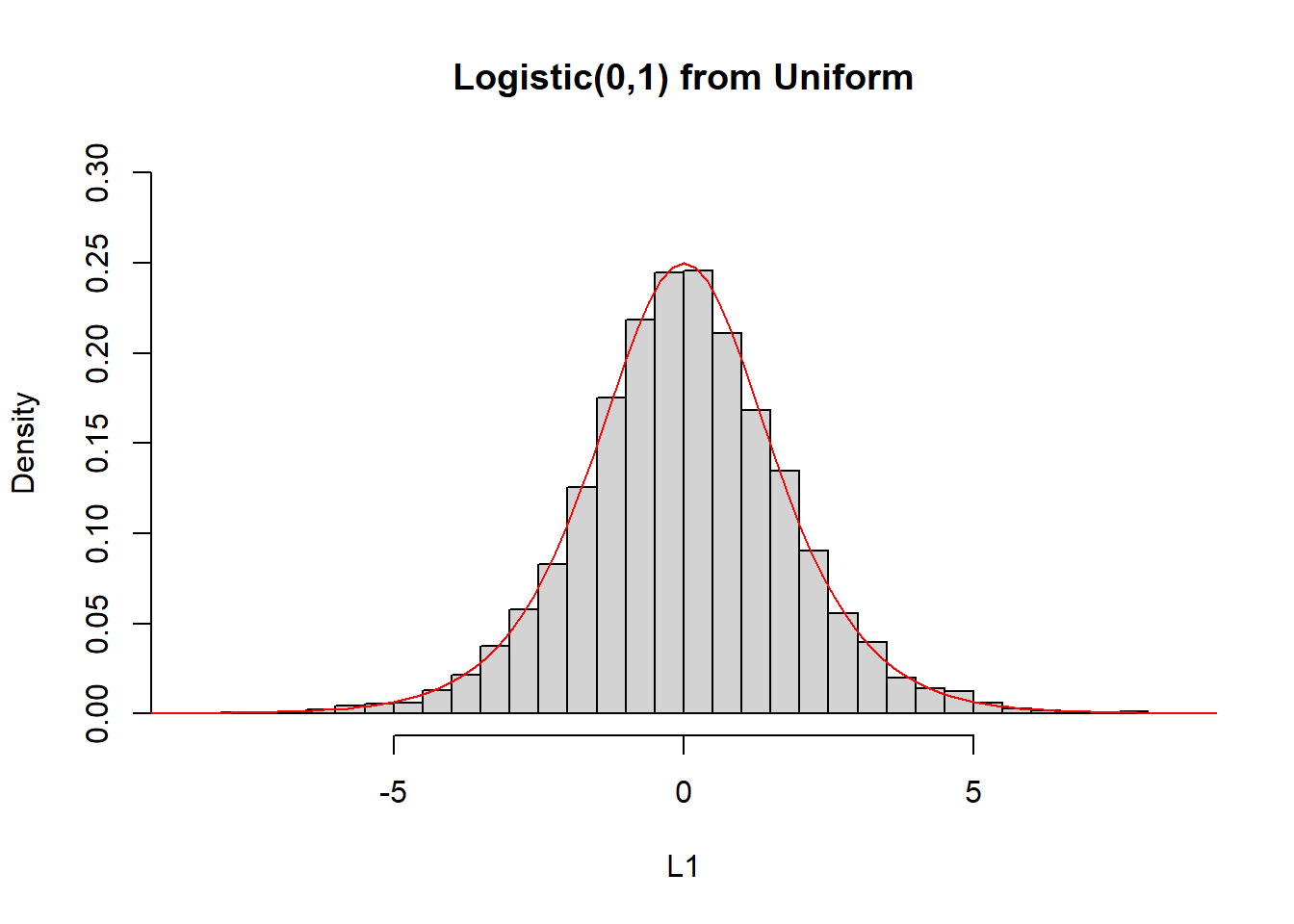

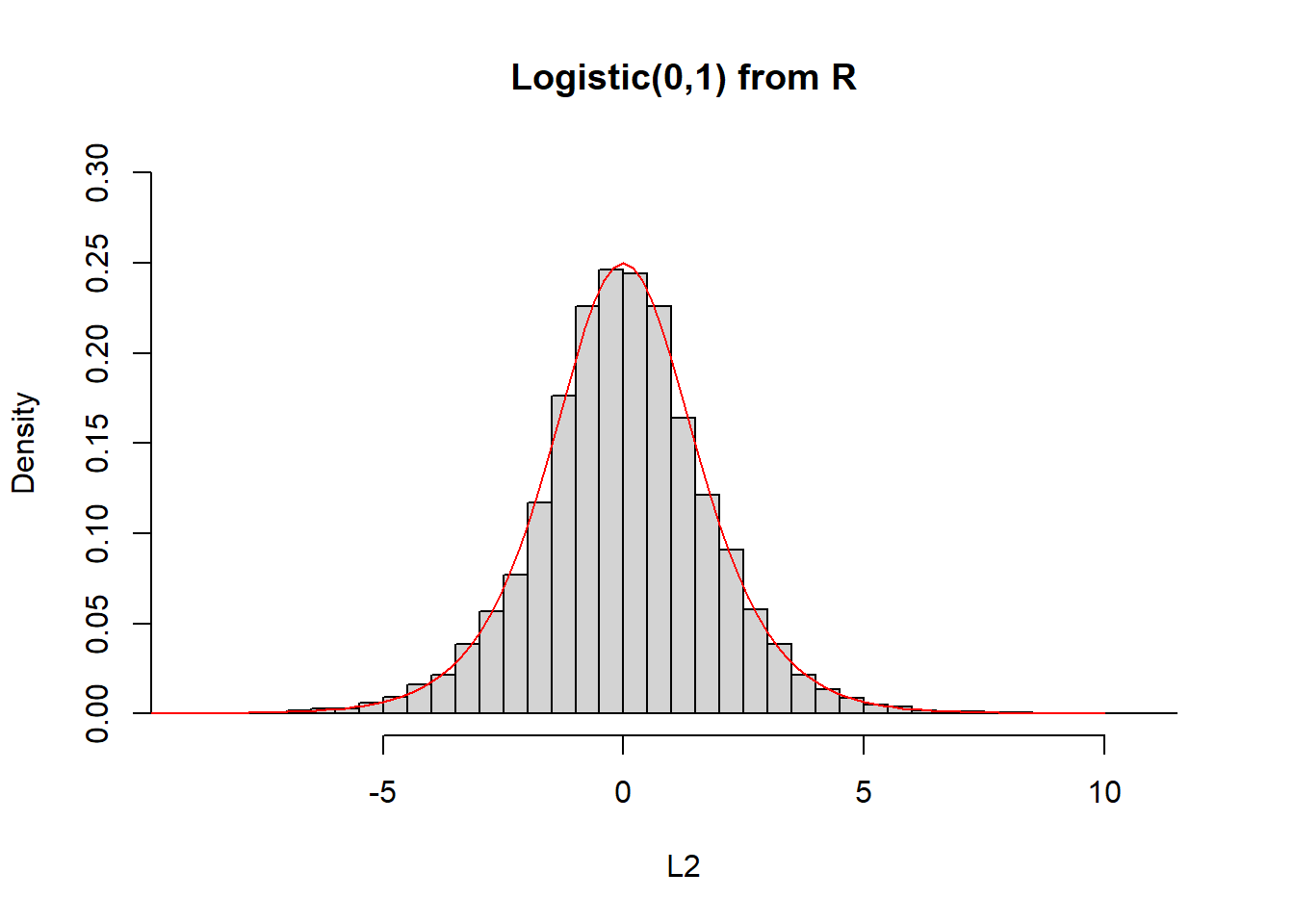
Κάνουμε τον έλεγχο Kolmogorov-Smirnov για να δούμε αν τα δύο δείγματα προέρχονται από την ίδια κατανομή. Για τον έλεγχο αυτό ισχύει:

\[\begin{align*} H_0 &: F_{L1}=F_{L2} \\ H_1 &: F_{L1}\neq F_{L2} \end{align*}\]

ks.test(L1, L2)
## 
##  Asymptotic two-sample Kolmogorov-Smirnov test
## 
## data:  L1 and L2
## D = 0.0103, p-value = 0.6637
## alternative hypothesis: two-sided

Όταν η p-value είναι μεγαλύτερη από 0.1 δεν έχουμε ενδείξεις υπέρ της εναλλακτικής υπόθεσης και άρα μπορούμε να δεχθούμε με σχετική ασφάλεια ότι τα 2 δείγματα προέρχονται από την ίδια κατανομή. Αν, από την άλλη, η p-value είναι μικρότερη από 0.1, τότε ανάλογα με το κατώφλι που καθορίζουμε (π.χ., 0.1, 0.05, 0.01, 0.001) ως επίπεδο στατιστικής σημαντικότητας \(\alpha\), απορρίπτουμε ή όχι τη μηδενική υπόθεση (ότι τα δείγματα προέρχονται από την ίδια κατανομή), ανάλογα με το αν η p-value είναι μικρότερη ή μεγαλύτερη από το \(\alpha\) αντίστοιχα. Σε πολλές περιπτώσεις βέβαια, μπορούμε να ‘μαντέψουμε’ τον τρόπο που η R προσομοιώνει, όπως είδαμε παραπάνω. Σε αυτές τις περιπτώσεις μπορούμε απλά να ελέγξουμε ότι οδηγούμαστε ακριβώς στις ίδιες παρατηρήσεις χρησιμοποιώντας τον ίδιο σπόρο.

set.seed(467)
mu <- 0
beta <- 1
U <- runif(10 ^ 4)
L1 <- mu + beta * log(U / (1 - U))
set.seed(467)
L2 <- rlogis(10 ^ 4)
identical(L1, L2)
## [1] TRUE

Το παραπάνω δείγμα είναι από την ‘τυπική’ λογιστική κατανομή. Θα μπορούσαμε να επιλέξουμε και \((\mu,\beta)\neq (0,1)\), π.χ.,

set.seed(467)
mu <- 1
beta <- 2
U <- runif(10 ^ 4)
L1 <- mu + beta * log(U / (1 - U))
set.seed(467)
L2 <- rlogis(10 ^ 4, mu, beta)
identical(L1, L2)
## [1] TRUE

Το παραπάνω αποτέλεσμα δείχνει βέβαια ότι έχουμε αναπαράγει με ακρίβεια τον τρόπο που η R προσομοιώνει τιμές από την οικογένεια θέσης - κλίμακας της λογιστικής κατανομής.

2.3.2 Παραγωγή Cauchy

Άσκηση 2.2 (Robert and Casella 2.2 b) Με παρόμοιο τρόπο, μπορούμε να παράγουμε παρατηρήσεις από την \(Cauchy(\mu, \sigma)\) μέσω της σχέσης:

\[\begin{equation*} X_i = \mu + \sigma \tan\left[\pi (U_i-0.5)\right], \end{equation*}\]

αφού αποτελεί την οικογένεια θέσης - κλίμακας που παράγεται από την τυπική Cauchy, με συνάρτηση κατανομής:

\[\begin{equation*} F_{C}(x) = \frac{1}{\pi}\arctan(x) + 1/2=\int_{-\infty}^{x}\frac{1}{\pi}\frac{1}{1+t^2}dt. \end{equation*}\]

και άρα αντίστροφη συνάρτηση κατανομής που βρίσκεται από τη σχέση \(u=1/\pi\, \arctan(x) + 1/2\), δίνοντας

\[\begin{equation*} F_{C}^{-1}(u) = tan\big(\pi(u-1/2)\big), \quad 0<u<1. \end{equation*}\]

mu <- 0
sigma <- 1
ssize <- 10 ^ 4
U <- runif(ssize)
C1 <- mu + sigma * tan(pi * (U - 0.5))
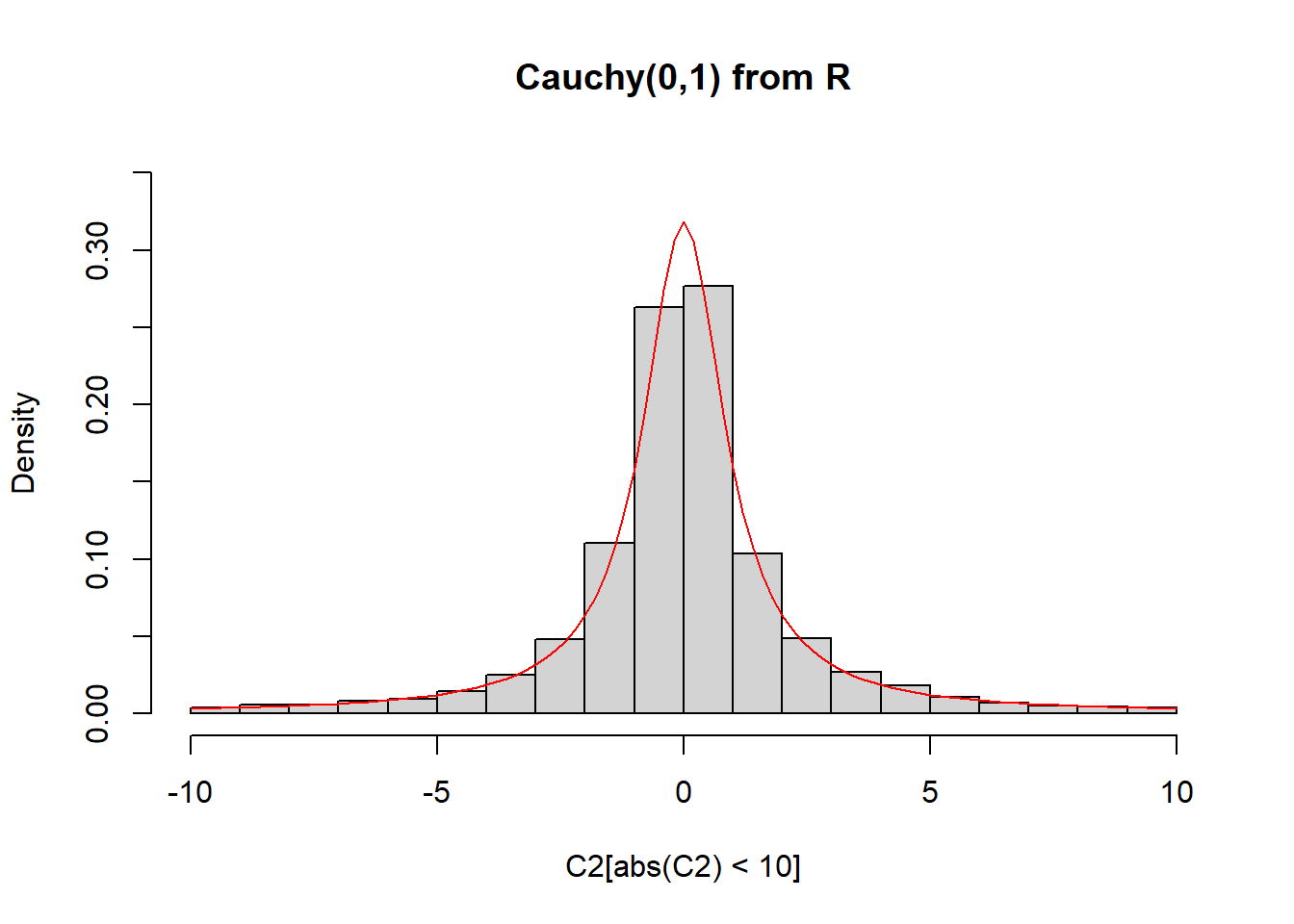
C2 <- rcauchy(ssize)
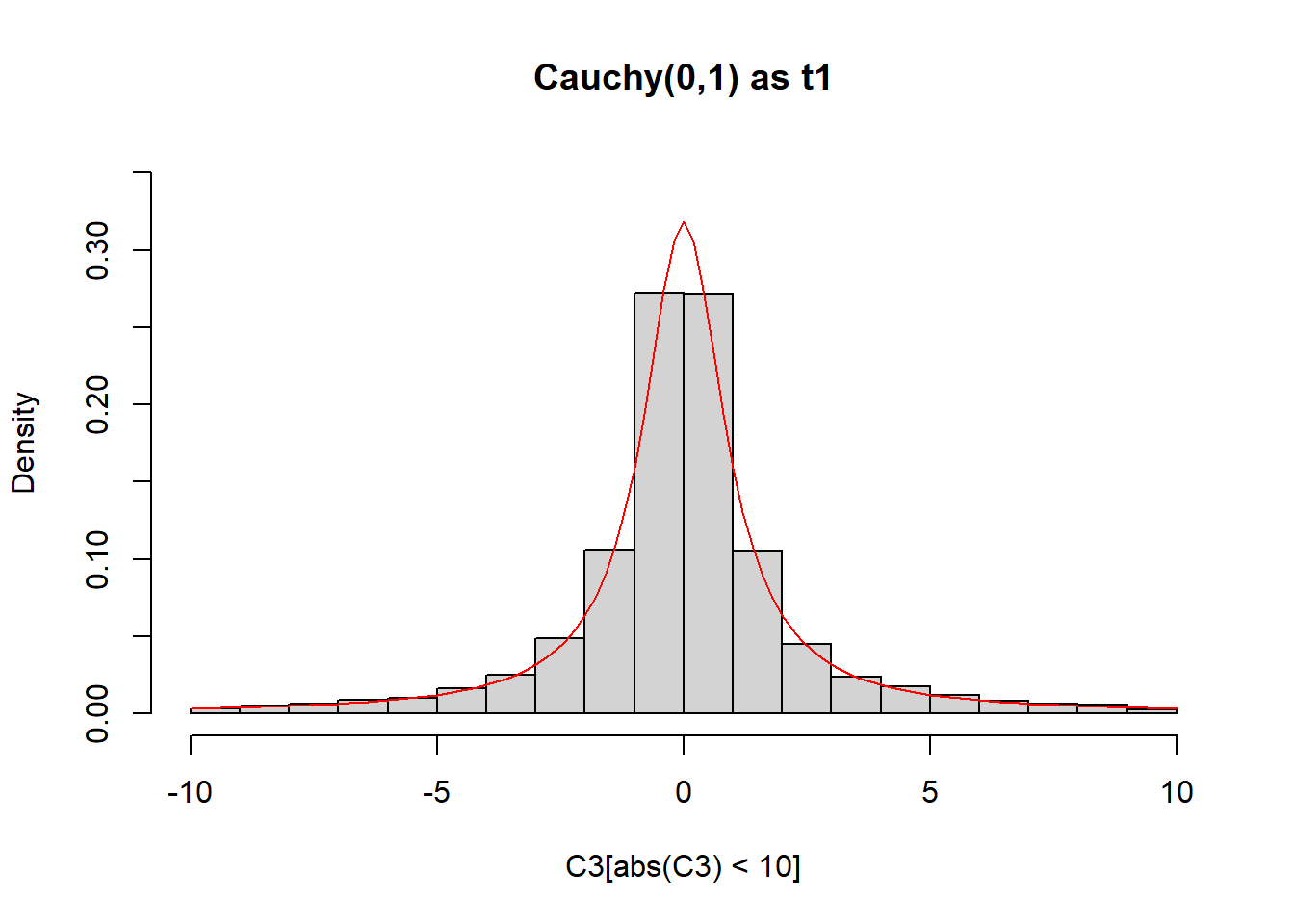
C3 <- rt(ssize, df = 1)
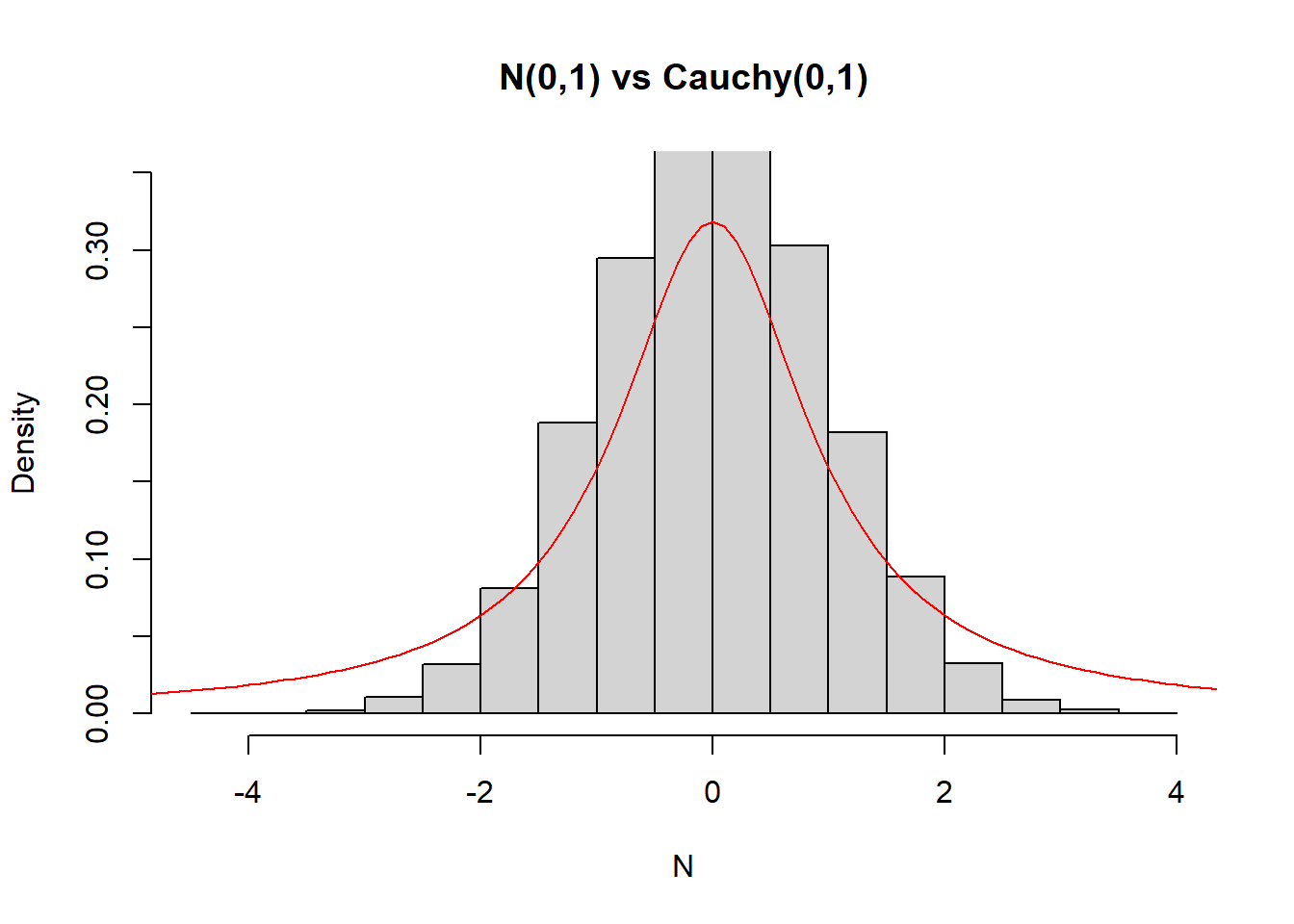
N <- rnorm(ssize)

hist(C1[abs(C1) < 10], freq = FALSE, ylim = c(0, 0.35), main = "Cauchy(0,1) from Uniform")
curve(dcauchy, from = -10, to = 10, lty= 1, lwd = 1, col = "red", add = TRUE)

hist(C2[abs(C2) < 10], freq = FALSE, ylim = c(0, 0.35), main = "Cauchy(0,1) from R")
curve(dcauchy, from = -10, to = 10, lty = 1, lwd = 1, col = "red", add = TRUE)

hist(C3[abs(C3) < 10], freq = FALSE, ylim = c(0, 0.35), main = "Cauchy(0,1) as t1")
curve(dcauchy, from = -10, to = 10, lty = 1, lwd = 1, col = "red", add = TRUE)

hist(N, freq = FALSE, ylim = c(0, 0.35), main = "N(0,1) vs Cauchy(0,1)")
curve(dcauchy, from = -5, to = 5, lty = 1, lwd = 1, col = "red", add = TRUE)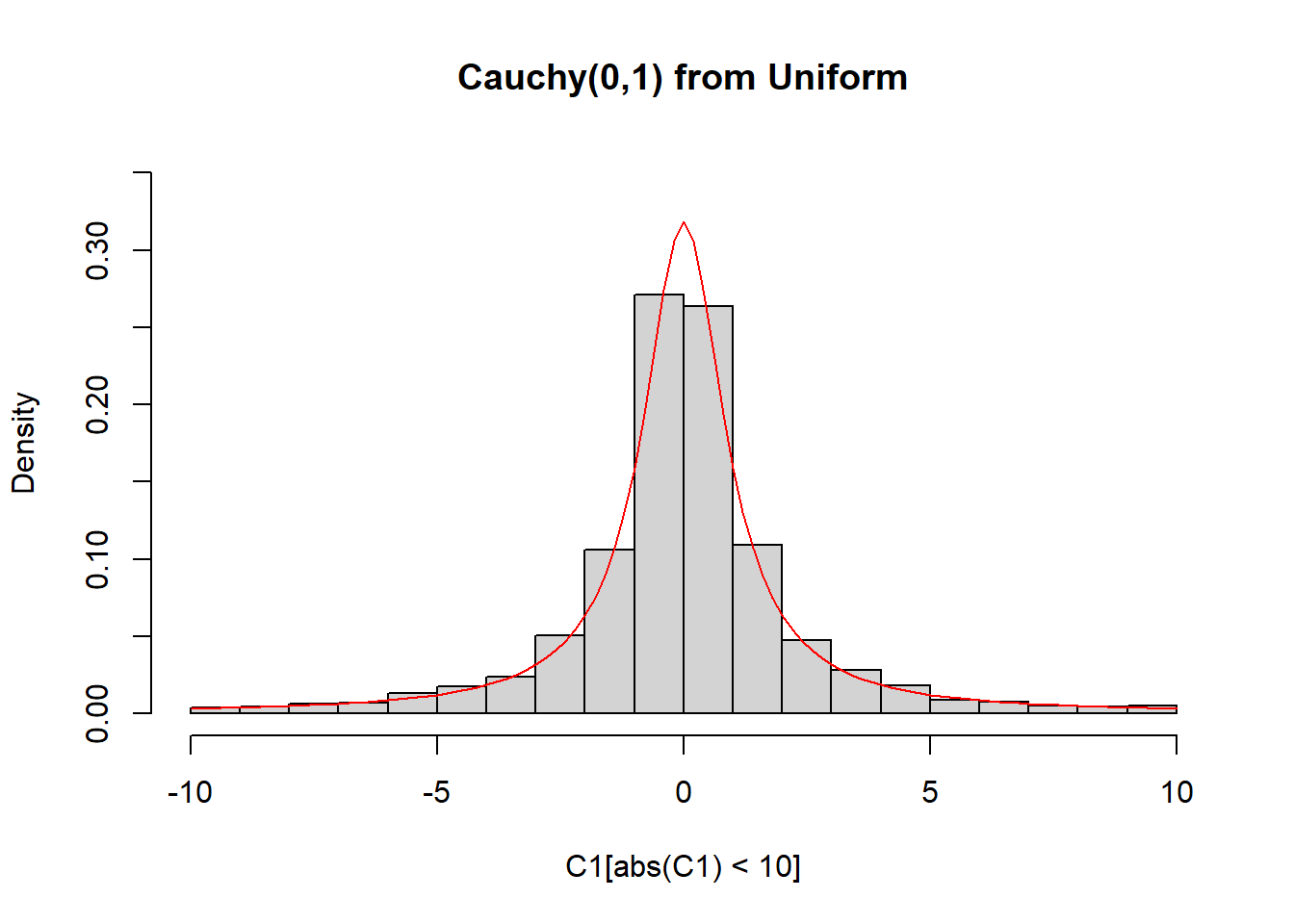

pcauchy(-10)
## [1] 0.03172552
sum(C1 < -10) / 10 ^ 4
## [1] 0.0329
ks.test(C1, C2)
## 
##  Asymptotic two-sample Kolmogorov-Smirnov test
## 
## data:  C1 and C2
## D = 0.0105, p-value = 0.6399
## alternative hypothesis: two-sided
ks.test(C2, C3)
## 
##  Asymptotic two-sample Kolmogorov-Smirnov test
## 
## data:  C2 and C3
## D = 0.0159, p-value = 0.1595
## alternative hypothesis: two-sided
ks.test(C3, N)
## 
##  Asymptotic two-sample Kolmogorov-Smirnov test
## 
## data:  C3 and N
## D = 0.1305, p-value < 2.2e-16
## alternative hypothesis: two-sided

Θα είναι χρήσιμο στα επόμενα να επεκτείνουμε τη μέθοδο εύρεσης της συνάρτησης πυκνότητας πιθανότητας αντιστρέψιμων μετασχηματισμών για διανυσματικές τυχαίες μεταβλητές. Για παράδειγμα, αν \(X=(X_1, X_2)\), \(Y=(Y_1, Y_2)\) και \[\begin{equation*} Y=(Y_1,Y_2)=(g_1(X),g_2(X))=g(X), \end{equation*}\] όπου \(g\) κατάλληλος μετασχηματισμός. Τότε, αν η \(g\) είναι 1-1, διαφορίσιμη και συμβολίζοντας με \(J_g(x)\) τον Ιακωβιανό πίνακα της \(g\) υπολογισμένο στο \(x\):

\[\begin{equation*} J_g(x) = \left(\begin{array}{cc} \frac{\partial g_1(x)}{\partial x_1} & \frac{\partial g_1(x)}{\partial x_2} \\ \frac{\partial g_2(x)}{\partial x_1} & \frac{\partial g_2(x)}{\partial x_2} \end{array} \right) \end{equation*}\]

υποθέσουμε επιπλέον ότι \(det J_g(x) \neq 0, \ \forall x \in S_x\), μπορεί να δειχθεί ότι η \(Y\) έχει σ.π.π. που δίνεται από τη σχέση \[\begin{equation*} f_Y(y)=f_X\left(g^{-1}(y)\right) \cdot \left| detJ_{g^{-1}}(y) \right| , \ \ \forall y\in g(S_X). \end{equation*}\]

Η παραπάνω σχέση ισχύει γενικότερα για διανυσματικές τυχαίες μεταβλητές.

2.3.3 Κατανομή της p-value υπό την \(H_0\)

Ας θυμηθούμε ότι \(p-value \equiv a(x)\), δηλαδή το παρατηρούμενο ε.σ.σ.. Είναι επομένως και αυτό μία τυχαία μεταβλητή, αν θεωρηθεί ως συνάρτηση του τυχαίου δείγματος, δηλ. στη μορφή \(a(X)\). Υπενθυμίζουμε τα εξής:

• Αν \(a(x) \leq a\) απορρίπτουμε την \(H_0\) σε ε.σ.σ. \(a\).
• Αν \(a(x) > a\) δεχόμαστε την \(H_0\) σε ε.σ.σ. \(a\).

Αν το θεωρήσουμε λοιπόν ως τ.μ., τότε απορρίπτουμε όταν πραγματοποιείται το ενδεχόμενο \(\{a(X)\leq a\} = \{ X \in C_a \}\), όπου \(C_a\) είναι η κρίσιμη περιοχή (περιοχή απόρριψης της \(H_0\)). Στην περίπτωση που η \(Η_0\) είναι απλή (αντιστοιχεί μόνο σε ένα δυνατό σενάριο) και το ε.σ.σ. συμπίπτει με το μέγεθος του ελέγχου (το \(\leq\) είναι ακριβώς ισότητα), τότε υπό την \(H_0\):

\[\begin{equation*} F_{a(X), Η_0}(a)=P_{H_0}(a(X)\leq a) = P_{H_0}(X\in C_a)=a, \ \ \forall 0<a<1. \end{equation*}\]

Τελικά συμπεραίνουμε ότι για απλή \(H_0\):

\[\begin{equation*} a(X) \thicksim U(0,1). \end{equation*}\]

Επιστρέφουμε λοιπόν στον παραπάνω έλεγχο για την λογιστική κατανομή. Τι αποτελέσματα αναμένουμε αν επαναλάβουμε τον ίδιο έλεγχο σε 1000 ανεξάρτητα δείγματα, το κάθε ένα με 1000 παρατηρήσεις;

ssize <- 10 ^ 3
ntests <- 10 ^ 3
U <- runif(ntests * ssize)
mu <- 0
beta <- 1
L1 <- matrix(mu + beta * log(U / (1 - U)), ncol = ntests)
L2 <- matrix(rlogis(ntests * ssize), ncol = ntests)

psample <- numeric(ntests)

for(i in 1:ntests){
  psample[i] <- ks.test(L1[ , i], L2[ , i])$p.value
}

a <- 0.1
sum(psample < a) / ntests
## [1] 0.11

hist(psample)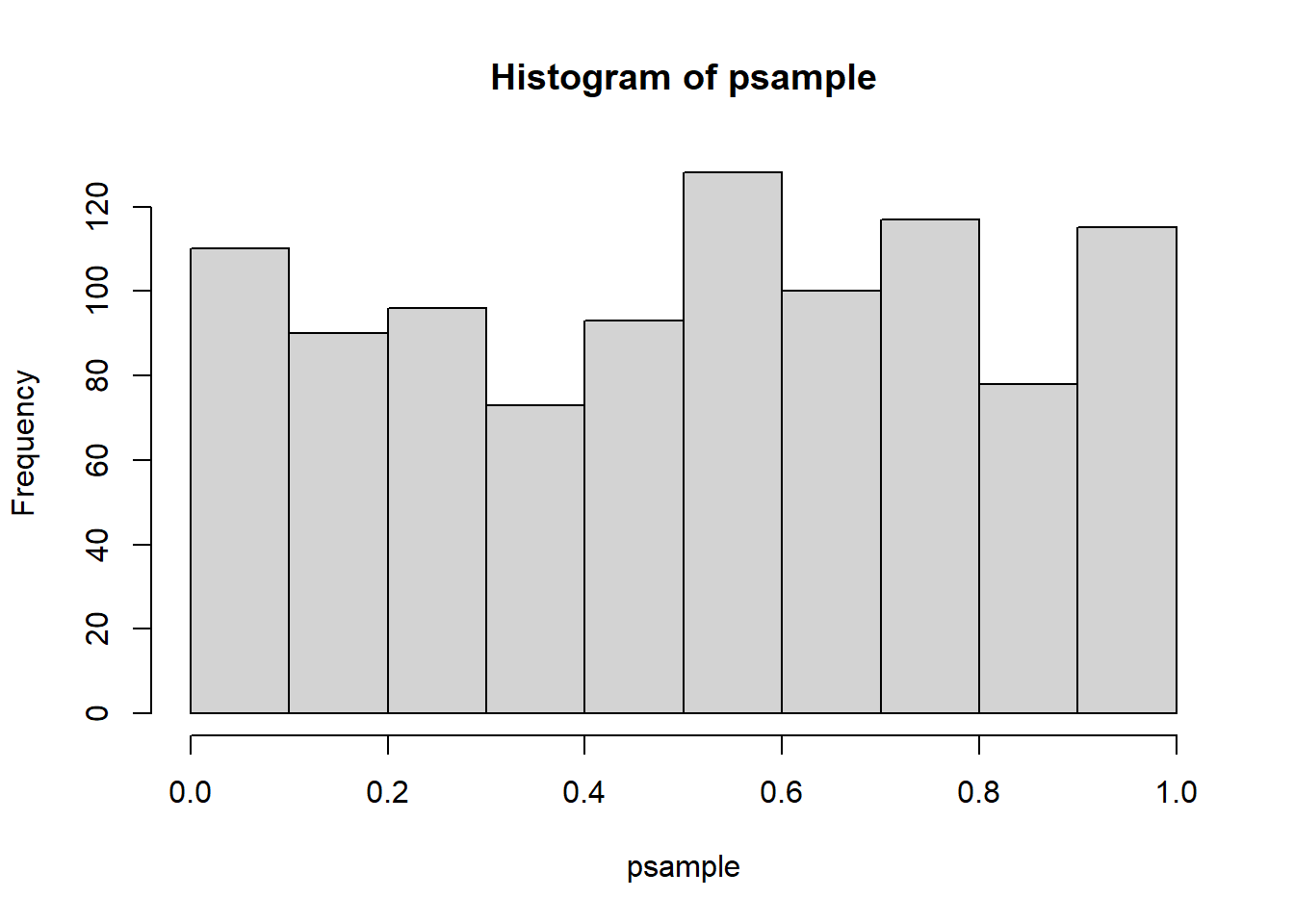

ks.test(psample, "punif") 
## 
##  Asymptotic one-sample Kolmogorov-Smirnov test
## 
## data:  psample
## D = 0.038359, p-value = 0.1054
## alternative hypothesis: two-sided

2.3.4 Παραγωγή Beta από Gamma

Παράδειγμα 2.8 Υποθέτουμε ότι ένας ασθενής φτάνει στο νοσοκομείο και πρέπει να κάνει 2 εξετάσεις, μία εξέταση αίματος και μία ακτινογραφία θώρακος. Ο χρόνος που θα χρειαστεί για να πραγματοποιήσει διαδοχικά αυτές τις 2 εξετάσεις υποθέτουμε ότι είναι \(X, Y\) αντίστοιχα, όπου \(X\thicksim G(a, \theta), Y\thicksim G(\beta, \theta)\) και \(X \perp \!\!\! \perp Y\). Το ερώτημα που θέλουμε να απαντήσουμε είναι ποιά είναι η κατανομή του ποσοστού του χρόνου \(W\) που καταλαμβάνει η 1η δραστηριότητα;

Ορίζουμε \(Z:=X+Y\) τον συνολικό χρόνο και για τις δύο εξετάσεις. Για το ποσοστό \(W\) ισχύει \(W=\frac{X}{X+Y}\). Παρατηρούμε ότι:

\[\begin{equation*} (Z, W) = g(X, Y) , (z,w) = (g_1(x,y), g_2(x,y))=\left(x+y, \frac{x}{x+y}\right). \end{equation*}\]

Επομένως:

\[\begin{equation*} \begin{array}{c} z=x+y \\ w=\frac{x}{x+y} \end{array} \Leftrightarrow \begin{array}{c} zw=x \\ y=z-x \end{array} \Leftrightarrow \begin{array}{c} x=zw \\ y=z(1-w) \end{array} \end{equation*}\]

H \(g\) είναι 1-1, διαφορίσιμη με \(det J_g(x) \neq 0\).

\[\begin{equation*} detJ_{g^{-1}}(z,w) = \left|\begin{array}{cc} w & z \\ 1-w & -z \end{array} \right| = -wz-z+zw=-z\neq 0. \end{equation*}\]

Τελικά,

\[\begin{align*} f_{Z,W}(z,w) & = f_{X,Y}(g^{-1}(z,w)) \cdot \left| detJ_{g^{-1}}(z,w) \right| \\ & \propto (zw)^{a-1} e^{-\theta zw} z^{\beta-1} (1-w)^{\beta-1} e^{-\theta z (1-w)}) \\ & = z^{a+\beta-1} e^{-\theta z} w^{a-1} (1-w)^{\beta-1} \\ & = h_1(z) \cdot h_2(w), \end{align*}\]

όπου

\[\begin{align*} h_1(z) &= z^{a+\beta-1} e^{-\theta z}, \ \ 0<z<+\infty, \\ h_2(w) &= w^{a-1} (1-w)^{\beta-1}, \ \ 0<w<1. \end{align*}\]

Επομένως \(Z\thicksim G(a+\beta, \theta)\), \(W\thicksim Beta(a, \beta)\) και \(Z \perp \!\!\! \perp W\).

Έστω \(X\thicksim G(a, \theta), Y \thicksim G(\beta, \theta)\) και \(X'\thicksim G(a, 1), Y' \thicksim G(\beta, 1)\). Τότε:

\[\begin{equation*} W = \frac{X}{X+Y} = \frac{\frac{1}{\theta}X'}{\frac{1}{\theta}X'+\frac{1}{\theta}Y'} = \frac{X'}{X'+Y'}. \end{equation*}\]

Άρα

\[\begin{equation*} W_i = \frac{X'_i}{X'_i+Y'_i}. \end{equation*}\]

Άρα η \(Beta(a, \beta)\) μπορεί να παραχθεί από 2 ανεξάρτητες \(G(a, 1)\), \(G(\beta, 1)\).

a <- 3
b <- 7
G1 <- rgamma(10 ^ 4, shape = a, rate = 1)
G2 <-  rgamma(10 ^ 4, shape = b, rate = 1)
B <- G1 / (G1 + G2)

hist(B, freq = FALSE, main = "Beta from Gamma")
curve(dbeta(x, shape1 = a, shape2 = b), from = 0, to = 1, lty = 1, lwd = 1, col = "red", add = TRUE)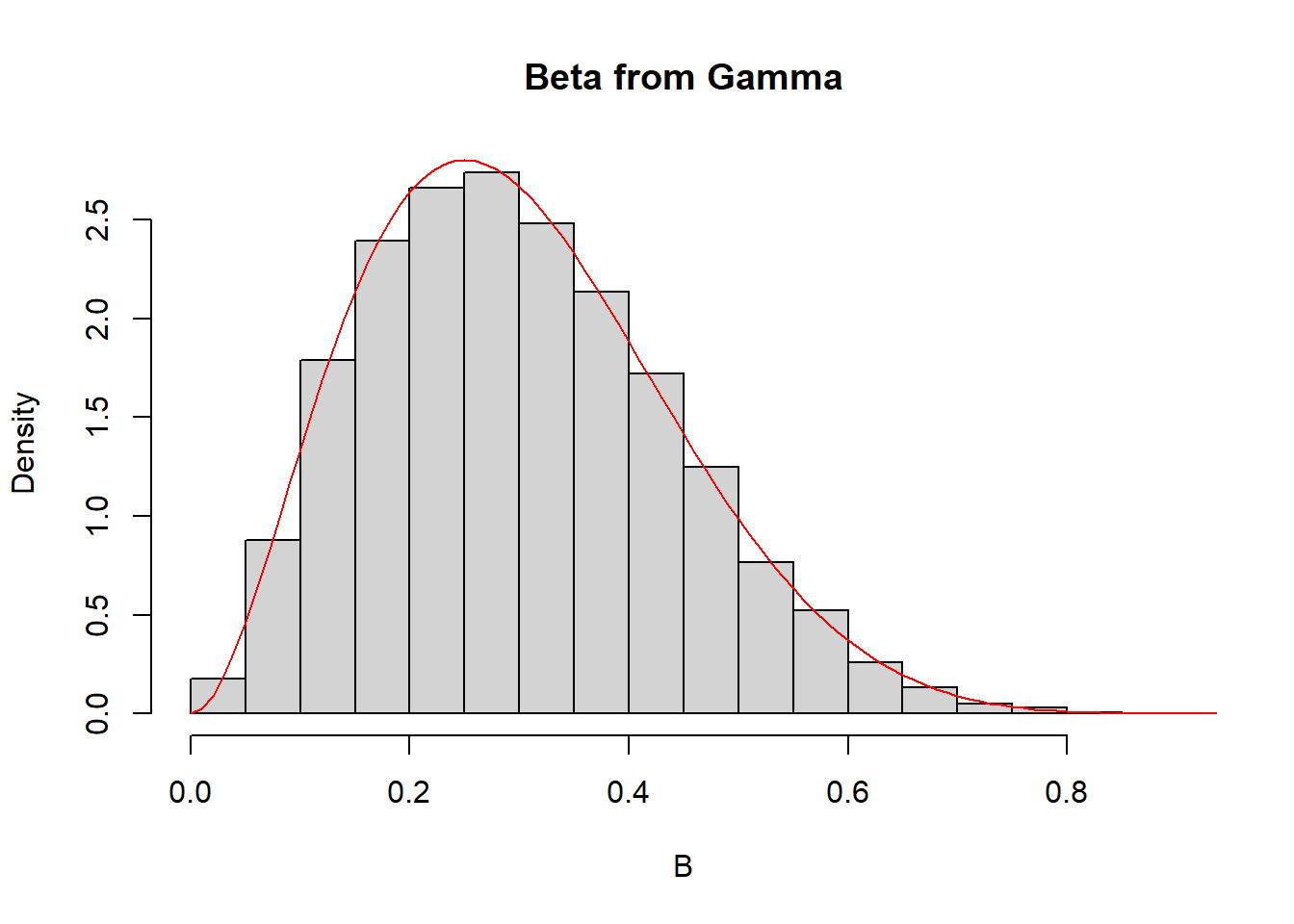

2.3.5 Παραγωγή Normal: Μετασχηματισμός Box-Muller

Θα δείξουμε ότι αν \((U_1, U_2)\) ανεξάρτητες τ.μ. από την \(Unif(0,1)\) και

\[\begin{align*} X_1 &= \sqrt{-2\log U_1} \cdot \cos(2\pi U_2), \\ X_2 &= \sqrt{-2\log U_1} \cdot \sin(2\pi U_2), \end{align*}\]

τότε \(X_1 \thicksim N(0,1), X_2 \thicksim N(0,1)\) και \(X_1 \perp \!\!\! \perp Χ_2\).

Έστω ότι έχουμε \(Χ_1, Χ_2 \thicksim N(0,1)\) και \(X_1 \perp \!\!\! \perp Χ_2\). Θα μελετήσουμε το ζεύγος τ.μ.

\[\begin{equation*} (R, \Theta) = (\sqrt{X_1^2 +X_2^2}, \arctan\frac{X_2}{X_1}). \end{equation*}\]

Ισχύει ότι

\[\begin{equation*} \begin{array}{c} x_1 = r \cos\theta \\ r=\sqrt{x_1^2+x_2^2} \end{array} \Leftrightarrow \begin{array}{c} x_2 = r \sin\theta \\ \theta=\arctan\frac{x_2}{x_1} \end{array}. \end{equation*}\]

\[\begin{equation*} detJ_g(x) = \left|\begin{array}{cc} \frac{\partial g_1(x)}{\partial x_1} & \frac{\partial g_1(x)}{\partial x_2} \\ \frac{\partial g_2(x)}{\partial x_1} & \frac{\partial g_2(x)}{\partial x_2} \end{array} \right| = ... = r \end{equation*}\]

Επομένως για $r $ έχουμε τον μετασχηματισμό:

\[\begin{align*} f_{R, \Theta}(R, \theta) &= f_{X_1, X_2}(r\cos\theta, r\sin\theta) \cdot r \\ &= \frac{1}{\sqrt{2\pi}} e^{-r^2\cos^2\theta} \cdot \frac{1}{\sqrt{2\pi}} e^{-r^2\sin^2\theta} \cdot r \\ &= \frac{1}{2\pi} r e^{-r^2} \\ &= f_\Theta (\theta) \cdot f_R (r). \end{align*}\]

όπου

\[\begin{align*} f_\Theta (\theta) &= \frac{1}{2\pi}, \ 0<r<+\infty, \\ f_R (r) &= r e^{-r^2} \ 0<\theta<2\pi. \end{align*}\]

Επομένως \(\Theta \perp \!\!\! \perp R\). Επιπλέον:

\[\begin{equation*} X_1^2, X_2^2 \thicksim N(0,1) \Rightarrow X_1^2+X_2^2 \thicksim \mathcal{X}_2^2 \equiv G\left(1,\frac{1}{2}\right) \equiv Exp\left(\frac{1}{2}\right). \end{equation*}\]

Άρα

\[\begin{align*} R &= \sqrt{X_1^2+X_2^2} \thicksim \sqrt{Exp(\frac{1}{2})} = \sqrt{2 \cdot Exp(1)} \\ \Theta &= \frac{1}{2\pi} \thicksim Unif(0, 2\pi)= 2\pi \cdot Unif(0,1). \end{align*}\]

Παρατήρηση:. Θα μπορούσαμε να παράγουμε παρατηρήσεις και με την αντίστροφη \(\Phi^{-1}\). Σε αυτή την περίπτωση όμως δεν θα ήταν ακριβής προσομοίωση, αλλά προσεγγιστική, αφού θα χρησιμοποιούσαμε αριθμητικές μεθόδους για τους υπολογισμούς μας (με μεγάλη ακρίβεια).

boxmuller <- function(size, nb) {
  theta <- runif(size, 0, 2 * pi) 
  U1 <- runif(size)
  samples <- matrix(ncol = 2, nrow = size)
  R <- sqrt(-2 * log(U1))
  # alternative transformation
  # R <- sqrt(rchisq(size,df=2)) [why this is equivalent ?] 
  X <- R * cos(theta)
  Y <- R * sin(theta)
  normal <- rnorm(size)
  label <- rep(c("x", "y", "normal"), size)
  value <- c(X, Y, normal)
  df <- data.frame(value, label)
  plt <- ggplot(df, aes(x = value, color = label, fill = label)) + 
     geom_histogram(aes(y = ..density..), bins = nb, position = "identity", alpha = 0.3) +
     labs(x = "Value", y = "Density") + theme_bw() +
      stat_function(fun = dnorm, colour = "red")
  print(plt)
}

size <- 10^4
nb <- 60
boxmuller(size, nb)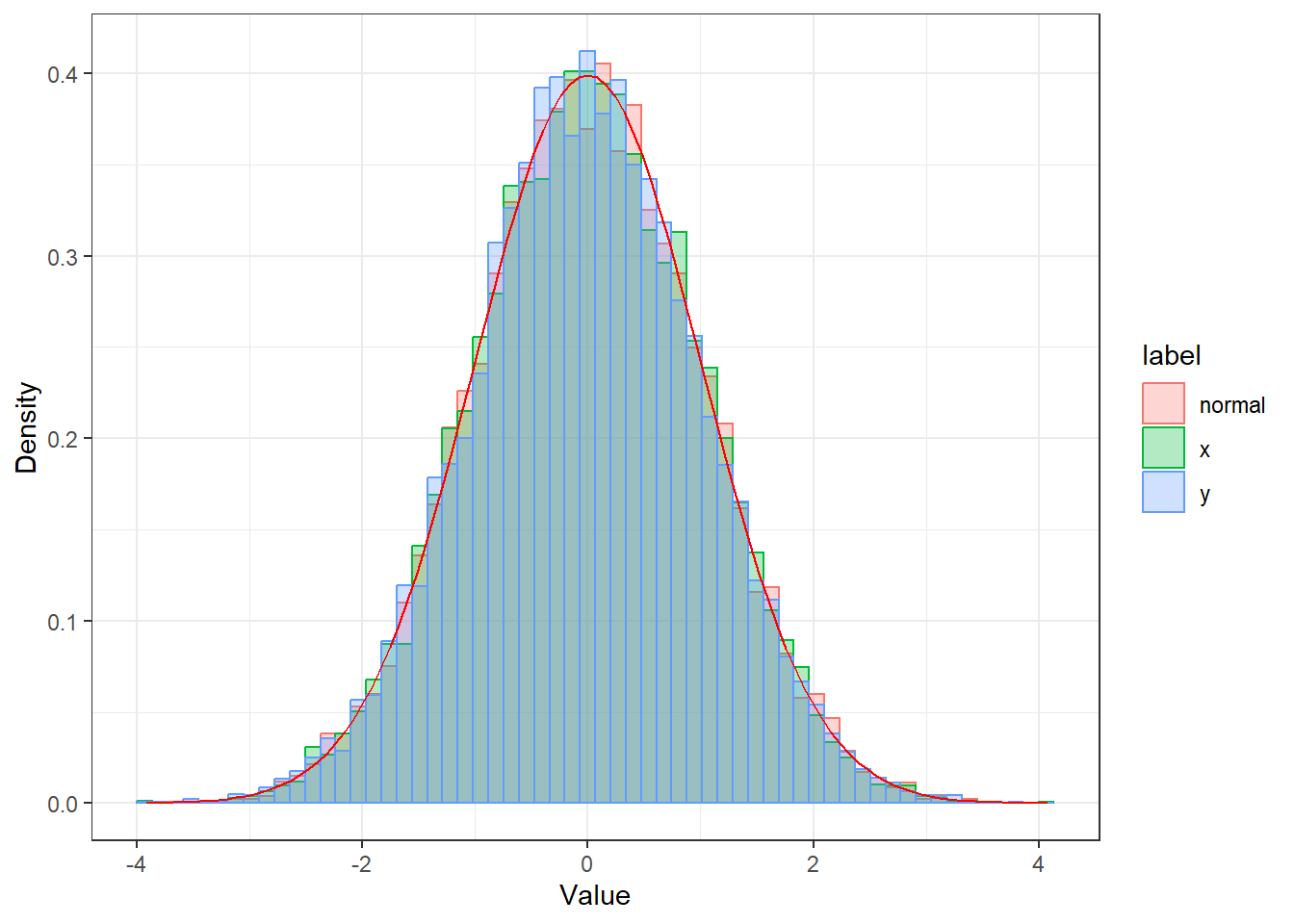

2.4 Προσομοίωση πολυδιάστατων κανονικών τ.μ.

Η κατανομή μίας p-διάστατης τ.μ. \(X=(X_1, X_2, ..., X_p)^\top\) περιγράφεται πλήρως από τις κατανομές όλων των γραμμικών συνδυασμών \(u^\top X= \sum_{i=1}^p u_i X_i\).

Ορισμός 2.2 Έστω \(\mu=(\mu_1, \mu_2, ..., \mu_p)^\top\) και \(\Sigma = \left(\sigma_{ij}\right)_{p\times p}\) με \(\Sigma\) συμμετρικό και θετικά ημιορισμένο. Θα λέμε ότι η \(X\) ακολουθεί p-διάστατη κανονική, με διάνυσμα μέσων τιμών \(\mu\) και πίνακα διασπορών-συνδιασπορών ή συνδιακύμανσης \(\Sigma\) και θα γράφουμε \(X\thicksim N_p(\mu, \Sigma)\), αν \(u^\top X\thicksim N_1(u^\top \mu, u^\top \Sigma u), \ \forall u \in \mathbb{R}^p\).

Παρατήρηση:. Εάν υπάρχουν οι μέσες τιμές και οι διασπορές, ισχύουν οι παρακάτω σχέσεις:

\[\begin{align*} \mathbf{E}(u^\top X) &= u^\top \mathbf{E}(X)=u^\top \mu \\ \mathbf{V}(u^\top X) &= u^\top \mathbf{V}(X) u = u^\top \Sigma u \end{align*}\]

Το γεγονός ότι ο \(\Sigma\) είναι θετικά ημιορισμένος εξασφαλίζει ότι \(u^\top \Sigma u \geq 0, \ \forall u \in \mathbb{R}^p\), ώστε να ισχύει \(\mathbf{V}(u^\top X) \geq 0\) (ως διασπορά). Η διασπορά επιτρέπεται να είναι μηδενική για \(u \neq 0\), σε περιπτώσεις που έχουμε εκφυλισμούς κάποιων γραμμικών συνδυασμών.

Για παράδειγμα, αν \(X=(Z, Z)^\top, Z\thicksim N(0,1)\), τότε:

\[\begin{equation*} X\thicksim N_2(\mathbf{0}, \Sigma), \ \mathbf{0}=\left(\begin{array}{c} 0 \\ 0 \end{array}\right), \ \Sigma =\left(\begin{array}{cc} 1 & 1 \\ 1 & 1 \end{array}\right). \end{equation*}\]

Για \(u=(1, -1)^\top\) παίρνουμε:

\[\begin{equation*} u^\top X = \left(\begin{array}{cc} 1 & -1 \end{array}\right) \cdot \left(\begin{array}{c} Z \\ Z \end{array}\right) = Z-Z=0. \end{equation*}\]

2.4.1 Παραγωγή p-διάστατων κανονικών από τυπική

Σε μονοδιάστατη γνωρίζουμε ότι:

\[\begin{equation*} X\thicksim N(\mu, \sigma^2) \Leftrightarrow X=\mu +\sigma Z, Z\thicksim N(0,1), \mu \in \mathbb{R}, \sigma>0. \end{equation*}\]

Για τις p-διάστατες χρησιμοποιούμε την σχέση:

\[\begin{equation*} Z\thicksim N_p(O_p, I_p) \Leftrightarrow Z=(Z_1, Z_2, ..., Z_p)^\top, Z_i\thicksim N(0,1), i=1,2,...,p \end{equation*}\]

όπου \(Z_i, Z_j\) ανεξάρτητες για \(i\neq j\).

Άρα

\[\begin{equation*} \mathbf{E}(Z)=\left(\begin{array}{c} \mathbf{E}(Z_1) \\ ... \\ \mathbf{E}(Z_p) \end{array}\right) = \left(\begin{array}{c} 0 \\ ... \\ 0 \end{array}\right) = O_p. \end{equation*}\]

\[\begin{equation*} \mathbf{V}(Z)=\left(\begin{array}{cccc} \mathbf{V}(Z_1) & \mathbf{C}(Z_1, Z_2) & \ldots & \mathbf{C}(Z_1, Z_p)\\ \mathbf{C}(Z_2, Z_1) & \mathbf{V}(Z_2) & \ldots & \mathbf{C}(Z_2, Z_p) \\ \vdots & \vdots & \ddots & \vdots \\ \mathbf{C}(Z_p, Z_1) & \mathbf{C}(Z_p, Z_2) & \ldots & \mathbf{V}(Z_p) \end{array}\right) = \left(\begin{array}{cccc} 1 & 0 & \ldots & 0 \\ 0 & 1 & \ldots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & 1 \end{array}\right) = I_p. \end{equation*}\]

Για μία μονοδιάστατη κατανομή, έχουμε ότι \(\sigma=\sqrt{\sigma^2}\). Για μία πολυδιάστατη πώς μπορεί να γενικευθεί αυτό;

Πρόταση 2.3 Αν \(\Sigma\) συμμετρικός και θετικά ημιορισμένος, τότε γράφεται στην μορφή \(\Sigma = A A^\top\), με γενικά πολλές επιλογές για τον Α. Από όλες τις επιλογές, υπάρχει “βολική” αναπαράσταση με Α κάτω τριγωνικό (παράγοντας  ανάλυση Choleski). Είναι μοναδική αν ο \(\Sigma\) είναι θετικά ορισμένος, δηλ \(x^\top \Sigma x>0, \ \forall x\neq 0\).

Πόρισμα 2.1 \[\begin{equation*} X\thicksim N_p(\mu, \Sigma) \Leftrightarrow X= \mu +A Z, Z\thicksim N_p(O_p, I_p), \mu \in \mathbb{R}, \Sigma=AA^\top, A \ \text{κάτω τριγωνικός}. \end{equation*}\]

Παράδειγμα 2.9 Ας μελετήσουμε την περίπτωση της δισδιάστατης. Θέλουμε

\[\begin{equation*} X\thicksim N_2(\mu, \Sigma), \mu=\left(\begin{array}{c} \mu_1 \\ mu_2 \end{array}\right), \Sigma=\left(\begin{array}{cc} \sigma_1^2 & p \sigma_1 \sigma_2 \\ p \sigma_1 \sigma_2 & \sigma_2^2 \end{array}\right), \end{equation*}\]

όπου

\[\begin{equation*} p=\frac{Cov(X_1, X_2)}{\sqrt{\mathbf{V}(X_1)\mathbf{V}(X_2)}}=\frac{\sigma_{1,2}}{\sigma_1 \sigma_2} \end{equation*}\]

Επιλέγουμε τον πίνακα

\[\begin{equation*} Α=\left(\begin{array}{cc} \sigma_1 & 0 \\ p \sigma_2 & \sqrt{1-p^2}\sigma_2 \end{array}\right). \end{equation*}\]

Εύκολα βλέπουμε ότι

\[\begin{equation*} X= \mu + AZ, Z=\left(\begin{array}{c} Z_1 \\ Z_2 \end{array}\right). \end{equation*}\]

Το παραπάνω γράφεται ως σύστημα:

\[\begin{align*} X_1 &= \mu_1 +\sigma_1 Z_1 \\ X_2 &= \mu_2 + p \sigma_2 Z_1 +\sqrt{1-p^2} \sigma_2 Z_2 = \mu_2 + \sigma_2 (pZ_1 + \sqrt{1-p^2}) Z_2 \end{align*}\]

Τελικά έχουμε:

\[\begin{equation*} \left(\begin{array}{c} Z_1 \\ Z_2 \end{array}\right) \rightarrow \left(\begin{array}{cc} 1 & 0 \\ p & \sqrt{1-p^2} \end{array}\right) \cdot \left(\begin{array}{c} Z_1 \\ Z_2 \end{array}\right) \equiv \left(\begin{array}{c} Z_1' \\ Z_2' \end{array}\right) \rightarrow \left(\begin{array}{cc} \sigma_1 & 0 \\ 0 & \sigma_2 \end{array}\right) \left(\begin{array}{c} Z_1' \\ Z_2' \end{array}\right) \rightarrow \mu + \left(\begin{array}{cc} \sigma_1 & 0 \\ 0 & \sigma_2 \end{array}\right) \left(\begin{array}{c} Z_1' \\ Z_2' \end{array}\right). \end{equation*}\]

Ας μελετήσουμε ένα παράδειγμα στην R

set.seed(2184)

Sigma <- cov(matrix(rnorm(30), nrow = 10))

# compare times for generating 1 vector
system.time(for(i in 1:10000) { t(chol(Sigma)) %*% rnorm(3) })
##    user  system elapsed 
##    0.20    0.04    0.24
system.time(for(i in 1:10000) { rmnorm(1, varcov = Sigma) })
##    user  system elapsed 
##    0.37    0.00    0.37

# compare times for generating a sample of 100 vectors
test_1 <- function(Nsim = 10 ^ 4) {
  for(i in 1:Nsim){
    A <- t(chol(Sigma))
    for(j in 1:100) {
      A %*% rnorm(3)
    }
  }
}

test_2 <- function(Nsim = 10 ^ 4) {
  for(i in 1:Nsim) {
    rmnorm(100, varcov = Sigma)
  }
}
system.time(test_1())
##    user  system elapsed 
##    2.94    0.31    3.34
system.time(test_2())
##    user  system elapsed 
##    0.62    0.03    0.65

2.5 Προσομοίωση με αναπαράσταση ως μίξη

Ας υποθέσουμε ότι θέλουμε να προσομοιώσουμε τιμές από κάποια τ.μ. \(X\). Υποθέτουμε ότι εξαρτάται από κάποια τ.μ. \(Y\) και μπορούμε να προσομοιώσουμε ευκολότερα τιμές τις \(Y\), αλλά και από την \(\left[X|Y=y\right]\). Τότε:

\[\begin{align*} f_X(x) &= \sum_{i=1}^k f_Y(y_i) f_{X|Y}(x|y_i),\ Y \ \text{διακριτή}, \\ f_X(x) &= \int_{\mathbb{R}} f_Y(y) f_{X|Y}(x|y),\ Y \ \text{συνεχής}. \end{align*}\]

Επειδή είναι δύσκολο να προσομοιώσουμε απ’ ευθείας από κατανομές αυτής της μορφής, αντί να προσομοιώσουμε τιμές της \(X\), προσομοιώνουμε από το ζεύγος \((Y,X)\) ξεκινώντας από την \(Y\) και μετά την \(\left[X|Y=y\right]\). Η διαδικασία αυτή αιτιολογείται μέσω της σχέσης:

\[\begin{equation*} f_{X,Y}(x,y)=f_Y(y) f_{X|Y}(x|y). \end{equation*}\]

Έτσι, η τιμή \(x\) της \(X\) έχει παραχθεί ισοδύναμα από την περιθώρια \(f_X\) της \(X\), με ‘κόστος’ την προσομοίωση μίας επιπλέον τιμής, της \(y\).

Παράδειγμα 2.10 Έστω ότι θέλουμε να προσoμοιώσουμε από την κατανομή Student \(t_n\). Ισχύει ότι:

\[\begin{equation*} T=\frac{Z}{\sqrt{Q/n}},\ Z\thicksim N(0,1),\ Q\thicksim \mathcal{X}^2_n,. \end{equation*}\]

Επομένως, \(\left[ T\mid Q=q\right]\thicksim N(0, n/q)\).

Nsim <- 10 ^ 4
n <- 10
q <- rchisq(Nsim, df = n)
t <- rnorm(Nsim, rep(0, Nsim), sqrt(n / q))

hist(t, main = "Student with df=10 as a mixture", freq = FALSE, col = "grey", breaks = 50)
curve(dt(x, df = n), from = -5, to = 5, lty = 1, lwd = 1, col = "red", add = TRUE)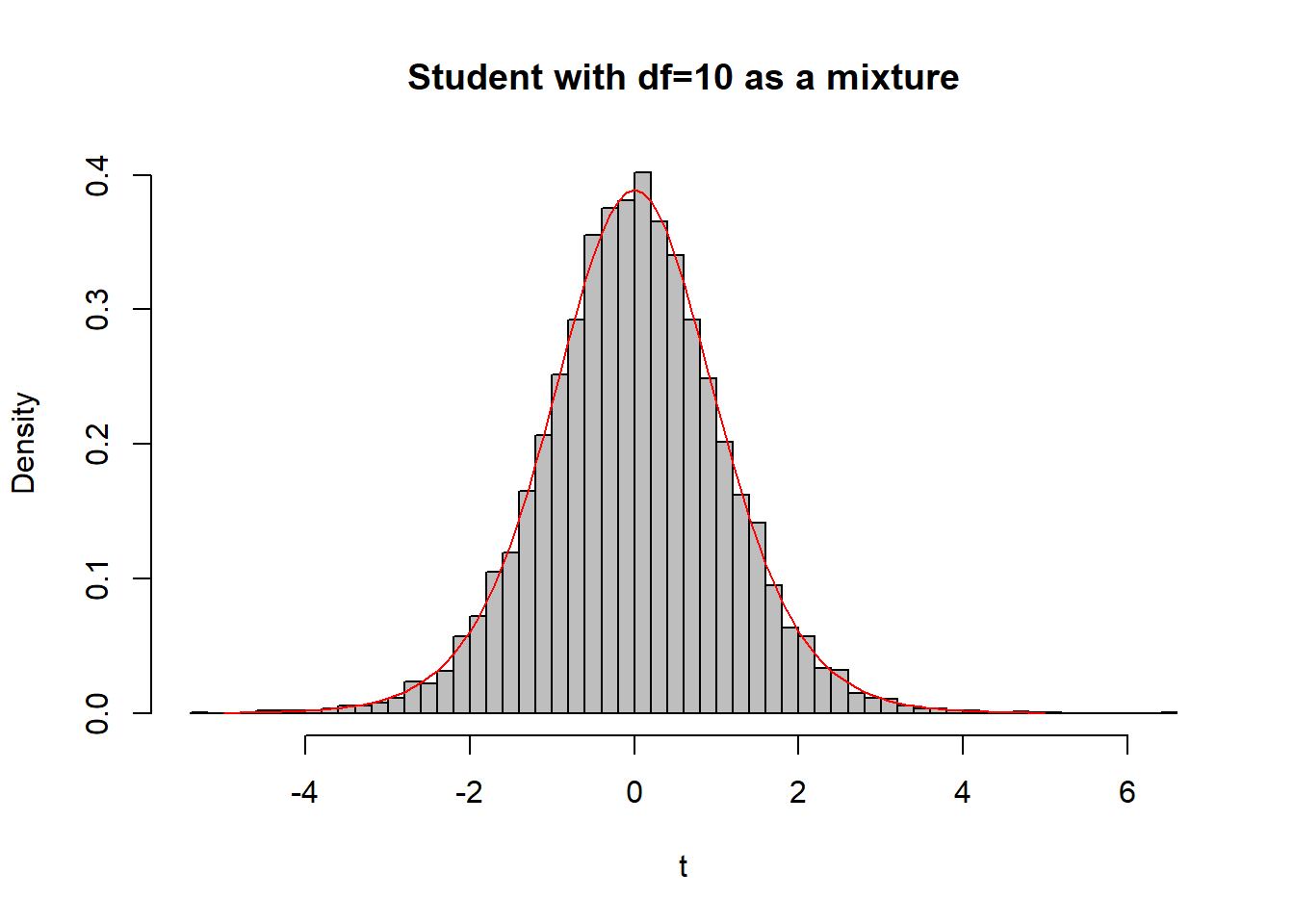

Παράδειγμα 2.11 Έστω ότι θέλουμε να προσoμοιώσουμε από την αρνητική διωνυμική \(NegBin(r,p)\) Ισχύει ότι:

\[\begin{equation*} X\thicksim Poisson(Y), \ Y\thicksim Gamma\left(r, \frac{p}{1-p}\right) \Rightarrow \ X \thicksim NegBin(r,p). \end{equation*}\]

Επομένως, μπορούμε να παράγουμε τιμές από την αρνητική διωνυμική ως μίξη Poisson με βάρη από κατανομή Gamma.

Nsim <- 10 ^ 4
r <- 6 ; p <- 0.3
y <- rgamma(Nsim, r, rate = p / (1 - p))
x <- rpois(Nsim, y)

hist(x, main = "", freq = FALSE, col = "grey", breaks = 40)
lines(1:50, dnbinom(1:50, r, p), lwd = 2, col = "sienna")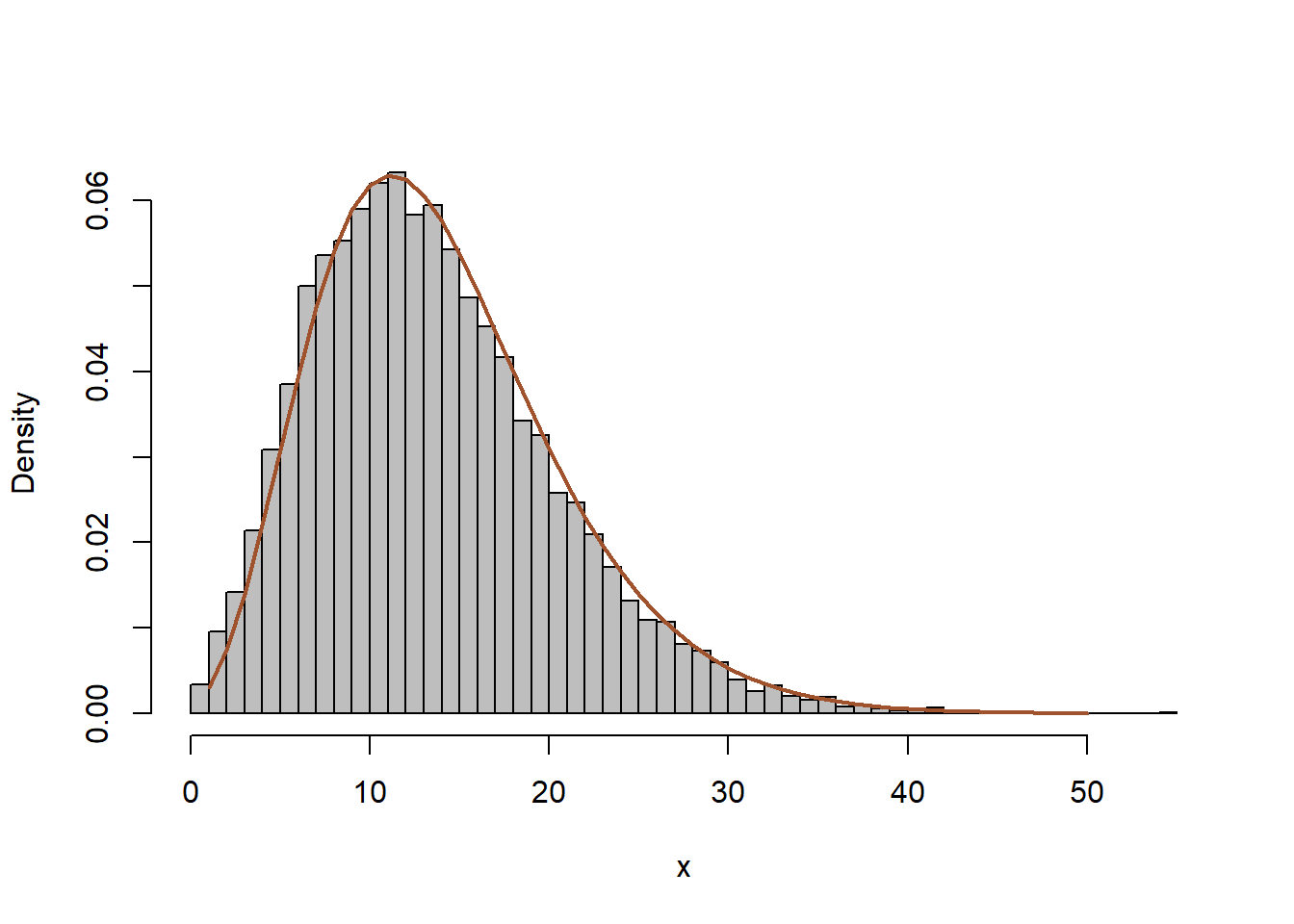

2.6 Μέθοδος Αποδοχής-Απόρριψης

Μέχρι τώρα, είτε μέσω του αντίστροφου μετασχηματισμού, είτε με κατάλληλους γενικούς μετασχηματισμούς παράγουμε άμεσα τιμές από μία τ.μ. \(X\). Οι μέθοδοι αποδοχής-απόρριψης μας προσφέρουν έναν πολύ γενικό τρόπο να παράγουμε έμμεσα από μία τ.μ. \(X\). Προϋπόθεση είναι να γνωρίζουμε τη συναρτησιακή μορφή της σ.π.π. / σ.π. της \(X\).

Για τη μέθοδο αποδοχής-απόρριψης χρειαζόμαστε:

• Μία πυκνότητα στόχο (target density) \(f\), γνωστή μέχρι κάποια πολλαπλασιαστική σταθερά (π.χ. \(f(x)=cx^3e^{-2x}, x>0\)),
• Μία υποψήφια (προτεινόμενη) πυκνότητα (instrumental / candidate density) \(g\), από την οποία μπορούμε να προσομοιώσουμε απ’ ευθείας.

Οι υποθέσεις του αλγορίθμου είναι:

\[\begin{align*} & S_f \subset S_g, \ \text{δηλ} \ f(x)>0 \Rightarrow g(x) >0 \\ & \exists M>0: f(x)\leq M\cdot g(x), \ \forall x \in S_g \Leftrightarrow \sup_{x\in S_g}\frac{f(x)}{g(x)}<+\infty. \end{align*}\]

Πρόταση 2.4 Γενικός Αλγόριθμος Αποδοχής-Απόρριψης

1. Προσομοιώνουμε \(Y\thicksim g\).
2. Προσομοιώνουμε ανεξάρτητα \(U\thicksim Unif(0,1)\).
3. Αν \(U\leq \frac{1}{M} \frac{f(Y)}{g(Y)}\), τότε αποδεχόμαστε την \(Y\), δηλ. \(X=Y\), διαφορετικά επιστρέφουμε στο Βήμα 1.

Ο αλγόριθμος τερματίζει όταν για 1η φορά γίνει αποδοχή κάποιας \(Y\). Οι παρατηρήσεις που παράγονται από τον αλγόριθμο ακολουθούν την \(f\).

Απόδειξη:. Η τελική αποδοχή της \(Y\) συμβαίνει όταν ικανοποιηθεί ο περιορισμός \(U\leq \frac{1}{M} \frac{f(Y)}{g(Y)}\). Επομένως, η κατανομή της αποδεκτής τιμής του αλγορίθμου εκφράζεται μέσα από την κατανομή της τ.μ. \(X=\left[Y\ \middle\vert \ U\leq \frac{1}{M} \frac{f(Y)}{g(Y)}\right]\). Υπολογίζουμε τη σ.κ. της \(X\). Συγκεκριμένα, έστω \(x\in \mathbb{R}\).

\[\begin{align*} \mathbf{P}(X\leq x) &= \mathbf{P}\left(Y\leq x \ \middle\vert \ U\leq \frac{1}{M} \frac{f(Y)}{g(Y)}\right) =\frac{\mathbf{P}\left(Y\leq x , U\leq \frac{1}{M} \frac{f(Y)}{g(Y)}\right)}{\mathbf{P}\left(U\leq \frac{1}{M} \frac{f(Y)}{g(Y)}\right)} =\frac{\mathbf{E}\left(\mathbf{1}_{ Y\leq x} \cdot \mathbf{1}_{U\leq \frac{1}{M} \frac{f(Y)}{g(Y)}}\right)}{\mathbf{E}\left(\mathbf{1}_{U\leq \frac{1}{M} \frac{f(Y)}{g(Y)}}\right)}\\ &=\frac{\mathbf{E}\left(\mathbf{1}_{Y\leq x} \cdot \mathbf{E}\left(\mathbf{1}_{U\leq \frac{1}{M} \frac{f(Y)}{g(Y)}}\ \middle \vert\ Y\right)\right)}{\mathbf{E}\left(\mathbf{E}\left(\mathbf{1}_{U\leq \frac{1}{M} \frac{f(Y)}{g(Y)}}\ \middle \vert \ Y\right)\right)} = \frac{\mathbf{E}\left(\mathbf{1}_{Y\leq x} \cdot \mathbf{P}\left(U\leq \frac{1}{M} \frac{f(Y)}{g(Y)}\ \middle \vert\ Y\right)\right)}{\mathbf{E}\left(\mathbf{E}\left(\mathbf{1}_{U\leq \frac{1}{M} \frac{f(Y)}{g(Y)}}\ \middle \vert \ Y\right)\right)} =\frac{\mathbf{E}\left(\mathbf{1}_{Y\leq x} \cdot \frac{1}{M} \frac{f(Y)}{g(Y)}\right)}{\mathbf{E}\left(\frac{1}{M} \frac{f(Y)}{g(Y)}\right)} \\ & = \frac{\int_{y\leq x}\frac{f(y)}{g(y)}\cdot g(y) dy}{\int_{y \in S_f}\frac{f(y)}{g(y)}\cdot g(y) dy} = F(x) \end{align*}\]

Γενικότερα,

\[\begin{equation*} \mathbf{E}\left[h(X)\right]=\mathbf{E}_f\left[ h(Y) \right]=\mathbf{E}_g\left[h(Y) \cdot \frac{f(Y)}{g(Y)} \right]. \end{equation*}\]

Άρα,

\[\begin{equation*} \mathbf{P}(X\leq x) = \mathbf{E}\left(\mathbf{1}_{X\leq x}\right) = \mathbf{E}_g\left( \mathbf{1}_{Y\leq x} \cdot \frac{f(Y)}{g(Y)} \right). \end{equation*}\]

Παρατήρηση:. Σημαντικό στην αποδοτικότητα ενός αλγορίθμου αποδοχής-απόρριψης είναι η πιθανότητα αποδοχής, όπου το ενδεχόμενο αποδοχής είναι το \(A=\left\{U \leq \frac{1}{M} \frac{f(Y)}{g(Y)} \right\}\).

\[\begin{equation*} \mathbf{P}(A) = \mathbf{P}\left( U \leq \frac{1}{M} \frac{f(Y)}{g(Y)} \right) = \mathbf{E}\left[ \mathbf{P}\left( U \leq \frac{1}{M} \frac{f(Y)}{g(Y)} \ \middle \vert \ Y \right) \right] = \mathbf{E}_g\left[ \frac{1}{M} \frac{f(Y)}{g(Y)} \right] = \frac{1}{M} \mathbf{E}_g\left[ \frac{f(Y)}{g(Y)} \right] = \frac{1}{M} \mathbf{E}_f\left[ 1 \right]=\frac{1}{M}. \end{equation*}\]

Παρατήρηση:. Στα προηγούμενα υποθέτουμε ότι οι σταθερές κανονικοποίησης είναι γνωστές και τότε η πιθανότητα αποδοχής είναι \(1/M\). Όμως ο αλγόριθμος εφαρμόζεται ακόμα και αν οι σταθερές είναι άγνωστες (τόσο για την \(f\) όσο και για την \(g\)). Έστω \(f=c_f \widetilde{f}, g=c_g \widetilde{g}\). Τότε:

\[\begin{equation*} \sup_{x\in S_{\widetilde{g}}}\frac{\widetilde{f}(x)}{\widetilde{g}(x)}= \frac{c_g}{c_f} \sup_{x\in S_g}\frac{f(x)}{g(x)}. \end{equation*}\]

Επομένως:

\[\begin{equation*} \sup_{x\in S_{\widetilde{g}}}\frac{\widetilde{f}(x)}{\widetilde{g}(x)} \leq M'\ \Longrightarrow \ \sup_{x\in S_g}\frac{f(x)}{g(x)} \leq \frac{c_f}{c_g} \cdot M'. \end{equation*}\]

Αν γνωρίζουμε ένα τέτοιο \(M'\), τότε ο αλγόριθμος αποδοχής-απόρριψης αποδέχεται την παραγόμενη παρατήρηση \(Y\) όταν \(U<\frac{1}{M'} \cdot \frac{\widetilde{f}(Y)}{\widetilde{g}(Y)}\).

Σε αυτή την περίπτωση, η πιθανότητα αποδοχής μεταβάλλεται:

\[\begin{equation*} \mathbf{P}(A) = \mathbf{P}\left( U \leq \frac{1}{M'} \frac{\widetilde{f}(Y)}{\widetilde{g}(Y)} \right) = \mathbf{E}_g\left[ \frac{1}{M'} \frac{\tilde{f}(Y)}{\tilde{g}(Y)} \right] = \frac{1}{M'} \frac{c_g}{c_f} \mathbf{E}_g\left[ \frac{f(Y)}{g(Y)} \right] = \frac{1}{M'} \cdot \frac{c_g}{c_f}. \end{equation*}\]

Πολλές φορές είναι άγνωστο μόνο το \(c_f\), και έτσι μπορούμε να εκτιμήσουμε τη σταθερά ολοκλήρωσης μέσα από μία σειρά διαδοχικών προσομοιώσεων. Αν είναι άγνωστος ο λόγος, τότε αντί για το \(c_f\), εκτιμάται ο λόγος \(c_f/c_g\) (ή \(c_g/c_f\)). Εφ’ όσον έχουμε πιθανότητα αποδοχής \(p=\frac{1}{M'} \cdot \frac{c_g}{c_f}\), αν σε ένα δείγμα \(n\) ανεξάρτητων προσομοιώσεων έχουμε ποσοστό αποδοχών \(\widehat{p}_n\), τότε:

\[\begin{equation*} \widehat{\left(\frac{c_g}{c_f}\right)}=M'\, \hat{p}_n. \end{equation*}\]

Παράδειγμα 2.12 (Robert & Casella 2.7.) Έστω ότι θέλουμε να προσoμοιώσουμε από την \(Beta(a,b), a,b>1\), χρησιμοποιώντας την \(Unif(0,1)\) ως υποψήφια.

Ας δούμε πώς υλοποιείται ο αλγόριθμος αποδοχής-απόρριψης στην R.

f <- function(x){
  dbeta(x, 2.7, 6.3)
}
optimize(f, interval = c(0, 1), maximum = TRUE)$objective
## [1] 2.669744

Nsim <- 2500
a <- 2.7
b <- 6.3
M <- 2.67
u <- runif(Nsim, max = M) # uniform over (0, M)
y <- runif(Nsim) # generation from g
x <- y[u < dbeta(y, a, b)] # accepted subsample

hist(x, main = "Beta(2.7, 6.3) sample with Accept-Reject", freq = FALSE, col = "grey")
curve(dbeta(x, 2.7, 6.3),  from = 0, to = 1, lty= 1, lwd = 1, col = "red", add = TRUE)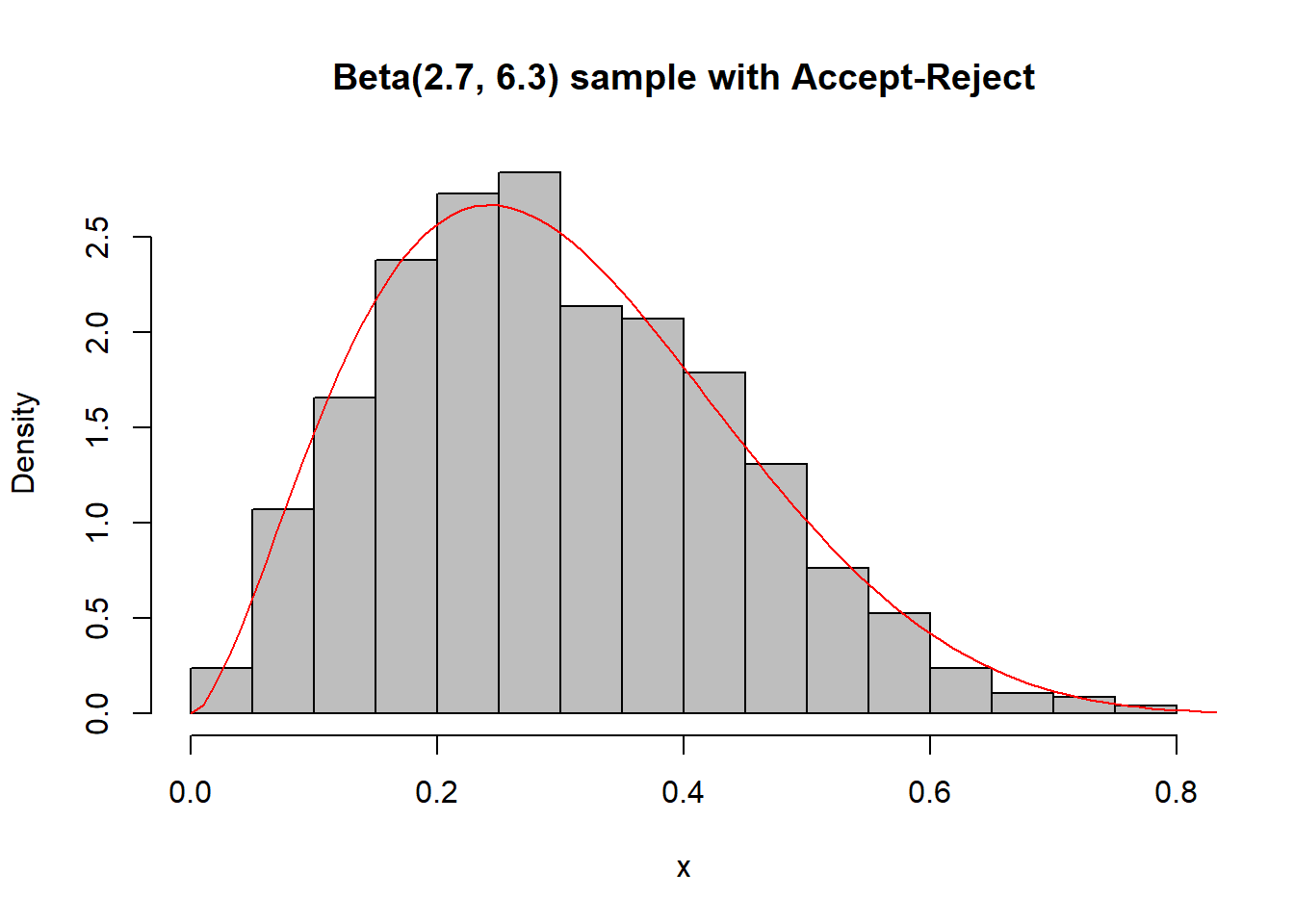

Στον παραπάνω κώδικα παράγουμε πολλές παρατηρήσεις από τις οποίες δεχόμαστε μόνο μερικές. Ένας πιο αποδοτικός τρόπος είναι ρυθμίζοντας τον αριθμό προσομοιώσεων να είναι τέτοιος ώστε ο μέσος αριθμός αποδεκτών καταστάσεων να συμπίπτει με το μέγεθος του δείγματος που θέλουμε να πάρουμε, όπως φαίνεται παρακάτω:

x <- NULL
while (length(x) < Nsim) {
y <- runif(Nsim * M)
x <- c(x, y[runif(Nsim * M) * M < dbeta(y, a, b)])}
x <- x[1:Nsim]

hist(x, main = "Beta(2.7, 6.3) sample with Accept-Reject", freq = FALSE, col = "grey")
curve(dbeta(x, 2.7, 6.3), from = 0, to = 1, lty= 1, lwd = 1, col = "red", add = TRUE)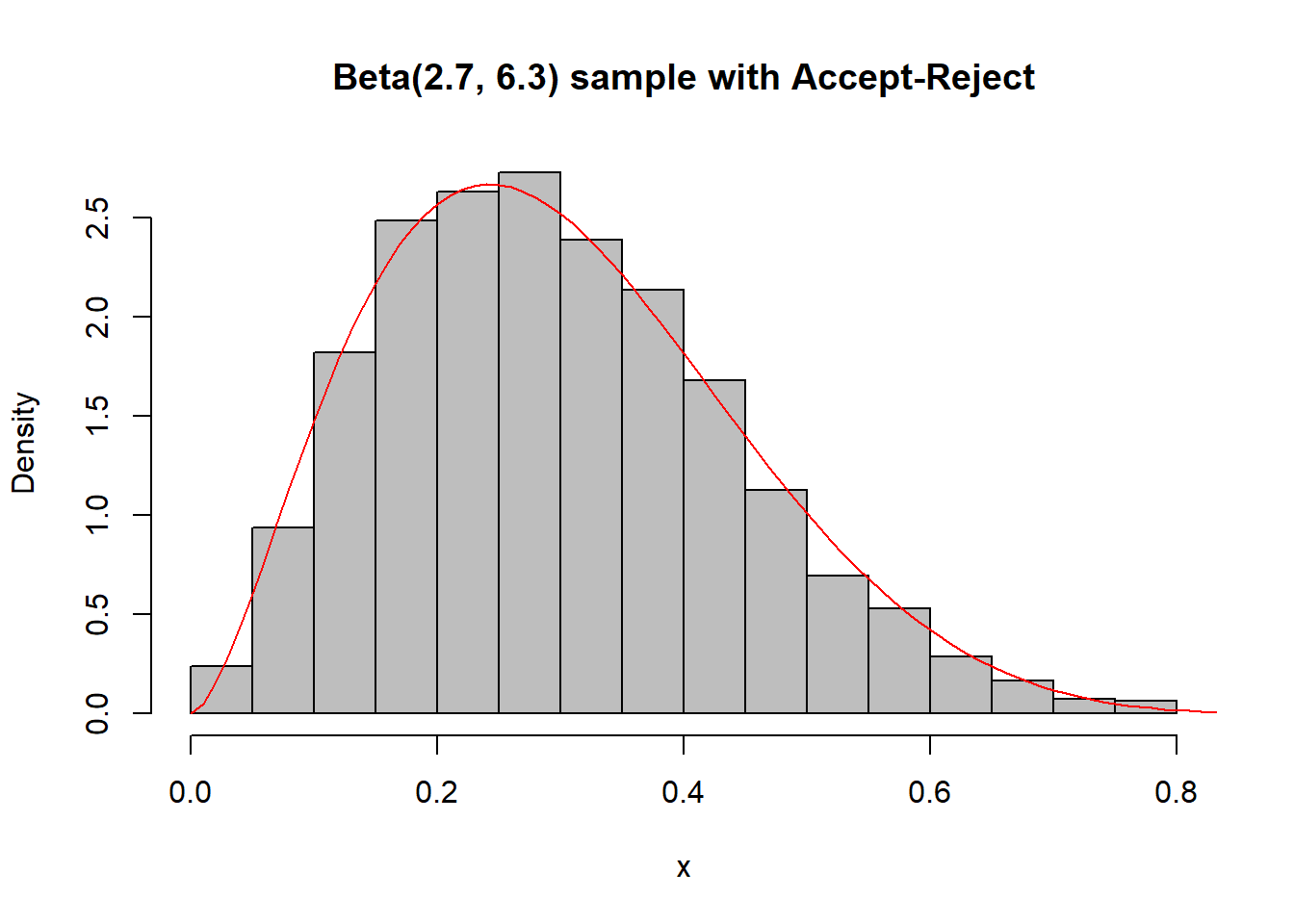

Άσκηση 2.3 Αποδείξτε ότι η \(\left[ Y\ \middle \vert \ U \leq \frac{1}{M'} \frac{\tilde{f}(Y)}{\tilde{g}(Y)} \right] \overset{d}{=} X\).

Άσκηση 2.4 Φτιάξτε δικό σας παράδειγμα προσομοίωσης από κάποια \(f=c\tilde{f}\) με άγνωστο c, χρησιμοποιώντας κάποια \(g\) που μπορεί να εφαρμοστεί ο αλγόριθμος αποδοχής-απόρριψης και εκτιμήστε τη σταθερά κανονικοποίησης \(c\) στην R με τη βοήθεια κάποιων προσομοιώσεων.

Παράδειγμα 2.13 (Robert and Casella, 2.8) Ας υποθέσουμε ότι θέλουμε να παράγουμε από \(N(0,1)\) με τον αλγόριθμο αποδοχής-απόρριψης και χρησιμοποιούμε κατανομή πρότασης τη διπλή εκθετική (Laplace) \(\mathcal{L}(a)\), με πυκνότητα

\[\begin{equation} g(x|a) = \frac{a}{2} \, e^{-a\,|x|}, \quad x\in \mathbb{R},\ a>0, \end{equation}\]

1. Να δειχθεί ότι

\[\begin{equation} \frac{f(x)}{g(x|a)}\leq \sqrt{\frac{2}{\pi}}a^{-1}e^{\frac{a^2}{2}} \end{equation}\]

και ότι το ελάχιστο του παραπάνω φράγματος (στο \(a\)) επιτυγχάνεται στο \(a=1\).

2. Να δειχθεί ότι η πιθανότητα αποδοχής γίνεται τότε \(\sqrt{\pi/2e}=0.76\) και συμπεράνετε ότι για να παραχθεί μία \(N(0,1)\) απαιτούνται κατά μέσο όρο \(1/0.76 \approx 1.3\) ομοιόμορφες τυχαίες μεταβλητές.

3. Να δειχθεί ότι η διπλή εκθετική \(\mathcal{L}(a)\) μπορεί να παραχθεί από τον αντίστροφο μετασχηματισμό πιθανότητας και συγκρίνετε αυτόν τον αλγόριθμο με τον αλγόριθμο Box-Muller του Παραδείγματος 2.3 ως προς το χρόνο εκτέλεσης.

Ερώτημα a

Σε πρώτη φάση υπολογίζουμε τον λόγο:

\[\begin{equation*} \frac{f(x)}{g(x|a)}=\frac{\frac{1}{\sqrt{2\pi}}e^{-x^2/2}}{\frac{a}{2} e^{-a|x|}}= \sqrt{\frac{2}{\pi}}a^{-1}e^{-\frac{x^2}{2}+a |x|} \end{equation*}\]

Όμως

\[\begin{equation*} e^{-\frac{x^2}{2}+a |x|}=e^{\frac{a^2}{2}}\cdot e^{-\frac{(|x|-a)^2}{2}}, \ \ \forall x \in \mathbb{R}, \end{equation*}\]

και

\[\begin{equation*} \sup_{x\in \mathbb{R}} e^{-\frac{(|x|-a)^2}{2}}=1, \end{equation*}\]

το οποίο επιτυγχάνεται για \(|x|=a.\) Συμπεραίνουμε ότι:

\[\begin{equation*} \sup_{x\in\mathbb{R}}\frac{f(x)}{g(x|a)}= \sqrt{\frac{2}{\pi}}a^{-1}e^{\frac{a^2}{2}}. \end{equation*}\]

Η χρήση μιας παραμετρικής οικογένειας \(g(x|a)\) αντί μιας συγκεκριμένης πυκνότητας μας επιτρέπει την περαιτέρω βελτίωση της σταθεράς \(M\) που παίζει σημαντικό ρόλο στην απόδοση του αλγορίθμου αποδοχής - απόρριψης.

Εδώ

\[\begin{equation*} M(a)=\sqrt{\frac{2}{\pi}} \frac{e^{\frac{a^2}{2}}}{a}, \end{equation*}\]

και έτσι ελαχιστοποιούμε την \(M(a)\) ως προς \(a>0\).

Παραγωγίζοντας την \(M(a)\) έχουμε

\[\begin{equation*} M'(a)=\sqrt{\frac{2}{\pi}} \frac{(a^2-1)e^{\frac{a^2}{2}}}{a^2}, \ \ a>0 \end{equation*}\]

και άρα

\[\begin{equation*} M'(a)=0 \Leftrightarrow a=1. \end{equation*}\]

Παρατηρούμε επίσης ότι \(M'(a)<0\), για \(a<1\) και \(M'(a)>0\), για \(a>1\). Συμπεραίνουμε λοιπόν ότι

\[\begin{equation*} \min_{a>0} M(a) = M(1) = \sqrt{\frac{2e}{\pi}} \cong 1.315 \end{equation*}\]

Ερώτημα b

Έχουμε δείξει ότι η πιθανότητα αποδοχής ενός αλγορίθμου αποδοχής - απόρριψης είναι

\[\begin{equation*} p = P\left[ U<\frac{1}{M} \cdot \frac{f(Y)}{g(Y)}\right]=\frac{1}{M}, \end{equation*}\]

και άρα εδώ

\[\begin{equation*} p=\frac{1}{M(1)}=\sqrt{\frac{\pi}{2e}}\cong 0.76 \ . \end{equation*}\]

Επίσης, αν \(N\) είναι το πλήθος των ανεξάρτητων ομοιόμορφων τ.μ. που παράγονται μέχρι να ικανοποιηθεί το κριτήριο και να γίνει για πρώτη φορά δεκτή, τότε

\[\begin{equation*} N\thicksim Geo(p), \quad N\in \mathbb{N}^{*}. \end{equation*}\]

Συμπεραίνουμε ότι

\[\begin{equation*} E(N)=\frac{1}{p}=M(1) \cong 1.315. \end{equation*}\]

Γενικότερα, ο μέσος αριθμός προσομοιώσεων ομοιόμορφων τ.μ. που χρειάζονται για να παραχθεί μία τιμή μίας τ.μ. \(X\) μέσω του αλγορίθμου αποδοχής - απόρριψης είναι \(M\). Θυμίζουμε βέβαια εδώ ότι αυτό ισχύει όταν οι σταθερές κανονικοποίησης των \(f,g\) είναι γνωστές.

Ερώτημα c

Η μέθοδος αντίστροφου μετασχηματισμού πιθανότητας για την προσομοίωση τυχαίων μεταβλητών στηρίζεται στη δυνατότητα υπολογισμού και αντιστροφής της σ.κ. της εν λόγω τ.μ..

Αν

\[\begin{equation*} X\thicksim \mathcal{L}(a), \ \ a>0, \end{equation*}\]

τότε

\[\begin{equation*} X=\frac{1}{a} \cdot Z, \ \text{όπου} \ \ Z\thicksim \mathcal{L}(1), \end{equation*}\]

άρα αρκεί να “αντιστρέψουμε” για \(a=1\).

Αν \(z<0,\) τότε

\[\begin{equation*} F_Z(z)=P(Z\leq z)=\int_{-\infty}^z\frac{1}{2}e^{-|u|}du=\frac{1}{2}\int_{-\infty}^ze^{u}du=\frac{1}{2}e^z. \end{equation*}\]

Για \(z\geq 0,\) έχουμε

\[\begin{align*} F_Z(z)=P(Z\leq z) &=P(Z \leq 0)+ P (0 \leq Z \leq z) \\ &= \frac{1}{2}+\frac{1}{2}\int_{0}^ze^{-u}du \\ &=\frac{1}{2}+\frac{1}{2}\left(1 - e^{-z}\right) \\ &= 1-\frac{1}{2} e^{-z}. \end{align*}\]

Τελικά,

\[\begin{equation*} F_Z(z)=\left\{\begin{array}{lcc} \frac{1}{2}e^z & , & z<0 \\ 1-\frac{1}{2}e^{-z} & , & z \geq 0 \end{array}\right. \ \ . \end{equation*}\]

Θέτοντας \(u=F_Z(z),\) έχουμε

\[\begin{equation*} z=F^{-1}_Z(u)=\left\{\begin{array}{lcc} \log(2u) & , & 0<u<\frac{1}{2} \\ -\log[2(1-u)] & , & \frac{1}{2} \leq u < 1 \end{array}\right. \ \ . \end{equation*}\]

Η παραπάνω σχέση μας οδηγεί στο συμπέρασμα ότι

\[\begin{equation*} Z=F^{-1}_Z(U)=\log(2u) \cdot 1_{\left(0, \frac{1}{2}\right)}(u)-\log[2(1-u)] \cdot 1_{\left[ \frac{1}{2}, 1\right)}(u), \end{equation*}\]

και άρα \(X=\frac{1}{a}F^{-1}_Z(U)\).

Σύγκριση Αλγορίθμων

Υλοποιούμε τον αλγόριθμο παραγωγής παρατηρήσεων από την τυπική κανονική μέσω της κατανομής Laplace.

Αρχικά, δημιουργούμε μία συνάρτηση για την πυκνότητα της Laplace:

dlaplace <- function(x) {
  exp( - abs(x)) / 2
}

Έπειτα, δημιουργούμε μία συνάρτηση για την παραγωγή τυχαίων παρατηρήσεων από την Laplace (μέσω αντίστροφου μετασχηματισμού):

rlaplace <- function(size) {
  u <- runif(size)
  log(2 * u) * I((0 < u) & (u < 1 / 2)) - log(2 * (1 - u)) * I((1 / 2 <= u) & (u < 1))
}

Τέλος, δημιουργούμε τη συνάρτηση που υλοποιεί τον αλγόριθμο αποδοχής - απόρριψης:

acc.rej <- function(size, plot = TRUE, report = TRUE) {
  
  # Arxikopoioume ta dianysmata kai to M
  u <- x <- y <- NULL
  M <- sqrt(2 * exp(1) / pi)
  
  while (length(x) < size) {
    
    # Dimiourgoume ton anamenomeno arithmo paratirisewn
    # pou tha xreiastoume, diladi (size-length(x))*M
    # kai eksetazoume posa tha ginoun dekta
    if (report) {
      cat(paste0("Number of trials: ", floor((size - length(x)) * M), "\n"))
    }
    
    u <- c(u, runif((size - length(x)) * M))
    y <- c(y, rlaplace((size - length(x)) * M))
    x <- y[u * M * dlaplace(y) < dnorm(y)]
    
    if (report) {
      cat(paste0("Total Accepted: ", length(x), "\n"))
    }
    
  }  
  
  # Kratame mono oses paratiriseis mas zitountai
  u<-u[1:size]
  x<-x[1:size]
  y<-y[1:size]
  
  # Kanoume to plot
  if (plot) { 
    data<-data.frame(pointx = y,
                     pointy = u * M * dlaplace(y), 
                     accept = (u * M * dlaplace(y) < dnorm(y)))
    
    a <- ggplot(data) +
      stat_function(fun = function(x) { dlaplace(x) * M }, xlim = c(-8,8)) +
      stat_function(fun = dnorm, xlim = c(-8,8)) +
      geom_point(aes(x = pointx, y = pointy, col = accept), size = 0.4) +
      xlab("x") + ylab("y") +
      theme_minimal()
    print(a)
  }
  
  x
}

x <- acc.rej(1000)
## Number of trials: 1315
## Total Accepted: 1023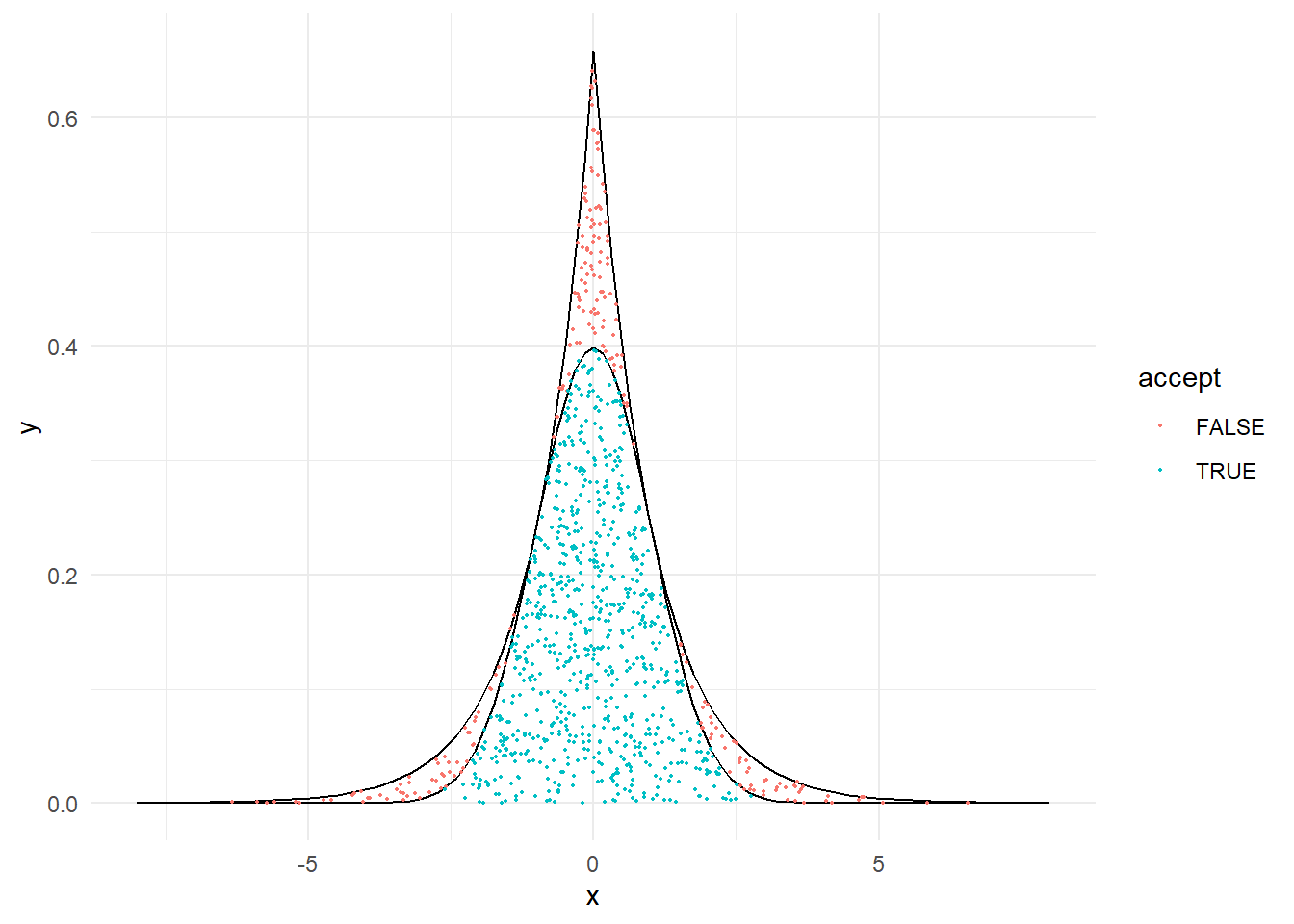

H παραπάνω συνάρτηση δημιουργεί τον αναμενόμενο αριθμό παρατηρήσεων που θα χρειαστούμε. Έτσι, γλυτώνει αρκετό χρόνο σε σύγκριση με την αντίστοιχη συνάρτηση που δημιουργεί τις παρατηρήσεις μία-μία:

acc.rej.1 <- function(size, plot = TRUE){
  
  # Arxikopoioume ta dianysmata kai to M
  u <- x <- y <- NULL
  M <- sqrt(2 * exp(1) / pi)
  
  # Dimiourgoume mia nea parathrhsh kai eksetazoume
  # an tha ginei dekth
  while (length(x)<size) {
    unew <- runif(1)
    ynew <- rlaplace(1)
    u <- c(u, unew)
    y <- c(y, ynew)
    x <- c(x, ynew[unew * M * dlaplace(ynew) < dnorm(ynew)])
  }  
  
  # Kanoume to plot
  if (plot) { 
    data<-data.frame(pointx = y,
                     pointy = u * M * dlaplace(y), 
                     accept = (u * M * dlaplace(y) < dnorm(y)))
    
    a <- ggplot(data) +
      stat_function(fun = function(x){ dlaplace(x) * M }, xlim = c(-8,8)) +
      stat_function(fun = dnorm, xlim = c(-8,8)) +
      geom_point(aes(x = pointx, y = pointy, col = accept), size = 0.4) +
      xlab("x") + ylab("y") +
      theme_minimal()
    print(a)
  }
  
  x
}

x <- acc.rej.1(1000)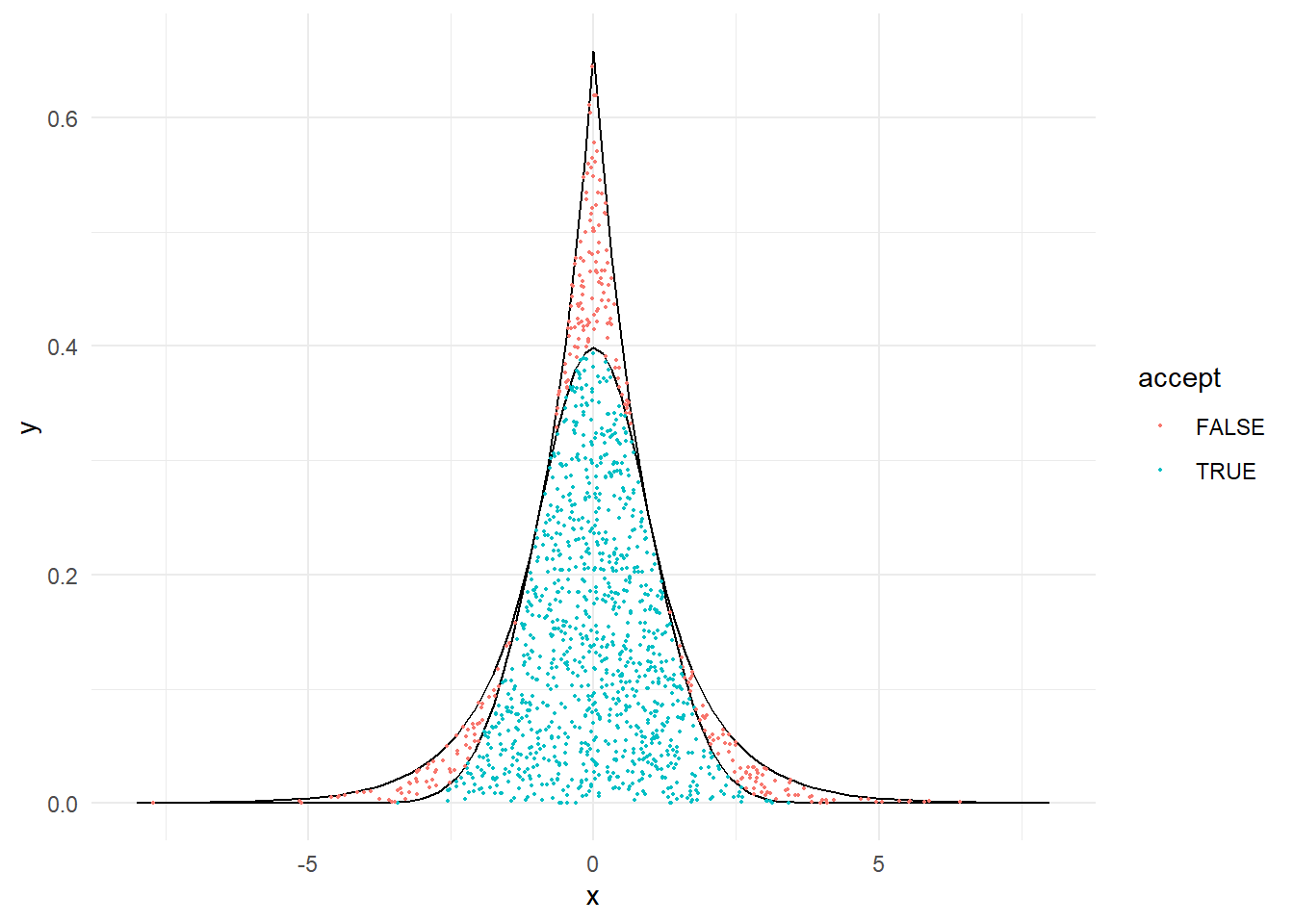

Ο αλγόριθμος Box-Muller μπορεί να εκτελεστεί στην R ως εξής:

boxmuller <- function(size) {
  
  if(size %% 2 == 1){
    size <- size + 1
  }
  
  theta <- runif(size / 2, 0, 2 * pi) 
  U1 <- runif(size / 2)
  R <- sqrt(-2 * log(U1))
  Z <- c(R * cos(theta), R * sin(theta))
  if(size %% 2 == 1){
    Z <- Z[-1]
  }
  Z
}

Συγκρίνουμε την ταχύτητα των τριών αλγορίθμων με το πακέτο microbenchmark:

microbenchmark(acc.rej(1000, plot = FALSE, report = FALSE), times = 100, unit = "us")
## Unit: microseconds
##                                         expr   min     lq    mean median    uq
##  acc.rej(1000, plot = FALSE, report = FALSE) 383.1 387.95 521.491 410.45 589.9
##    max neval
##  959.8   100
microbenchmark(acc.rej.1(1000, plot = FALSE), times = 100, unit = "us")
## Unit: microseconds
##                           expr     min       lq     mean   median       uq
##  acc.rej.1(1000, plot = FALSE) 31170.2 35840.15 39810.97 37498.15 43668.55
##      max neval
##  55160.8   100
microbenchmark(boxmuller(1000), times = 100, unit = "us")
## Unit: microseconds
##             expr   min    lq    mean median    uq    max neval
##  boxmuller(1000) 116.3 117.5 209.156  118.1 120.4 9105.6   100

---

2.6.1 Εφαρμογή στη Μπεϋζιανή Στατιστική

Στη Μπεϋζιανή Στατιστική η παράμετρος \({\theta}\), που στην κλασική Στατιστική είναι άγνωστη σταθερά, θεωρείται τυχαία μεταβλητή με μία εκ των προτέρων (prior) κατανομή \(f(\theta)\). Μόλις τα δεδομένα γίνουν διαθέσιμα, τότε η κατανομή της \(\Theta\) μεταβάλλεται φυσιολογικά σε \(f(\theta|x)\). Η κατανομή της \(\left[\Theta|X=x\right]\) λέγεται εκ των υστέρων (posterior) κατανομή της \(\Theta\) (δεδομένου του \(X=x\)), και η εύρεση αυτής της κατανομής αποτελεί το διακαή πόθο μίας μπεϋζιανής προσέγγισης.

Με τη βοήθεια της εκ των υστέρων κατανομής μπορούμε να απαντήσουμε στα ίδια ερωτήματα που θέτει η κλασική στατιστική, εφαρμόζοντας όμως τώρα τη μπεϋζιανή προσέγγιση.

Ένα από τα “μειονεκτήματα” της μπεϋζιανής προσέγγισης αποτελεί η αυθαιρεσία στην επιλογή της prior \(f(\theta)\), κάτι όμως που μπορεί να αποδειχθεί ένα από τα μεγαλύτερα “πλεονεκτήματά” της, καθώς μπορεί να αποτυπώσει με τη μορφή μιας κατανομής, εκ των προτέρων πληροφορία που μπορεί ένας ειδικός να διαθέτει για τις πιο πιθανές τιμές που μπορεί να πάρει το άγνωστο \(\theta\), πριν ακόμα τα δεδομένα γίνουν διαθέσιμα. Τελικά, η \(\Theta\) με prior \(f(\theta)\) αλληλεπιδρά με τα δεδομένα \(x\) και μέσω του Bayes καταλήγουμε στην εκ των υστέρων σ.π. / σ.π.π. της \(\Theta\) δοθείσης της \(X=x\)

\[\begin{equation} f(\theta|x)=\frac{f(\theta)\cdot f(x|\theta)}{f(x)}, \tag{2.1} \end{equation}\]

όπου

\[\begin{equation} f(x)=\int_{\theta} f(\theta) f(x|\theta) d\theta. \tag{2.2} \end{equation}\]

Η γνώση της \(f(\theta|x)\) είναι ό,τι χρειάζεται να γνωρίζουμε για να εφαρμόσουμε μπεϋζιανή συμπερασματολογία σε κάποιο στατιστικό πρόβλημα. Να σημειώσουμε εδώ ότι η \(f(x|\theta)\) παίζει το ρόλο που έπαιζε η συνάρτηση πιθανοφάνειας στην κλασική στατιστική. Οι πιο συχνά χρησιμοποιούμενες σημειακές εκτιμήτριες της μπεϋζιανής προσέγγισης προκύπτουν από την εκ των υστέρων μέση τιμή \(E\left[\theta|x\right]\) και το εκ των υστέρων μέγιστο \(\arg\max_{\theta}f(\theta|x)\).

Με γνώση / καθορισμό της prior \(f(\theta)\) και της \(f(x|\theta)\), είναι φανερό ότι ο υπολογισμός της posterior \(f(\theta|x)\) είναι στενά συνδεδεμένος με τη δυνατότητα υπολογισμού της (2.2), που παίζει το ρόλο της σταθεράς κανονικοποίησης, εφ’όσον

\[\begin{equation*} f(\theta|x)\overset{\theta}{\propto} f(\theta)\cdot f(x|\theta). \end{equation*}\]

Χωρίς να μπούμε σε λεπτομέρειες για τον τρόπο επιλογής της prior και και καλές πρακτικές μπεϋζιανής μεθοδολογίας, δίνουμε τώρα ένα πολύ απλό παράδειγμα εφαρμογής της στην περίπτωση ενός τυχαίου δείγματος \(Χ=(Χ_1,\ldots,X_n)\) που προέρχεται από την κατανομή \(Bernoulli(\theta)\), \(\theta\in (0,1)\).

Θυμίζουμε ότι αν \(x=(x_1,\ldots,x_n)\in \{0,1\}^{n}\) είναι οι παρατηρούμενες τιμές, τότε η συνάρτηση πιθανοφάνειας που αντιστοιχεί στο \(x\) δίνεται από τη σχέση:

\[\begin{equation*} f(x|\theta) = \theta^{s_n}(1-\theta)^{s_n},\qquad \theta \in (0,1), \end{equation*}\]

όπου \(s_n = x_1+x_2 +\ldots x_n,\) και έτσι η εκτιμήτρια μέγιστης πιθανοφάνειας \(\widehat{\theta}_n\) του \(\theta\) που προκύπτει με μεγιστοποίηση της παραπάνω είναι

\[\begin{equation*} \widehat{\theta}_n = \frac{S_n}{n}= \overline{X}_n, \end{equation*}\]

επιτρέποντας και τις οριακές τιμές \(\theta\in \{0,1\}\) με συμπαγοποίηση του παραμετρικού χώρου. Η μέθοδος της μέγιστης πιθανοφάνειας είναι αρκετά δημοφιλής λόγω των καλών ασυμπτωτικών ιδιοτήτων των εκτιμητριών που προκύπτουν με τη μέθοδο αυτή. Σε πολλές περιπτώσεις λοιπόν, αργεί να φανεί η δύναμή της, καθώς το δείγμα μπορεί να είναι σχετικά μικρό. Ως ακραία περίπτωση, σκεφτείτε την περίπτωση που διαθέτουμε μία μόνο παρατήρηση \(X_1\sim Bernoulli(\theta)\). Τότε, αν γνωρίζαμε ότι \(\theta \in (0,1)\), η ε.μ.π. δεν θα μπορούσε καν να δώσει τιμή στο \((0,1)\), καθώς \(\widehat{\theta}_1=X_1\in \{0,1\}\). Η μπεϋζιανή προσέγγιση μπορεί λοιπόν πολλές φορές να μας εξασφαλίσει εκτιμήτριες που έχουν καλύτερη συμπεριφορά, ιδιαιτέρως σε περιπτώσεις που το δείγμα είναι σχετικά μικρό.

Από την άλλη μεριά, λόγω της ποικιλίας των διαφορετικών prior που μπορούν να επιλεγούν είναι πολλές φορές εφικτό να πλησιάσουμε πάρα πολύ τη συμπεριφορά της ε.μ.π., επιλέγοντας κατάλληλη prior και κατάλληλη σημειακή εκτιμήτρια μέσα από την posterior κατανομή. Στο συγκεκριμένο παράδειγμα έχουμε

\[\begin{equation*} f(\theta|x)\propto f(\theta)\cdot f(x|\theta)=f(\theta)\cdot \theta^{s_n}(1-\theta)^{n-s_n}. \end{equation*}\]

Είναι λοιπόν φανερό ότι με την επιλογή της ομοιόμορφης κατανομής \(Unif(0,1)\) ως prior κατανομής της παραμέτρου \(\theta\), η posterior κατανομή γίνεται ανάλογη της συνάρτησης πιθανοφάνειας. Έτσι αν χρησιμοποιηθεί το εκ των υστέρων μέγιστο (posterior max ή MAP) \(\arg \max_{\theta} f(\theta|x)\) ως σημειακή εκτιμήτρια του \(\theta\), έχουμε

\[\begin{equation*} \arg \max_{\theta} f(\theta|x) = \arg \max_{\theta} f(x|\theta), \end{equation*}\]

και άρα

\[\begin{equation*} \widehat{\theta}^{mle}_{n}=\widehat{\theta}^{map}_n=\overline{X}_n. \end{equation*}\]

Η επιλογή αυτή μας οδηγεί ακριβώς στην ε.μ.π. και έτσι παρουσιάζει τα ίδια προβλήματα. Από την άλλη μεριά η χρήση του posterior mean μας οδηγεί σε διαφορετική εκτιμήτρια. Για την εύρεση του μέσου, παρατηρούμε κατ’αρχήν ότι αν \(\Theta \sim Unif(0,1)\), τότε

\[\begin{equation*} f(\theta|x)\propto \theta^{s_n}(1-\theta)^{n-s_n}, \end{equation*}\]

από το οποίο συμπεραίνουμε ότι

\[\begin{equation*} \big[\Theta\,|\,\underbrace{X_1=x_1,\ldots,X_n=x_n}_{X=x}\big]\sim Beta\big(\,\underbrace{s_n+1}_{=\alpha},\ \underbrace{n-s_n+1}_{=\beta}\big), \end{equation*}\]

και άρα

\[\begin{equation*} \widehat{\theta}^{bayes}_{n} = E[\Theta|X]= \frac{\alpha}{\alpha+\beta}=\frac{S_n+1}{n+2}= \frac{n}{n+2}\widehat{\theta}^{mle}_{n}+\frac{2}{n+2}E(\Theta), \end{equation*}\]

που είναι η ζητούμενη σημειακή εκτιμήτρια.

2.6.1.1 Αριθμητική Εφαρμογή και προσομοίωση μέσω Accept-Reject

Υποθέτουμε λοιπόν τώρα ότι στο παραπάνω πρόβλημα πήραμε τις εξής παρατηρήσεις:

##  [1] 1 1 0 1 1 1 0 0 1 0

Έχουμε \(n=10\), \(s_{10}=6\) και άρα \(f(\theta|x)\propto \theta^6 (1-\theta)^4, \qquad \theta \in (0,1)\). Σε αυτό το παράδειγμα υποθέτουμε λοιπόν ότι η σταθερά κανονικοποίησης είναι άγνωστη, αλλά εμείς παρ’όλα αυτά θέλουμε να προσομοιώσουμε από την \(f(\theta|x)\). Όπως έχει ήδη ειπωθεί ο αλγόριθμος Accept-Reject μπορεί να εφαρμοστεί και σε τέτοιες περιπτώσεις.

f_tilde <- function(x) {
  x ^ 6 * (1 - x) ^ 4 * I((x > 0) & (x < 1))
}

Μετά σταθμίζουμε κατάλληλα τη συνάρτηση διαιρώντας με τη μέγιστη τιμή της:

f_tilde_max <- optimize(f_tilde, interval = c(0, 1), maximum = TRUE)$objective
f_tilde_max
## [1] 0.001194394

και άρα

fb_tilde <- function(x) {
  f_tilde(x) / optimize(f_tilde, interval = c(0, 1), maximum = TRUE)$objective 
}

Τέλος, δημιουργούμε τη συνάρτηση που υλοποιεί τον αλγόριθμο αποδοχής - απόρριψης με κατανομή πρότασης την Unif(0,1)

acc.rej.beta <- function(size, plot = TRUE, report = TRUE){
  
  # Arxikopoioume ta dianysmata kai to M
  u <- x <- y <- NULL
  M_pr <- 1 + 0.00000001
  
  while (length(x) < size) {
    
    # Dimiourgoume ton anamenomeno arithmo paratirisewn
    # pou tha xreiastoume, diladi (size-length(x))*M
    # kai eksetazoume posa tha ginoun dekta
    M <- M_pr
    c <- f_tilde_max/beta(7, 5)
    if (report) {
      cat(paste0("Number of trials: ", floor((size - length(x)) * M * c), "\n"))
    }
    
    u <- c(u, runif((size - length(x)) * M * c))
    y <- c(y, runif((size - length(x)) * M * c))
    x <- y[u * M < fb_tilde(y)]
    beta_est <- (length(x) * f_tilde_max) / length(y)
    
    if (report) {
      cat(paste0("Total Accepted: ", length(x), "\n"))
    }
    
  }  
  
  # Kratame mono oses paratiriseis mas zitountai
  u <- u[1:size]
  x <- x[1:size]
  y <- y[1:size]
  
  # Kanoume to plot
  
  if (plot) { 
    
    data<-data.frame(pointx = y,
                     pointy = u * M, 
                     accept = (u * M < fb_tilde(y)))
    
    a <- ggplot(data) +
      stat_function(fun = function(x){ dunif(x) * M }, xlim = c(0,1)) +
      stat_function(fun = fb_tilde, xlim = c(0,1)) +
      geom_point(aes(x = pointx, y = pointy, col = accept), size = 0.4) +
      xlab("x") + ylab("y") +
      theme_minimal()
    print(a)
  }
  
  list(x,beta_est)
}

AR <- acc.rej.beta(10000)
## Number of trials: 27590
## Total Accepted: 9913
## Number of trials: 240
## Total Accepted: 10000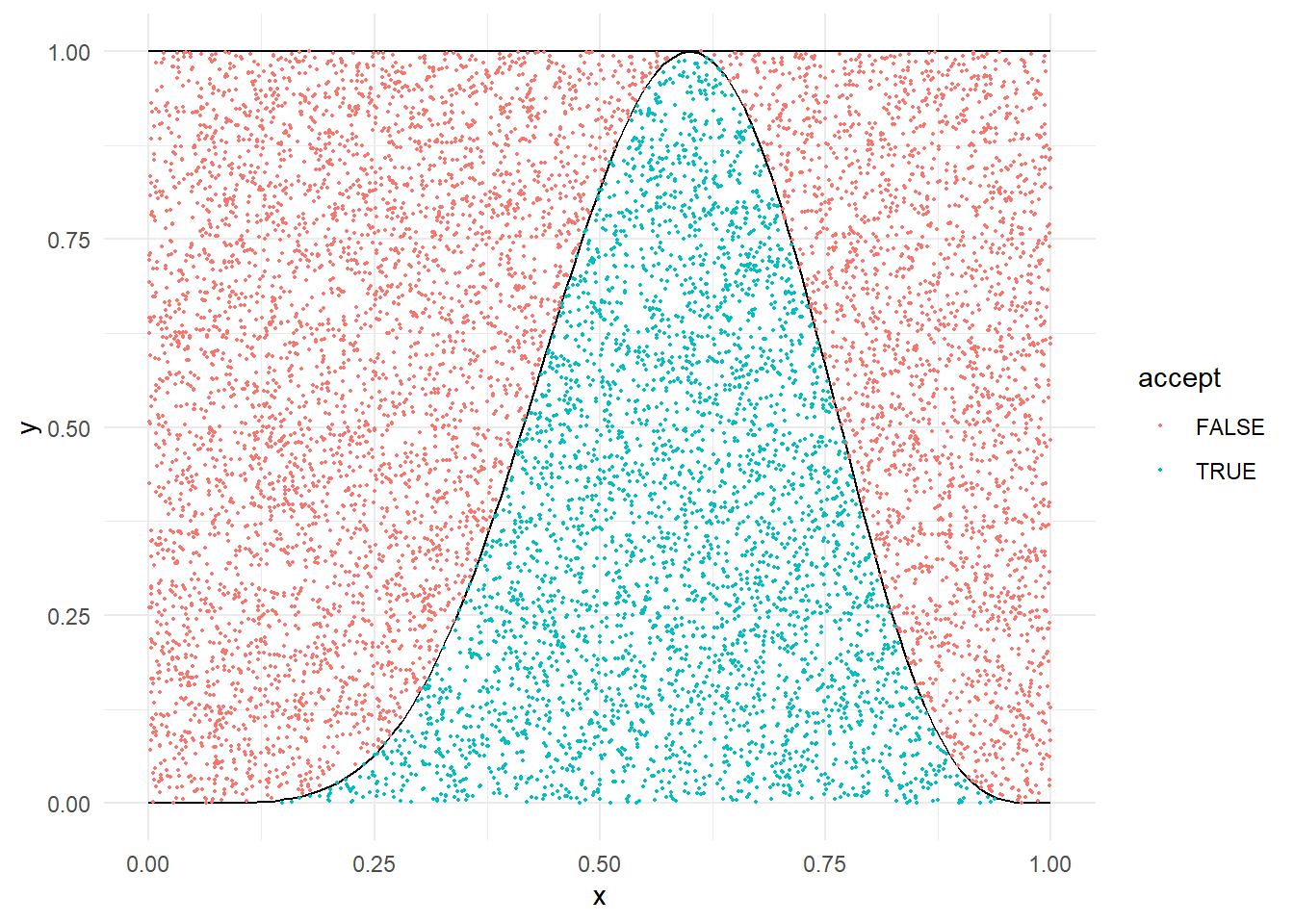

H εκτίμηση του \(B(7,5)\approx 0.0004329\) είναι εφικτή (όπως είδαμε) από το ποσοστό αποδοχής του Accept-Reject και ο αλγόριθμος έδωσε

AR[[2]]
## [1] 0.0004291748

Μπορεί να θεωρηθεί το παραγόμενο δείγμα ότι προέρχεται από την αντίστοιχη κατανομή Βήτα;

hist(AR[[1]], main = "Beta(7, 5) sample with Accept-Reject", freq = FALSE, col = "grey", breaks = 20)
curve(dbeta(x, 7, 5),  from = 0, to = 1, lty= 1, lwd = 1, col = "red", add = TRUE)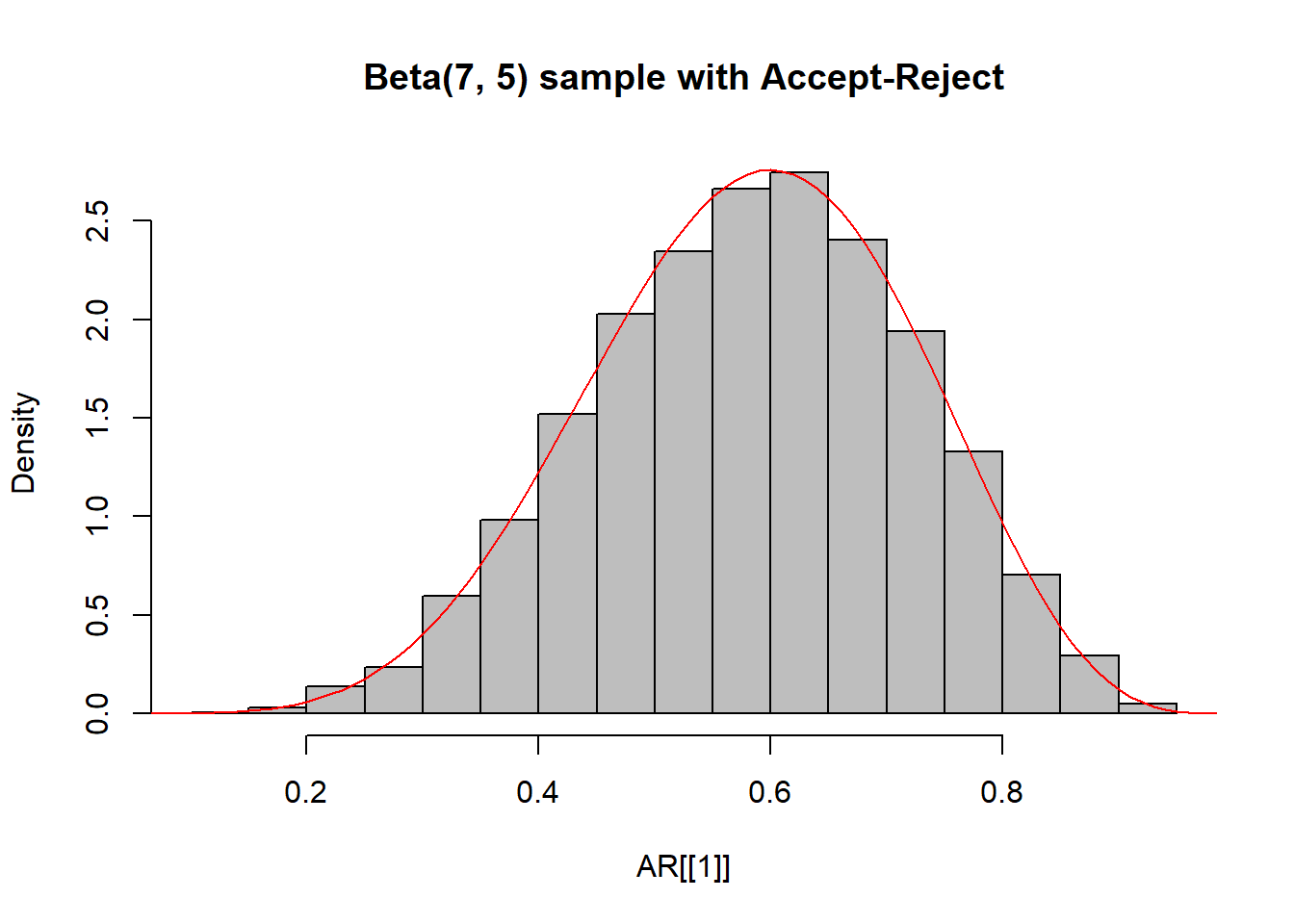

ks.test(AR[[1]],"pbeta", 7, 5)
## 
##  Asymptotic one-sample Kolmogorov-Smirnov test
## 
## data:  AR[[1]]
## D = 0.0087441, p-value = 0.429
## alternative hypothesis: two-sided

2.7 Ασκήσεις

Άσκηση 2.5 (Robert and Casella 2.18) Η παρακάτω “περίεργη” συνάρτηση πυκνότητας

\[\begin{equation*} f(x)\propto e^{-x^2/2} \cdot \left(\sin(6x)^2 +3 \cos(x)^2 sin(4x)^2 +1 \right), \end{equation*}\]

μπορεί να προσομοιωθεί χρησιμοποιώντας τον αλγόριθμο Αποδοχής - Απόρριψης.

1. Σχεδιάστε την \(f(x)\) και δείξτε ότι μπορούμε να τη φράξουμε από τη \(M g(x)\), όπου \(g\) είναι η σ.π.π. της τυπικής κανονικής \(g(x)=e^{-x^2/2}/\sqrt{2\pi}\). Βρείτε μία αποδεκτή, αν όχι βέλτιστη, τιμή για το \(M\) (Υπόδειξη: Χρησιμοποιήστε τη συνάρτηση optimise).

2. Προσομοιώστε 2500 τυχαίες παρατηρήσεις από την \(f\) χρησιμοποιώντας τον αλγόριθμο Αποδοχής - Απόρριψης.

3. Από το ποσοστό αποδοχής του αλγορίθμου εκτιμήστε τη σταθερά κανονικοποίησης της \(f\) και συγκρίνετε το ιστόγραμμα του τυχαίου δείγματος με την κανονικοποιημένη καμπύλη \(f\).

Λύση:

Θα σχεδιάσουμε τις συναρτήσεις \(c\cdot f\) και \(M\cdot g\), δίνοντας τη δυνατότητα στα \(c\) και \(M\) να μεταβάλλονται.

Παρατηρούμε ότι η \(f\) είναι δικόρυφη (το μέγιστο επιτυγχάνεται σε 2 διαφορετικές θέσεις) και για \(c=1\) βρίσκεται γενικά πάνω από τη \(g\). Επομένως, προκειμένου η \(f\) να ολοκληρώνει στη μονάδα, έχουμε ότι \(c<1\). Για \(c=1\) μπορούμε να βρούμε κατάλληλο \(M>1\) ώστε \(f<=M\cdot g\). Μπορούμε να βρούμε ένα τέτοιο \(M\) με τον παρακάτω κώδικα:

# target density
f <- function(x, c = 1) {
  c * exp(- x ^ 2 / 2) * (sin(6 * x) ^ 2 + 3 * cos(x) ^ 2 * sin(4 * x) ^ 2 + 1)
}

# candidate density N(0,1)
g <- function(x, M = 1) {
  M * exp(- x ^ 2 / 2) / sqrt( 2 * pi)
}

# ratio f/g
ratio <- function(x) {
  f(x) / g(x)
}

opt <- optimize(ratio, interval = c(-5, 5), maximum = TRUE)
M <- opt$objective
M
## [1] 10.94031

Σύμφωνα με τα παραπάνω, εργαζόμαστε με \(M=\) 10.9403062. Προσέχουμε ότι το \(M\) αυτό θα ήταν βέλτιστο αν η πραγματική τιμή της σταθεράς ήταν \(c=1\). Γνωρίζοντας όμως ότι είναι μικρότερη, το ίδιο ισχύει και για το βέλτιστο \(Μ\).

Είμαστε τώρα έτοιμοι να υλοποιήσουμε τον αλγόριθμο Αποδοχής - Απόρριψης.

y <- NULL
n <- 2500
trials <- 0

while (length(y) < n) {
  x <- rnorm(1)
  u <- runif(1)
  y <- c(y, x[u < f(x) / (M * g(x))])
  trials <- trials + 1
}

Έχοντας παράγει το δείγμα, θα εκτιμήσουμε τη σταθερά κανονικοποίησης

\[\begin{equation*} \hat{c}=\frac{1}{\hat{p}M}, \end{equation*}\]

όπου \(\hat{p}\) το ποσοστό αποδοχών.

acc <- n / trials
chat <- 1 / (acc * M)
acc ; chat
## [1] 0.544781
## [1] 0.1677832

Επομένως η κανονικοποιημένη f και το ιστόγραμμά της έχουν τη μορφή:

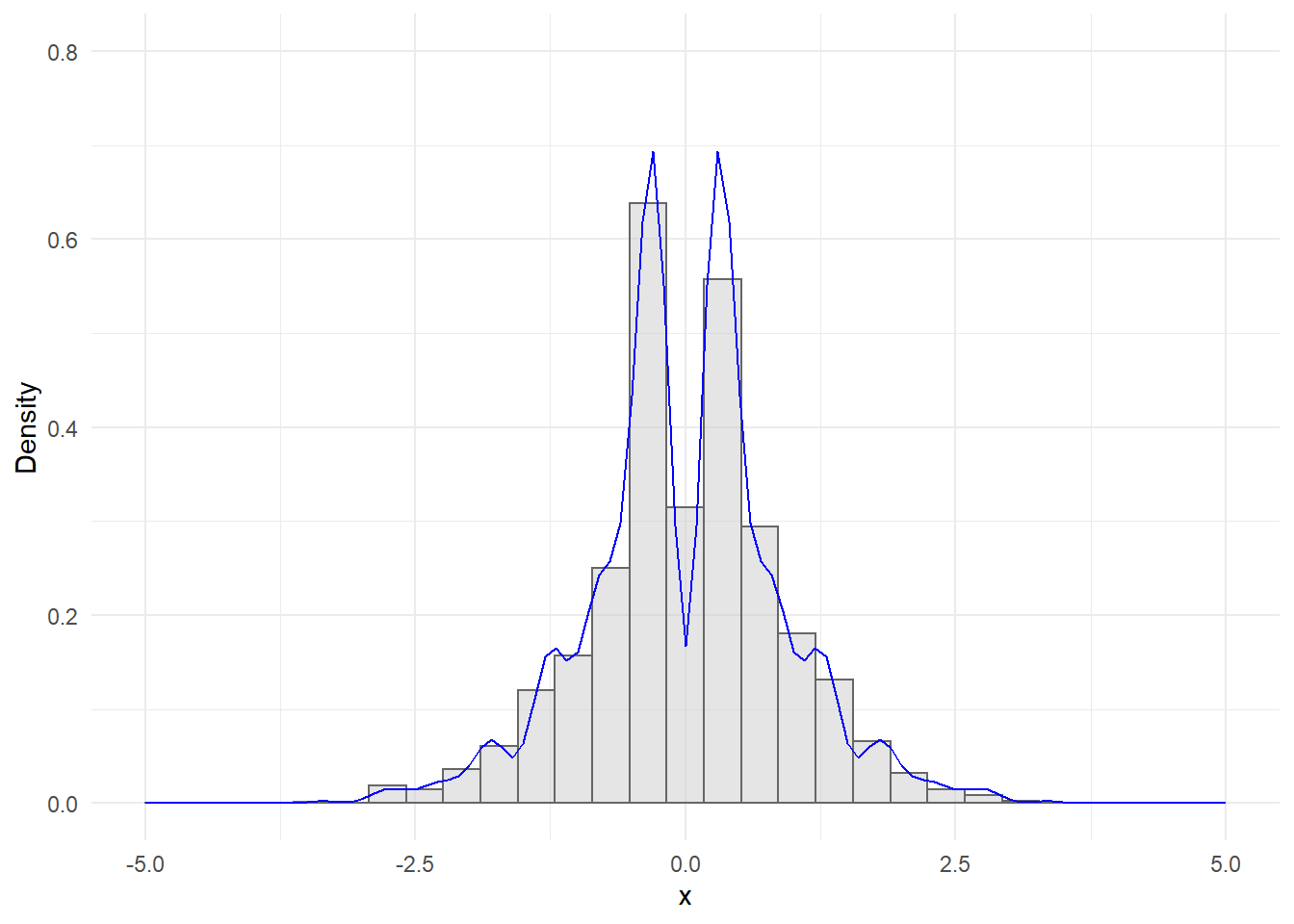
Άσκηση 2.6 (Robert and Casella 2.23) Έστω ότι έχουμε μία πυκνότητα \(f(x|\theta)\), όπου το \(\theta\) είναι η υπό εκτίμηση παράμετρος, και μία prior \(\pi(\theta)\). Αν παρατηρήσουμε \(x=(x_1, x_2, ..., x_n)\), τότε η posterior του \(\theta\) είναι:

\[\begin{equation*} \pi(\theta|x)=\pi(\theta|x_1, x_2, ..., x_n) \propto \prod_{i} f(x_i|\theta) \pi(\theta), \end{equation*}\]

όπου \(\prod_{i} f(x_i|\theta) = L(\theta|x_1, x_2, ..., x_n)\) είναι η συνάρτηση πιθανοφάνειας.

1. Αν \(\pi(\theta|x)\) είναι η πυκνότητα στόχος σε ένα αλγόριθμο Αποδοχής - Απόρριψης και αν \(\pi(\theta)\) είναι η υποψήφια πυκνότητα, δείξτε ότι το βέλτιστο φράγμα \(M\) είναι η συνάρτηση πιθανοφάνειας στο σημείο μέγιστης πιθανοφάνειας.

2. Για την εκτίμηση του \(\mu\) σε μία κανονική κατανομή, μία καλή prior (ανθεκτική στις ακραίες παρατηρήσεις) είναι η Cauchy. Για \(X_i \thicksim N(\theta, 1), \theta \thicksim C(0,1)\), η posterior είναι η

\[\begin{equation*} \pi(\theta|x)=\propto \frac{1}{\pi} \frac{1}{1+\theta^2} \prod_{i=1}^n e^{-(x_i-\theta)^2/2}. \end{equation*}\]

Θέστε \(\theta_0=3, n=10\) και προσομοιώστε \(X_1, X_2, ..., X_n \thicksim Ν(\theta_0, 1)\). Χρησιμοποιήστε τον αλγόριθμο Αποδοχής - Απόρριψης με την Cauchy \(C(0,1)\) ως υποψήφια πυκνότητα και προσομοιώστε ένα δείγμα από την posterior. Αξιολογήστε πόσο καλά εκτιμάται το \(\theta_0\). Πόσο βελτιώνεται η εκτίμηση καθώς το \(n\) αυξάνεται;

Λύση:

Αρχικά, ας γράψουμε την posterior στην πλήρη της μορφή:

\[\begin{equation*} \pi(\theta|x)= \frac{\prod_{i} f(x_i|\theta) \pi(\theta)}{\prod_{i} f(x_i)} = c_{post} \prod_{i} f(x_i|\theta) \pi(\theta) = c_{post} L(\theta| x) \pi(\theta), \ \theta \in S_\theta, \end{equation*}\]

θέτοντας \(c_{post}=\frac{1}{\prod_{i} f(x_i)}\).

Μας ενδιαφέρει να βρούμε ένα άνω φράγμα για το λόγο

\[\begin{equation*} \frac{\pi(\theta|x)}{\pi(\theta)} = c_{post} L(\theta| x), \ \theta \in S_\theta. \end{equation*}\]

Επομένως το βέλτιστο φράγμα επιτυγχάνεται για \(\theta=\arg\max_\theta L(\theta|x)\), δηλαδή για την ΕΜΠ \(\widehat{\theta}\).

Ας εφαρμόσουμε το παραπάνω στην εκτίμηση του \(\theta_0=3\) στο τυχαίο δείγμα κανονικών όταν προτείνουμε με prior κατανομή την Cauchy. Εδώ πρέπει να προσέξουμε ότι η ε.μ.π. \(\widehat{\theta}=\overline{x}\) είναι γνωστή και άρα \[\begin{equation*} M = L(\widehat{\theta})= (2\pi)^{-n/2} e^{-0.5\sum_{i=1}^{n}(x_i-\overline{x})^2} \end{equation*}\] Δημιουργούμε στην R όλα τα απαραίτητα στοιχεία:

# sample and mle
theta0 <- 3
n <- 10
x0 <- rnorm(n, mean = theta0, sd = 1)
mle <- mean(x0)
M <- prod(dnorm(x0, mean = mle, sd = 1))

Για να απαλλαγούμε προσωρινά από το \(c_{post}\) ορίζουμε την \(\widetilde{\pi}(\theta|x):\)

\[\begin{equation*} \pi(\theta|x)=c_{post}\widetilde{\pi}(\theta|x). \end{equation*}\]

Δημιουργούμε στην R την μη κανονικοποιημένη posterior της \(\pi(\theta|x)\), με αρχική τιμή \(c_{post}=1\) (δηλαδή \(\widetilde{\pi}(\theta|x)\)):

# posterior
post <- function(theta, x0, c = 1) {
  c * sapply(theta, function(theta) prod(dnorm(x0, mean = theta, sd = 1))) * dcauchy(theta) 
}

Είμαστε έτοιμοι να τρέξουμε τον αλγόριθμο:

# Accept - Reject
theta <- NULL
trials <- 0
size <- 5000

while(length(theta) < size){
  cand <- rcauchy(1, 0, 1)
  u <- runif(1)
  theta <- c(theta, cand[u < (post(cand, x0) / (M * dcauchy(cand)))])
  trials <- trials + 1
}

Μέσα από το ποσοστό αποδοχής εκτιμούμε τη σταθερά κανονικοποίησης

acc <- size / trials
chat <- 1 / (acc * M)
acc ; chat
## [1] 0.0213398
## [1] 4248986

Δημιουργούμε το γράφημα: