7 Δειγματολήπτες Gibbs

7.1 Εισαγωγή

Σε αυτό το κεφάλαιο θα διευρύνουμε το πλαίσιο των αλγορίθμων MCMC, μελετώντας μία άλλη κατηγορία τέτοιων μεθόδων, τους δειγματολήπτες Gibbs. Οι αλγόριθμοι αυτοί έχουν δύο πολύ σημαντικά χαρακτηριστικά. Πρώτον, η ρύθμισή τους εστιάζει στην πυκνότητα-στόχο και δεύτερον, μας επιτρέπουν να σπάσουμε ένα πολύπλοκο πρόβλημα (π.χ. κατανομή μεγάλης διάστασης, για την οποία ένας τυχαίος περίπατος Metropolis - Hastings θα ήταν σχεδόν αδύνατο να κατασκευαστεί) σε μία σειρά από ευκολότερα προβλήματα. Το αρνητικό που συχνά συνοδεύει τους δειγματολήπτες Gibbs είναι ότι αυτή η σειρά εύκολων προβλημάτων γενικά χρειάζεται αρκετή ώρα για να συγκλίνει.

7.2 Δειγματολήπτης Gibbs Δύο Σταδίων

Ας θεωρήσουμε δύο τυχαίες μεταβλητές \(X\) και \(Y\) με από κοινού συνάρτηση πυκνότητας \(f(x,y)\) και αντίστοιχες δεσμευμένες πυκνότητες \(f_{Y|X}, f_{X|Y}\). Ο δειγματολήπτης Gibbs δύο σταδίων δημιουργεί μία μαρκοβιανή αλυσίδα \((X_t, Y_t)\) από την απο κοινού κατανομή των \((X,Y)\) σύμφωνα με τα παρακάτω βήματα:

---

Αλγόριθμος Gibbs Δύο Σταδίων Παίρνουμε \(X_0=x_0\) Για \(t=1, 2, \dots\) προσομοιώνουμε

1. \(Y_t \sim f_{Y|X}(\cdot |x_{t-1})\),
2. \(X_t \sim f_{X|Y}(\cdot |y_t)\).

---

Παρατηρούμε λοιπόν ότι για την εφαρμογή του αλγορίθμου, χρειαζόμαστε τις δεσμευμένες συναρτήσεις πυκνότητας \(f_{Y|X}, f_{X|Y}\). Όταν η από κοινού συνάρτηση πυκνότητας είναι διαθέσιμη σε κλειστή μορφή, έως μία σταθερά κανονικοποίησης \(c\), το ίδιο ισχύει και για τις δεσμευμένες πυκνότητες. Εάν η άμεση προσομοίωση από τις δεσμευμένες σ.π. δεν είναι δυνατή, τότε μπορούμε να εφαρμόσουμε προσεγγίσεις Monte Carlo ή MCMC, όπως θα δούμε στην πορεία. Είναι επίσης εύκολο να δούμε ότι, αν η \((X_t, Y_t)\) προέρχεται από την \(f\), το ίδιο ισχύει και για την \((X_{t+1}, Y_{t+1})\), καθώς ο αλγόριθμος χρησιμοποιεί τις πραγματικές δεσμευμένες συναρτήσεις πυκνότητας. Η σύγκλιση της μαρκοβιανής αλυσίδας (και επομένως του αλγορίθμου) είναι λοιπόν βέβαιη, εκτός κι αν τα στηρίγματα των δεσμευμένων κατανομών δεν συνδέονται.

Παράδειγμα 7.1 (Robert & Casella 7.1.) Ας θεωρήσουμε το τυχαίο διάνυσμα \((X,Y)\) για το οποίο ισχύει \[\begin{equation*} (X,Y) \sim \mathcal{N}_2 \left(0, \left( \begin{array}{cc} 1 & p \\ p & 1 \end{array} \right) \right). \end{equation*}\]

Ένα βήμα του δειγματολήπτη Gibbs, για δεδομένο \(x_t\) έχει ως εξής: \[\begin{align*} Y_{t+1}|x_t &\sim \mathcal{N} (p x_t, 1-p^2), \\ X_{t+1}|y_{t+1} &\sim \mathcal{N} (p y_{t+1}, 1-p^2). \end{align*}\]

Επομένως, για την υποαλυσίδα \((X_t)_t\) ισχύει \[\begin{equation*} X_{t+1}|X_t=x_t \sim \mathcal{N} (p^2 x_t, 1-p^4), \end{equation*}\]

που αναδρομικά οδηγεί στο αποτέλεσμα \[\begin{equation*} X_{t+1}|X_0=x_0 \sim \mathcal{N} (p^{2t} x_0, 1-p^{4t}), \end{equation*}\] το οποίο τείνει στην κατανομή \(\mathcal{N}(0,1)\) καθώς το \(t\) τείνει στο άπειρο.

Όπως γίνεται εμφανές από το παραπάνω παράδειγμα, η ακολουθία \((X_t, Y_t)\) που προσομοιώνεται με το δειγματολήπτη Gibbs συγκλίνει στην από κοινό κατανομή \(f\) και επομένως, οι \(X_t\) και \(Y_t\) συγκλίνουν στις περιθώριες κατανομές τους.

Ίσως ο κύριος λόγος που οι δειγματολήπτες Gibbs έγιναν τόσο δημοφιλείς στην δεκαετία του 90 ως ο κατ’ εξοχήν αλγόριθμος MCMC, είναι η εφαρμογή τους στα ιεραρχικά μοντέλα, στα οποία μία από κοινού κατανομή ορίζεται μέσα από διαδοχικά στρώματα δεσμευμένων κατανομών. Το παρακάτω παράδειγμα αποτελεί μία εισαγωγή στα ιεραρχικά μοντέλα.

Παράδειγμα 7.2 (Robert & Casella 7.2.) Θεωρούμε το τυχαίο διάνυσμα \((X, \theta)\) για το οποίο ισχύει \[\begin{equation*} X|\theta \sim Bin(n, \theta), \ \theta\sim Be(a,b). \end{equation*}\] Η προκύπτουσα από κοινού συνάρτηση πυκνότητας είναι η \[\begin{equation*} f(x,\theta) = \left(\begin{array}{c} n \\ k \end{array} \right) \frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)} \theta^{x+a-1} (1-\theta)^{n-x+b-1}, \end{equation*}\] ενώ η δεσμευμένη κατανομή \(\theta|X=x\sim Be(x+a, n-x+b)\). Ο δειγματολήπτης Gibbs μπορεί να υλοποιηθεί ως εξής:

set.seed(1194)
nsim <- 10^4                        # initial values
n <- 15 ; a <- 3 ; b <- 7

X <- Th <- rep(0,nsim)                 # initialize the arrays

Th[1] <- rbeta(1, a, b)               # initialize the Theta chain
X[1] <- rbinom(1, n, Th[1])           # initialize the X     chain

for (i in 2:nsim){               # sampling loop
  X[i] <- rbinom(1, n, Th[i - 1])
  Th[i] <- rbeta(1, a + X[i], n - X[i] + b)
}

Όπως βλέπουμε στην εικόνα 7.1, τα δείγματα των \(X\) και \(\theta\) προσαρμόζονται πολύ καλά στις καμπύλες των περιθώριων πυκνοτήτων τους.

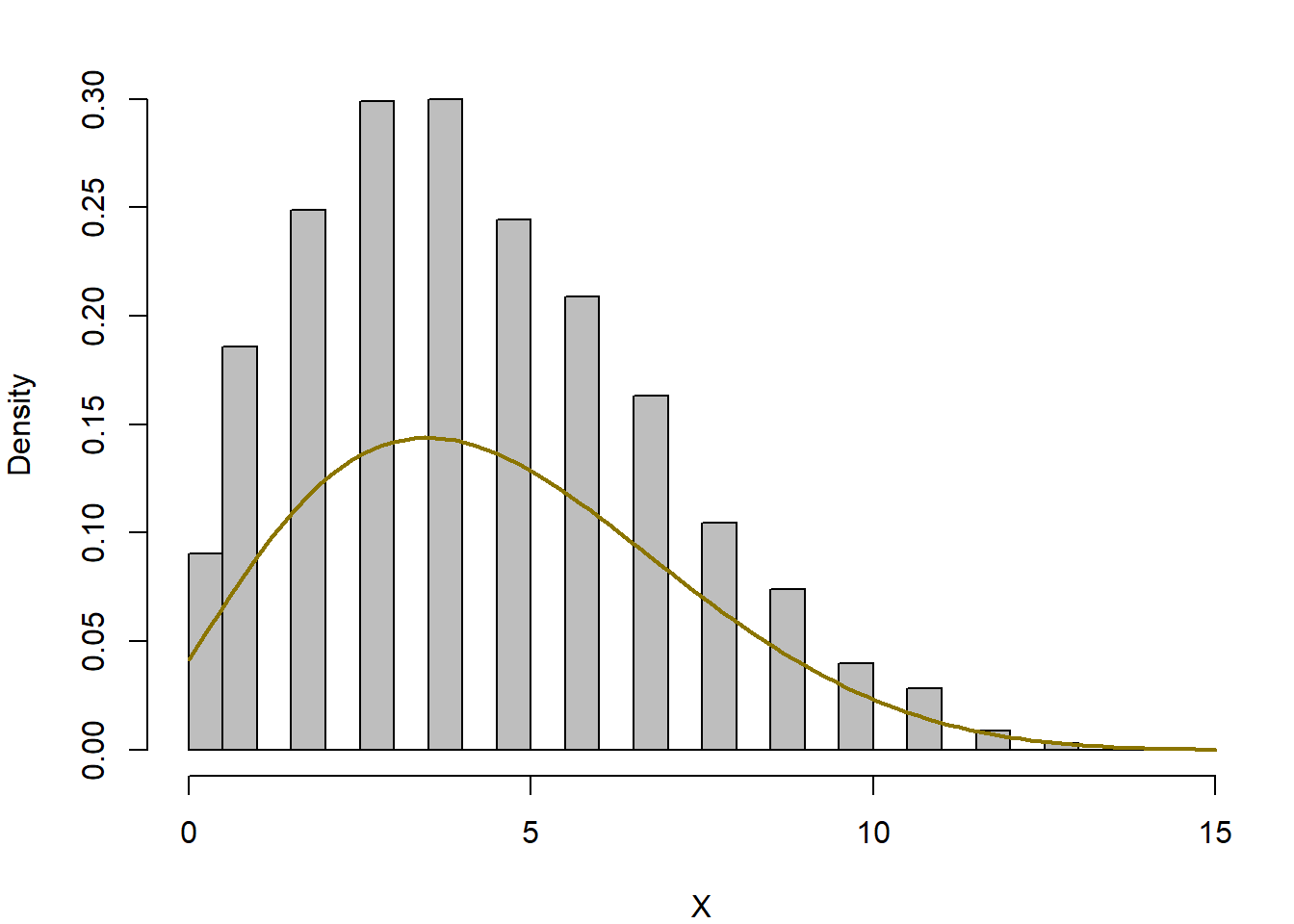
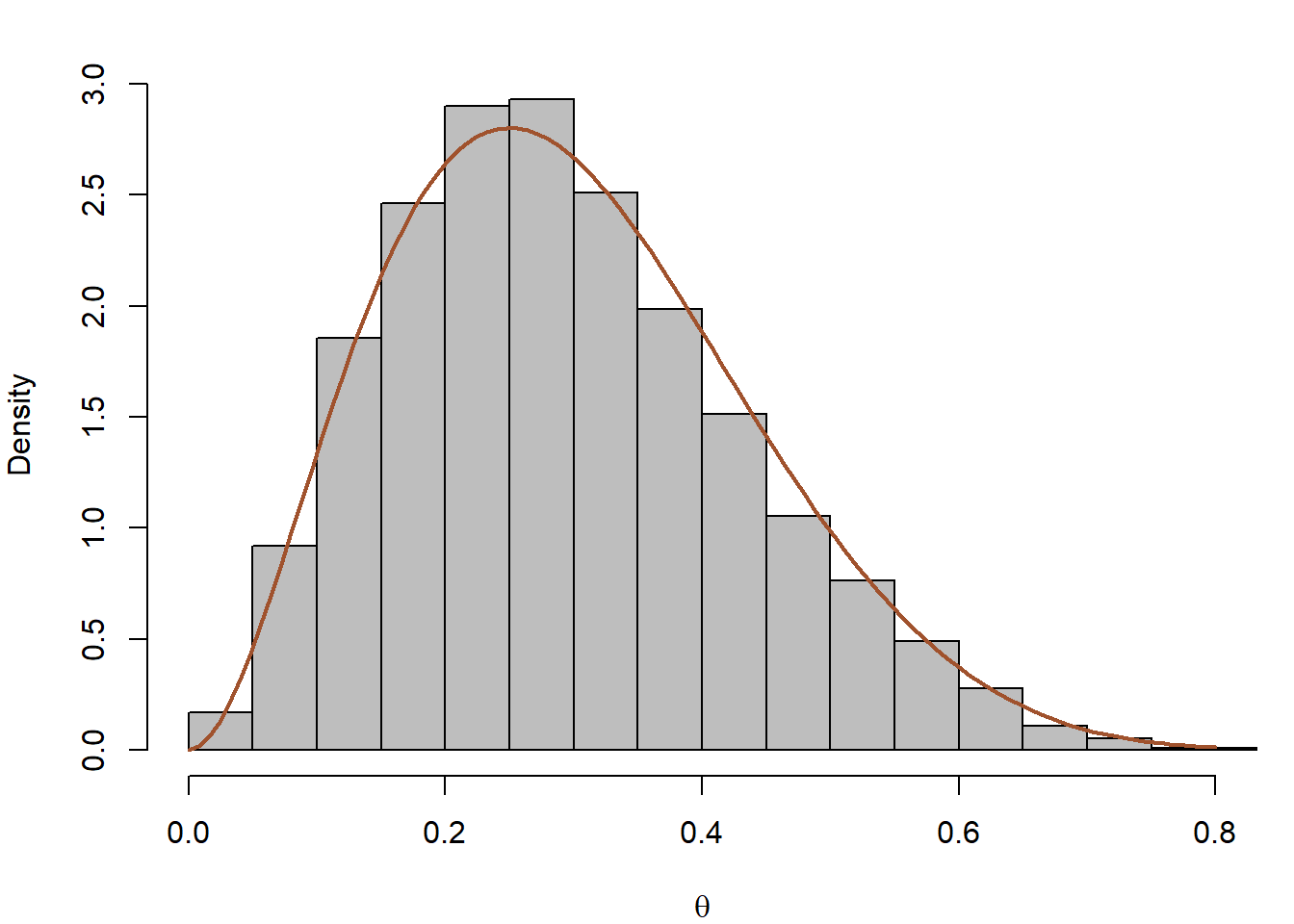
Εικόνα 7.1: Histograms of marginal distributions from the Gibbs sampler of Example 7.2 based on \(10^4\) iterations of the Gibbs sampler for \(n = 15, a = 3, b = 7\). The true marginal distribution of \(\theta\) is \(Be(a, b)\) and the marginal distribution of \(X\) is betabinomial.

Παράδειγμα 7.3 (Robert & Casella 7.3.) Θεωρούμε την posterior κατανομή των \((\theta, \sigma^2)\) του μοντέλου \[\begin{align*} X_i &\sim \mathcal{N}(\theta, \sigma^2), \ i=1, 2, \dots, n \\ \theta &\sim \mathcal{N}(\theta_0, \tau^2), \ \sigma^2 \sim IG(a,b), \end{align*}\]

όπου τα \(\theta_0, \tau^2, a, b\) είναι γνωστά, και με \(IG(a,b)\) συμβολίζουμε την αντιστραμμένη γάμμα κατανομή (δηλαδή \(1/\sigma^2\sim \Gamma(a,b)\)), με συνάρτηση πυκνότητας \[\begin{equation*} f(x) = \frac{1}{\Gamma (a)} b^a \left(\frac{1}{x}\right)^{a-1} e^{-b/x}. \end{equation*}\]

Γράφοντας \(x=(x_1, \dots, x_n)\), η posterior κατανομή του \((\theta, \sigma^2)\) δίνεται από την

\[\begin{equation*} f(\theta, \sigma^2 |x) \propto \left[ \frac{1}{\left(\sigma^2\right)^{n/2}}e^{-\sum_i (x_i-\theta)^2/(2\sigma^2)} \right] \times \left[ \frac{1}{\tau} e^{-(\theta-\theta_0)^2/(2\tau^2)}\right] \times \left[ \frac{1}{(\sigma^2)^{a-1}} e^{-b/\sigma^2} \right], \end{equation*}\]

από την οποία μπορούμε να βρούμε τις δεσμευμένες πυκνότητες του \(\theta\) και του \(\sigma^2\). Γράφοντας \(x=(x_1, \dots, x_n)\) έχουμε \[\begin{align*} \pi(\theta|x, \sigma^2) &\propto e^{-\sum_i (x_i-\theta)^2/(2\sigma^2)-(\theta-\theta_0)^2/(2\tau^2)} \\ \pi(\sigma^2|x, \theta) &\propto \left(\frac{1}{\sigma^2}\right)^{n/2+a-1} e^{-\frac{1}{2\sigma^2}\left(\sum_i (x_i-\theta)^2 \right)-b/sigma^2 }. \end{align*}\]

Οι πυκνότητες αυτές αντιστοιχούν στις κατανομές \[\begin{align*} \theta |x, \sigma^2 &\sim \mathcal{N}\left(\frac{\sigma^2}{\sigma^2+n\tau^2} \theta_0 +\frac{n\tau^2}{\sigma^2+n\tau^2} \overline{x}, \frac{\sigma^2\tau^2}{\sigma^2+n\tau^2} \right), \\ \sigma^2|x, \theta &\sim IG\left( \frac{n}{2} +a, \frac{1}{2} \sum_i (x_i-\theta)^2 +b \right), \end{align*}\] όπου το \(\overline{x}\) είναι ο δειγματικός μέσος των παρατηρήσεων, καθώς στον δειγματολήπτη Gibbs χρησιμοποιούνται οι πλήρεις δεσμευμένες κατανομές.

Μία μελέτη του μεταβολισμού σε γυναίκες ηλικίας 15 ετών έδωσε τα παρακάτω δεδομένα πρόσληψης ενέργειας μέσα σε 24 ώρες, μετρημένα σε Mega Joule.

x <- c(91,504,557,609,693,727,764,803,857,929,970,1043,1089,1195,1384,1713)

Χρησιμοποιώντας το παραπάνω κανονικό μοντέλο, με το \(\theta\) να αντιστοιχεί στην πραγματική μέση πρόσληψη ενέργειας, ο δειγματολήπτης Gibbs μπορεί να υλοποιηθεί ως

n <- length(x) ; nsim <- 10 ^ 4
a <- b <- 3 ; tau2 <- 10 ; theta0 <- 5
xbar <- mean(x) ; sh1 <- (n / 2) + a
sigma <- theta <- rep(0, nsim)                  #init arrays
sigma[1] <- 1 / rgamma(1, shape = a, rate = b)      #init chains
B <- sigma[1] / (sigma[1] + n * tau2)
theta[1] <- rnorm(1, m = B * theta0 + (1 - B) * xbar, sd = sqrt(tau2 * B))

for (i in 2:nsim){
  B <- sigma[i - 1] / (sigma[i - 1] + n * tau2)
  theta[i] <- rnorm(1, m = B * theta0 + (1 - B) * xbar, sd = sqrt(tau2 * B))
  ra1 <- (1 / 2) * (sum((x - theta[i]) ^ 2)) + b
  sigma[i] <- 1/rgamma(1, shape = sh1, rate = ra1)
}

όπου τα theta0, tau2, a, b, είναι προκαθορισμένες τιμές. Ο posterior δειγματικός μέσος του \(\theta\) και του \(\sigma\) είναι 5.3639 και 7.0477706^{5}, αντίστοιχα. Στην εικόνα 7.2 βλέπουμε τα ιστογράμματα των posterior κατανομών των \(\log (\theta)\) και \(\log(\sigma)\).

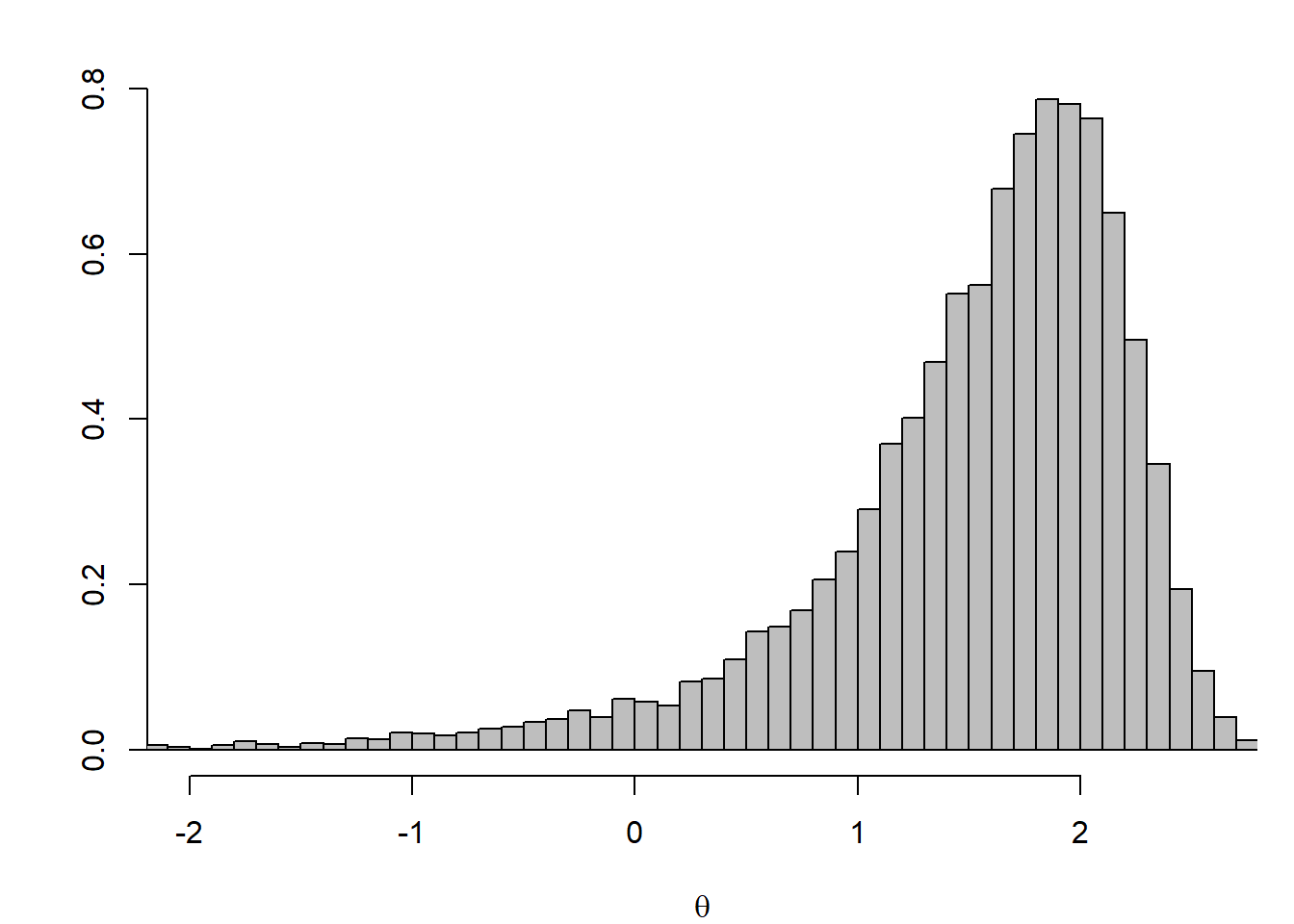
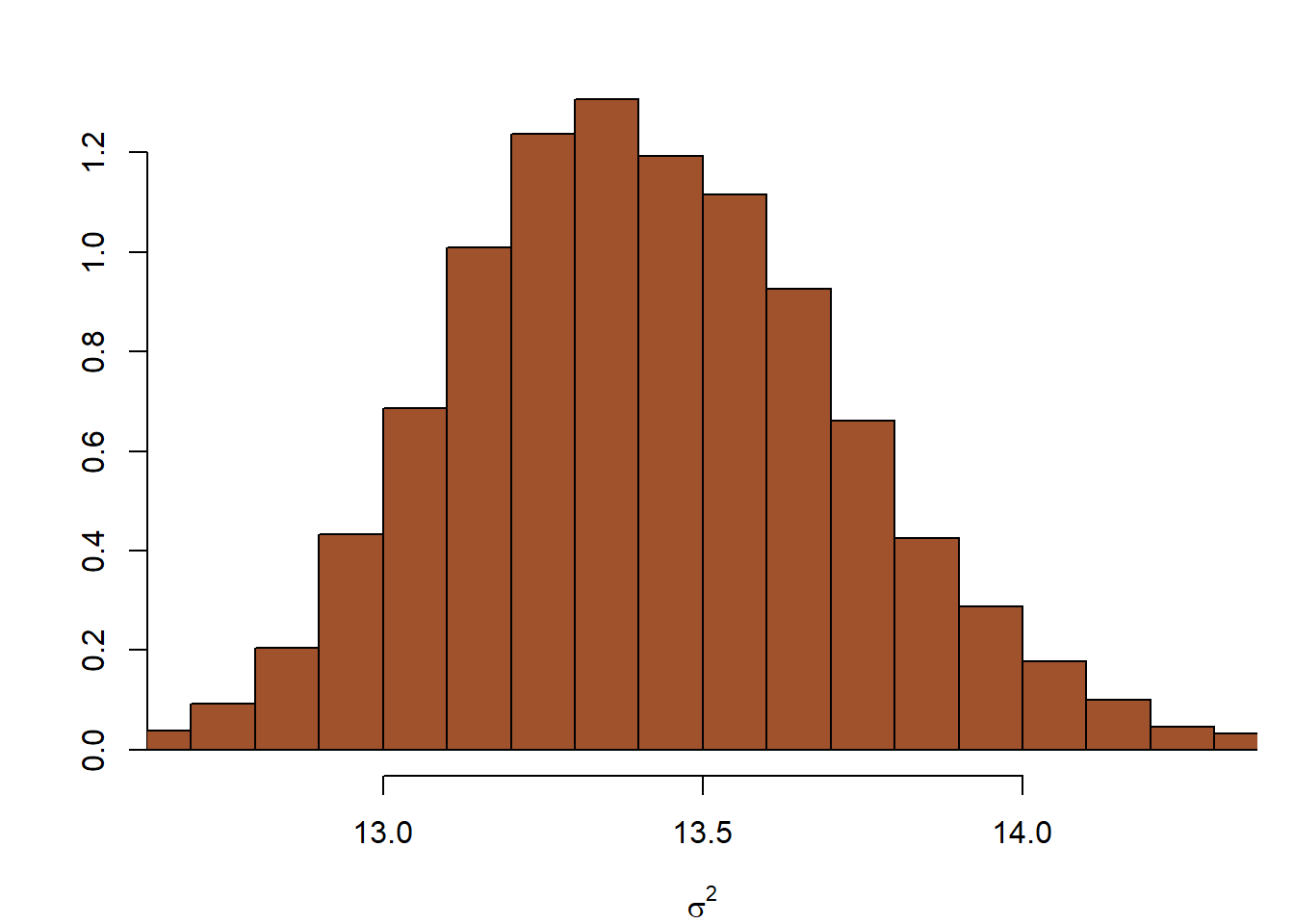
Εικόνα 7.2: Histograms of marginal posterior distributions of the log-mean and log-standard deviation from the Gibbs sampler of Example 7.3 based on 5000 iterations, with \(a = b = 3, \tau^2 = 10\) and \(\theta_0 = 5\). The 90% interval for \(\log(\theta)\) is \((6.299, 6.960)\) and for \(\log(\sigma)\) it is \((0.614, 1.029)\)

Σε αυτό το σημείο καλό είναι να τονιστεί πως το να αναγνωρίσουμε τις πλήρεις δεσμευμένες κατανομές από μία από κοινού κατανομή δεν είναι τόσο δύσκολο. Για παράδειγμα, η posterior κατανομή ανάλογη της \(f(\theta, \sigma^2|x)\) προκύπτει πολλαπλασιάζοντας τις πυκνότητες \(f(x|\theta, \sigma), f(\theta)\) και \(f(\sigma^2)\). Για να βρούμε μία πλήρη δεσμευμένη κατανομή (δηλαδή, τη κατανομή μίας παραμέτρου δεσμευμένη ως προς όλες τις άλλες), απλά επιλέγουμε τους όρους της από κοινού πυκνότητας που περιλαμβάνουν την εν λόγω παράμετρο. Για παράδειγμα, βλέπουμε ότι \[\begin{align*} f(\theta| \sigma^2, x) &\propto \left[ \frac{1}{\left(\sigma^2\right)^{n/2}}e^{-\sum_i (x_i-\theta)^2/(2\sigma^2)} \right] \times \left[ \frac{1}{\tau} e^{-(\theta-\theta_0)^2/(2\tau^2)}\right], \\ f(\theta, \sigma^2 |x) &\propto \left[ \frac{1}{\left(\sigma^2\right)^{n/2}}e^{-\sum_i (x_i-\theta)^2/(2\sigma^2)} \right] \times \left[ \frac{1}{(\sigma^2)^{a-1}} e^{-b/\sigma^2} \right]. \end{align*}\]

Είναι επομένως εύκολο να δούμε ότι η πλήρης δεσμευμένη της \(\sigma^2\) είναι μία αντιστραμμένη γάμμα κατανομή. Για το \(\theta\), παρότι χρειάζονται κάποιες πράξεις, μπορούμε να δούμε ότι η πλήρης δεσμευμένη θα είναι κανονική.