1 Εισαγωγή
H προσομοίωση δεδομένων και η χρήση αριθμητικών μεθόδων αποτελούν απαραίτητα εργαλεία στατιστικών αναλύσεων και έτσι ένας σύγχρονος στατιστικός πρέπει να έχει μία καλή εξοικείωση με τις πιο βασικές μεθόδους. Στο επόμενο κεφάλαιο γίνεται μία εισαγωγή σε μεθόδους προσομοίωσης. Θα πρέπει επίσης να γίνει σαφές από την αρχή, ότι η χρήση έτοιμων συναρτήσεων από τα βασικά πακέτα της R, ή από πακέτα που μπορούν να εγκατασταθούν σε μεταγενέστερο χρόνο θα πρέπει να προτιμάται, τουλάχιστον όταν αυτό που θέλουμε να κάνουμε είναι γενικού σκοπού, και υπάρχουν ήδη έτοιμες συναρτήσεις της R. Δίνουμε ένα παράδειγμα σε αυτήν την κατεύθυνση που αφορά τον υπολογισμό της τετραγωνικής ρίζας ενός αριθμού. Όπως σε κάθε προγραμματιστικό περιβάλλον, έτσι και εδώ, αναμένουμε η R να μπορεί να κάνει αυτήν την εργασία αρκετά αποτελεσματικά και γρήγορα. Παρόλα αυτά, ενώ θα ήταν μη αποδοτικό να προσπαθήσουμε να ανταγωνιστούμε την R στον υπολογισμό αυτό με μία δική μας συνάρτηση, είναι χρήσιμο πολλές φορές να ξεκινάμε την εκμάθηση με πολύ απλά παραδείγματα, ώστε να κατανοούμε κάποιες καινούριες μεθόδους (γενικού σκοπού) που μαθαίνουμε και να επαληθεύουμε ότι λειτουργούν σωστά σε περιπτώσεις που υπάρχει ήδη άλλη μέθοδος που κάνει την ίδια δουλειά πιο αποδοτικά σε ένα συγκεκριμένο παράδειγμα.
1.1 Παράδειγμα Αριθμητικής Επίλυσης
Παράδειγμα 1.1 Θέλουμε να υπολογίσουμε την τετραγωνική ρίζα ενός θετικού αριθμού \(p\). Αναζητούμε δηλαδή τη θετική λύση της εξίσωσης \(x^2=p\). Μία μέθοδος γενικού σκοπού για την εύρεση ριζών μίας συνάρτησης είναι η μέθοδος του Νεύτωνα, γνωστή και ως μέθοδος Newton-Raphson. Η μετατροπή του αρχικού προβλήματος, σε ένα πρόβλημα εύρεσης ριζών κατάλληλης συνάρτησης γίνεται άμεσα. Θέτουμε
\[\begin{equation} f(x)=x^2-p, \end{equation}\]
και η λύση του αρχικού προβλήματος μετατρέπεται σε ένα πρόβλημα εύρεσης της θετικής λύσης της εξίσωσης \(f(x)=0\).
## Warning: Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
## ℹ Please use `linewidth` instead.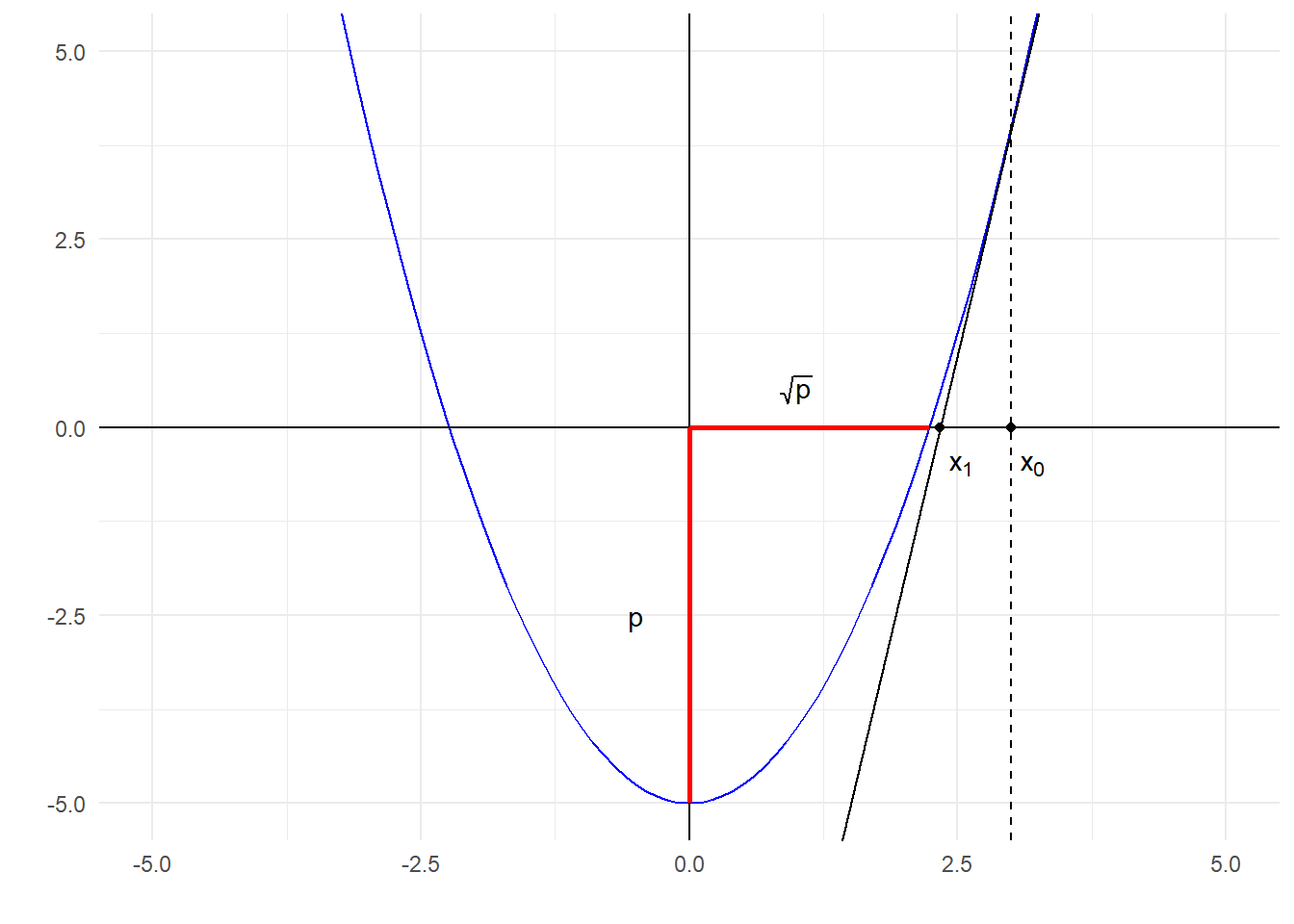
Η ιδέα που βρίσκεται στη βάση κατασκευής του αλγορίθμου Newton-Raphson είναι η δυνατότητα ικανοποιητικής γραμμικής προσέγγισης της εν λόγω συνάρτησης σε μία περιοχή που περιλαμβάνει τη ρίζα της.
Αν \(x_0\) είναι ένα αρχικό σημείο εντός αυτής της περιοχής, τότε
\[\begin{equation} f(x)\cong f(x_0) +f'(x_0)(x-x_0). \end{equation}\]
Επομένως, αντί να λύσουμε την εξίσωση \(f(x)=0\), λύνουμε την:
\[\begin{equation*} f(x_0) +f'(x_0)(x-x_0) = 0. \end{equation*}\]
Yποθέτοντας λοιπόν ότι \(f'(x_0)\neq 0\), επιλέγουμε ως επόμενο σημείο το
\[\begin{equation} x_1 = x_0 - \frac{f(x_0)}{f'(x_0)}, \end{equation}\]
και επαναλαμβάνοντας τη διαδικασία γραμμικών προσεγγίσεων της \(f\) στα σημεία που παίρνουμε κάθε φορά, καταληγούμε στον εξής αναδρομικό ορισμό της ακολουθίας:
\[\begin{equation} x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}, \quad \forall n\geq 0. \end{equation}\]
Αν εφαρμόσουμε τον αλγόριθμο αυτό στο παράδειγμα εύρεσης της τετραγωνικής ρίζας, τότε με \(f'(x)=2x\), καταλήγουμε στην αναδρομή:
\[\begin{equation} x_{n+1} = x_n - \frac{x^2_n-p}{2x_n} = \frac{x_n+\frac{p}{x_n}}{2}. \end{equation}\]
Μπορούμε τώρα να δημιουργήσουμε μία συνάρτηση στην R, η οποία υλοποιεί τη μέθοδο του Νεύτωνα και υπολογίζει την τετραγωνική ρίζα ενός θετικού αριθμού με συγκεκριμένη ακρίβεια.
sqrnt <- function(p, tol = 1e-5){
x <- p / 2
y <- (x + p / x) / 2
while (abs(y - x) > tol) {
x <- y
y <- (x + p / x) / 2
}
y
}
sqrnt(2)
## [1] 1.414214Το κριτήριο τερματισμού που αντιστοιχεί στον παραπάνω αλγόριθμο αφορά την απόσταση μεταξύ δύο διαδοχικών όρων της ακολουθίας. Στην περίπτωση που ο αλγόριθμος συγκλίνει, τότε και η απόσταση των διαδοχικών όρων \(|x_{n+1}-x_n|\) συγκλίνει στο \(0\). Είναι επίσης δυνατό να χρησιμοποιηθεί ένα κριτήριο τερματισμού που στηρίζεται στις τιμές της αρχικής συνάρτησης \(f(x)\).
sqrnt2 <- function(p, tol = 1e-5){
x <- p / 2
while (abs(x * x - p) > tol) {
x <- (x + p / x) / 2
}
x
}
sqrnt2(2)
## [1] 1.414216Θα πρέπει βέβαια να σημειωθεί ότι γενικότερα σε κάποιον αλγόριθμο μπορούμε να συνδυάζουμε και τα 2 κριτήρια, απαιτώντας ο αλγόριθμος να σταματά όταν και οι 2 συνθήκες παύουν να ισχύουν. Αυτό θα δίνει μία περαιτέρω εγγύηση στο ότι μικρές αποστάσεις διαδοχικών όρων, δε σημαίνει κατ’ανάγκη ότι έχουμε καλή προσέγγιση της λύσης.
Στο σημείο αυτό αξίζει να σημειώσουμε την ανταλλαγή ακρίβειας-ταχύτητας που αποτελεί γενικό χαρακτηριστικό των υπολογιστικών μεθόδων. Καθώς αυξάνεται η ακρίβεια της προσέγγισης που απαιτούμε από τον αλγόριθμο, ελαττώνεται η ταχύτητα διεκπεραίωσης της εργασίας που έχει αναλάβει το πρόγραμμα, αυξάνοντας έτσι το συνολικό χρόνο ολοκλήρωσης του προγράμματος.
Στη συνάρτηση που κατασκευάσαμε έχουμε επιτρέψει τον έλεγχο της ακρίβειας του αλγορίθμου Newton-Raphson μέσα από το όρισμα tol, με αρχική τιμή \(10^{-5}\). Ας ζητήσουμε από την R να τρέξει τη συνάρτηση με διαφορετικές ακρίβειες και να τις χρονομετρήσει. Σε αυτό θα μας βοηθήσει το πακέτο microbenchmark, που τρέχει μία συνάρτηση πολλές φορές και υπολογίζει βασικά στατιστικά όπως ο μέσος χρόνος εκτέλεσης.
library(microbenchmark)
microbenchmark(sqrnt(2, tol = 1e-1), times = 10000, unit = 'ns')
## Unit: nanoseconds
## expr min lq mean median uq max neval
## sqrnt(2, tol = 0.1) 500 600 668.76 600 700 47100 10000
microbenchmark(sqrnt(2, tol = 1e-3), times = 10000, unit = 'ns')
## Unit: nanoseconds
## expr min lq mean median uq max neval
## sqrnt(2, tol = 0.001) 700 800 866.99 800 900 22600 10000
microbenchmark(sqrnt(2, tol = 1e-10), times = 10000, unit = 'ns')
## Unit: nanoseconds
## expr min lq mean median uq max neval
## sqrnt(2, tol = 1e-10) 800 900 987.46 900 1000 19400 10000
#print.microbenchmark to display and boxplot.microbenchmark or autoplot.microbenchmark to plot the results.Πράγματι, καθώς αυξάνουμε την επιθυμητή ακρίβεια, αυξάνεται και ο χρόνος εκτέλεσης. Οι διαφορές βέβαια εδώ είναι πολύ μικρές, καθώς ο αλγόριθμος αυτός έχει μεγάλη ταχύτητα σύγκλισης. Θα επανέλθουμε στο σημείο αυτό αργότερα.
Έχοντας δημιουργήσει τη συνάρτηση, είμαστε έτοιμοι να κάνουμε τη σύγκριση με την έτοιμη εντολή της R για τον υπολογισμό της τετραγωνικής ρίζας.
sqrnt(2) # our function
## [1] 1.414214
sqrt(2) # base R function
## [1] 1.414214Οι δύο συναρτήσεις φαίνεται να παράγουν το ίδιο αποτέλεσμα. Αυτό είναι σωστό, μέχρι την ακρίβεια που καθορίσαμε. Για να συγκρίνουμε τις δύο προσεγγίσεις, μπορούμε να εμφανίσουμε περισσότερα ψηφία από τα 6 που εμφανίζει by default η R και να εμφανίσουμε και τα 20 πραγματικά δεκαδικά ψηφία του \(\sqrt{2}\)
format(sqrnt(2),nsmall = 20)
## [1] "1.41421356237468986983"
format(sqrt(2),nsmall = 20)
## [1] "1.41421356237309514547"
1.41421356237309504880
## [1] 1.414214H προσέγγιση της R είναι σωστή μέχρι και το 15ο ψηφίο και βλέπουμε ότι ο αλγόριθμος πέτυχε σωστά τα 11 πρώτα. Αυτό δεν είναι περίεργο, καθώς η προσέγγιση στα 5 που ζητήσαμε αποτελεί την ελάχιστη ακρίβεια που εμείς επιζητάμε. Η τελευταία επανάληψη του αλγορίθμου που προκύπτει όταν για πρώτη φορά θα ικανοποιηθεί το κριτήριο τερματισμού (της ζητούμενης ακρίβειας), μπορεί να οδηγήσει σε αριθμό που έχει αρκετά καλύτερη ακρίβεια από αυτήν που θέσαμε. Αυτό είναι εμφανές σε αυτό το παράδειγμα. Αν από την άλλη, αυξήσουμε την ακρίβεια, π.χ., στα 18 ψηφία, τότε έχουμε αντίστοιχα
format(sqrnt(2, tol = 1e-18), nsmall = 20)
## [1] "1.41421356237309492343"
format(sqrt(2), nsmall = 20)
## [1] "1.41421356237309514547"
1.41421356237309504880
## [1] 1.414214φτάνοντας στο όριο των 15 ψηφίων, όσο μπορεί δηλ. και η R. Ας συγκρίνουμε τώρα τους χρόνους εκτέλεσης των δύο αλγορίθμων:
microbenchmark(sqrnt(2, tol = 1e-12), unit = "ns")
## Unit: nanoseconds
## expr min lq mean median uq max neval
## sqrnt(2, tol = 1e-12) 900 1000 1142 1000 1100 9000 100
microbenchmark(sqrt(2), unit = "ns")
## Unit: nanoseconds
## expr min lq mean median uq max neval
## sqrt(2) 0 0 50 0 100 1200 100Βλέπουμε πως η συνάρτηση που φτιάξαμε είναι πιο αργή στο μέσο χρόνο εκτέλεσης από την έτοιμη συνάρτηση της R. Επιπλέον, προγραμματιστικά δεν είναι πλήρης, αφού είναι πολύ πιθανό να μην λειτουργήσει με τον επιθυμητό τρόπο σε όλα τα σενάρια που μπορεί να προκύψουν. Για παράδειγμα, αν τρέξουμε τις παρακάτω γραμμές κώδικα, θα δούμε πως η συνάρτησή μας παγιδεύεται μέσα στο while και δε σταματά ποτέ.
sqrnt(-1)
sqrt(-1)Μπορούμε βέβαια να τροποποιήσουμε τη συνάρτηση για να χειριστούμε κάποια σημεία που είναι προβληματικά.
1.2 Παράδειγμα Επίλυσης με Monte-Carlo
Το βασικό αντικείμενο μελέτης του Σεμιναρίου είναι η επίλυση προβλημάτων με τεχνικές Monte-Carlo. Σε αντίθεση με τη ‘ντετερμινιστική’ αριθμητική επίλυση ενός προβλήματος που είδαμε στο προηγούμενο παράδειγμα, οι μέθοδοι Monte-Carlo επιλύουν στοχαστικά ένα πρόβλημα. Έτσι, αν ο αλγόριθμος επαναληφθεί κάτω από τις ίδιες αρχικές συνθήκες (με διαφορετικό σπόρο (seed) βέβαια), τότε το αποτέλεσμα θα είναι γενικά διαφορετικό. Στο ακόλουθο παράδειγμα γίνεται μία εκτίμηση του αριθμού \(\pi\). Είναι φανερό ότι αν γίνεται τυχαία επιλογή σημείων εντός ενός τετραγώνου \(T\) με πλευρά 2 και \(K\) είναι ο εγγεγραμμένος κύκλος του τετραγώνου \(T\) (άρα ακτίνας 1), τότε αναμένουμε το ποσοστό των σημείων που πέφτουν μέσα στον κύκλο να είναι περίπου \[\begin{equation*} \lambda = \frac{\text{Εμβ}(K)}{\text{Εμβ}(T)}=\frac{\pi}{4}, \end{equation*}\]
όσο και ο λόγος των εμβαδών του κύκλου προς το τετράγωνο. Για να συμβεί βέβαια αυτό θα πρέπει το πλήθος των σημείων που έχουν επιλεγεί τυχαία να είναι επαρκώς μεγάλο. Αυτό το σημείο χρειάζεται προσοχή, καθώς ναι μεν ο υπολογιστής μας δίνει τη δυνατότητα να προσομοιώνουμε ένα πολύ μεγάλο πλήθος αριθμών από μία κατανομή ενδιαφέροντος, αλλά η ακρίβεια με την οποία θέλουμε να εκτιμήσουμε μία ποσότητα παίζει ρόλο καθοριστικό για το αν η χρήση των υπολογιστικά εντατικών μεθόδων Monte-Carlo μπορεί να δώσει μία ικανοποιητική απάντηση στο πρόβλημα που μας απασχολεί. Είναι φανερό ότι για καλές προσεγγίσεις του \(\pi\), με αρκετά δεκαδικά ψηφία, η χρήση στοχαστικών αλγορίθμων δεν ενδείκνυται, αλλά παρ’όλα αυτά η προσέγγιση του \(\pi\) με Monte-Carlo παραμένει διδακτικά ενδιαφέρουσα. H εκτίμηση \(\widehat{\pi}\) του \(\pi\) θα δίνεται τελικά από τη σχέση \(\widehat{\pi}=4\widehat{\lambda}\), όπου \(\widehat{\lambda}\) αντιστοιχεί στο ποσοστό των σημείων που βρίσκονται στο εσωτερικό του κύκλου. Ο παρακάτω αλγόριθμος υλοποιεί την εκτίμηση του \(\pi\).
set.seed(102)
N <- 1e4
radius <- 1
side <- 2 * radius
x <- runif(N, -radius, radius)
y <- runif(N, -radius, radius)
inside <- sqrt(x ^ 2 + y ^ 2) <= radius
percent <- sum(inside) / N
pi2 <- 4 * percent
pi2
## [1] 3.1556
pi
## [1] 3.141593Παρατηρούμε ότι όταν το μέγεθος του Monte-Carlo δείγματος είναι \(10^4\), τότε η ακρίβεια εκτίμησης του \(\pi\) είναι περίπου \(10^{-2}\). Μπορείτε να επαναλάβετε την εκτίμηση του \(\pi\) με διαφορετικούς σπόρους (είτε απλά να ξανατρέξετε πολλές φορές τον παραπάνω κώδικα, αγνοώντας την πρώτη γραμμή), ώστε να διαπιστώσετε ότι οι εκτιμήσεις διαφοροποιούνται. Αυτό είναι ένα βασικό χαρακτηριστικό των στοχαστικών αλγορίθμων. Το αποτέλεσμά τους αλλάζει κάθε φορά που επαναλαμβάνουμε το πείραμα. Για το λόγο αυτό, το αποτέλεσμα είναι τυχαία μεταβλητή.
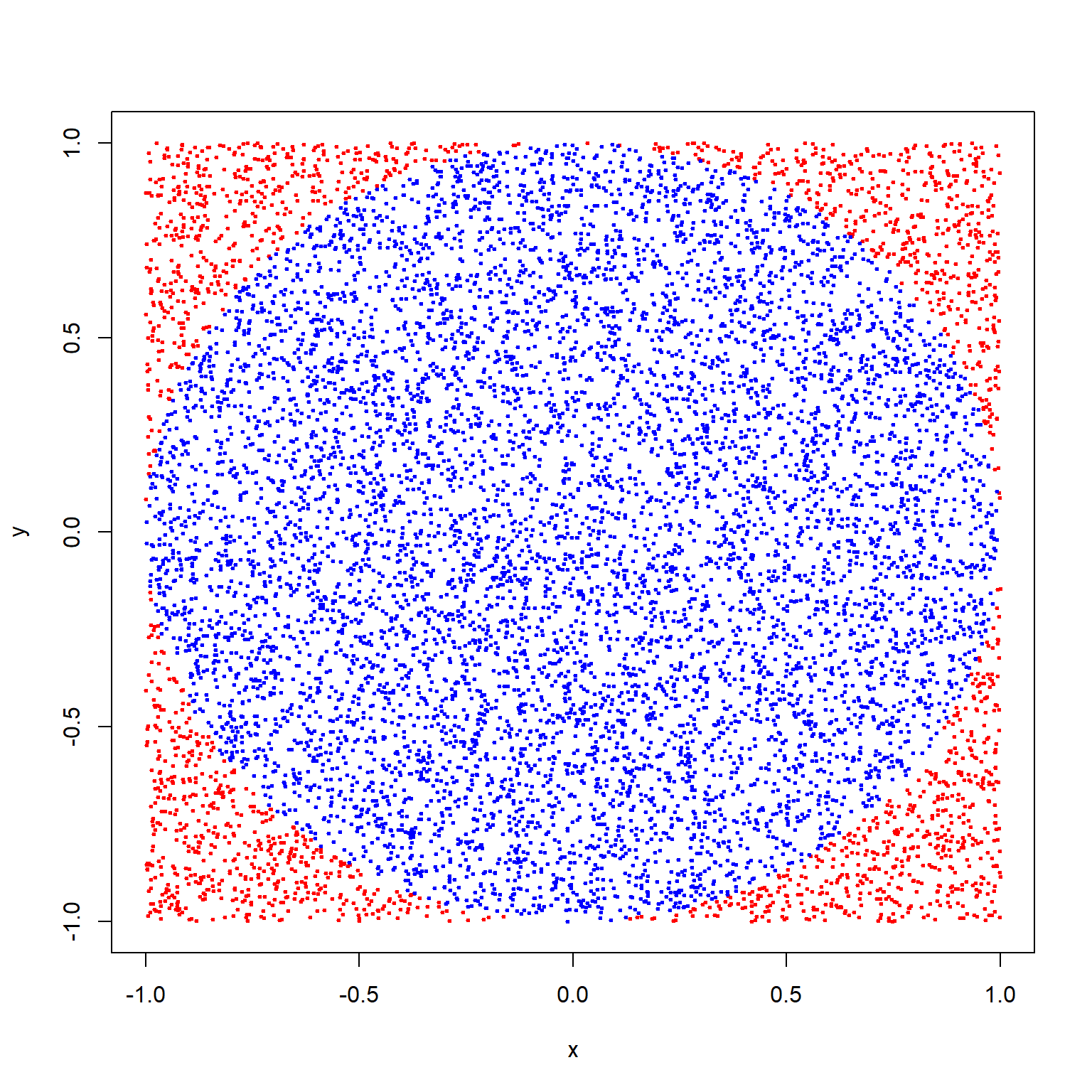
Στο παρακάτω σχήμα απεικονίζεται γραφικά η παραγωγή τυχαίων σημείων. Όσα σημεία έχουν μπλε χρώμα ικανοποίησαν τη συνθήκη ότι η απόστασή τους από το κέντρο του κύκλου ήταν μικρότερη (ή ίση) από την ακτίνα, ενώ αντίθετα όσα έχουν κόκκινο χρώμα δεν ικανοποίησαν τη συνθήκη.
Για μία καλύτερη εκτίμηση του \(\pi\) θα χρειαστεί βέβαια να αυξήσουμε το μέγεθος του δείγματος.
N <- 1e6
x <- runif(N, -radius, radius)
y <- runif(N, -radius, radius)
inside <- sqrt(x ^ 2 + y ^ 2) <= radius
percent <- sum(inside) / N
area <- percent * side ^ 2
pi2 <- area / radius ^ 2
pi2
## [1] 3.13904
pi
## [1] 3.141593Παρατηρούμε ότι όταν το μέγεθος του Monte-Carlo δείγματος είναι \(10^6\), τότε η ακρίβεια εκτίμησης του \(\pi\) είναι περίπου \(10^{-3}\). Θα μπορούσε να σκεφτεί λοιπόν κάποιος, αν συνδυάσει και το αποτέλεσμα για μέγεθος δείγματος \(10^4\), ότι όσο μεγαλώνει το μέγεθος του δείγματος, τόσο καλύτερα προσεγγίζουμε το \(\pi\) και μάλιστα για μέγεθος δείγματος \(N\), η ακρίβεια της εκτίμησης είναι κοντά στο \(1/\sqrt{N}\). Η πρώτη παρατήρηση θα αιτιολογηθεί αργότερα από τον Ισχυρό Νόμο των Μεγάλων Αριθμών και η δεύτερη από το Κεντρικό Οριακό Θεώρημα, που είναι τα σημαντικότερα αποτελέσματα της Θεωρίας Πιθανοτήτων.
Μπορείτε να επαναλάβετε πάλι την εκτίμηση κάποιες φορές για να διαπιστώσετε ακόμα μία φορά τη ‘στοχαστικότητα’ του αποτελέσματος. Για να γίνετε πιο αποδοτικοί, απλά φτιάξτε μία συνάρτηση εκτίμησης του \(\pi\) με κατάλληλα ορίσματα, συμπεριλαμβάνοντας ως όρισμα και το μέγεθος του δείγματος, αλλά και το πλήθος των επεναλήψεων που θέλετε.