4 Μέθοδοι Ελέγχου Σύγκλισης
4.1 Αποτίμηση της Monte Carlo Μεταβλητότητας
Είναι σημαντικό να κατανοήσουμε πως υπάρχει ένας απλός και άμεσος τρόπος να αξιολογήσουμε τη μεταβλητότητα μιας ακολουθίας εκτιμήσεων Monte Carlo, και αυτός είναι να προσομοιώσουμε αρκετές ανεξάρτητες ακολουθίες. Η μέθοδος αυτή, παρότι θεωρητικά απλή, είναι ιδιαίτερα χρονοβόρα και υπολογιστικά απαιτητική. Αυτό είναι κάτι που θα συναντάμε συχνά στην προσομοίωση Monte Carlo, ότι δηλαδή η πολυπλοκότητα εκτίμησης της μεταβλητότητας μίας εκτιμήτριας είναι μεγαλύτερη από τη μελέτη της σημειακής της συμπεριφοράς.
Παράδειγμα 4.1 (Robert & Casella 4.1) Υπενθυμίζουμε το παράδειγμα Robert & Casella 3.3, όπου εκτιμήσαμε το ολοκλήρωμα της
\[\begin{equation*} h(x)=\left[cos(50x)+sin(20x)\right]^2, \end{equation*}\]
στο \(\left[ 0, 1 \right]\) (Εικόνα 4.1).
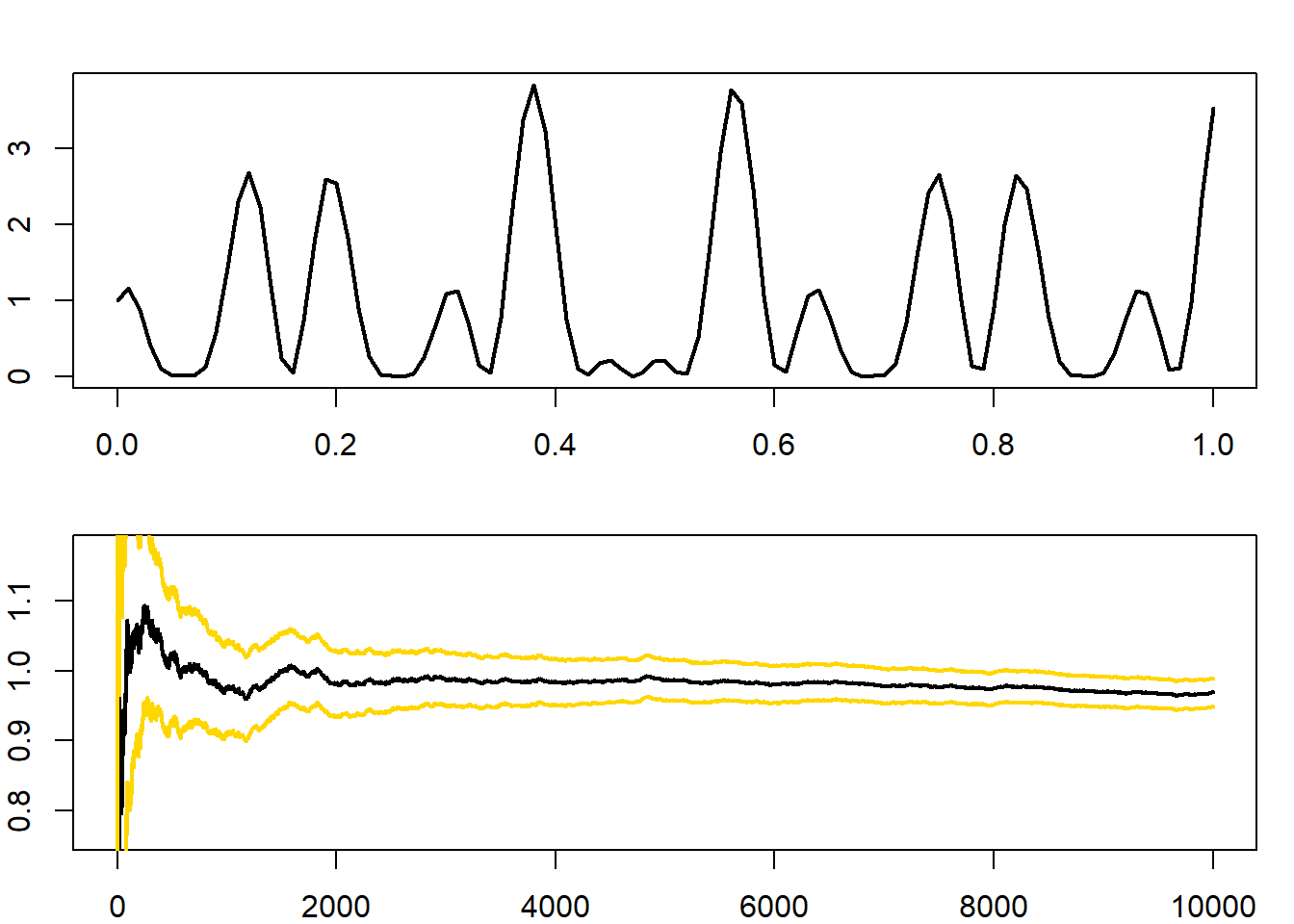
Εικόνα 4.1: (Up) Plot of the h function. (Down) Monte Carlo estimation of the integral, along with the 95% confidence interval based on asymptotic normality.
Επαναλαμβάνουμε την εκτίμηση αυτή, προσομοιώνοντας όχι ένα, αλλά πολλά ανεξάρτητα δείγματα, κάθε ένα μεγέθους \(10^4\). Με αυτά, δημιουργούμε το \(95\%\) ποσοστημοριακό εύρος, δηλαδή το διάστημα \((q_{0.025}, q_{0.975})\) μέσα στο οποίο συγκεντρώνονται το \(95\%\) των τιμών της εκτιμήτριας \(\overline{h(X)}_n\). Αξίζει ιδιαίτερη προσοχή στη διαφορά ανάμεσα στο ποσοστημοριακό εύρος, το οποίο δημιουργείται από ένα μεγάλο αριθμό ανεξάρτητων προσομοιωμένων δειγμάτων και στηρίζεται στην εμπειρική κατανομή του δειγματικού μέσου \(\overline{h(X)}_n\), για κάθε \(n\), και στο ασυμπτωτικό \(95\%\) διάστημα εμπιστοσύνης, το οποίο δημιουργείται από ένα μοναδικό προσομοιωμένο δείγμα και στηρίζεται στην ασυμπτωτική κανονικότητα του δειγματικού μέσου \(\overline{h(X)}_n\), καθώς \(n\rightarrow +\infty\). Επομένως, το διάστημα εμπιστοσύνης επηρεάζεται από τη μεταβλητότητα του ενός δείγματος από το οποίο κατασκευάστηκε.
Προσομοιώνουμε \(10^4\) μονοπάτια και συγκρίνουμε το ασυμπτωτικό \(95\%\) διάστημα εμπιστοσύνης στο πρώτο προσομοιωμένο μονοπάτι \(\left(\overline{h(X_{n,1})}-z_{0.025}\frac{\widehat{\sigma}}{n}, \overline{h(X_{n,1})}+z_{0.025}\frac{\widehat{\sigma}}{n}\right)\) με τα διαστήματα που δημιουργούνται από 200 και \(10^4\) ανεξάρτητα δείγματα, όπως περιγράφηκε παραπάνω.
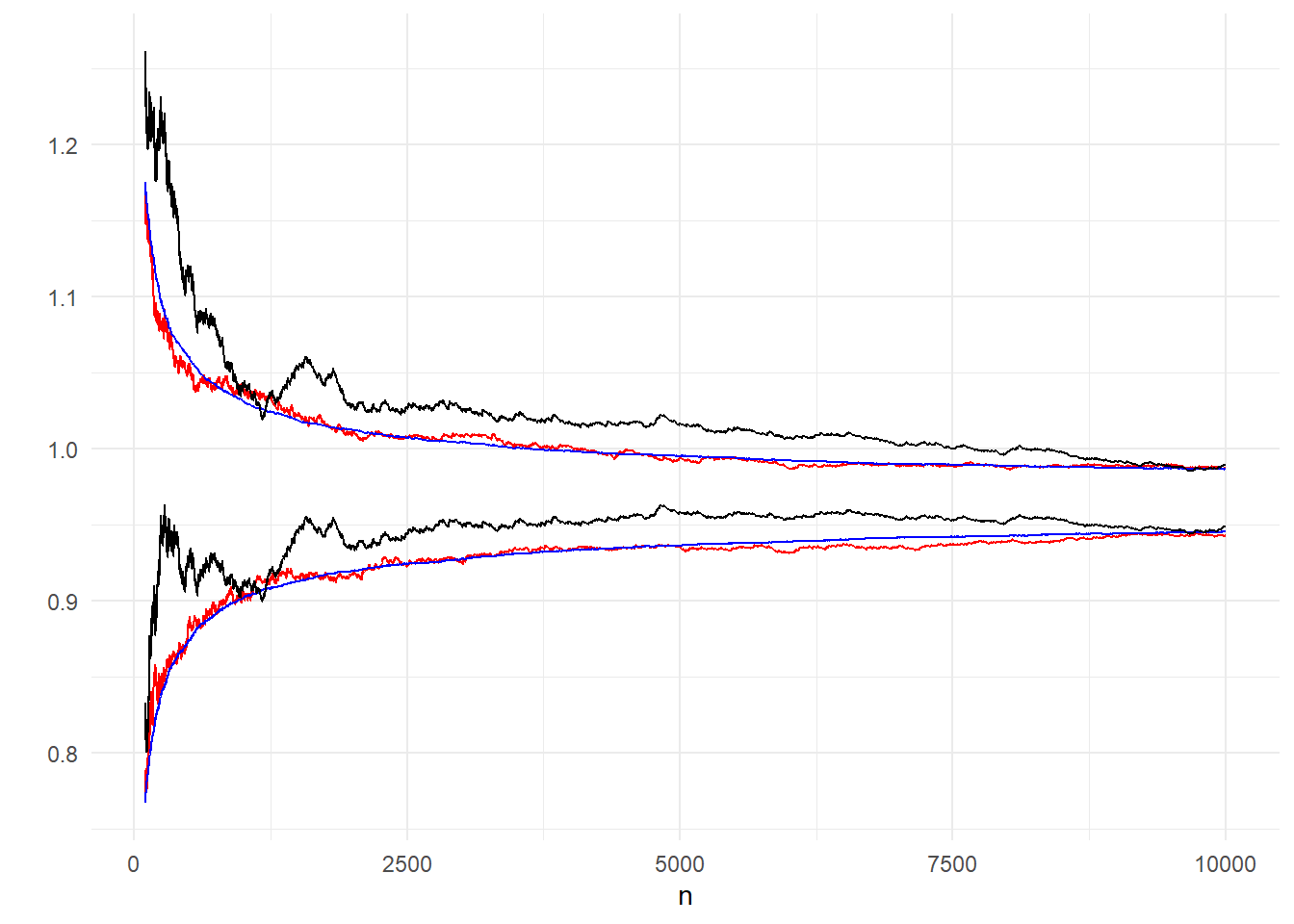
Εικόνα 4.2: Comparison of the 95% inter-quantile range from 200 (red), 10000 (blue) independent paths and 95% confidence interval from one path, based on asymptotic normality (black).
Στην εικόνα 4.2 φαίνεται μία αισθητή διαφορά ανάμεσα στο ασυμπτωτικό διάστημα εμπιστοσύνης, το οποίο είναι επηρεασμένο από τα σφάλματα του πρώτου μονοπατιού, με τα άλλα δύο που δημιουργήθηκαν από ανεξάρτητα μονοπάτια, οδηγώντας σε μικρότερο σφάλμα. Καθώς το μέγεθος \(n\) αυξάνεται, το διάστημα που παράγεται από 200 ανεξάρτητα μονοπάτια έρχεται πολύ κοντά στο διάστημα των \(10^4\) ανεξάρτητων μονοπατιών και αποτελεί μία καλή προσέγγιση.
Στο παραπάνω παράδειγμα συγκρίναμε το διάστημα \((q_{0.025}, q_{0.975})\) που προκύπτει από μία μη παραμετρική εκτίμηση 200 μονοπατιών με το παραμετρικό διάστημα ενός μόνο μονοπατιού. Εναλλακτικά, μπορούμε να κατασκευάσουμε ένα παραμετρικό διάστημα χρησιμοποιώντας και τα 200 μονοπάτια, αφού γνωρίζουμε πως καθώς το μέγεθος του δείγματος \(n\) αυξάνει, η κατανομή του Monte Carlo σφάλματος συγκλίνει στην κανονική. Συγκεκριμένα, για ένα σταθερό \(n\) παίρνουμε τον δειγματικό μέσο των \(s\) μονοπατιών \(Y_n=\frac{1}{s}\sum_{j=1}^s X_{n,j}\) και χρησιμοποιούμε την ασυμπτωτική κανονικότητα του δειγματικού μέσου \(\overline{Y_{n}}\) για να πάρουμε το διάστημα \(\left(\overline{Y_{n}}-z_{0.025}\frac{\widehat{\sigma}}{n}, \overline{Y_{n}}+z_{0.025}\frac{\widehat{\sigma}}{n}\right)\).
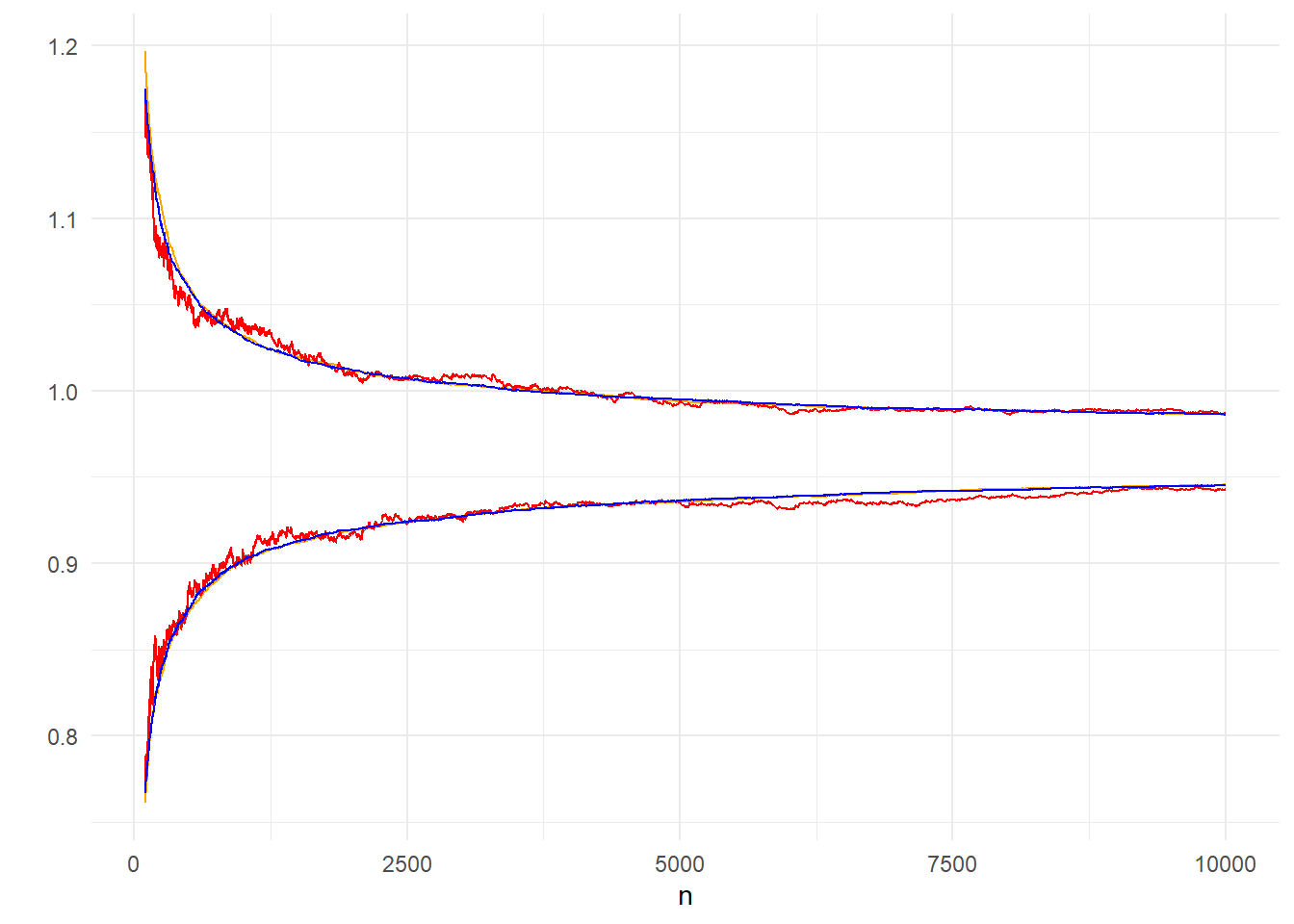
Εικόνα 4.3: Comparison of 95% CI of 200 paths (orange) based on asymptotic normality and 95% inter-quantile range of 200 (red) and 10000 (blue) paths.
Στην εικόνα 4.3 είναι εμφανές πως η ποιότητα της παραμετρικής εκτίμησης είναι καλύτερη, ήδη από μικρά \(n\). Επομένως, αν έχουμε 200 μονοπάτια, προτιμούμε την παραμετρική προσέγγιση από την μη-παραμετρική. Αυτό οφείλεται στην καλή προσέγγιση της κανονικής κατανομής από μικρά \(n\), κάτι που μπορεί να ελεγχθεί και με ένα έλεγχο κανονικότητας.
Μία διαφορετική μέθοδος εκτίμησης της μεταβλητότητας, χρησιμοποιώντας μόλις μία προσομοιωμένη ακολουθία, είναι το bootstrap, το οποίο εφαρμόζει επαναδειγματοληψία σε ένα ήδη υπάρχον δείγμα για να δημιουργήσει τον επιθυμητό αριθμό ακολουθιών. Έτσι, μπορούμε να παράγουμε μόλις ένα μονοπάτι και από αυτό να δημιουργήσουμε με Bootstrap τα 200 μονοπάτια που θέλουμε για τον υπολογισμό των δειγματικών ποσοστημορίων.
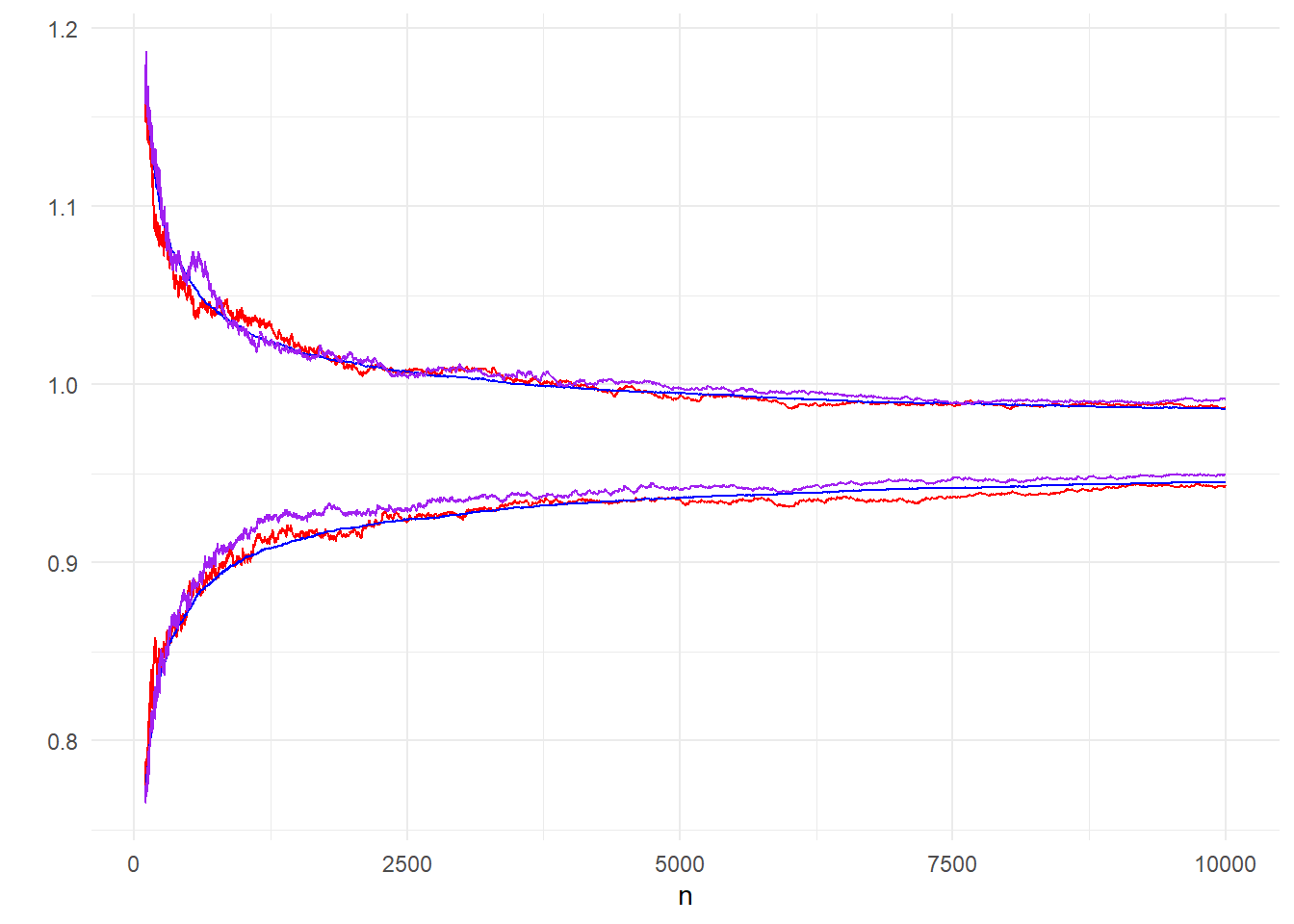
Εικόνα 4.4: Comparison of 95% inter-quantile ranges made from 200 bootstrap paths (purple), 200 (red) and 10000 (blue) independent paths.
Στην εικόνα 4.4 γίνεται φανερό ότι το bootstrap μας οδηγεί σε αντίστοιχα αποτελέσματα με αυτά που πήραμε με τα ανεξάρτητα μονοπάτια Monte Carlo και επομένως θα λέγαμε ότι είναι προτιμητέο.
Επιπλέον, με τα Bootstrap μονοπάτια μπορούμε να δημιουργήσουμε παραμετρικά διαστήματα εμπιστοσύνης στηριζόμενοι στην ασυμπτωτική κανονικότητα της εκτιμήτριας, ακριβώς όπως πριν. Έτσι αναπαράγουμε την εικόνα 4.3 με τα αντίστοιχα Bootstrap μονοπάτια, αντιπαραβάλοντας τα διαφορετικά διαστήματα εμπιστοσύνης που παίρνουμε μέσω Bootstrap, από μόλις ένα προσομοιωμένο μονοπάτι.
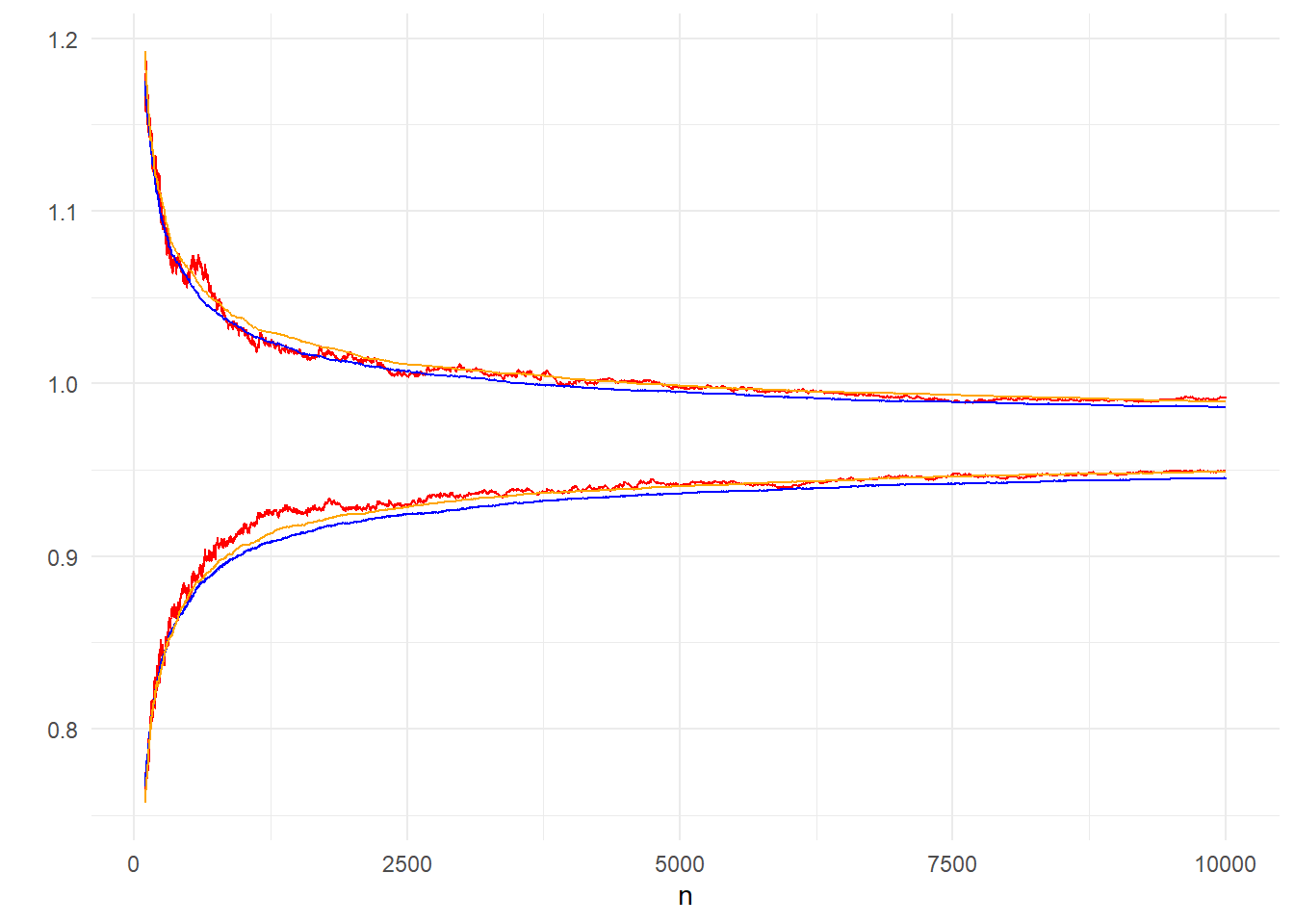
Εικόνα 4.5: Comparison of 95% CI (orange), 95% inter-quantile range (red) from 200 bootstrap paths and inter-quantile range from 10000 (blue) independent paths.
Η εικόνα 4.5 των διαστημάτων από 200 Bootstrap μονοπάτια μας οδηγεί σε τελείως ανάλογα συμπεράσματα με την 4.4 των διαστημάτων από 200 ανεξάρτητα μονοπάτια, με το παραμετρικό διάστημα εμπιστοσύνης να επιτυγχάνει πολύ καλές προσεγγίσεις ήδη από μικρά \(n\).
Στο παραπάνω παράδειγμα δεν είναι εμφανής ο λόγος για τον οποίο κάποιος θα προτιμούσε το bootstrap αντί της προσομοίωσης παράλληλων αλυσίδων, διότι το υπολογιστικό κόστος είναι συγκρίσιμο. Παρ’ όλα αυτά, σε πιο πολύπλοκα προβλήματα, η δημιουργία παράλληλων αλυσίδων μπορεί να είναι υπολογιστικά πολύ πιο ακριβή από την επαναδειγματοληψία ενός υπάρχοντος δείγματος.
4.2 Ασυμπτωτική Διασπορά Εκτιμητριών Σπουδαιότητας
Παράδειγμα 4.2 (Robert & Casella 4.2) Θεωρούμε μία τ.μ. \(X\sim \mathcal{N}(\theta,1)\), με prior \(\theta\sim\mathcal{C}(0,1)\), καθώς και μία παρατήρηση \(x=2.5\).
Σε αυτή την περίπτωση έχουμε posterior πυκνότητα
\[\begin{equation*} f(\theta|x)=\frac{\frac{1}{1+\theta^2} e^{-(x-\theta)^2/2}}{\int_{-\infty}^{+\infty} \frac{1}{1+\theta^2} e^{-(x-\theta)^2/2}}, \end{equation*}\]
δηλαδή posterior μέση τιμή
\[\begin{equation*} \delta(x)=\frac{\int_{-\infty}^{+\infty} \frac{\theta}{1+\theta^2} e^{-(x-\theta)^2/2} d\theta}{\int_{-\infty}^{+\infty} \frac{1}{1+\theta^2} e^{-(x-\theta)^2/2} d\theta}. \end{equation*}\]
Επομένως, μία προσέγγιση του \(\delta(x)\) βασισμένη στην προσομοίωση ανεξάρτητων και ισόνομων \(\theta_1, \theta_2, \dots, \theta_n \sim\mathcal{N}(x,1)\) είναι η
\[\begin{equation*} \widehat{\delta}(x)=\frac{\sum_{i=1}^{n} \frac{\theta_i}{1+\theta_i^2}}{\sum_{i=1}^{n} \frac{1}{1+\theta_i^2}}, \end{equation*}\]
αφού και τα δύο αθροίσματα συγκλίνουν. Η εκτιμήτρια αυτή μπορεί να ερμηνευθεί ως μία κανονικοποιημένη προσέγγιση επαναδειγματοληψίας σπουδαιότητας με την κανονική σ.π.π. ως συνάρτηση σπουδαιότητας και λόγο \(1/(1+\theta^2)\). Σημειώνουμε εδώ ότι η εκτιμήτρια \(\widehat{\delta}(x)\) είναι λόγος εκτιμητριών και γενικά η διασπορά ενός λόγου δεν είναι ο λόγος των διασπορών. Το πρόβλημα αυτό συναντάται συχνά στην Μπεϋζιανή Στατιστική.
Θεωρούμε λοιπόν την εκτιμήτρια
\[\begin{equation*} \widehat{\delta}(x)=\frac{\sum_{i=1}^{n} w_ih(x_i)}{\sum_{i=1}^{n} w_i}, \end{equation*}\]
όπου \(x_i\) οι πραγματοποιήσεις των τυχαίων μεταβλητών \(X_i\) από την υποψήφια πυκνότητα \(g\). Επιπλέον, τα \(w_i\) είναι οι πραγματοποιήσεις των τυχαίων μεταβλητών \(W_i\) για τις οποίες ισχύει \(\mathbf{E}\left[W_i|x_i=x\right]=k f(x)/g(x)\), όπου \(k\) μία αυθαίρετη σταθερά (η οποία εμπεριέχει τις πιθανώς άγνωστες σταθερές των \(f,g\)). Συμβολίζουμε
\[\begin{equation*} S_{h,n}=\sum W_i h(X_i), \ \ S_{1,n}=\sum_{i=1}^n W_i. \end{equation*}\]
Σημειώνουμε εδώ πως δεν έχουμε υποθέσει ανεξαρτησία ανάμεσα στις \(X_i\), σε αντίθεση με την δειγματοληψία σπουδαιότητας. Τότε, η ασυμπτωτική διασπορά της \(\delta_{h,n}\) είναι (Liu 1996, Robert & Casella 2002 Chapter 4)
\[\begin{equation*} \mathbf{V}\left(\delta_{h,n}\right) = \frac{1}{n^2k^2}\left[ \mathbf{V}\left(S_{h,n}\right) -2\mathbf{E}_f[h] Cov(S_{h,n}, S_{1,n}) +\mathbf{E}_f[h]^2 \mathbf{V}\left(S_{1,n}\right) \right]. \end{equation*}\]
Μπορούμε να συμπεράνουμε ότι, αν οι \(X_i\) είναι ανεξάρτητες και ισόνομες, μία αδρή εκτίμηση της διασποράς της \(\delta_{h,n}\) είναι
\[\begin{equation*} \mathbf{V}\left(\delta_{h,n}\right) \approx \frac{1}{n} \mathbf{V}_f\left(h(X)\right) \left[1+\mathbf{V}_g\left(W\right) \right]. \end{equation*}\]
Η παραπάνω προσέγγιση είναι έγκυρη μόνο για την κανονικοποιημένη μορφή των βαρών \(w_i\), καθώς διαφορετικά εξαρτάται από την άγνωστη σταθερά \(k\). Η εκτίμηση Monte Carlo που παίρνουμε είναι
\[\begin{equation*} \frac{\sum_{i=1}^n w_i \left(h(x_i)-\delta_{h,n}\right)^2}{n \sum_{i=1}^n w_i} \cdot \left[ 1+\frac{n \widehat{\mathbf{V}}(W)}{\left(\sum_{i=1}^n w_i\right)^2}\right]. \end{equation*}\]
Η παραπάνω έκφραση δεν αποτελεί μια καλή προσέγγιση της διασπορά, αφού όπως είναι φανερό είναι πάντοτε μεγαλύτερη από την \(\mathbf{V}_f\left(h(X)\right)\), την διασπορά ενός ανεξάρτητου και ισόνομου δείγματος μεγέθους \(n\).
Παράδειγμα 4.3 (Robert & Casella 4.3) Εάν προσομοιώσουμε ένα δείγμα από την \(\mathcal{N}(x,1)\), η προσέγγιση της διασποράς που δόθηκε μπορεί να χρησιμοποιηθεί για να αξιολογήσουμε την μεταβλητότητα της εκτίμησής μας, αλλά και πάλι, η ασυμπτωτική φύση αυτών των προσεγγίσεων πρέπει να ληφθεί υπ’ όψιν.
Αν πάρουμε 500 ακολουθίες των εκτιμητριών των \(\delta (x)\) μπορούμε να βρούμε το \(95\%\) ποσοστημοριακό εύρος (γκρι λωρίδα) και να το αντιπαραβάλουμε με το \(95\%\) ασυμπτωτικό διάστημα εμπιστοσύνης βασισμένο σε μία ακολουθία χρησιμοποιώντας τη συνήθη εκτίμηση διασποράς (μαύρες γραμμές) καθώς και το αντίστοιχο δ.ε. με την διόρθωση βαρών (καφέ γραμμές).
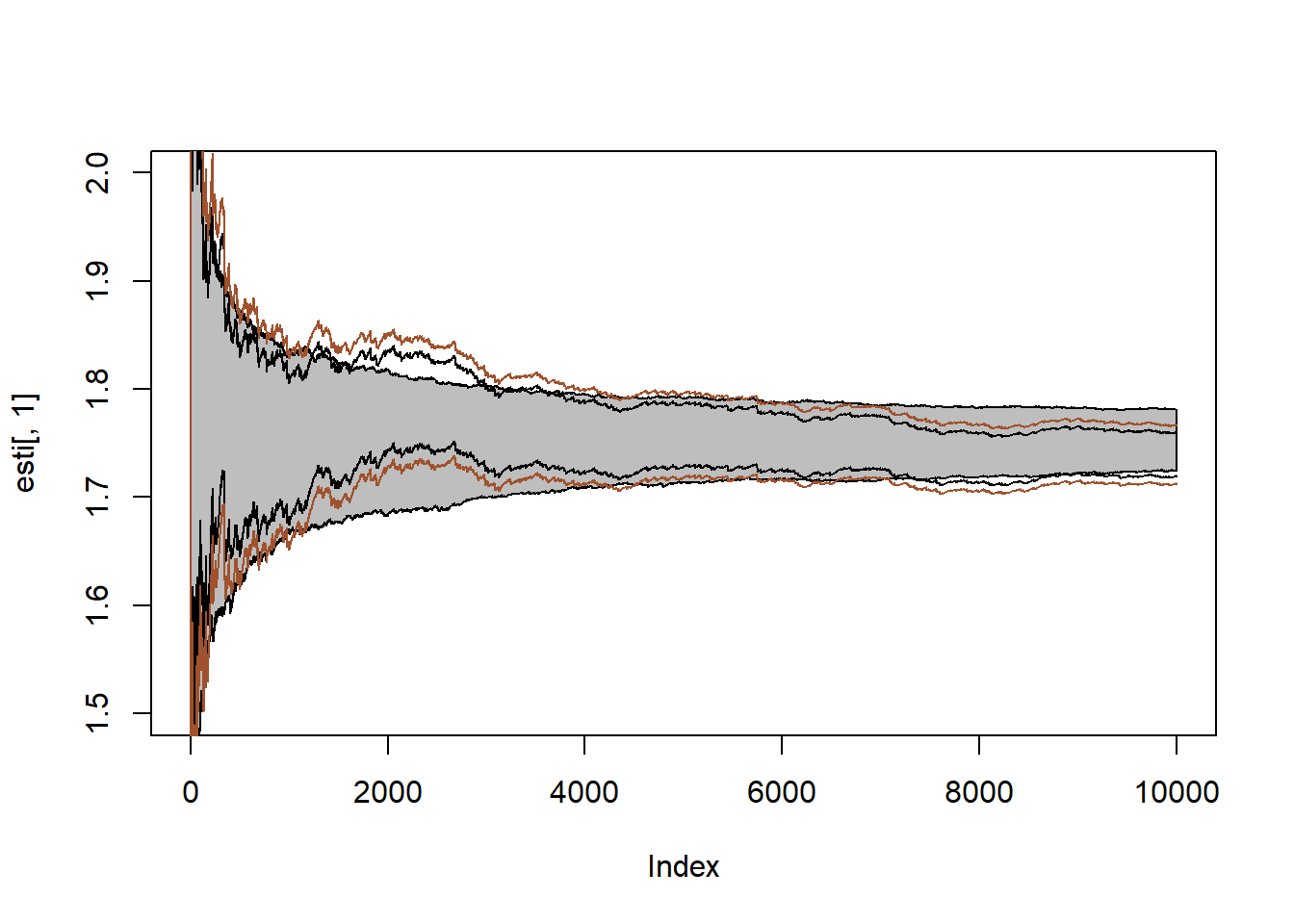
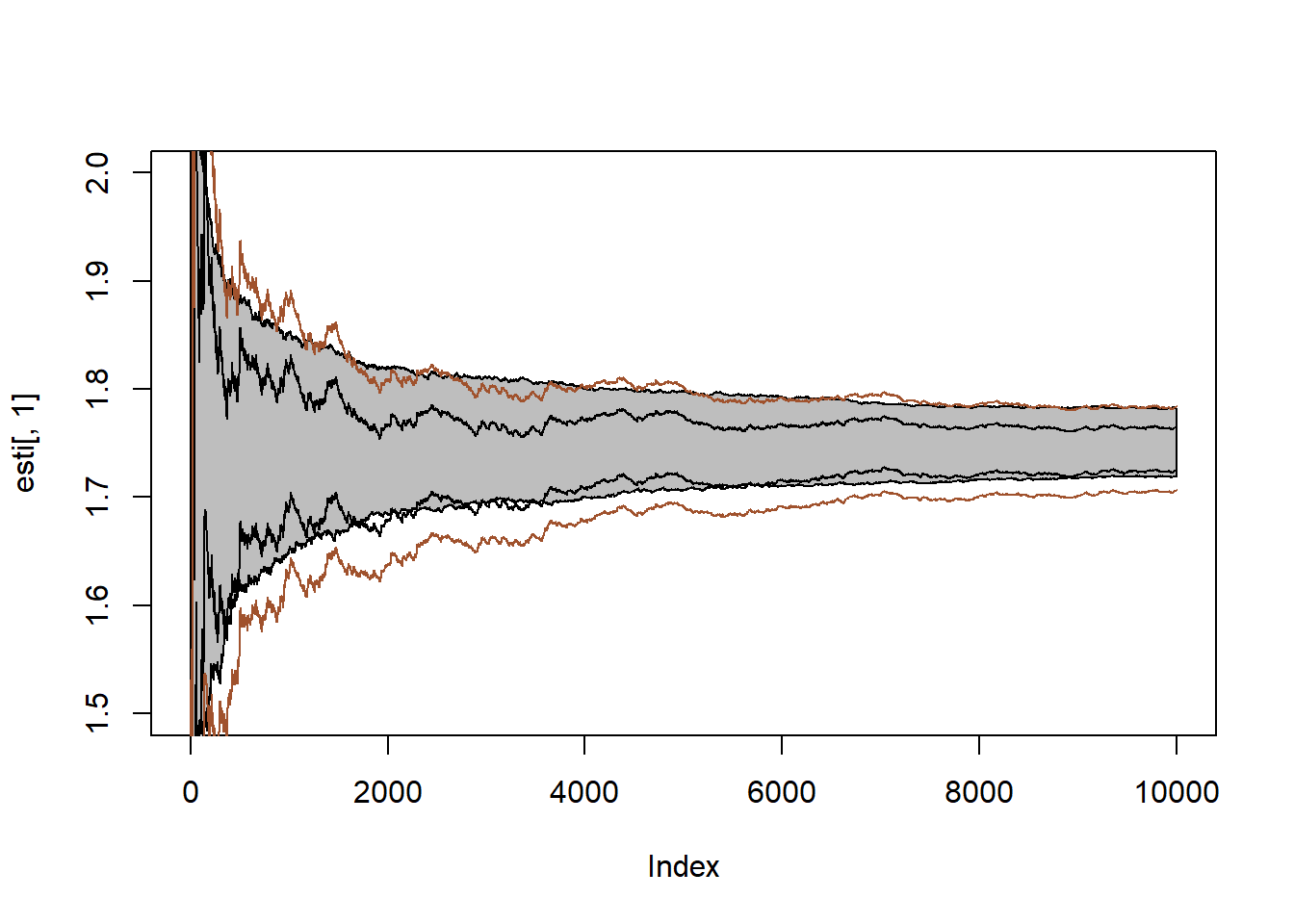
Μπορούμε να επαναλάβουμε την διαδικασία, αυτή τη φορά προσομοιώνοντας τα \(\theta_i\) από την prior \(\mathcal{C}(0,1)\) και χρησιμοποιώντας την εκτιμήτρια της επαναδειγματοληψίας σπουδαιότητας
\[\begin{equation*} \tilde{\delta}_{h,n} = \frac{\sum_{i=1}^n \theta_i e^{-\frac{1}{2}(x-\theta_i)^2}}{\sum_{i=1}^n e^{-\frac{1}{2}(x-\theta_i)^2}}. \end{equation*}\]
4.3 Αποτελεσματικό Μέγεθος Δείγματος
Η αναπαράσταση
\[\begin{equation*} \frac{\sum_{i=1}^n w_i \left(h(x_i)-\delta_{h,n}\right)^2}{n \sum_{i=1}^n w_i} \cdot \left[ 1+ \frac{n \widehat{\mathbf{V}}(W)}{\left(\sum_{i=1}^n w_i\right)^2}\right]. \end{equation*}\]
που προτάθηκε για την προσέγγιση της διασποράς της εκτιμήτριας που προκύπτει από τη δειγματοληψία σπουδαιότητας μας οδηγεί σε ένα αναγκαίο εργαλείο αξιολόγησης της απόδοσης των συναρτήσεων σπουδαιότητας. Για την \(\widehat{\mathbf{V}}(W)\) ισχύει
\[\begin{equation*} \widehat{\mathbf{V}}(W) = \frac{1}{n} \sum_{i=1}^n w_i^2 - \frac{1}{n^2} \left( \sum_{i=1}^n w_i \right)^2, \end{equation*}\]
επομένως
\[\begin{equation*} 1+\widehat{\mathbf{V}}_g(W) = \frac{n \sum_{i=1}^n w_i^2}{\left( \sum_{i=1}^n w_i \right)^2}. \end{equation*}\]
Συμβολίζοντας τα κανονικοποιημένα βάρη \(w_{i,n} = w_i/\sum_{j=1}^n w_j\), ορίζουμε το αποτελεσματικό μέγεθος δείγματος ως
\[\begin{equation*} ESS_n = \frac{1}{\sum_{i=1}^n w_{i,n}^2}. \end{equation*}\]
Το αποτελεσματικό μέγεθος δείγματος είναι χρήσιμο στην αξιολόγηση της επιβάρυνσης της διασποράς εξαιτίας των βαρών σπουδαιότητας, κάτι που παράλληλα μας δίνει μια αξιολόγηση για της συνάρτησης σπουδαιότητας. Για ένα δείγμα με ίσα βάρη, έχουμε \(ESS_n=n\), ενώ για ένα εκφυλισμένο δείγμα με όλα τα βάρη ίσα με 0 εκτός από ένα, έχουμε \(ESS_n=1\). Επομένως, το αποτελεσματικό μέγεθος δείγματος αντιστοιχεί το δείγμα σπουδαιότητας με το μέγεθος ενός ισοδύναμου δείγματος ανεξάρτητων και ισόνομων παρατηρήσεων.
Ένα ακόμα μέτρο αξιολόγησης παρέχεται από την perplexity \(e^{PP}/n\), όπου
\[\begin{equation*} PP_n = -\sum_{i=1}^n w_{i,n} \log(w_{i,n}), \end{equation*}\]
είναι η εντροπία των κανονικοποιημένων βαρών σπουδαιότητας. (Το εργαλείο αυτό χρησιμοποιείται κυρίως στην θεωρία πληροφόρησης και την αναγνώριση λόγου, βλ Jelinek 1999). Το perplexity παρέχει μία εκτίμηση της \(e^{D_{KL}(f,g)}\), όπου
\[\begin{equation*} D_{KL}(f,g) = \int \log\left\{\frac{f(x)}{g(x)}\right\} f(x) dx, \end{equation*}\]
είναι η απόκλιση Kullback-Leibler ανάμεσα στην συνάρτηση-στόχο \(f\) και την συνάρτηση σπουδαιότητας \(g\). Επομένως, όσο πιο κοντά βρίσκεται το perplexity στο 1, τόσο πιο κατάλληλη η συνάρτηση σπουδαιότητας.
Παράδειγμα 4.4 (Robert & Casella 4.3) Αν συγκρίνουμε το αποτελεσματικό μέγεθος δείγματος για τις προσομοιώσεις από κανονική και Cauchy των προηγούμενων παραδειγμάτων, η διαφορά στην αποδοτικότητα είναι πολύ πιο καθαρή απ’ ότι με την σύγκριση των γραφημάτων.
Για τα αποτελεσματικά μεγέθη δειγμάτων (αριστερά) και για τα perplexity (δεξιά) της κανονικής (κόκκινο) και της Cauchy (μπλε), έχουμε:
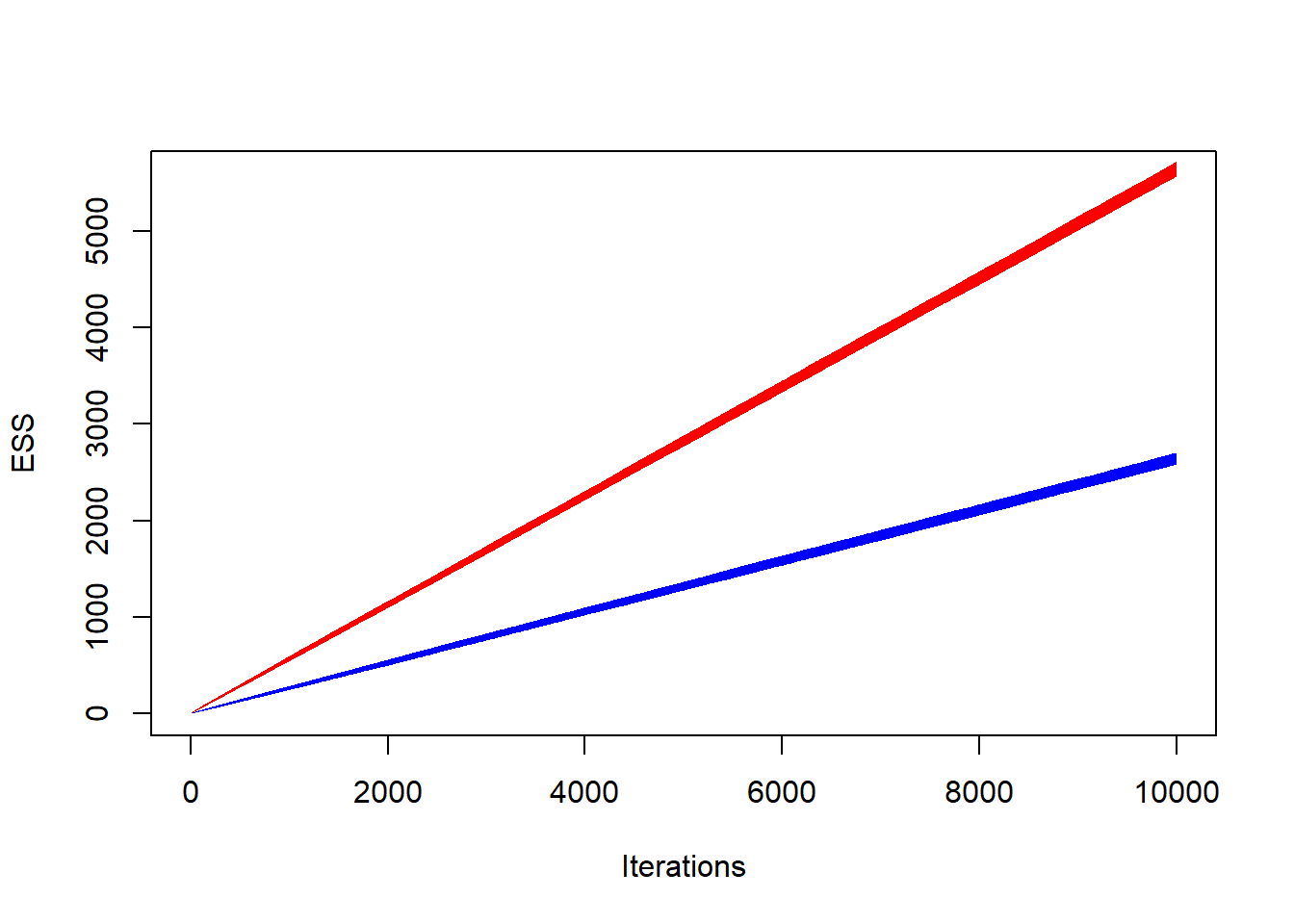
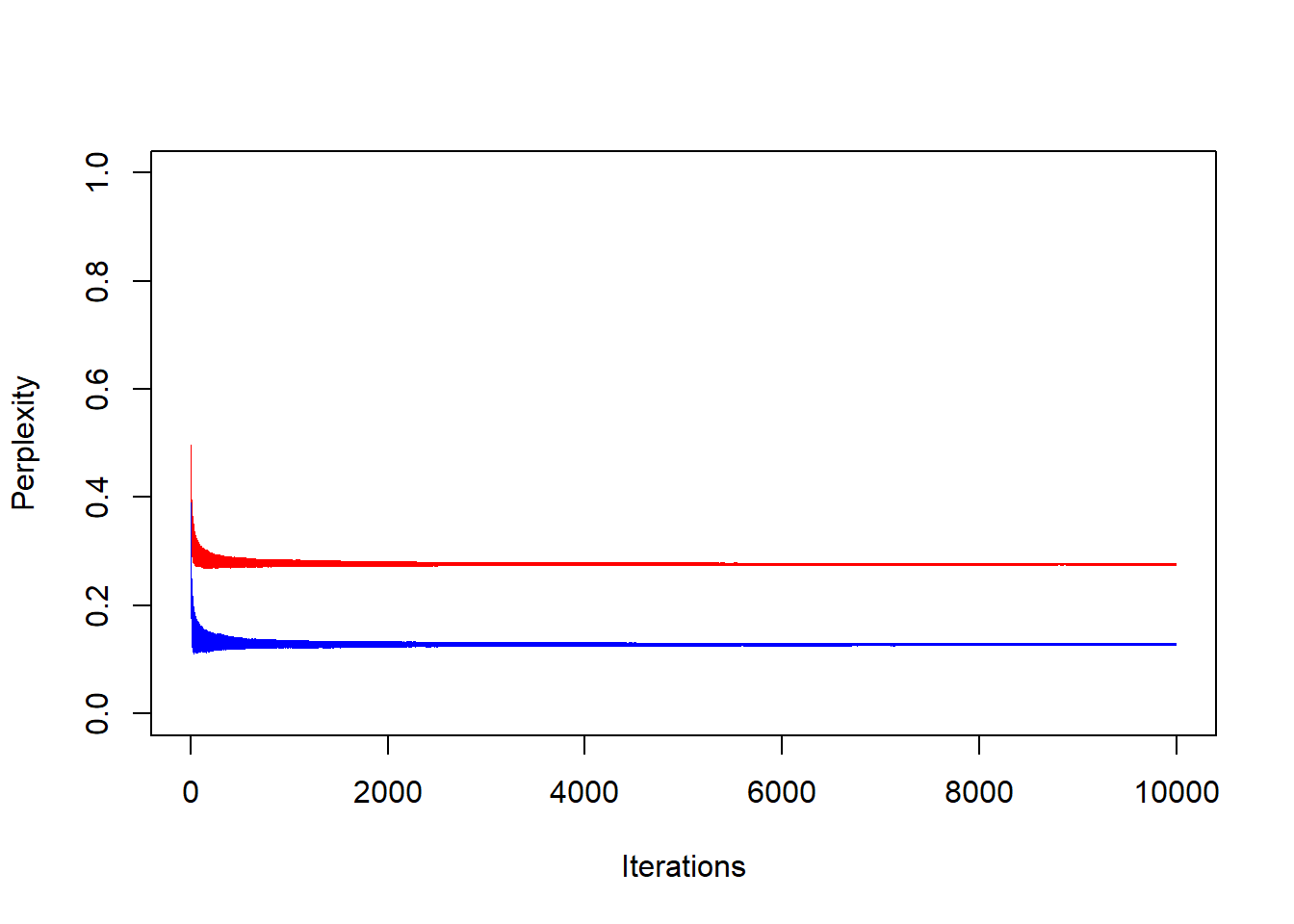
Όπως είναι φανερό, η προσομοίωση βασισμένη στην κανονική είναι περίπου διπλά αποδοτική από την προσομοίωση που βασίστηκε στην Cauchy.
4.4 Rao-Blackwellization
Θεώρημα 4.1 (Rao-Blackwell) Έστω ένα τυχαίο δείγμα \(X\) και μία εκτιμήτρια \(\delta(X)\). Αν \(Y\) μία επαρκής στατιστική συνάρτηση, τότε
\[\begin{equation*} \mathbf{V}\left(\mathbf{E}\left(\delta(X)|Y\right)\right) \leq \mathbf{V}\left(\delta(X)\right). \end{equation*}\]
Το θεώρημα Rao-Blackwell δείχνει ότι δεσμεύοντας μία εκτιμήτρια ως προς μία επαρκή στατιστική συνάρτηση οδηγεί σε εκτιμήτριες με μικρότερη ίση διασπορά. Αυτό το θεώρημα μας οδηγεί άμεσα σε μία τεχνική μείωσης της διασποράς των Monte Carlo εκτιμητριών χρησιμοποιώντας δέσμευση. Η τεχνική αυτή ονομάζεται Rao-Blackwellization, παρότι στο πλαίσιο του Monte Carlo η δέσμευση δεν γίνεται πάντα ως προς επαρκείς στατιστικές συναρτήσεις. Η βασική ιδέα είναι ότι χρησιμοποιώντας δεσμευμένη μέση τιμή (η οποία μπορεί να υπολογιστεί) οδηγούμαστε εκτιμήσεις μικρότερης μεταβλητότητας, χωρίς να επηρεάζεται η αμεροληψία των εκτιμήσεων αυτών.
Πιο αυστηρά, αν \(\delta(X)\) είναι μία εκτιμήτρια της ποσότητας \(m=\mathbf{E}_f\left(h(X)\right)\) και η \(X\) μπορεί να προσομοιωθεί με την από κοινού κατανομή \(f^\star(x,y)\) η οποία ικανοποιεί η σχέση
\[\begin{equation*} f(x)=\int f^\star (x,y) dy, \end{equation*}\]
τότε η νέα εκτιμήτρια \(\delta^\star (Y) = \mathbf{E}\left(\delta(X)|Y\right)\) κυριαρχεί της \(\delta\) ως προς τη διασπορά, ενώ η μεροληψία παραμένει η ίδια. Φυσικά, αυτό το αποτέλεσμα είναι ιδιαίτερα χρήσιμο όταν η \(\delta^\star (Y)\) μπορεί να υπολογιστεί αναλυτικά.
Παράδειγμα 4.5 (Robert & Casella 4.6.) Επιθυμούμε να υπολογίσουμε τη μέση τιμή της \(h(X)=e^{-X^2}\), όπου \(X\sim\mathcal{T}_n(\mu, \sigma^2)\). Αρχικά ας μελετήσουμε την κατανομή αυτή. Γνωρίζουμε ότι η κατανομή Student \(t_n\) κατασκευάζεται από τον λόγο μίας τυπικής κανονικής προς την ρίζα μίας \(\mathcal{X}^2_n\), διαιρεμένη με τους βαθμούς ελευθερίας της, δηλαδή:
\[\begin{equation*} T=\frac{Z}{\sqrt{Q}/n}, \ Z\sim\mathcal{N}(0,1), Q\sim\mathcal{X}^2_n. \end{equation*}\]
Η οικογένεια των κανονικών κατανομών μπορεί να βασιστεί στην τυπική κατανομή χρησιμοποιώντας μετασχηματισμούς θέσης-κλίμακας, δηλαδή
\[\begin{equation*} Z\sim N(0,1) \Rightarrow X=\mu+\sigma Z \sim\mathcal{N}(\mu,\sigma^2). \end{equation*}\]
Ανάλογα, κάνοντας μετασχηματισμό θέσης κλίμακας στην \(Τ~t_n\) που κατασκευάσαμε παραπάνω, έχουμε
\[\begin{equation*} T=\frac{Z}{\sqrt{Q}/n}\sim t_n \Rightarrow X=\mu+\sigma T= \mu+\sigma \frac{Z}{\sqrt{Q}/n} \sim\mathcal{T}_n(\mu, \sigma^2). \end{equation*}\]
Ορίζουμε την τ.μ. \(Y=Q/n\) και παρατηρούμε ότι
\[\begin{equation*} X|Y=y = \mu +\frac{\sigma}{\sqrt{y}}Z \sim \mathcal{N}\left(\mu, \frac{\sigma^2}{y}\right). \end{equation*}\]
Επομένως μπορούμε να υπολογίσουμε την από κοινού συνάρτηση πυκνότητας των \(X, Y\) δεσμεύοντας ως προς \(Y\) (Dikey’s Decomposition),
\[\begin{equation*} f_{X,Y}^\star (x,y) = f_{X|Y} (x|y) \cdot f_Y(y) = \frac{\sqrt{y}}{\sqrt{2\pi\sigma^2}} e^{-\frac{y}{2\sigma^2}(x-\mu)^2} \cdot \frac{(n/2)^{n/2}}{\Gamma(n/2)} y^{n/2 - 1} e^{-yn/2}. \end{equation*}\]
Η εφαρμογή του παραπάνω στην R είναι άμεση
Nsim <- 10 ^ 4 ; nu <- 5 ; mu <- 3 ; sigma <- 0.5
y <- sqrt(rchisq(Nsim, df = nu) / nu)
x <- rnorm(Nsim, mu, sigma / y)Ο παραπάνω κώδικας προσομοιώνει ζευγάρια τ.μ. \((X_i, Y_i), i=1,2, \ldots, n\). Στηριζόμενοι μόνο στις παρατηρήσεις της \(X\), εκτιμούμε την \(\mathbf{E}_f\left(h(X)\right)\) ως
\[\begin{equation*} \delta_n = \frac{1}{n} \sum_{j=1}^n e^{-X_j^2}. \end{equation*}\]
Η εκτίμηση αυτή μπορεί να βελτιωθεί χρησιμοποιώντας Rao-Blackwellization
\[\begin{equation*} \delta_n^\star = \frac{1}{n} \sum_{j=1}^n \mathbf{E}\left(e^{-X_j^2} | Y_j\right), \end{equation*}\]
όπου η \(\mathbf{E}\left(e^{-X^2} | Y\right)\) υπολογίζεται αναλυτικά
\[\begin{align*} \mathbf{E}\left(e^{-X^2} | Y=y\right) &= \int_{-\infty}^{+\infty} e^{-x^2} \frac{\sqrt{y}}{\sqrt{2\pi \sigma^2}} e^{-\frac{y}{2\sigma^2}(x-mu)^2} dx = \int_{-\infty}^+{+\infty} \frac{\sqrt{y}}{\sqrt{2\pi \sigma^2}} e^{(-\frac{y}{2\sigma^2}-1)x^2+\frac{y}{2\sigma^2}2x\mu-\frac{y}{2\sigma^2}\mu^2} dx \\ &=\ldots=\frac{\sqrt{y}}{\sqrt{2\pi \sigma^2}} e^{-\frac{y}{2\sigma^2}\mu^2+\frac{(y\mu)^2}{2\sigma^2(y+2\sigma^2)}} \int_{-\infty}^{+\infty} e^{-\frac{y+2\sigma^2}{2\sigma^2}(x-\frac{y\mu}{y+2\sigma^2})^2}dx = \frac{\sqrt{y}}{\sqrt{2\pi \sigma^2}} e^{-\frac{y}{2\sigma^2}\mu^2+\frac{(y\mu)^2}{2\sigma^2(y+2\sigma^2)}}\cdot \sqrt{2\pi \frac{\sigma^2}{y+2\sigma^2}} \\ &= \ldots = \frac{1}{\sqrt{\frac{2\sigma^2}{y}+1}} e^{-\frac{\mu^2}{\frac{2\sigma^2}{y}+1}}. \end{align*}\]
Επομένως έχουμε την εκτιμήτρια
\[\begin{equation*} \delta_n^\star = \frac{1}{n}\sum_{j=1}^n \mathbf{E}\left(e^{-X^2}|Y_j\right) = \frac{1}{n}\sum_{j=1}^n \frac{1}{\sqrt{\frac{2\sigma^2}{Y_j}+1}} e^{-\frac{\mu^2}{\frac{2\sigma^2}{Y_j}+1}}, \end{equation*}\]
η οποία υπολογίζεται αναλυτικά.
d1 <- cumsum(exp( - x ^ 2)) / (1:Nsim)
d2 <- cumsum(exp(- mu ^ 2 / (1 + 2 * (sigma / y) ^ 2)) / sqrt(1 + 2 * (sigma / y) ^ 2)) / (1:Nsim)Στην εικάνα 4.6 γίνεται σύγκριση των εκτιμητριών των δύο εκτιμητριών \(\delta_n, \delta_n^\star\) για τις τιμές \(n=5, \mu=3, \sigma=0.5\). Είναι εμφανής η μείωση της μεταβλητότητας που επιτεύχθηκε με τη μέθοδο Rao-Blackwellization. Εκτιμώντας τις διασπορές τους έχουμε \(\widehat{\mathbf{V}(\delta_n)}=0.00279\) και \(\widehat{\mathbf{V}(\delta_n^\star)}=0.00022\), δηλαδή επιτύχαμε μείωση της διασποράς περίπου στο 1/10 της αρχικής.
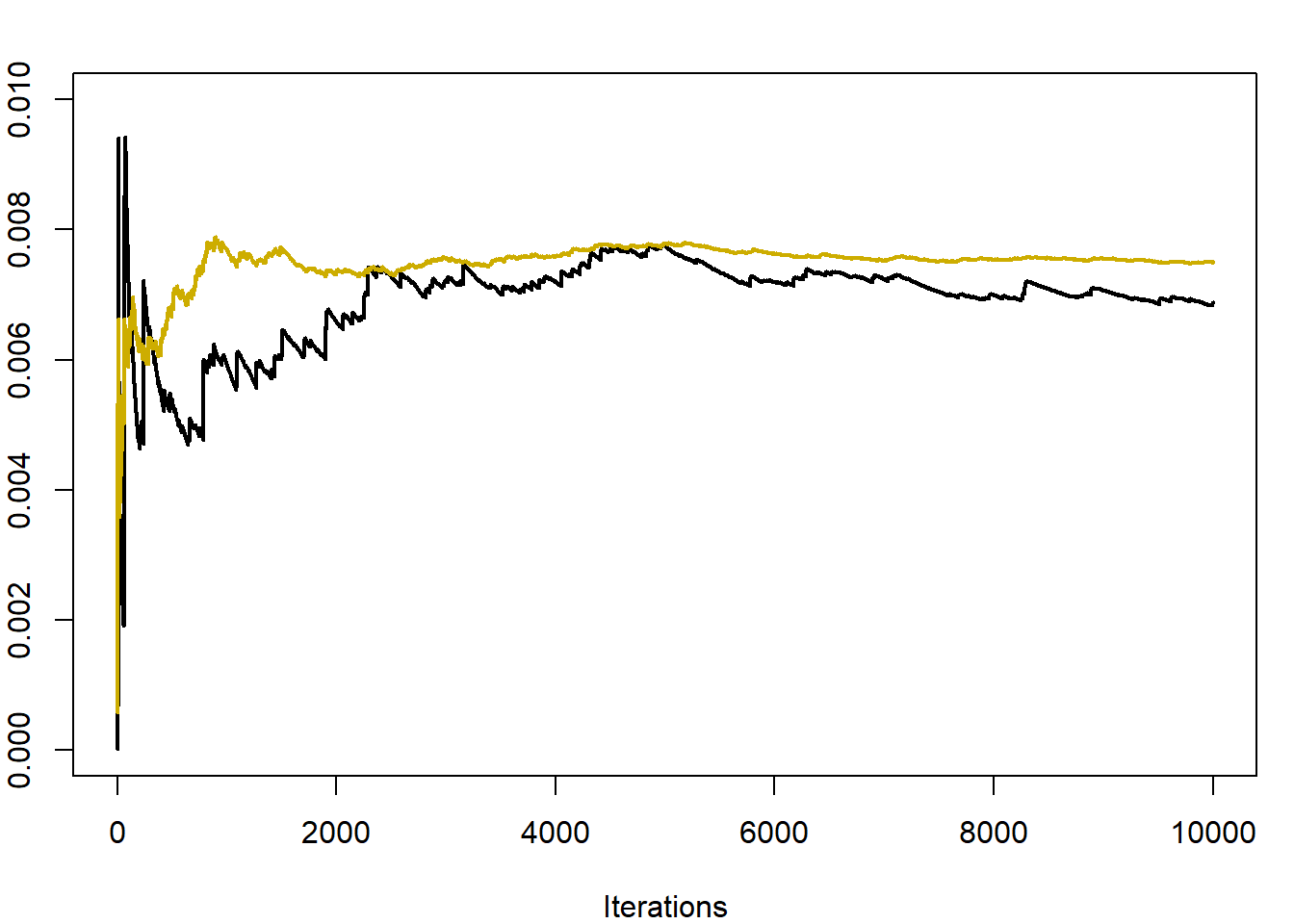
Εικόνα 4.6: Convergence of the estimators \(\delta_n\) (darker) and \(\delta_n^\star\) (lighter), for \(n=5, \mu=3, \sigma=0.5\).
Άσκηση 4.1 (Robert & Casella 4.10) Έστω ένας αλγόριθμος αποδοχής-απόρριψης στον οποίο έχουμε πυκνότητα-στόχο την \(f\) και υποψήφια πυκνότητα την \(g\).
Δείξτε ότι το δείγμα \((X_1, X_2, ..., X_n)\) μπορεί να περιγραφεί πλήρως από ένα τυχαίο δείγμα \((U_1, U_2, ..., U_N)\) από την \(Unif(0,1)\), και ένα τυχαίο δείγμα \((Y_1, Y_2, ..., Y_N)\) από την κατανομή με σ.π.π. τη \(g\). Με \(N\) συμβολίζουμε την τ.μ. του πλήθος παρατηρήσεων που πρέπει να προσομοιωθούν μέχρι να υπάρξουν \(n\) αποδεκτές παρατηρήσεις.
Συμπεράνετε ότι η εκτιμήτρια της \(\mathbf{E}\left(h(X)\right)\) που βασίζεται στο παραπάνω δείγμα \((X_1, X_2, ..., X_n)\) μπορεί να γραφτεί ως
\[\begin{equation*} \delta_1 = \frac{1}{n} \sum_{i=1}^n h(X_i) = \frac{1}{n} \sum_{j=1}^N h(Y_j) 1_ {U_j\leq w_j}, \end{equation*}\] όπου \(w_j=f(Y_j)/Mg(Y_j)\).
Λύση:
Ας θυμηθούμε κάποια βασικά στοιχεία του αλγορίθμου αποδοχής-απόρριψης. Για να προσομοιώσουμε την παρατήρηση \(X_i\), προσομοιώνουμε τις \(Y_{i,1}\) και \(U_{i,1}\). Αν \(U_{i,1}\leq f(Y_{i,1})/Mg(Y_{i,1})\), τότε δεχόμαστε την υποψήφια παρατήρηση και έχουμε \(X_i=Y_{i,1}\), ενώ διαφορετικά προσομοιώνουμε τις \(Y_{i,2}\) και \(U_{i,2}\) και επαναλαμβάνουμε τη διαδικασία. Αυτό οδηγεί σε ένα τυχαίο πλήθος \(N_i\) προσομοιώσεων, μέχρι να έχουμε την πρώτη αποδοχή, ενώ σε κάθε επανάληψη έχουμε πιθανότητα αποδοχής \(p=1/M\). Επομένως, το \(N_i\) ακολουθεί γεωμετρική κατανομή με παράμετρο \(p\), δηλαδή \(N_i~Geo(p)\). Τα παραπάνω μας οδηγούν στη σχέση:
\[\begin{equation*} X_i = \sum_{j=1}^{N_i} Y_j 1_{U_j\leq w_j}, \ i=1, 2, \dots, n. \end{equation*}\]
Η παραπάνω διαδικασία πρέπει να επαναληφθεί συνολικά \(N=N_1 +N_2 +... +N_n\) φορές εώς ότου έχουμε συνολικά \(n\) αποδεκτές παρατηρήσεις (όπου \(N_i, N_j\) ανεξάρτητα για \(i\neq j\)). Επομένως, το συνολικό πλήθος επαναλήψεων είναι μία τ.μ. που ακολουθεί αρνητική διωνυμική, δηλ. \(N~NegBin(n,p)\). Η εκτιμήτριά μας επομένως μπορεί να περιγραφεί ως
\[\begin{equation*} \delta_1 = \frac{1}{n} \sum_{i=1}^n h(X_i) = \frac{1}{n} \sum_{i=1}^n \sum_{j=1}^ {N_i} h(Y_{i,j}) 1_{U_{i,j}\leq w_{i,j}}, \end{equation*}\]
το οποίο με αλλαγή αρίθμησης των δεικτών \((i,j)\) γίνεται
\[\begin{equation*} \delta_1 = \frac{1}{n} \sum_{i=1}^n h(X_i) = \frac{1}{n} \sum_{j=1}^N h(Y_j) 1_ {U_j\leq w_j}. \end{equation*}\]
Το Rao-Blackwellization βρίσκει μία ακόμα εφαρμογή στα πλαίσια της αμυντικής δειγματοληψίας (defensive sampling, Hesterberg, 1995), μία παραλλαγή της δειγματοληψίας σπουδαιότητας. Έχουμε δει πως όταν προσομοιώνουμε με δειγματοληψία σπουδαιότητας από μία σ.π.π. \(f\) χρησιμοποιώντας τη σ.π.π. \(g\), οι ουρές της \(g\) πρέπει να είναι βαρύτερες από εκείνες της \(f\), προκειμένου η εκτιμήτρια που θα προκύψει να έχει πεπερασμένη διασπορά. Καθώς αυτό μπορεί να είναι δύσκολο, μία γενική τεχνική που συχνά επιστρατεύεται είναι αυτή της αμυντικής δειγματοληψίας η οποία στην θέση της \(g\) χρησιμοποιεί τη μίξη
\[\begin{equation*} pg(x) + (1-p) \ell(x), \ 0<p<1, \end{equation*}\]
όπου η \(\ell\) είναι μία πυκνότητα με βαριές ουρές (όπως η Cauchy ή η Pareto) και το \(p\) είναι κοντά στη μονάδα. Από τεχνική σκοπιά, εάν μπορούμε να προσομοιώσουμε από τις \(g, \ell\), μπορούμε εύκολα να προσομοιώσουμε από την μίξη τους προσομοιώνοντας μία παρατήρηση από την \(Bin(n, p)\) η οποία θα κρίνει πόσες παρατηρήσεις θα προέρχονται από την \(g\) και πόσες από την \(\ell\).
mix <- function(n = 1, p = 0.5) {
m <- rbinom(1, size, pro = p) # simg and siml simulate from
c(simg(m), siml(n - m)) # g and l, respectively.
}Αξίζει προσοχή το γεγονός πως τα βάρη σπουδαιότητας είναι ίσα με
\[\begin{equation*} w_i(x_i) = \frac{f(x_i)}{pg(x_i) + (1-p) \ell(x_i)}, \ i=1, 2, \dots, n, \end{equation*}\]
ανεξάρτητα από το αν η παρατήρηση \(x_i\) προσομοιώθηκε από την \(g\) ή την \(\ell\). Η εισαγωγή της τυχαιότητας στο πλήθος των παρατηρήσεων που προέρχονται από κάθε πυκνότητα επιβαρύνει την μεταβλητότητα της εκτίμησής μας. Γι’ αυτό, μπορούμε να επιλέξουμε από τις \(n\) παρατηρήσεις οι \(x_1, x_2, \dots, x_{pn}\) να προέρχονται από την \(g\) και οι \(y_1, y_2, \dots, y_{(1-p)n}\) από την \(\ell\) (υποθέτοντας ότι το \(pn\) είναι ακέραιος). Κάτι τέτοιο οδηγεί στην εκτιμήτρια
\[\begin{equation*} \frac{1}{n}\sum_{i=1}^{pn} h(x_i) \frac{f(x_i)}{pg(x_i)+(1-p)\ell(x_i)} + \frac{1}{n}\sum_{i=1}^{(1-p)n} h(y_i) \frac{f(y_i)}{pg(y_i)+(1-p)\ell(y_i)}, \end{equation*}\]
η οποία είναι αμερόληπτη. Επομένως, προσομοιώνοντας ένα σταθερό αριθμό παρατηρήσεων από κάθε κατανομή εξαλείφει την μεταβλητότητα που εισήγαγε η διωνυμική κατανομή.
Παράδειγμα 4.6 (Robert & Casella 3.9.) Έστω \(f\) η πυκνότητα της κατανομής \(\mathcal{T}_n\) και η υπό εκτίμηση ποσότητα \(\mathbf{E}\left(h(X)\right)\), όπου \(h(x)=\sqrt{x/(1-x)}\). Εάν προσπαθήσουμε να κάνουμε δειγματοληψία σπουδαιότητας με συνάρτηση σπουδαιότητας \(g: g(1)<+\infty\), η εκτίμηση που θα προκύψει θα έχει άπειρη διασπορά. Συγκεκριμένα, η εκτίμηση του ολοκληρώματος
\[\begin{equation*} \int_1^{+\infty} \sqrt{\frac{x}{x-1}}t_2(x) dx = \int_1^{+\infty} \sqrt{\frac{x}{x-1}} \frac{\Gamma(3/2)/\sqrt{2\pi}}{(1+x^2/2)^{3/2}} dx, \end{equation*}\]
δεν μπορεί να γίνει άμεσα, αφού η συνάρτηση \(h(x)=\sqrt{1/(x-1)}\) δεν είναι δύο φορές ολοκληρώσιμη και επομένως αν προσομοιώσουμε από την κατανομή \(\mathcal{T}_2\) θα προκύψει μία εκτιμήτρια του ολοκληρώματος με άπειρη διασπορά. Για τον λόγο αυτό, θα χρησιμοποιήσουμε μία μίξη της σ.π.π. της \(\mathcal{T}_2\) με μία \(\ell\). Προκειμένου η \(h^2(x)f(x)/\ell(x)\) να είναι ολοκληρώσιμη, η \(\ell\) πρέπει να αποκλίνει καθώς το \(x\) τείνει στο 1 (όπως και η \(h(x)\)) και να φθίνει πιο γρήγορα από το \(x^5\) όταν το \(x\) τείνει στο άπειρο. Με βάση τα παραπάνω, η
\[\begin{equation*} \ell(x) \propto \frac{1}{\sqrt{x-1}} \frac{1}{x^{3/2}} 1_{x>1}, \end{equation*}\]
είναι μία αποδεκτή πυκνότητα. Παρατηρούμε ότι
\[\begin{equation*} \int_1^y \frac{1}{\sqrt{x-1}x^{3/2}} dx = \int_0^{y-1} \frac{1}{\sqrt{w}(w+1)^{3/2}} dw = \int_0^{\sqrt{y-1}} \frac{2}{(u^2+1)^{3/2}} du = \int_0^{\sqrt{2(y-1)}} \frac{2}{(1+t^2/2)^{3/2}} dt. \end{equation*}\]
Από αυτό συμπεραίνουμε ότι η \(\ell(x)\) είναι η πυκνότητα μίας \(1+T^2/2\), όπου \(T\sim\mathcal{T}_3\), δηλαδή
\[\begin{equation*} \ell(x) = \frac{\sqrt{2}\Gamma(3/2)/\sqrt{2\pi}}{\sqrt{x-1}x^{3/2}} 1_{(1, +\infty)}(x). \end{equation*}\]
Παρατηρήστε πως οι προσομοιώσεις που είναι μικρότερες της μονάδας στην αμυντική δειγματοληψία παίρνουν ένα βάρος ίσο με \(1/0.95\), αφού \(\ell(x)=0\) για \(x\leq 1\). Η σύγκριση της αμυντικής δειγματοληψίας με την δειγματοληψία σπουδαιότητας μπορεί να γίνει προσθέτοντας ένα μικρό δείγμα από την \(\ell\) στο αρχικό δείγμα από την \(g\). Συγκρίνοντας τις δύο εκτιμήτριες, είναι εμφανές ότι η αμυντική δειγματοληψία λύνει το πρόβλημα της διασποράς (Εικόνα 4.7).
h <- function(x){
(x > 1) / sqrt(abs(x - 1))
}
sam1 <- rt(.95 * 10 ^ 4, df = 2)
sam2 <- 1 + .5 * rt(.05 * 10 ^ 4, df = 2) ^ 2
sam <- sample(c(sam1, sam2), .95 * 10 ^ 4)
weit <- dt(sam, df = 2) / (0.95 * dt(sam, df = 2) + .05 * (sam > 0) * dt(sqrt(2 * abs(sam - 1)), df = 2) * sqrt(2) / sqrt(abs(sam - 1)))
plot(cumsum(h(sam1)) / (1:length(sam1)), ty = "l", xlab = "Iterations", ylab = "", lwd = 2)
lines(cumsum(weit * h(sam)) / 1:length(sam1), col = "blue", lwd = 2)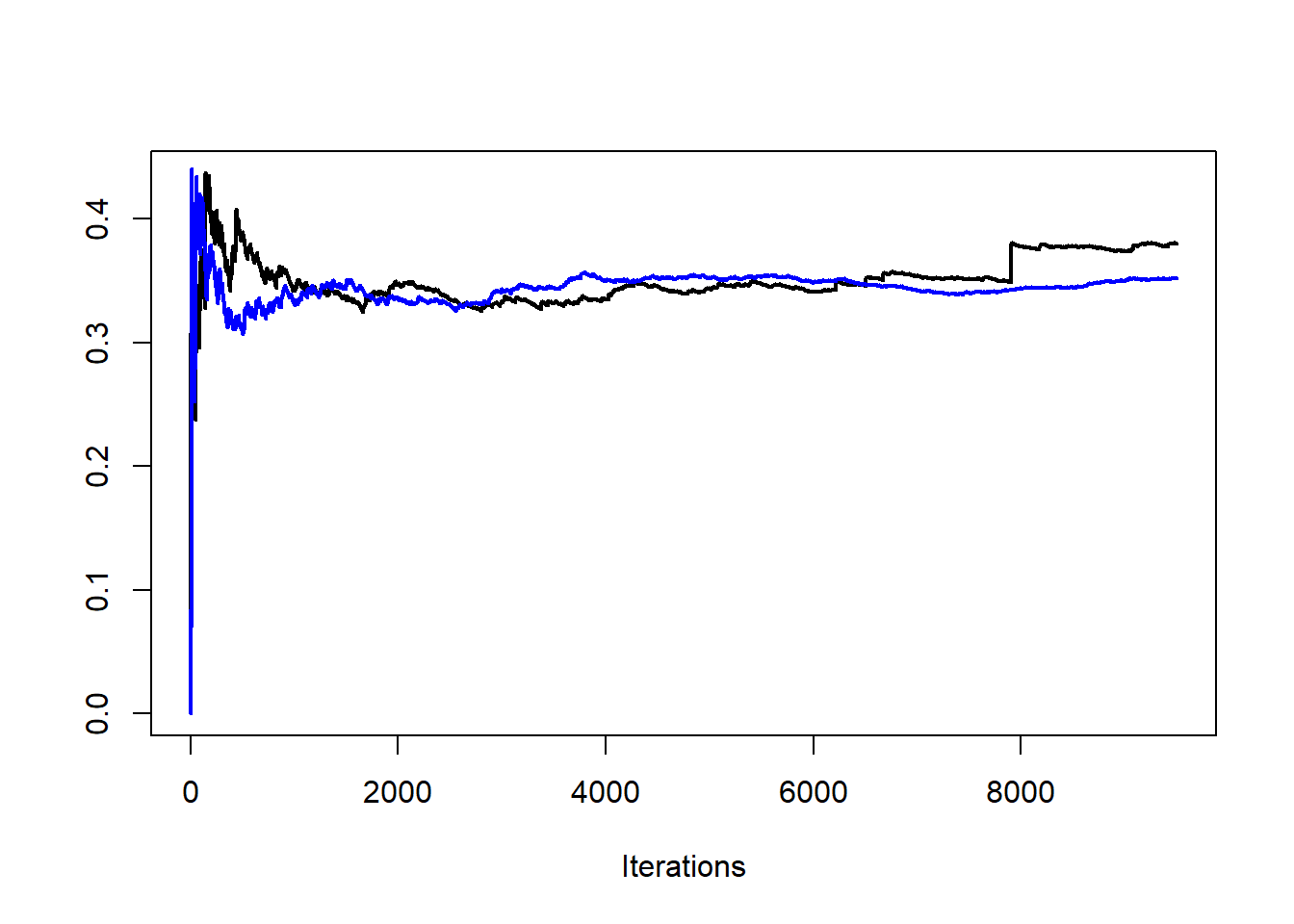
Εικόνα 4.7: Convergence of two estimators based on a sample from \(\mathcal{T}_2\) (black) and a defensive version (blue).
Υποθέτουμε τώρα ότι θέλουμε να προσομοιώσουμε από μία μίξη κατανομών \(g(x)=pg_1(x)+(1-p)g_2(x)\), όπου το \(p\) είναι γνωστό, με την προσθήκη μίας βοηθητικής, δίτιμης τ.μ. \(Y\). Έτσι, αν η εκτιμήτρια σπουδαιότητας είναι η
\[\begin{equation*} \delta_n = \frac{1}{n} \sum_{i=1}^n h(X_i) \left\{ \frac{f(X_i)}{g_1(X_i)} 1_{Y_i=1} + \frac{f(X_i)}{g_2(X_i)} 1_{Y_i=2}\right\}, \end{equation*}\]
τότε η βελτιωμένη εκδοχή της είναι η
\[\begin{align*} \delta_n^\star &= \frac{1}{n} \sum_{i=1}^n h(X_i) \mathbf{E}\left( \frac{f(X_i)}{g_{Υ_i}(X_i)} | X_i \right) = \frac{1}{n} \sum_{i=1}^n h(X_i) f(X_i) \mathbf{E}\left( \frac{1}{g_{Υ_i}(X_i)} | X_i \right) \\ &= \frac{1}{n} \sum_{i=1}^n h(X_i)f(X_i) \left[\mathbf{P}(Y_i=1|X_i) \frac{1}{g_1(X_i)} + \mathbf{P}(Y_i=2|X_i) \frac{1}{g_2(X_i)} \right] \\ &= \frac{1}{n} \sum_{i=1}^n h(X_i)f(X_i) \left[\frac{f(X_i|Y_i=1)\mathbf{P}(Y_i=1)}{f(X_i)} \frac{1}{g_1(X_i)} + \frac{f(X_i|Y_i=2)\mathbf{P}(Y_i=2)}{f(X_i)} \frac{1}{g_2(X_i)} \right] \\ &=\frac{1}{n} \sum_{i=1}^n h(X_i)f(X_i) \left[\frac{pg_1(X_i)}{pg_1(X_i)+(1-p)g_2(X_i)} \frac{1}{g_1(X_i)} + \frac{(1-p)g_2(X_i)}{pg_1(X_i)+(1-p)g_2(X_i)} \frac{1}{g_2(X_i)} \right] \\ &=\frac{1}{n} \sum_{i=1}^n h(X_i)f(X_i) \frac{1}{pg_1(X_i)+(1-p)g_2(X_i)} = \frac{1}{n} \sum_{i=1}^n h(X_i)\frac{f(X_i) }{pg_1(X_i)+(1-p)g_2(X_i)} \end{align*}\]
Σε αυτό το σημείο αξίζει να σημειώσουμε ότι δέσμευση ως προς το πλήθος των παρατηρήσεων που προέρχονται από κάθε κατανομή που είδαμε στο προηγούμενο παράδειγμα, δεν αποτελεί Rao-Blackwellization, παρότι οδηγεί σε μία αμερόληπτη εκτιμήτια με μικρότερη διασπορά από εκείνη που στηρίζεται στην διωνυμική \(Bin(n,p)\) για το μοίρασμα των παρατηρήσεων στις \(g_1\) και \(g_2\).
4.5 Μέθοδοι Επιτάχυνσης Σύγκλισης
Θα μελετήσουμε μερικές μεθόδους επιτάχυνσης σύγκλισης, οι οποίες λειτουργούν ανεξάρτητα από τις ιδιαίτερες συνθήκες μία προσομοίωσης και επομένως μπορούν (και συνιστάται) να χρησιμοποιούνται.
4.5.1 Συσχετισμένες Παρατηρήσεις
Παρότι το γενικό πλαίσιο των Monte Carlo προσομοιώσεων στηρίζεται σε τυχαία δείγματα (παρατηρήσεις από ανεξάρτητες και ισόνομες τ.μ.), μπορεί να είναι ιδιαίτερα επιθυμητό να προσομοιώσουμε δείγματα από αρνητικά ή θετικά συσχετισμένες τ.μ., καθώς αυτό μπορεί να οδηγήσει σε μείωση της διασποράς της προκύπτουσας εκτιμήτριας. Ας μελετήσουμε ένα τέτοιο πλαίσιο.
Έστω δύο ποσότητες \(m_1, m_2\),
\[\begin{equation*} m_1=\int g_1(x)f_1(x)dx, m_2=\int g_2(x)f_2(x)dx, \end{equation*}\]
και οι αντίστοιχες εκτιμήτριες \(\delta_1, \delta_2\), οι οποίες είναι ανεξάρτητες μεταξύ τους. Ενδιαφερόμαστε να εκτιμήσουμε την διαφορά \(m_2-m_1\). Εάν χρησιμοποιήσουμε ως εκτιμήτρια την \(\delta=\delta_2-\delta_1\), παρατηρούμε ότι η διασπορά της είναι
\[\begin{equation*} \mathbf{V}(\delta)=\mathbf{V}(\delta_2-\delta_1)=\mathbf{V}(\delta_2)+\mathbf{V}(\delta_1), \end{equation*}\]
λόγω της ανεξαρτησίας των \(\delta_1, \delta_2\). Η διασπορά αυτή είναι πιθανώς πολύ μεγάλη για να υποστηρίξει μία ακριβή εκτίμηση της διαφοράς \(m_2-m_1\), ιδιαίτερα οι δύο αυτές ποσότητες είναι σχεδόν ίσες. Εάν οι \(\delta_1, \delta_2\) είναι θετικά συσχετισμένες, τότε η διασπορά της \(\delta\) είναι
\[\begin{equation*} \mathbf{V}(\delta)=\mathbf{V}(\delta_2-\delta_1)=\mathbf{V}(\delta_2)+\mathbf{V}(\delta_1)-2Cov(\delta_1, \delta_2), \end{equation*}\]
έχει δηλαδή μειωθεί κατά \(2Cov(\delta_1, \delta_2)\). Γενικότερα, στο πλαίσιο της στατιστικής συμπερασματολογίας, μία εκτιμήτρια \(\delta\) της παραμέτρου \(\theta\) αξιολογείται μέσω του ρίσκου \(R(\delta, \theta)=\mathbf{E}\left(L(\delta, \theta)\right)\), όπου \(L(\delta, \theta)\) μία συνάρτηση σφάλματος (π.χ. τετραγωνικό σφάλμα \(L(\delta, \theta)=(\delta-\theta)^2\)). Επομένως η σύγκριση δύο εκτιμητριών \(\delta_1, \delta_2\) μίας παραμέτρου \(\theta\) ανάγεται στην σύγκριση των ρίσκων \(R(\delta_1, \theta), R(\delta_2, \theta)\) και συγκεκριμένα στη διαφορά τους. Όμως, το ρίσκο είναι μία μέση τιμή, η οποία συχνά δεν μπορεί να υπολογιστεί αναλυτικά. Αν προσομοιώσουμε λοιπόν από την \(f(\cdot|\theta)\) δύο τυχαία δείγματα \(X_1, X_2, \dots, X_n\) και \(Y_1, Y_2, \dots, Y_n\), ανεξάρτητα μεταξύ τους, παίρνουμε τις εκτιμήσεις
\[\begin{equation*} \widehat{R}(\delta_1, \theta) = \frac{1}{n} \sum_{i=1}^n L\left( \delta_1 (X_i), \theta \right), \widehat{R}(\delta_2, \theta) = \frac{1}{n} \sum_{i=1}^n L\left( \delta_2 (Y_i), \theta \right). \end{equation*}\]
Επομένως εκτιμάμε την διαφορά \(R(\delta_2, \theta)-R(\delta_1, \theta)\) με την διαφορά \(\widehat{R}(\delta_2, \theta)-\widehat{R}(\delta_1, \theta)\), οπότε θετική συσχέτιση ανάμεσα στις ποσότητες \(L(\delta_1(X_i), \theta)\) και \(L(\delta_2(Y_i), \theta)\) οδηγεί σε μικρότερη διασπορά της εκτιμήτριας.