3 Ολοκλήρωση Monte Carlo

3.1 Εισαγωγή

Οι μέθοδοι Monte Carlo αποτελούν μία σημαντική κατηγορία εντατικών υπολογιστικών μεθόδων της Στατιστικής που έχουν ως βασικό στόχο την προσέγγιση πολύπλοκων ολοκληρωμάτων και την εύρεση βέλτιστων λύσεων σε προβλήματα βελτιστοποίησης με τη βοήθεια προσομοιώσεων.

Στο κεφάλαιο αυτό εστιάζουμε στη χρήση τους ως μεθόδων προσεγγιστικής ολοκλήρωσης. Ας υποθέσουμε λοιπόν ότι θέλουμε να υπολογίσουμε ένα ολοκλήρωμα της μορφής \(\int_Ag(x)dx\) κάποιας συνάρτησης \(g: A\rightarrow \mathbb{R}\), όπου \(A\subset \mathbb{R}^d\). Αν υποθέσουμε ότι \(\int_A |g(x)|dx<+\infty\) (δηλ. συγκλίνει απόλυτα), τότε

\[\begin{equation*} I=\int_Ag(x)dx = \int_A \frac{g(x)}{f(x)} \cdot f(x) dx = \int_{\mathbb{R}^d}h(x)f(x)dx, \end{equation*}\]

όπου η \(f(x)\) μπορεί να επιλεγεί ως σ.π.π. στον \(\mathbb{R}^d\) με στήριγμα το \(A\) και \(h(x)=g(x)/f(x)\). Έτσι λοιπόν, \(I=\mathbf{E}_f\left[h(X)\right]\), συμπεραίνοντας ότι το ζητούμενο ορισμένο ολοκλήρωμα γράφεται ως μία μέση τιμή μιας κατάλληλης συνάρτησης μιας τυχαίας μεταβλητής.

Θα πρέπει να γίνει σαφές από την αρχή ότι σε πολλές τέτοιες περιπτώσεις μπορεί να υπάρχουν πολύ αποτελεσματικές μέθοδοι αριθμητικής ολοκλήρωσης που υπερτερούν της Monte Carlo ολοκλήρωσης. Γρήγορα όμως οι τελευταίες μπορούν να αποδειχθούν πιο αποτελεσματικές καθώς η διάσταση \(d\) αυξάνει. Δύο συναρτήσεις στην R που μπορούν να χρησιμοποιηθούν για υπολογισμό απλών ολοκληρωμάτων (\(d=1\)) είναι η area και η integrate. Η πρώτη όμως προϋποθέτει ολοκλήρωση σε φραγμένο διάστημα, ενώ η δεύτερη μπορεί να αποδειχθεί αναξιόπιστη, όπως δείχνουμε στο επόμενο παράδειγμα.

Παράδειγμα 3.1 (Robert & Casella 3.2) Έστω ένα δείγμα 10 παρατηρήσεων από την Cauchy, \(x_i, 1\leq i \leq 10\), με παράμετρο θέσης \(\theta=350\). H περιθώρια κατανομή του (ψευδο-)δείγματος υπό μία επίπεδη (flat) prior είναι

\[\begin{equation*} m(x)=\int_{-\infty}^{+\infty} \prod_{i=1}^{10} \frac{1}{\pi} \frac{1}{1+(x_i-\theta)^2} d\theta. \end{equation*}\]

Όμως, η συνάρτηση integrate επιστρέφει λάθος αριθμητική τιμή:

cac <- rcauchy(10) + 350

lik <- function(the) {
  u <- dcauchy(cac[1] - the)
  for (i in 2:10)
    u <- u * dcauchy(cac[i] - the)
    return(u)
}

integrate(lik, -Inf, Inf)
## 4.016188e-44 with absolute error < 7.9e-44
integrate(lik, 200, 400) 
## 2.00427e-11 with absolute error < 3.7e-11

Επιπλέον, η συνάρτηση αποτυγχάνει να μας δείξει την αδυναμία της να υπολογίσει το ολοκλήρωμα, επιστρέφοντας ένα πολύ μικρό σφάλμα. Συγκρίνουμε τις εκτιμήσεις των integrate και area:

cac <- rcauchy(10)
nin <- function(a){ integrate(lik, -a, a)$val }
nan <- function(a){ area(lik, -a, a)}

x <- seq(1, 10 ^ 3,le = 10 ^ 4)
y <- log(apply(as.matrix(x), 1, nin))
z <- log(apply(as.matrix(x), 1, nan))

plot(x, y, type = "l", ylim = range(cbind(y, z)),lwd = 2)
lines(x, z, lty = 2, col = "sienna", lwd = 2) 

Χρησιμοποιώντας την εντολή area παράγουμε μια πιο αξιόπιστη εκτίμηση, αφού εκτιμήτρια δείχνει να συγκλίνει καθώς το \(n\) αυξάνεται. Η area όμως μπορεί να λειτουργήσει μόνο για φραγμένα διαστήματα, κάτι που απαιτεί κάποια prior γνώση για την περιοχή μεγίστου της ολοκληρωτέας ποσότητας.

Στο παράδειγμα αυτό η χρήση της area είναι περισσότερο αξιόπιστη και διορθώνει το πρόβλημα. Η κατάσταση γίνεται δυσκολότερη σε πολλαπλά ολοκληρώματα που τυπικά εμφανίζονται στην Στατιστική όταν έχουμε μεγάλα μεγέθη δείγματος (ακόμα και μεσαίου μεγέθους).

3.2 Ασυμπτωτική θεωρία

Η πλήρης κατανόηση της λειτουργίας των μεθόδων Monte Carlo επιτυγχάνεται με τη γνώση των βασικών τρόπων σύγκλισης ακολουθιών τυχαίων μεταβλητών, βασικών οριακών θεωρημάτων και ασυμπτωτικών ιδιοτήτων εκτιμητριών. Για το λόγο αυτό στην επόμενη παράγραφο παραθέτουμε τα πιο σημαντικά από αυτά.

3.2.1 Ασυμπτωτικές Ιδιότητες Εκτιμητριών

Η μελέτη εκτιμητριών σε στατιστικά μοντέλα οδηγεί φυσιολογικά στη διερεύνηση της ασυμπτωτικής έκφρασης των ιδιοτήτων που χαρακτηρίζουν μία καλή εκτιμήτρια. Όταν μία εκτιμήτρια δεν είναι αμερόληπτη, θα θέλαμε τουλάχιστον ασυμπτωτικά να απολαμβάνει αυτήν την ιδιότητα, δηλαδή να μηδενίζεται το μέσο σφάλμα της. Ο ασυμπτωτικός μηδενισμός θα θέλαμε να συμβαίνει και με το μέσο τετραγωνικό σφάλμα (ή το μέσο απόλυτο σφάλμα) που αποτελεί κριτήριο επιλογής εκτιμητριών. Έτσι οδηγούμαστε φυσιολογικά στις έννοιες της ασυμπτωτικής αμεροληψίας και της \(L^2\)-συνέπειας.

Ορισμός 3.1 Μία εκτιμήτρια \(\widehat{\theta}_n\) μιας παραμέτρου \(\theta\in \Theta\) θα λέμε ότι είναι ασυμπτωτικά αμερόληπτη εκτιμήτρια (α.α.ε.), αν η συνάρτηση μεροληψίας της \(b_n\) μηδενίζεται ασυμπτωτικά, δηλ., αν \[\begin{equation*} b_{n} \xrightarrow[n\rightarrow \infty]{p.w.} 0 \qquad \textrm{ή ισοδύναμα} \qquad \mathbf{E}_{\theta}(\widehat{\theta}_n) \xrightarrow[n\rightarrow \infty]{} \theta, \quad \textrm{για κάθε } \theta \in \Theta. \end{equation*}\]

Ορισμός 3.2 Μία εκτιμήτρια \(\widehat{\theta}_n\) μιας παραμέτρου \(\theta\in \Theta\) λέγεται \(L^2\)-συνεπής, αν το μέσο τετραγωνικό της σφάλμα \(MSE_n\) μηδενίζεται ασυμπτωτικά, δηλ., αν \[\begin{equation*} MSE_{n} \xrightarrow[n\rightarrow \infty]{p.w.} 0 \qquad \textrm{ή ισοδύναμα} \qquad \mathbf{E}_{\theta}\left(\widehat{\theta}_n-\theta\right)^2 \xrightarrow[n\rightarrow \infty]{} 0, \quad \textrm{για κάθε } \theta \in \Theta. \end{equation*}\]

Είναι φανερό ότι οι παραπάνω ασυμπτωτικές ιδιότητες είναι επιθυμητές για μία εκτιμήτρια, αλλά δεν μας λένε τίποτα για την ταχύτητα σύγκλισης, η οποία πρέπει να εξετάζεται ταυτόχρονα. Σχετικά έχουμε τον ακόλουθο ορισμό.

Ορισμός 3.3 Μία ακολουθία \((\alpha_n)\) πραγματικών αριθμών λέγεται \(O(\beta_n)\) (κεφαλαίο όμικρον της \(\beta_n\)), όπου \((\beta_n)\) είναι μία συνήθως “απλούστερη” ακολουθία θετικών πραγματικών αριθμών, αν υπάρχει μία σταθερά \(M>0\), έτσι ώστε (τελικά για κάθε \(n\)) \[\begin{equation*} |\alpha_n| \leq M\beta_n. \end{equation*}\]

Ερμηνεία: H κλάση \(O(\beta_n)\) συμπεριλαμβάνει όλες τις ακολουθίες των οποίων η ασυμπτωτική συμπεριφορά κυριαρχείται από αυτήν που καθορίζεται από τη \((\beta_n)\). Είναι λοιπόν ένας συμβολισμός που αντιστοιχεί σε μία απλή περιγραφή του “χειρότερου” σεναρίου, αφού συνήθως εκφράζει κάποια πολυπλοκότητα αλγορίθμου (για \(\beta_n \rightarrow \infty\)) ή κάποιο σφάλμα (για \(\beta_n \rightarrow 0\)).

Παράδειγμα 3.2 Η κλάση \(O(1)\) είναι όλες οι φραγμένες ακολουθίες, η κλάση \(O(n)\) περιλαμβάνει όλες εκείνες που αποκλίνουν το πολύ γραμμικά στο \(+\infty\), ενώ η κλάση \(O(1/n)\) αφορά εκείνες που συγκλίνουν τουλάχιστον γραμμικά στο \(0\).

3.2.2 Τρόποι Σύγκλισης Ακολουθιών Τυχαίων Μεταβλητών

Σε αυτήν την ενότητα υπενθυμίζουμε τους σημαντικότερους τρόπους σύγκλισης ακολουθιών τ.μ., δίνουμε κάποιες πολυδιάστατες επεκτάσεις και υπενθυμίζουμε τους νόμους μεγάλων αριθμών και το κλασικό κεντρικό οριακό θεώρημα.

Ορισμός 3.4 Μία ακολουθία τ.μ. \((X_n)\) λέμε ότι συγκλίνει με πιθανότητα 1 ή σχεδόν βεβαίως, ή ισχυρά, σε μία τ.μ. \(X\), και γράφουμε \(X_n\xrightarrow[]{a.s.}X\), αν

\[\begin{equation*} \mathbf{P}\big(\big\{\omega \in \Omega: \exists \lim X_n(\omega) \ \textrm{και} \ \lim X_n(\omega)=X(\omega) \big\}\big) = 1. \end{equation*}\]

Ερμηνεία: Μία σύγκλιση με πιθανότητα 1 μας εξασφαλίζει ότι τυπικά κάθε πραγματοποίηση \((X_n(\omega))\) αντιστοιχεί σε μία συγκλίνουσα ακολουθία πραγματικών αριθμών. Αν γνωρίζουμε ότι η οριακή τυχαία μεταβλητή είναι η \(X\), τότε πρακτικά κάθε μονοπάτι οδηγεί στο \(X(\omega)\).

Το παραπάνω ενδεχόμενο γράφεται και συνοπτικά ως \(\{\lim X_n=X\}\) και έτσι σύντομα γράφουμε \(\mathbf{P}(\lim X_n=X)=1\) για να δηλώσουμε την παραπάνω σύγκλιση. Από τον ορισμό αυτό είναι φανερό ότι το μόνο που χρειάζεται να ορίσει κανείς είναι η σύγκλιση στο \(0\), αφού

\[\begin{equation*} X_n\xrightarrow[]{a.s.}X \quad \Longleftrightarrow \quad |X_n - X| \xrightarrow[]{a.s.} 0. \end{equation*}\]

Ο τρόπος αυτός σύγκλισης χαρακτηρίζει την ασυμπτωτική συμπεριφορά της ακολουθίας των δειγματικών μέσων μιας ακολουθίας ανεξάρτητων και ισόνομων τυχαίων μεταβλητών, έτσι όπως διατυπώνεται στον Ισχυρό Νόμο των Μεγάλων Αριθμών.

Θεώρημα 3.1 (Strong Law of Large Numbers) Έστω \((X_n)\) μία ακολουθία ανεξάρτητων και ισόνομων τυχαίων μεταβλητών με \(\mathbf{E}|X_1|< +\infty\). Αν \(\overline{X}_n\) είναι ο δειγματικός μέσος, τότε

\[\begin{equation*} \overline{X}_n \xrightarrow[]{a.s.} \mathbf{E}(X_1). \end{equation*}\]

Στη στατιστική, ο παραπάνω τρόπος σύγκλισης μιας ακολουθίας τυχαίων μεταβλητών έχει μία άμεση εφαρμογή σε έναν ισχυρό τρόπο σύγκλισης εκτιμητριών στην υπό εκτίμηση παράμετρο. Είμαστε τώρα σε θέση να ορίσουμε την ισχυρή συνέπεια μιας εκτιμήτριας.

Ορισμός 3.5 Μία εκτιμήτρια \(\widehat{\theta}_n\) μιας παραμέτρου \(\theta\in \Theta\) λέγεται ισχυρά συνεπής, αν \[\begin{equation*} \widehat{\theta}_n \xrightarrow[n\rightarrow \infty]{a.s.} \theta, \qquad \quad \textrm{για κάθε } \theta \in \Theta. \end{equation*}\]

Ερμηνεία: Όταν μία εκτιμήτρια είναι ισχυρά συνεπής, τότε πρακτικά κάθε δυνατό μονοπάτι εκτίμησης καταλήγει στην άγνωστη παράμετρο, όποια και αν είναι αυτή.

Στην περίπτωση που έχουμε πολυπαραμετρικά προβλήματα, μία εκτιμήτρια αντιστοιχεί σε μία ακολουθία τυχαίων διανυσμάτων. Οι παραπάνω έννοιες επεκτείνονται φυσιολογικά για διανύσματα. Ο ισχυρός τρόπος σύγκλισης επεκτείνεται εντελώς φυσιολογικά για ακολουθίες τυχαίων διανυσμάτων. Ο τυπικός ορισμός είναι όπως και στη μονοδιάστατη περίπτωση, απλά η έννοια του ορίου νοείται ως προς την ευκλείδια νόρμα.

Ορισμός 3.6 Μία ακολουθία τ.δ. \((X_n)\) λέμε ότι συγκλίνει ή σχεδόν βεβαίως, ή ισχυρά, σε ένα τ.δ. \(X\), και γράφουμε \(X_n\xrightarrow[]{a.s.}X\), αν

\[\begin{equation*} ||X_n - X|| \xrightarrow[]{a.s.} 0 \quad \textrm{ή ισοδύναμα} \quad \mathbf{P}(\lim X_n=X)=1. \end{equation*}\]

Ασθενέστερη της παραπάνω σύγκλισης είναι η στοχαστική σύγκλιση.

Ορισμός 3.7 Μία ακολουθία τ.μ. \((X_n)\) λέμε ότι συγκλίνει κατά πιθανότητα ή στοχαστικά σε μία τ.μ. \(X\), και γράφουμε \(X_n\xrightarrow[]{p}X\), αν για κάθε \(\epsilon > 0\)

\[\begin{equation*} \mathbf{P}\big(\lvert \, X_n - X \rvert > \epsilon \big) \xrightarrow[n \rightarrow\infty]{} 0 \quad \textrm{ή ισοδύναμα} \quad \mathbf{P}\big(\lvert \, X_n - X \rvert \leq \epsilon \big) \xrightarrow[n \rightarrow\infty]{} 1. \end{equation*}\]

Όπως για την ισχυρή σύγκλιση, έτσι και για τη στοχαστική, έχουμε

\[\begin{equation*} X_n\xrightarrow[]{p}X \quad \Longleftrightarrow \quad |X_n - X|\xrightarrow[]{p} 0. \end{equation*}\]

Ο τρόπος αυτός σύγκλισης εμφανίζεται στην ασυμπτωτική συμπεριφορά της ακολουθίας των δειγματικών μέσων μιας ακολουθίας ανεξάρτητων και ισόνομων τυχαίων μεταβλητών, έτσι όπως διατυπώνεται στον Ασθενή Νόμο των Μεγάλων Αριθμών.

Θεώρημα 3.2 (Weak Law of Large Numbers) Έστω \((X_n)\) μία ακολουθία ανεξάρτητων και ισόνομων τυχαίων μεταβλητών με \(\mathbf{E}|X_1|< +\infty\). Αν \(\overline{X}_n\) είναι ο δειγματικός μέσος, τότε

\[\begin{equation*} \overline{X}_n \xrightarrow[]{p} \mathbf{E}(X_1). \end{equation*}\]

Στη στατιστική, ο παραπάνω τρόπος σύγκλισης μιας ακολουθίας τυχαίων μεταβλητών έχει μία άμεση εφαρμογή σε έναν ασθενέστερο τρόπο σύγκλισης εκτιμητριών στην υπό εκτίμηση παράμετρο από αυτόν που αντιστοιχεί στην ισχυρή συνέπεια. Είμαστε τώρα σε θέση να ορίσουμε την (ασθενή) συνέπεια μιας εκτιμήτριας.

Ορισμός 3.8 Μία εκτιμήτρια \(\widehat{\theta}_n\) μιας παραμέτρου \(\theta\in \Theta\) λέγεται (ασθενώς) συνεπής, αν \[\begin{equation*} \widehat{\theta}_n \xrightarrow[n\rightarrow \infty]{p} \theta, \qquad \quad \textrm{για κάθε } \theta \in \Theta. \end{equation*}\]

Ερμηνεία: Όταν μία εκτιμήτρια είναι συνεπής, τότε θεωρητικά, καθώς το μέγεθος του δείγματος αυξάνει, γίνεται όλο και πιο σπάνιο το ενδεχόμενο να βρεθεί η εκτιμήτρια \(\epsilon\)-μακριά από την άγνωστη παράμετρο, όποια και αν είναι αυτή. Ισοδύναμα, γίνεται όλο και πιο συχνό το ενδεχόμενο να βρεθεί η εκτιμήτρια \(\epsilon\)-κοντά στην υπό εκτίμηση παράμετρο.

Καθώς θέλουμε να αντιμετωπίσουμε και προβλήματα πολυπαραμετρικά οδηγούμαστε στην ακόλουθη επέκταση της στοχαστικής σύγκλισης, όπως κάναμε και για την ισχυρή.

Ορισμός 3.9 Μία ακολουθία τ.δ. \((X_n)\) λέμε ότι συγκλίνει κατά πιθανότητα ή στοχαστικά σε ένα τ.δ. \(X\), και γράφουμε \(X_n\xrightarrow[]{p}X\), αν

\[\begin{equation*} ||X_n - X|| \xrightarrow[]{p} 0. \end{equation*}\]

Παρόλο που η ισχυρή και η στοχαστική σύγκλιση εμπλέκουν τη συμπεριφορά της νόρμας στον \(\mathbb{R}^{d}\), η μελέτη τους απλοποιείται και είναι ισοδύναμη με την εξέταση των αντίστοιχων ορίων κατά συνιστώσα. Συγκεκριμένα, είναι εύκολο να δειχθεί το επόμενο αποτέλεσμα.

Πρόταση 3.1 Έστω \((X_n)=(X_{n,1},X_{n,2},\ldots,X_{n,d})\) μία ακολουθία τυχαίων διανυσμάτων και \(X=(X_{1},X_{2},\ldots,X_{d})\) ένα ακόμα τυχαίο διάνυσμα. Τότε, \[\begin{equation*} X_n \xrightarrow[]{a.s./p} X \quad \Longleftrightarrow \quad X_{n,i} \xrightarrow[]{a.s./p} X_{i}, \quad \textrm{για κάθε} \ i=1,2,\ldots,d, \end{equation*}\] δηλαδή, και οι δύο συγκλίσεις είναι ισοδύναμες με τις αντίστοιχες συγκλίσεις κατά συνιστώσα.

Με βάση την παραπάνω πρόταση καταλήγουμε άμεσα σε πολυδιάστατες επεκτάσεις του Ισχυρού Νόμου των Μεγάλων Αριθμών (Ι.Ν.Μ.Α.), αλλά και του Ασθενή Νόμου των Μεγάλων Αριθμών (Α.Ν.Μ.Α.).

Πόρισμα 3.1 Έστω \((X_n)\) μία ακολουθία ανεξάρτητων και ισόνομων τ.δ. με \(\mathbf{E}||X_1||< +\infty\). Αν \(\overline{X}_n\) είναι ο δειγματικός μέσος, τότε

\[\begin{equation*} \overline{X}_n \xrightarrow[]{a.s.} \mathbf{E}(X_1) \qquad (\textrm{I.N.M.A}) \end{equation*}\]

και

\[\begin{equation*} \overline{X}_n \xrightarrow[]{p} \mathbf{E}(X_1) \qquad (\textrm{Α.N.M.A}) \end{equation*}\]

Όπως βέβαια και στη μονοδιάστατη περίπτωση ο Α.Ν.Μ.Α. είναι συνέπεια του Ι.Ν.Μ.Α., καθώς η στοχαστική σύγκλιση προκύπτει άμεσα από την ισχυρή.

Πιο σύνθετη είναι η κατάσταση στη σύγκλιση κατά κατανομή. Η σημασία βέβαια της σύγκλισης αυτής είναι τεράστια και έχει πολλές εφαρμογές, ιδιαίτερα δε στη Στατιστική. Έτσι έχουν δοθεί αρκετοί ισοδύναμοι χαρακτηρισμοί. Υπενθυμίζουμε πρώτα τον ορισμό που συνήθως δίνεται για ακολουθίες πραγματικών τυχαίων μεταβλητών.

Ορισμός 3.10 Μία ακολουθία τ.μ. \((X_n)\) λέμε ότι συγκλίνει κατά κατανομή ή ασθενώς σε μία τ.μ. \(X\), και γράφουμε \(X_n\xrightarrow[]{d}X\), αν για κάθε \(x\in \mathbb{R}\) με \(F(x-)=F(x)\) (σημεία συνεχείας της \(F\)),

\[\begin{equation*} F_{n}(x) \xrightarrow[n \rightarrow \infty]{} F(x), \end{equation*}\]

όπου \(F_n\) είναι η συνάρτηση κατανομής της \(X_n\) και \(F\) είναι η σ.κ. της \(X\).

Η συνάρτηση κατανομής είναι ένα βολικό αντικείμενο περιγραφής της κατανομής μιας πραγματικής τ.μ. (επεκτείνεται και στις διανυσματικές), με το πλεονέκτημα ότι ορίζεται με ενιαίο τρόπο για συνεχείς και διακριτές τ.μ..

Στην ισχυρή και στη στοχαστική σύγκλιση, όλες οι τ.μ. πρέπει να είναι ορισμένες στον ίδιο χώρο πιθανότητας. Στην ασθενή σύγκλιση αυτό δεν είναι απαραίτητο, αλλά δεν θα επεκταθούμε άλλο σε αυτό το θέμα.

Στην παρακάτω πρόταση υπενθυμίζουμε τη σχέση που έχουν οι διάφοροι τρόποι σύγκλισης μεταξύ τους.

Πρόταση 3.2 Έστω \((X_n)\) μία ακολουθία τ.μ. και \(X\) μία ακόμα τ.μ. ορισμένες σε κοινό χώρο πιθανότητας. Τότε

\[\begin{equation*} X_n \xrightarrow[]{a.s.}X \ \ \Rightarrow \ \ X_n \xrightarrow[]{p} X \ \ \Rightarrow \ \ X_n \xrightarrow[]{d} X. \end{equation*}\]

Στην ειδική περίπτωση που \(X\stackrel{a.s.}=c\), όπου \(c\) σταθερά, τότε \[\begin{equation*} X_n \xrightarrow[]{p} c \ \Longleftrightarrow \ X_n \xrightarrow[]{d} c. \end{equation*}\]

Υπενθυμίζουμε τώρα το κλασικό Κεντρικό Οριακό Θεώρημα (Lindeberg-Levy) σε δύο ισοδύναμες μορφές.

Πρόταση 3.3 Έστω \((X_n)\) μία ακολουθία ανεξάρτητων και ισόνομων τ.μ. με \(\mathbf{E}(X_1 ^{2})< +\infty\). Θέτουμε \(\mu_X=\mathbf{E}(X)\) και \(\sigma_{X}^{2}=\mathbf{V}(X)\). Αν \(\left(\overline{X}_n\right)\) είναι η ακολουθία των δειγματικών μέσων και \((S_n)\) η ακολουθία των μερικών αθροισμάτων της \((X_n)\), τότε

\[\begin{equation*} \sqrt{n}\left(\,\overline{X}_n-\mu_X\right) \xrightarrow[]{d} \mathcal{N}\,(0, \, \sigma_{X}^{2}), \end{equation*}\]

και

\[\begin{equation*} \frac{S_n- n\,\mu_X}{\sqrt{n}} \xrightarrow[]{d} \mathcal{N}\,(0, \, \sigma_{X}^{2}). \end{equation*}\]

3.2.3 Θεώρημα Συνεχούς Απεικόνισης

Το επόμενο θεώρημα είναι πολύ χρήσιμο για να βρίσκουμε τις ασυμπτωτικές ιδιότητες συνεχών συναρτήσεων τυχαίων μεταβλητών ή τυχαίων διανυσμάτων, όταν γνωρίζουμε τις ασυμπτωτικές ιδιότητες των τελευταίων. Μπορούμε να το δούμε και ως γενίκευση της αρχής της μεταφοράς.

Θεώρημα 3.3 (Continuous Mapping Theorem) Έστω \((X_n)\), \(X\) τυχαία διανύσματα με τιμές στον \(\mathbb{R}^d\). Αν \(g: \mathbb{R}^d\rightarrow \mathbb{R}^{\ell}\) και η \(g\) είναι συνεχής σε κάποιο \(C\in \mathcal{B}(\mathbb{R}^d)\), τέτοιο ώστε \(\textbf{P}(X\in C)=1\), τότε

\[\begin{equation}\label{continuity-theorem} X_n \xrightarrow{a.s./p/d} X \quad \Rightarrow \quad g(X_n) \xrightarrow{a.s./p/d} g(X). \end{equation}\]

Λήμμα 3.1 Αν \(X_n\xrightarrow{d} X\) και \(X_n-Y_n\xrightarrow{p} 0\), τότε \(Y_n\xrightarrow{d}X\).

Λήμμα 3.2 Αν \(X_n\xrightarrow{d} X\) και \(Y_n\xrightarrow{p} c\), τότε \((X_n, Y_n)\xrightarrow{d} (X, c)\).

Θεώρημα 3.4 (Slutsky) Αν \(X_n, Y_n, X, c\) τυχαία διανύσματα ή πίνακες με κατάλληλες διαστάσεις και \(X_n\xrightarrow{d} X\), \(Y_n\xrightarrow{p}c\), τότε \(X_n+Y_n\xrightarrow{d} X+c\), \(Y_n X_n \xrightarrow{d} cX\) και, αν \(c\) αντιστρέψιμος, τότε \(Y_n^{-1} X_n \xrightarrow{d} c^{-1} X\).

Παρατήρηση:. Αν \(X_n\xrightarrow{as/p} X\), \(Y_n\xrightarrow{as/p} Y\), τότε \(X_n+Y_n \xrightarrow{as/p} X+Y\), \(X_n Y_n \xrightarrow{as/p} XY\) και \(Y_n^{-1} X_n \xrightarrow{as/p} Y^{-1} X\), αν υπάρχουν τα αντίστροφα. Γενικά όμως δεν ισχύει για τη σύγκλιση κατά κατανομή.

3.2.4 Μέθοδος Δέλτα

H μέθοδος δέλτα είναι μία από τις πιο χρήσιμες μεθόδους για να βρίσκουμε την ασυμπτωτική κατανομή μιας εκτιμήτριας που μπορεί να εκφραστεί ως διαφορίσιμη συναρτηση κάποιας άλλης εκτιμήτριας (συνήθως μέσω plug-in) της οποίας γνωρίζουμε την ασυμπτωτική της κατανομή. Παρουσιάζουμε τη μέθοδο κατ’ευθείαν στην πολυδιάστατη περίπτωση.

Θεώρημα 3.5 Έστω \(\phi: D_{\phi}\subset \mathbb{R}^d \rightarrow \mathbb{R}^m\) μία διαφορίσιμη απεικόνιση στο \(\theta\in D_{\phi}\) και \(X_n\in D_{\phi}\) για κάθε \(n\geq 1\). Αν \((r_n)\) ακολουθία με \(r_n\rightarrow \infty\) και \(r_n(X_n-\theta)\xrightarrow{d} X\), τότε \[\begin{equation}\label{delta} r_n\Big(\phi(X_n)-\phi(\theta)\Big)\, \xrightarrow{d}\, \Phi'_{\theta} \cdot X, \end{equation}\] όπου \(\Phi'_{\theta} := \left(\dfrac{\partial \phi_i}{\partial x_j} \right)\Bigg\vert_{x=\theta}\) είναι ο Ιακωβιανός πίνακας της \(\phi\) υπολογισμένος στο \(\theta\). Ειδικά για \(d=m=1\), έχουμε \[\begin{equation}\label{delta_alternative_1} r_n\Big(\phi(X_n)-\phi(\theta)\Big)\, \xrightarrow{d}\, \phi^{'}(\theta)\cdot X, \end{equation}\]

Σε πολλές περιπτώσεις έχουμε \(r_n=\sqrt{n}\) και οριακή κανονική κατανομή.

Πόρισμα 3.2 Με υποθέσεις όπως πριν, αν \(\sqrt{n}(X_n-\theta)\xrightarrow{d} N_d(0, \Sigma),\) τότε \[\begin{equation}\label{delta_corollary} \sqrt{n}\, \Big(\phi(X_n)-\phi(\theta)\Big)\, \xrightarrow{d}\, N_d\Big( 0, \Phi'_{\theta}\,\Sigma\, (\Phi'_{\theta})^{\top} \Big). \end{equation}\] Ειδικά για \(d=m=1\) και \(\Sigma=\sigma^2\), έχουμε \[\begin{equation}\label{delta_corollary2} \sqrt{n}\, \Big(\phi(X_n)-\phi(\theta)\Big)\, \xrightarrow{d}\, N\Big( 0, (\phi'(\theta))^2\,\sigma^2 \Big). \end{equation}\]

3.3 Κλασική Monte Carlo Ολοκλήρωση

Όπως είδαμε στην προηγούμενη παράγραφο, το ζητούμενο των μεθόδων ολοκλήρωσης Monte Carlo είναι η προσέγγιση του ολοκληρώματος

\[\begin{equation*} I=\mathbf{E}_f\left[h(X)\right]=\int_\mathcal{X} h(x)f(x) dx, \end{equation*}\]

όπου \(X\) τυχαία μεταβλητή με σ.π.π. \(f\) και τιμές στο \(\mathcal{X}\). Θα πρέπει να είναι σαφές από την αρχή ότι η αναπαράσταση του \(I\) στη μορφή αυτή δεν είναι μοναδική και έτσι αλλάζοντας τις \(h\) και \(f\) μπορούμε να οδηγηθούμε στην ίδια ολοκληρωτέα συνάρτηση \(h\cdot f\).

Η ανάλυση της αποδοτικότητας τέτοιων αναπαραστάσεων είναι ένα θέμα που θα μας απασχολήσει αργότερα. Ας ξεκινήσουμε με το πρόβλημα εκτίμησης του \(I\) στη μορφή αυτή. Είναι φανερό λοιπόν, ότι αν μπορούμε να προσομοιώσουμε από την \(f\) χρησιμοποιώντας ένα (ψευδο)τυχαίο δείγμα \(X_1, X_2, ..., X_n\) από αυτήν την κατανομή θα έχουμε ότι ο δειγματικός μέσος

\[\begin{equation*} \overline{h}_n = \frac{1}{n}\sum_{j=1}^n h(X_j), \end{equation*}\]

αποτελεί μία αμερόληπτη εκτιμήτρια του \(I\).

Η μεγάλη υπολογιστική ισχύς που διαθέτουμε σήμερα μας δίνει τη δυνατότητα να παράγουμε εκατομμύρια παρατηρήσεις από μία κατανομή ενδιαφέροντος και έτσι τίθεται σε ισχύ η ασυμπτωτική θεωρία.

Συγκεκριμένα, αν \(\mathbf{E}_f|h(X)|<+\infty\), συνθήκη η οποία είναι αναγκαία για την ύπαρξη του ολοκληρώματος \(I\) που θέλουμε να υπολογίσουμε, τότε γνωρίζουμε ότι εφαρμόζεται ο Ισχυρός Νόμος των Μεγάλων Αριθμών (I.N.M.A.) και άρα,

\[\begin{equation*} \overline{h}_n \overset{a.s.}{\longrightarrow} \mathbf{E}_f\left[h(X)\right] = I, \quad n\rightarrow +\infty. \end{equation*}\]

Το παραπάνω αποτέλεσμα μας εξασφαλίζει ότι τυπικά (σχεδόν για κάθε πραγματοποίηση) θα έχουμε σύγκλιση της ακολουθίας \(\left(\overline{h}_n(\omega)\right)_n\) στην τιμή \(I\). Το ισχυρό αυτό αποτέλεσμα μας εξασφαλίζει ότι πρακτικά όποια προσομοίωση και να κάνουμε στον υπολογιστή, μπορούμε να βρεθούμε οσοδήποτε κοντά θέλουμε στο \(I\), χρησιμοποιώντας επαρκώς μεγάλο μέγεθος δείγματος.

Παράδειγμα 3.3 Για να έχουμε μία εικόνα του παραπάνω αποτελέσματος σε ένα απλό παράδειγμα ας υποθέσουμε ότι θέλουμε να υπολογίσουμε το

\[\begin{equation*} I = \int_{-\infty}^{+\infty} e^{-x^2/2} dx. \end{equation*}\]

Είναι γνωστό ότι \(I=\sqrt{2\pi}\), αφού το \(1/I\) αποτελεί τη σταθερά κανονικοποίησης της τυπικής κανονικής κατανομής. Έχουμε λοιπόν

\[\begin{equation*} I = \int_{-\infty}^{+\infty} \underbrace{\frac{2\,e^{-x^2/2}}{ e^{-|x|}}}_{h(x)} \cdot \underbrace{\frac{1}{2} e^{-|x|}}_{f(x)} dx = \mathbf{E}_f\left[h(X)\right], \end{equation*}\]

όπου \(f(x)\) είναι η σ.π.π. της διπλής εκθετικής (Laplace) και

\[\begin{equation*} h(x) = 2 e^{-\frac{x^2}{2}+|x|}, \ \forall x \in \mathbb{R}. \end{equation*}\]

Στο παρακάτω γράφημα μπορούμε να δούμε 4 προσομοιωμένα μονοπάτια της εξέλιξης του δειγματικού μέσου \(\overline{h}_{1,n}\), όταν η κατανομή πρότασης αντιστοιχεί στη διπλή εκθετική.

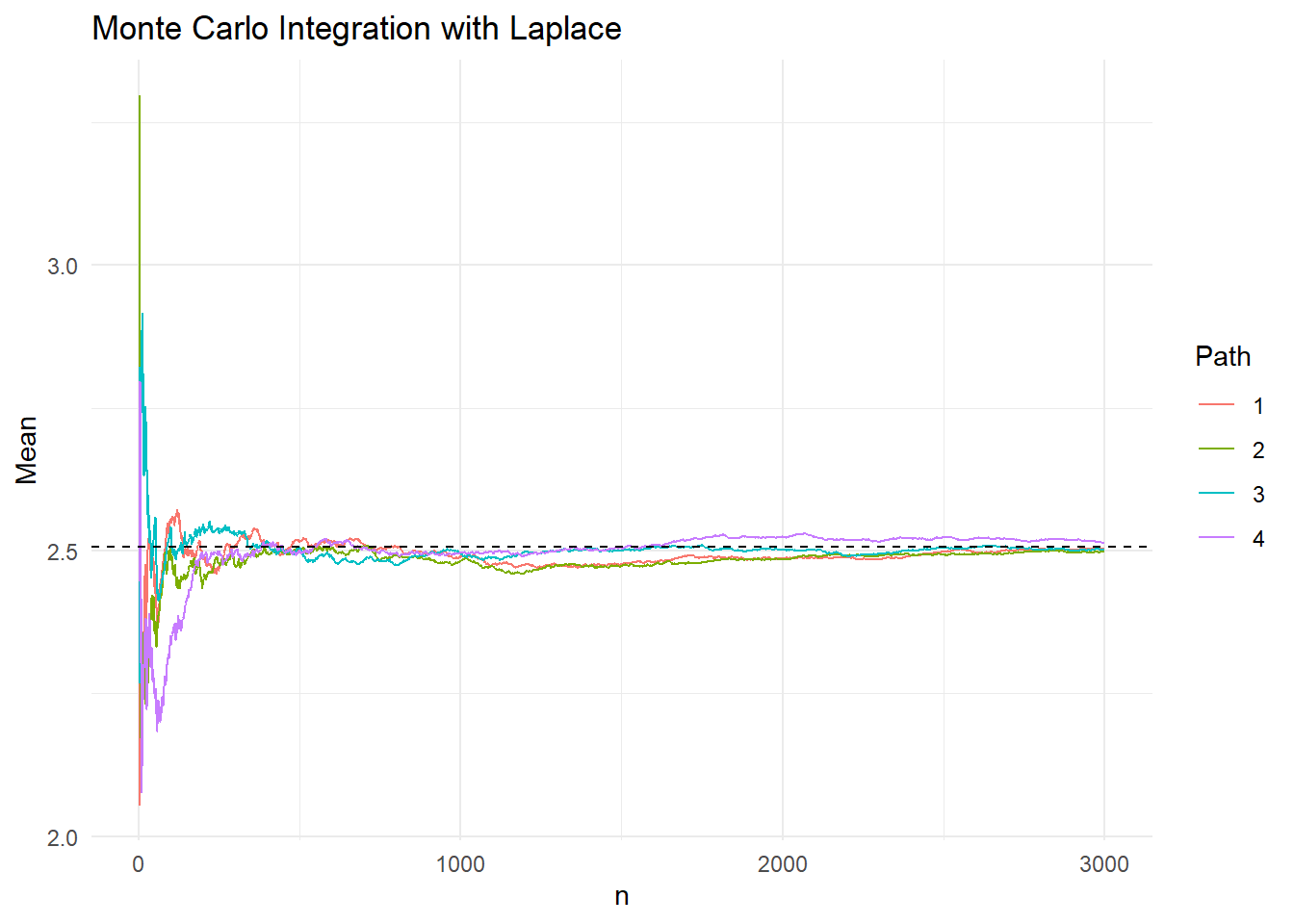
Η επιλογή \(f=f_1\) με \(f_1\) την σ.π.π. της διπλής εκθετικής είναι μία δυνατή από πολλές διαφορετικές επιλογές (προφανώς άπειρες). Ας δούμε μία διαφορετική επιλογή \(f=f_2\) με \(f_2\) τη σ.π.π. της τυπικής Cauchy. Με αυτήν την επιλογή της \(f\), έχουμε \(h_2=g/f_2\) και

\[\begin{equation*} I=\int_{-\infty}^{+\infty} \underbrace{e^{-x^2/2}}_{g(x)} dx = \int_{-\infty}^{+\infty} \underbrace{\pi (1+x^2) e^{-x^2/2}}_{g/f_2=h_2} \cdot \underbrace{\frac{1}{\pi(1+x^2)}}_{f_2} dx = \mathbf{E}_{f_2}\left[h_2(X)\right]. \end{equation*}\]

Στο παρακάτω γράφημα βλέπουμε 4 προσομοιωμένα μονοπάτια της εξέλιξης του δειγματικού μέσου \(\overline{h}_{2,n}\), όταν η κατανομή πρότασης αντιστοιχεί στην κατανομή Cauchy.

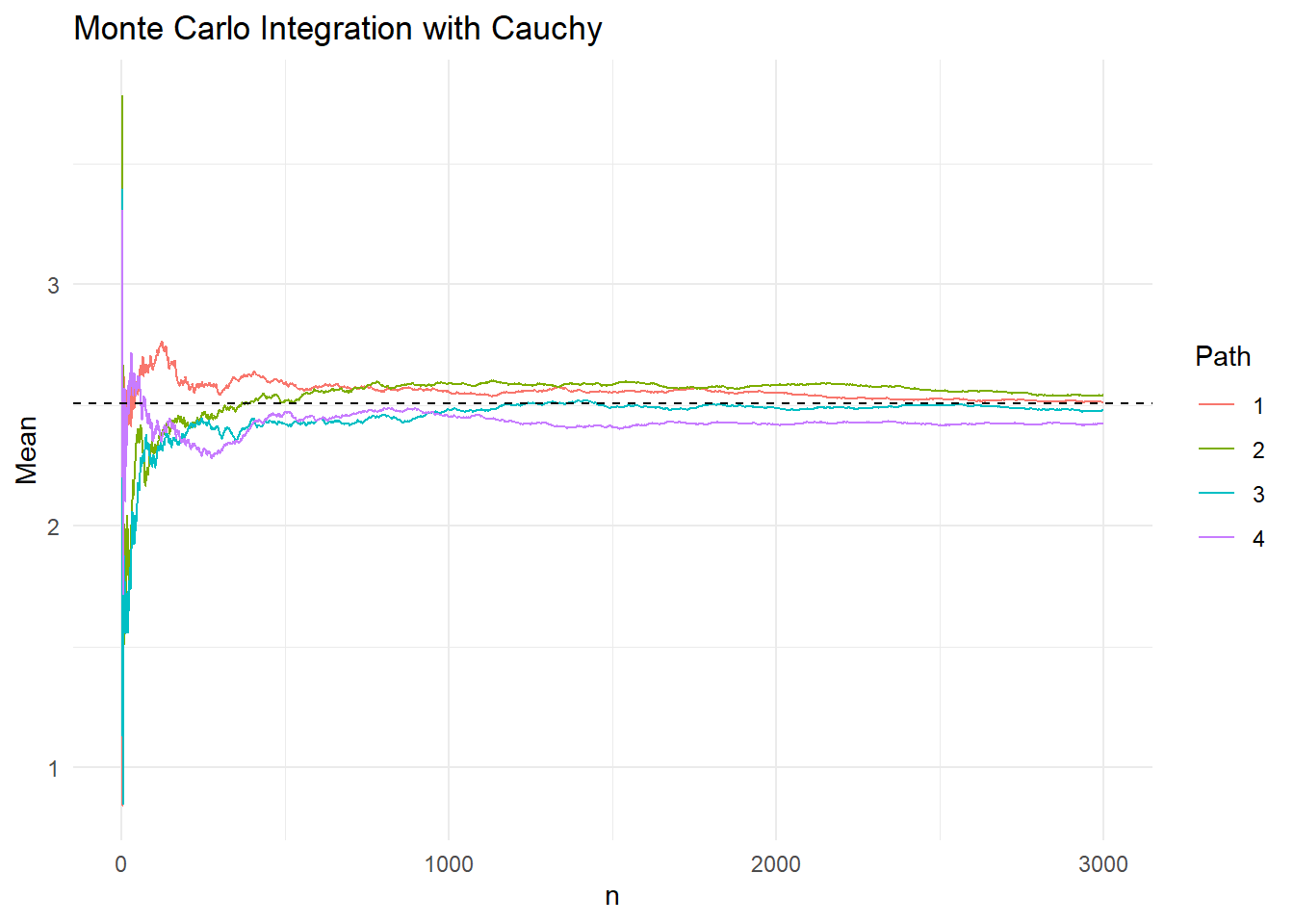
Αν και με τις δύο κατανομές πρότασης οι εκτιμήτριες που προκύπτουν είναι αμερόληπτες, μπορούμε εύκολα να παρατηρήσουμε ότι παρουσιάζουν διαφορετική μεταβλητότητα. Για να γίνει περισσότερο εμφανές, αντιπαραβάλλουμε τη συμπεριφορά των μονοπατιών σε ένα κοινό γράφημα

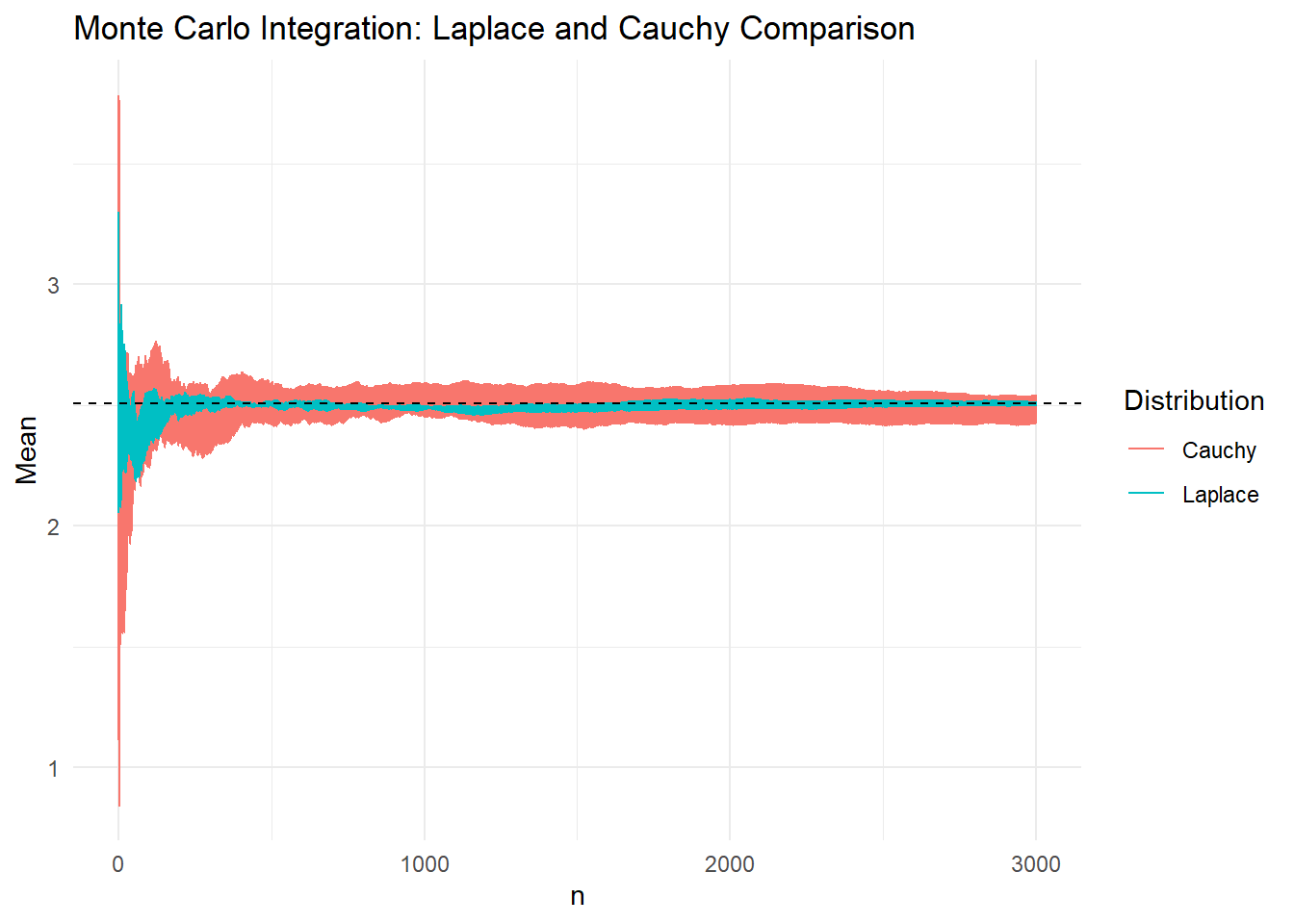
Στο παραπάνω γράφημα έχουν προσομοιωθεί 4 μονοπάτια από κάθε κατανομή και χρωματίζεται η περιοχή από την μικρότερη μέχρι την μεγαλύτερη τιμή των μονοπατιών σε κάθε βήμα \(n\). Είναι εμφανές ότι προσομοιώνοντας από τη Laplace επιτυγχάνουμε γρηγορότερη σύγκλιση στη σταθερά \(I\) απ’ ότι με την Cauchy.

Για να μπορέσουμε να συγκρίνουμε την απόδοση των δύο διαφορετικών τρόπων προσέγγισης χρειάζεται η σύγκριση των διασπορών τους. Ως αμερόληπτες εκτιμήτριες, εκείνη που θα έχει τη μικρότερη διασπορά, θα έχει και το μικρότερο μέσο τετραγωνικό σφάλμα. Σε κάποιες απλές περιπτώσεις, όπως εδώ, είναι δυνατός ο απ’ευθείας υπολογισμός της διασποράς. Σε κάποιες άλλες, που είναι η πλειοψηφία των περιπτώσεων σε πρακτικές εφαρμογές, είναι αναγκαία η εκτίμηση της διασποράς. Ας συγκρίνουμε πρώτα εδώ τις θεωρητικές τους διασπορές. Εφ’ όσον και οι δύο είναι αμερόληπτες εκτιμήτριες, η σύγκριση των διασπορών τους ανάγεται στη σύγκριση των ροπών δεύτερης τάξης.

\[\begin{align*} \mathbf{E}_{f_1}\left[h_1^2(X)\right] &= 4\int_{-\infty}^{+\infty} \left( e^{-x^2/2+|x|}\right)^2 \frac{1}{2} e^{-|x|} dx = 2 \int_{-\infty}^{+\infty} e^{-x^2+|x|} dx = 2 e^{1/4} \int_{-\infty}^{+\infty} e^{-x^2+|x|-1/4} dx \\ & = 2 e^{1/4} \int_{-\infty}^{+\infty} e^{-\frac{(\sqrt{2}|x|-1/\sqrt{2})^2}{2}} dx = 2 \sqrt{\pi} e^{1/4} \int_{-\infty}^{+\infty} \frac{\sqrt{2}}{\sqrt{2\pi}} e^{-\frac{(\sqrt{2}|x|-1/\sqrt{2})^2}{2}} dx \\ & = 2 \sqrt{\pi} e^{1/4} \left( \int_{-\infty}^{0} \frac{\sqrt{2}}{\sqrt{2\pi}} e^{-\frac{(\sqrt{2}x+1/\sqrt{2})^2}{2}} dx +\int_{0}^{+\infty} \frac{\sqrt{2}}{\sqrt{2\pi}} e^{-\frac{(\sqrt{2}x-1/\sqrt{2})^2}{2}} dx \right) \\ &= 2\sqrt{\pi} e^{1/4} \left( \int_{-\infty}^{1/\sqrt{2}} \frac{1}{\sqrt{2\pi}} e^{-y^2/2} dy + \int_{-1/\sqrt{2}}^{+\infty} \frac{1}{\sqrt{2\pi}} e^{-y^2/2} dy \right) \\ &= 2 \sqrt{\pi} e^{1/4} \left[ \Phi\left(1/\sqrt{2}\right) +1 -\Phi\left(-1/\sqrt{2}\right) \right] \\ &= 4 \sqrt{\pi} e^{1/4} \cdot \Phi\left(1/\sqrt{2}\right) \end{align*}\]

Από την άλλη μεριά,

\[\begin{align*} \mathbf{E}_{f_2}\left[h_2^2(X)\right] &= \int_{-\infty}^{+\infty} \pi^2 (1+x^2)^2 e^{-x^2} \frac{1}{\pi (1+x^2)} dx = \pi \int_{-\infty}^{+\infty} (1+x^2) e^{-x^2} dx \\ &= \pi \left( \int_{-\infty}^{+\infty} e^{-x^2} dx + \int_{-\infty}^{+\infty} x^2 e^{-x^2} dx \right) = \pi \left( \sqrt{\pi} + \sqrt{\pi} \underbrace{\int_{-\infty}^{+\infty} \frac{y^2}{\sqrt{2\pi}} e^{-y^2/2} dy}_{\mathbf{E}(Z^2)=1} \right) \\ &= 2\pi \sqrt{\pi}. \end{align*}\]

Η σύγκριση αυτή μας οδηγεί στο συμπέρασμα ότι \[\begin{equation*} \mathbf{E}_{f_1}\left[h_1^2(X)\right] \approx 6.92 < 11.14 \approx \mathbf{E}_{f_2}\left[h_2^2(X)\right] \end{equation*}\]

και συνεπώς \[\begin{equation*} \mathbf{V}_{f_1}\left[h_1(X)\right] \approx 0.64 < 4.85 \approx \mathbf{V}_{f_2}\left[h_2(X)\right] \end{equation*}\]

Όταν μία μέθοδος προσομοίωσης μας εξασφαλίζει μικρότερη διασπορά, τότε αυτό σημαίνει πρακτικά ότι θα χρειαζόμαστε μικρότερο πλήθος προσομοιώσεων για να εξασφαλίσουμε μία δεδομένη ακρίβεια και έτσι η μέθοδος αυτή είναι πιο αποδοτική. Τις περισσότερες φορές η διασπορά θα είναι άγνωστη και θα πρέπει να εκτιμηθεί από το ίδιο δείγμα. Αν \(\overline{h}_n\) είναι ο δειγματικός μέσος, τότε

\[\begin{equation*} \sigma^2_{\overline{h}_n}=\mathbf{V}_f\left(\overline{h}_n\right) = \frac{\mathbf{V}_f\left[h(X)\right]}{n} = \frac{\sigma^2_h}{n}. \end{equation*}\]

Με την προϋπόθεση λοιπόν ότι η παραπάνω διασπορά είναι πεπερασμένη, μπορούμε να την εκτιμήσουμε με χρήση της δειγματικής διασποράς. Αν

\[\begin{equation*} \widehat{\sigma^2}_{h,n}=\frac{1}{n} \sum_{j=1}^n\left(h(X_j)-\overline{h}_n\right)^2, \end{equation*}\]

είναι η (μη αμερόληπτη) εκτιμήτρια της \(\mathbf{V}_f\left[h(X)\right]\), τότε η εκτιμήτρια της \(\mathbf{V}_f\left(\overline{h}_n\right)\) προκύπτει από τη σχέση

\[\begin{equation*} \widehat{\sigma^2}_{\overline{h}_n}=\frac{\widehat{\sigma^2}_{h,n}}{n}= \frac{1}{n^2} \sum_{j=1}^n\left(h(X_j)-\overline{h}_n\right)^2. \end{equation*}\]

Παρατηρούμε επίσης ότι

\[\begin{equation*} \widehat{\sigma^2}_{h,n} = \overline{h^{2}_{n}} - (\overline{h}_n)^2 \xrightarrow[n\rightarrow \infty]{a.s.}\mathbf{E}_{f}\left[h^2(X)\right] - \mathbf{E}_{f}^2\left[h(X)\right]=\mathbf{V}_f\left[h(X)\right], \end{equation*}\]

όπου χρησιμοποιήσαμε τον Ι.Ν.Μ.Α. για την ακολουθία \(\{h^2(X_j)\}\) και το θεώρημα συνεχούς απεικόνισης. Η (ισχυρή) συνέπεια της δειγματικής διασποράς μας επιτρέπει να εκτιμήσουμε την άγνωστη διασπορά \(\mathbf{V}_f\left[h(X)\right]\) και να κατασκευάσουμε ασυμπτωτικά διαστήματα εμπιστοσύνης για την τιμή του \(I\). Πράγματι, από το κλασικό κεντρικό οριακό θεώρημα έχουμε

\[\begin{equation*} \sqrt{n}\, \Big(\overline{h}_n - Ι \Big)\, \xrightarrow{d}\, N( 0, \sigma^2_h ) \end{equation*}\] ή ισοδύναμα \[\begin{equation*} \sqrt{n}\ \frac{\overline{h}_n - Ι }{\sigma_h}\, \xrightarrow{d}\, N( 0,1) \end{equation*}\]

Από το θεώρημα του Slutsky και το Θ.Σ.Α. προκύπτει ότι \[\begin{equation*} \sqrt{n}\ \frac{\overline{h}_n - Ι }{\widehat{\sigma}_{h,n}}\, \xrightarrow{d}\, N( 0,1), \end{equation*}\]

δίνοντας ασυμπτωτικά (1-α)-Δ.Ε. της μορφής \[\begin{equation*} \overline{h}_n \pm z_{a/2}\frac{\widehat{\sigma}_{h,n}}{\sqrt{n}} \end{equation*}\]

Παράδειγμα 3.4 (Robert & Casella 3.3) Έστω ότι θέλουμε να εκτιμήσουμε το ολοκλήρωμα της

\[\begin{equation*} h(x)=\left[cos(50x)+sin(20x)\right]^2, \end{equation*}\]

στο \(\left[ 0, 1 \right]\). Μπορούμε να δούμε το ολοκλήρωμα ως μέση τιμή συνάρτησης μιας ομοιόμορφης τ.μ., και επομένως να προσομοιώσουμε \(U_1, U_2, ..., U_n\) από την \(\mathcal{Unif}(0,1)\) και να εκτιμήσουμε το \(\int h(x) dx\) με το \(\sum h(U_i)/n\). Υλοποιούμε την προσομοίωση στην R και παρουσιάζουμε το γράφημα της h(x) και της σύγκλισης του δειγματικού μέσου.

h <- function(x){
  (cos(50 * x) + sin(20 * x)) ^ 2
}
par(mar = c(2, 2, 2, 1), mfrow = c(2, 1))
curve(h, xlab = "Function", ylab = "", lwd = 2)
integrate(h, 0, 1)
## 0.9652009 with absolute error < 1.9e-10

x <- h(runif(10 ^ 4))
estint <- cumsum(x) / (1:(10 ^ 4))
esterr <- sqrt(cumsum((x - estint) ^ 2))/(1:(10 ^ 4))

plot(estint, xlab = "Mean and error range", type = "l", lwd = 2,
     ylim = mean(x) + 20 * c(-esterr[10 ^ 4], esterr[10 ^ 4]), ylab = "") 
lines(estint + 1.96 * esterr, col = "gold", lwd = 2)
lines(estint - 1.96 * esterr, col = "gold", lwd = 2)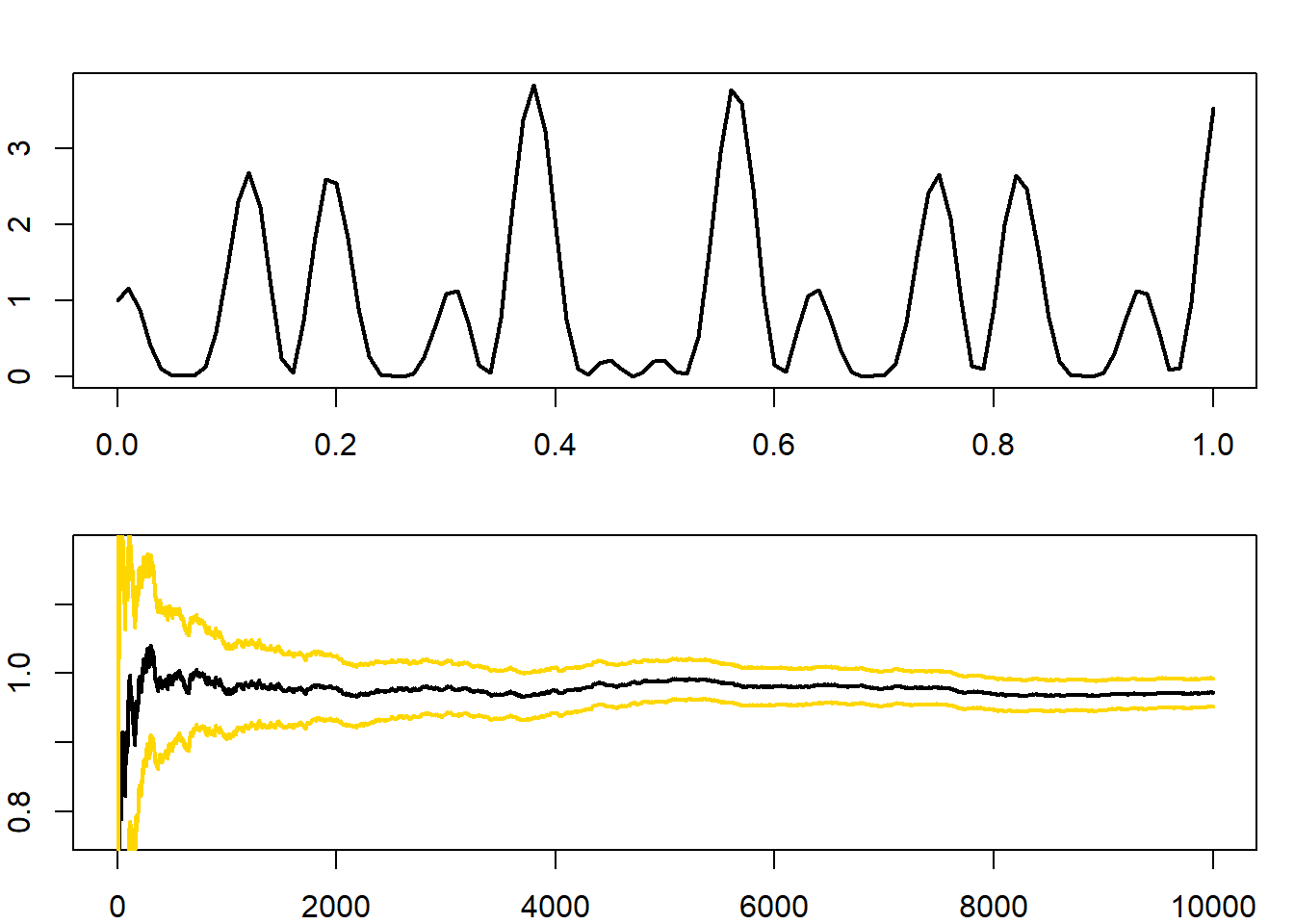

Σημειώνουμε ότι η λωρίδα εμπιστοσύνης που φαίνεται στο γράφημα δεν είναι μία ταυτόχρονη ασυμπτωτική \(95\%\) λωρίδα εμπιστοσύνης (simultaneous confidence band) αλλά μία σημειακή ασυμπτωτική (pointwise) \(95\%\) λωρίδα εμπιστοσύνης (δηλάδή υποδεικνύει το ασυμπτωτικό \(95\%\) διάστημα εμπιστοσύνης για κάθε μέγεθος δείγματος \(n\), εάν σταματούσαμε την προσομοίωση εκεί).

Παράδειγμα 3.5 (Robert & Casella 3.4) Δοθέντος ενός δείγματος \((x_1, x_2, ..., x_n)\) από την κανονική \(\mathcal{N}(0,1)\), η προσέγγιση του

\[\begin{equation*} \Phi(t)=\int_{-\infty}^t \frac{1}{\sqrt{2\pi}} e^{-y^2/2} dy, \end{equation*}\]

από την μέθοδο Monte Carlo είναι

\[\begin{equation*} \widehat{\Phi}(t)=\frac{1}{n} \sum_{i=1}^n \mathbb{I}_{x_i\leq t}, \end{equation*}\]

με (ακριβή) διασπορά \(\Phi(t)\left[1-\Phi(t)\right]/n\) (αφού οι \(\mathbb{I}_{x_i\leq t}\) είναι ανεξάρτητες Bernoulli με πιθανότητα επιτυχίας \(\Phi(t)\)).

x <- rnorm(10 ^ 8) # whole sample
bound <- qnorm(c(.5, .75, .8, .9, .95, .99, .999, .9999))
res <- matrix(0, ncol = 8, nrow = 7)
for (i in 2:8) { # lengthy loop!!
  for (j in 1:8) {
    res[i - 1, j] <- mean(x[1:(10 ^ i)] < bound[j])
  }
}
m <- matrix(as.numeric(format(res, digi = 4)), ncol = 8) 

(#tab:example_3_4_kable)Monte Carlo Approximations

	0.0	0.67	0.84	1.28	1.65	2.32	3.09	3.72
100	0.4900	0.7600	0.8500	0.9000	0.9500	0.9900	1.0000	1.0000
1000	0.5030	0.7380	0.8000	0.8870	0.9420	0.9880	0.9990	1.0000
10000	0.4911	0.7452	0.7987	0.9006	0.9514	0.9909	0.9988	1.0000
100000	0.4987	0.7502	0.8009	0.9011	0.9513	0.9907	0.9990	0.9999
1000000	0.5003	0.7497	0.8000	0.9003	0.9500	0.9901	0.9990	0.9999
10000000	0.5002	0.7501	0.8000	0.9001	0.9501	0.9900	0.9990	0.9999
100000000	0.5000	0.7499	0.7999	0.9000	0.9500	0.9900	0.9990	0.9999

Για τιμές του \(t\) γύρω από το \(0\), η διασπορά είναι κατά προσέγγιση \(1/4n\), και για να επιτύχουμε ακρίβεια τεσσάρων δεκαδικών, χρειαζόμαστε \(2\cdot \sqrt{1/4n}\le 10^{-4}\) προσομοιώσεις, δηλαδή περίπου \(n=(10^4)^2=10^8\) προσομοιώσεις. Ο πίνακας δείχνει την εξέλιξη αυτής της προσέγγισης για αρκετές τιμές του \(t\) και δίνει μία εκτίμηση (με ακρίβεια 4 δεκαδικών ψηφίων) για 100 εκατομμύρια επαναλήψεις. Σημειώνουμε ότι καλύτερη (απόλυτη) ακρίβεια επιτυγχάνεται στις ουρές και ότι η συγκεκριμένη προσέγγιση μπορεί να υλοποιηθεί με πολύ πιο αποδοτικές μεθόδους.

3.4 Εκτίμηση με Monte Carlo

Ενώ η χρήση των μεθόδων Monte Carlo ξεκίνησε ως μία διαδικασία προσεγγιστικής ολοκλήρωσης, μπορεί να χρησιμοποιηθεί για ποικίλους σκοπούς. Ας επιστρέψουμε τώρα στο παράδειγμα υπολογισμού του ολοκληρώματος \(I\) (3.3). Έχουμε:

\[\begin{equation*} I=\sqrt{2\pi} \Rightarrow \pi = \frac{I^2}{2} = \phi(I). \end{equation*}\]

Είναι φανερό λοιπόν, ότι έχοντας εκτιμήσει το \(I\) με κάποια Monte Carlo εκτιμήτρια \(\widehat{I}_n\), τότε μπορούμε να πάρουμε άμεσα μία εκτιμήτρια για το \(\pi\) με τη μέθοδο της αντικατάστασης (plug-in). Συγκεκριμένα,

\[\begin{equation*} \widehat{\pi}_n=\phi(\widehat{I_n}) = \frac{\left(\widehat{I_n}\right)^2}{2}. \end{equation*}\]

Εφόσον η \(\widehat{I}_n\) είναι ισχυρά συνεπής εκτιμήτρια του \(I\) και η \(\phi\) είναι συνεχής, από το Θ.Σ.Α. έχουμε μία ισχυρά συνεπή εκτιμήτρια του \(\pi\) καθώς

\[\begin{equation*} \widehat{\pi}_n=\phi(\widehat{I_n}) \overset{a.s.}{\longrightarrow} \phi(I) = \pi, \end{equation*}\]

και από την ασυμπτωτική κανονικότητα της \(\widehat{I}_n\) και τη μέθοδο Δέλτα για τη διαφορίσιμη \(\phi\), έχουμε

\[\begin{equation*} \sqrt{n}\left(\widehat{\pi}_n-\pi\right)=\sqrt{n}\left(\phi(\widehat{I_n})-\phi(I)\right)\overset{d}{\longrightarrow} \mathcal{N}\left(0, \left(\phi'(I)\right)^2 \sigma_h^2\right) = \mathcal{N}\left(0, I^2 \sigma_h^2\right). \end{equation*}\]

Ο προσδιορισμός της ακρίβειας της εκτίμησης γίνεται ασυμπτωτικά, χρησιμοποιώντας plug-in εκτιμήτρια της τυπικής απόκλισης \(Ι\, \sigma_h\). Από τη σχέση

\[\begin{equation*} \sqrt{n}\, \frac{\widehat{\pi}_n-\pi}{\widehat{Ι_n}\widehat{\sigma}_{h,n}}\overset{d}{\longrightarrow} \mathcal{N}(0,1), \end{equation*}\]

προσδιορίζουμε το ασυμπτωτικό (1-α)-Δ.Ε. για το \(\pi\):

\[\begin{equation*} \widehat{\pi}_n \pm z_{a/2} \frac{\widehat{Ι_n}\widehat{\sigma}_{h,n}}{\sqrt{n}}. \end{equation*}\]

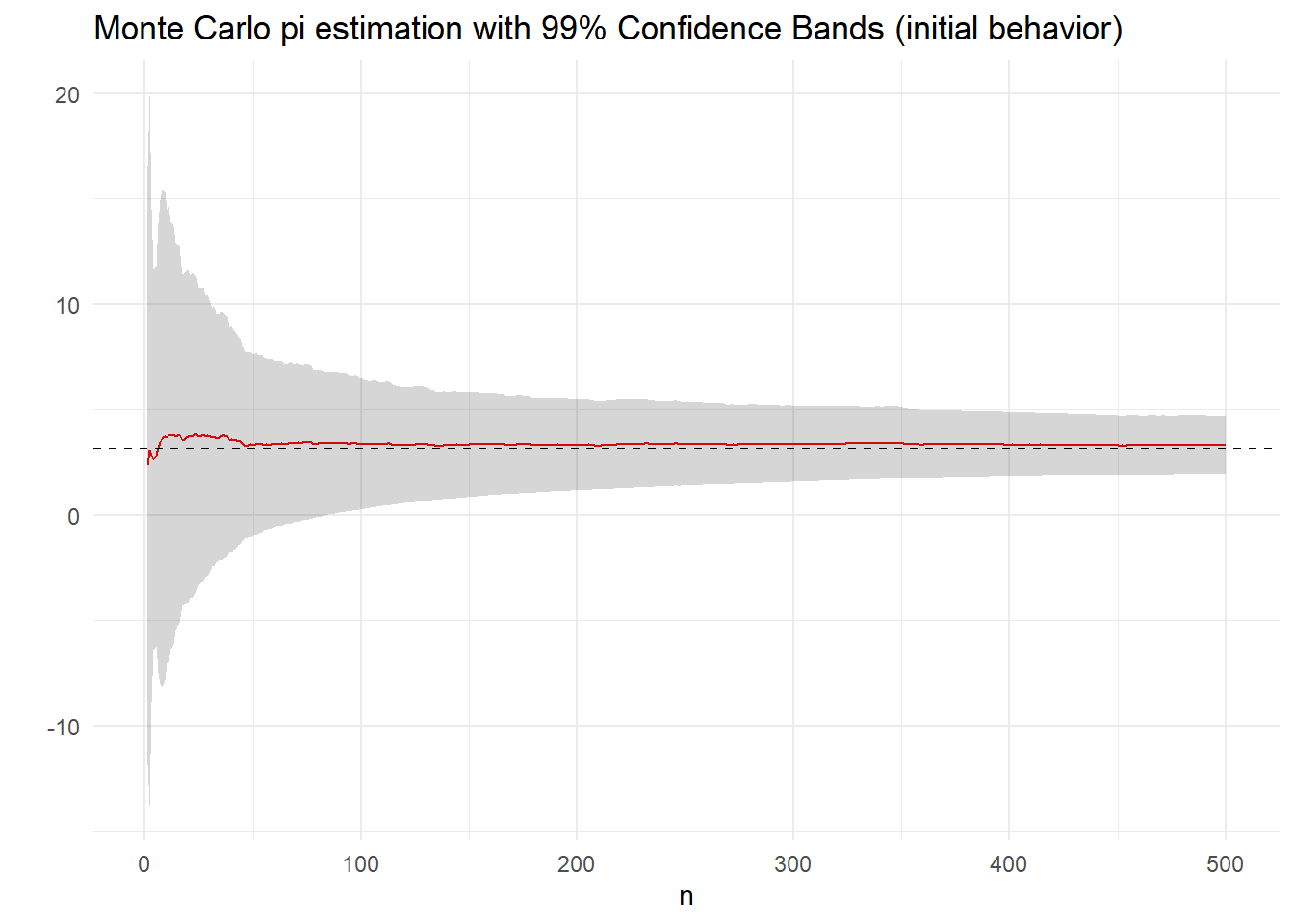
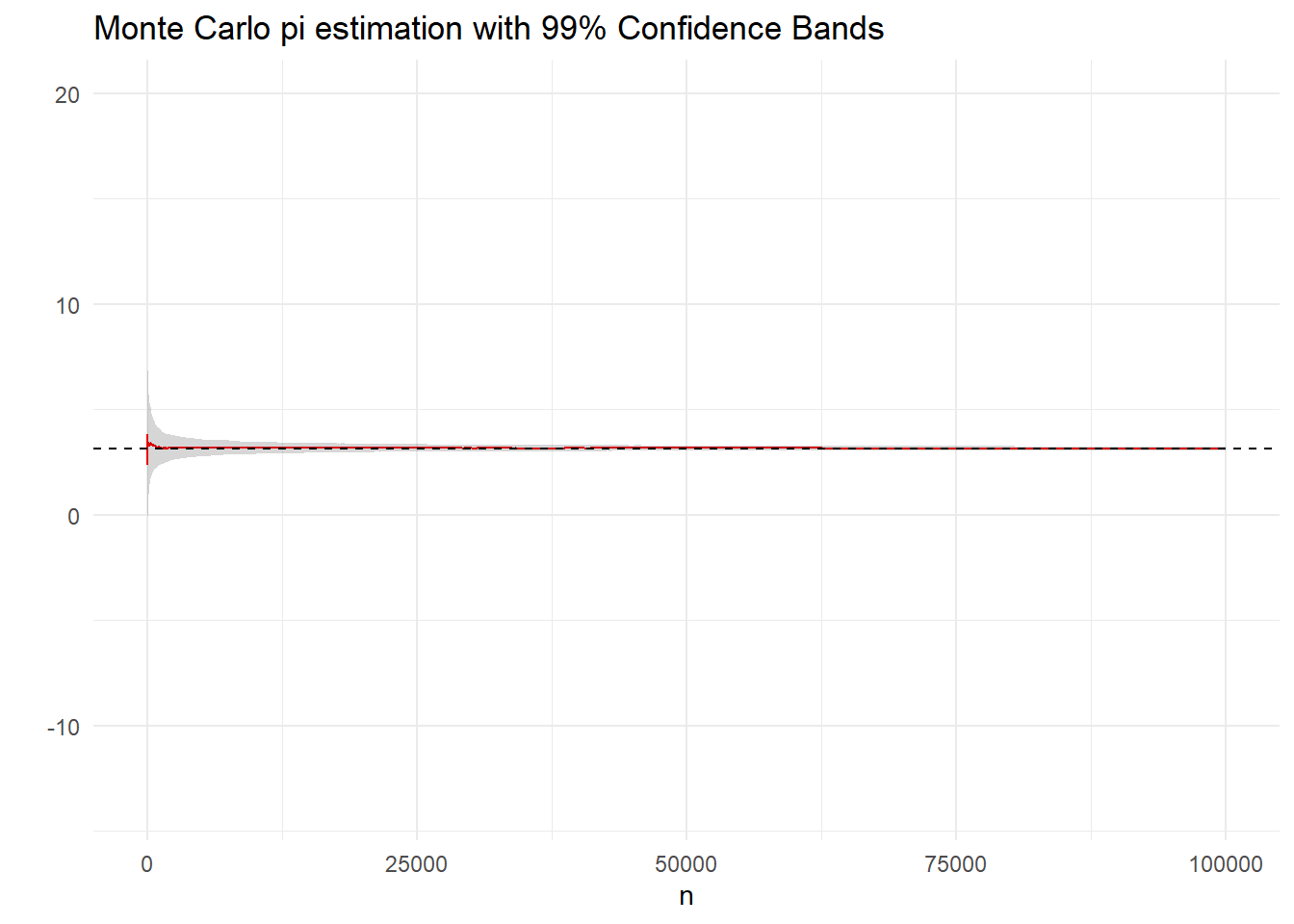
Στο παρακάτω γράφημα δείχνουμε μία πορεία εκτίμησης του \(\pi\), μαζί με την εξέλιξη των ασυμπτωτικών \(99\%\)-λωρίδων εμπιστοσύνης για το \(\pi\) όταν χρησιμοποιούμε \(10^5\) προσομοιώσεις από τη διπλή εκθετική. Η προσέγγιση του \(\pi\) είναι 3.1455051 και επομένως είναι σωστή σε 2 δεκαδικά ψηφία.

Αντίστοιχα μας ενδιαφέρει η ασυμπτωτική κατανομή της (μη αμερόληπτης) δειγματικής διασποράς \(\widehat{\sigma^2}_{h,n}=\frac{1}{n}\sum_{j=1}^n\left(h(X_j)-\overline{h}_n\right)^2\) της \(\mathbf{V}_f\left[ h(X) \right]\). Εκμεταλλευόμενοι το γεγονός ότι η παραπάνω έχει την ίδια ασυμπτωτική κατανομή με την \(\frac{1}{n}\sum_{j=1}^n\left(h(X_j)-Ι\right)^2\), για την οποία ισχύει \(\mathbf{E}_f\left[\left(h(X)-Ι\right)^2\right]=\sigma_h^2\) και \(\mathbf{V}_f\left[\left(h(X)-Ι\right)^2\right]=\mathbf{E}_f\left[\left(h(X)-Ι\right)^4\right]-\left(\mathbf{E}_f\left[h(X)-Ι\right]^2\right)^2=\mu_{4,h}-\sigma_h^4\), εφαρμόζεται άμεσα το (μονοδιάστατο) ΚΟΘ και παίρνουμε ότι

\[\begin{equation*} \sqrt{n}\left(\widehat{\sigma^2}_{h,n}-\sigma^2_h\right) \overset{d}{\longrightarrow} \mathcal{N}\left(0, \mu_{4,h}-\sigma_h^4 \right). \end{equation*}\]

Θα ήταν ενδιαφέρον να μελετήσουμε επίσης την από κοινού συμπεριφορά της εκτιμήτριας \(\widehat{I_n}\) και της εκτιμημένης διασποράς \(\widehat{\sigma^2}_{h,n}\). Προκειμένου να είμαστε σε θέση να τις μελετήσουμε, θα χρειαστούμε κάποια βασικά εργαλεία πολυδιάστατης στατιστικής, όπως επίσης και τον ορισμό και στοιχειώδεις ιδιότητες της πολυδιάστατης κανονικής.

3.5 Κατανομή τυχαίων διανυσμάτων και Πολυδιάστατη Κανονική

Προτού παρουσιάσουμε την πολυδιάστατη κανονική, κάνουμε μία επέκταση γνωστών εννοιών όπως η συνάρτηση κατανομής, η μέση τιμή και η διασπορά, στην περίπτωση των πολυδιάστατων τυχαίων μεταβλητών.

3.5.1 Κατανομή τυχαίων διανυσμάτων

Η έννοια της συνάρτησης κατανομής επεκτείνεται φυσιολογικά και για τυχαία διανύσματα. Σε ότι ακολουθεί θεωρούμε το \(\mathbb{R}^{d}\) εφοδιασμένο με τη σχέση μερικής διάταξης που προκύπτει μέσω της σχέσης \(x\leq y\), αν και μόνο αν, \(x_i\leq y_i\), για κάθε \(1\leq i \leq d\).

Ορισμός 3.11 Έστω \(X\) ένα τυχαίο διάνυσμα με τιμές στον \(\mathbb{R}^{d}\). Η συνάρτηση \(F_X:\mathbb{R}^{d}\rightarrow [0,1]\), όπου

\[\begin{equation*} F_X(x):=\mathbf{P}(X\leq x)=\mathbf{P}(X_1\leq x_1,X_2 \leq x_2,\ldots,X_d \leq x_d) = \mathbf{P}\left(\bigcap_{i=1}^{d}\{X_i \leq x_i\}\right), \end{equation*}\]

λέγεται συνάρτηση κατανομής του τ.δ. \(X\) ή των \(X_1,X_2,\ldots,X_d\). Όταν θέλουμε να δώσουμε έμφαση στις συνιστώσες τ.μ. γράφεται και ως \(F_{X_1,\ldots,X_n}(x_1,\ldots,x_n)\).

Δίνουμε παρακάτω χωρίς απόδειξη τρεις χρήσιμους χαρακτηρισμούς της ισονομίας τυχαίων διανυσμάτων.

Πρόταση 3.4 Δύο τυχαία διανύσματα \(X\),\(Y\) είναι ισόνομα, αν και μόνο αν,

1. \(F_X = F_Y\), δηλαδή, έχουν κοινή συνάρτηση κατανομής.
2. \(u^{\top}X \stackrel{d}{=} u^{\top}Y\), για κάθε \(u\in \mathbb{R}^{d}\), δηλαδή, κάθε γραμμικός συνδιασμός των συνιστωσών της \(X\) είναι ισόνομος με τον αντίστοιχο γραμμικό συνδιασμό των συνιστωσών της \(Y\).
3. \(\mathbf{E}[f(X)]=\mathbf{E}[f(Y)]\), για κάθε \(f:\mathbb{R}^{d}\rightarrow \mathbb{R}\) συνεχή και φραγμένη συνάρτηση.

Ο πρώτος χαρακτηρισμός είναι φυσιολογική γενίκευση του αντίστοιχου χαρακτηρισμού για μονοδιάστατες τ.μ.. Ο δεύτερος είναι αρκετά χρήσιμος σε αποδείξεις και δίνει τη δυνατότητα χαρακτηρισμού της κατανομής ενός τ.δ. μέσω της γνώσης μιας (άπειρης) οικογένειας κατανομών μονοδιάστατων τ.μ. που προκύπτουν μάλιστα μόνο μέσω γραμμικών μετασχηματισμών. Είναι μάλιστα θεωρητικά πιο γόνιμος, αφού επεκτείνεται και σε απειροδιάστατους διανυσματικούς χώρους με νόρμα μέσω της έννοιας του γραμμικού φραγμένου τελεστή (αντικείμενο μελέτης της συναρτησιακής ανάλυσης). Ο τελευταίος χαρακτηρισμός είναι ο πιο γενικός και μπορεί να χρησιμοποιηθεί γενικότερα σε μετρικούς χώρους.

3.5.2 Μέση τιμή και διασπορά τυχαίων διανυσμάτων

Οι έννοιες της μέσης τιμής και της διασποράς, όπως και της ροπής οποιασδήποτε τάξης, επεκτείνονται σε τυχαία διανύσματα. Θα περιοριστούμε εδώ μόνο στη μέση τιμή και τη διασπορά που είναι και οι πιο χρήσιμες. Είναι φανερό από τον χαρακτηρισμό της κατανομής που δίνεται στην Πρόταση 3.4-(2) ότι μία επέκταση κάποιας έννοιας στην πολυδιάστατη περίπτωση θα μπορούσε να εμπνέεται απο την εφαρμογή της αντίστοιχης έννοιας στη μονοδιάστατη περίπτωση σε όλους τους γραμμικούς συνδιασμούς \(u^{\top}X\). Λόγω της γραμμικότητας της μέσης τιμής, η μέση τιμή \(\mathbf{E}(u^{\top}X)\) καθορίζεται πλήρως από το διάνυσμα των μέσων τιμών \(\left(\mathbf{E}(X_1),\ldots,\mathbf{E}(X_d)\right)\). Στην περίπτωση της διασποράς, δεν αρκεί η γνώση των συνιστωσών διασπορών, αλλά χρειάζεται η γνώση και των συνδιακυμάνσεων \(\text{Cov}(X_i,X_j)\). Παρόλα αυτά, η γνώση του πίνακα \(\left(\text{Cov}(X_i,X_j)\right)_{i,j}\) είναι αρκετή για τον καθορισμό της διασποράς \(\mathbf{V}(u^{\top}X)\), δηλαδή, της διασποράς όλων των γραμμικών συνδιασμών της \(X\). Οδηγούμαστε λοιπόν στους επόμενους ορισμούς.

Ορισμός 3.12 Έστω \(X\) ένα τυχαίο διάνυσμα με τιμές στον \(\mathbb{R}^{d}\).

1. Αν \(\mathbf{E}|X_i|< +\infty\) για κάθε \(1\leq i \leq d\), τότε λέμε ότι το \(X\) έχει μέση τιμή \(\mathbf{E}(X)\) που ορίζεται από τη σχέση: \[\begin{equation*} \mu_X \equiv \mathbf{E}(X):=\left(\mathbf{E}(X_1),\mathbf{E}(X_2), \ldots, \mathbf{E}(X_d)\right). \end{equation*}\] Η συνθήκη ύπαρξης μέσης τιμής είναι ισοδύναμη με τη συνθήκη \(\mathbf{E}||X||< +\infty\), όπου \(||\cdot||\) είναι η ευκλείδια νόρμα στον \(\mathbb{R}^{d}\), την οποία και θα χρησιμοποιούμε για απλότητα.

2. Αν \(\mathbf{E}(X_i^2)< +\infty\) για κάθε \(1\leq i \leq d\), τότε ορίζουμε ως διασπορά του \(X\) τον πίνακα: \[\begin{equation*} \Sigma_X \equiv \mathbf{V}(X):=\left(\text{Cov}(X_i,X_j)\right)_{1\leq i,j \leq d}. \end{equation*}\] Ο πίνακας \(\mathbf{V}(X)\) λέγεται και πίνακας διασπορών–συνδιασπορών (για εμφανείς λόγους) ή πίνακας συνδιακύμανσης και συμβολίζεται και με \(\text{Cov}(X)\). Η συνθήκη ύπαρξης της διασποράς είναι ισοδύναμη με τη συνθήκη \(\mathbf{E}||X||^{2}< +\infty\), την οποία και θα χρησιμοποιούμε για απλότητα.

3. Αν \(Y\) είναι ένα ακόμα τυχαίο διάνυσμα με τιμές στον \(\mathbb{R}^{s}\) και \(\mathbf{E}||X||^{2}< +\infty\), τότε ορίζουμε ως (σταυρωτή) συνδιακύμανση των τ.δ. \(X\) και \(Y\), τον πίνακα \[\begin{equation*} \Sigma_{X,Y} \equiv \mathbf{C}(X,Y) := \begin{pmatrix} \text{Cov}(X_1,Y_1) & \text{Cov}(X_1,Y_2) & \ldots & \text{Cov}(X_1,Y_s) \\ \text{Cov}(X_2,Y_1) & \text{Cov}(X_2,Y_2) & \ldots & \text{Cov}(X_2,Y_s) \\ \vdots & \vdots & \ddots & \vdots \\ \text{Cov}(X_d,Y_1) & \text{Cov}(X_d,Y_2) & \ldots & \text{Cov}(X_d,Y_s). \end{pmatrix} \end{equation*}\] Τα τ.δ. \(X\) και \(Y\) λέγονται , αν o \(C(X,Y)\) είναι ο μηδενικός πίνακας.

Παρατήρηση:. Από τους παραπάνω ορισμούς είναι φανερό ότι \(\mathbf{C}(X,X)=\mathbf{V}(X)\) και \(\mathbf{C}(Y,X)=\mathbf{C}(X,Y)^{\top}\). Παρατηρούμε λοιπόν εδώ ότι ο πίνακας συνδιακύμανσης μεταξύ δύο τ.δ. (έτσι όπως τον ορίσαμε) δεν είναι γενικά συμμετρικός, εκτός αν \(X=Y\), οπότε ταυτίζεται με τον συμμετρικό πίνακα \(\mathbf{V}(X)\).

Στην επόμενη πρόταση δίνουμε κάποιες στοιχειώδεις ιδιότητες της μέσης τιμής τυχαίων διανυσμάτων.

Πρόταση 3.5 Έστω \(X,Y\) τυχαία διανύσματα με τιμές στον \(\mathbb{R}^{d}\) με \(\mathbf{E}||X||, \mathbf{E}||Y||< +\infty\) και \(A, \, b\) πίνακας και διάνυσμα κατάλληλης διάστασης. Τότε ισχύουν τα εξής:

\[\begin{eqnarray*} \mathbf{E}(AX + b) & = & A \mathbf{E}(X) + b, \\ \mathbf{E}(X+Y) & = & \mathbf{E}(X) + \mathbf{E}(Y). \end{eqnarray*}\]

Στην επόμενη πρόταση δίνουμε στοιχειώδεις ιδιότητες της διασποράς τυχαίων διανυσμάτων.

Πρόταση 3.6 Έστω \(X,Y\in\mathbb{R}^{d}\) τυχαία διανύσματα με \(\mathbf{E}||X||^{2}, \mathbf{E}||Y||^{2}< +\infty\) και \(A, \, b\) πίνακας και διάνυσμα κατάλληλης διάστασης. Τότε ισχύουν τα εξής:

\[\begin{eqnarray*} \mathbf{V}(X) & = & \mathbf{E}\left((X-\mu_X)(X-\mu_X)^{\top}\right) = \mathbf{E}(X X^{\top}) - \mathbf{E}(X)\mathbf{E}(X^{\top}),\\ \mathbf{V}(AX + b) & = & A \mathbf{V}(X)\, A^{\top}, \\ \mathbf{V}(X+Y) & = & \mathbf{V}(X) +\mathbf{V}(Y) + \mathbf{C}(X,Y) + \mathbf{C}(Y,X). \end{eqnarray*}\]

Ακολουθούν ιδιότητες που συνδέονται με τη συνδιακύμανση δύο τυχαίων διανυσμάτων.

Πρόταση 3.7 Έστω \(X,\,Y\) τυχαία διανύσματα με τιμές στον \(\mathbb{R}^{d}\) και \(\mathbb{R}^{s}\) αντίστοιχα. Αν υποθέσουμε ότι \(\mathbf{E}||X||^{2},\mathbf{E}||Y||^{2}< +\infty\), τότε ισχύουν τα εξής:

\[\begin{eqnarray*} \mathbf{C}(X, Y) & = & \mathbf{E}\left((X-\mu_X)(Y-\mu_Y)^{\top}\right) = \mathbf{E}(X Y^{\top}) - \mathbf{E}(X)\mathbf{E}(Y^{\top}), \\ \mathbf{C}(AX + b, BY + c ) & = & A \mathbf{C}(X,Y)\, B^{\top}. \end{eqnarray*}\]

3.5.3 Σύγκλιση κατά κατανομή

Η σύγκλιση κατά κατανομή για ακολουθίες τυχαίες διανυσμάτων δε μπορεί να αναχθεί σε σύγκλιση κατά κατανομή των συνιστωσών ακολουθιών τυχαίων μεταβλητών, καθώς είναι σημαντικό να ληφθεί υπόψη η εξάρτησή τους. Παρουσιάζει λοιπόν μεγαλύτερο ενδιαφέρον η μελέτη αυτής της σύγκλισης και έχουν δοθεί αρκετοί ισοδύναμοι χαρακτηρισμοί που είναι βολικοί κατά περίπτωση. Δίνουμε τώρα μερικούς από αυτούς σε αντιστοιχία με την πρόταση 3.4.

Θεώρημα 3.6 Μία ακολουθία τ.δ. \((X_n)\) συγκλίνει κατά κατανομή σε ένα τ.δ. \(X\in \mathbb{R}^{d}\), αν και μόνο αν,

1. για κάθε σημείο συνεχείας \(x\in \mathbb{R}^{d}\) της \(F\) \[\begin{equation*} F_n(x) \xrightarrow[n\rightarrow \infty]{} F(x), \end{equation*}\] όπου \(F_n,F\) είναι οι σ.κ. των \(X_n,X\),

2. (τέχνασμα Cramér–Wold) κάθε γραμμικός συνδιασμός των συνιστωσών της \(X_n\) συγκλίνει κατά κατανομή στον αντίστοιχο γραμμικό συνδιασμό των συνιστωσών της \(X\), δηλαδή, για κάθε \(u\in \mathbb{R}^{d}\) \[\begin{equation*} u^{\top}X_n \xrightarrow[]{d} u^{\top}X, \end{equation*}\]

3. για κάθε \(f:\mathbb{R}^{d}\rightarrow \mathbb{R}\) συνεχή και φραγμένη συνάρτηση

\[\begin{equation*} \mathbf{E}[f(X_n)] \xrightarrow[n\rightarrow \infty]{} \mathbf{E}[f(X)]. \end{equation*}\]

3.5.4 Πολυδιάστατη Κανονική Κατανομή

Η πιο σημαντική συνεχής πολυδιάστατη κατανομή είναι η κανονική κατανομή για τους ίδιους λόγους που είναι και στη μονοδιάστατη περίπτωση. Θα στηρίξουμε τον επόμενο ορισμό της κανονικής κατανομής στην Πρόταση 3.4–(2), χρησιμοποιώντας τις κατανομές όλων των γραμμικών συνδιασμών των συνιστωσών ενός τ.δ..

Ορισμός 3.13 Έστω \(X=(X_1,X_2,\ldots,X_d)\) ένα τ.δ. με \(d\geq 1\), \(\mu \in \mathbb{R}^{d}\) ένα διάνυσμα και \(\Sigma\) ένας συμμετρικός και θετικά ημιορισμένος πίνακας. Θα λέμε ότι το \(X\) ακολουθεί την κανονική κατανομή \(\mathcal{N}_{d}(\mu, \Sigma)\) με παραμέτρους \(\mu\) και \(\Sigma\), αν για κάθε \(u \in \mathbb{R}^{d}\)

\[\begin{equation} u^{\top}X \sim \mathcal{N}_{1}(u^{\top} \mu, \, u^{\top}\Sigma \, u). \end{equation}\]

Αν ο \(\Sigma\) είναι θετικά ορισμένος (και όχι απλά ημιορισμένος), τότε αν θέλουμε να το δηλώσουμε ξεκάθαρα θα γράφουμε ότι \(X\sim \mathcal{Ν}_{d}^{*}(\mu, \Sigma)\).

Πρόταση 3.8 Αν ένα τ.δ. \(X\sim \mathcal{N}_d(\mu, \, \Sigma)\), τότε \(\mathbf{E}(X)=\mu\) και \(\mathbf{V}(X)=\Sigma\).

Απόδειξη:. Από τον ορισμό 3.13 για \(u=e_i\), \(i=1,\ldots,d\), έχουμε

\[\begin{equation*} X_i = e_i^{\top}X \sim \mathcal{N}_{1}\left(e_i^{\top} \mu, \, e_i^{\top}\Sigma \, e_i\right) = \mathcal{N}_{1}(\mu_i, \, \Sigma_{ii}), \end{equation*}\]

από το οποίο συμπεραίνουμε ότι \(\mathbf{E}(X_i)=\mu_i\) και \(\mathbf{V}(X_i)=\Sigma_{ii}\). Από τις συνιστώσες μέσες τιμές συμπεραίνουμε ότι \(\mathbf{E}(X)=\mu\) και από τις διασπορές ότι τα διαγώνια στοιχεία του \(\Sigma\) συμπίπτουν με αυτές. Θέτοντας τώρα \(u=e_i+e_j\), \(i,j=1,\ldots,d\), \(i\neq j\) έχουμε

\[\begin{equation*} \mathbf{V}(X_i+X_j)= \mathbf{V}[(e_i+e_j)^{\top}X] = (e_{i}^{\top}+e_j^{\top})\, \Sigma \, (e_{i}+e_j)=\Sigma_{ii}+\Sigma_{jj}+2\Sigma_{ij}. \end{equation*}\]

Από τη σχέση

\[\begin{equation*} \mathbf{V}(X_i+X_j)= \mathbf{V}(X_i) + \mathbf{V}(X_j) + 2\,\text{Cov}(X_i,X_j), \end{equation*}\]

και τα παραπάνω καταλήγουμε στο ότι \(\text{Cov}(X_i,X_j)=\Sigma_{ij}\) και έτσι φτάνουμε στο ζητούμενο και για τον πίνακα διασποράς.

Παρατήρηση:. Γίνεται σαφές από την παραπάνω απόδειξη ότι αν για ένα οποιοδήποτε τ.δ. \(X\) ισχύει ότι για κάθε \(u\in \mathbb{R}^{d}\), η μέση τιμή \(\mathbf{E}(u^{\top}X)=u^{\top}\mu\) και η διασπορά \(\mathbf{V}(u^{\top}X)=u^{\top}\,\Sigma \, u\), τότε \(\mathbf{E}(X)=\mu\) και \(\mathbf{V}(X)=\Sigma\).

Η πιο απλή περίπτωση πολυδιάστατης κανονικής είναι βέβαια ένα τ.δ. \(Z\) που αποτελείται από ανεξάρτητες τ.μ. που ακολουθούν την τυπική κανονική.

Πόρισμα 3.3 Αν \(Z\sim \mathcal{N}_d(0_d,I_d)\), όπου \(0_d\) είναι το μηδενικό διάνυσμα και \(I_d\) είναι ο ταυτοτικός πίνακας \(d\)-τάξης, τότε οι συνιστώσες του \(Ζ\) είναι ανεξάρτητες και ισόνομες τ.μ. που ακολουθούν την τυπική κανονική. Λέμε ότι το \(Z\) ακολουθεί την τυπική κανονική διάστασης \(d\).

Απόδειξη:. Ας υποθέσουμε ότι \(Z\sim \mathcal{N}_d(0_d,I_d)\). Τότε από τον ορισμό της πολυδιάστατης κανονικής έχουμε \(u^{\top}Z \sim \mathcal{N}_1(0,u^{\top}u)\). Ας υποθέσουμε τώρα ότι παίρνουμε ένα τ.δ. \(W=(W_{1},\ldots,W_{d})\) που αποτελείται από τ.μ. \(W_{i}\) ανεξάρτητες τυπικές κανονικές. Τότε \(u^{\top}W \sim \mathcal{N}_1(0,u^{\top}u)\), από γνωστό αποτέλεσμα για γραμμικούς συνδιασμούς ανεξάρτητων τ.μ. που ακολουθούν κανονική κατανομή. Καταλήγουμε στο συμπέρασμα ότι \(u^{\top}Z \stackrel{d}{=} u^{\top}W\) για κάθε \(u\in \mathbb{R}^{d}\) και άρα \(Ζ\stackrel{d}{=} W\).

Στην επόμενη πρόταση δίνονται κάποιες σημαντικές ιδιότητες της πολυδιάστατης κανονικής κατανομής.

Πρόταση 3.9 Έστω \(X\sim \mathcal{N}_d(\mu,\Sigma)\), με μέση τιμή \(\mu \in \mathbb{R}^d\) και πίνακα διασποράς \(\Sigma\).

1. Αν \(Α\in \mathbb{R}^{s\times d}\) και \(b\in \mathbb{R}^{s}\), τότε

\[\begin{equation} AX + b \sim \mathcal{N}_s\left(A\mu + b,\, A\,\Sigma \, A^{\top}\right) \tag{3.1} \end{equation}\]

2. Aν ο \(\Sigma\) είναι θετικά ορισμένος (αντιστρέψιμος), τότε το τ.δ. \(X\) έχει συνάρτηση πυκνότητας πιθανότητας στον \(\mathbb{R}^d\) της μορφής

\[\begin{equation} f_{X}(x) = (2\pi)^{-d/2}\left(\det\,(\Sigma)\right)^{-1/2} \exp\left\{-\,\frac{1}{2}(x-\mu)^{\top}\,\Sigma^{-1}(x-\mu) \right\} \quad \forall x\in \mathbb{R}^{d}. \tag{3.2} \end{equation}\]

Απόδειξη:.

1. Έστω \(u\in \mathbb{R}^{s}\). Tότε, \[\begin{equation*} u^{\top}(AX + b) = (u^{\top}A)X + u^{\top}b = (A^{\top}u)^{\top}X + u^{\top}b \sim \mathcal{N}_1\left(\,(A^{\top}u)^{\top}\mu,\, (A^{\top}u)^{\top}\,\Sigma \, A^{\top}u\right) + u^{\top}b, \end{equation*}\] όπου η τελευταία σχέση έπεται από την υπόθεση ότι \(X\sim \mathcal{N}_d(\mu,\Sigma)\) και άρα \(v^{\top}X \sim \mathcal{N}_1\left(v^{\top}\mu,v^{\top} \Sigma v\right)\) για \(v=A^{\top}u \in \mathbb{R}^{d}\). Τελικά, η παραπάνω σχέση ξαναγράφεται στη μορφή \[\begin{equation*} u^{\top}(AX + b) \sim \mathcal{N}_1\left(\,u^{\top}(Α\mu+b),\, u^{\top}A\Sigma \, A^{\top}u\right), \end{equation*}\] από την οποία συμπεραίνουμε την (3.1).

2. Aν ο \(\Sigma\) είναι θετικά ορισμένος, τότε γράφεται στη μορφή \(\Sigma = AA^{\top}\), με \(Α\) αντιστρέψιμο. Ο πίνακας \(Α\) παίζει το ρόλο μιας τετραγωνικής ρίζας του \(\Sigma\). Συμπεραίνουμε λοιπόν από το ερώτημα (1) ότι το τ.δ. \[\begin{equation*} Z = A^{-1}(X-\mu) \sim \mathcal{N}_d\left(0_d,\, A^{-1}\,\Sigma \, (A^{-1})^{\top}\right) \end{equation*}\] και επειδή \(A^{-1}\,\Sigma \, (A^{-1})^{\top}=A^{-1}AA^{\top}(A^{-1})^{\top}=I_d\), καταλήγουμε στο ότι \(Ζ\sim \mathcal{N}_d(0_d,I_d)\). Η σ.π.π. του \(Ζ\) είναι \[\begin{equation*} f_{Z}(z) = \prod_{i=1}^{d}f_{Z_i}(z_i)=\prod_{i=1}^{d}(2\pi)^{-1/2}e^{-z_i^2/2}=(2\pi)^{-d/2} \exp\left\{-\,\frac{1}{2}z^{\top}z \right\} \quad \forall z\in \mathbb{R}^{d}. \end{equation*}\] Συμπεραίνουμε ότι το τ.δ. \(X=AZ + \mu\) έχει σ.π.π. στον \(\mathbb{R}^d\) της μορφής \[\begin{equation*} f_{X}(x) = (2\pi)^{-d/2}\vert \det\,(A)\vert^{-1} \exp\left\{-\,\frac{1}{2}\left(A^{-1}(x-\mu)\right)^{\top}\left(A^{-1}(x-\mu)\right) \right\}. \end{equation*}\] Η παραπάνω έκφραση συμπίπτει με την (3.2).

Παράδειγμα 3.6 Ας μελετήσουμε γραφικά τη διδιάστατη κανονική \(\mathcal{N}_2(0, \Sigma)\), με πίνακα διασπορών - συνδιασπορών

\[\begin{equation*} \Sigma = \left( \begin{array}{cc} 1 & p \\ p & 1 \end{array} \right), \end{equation*}\]

για τις διάφορες τιμές της παραμέτρου \(p\).

Θα προσομοιώσουμε με Monte Carlo από την δισδιάστατη κανονική κατανομή. Εύκολα μπορεί κάποιος να παρατηρήσει την μεταβολή των προσομοιωμένων τιμών καθώς η τιμή του \(p\) μεταβάλλεται από το \(-1\) στο \(1\). Η προσομοίωση των ανεξάρτητων τ.μ. \((Ζ_1, Ζ_2)\) έγινε με τον μετασχηματισμό Box-Muller, όπου για μηδενικές μέσες τιμές και μοναδιαίες τυπικές αποκλίσεις οι εξαρτημένες \((Χ_1, Χ_2)\) δίνονται από τις σχέσεις:

\[\begin{align*} X_1 &= Z_1, \\ X_2 &= pZ_1 +\sqrt{1-p^2} Z_2 \end{align*}\]

boxmuller <- function(n, p){
  
  theta <- runif(n, min = 0, max = 2 * pi) 
  U <- runif(n)
  R <- sqrt( - 2 * log(U))
  
  Z1 <- R * cos(theta)
  Z2 <- R * sin(theta)
  
  X1 <- Z1
  X2 <- p * Z1 + sqrt(1 - p ^ 2) * Z2
  
  data.frame(x = X1, y = X2)
}

3.5.5 Πολυδιάστατο Κεντρικό Οριακό Θεώρημα

Είμαστε τώρα σε θέση να παρουσιάσουμε το πολυδιάστατο Κεντρικό Οριακό Θεώρημα σε δύο ισοδύναμες μορφές.

Πρόταση 3.10 Έστω \((X_n)\) μία ακολουθία ανεξάρτητων και ισόνομων τ.δ. με \(\mathbf{E} \lVert X_1 \rVert ^{2}< +\infty\). Θέτουμε \(\mu_X=\mathbf{E}(X)\) και \(\Sigma_{X}=\mathbf{V}(X)\). Αν \(\left(\overline{X}_n\right)\) είναι η ακολουθία των δειγματικών μέσων και \((S_n)\) η ακολουθία των μερικών αθροισμάτων της \((X_n)\), τότε

\[\begin{equation*} \sqrt{n}\left(\,\overline{X}_n-\mu_X\right) \xrightarrow[]{d} \mathcal{N}_{d}\,(0_{d}, \, \Sigma_{X}), \end{equation*}\]

και

\[\begin{equation*} \frac{S_n- n\,\mu_X}{\sqrt{n}} \xrightarrow[]{d} \mathcal{N}_{d}\,(0_{d}, \, \Sigma_{X}). \end{equation*}\]

Απόδειξη:. Θα αποδείξουμε την πρώτη από τις δύο ισοδύναμες μορφές. Η δεύτερη έπεται από την παρατήρηση ότι \(S_n = n \overline{X}_n\). Έστω λοιπόν \(U\) ένα τ.δ. με \(U\sim \mathcal{N}_{d} (0_{d}, \Sigma_{X})\) και \(u\in \mathbb{R}^{d}\). Από το Θεώρημα 3.6 αρκεί να δείξουμε ότι

\[\begin{equation} u^{\top}\left\{\sqrt{n}\left(\overline{X}_n-\mu_X\right)\right\} \xrightarrow[]{d} u^{\top} U \sim \mathcal{N}_{1}(0, u^{\top}\Sigma_{X}u). \tag{3.3} \end{equation}\]

Παρατηρούμε όμως ότι

\[\begin{equation*} u^{\top}\left\{\sqrt{n}\left(\,\overline{X}_n-\mu_X\right)\right\} = \sqrt{n}\left(\overline{u^{\top}X_n}-u^{\top}\mu_X\right) = \sqrt{n}\left(\overline{Y}_n-\mu_Y\right), \end{equation*}\]

όπου \((Y_n)\) είναι ακολουθία ανεξάρτητων και ισόνομων τ.μ. με \(Y_n=u^{\top}X_n\) και \(\mu_Y = \mathbf{E}(Y_1) = u^{\top}\mu_X\). Από το κλασσικό Κεντρικό Οριακό Θεώρημα έχουμε

\[\begin{equation*} \sqrt{n}\left(\overline{Y}_n-\mu_Y\right) \xrightarrow[]{d} \mathcal{N}_{1}(0, \mathbf{V}(Y_1)) = \mathcal{N}_{1}(0, u^{\top}\Sigma_{X}u ), \end{equation*}\]

που είναι η οριακή κατανομή (3.3) που θέλαμε να φτάσουμε.

Ας μελετήσουμε μία εφαρμογή που συνδιάζει το πολυδιάστατο ΚΟΘ με το λήμμα του Slutsky.

Παράδειγμα 3.7 Έστω \((X_n)\) ακολουθία α.ι.τ.μ. με \(\mathbb{E}(X_1^4)<+\infty\), όπου τα \(\mu=\mathbb{E}(X_1)\) και \(\sigma^2=\textbf{V}(X_1)\) είναι άγνωστα. Θέτουμε \(\widehat{\theta}_n=\left(\widehat{\mu}_n,\, \widehat{\sigma_n^2} \right)^{\top} = \left( \overline{X}_n,\, M_n\right)^{\top}\), όπου \(\overline{X}_n\) και \(M_n=\dfrac{1}{n}\sum\limits_{i=1}^{n}(X_i-\overline{X}_n)^2\) είναι οι εκτιμήτριες ροπών. Σε τυχαίο δείγμα από την κανονική κατανομή \(N(\mu, \sigma^2)\) οι \(\widehat{\mu}_n\) και \(\widehat{\sigma_n^2}\) είναι ανεξάρτητες, γενικά όμως όχι. Αναζητούμε την ασυμπτωτική κατανομή του \(\sqrt{n}\left(\widehat{\theta}_n-\theta\right)\). Θέτουμε \(N_n=\dfrac{1}{n}\sum\limits_{i=1}^{n}(X_i-\mu)^2\), και τότε

\[\begin{equation*} M_n-N_n=\dfrac{1}{n}\sum\limits_{i=1}^{n}\Big[ (X_i-\overline{X}_n)^2 - (X_i-\mu)^2\Big] = -\, (\overline{X}_n-\mu)^2 \end{equation*}\]

\[\begin{align*} \sqrt{n}\left(\hat{\theta}_n-\theta\right) &= \sqrt{n}\left[ \begin{pmatrix} \overline{X}_n \\ M_n \end{pmatrix} - \begin{pmatrix} \mu \\ \sigma^2 \end{pmatrix} \right] \\ &= \sqrt{n}\left[ \begin{pmatrix} \overline{X}_n \\ N_n \end{pmatrix} - \begin{pmatrix} \mu \\ \sigma^2 \end{pmatrix} \right] - \sqrt{n} \begin{pmatrix} 0 \\ (\overline{X}_n-\mu)^2 \end{pmatrix}. \end{align*}\]

Έχουμε ότι \(\sqrt{n}(\overline{X}_n-\mu)\xrightarrow{d} \mathcal{N}(0, \sigma^2)\) και \(\overline{X}_n-\mu\xrightarrow{p} 0\). Από το μονοδιάστατο Slutsky έχουμε

\[\begin{equation*} \sqrt{n}(\overline{X}_n-\mu)^2 = (\overline{X}_n-\mu)\cdot \sqrt{n}\,(\overline{X}_n-\mu) \xrightarrow{d} 0 \cdot \mathcal{N}(0, \sigma^2)=0, \end{equation*}\]

και άρα συμπεραίνουμε ότι

\[\begin{equation*} \begin{pmatrix} 0 \\ -\sqrt{n}(\overline{X}_n-\mu)^2 \end{pmatrix} \xrightarrow{p} \begin{pmatrix} 0 \\ 0 \end{pmatrix}. \end{equation*}\]

Από τα παραπάνω, το αρχικό πρόβλημα ανάγεται στην εύρεση της οριακής κατανομής της \(\sqrt{n}\left[ (\overline{X}_n \ \ N_n)^{\top} - (\mu \ \ \sigma^2)^{\top} \right]\). Παρατηρούμε τώρα ότι

\[\begin{equation*} N_n=\dfrac{1}{n}\sum\limits_{i=1}^{n}(X_i-\mu)^2=:\overline{(X-\mu)^{2}_{[n]}}, \end{equation*}\]

άρα

\[\begin{equation*} \sqrt{n}\left[ \begin{pmatrix} \overline{X}_n \\ \\ \overline{(X-\mu)^{2}_{[n]}} \end{pmatrix} - \begin{pmatrix} \mu \\ \\ \sigma^2 \end{pmatrix} \right]=\sqrt{n}\,\Big(\overline{Y_n}-\mathbf{E}(Y_1)\Big), \end{equation*}\]

όπου \(Y_n=\begin{pmatrix} X_n \\ (X_n-\mu)^2 \end{pmatrix}=g(X_n)\) για \(g(x)=(x,\ (x-\mu)^2)^{\top}\) και οι \(g(X_n)\) είναι α.ι.τ.δ. (διότι οι \(X_n\) είναι α.ι.τ.μ.), με

\[\begin{equation*} \mathbf{E}(Y_n)=\mathbf{E}(Y_1)=\begin{pmatrix} \mathbf{E}(X_1) \\ \mathbf{E}(X_1-\mu)^2 \end{pmatrix}=\begin{pmatrix} \mu \\ \sigma^2 \end{pmatrix}. \end{equation*}\]

Προφανώς, ο πίνακας διασπορών-συνδιασπορών \(\Sigma\) υπάρχει και

\[\begin{equation*} \Sigma:=\textbf{V}(Y_1)=\begin{pmatrix} \textbf{V}(X_1) & \textbf{C}\big(X_1, (X_1-\mu)^2\big) \\ \textbf{C}\big(X_1, (X_1-\mu)^2\big) & \textbf{V}\big((X_1-\mu)^2\big) \end{pmatrix}. \end{equation*}\]

Υπολογίζουμε τα στοιχεία του πίνακα:

• \(\mathbf{C}\big(X_1, (X_1-\mu)^2\big)= \mathbf{C}\big(X_1-\mu, (X_1-\mu)^2 \big)= \underbrace{ \mathbf{E}\big((X_1-\mu)^3 \big)}_{\mu_3}-\underbrace{ \mathbf{E}(X_1-\mu)}_{0}\mathbf{E}(X_1-\mu)^2=\mu_3\)
• \(\mathbf{V}\big( (X_1-\mu)^2 \big)=\mathbf{E}(X_1-\mu)^4-\mathbf{E}^2(X_1-\mu)^2=\mu_4-\sigma^4\).

Από τα παραπάνω συμπεραίνουμε ότι

\[\begin{equation*} \Sigma=\begin{pmatrix} \sigma^2 & \mu_3 \\ \mu_3 & \mu_4-\sigma^4 \end{pmatrix}. \end{equation*}\]

Είναι χρήσιμο πολλές φορές να χρησιμοποιούνται ως παράμετροι μίας κατανομής ο συντελεστής λοξότητας \(\lambda=\mathbf{E}\left(\frac{X-\mu}{\sigma}\right)^3\) και ο συντελεστής κύρτωσης \(\kappa=\mathbf{E}\left(\frac{X-\mu}{\sigma}\right)^4\). Έτσι, ο πίνακας \(\Sigma\) μπορεί να γραφεί στη μορφή

\[\begin{equation*} \Sigma=\begin{pmatrix} \sigma^2 & \lambda \sigma^3 \\ \lambda \sigma^3 & (\kappa-1)\sigma^4 \end{pmatrix}. \end{equation*}\]

Με εφαρμογή του πολυδιάστατου Κεντρικού Οριακού Θεωρήματος για την ακολουθία των α.ι.τ.δ. \((Y_n)\) και λόγω των παραπάνω σχέσεων, έχουμε τελικά ότι

\[\begin{equation*} \sqrt{n}\left(\hat{\theta}_n-\theta\right) \xrightarrow{d} \mathcal{N}_2(0, \Sigma), \end{equation*}\]

ή γραμμένο αναλυτικά,

\[\begin{equation*} \sqrt{n}\left[ \left(\widehat{\mu}_n, \widehat{\sigma^2}_{n}\right)^\top - \left( \mu, \sigma^2\right)^\top \right] \xrightarrow{d} \mathcal{N}_2(0, \Sigma). \end{equation*}\]

Εφαρμόζοντας μέθοδο Δέλτα για την συνάρτηση \(\phi(x,y)=(x, \sqrt{y})\) με Ιακωβιανό πίνακα \(\Phi'=\left[\begin{array}{cc} 1 & 0 \\ 0 & \frac{1}{2\sigma} \end{array} \right]\), και λαμβάνοντας υπ’ όψιν το αναλλοίωτο της ε.μ.π., μπορούμε να έχουμε το αντίστοιχο αποτέλεσμα για την τυπική απόκλιση

\[\begin{equation*} \sqrt{n}\left(\phi\left(\hat{\theta}_n\right)-\phi\left(\theta\right)\right) \xrightarrow{d} \mathcal{N}_2\left(0, \Phi'\Sigma\Phi'^\top\right), \end{equation*}\]

ή γραμμένο αναλυτικά,

\[\begin{equation*} \sqrt{n}\left[ \left(\widehat{\mu}_n, \widehat{\sigma}_{n}\right)^\top - \left( \mu, \sigma\right)^\top \right] \xrightarrow{d} \mathcal{N}_2(0, \Sigma'), \tag{3.4} \end{equation*}\]

όπου

\[\begin{equation*} \Sigma'=\sigma^2\begin{pmatrix} 1 & \lambda/2 \\ \lambda/2 & (\kappa-1)/4 \end{pmatrix}. \end{equation*}\]

Από τα παραπάνω εξάγουμε άμεσα και τις περιθώριες οριακές κατανομές των \(\widehat{\sigma^2}_n\) και \(\widehat{\sigma}_n\):

\[\begin{equation*} \sqrt{n}\left(\widehat{\sigma^2}_n-\sigma^2\right)\overset{d}{\longrightarrow}\mathcal{N}\left(0, (\kappa-1)\sigma^4\right). \end{equation*}\]

\[\begin{equation*} \sqrt{n}\left(\widehat{\sigma}_n-\sigma\right)\overset{d}{\longrightarrow}\mathcal{N}\left(0, \frac{\kappa-1}{4}\sigma^2\right). \end{equation*}\]

3.5.6 Εφαρμογή στην ολοκλήρωση Monte Carlo

Εφαρμόζουμε τα αποτελέσματα της προηγούμενης παραγράφου στην εύρεση της από κοινού ασυμπτωτικής κατανομής των \(\widehat{I}_n\) και \(\widehat{\sigma^2}_{h,n}\) του παραδείγματος (3.3). Από την (3.4) έχουμε:

\[\begin{equation*} \sqrt{n}\left[ \left(\widehat{I_n}, \widehat{\sigma}_{h,n}\right)^\top - \left( I, \sigma_h\right)^\top \right] \xrightarrow{d} \mathcal{N}_2(0, \Sigma_h'), \end{equation*}\]

όπου

\[\begin{equation*} \Sigma_h'=\sigma^2\begin{pmatrix} 1 & \lambda_h/2 \\ \lambda_h/2 & (\kappa_h-1)/4 \end{pmatrix}. \end{equation*}\]

Επομένως, για αρκετά μεγάλο \(n\) θα έχουμε

\[\begin{equation*} \left(\widehat{I_n}, \widehat{\sigma}_{h,n}\right)^\top \overset{d}{\approx} \mathcal{N}_2(\left( I, \sigma_h\right)^\top, \Sigma_h'/n). \end{equation*}\]

Έχοντας μία προσέγγιση της ασυμπτωτικής κατανομής των παραπάνω εκτιμητριών, μετά μπορούμε να βρούμε προσεγγιστικές κατανομές συναρτήσεών τους. Για παράδειγμα, μία προσέγγιση της κατανομής του ανώτερου και κατώτερου ορίου \(\widehat{I_n} \pm\frac{z_{a/2}}{\sqrt{n}} \widehat{\sigma}_{h,n}\) των \((1-a)-\)λωρίδων εμπιστοσύνης. Για το σκοπό αυτό εφαρμόζουμε το γραμμικό μετασχηματισμό για \(u=\left(1, \pm \frac{z_{a/2}}{\sqrt{n}}\right)^\top\) και παίρνουμε:

\[\begin{equation*} \widehat{I_n} \pm\frac{z_{a/2}}{\sqrt{n}} \widehat{\sigma}_{h,n} \overset{d}{\approx} \mathcal{N}\left(I\pm\frac{z_{a/2}}{\sqrt{n}} \sigma_h,\ \frac{\sigma_h^2}{n} \left(1\pm \frac{ z_{a/2}\lambda_h}{\sqrt{n}} +\frac{z^2_{a/2}(k_h-1)}{4n}\right)\right). \end{equation*}\]

Σε αυτό το πρόβλημα οι συντελεστές λοξότητας και κύρτωσης για την \(h_1(X)\) υπολογίζονται ακριβώς, αφού μπορούμε να βρούμε αναλυτικό τύπο για τις ροπές \(k-\)τάξης:

\[\begin{align*} \mathbf{E}_{f}\left[h_1^k(X)\right] &= \int_{-\infty}^{+\infty} 2^k e^{-\frac{k}{2}x^2 + k|x|} \frac{1}{2}e^{-|x|} dx = \int_{-\infty}^{+\infty} 2^{k-1} e^{-\frac{k}{2}x^2 + (k-1)|x|} dx = \int_{-\infty}^{+\infty} 2^{k-1} e^{-\frac{1}{2}\left(\sqrt{k}|x|-\frac{k-1}{\sqrt{k}}\right)^2 +\frac{(k-1)^2}{2k}} dx \\ &=2^{k-1} e^{\frac{(k-1)^2}{2k}} \int_{-\infty}^{+\infty}e^{-\frac{1}{2}\left(\sqrt{k}|x|-\frac{k-1}{\sqrt{k}}\right)^2} dx =2^{k-1} e^{\frac{(k-1)^2}{2k}} \int_{-\infty}^{0}e^{-\frac{1}{2}\left(\sqrt{k}x+\frac{k-1}{\sqrt{k}}\right)^2} + 2^{k-1} e^{\frac{(k-1)^2}{2k}} \int_{0}^{+\infty}e^{-\frac{1}{2}\left(\sqrt{k}x-\frac{k-1}{\sqrt{k}}\right)^2} dx \\ &=2^{k-1} e^{\frac{(k-1)^2}{2k}} \int_{-\frac{k-1}{\sqrt{k}}}^{+\infty} \frac{1}{\sqrt{k}} e^{-\frac{1}{2}y^2} dy +2^{k-1} e^{\frac{(k-1)^2}{2k}} \int_{-\infty}^{+\frac{k-1}{\sqrt{k}}} \frac{1}{\sqrt{k}} e^{-\frac{1}{2}y^2} dy =\frac{\sqrt{2\pi}}{\sqrt{k}}2^{k-1} e^{\frac{(k-1)^2}{2k}} \int_{-\frac{k-1}{\sqrt{k}}}^{+\infty} \frac{1}{\sqrt{2\pi}} e^{-\frac{1}{2}y^2} dy +\frac{\sqrt{2\pi}}{\sqrt{k}}2^{k-1} e^{\frac{(k-1)^2}{2k}} \int_{-\infty}^{+\frac{k-1}{\sqrt{k}}} \frac{1}{\sqrt{2\pi}} e^{-\frac{1}{2}y^2} dy \\ &=\frac{\sqrt{2\pi}}{\sqrt{k}}2^{k-1} e^{\frac{(k-1)^2}{2k}} \left(1-\Phi\left(-\frac{k-1}{\sqrt{k}}\right) \right) +\frac{\sqrt{2\pi}}{\sqrt{k}}2^{k-1} e^{\frac{(k-1)^2}{2k}}\Phi\left(\frac{k-1}{\sqrt{k}}\right) = \frac{\sqrt{2\pi}}{\sqrt{k}}2^{k-1} e^{\frac{(k-1)^2}{2k}} \cdot 2 \Phi\left(\frac{k-1}{\sqrt{k}}\right) \\ &=2^{k}\frac{\sqrt{2\pi}}{\sqrt{k}} e^{\frac{(k-1)^2}{2k}} \Phi\left(\frac{k-1}{\sqrt{k}}\right). \end{align*}\]

Αρχικά, επαληθεύουμε για \(k=1, 2\):

\[\begin{align*} \mathbf{E}_{f}\left[h_1(X)\right] &=\sqrt{2\pi} = I, \\ \mathbf{E}_{f}\left[h_1^2(X)\right] &=4\sqrt{\pi}e^{1/4} \Phi\left(\frac{1}{\sqrt{2}}\right). \end{align*}\]

Για \(k=3, 4\) έχουμε:

\[\begin{align*} \mathbf{E}_{f}\left[h_1^3(X)\right] &=8\frac{\sqrt{2\pi}}{\sqrt{3}}e \Phi\left(\frac{2}{\sqrt{3}}\right), \\ \mathbf{E}_{f}\left[h_1^4(X)\right] &=8\sqrt{2\pi}e^{9/8} \Phi\left(\frac{3}{2}\right). \end{align*}\]

Αφήνεται τώρα ως άσκηση ο υπολογισμός των \(\lambda_h\) και \(k_h\). Σε άλλες περιπτώσεις οι συντελεστές αυτοί πρέπει να εκτιμηθούν από το προσομοιωμένο δείγμα χρησιμοποιώντας τους αντίστοιχους δειγματικούς.

3.6 Δειγματοληψία Σπουδαιότητας

Πριν ορίσουμε την έννοια της δειγματοληψίας σπουδαιότητας είναι σημαντικό να κατανοηθεί ότι το ίδιο το δείγμα που προσομοιώνεται από μία κατανομή μπορεί να χρησιμοποιηθεί για την προσέγγιση της κατανομής αυτής. Υπάρχουν πολλές περιπτώσεις που η συνάρτηση κατανομής \(F\), από την οποία προσομοιώνουμε, είναι άγνωστη. Πώς μπορούμε λοιπόν να χρησιμοποιήσουμε τις προσομοιωμένες τιμές για το σκοπό αυτό;

Έστω λοιπόν ότι διαθέτουμε ένα Monte Carlo δείγμα \(x_1,x_2,\ldots,x_n\) με ανεξάρτητες παρατηρήσεις που έχουνε προσομοιωθεί από την \(F\). Η μόνη πληροφορία που έχουμε είναι ότι η κατανομή μπορεί να πάρει αυτές τις τιμές. Αν κάποιος τώρα μας ζητήσει μία τιμή από την κατανομή δεν θα είχαμε κάποιο λόγο να ευνοήσουμε κάποια από αυτές. Θα μπορούσαμε να τις βάλουμε σε μία κληρωτίδα και να τραβήξουμε στην τύχη μία από αυτές. Με άλλα λόγια θα επιλέγαμε κάποια απο αυτές ισοπίθανα. Αυτή η απλή σκέψη μάς οδηγεί στην κατασκευή μίας καινούριας τ.μ. \(X^{*}_{n}\) που έχει τη διακριτή ομοιόμορφη κατανομή στο σύνολο \(\{x_1,x_2,\ldots x_n\}\). Θα ήταν βέβαια ιδιαίτερα επιθυμητό η συνάρτηση κατανομής \(F^{*}_{n}\) της \(X^{*}_{n}\) να προσεγγίζει (με κάποια έννοια) την άγνωστη συνάρτηση κατανομής \(F\) για μεγάλο \(n\). Εφόσον βέβαια η \(X^{*}_{n}\) είναι διακριτή τ.μ. έχουμε ότι \(\forall x\in \mathbb{R}\),

\[\begin{equation}\label{edfr}\displaystyle F^{*}_{n}(x) = \mathbf{P}(X^{*}_{n} \leq x)= \sum_{i: x_i \, \leq \, x } \mathbf{P}(X^{*}_{n} = x_i)= \sum_{i=1}^{n} \frac{1}{n}\,\mathbb{I}_{x_i \, \leq \, x} = \frac{\sum_{i=1}^{n}\mathbb{I}_{x_i \, \leq \, x}}{n}. \end{equation}\]

Είναι φανερό ότι η παραπάνω διαδικασία μας οδηγεί σε μία εκτιμήτρια του \(F(x)\). Συγκεκριμένα, αντικαθιστώντας με τ.μ. ορίζουμε

\[\begin{equation}\label{edf}\displaystyle \mathbb{F}_{n}(x) = \frac{\sum_{i=1}^{n}\mathbb{I}_{X_i \, \leq \, x}}{n}\qquad \forall x\in \mathbb{R}. \end{equation}\]

H \(\mathbb{F}_{n}\) λέγεται εμπειρική συνάρτηση κατανομής. Κάθε πραγματοποίηση \(F^{*}_{n}\) της \(\mathbb{F}_{n}\) αντιστοιχεί σε μία συνάρτηση κατανομής όπως προαναφέραμε και άρα παίρνει τιμές στο χώρο συναρτήσεων \(\mathcal{F}\). Μπορούμε λοιπόν να σκεφτόμαστε την \(\mathbb{F}_{n}\) ως μία τυχαία συνάρτηση του \(x\) ή ισοδύναμα ως μία τυχαία μεταβλητή με τιμές συναρτήσεις στον χώρο \(\mathcal{F}\). Αξίζει βέβαια να μελετηθούν οι οριακές ιδιότητες της \(\mathbb{F}_{n}\). Μας ενδιαφέρει λοιπόν να δούμε αν και με ποιό τρόπο συγκλίνει η \(\mathbb{F}_{n}\) στην \(F\).

3.6.1 Σημειακές ιδιότητες της εμπειρικής συνάρτησης κατανομής

Είδαμε ότι τη συνάρτηση κατανομής \(F\) μπορούμε να την εκτιμήσουμε με την εμπειρική συνάρτηση κατανομής \(\mathbb{F}_n\). Εξετάζουμε πρώτα τις σημειακές ιδιότητες της \(\mathbb{F}_n\).

Πρόταση 3.11 Για κάθε \(x\in\mathbb{R}\) ισχύει ότι \(n\,\mathbb{F}_n(x)\sim\text{Bin}(n, F(x))\).

Απόδειξη:. Έχουμε ότι \[\begin{equation}\label{edf-as-sample-mean} \mathbb{F}_n(x)=\dfrac{1}{n}\sum\limits_{k=1}^{n}\textbf{1}_{(-\infty, x]}(X_k)=\dfrac{1}{n}\sum\limits_{k=1}^{n}Y_k, \end{equation}\] όπου \(Y_k=\textbf{1}_{(-\infty, x]}(X_k)\) για κάθε \(1\leq k \leq n\). Είναι φανερό ότι \(Y_k\sim \text{Be}(F(x))\) για κάθε \(1\leq k \leq n\), και οι \(Y_1, \dots, Y_n\) είναι ανεξάρτητες τυχαίες μεταβλητές, αφού \(Y_k\in\{0, 1\}\) και ισχύει ότι \(\textbf{P}_F(Y_k=1)=\textbf{P}_F(X_k\leq x)=F(x)\), ενώ η ανεξαρτησία των \(Y_1, \dots, Y_n\) έπεται από την ανεξαρτησία των \(X_1, \dots, X_n\). Από τη σχέση (\(\ref{edf-as-sample-mean}\)) συμπεραίνουμε ότι \[n\,\mathbb{F}_n(x)=\sum\limits_{k=1}^{n}Y_k\sim \text{Bin}(n, F(x))\] ως άθροισμα \(n\) το πλήθος ανεξάρτητων τυχαίων μεταβλητών από την κατανομή \(\text{Be}(F(x))\). Το ζητούμενο έπεται.

Πόρισμα 3.4 Έστω \(F\) συνάρτηση κατανομής. Ισχύουν τα εξής:

1. \(\mathbf{E}_F(\mathbb{F}_n(x))=F(x)\), για κάθε \(x\in\mathbb{R}\).
2. \(\textbf{V}_F(\mathbb{F}_n(x))=\dfrac{F(x)(1-F(x))}{n}\), για κάθε \(x\in\mathbb{R}\).

Παρατήρηση:.

1. Ο δείκτης \(F\) στα \(\mathbf{E}_F\) και \(\textbf{V}_F\) που μπαίνουν στη μέση τιμή και τη διασπορά αφορούν τον υπολογισμό, αντίστοιχα, μέσης τιμής και διασποράς με \(X_1, \dots, X_n\sim F\) και συνήθως θα παραλείπεται.

2. Το παραπάνω πόρισμα εκφράζει την αμεροληψία της \(\mathbb{F}_n(x)\) ως εκτιμήτριας του \(F(x)\), για κάθε \(x\in \mathbb{R}\). Αυτό φαίνεται από τη σχέση (i). Από τη σχέση (ii) και τη σχέση (i) συμπεραίνουμε ότι είναι και συνεπής εκτιμήτρια του \(F(x)\), για κάθε \(x\in\mathbb{R}\). Πράγματι, ισχύει ότι \(\mathbf{V}(\mathbb{F}_n(x))\rightarrow 0\) και η \(\mathbb{F}_n(x)\) είναι αμερόληπτη εκτιμήτρια του \(\mathbb{F}(x)\). Αυτό το αποτέλεσμα μπορούμε να το δείξουμε και ανεξάρτητα. Μάλιστα, όπως φαίνεται στην επόμενη πρόταση, έχουμε ισχυρή συνέπεια.

Πρόταση 3.12 Για κάθε \(x\in\mathbb{R}\) ισχύει ότι \(\mathbb{F}_n(x)\stackrel{a.s.}{\longrightarrow}F(x)\).

Για κάθε \(x\in\mathbb{R}\) ισχύει ότι \(\sqrt{n}\,\left( \mathbb{F}_n(x)-F(x) \right) \stackrel{d}{\longrightarrow} \mathcal{N}\Big(0,\, F(x)(1-F(x)) \Big)\).

3.6.2 Ομοιόμορφη σύγκλιση της εμπειρικής συνάρτησης κατανομής

Τα παραπάνω αποτελέσματα μας δείχνουν τη σημειακή συμπεριφορά της εκτιμήτριας \(\mathbb{F}_n(x)\) της \(F\), δηλαδή το πώς συμπεριφέρονται οι ακολουθίες των τυχαίων μεταβλητών \(\mathbb{F}_n(x)\) για κάθε \(x\in\mathbb{R}\). Η \(\mathbb{F}_n\) είναι μία συλλογή τυχαίων μεταβλητών \(\{\mathbb{F}_n(x)\}_{x\in\mathbb{R}}\), οι οποίες είναι συσχετισμένες. Στην πραγματικότητα με το Monte Carlo δείγμα μπορούμε να προσεγγίσουμε όχι μόνο κατά σημείο αλλά και ομοιόμορφα. Σχετικά, είναι γνωστό το παρακάτω θεώρημα.

Θεώρημα 3.7 (Glivenko-Cantelli) Η εμπειρική συνάρτηση κατανομής \(\mathbb{F}_{n}\) συγκλίνει με πιθανότητα 1 ομοιόμορφα στην \(F\), δηλαδή,

\[\begin{equation}\label{unif-conv} \sup_{x\in\mathbb{R}}|\mathbb{F}_{n}-F| \xrightarrow[]{a.s.} 0. \end{equation}\]

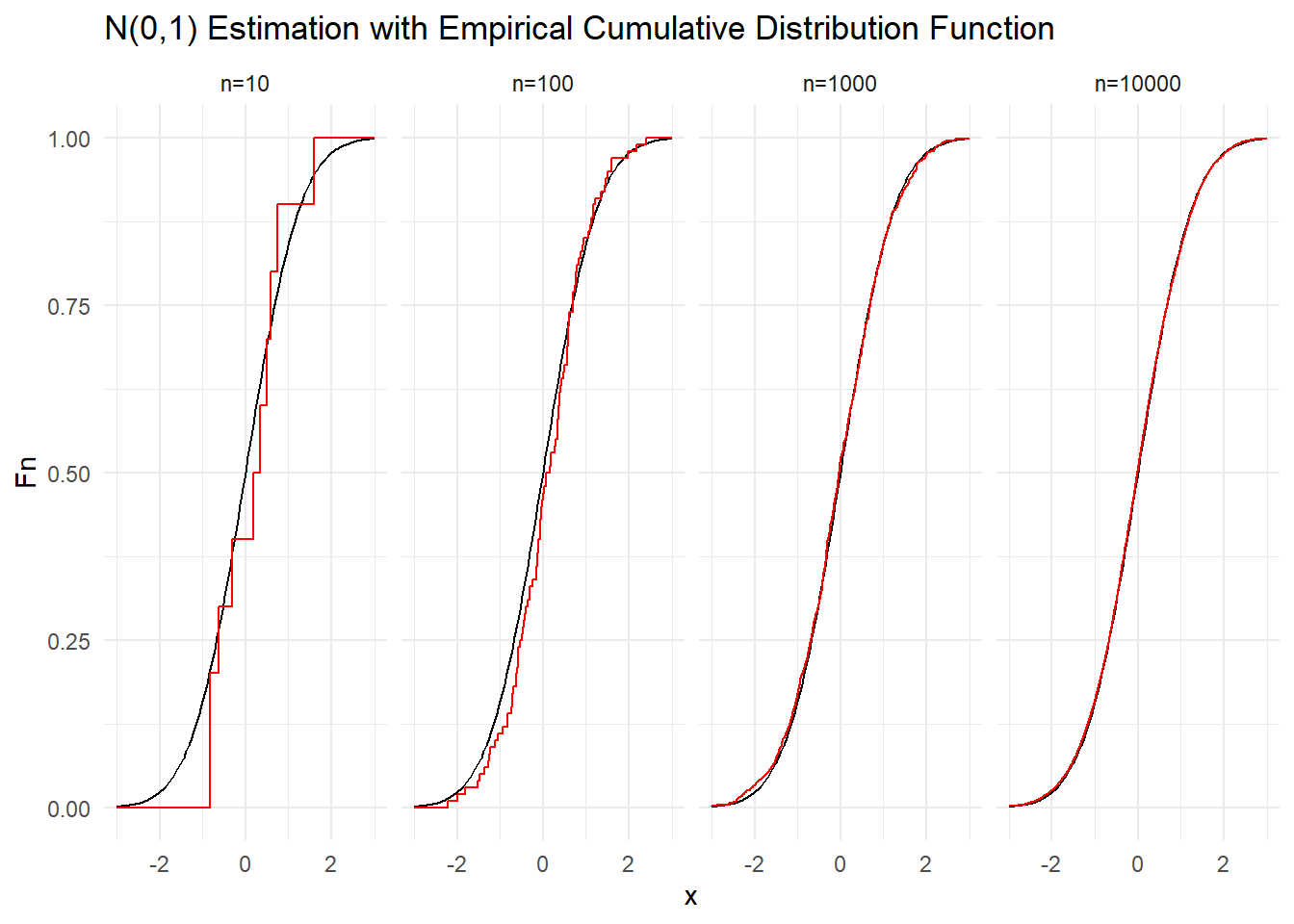
Παράδειγμα 3.8 Ας επαληθεύσουμε την σύγκλιση της \(\mathbb{F}_{n}\) στην \(F\) παίρνοντας όλο και μεγαλύτερα Monte Carlo δείγματα από την \(\mathcal{N}(0,1)\). Συγκεκριμένα, προσομοιώνουμε δείγματα μεγέθους \(n=10, 100, 1000\) και \(10000\).

Στα παρακάτω γραφήματα βλέπουμε μία πραγματοποίηση της εξέλιξης της εμπειρικής σ.κ. (κόκκινο), καθώς το μέγεθος του Monte Carlo δείγματος της \(N(0,1)\) αυξάνει, μαζί με τη θεωρητική συνάρτηση κατανομής (μαύρο) της τυποποιημένης κανονικής κατανομής \(N(0, 1)\). Βλέπουμε ότι με δείγμα μεγέθους \(n=10\) η προσέγγιση της θεωρητικής από την εμπειρική σ.κ. δεν είναι καλή, βελτιώνεται αισθητά με \(n=100\), δύσκολα ξεχωρίζουμε τις καμπύλες με \(n=1000\) , ενώ με \(n=10000\) σχεδόν επιτυγχάνεται ταύτιση.

3.6.3 Δειγματοληψία σπουδαιότητας

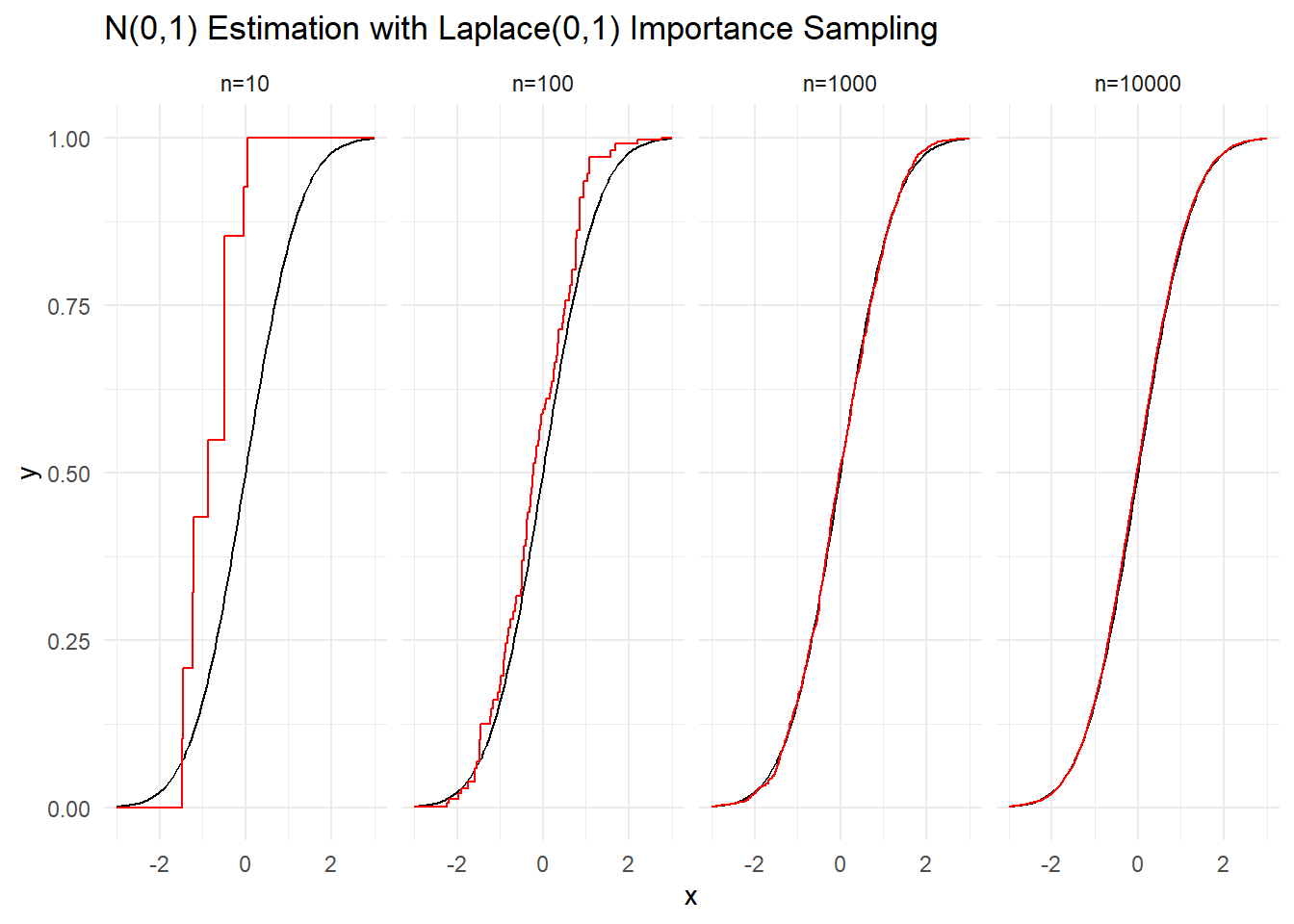
Ας υποθέσουμε τώρα ότι δε μπορούμε να προσομοιώσουμε από τη \(\mathcal{N}(0,1)\). Παρ’ όλα αυτά έχουμε τη δυνατότητα να προσομοιώνουμε από τη διπλή εκθετική. Το ερώτημα που τίθεται είναι κατά πόσον μπορούμε να φτάσουμε στο ίδιο αποτέλεσμα, δηλαδή μετά από ένα κατάλληλα μεγάλο μέγεθος δείγματος να μπορούμε να βρεθούμε οσοδήποτε κοντά θέλουμε στην κανονική κατανομή, και συγκεκριμένα στην σ.κ. \(\Phi\). Η πρώτη μας σκέψη θα ήταν ότι αν προσομοιώναμε από τη διπλή εκθετική, τότε χρησιμοποιώντας την εμπειρική συνάρτηση κατανομής της, θα μπορούσαμε να προσεγγίσουμε όσο καλά θέλουμε την \(F_L\), δηλαδή τη σ.κ. της \(Laplace(0,1)\) (δηλ. τη διπλή εκθετική) και όχι τη \(\Phi\). Με κάποιο τρόπο πρέπει να αντισταθμίσουμε ότι προσομοιώνουμε από διαφορετική κατανομή από αυτήν που ζητάμε. Παρατηρούμε ότι

\[\begin{equation*} \Phi(x) = \mathbf{E}_f\left[\mathbb{I}_{X\leq x}\right] = \mathbf{E}_g\left[\mathbb{I}_{X\leq x} \cdot \frac{f(X)}{g(X)}\right]. \end{equation*}\]

Προκειμένου λοιπόν να “στοχεύσουμε” με Monte Carlo στην \(\Phi\) θα μπορούσαμε να “προτείνουμε” από τη \(g\) και να αντισταθμίσουμε αυτή τη διαφορά εισάγοντας τη συνάρτηση “βάρους”

\[\begin{equation*} w(x)=\frac{f(x)}{g(x)}. \end{equation*}\]

Ο όρος importance function (συνάρτηση σπουδαιότητας) χρησιμοποιείται συχνά σε αυτό το πλαίσιο για τη \(g\) και ο όρος importance weight (βάρος σπουδαιότητας) για τη \(w=f/g\). Η ερμηνεία του βάρους σπουδαιότητας είναι αρκετά διαισθητική, αφού οι τιμές τις οποίες προσομοιώνει η \(g\) με μικρότερη (μεγαλύτερη) πυκνότητα από την \(f\) πρέπει να “ενισχυθούν” (“αποδυναμωθούν”) με μεγαλύτερο βάρος, έτσι ώστε τελικά ο “στόχος” να παραμένει στην \(f\). Γενικά, αυτό εκφράζεται ως

\[\begin{equation*} \mathbf{E}_f\left[h(X)\right] = \mathbf{E}_g\left[h(X) w(X)\right]. \end{equation*}\]

Παράδειγμα 3.9 Ας επαληθεύσουμε ότι με δειγματοληψία σπουδαιότητας από την \(Laplace(0,1)\) πετυχαίνουμε σύγκλιση στην \(\Phi\). Συγκεκριμένα, προσομοιώνουμε δείγματα μεγέθους \(n=10, 100, 1000\) και \(10000\).

# Importance weight
w <- function(s) {
  dnorm(s) / dlaplace(s)
}

# ecdf
Fn <- function(x, s) {
  sapply(x, FUN = function(x) { sum((s <= x) * w(s)) / sum(w(s)) })
}

Άσκηση 3.1 (Robert & Casella 3.3) Μας ενδιαφέρει να εκτιμήσουμε την πιθανότητα \(\mathbf{P}(X>5)\) όταν \(X\sim \mathcal{N}(0,1)\), η οποία σύμφωνα με την R είναι \(p=2.8665\cdot 10^{-7}\). Σε αυτή την περίπτωση, η άμεση προσομοίωση από την \(\mathcal{N}(0,1)\) είναι ιδιαίτερα δύσκολη, αφού το ενδεχόμενο που θέλουμε να μελετήσουμε εμφανίζεται κατά μέσο όρο 1 φορά στις \(1/p=3488556\) παρατηρήσεις, δηλαδή θα χρειαστούμε περίπου 3.5 εκατομμύρια παρατηρήσεις για την εμφάνιση μίας παρατήρησης \(x_i>5\). Για τον λόγο αυτό, προτιμάμε να εκφράσουμε την πιθανότητα ως ολοκλήρωμα και να χρησιμοποιήσουμε Monte Carlo προσομοίωση.

\[\begin{equation*} \mathbf{P}(X>5) = \int_5^{+\infty} f(x) dx \overset{y=1/x}{=} \int_{1/5}^{0} f(1/y) \cdot \left(-\frac{1}{y^2}\right) dy = \int_0^{1/5} f(1/y) \frac{1}{y^2} dy. \end{equation*}\]

Σε αυτό το σημείο, μπορούμε να εκφράσουμε το ολοκλήρωμα ως μέση τιμή μιας τ.μ. \(Y\sim Unif(0, 1/5)\) με σ.π.π. \(g(y)=5\) στο διάστημα \((0, 1/5)\), και να πάρουμε

\[\begin{equation*} \int_0^{1/5} f(1/y) \frac{1}{y^2} dy = \int_0^{1/5} f(1/y) \frac{1}{5y^2} \cdot 5 dy = \int_0^{1/5} h(y)\cdot g(y) dy = \mathbf{E}_g\left[h(Y)\right)], \end{equation*}\]

όπου \(h(y)=f(1/y) \frac{1}{5y^2}\). Επομένως είμαστε έτοιμοι να προσομοιώσουμε από την \(Y\) και να λάβουμε την εκτίμησή μας καθώς και το εκτιμημένο τυπικό σφάλμα της εκτιμήτριας.

Στο παρακάτω γράφημα βλέπουμε την πορεία της εκτίμησης καθώς και την ασυμπτωτική σημειακή \(95\%\) λωρίδα εμπιστοσύνης για μέγεθος δείγματος \(n=10^5\). Η εκτίμηση που παίρνουμε είναι \(\widehat{p}_n=\) 2.9021 \(\cdot 10^{-7}\) με εκτιμημένο τυπικό σφάλμα \(\widehat{\sigma}_{\widehat{p}_n}=\) 0.0326\(\cdot 10^{-7}\).

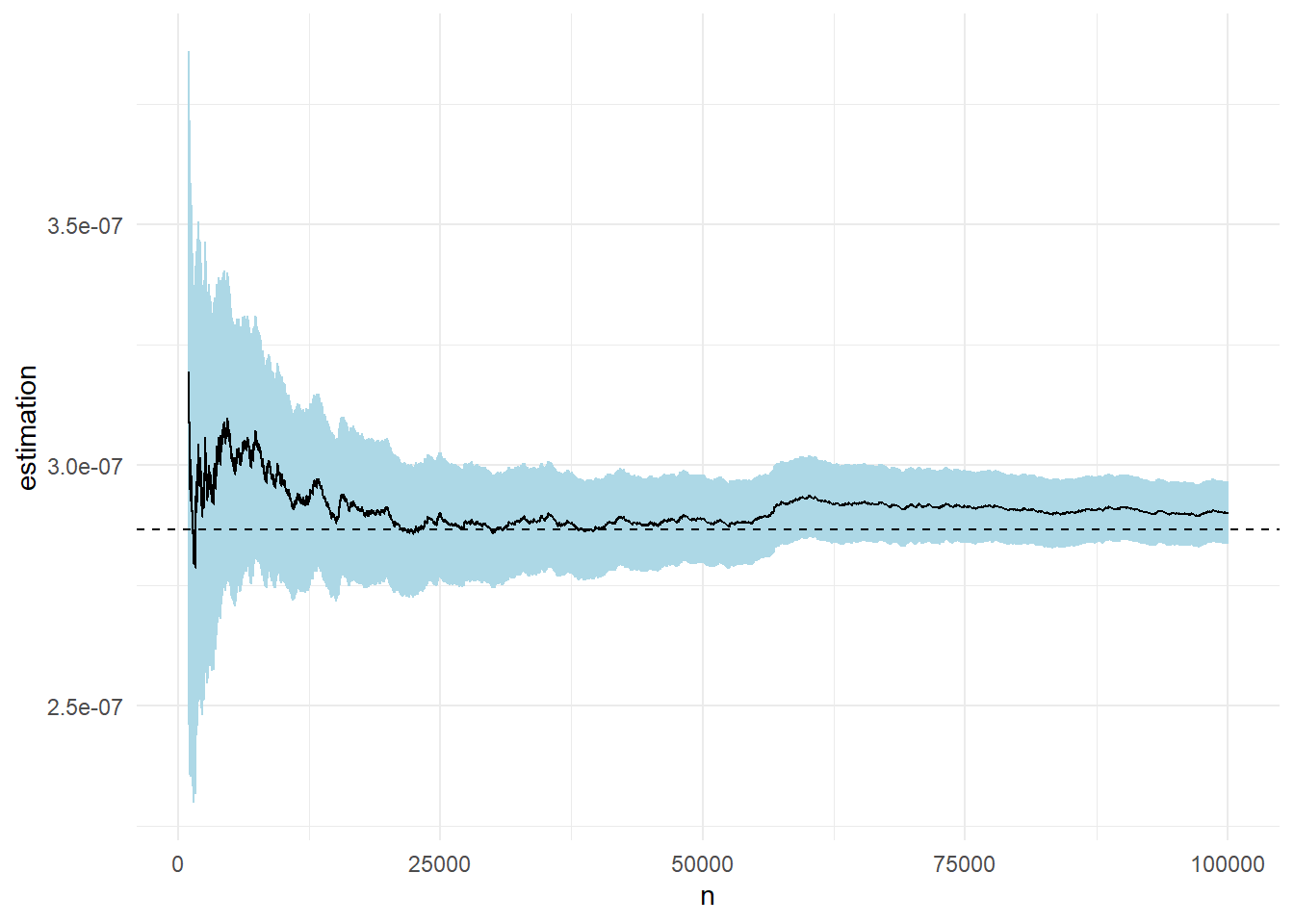
Άσκηση 3.2 (Robert & Casella 3.5) Σε συνέχεια της προηγούμενης άσκησης, επιθυμούμε να επαναλάβουμε την εκτίμηση της πιθανότητας \(\mathbf{P}(X>5)\) όταν \(X\sim \mathcal{N}(0,1)\), αυτή τη φορά χρησιμοποιώντας δειγματοληψία σπουδαιότητας, με συνάρτηση σπουδαιότητας \(g\) από την περικεκκομένη εκθετική με παράμετρο 1 στο διάστημα \((5, +\infty)\).

Σημείωση: Έστω η τ.μ. \(Y\) που ακολουθεί μία συγκεκριμένη κατανομή. Η περικεκκομένη (truncated) κατανομή στο διάστημα \((a, \beta)\), το οποίο πρέπει να είναι υποσύνολο του στηρίγματος, όπου το \(a\) (αντίστοιχα, \(\beta\)) μπορεί να είναι και \(-\infty\) (αντίστοιχα, \(+\infty\)), χαρακτηρίζεται από την συνάρτηση κατανομής

\[\begin{equation*} F_{tr}(y) = \mathbf{P}\left(Y\leq y |Y\in (a, \beta)\right) = \frac{\int_a^y f(y) dy}{\int_a^\beta f(y) dy}, \ \ y\in (a, \beta). \end{equation*}\]

Ειδικά στην περίπτωση της εκθετικής κατανομής (που έχει την αμνήμονη ιδιότητα), έχουμε σημαντικές απλοποιήσεις. Έτσι, η περικεκκομένη εκθετική στο διάστημα \((a, +\infty)\) έχει συνάρτηση κατανομής

\[\begin{equation*} F_{tr}(y) = 1-e^{-\lambda(y-a)}\ \ y>a, \end{equation*}\]

και συνάρτηση πυκνότητας πιθανότητας

\[\begin{equation*} f(y) = \lambda e^{-\lambda (y-a)}, \ \ y>a. \end{equation*}\]

Τα παραπάνω υποδηλώνουν ότι αν \(Y\sim Exp(1)\), τότε η \((Y+a)\) ακολουθεί την περικεκκομένη εκθετική στο επιθυμητό διάστημα \((a, +\infty)\). Επομένως είναι ιδιαίτερα εύκολο να προσομοιώσουμε από την συγκεκριμένη κατανομή και να εφαρμόσουμε δειγματοληψία σπουδαιότητας. Έχουμε:

\[\begin{equation*} \mathbf{P}(X>5) = \mathbf{E}_f \left[\mathbb{I}_{\{X>5\}} \right] = \mathbf{E}_g \left[\mathbb{I}_{\{X>5\}} \cdot \frac{f(X)}{g(X)} \right] = \mathbf{E}_g \left[h(X) w(X) \right]=\mathbf{E}_g \left[w(X) \right], \end{equation*}\]

όπου \(h(x)=\mathbb{I}_{\{x>5\}}\) και \(w(x)=f(x)/g(x)\).

Στο παρακάτω γράφημα βλέπουμε την πορεία της εκτίμησης καθώς και την ασυμπτωτική σημειακή \(95\%\) λωρίδα εμπιστοσύνης για μέγεθος δείγματος \(n=10^5\). Η εκτίμηση που παίρνουμε είναι \(\widehat{p}_n=\) 2.869 \(\cdot 10^{-7}\) με εκτιμημένο τυπικό σφάλμα \(\widehat{s}_n=\) 0.0126\(\cdot 10^{-7}\).

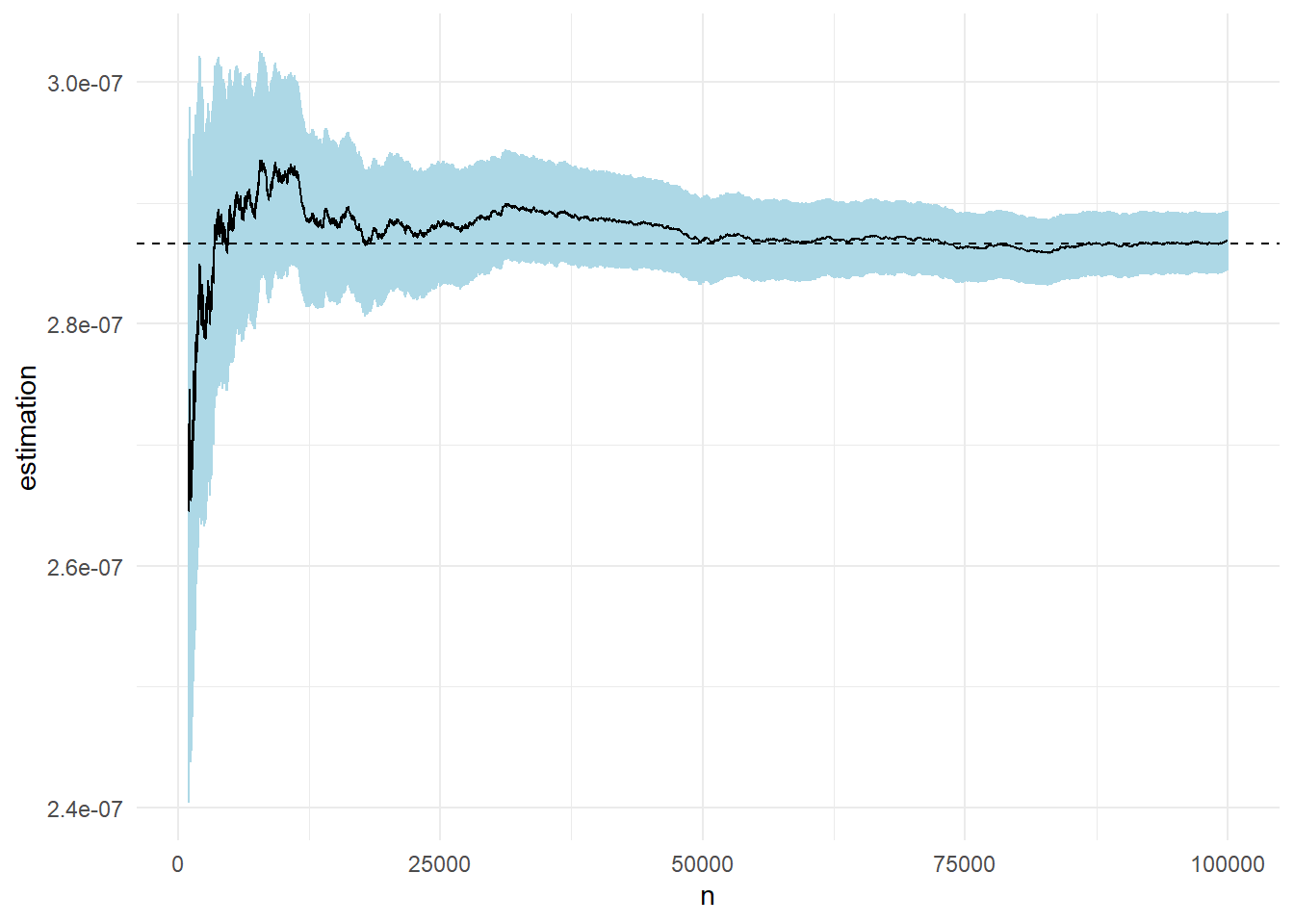
Παρατηρούμε ότι η σύγκλιση με αυτόν τον τρόπο είναι ταχύτερη σε σχέση με το προηγούμενο παράδειγμα, καθώς έχει μικρότερη ασυμπτωτική διασπορά, κάτι που φαίνεται και στα γραφήματα.

Άσκηση 3.3 (Robert & Casella 3.4) Θέλουμε να υπολογίσουμε την \(\mathbf{E}_f\left[h(X)\right]\), όπου \(f\) είναι η σ.π.π. της τυπικής κανονικής και \(h(x)=e^{-(x-3)^2/2}+e^{-(x-6)^2/2}\). Η συγκεκριμένη μέση τιμή μπορεί να γραφεί σε κλειστή μορφή και να υπολογιστεί ως εξής:

\[\begin{align*} \mathbf{E}_f\left[h(X)\right] &= \int_{-\infty}^{+\infty} \left(e^{-(x-3)^2/2}+e^{-(x-6)^2/2}\right) \cdot \frac{1}{\sqrt{2\pi}} e^{-\frac{1}{2}x^2} dx \\ &= \int_{-\infty}^{+\infty} \frac{1}{\sqrt{2\pi}} e^{-\frac{1}{2}\left[ (x-3)^2 +x^2 \right]} dx + \int_{-\infty}^{+\infty} \frac{1}{\sqrt{2\pi}} e^{-\frac{1}{2}\left[ (x-6)^2 +x^2 \right]} dx \\ &=\int_{-\infty}^{+\infty}\frac{1}{\sqrt{2\pi}} e^{-\frac{1}{2} \cdot 2 \cdot \left[ (x-3/2)^2 +9/4\right]} dx + \int_{-\infty}^{+\infty}\frac{1}{\sqrt{2\pi}} e^{-\frac{1}{2} \cdot 2 \cdot \left[(x-3)^2 +9\right]} dx \\ &= \frac{e^{-9/4}}{\sqrt{2}} \int_{-\infty}^{+\infty} \frac{1}{\sqrt{\pi}} e^{-\frac{1}{2} \cdot 2 \cdot (x-3/2)^2} dx + \frac{e^{-9}}{\sqrt{2}} \int_{-\infty}^{+\infty} \frac{1}{\sqrt{\pi}} e^{-\frac{1}{2} \cdot 2 \cdot (x-3)^2} dx \\ &= \frac{e^{-9/4}}{\sqrt{2}} \int_{-\infty}^{+\infty} \underbrace{\frac{1}{\sqrt{2\pi \frac{1}{2}}} e^{-\frac{1}{2 \cdot \frac{1}{2}} \cdot (x-3/2)^2}}_{\mathcal{N}\left(\cdot \ ; \ \mu=3/2, \sigma^2=1/2\right)} dx + \frac{e^{-9}}{\sqrt{2}} \int_{-\infty}^{+\infty} \underbrace{\frac{1}{\sqrt{2\pi \frac{1}{2}}} e^{-\frac{1}{2 \cdot \frac{1}{2}} \cdot (x-3)^2}}_{\mathcal{N}\left(\cdot \ ; \ \mu=3, \sigma^2=1/2\right)} dx \\ &= \frac{e^{-9/4}+e^{-9}}{\sqrt{2}} \approx 0.0746 \end{align*}\]

Θέλουμε να εκτιμήσουμε την παραπάνω ποσότητα με ολοκλήρωση Monte Carlo προσομοιώνοντας από την \(\mathcal{N}(0,1)\) ένα δείγμα μεγέθους \(n=10^4\).

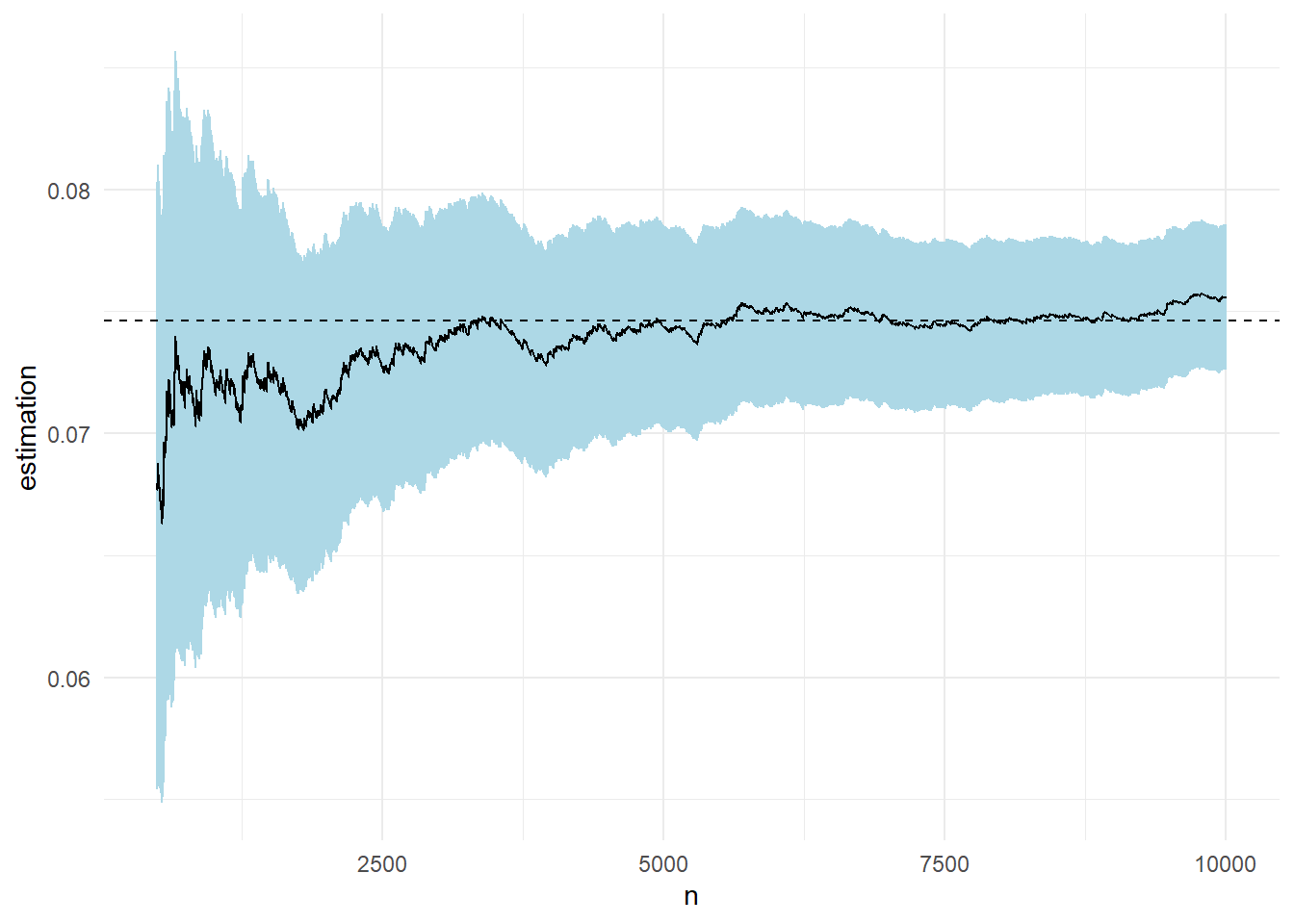
Θα προσπαθήσουμε τώρα να εκτιμήσουμε την ίδια ποσότητα με δειγματοληψία σπουδαιότητας, χρησιμοποιώντας ως συνάρτηση σπουδαιότητας \(g\) την σ.π.π. της \(Unif(-8, -1)\). Φυσικά, με το να επιλέξουμε μία \(g\) με στήριγμα υποσύνολο του στηρίγματος της \(h\times f\) εισάγουμε μεροληψία στην εκτίμησή μας. Αρχικά, παρατηρούμε ότι οι συναρτήσεις \(h, w\) είναι γνησίως αύξουσες στο διάστημα \((-8, -1)\), επομένως το ίδιο και η \(h\cdot w\).

h <- function(x) { 
  exp( - (x - 3) ^ 2 / 2) + exp( - (x - 6) ^ 2 / 2)
}
w <- function(x) { 
  dnorm(x) / dunif(x, min = -8, max = -1)
}

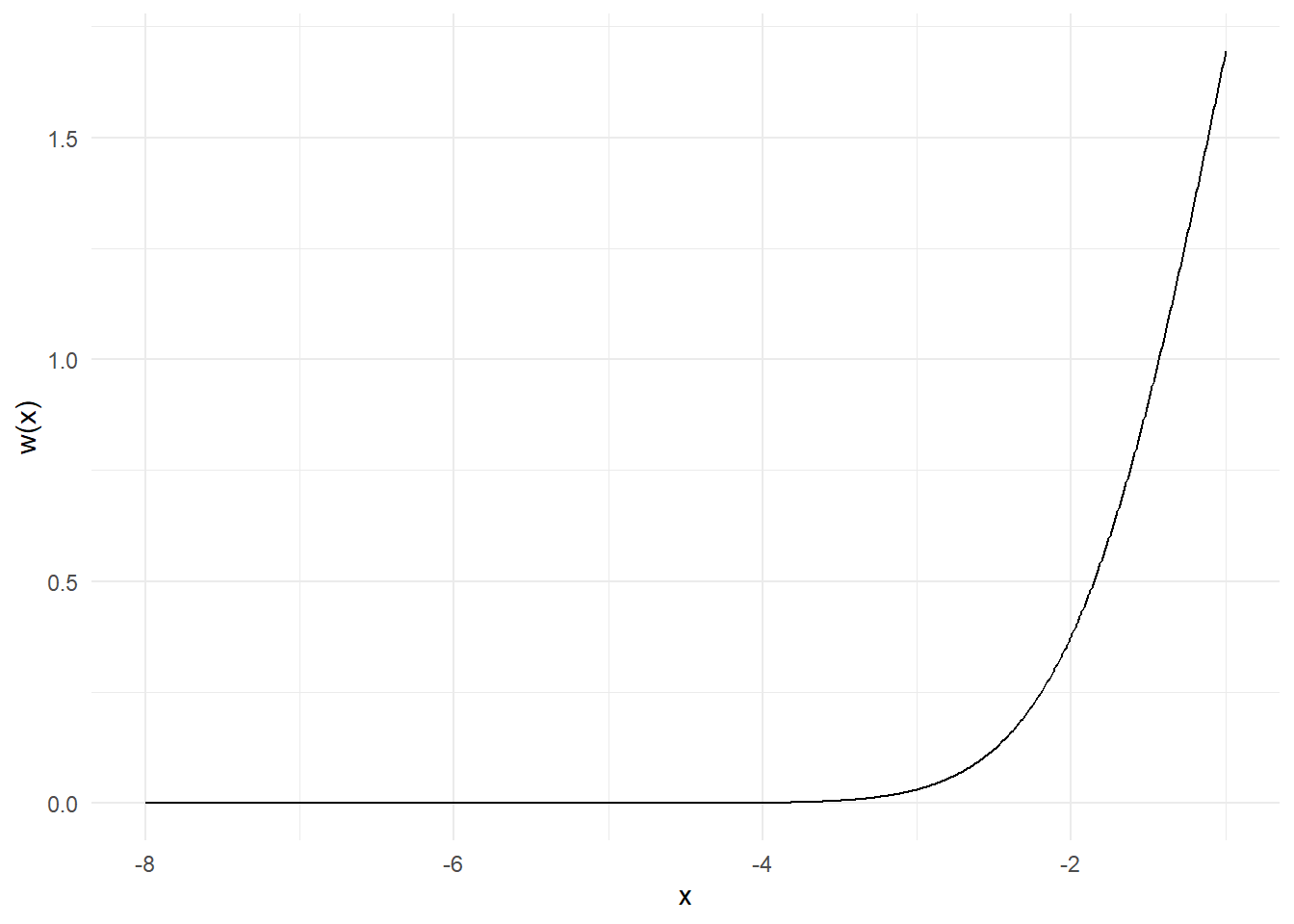
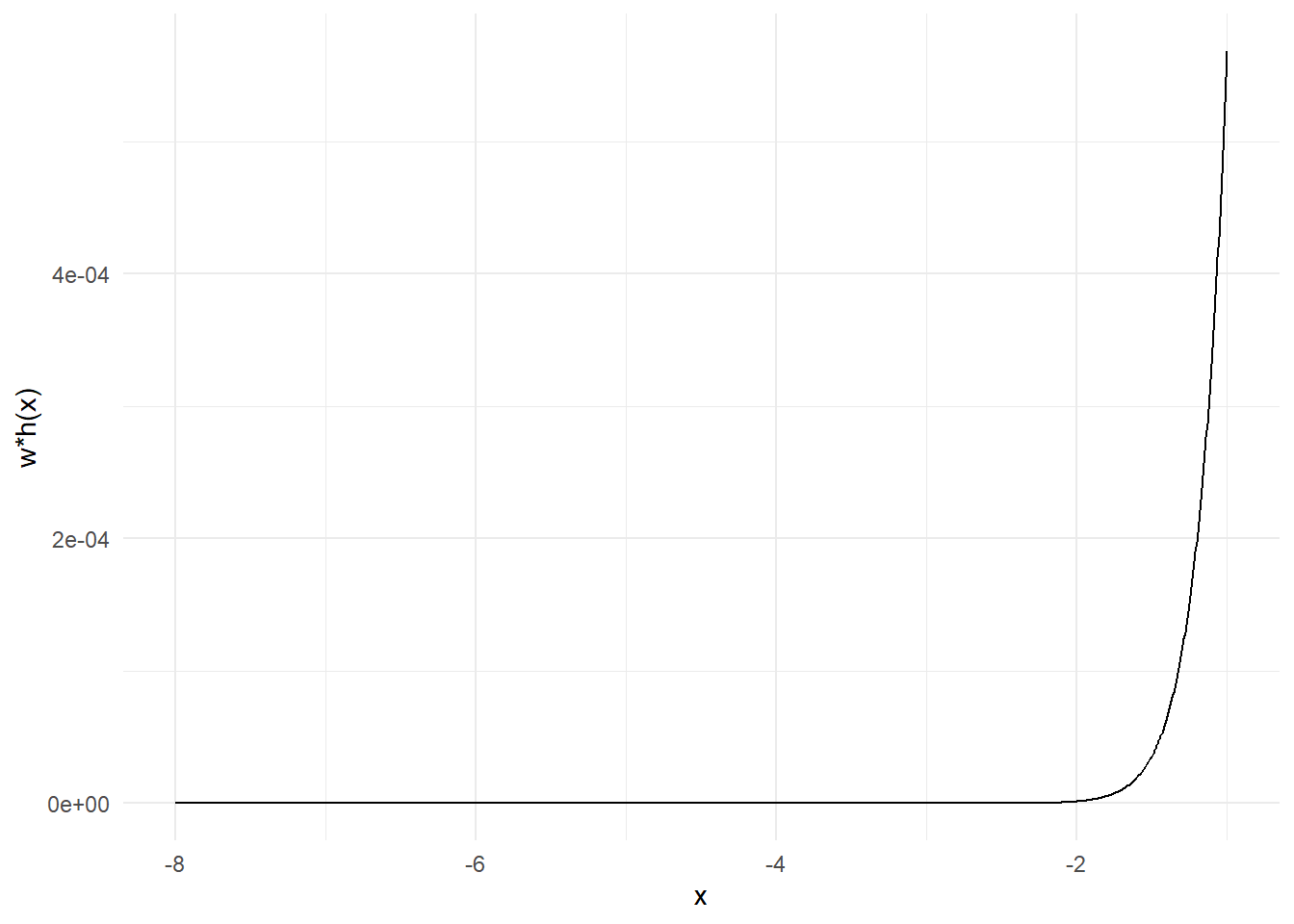
Παρατηρούμε πως υπάρχει πολύ μεγάλη διαφορά ανάμεσα στα βάρη που αντιστοιχούν στις τιμές του διαστήματος, κάτι που μπορεί να οδηγήσει σε πολύ μεγάλες αλλαγές στην εκτίμησή μας με την εισαγωγή μίας μόνο παρατήρησης. Ως παράδειγμα, έχουμε \(w(-6)=4.2531\cdot 10^{-8}\) και \(w(-2)=0.3779\), δηλαδή τα δύο βάρη έχουν λόγο \(\frac{w(-2)}{w(-6)}=8886111\).

Επιπλέον, για \(x \in [-8, -1]\), οι παρατηρήσεις \(h(x)\cdot w(x)\) θα παίρνουν τιμές στο διάστημα \([h(-8)\cdot w(-8), h(-1)\cdot w(-1)]=[1.8783\cdot 10^{-40}, 0.0005682]\), τη στιγμή που η υπό εκτίμηση ποσότητα υπολογίστηκε ίση με \(0.0746\), δηλαδή η πραγματική μέση τιμή βρίσκεται εκτός του στηρίγματος της εκτιμήτριας που κατασκευάσαμε.

Η συγκεκριμένη δειγματοληψία σπουδαιότητας μας δίνει εκτίμηση \(\widehat{p}_n=\) 1.5576 \(\cdot 10^{-5}\) με εκτιμημένο τυπικό σφάλμα \(\widehat{s}_n=\) 0.0654\(\cdot 10^{-5}\) (σχήμα αριστερά). Η εκτίμηση αυτή πέφτει τόσο έξω από την πραγματική τιμή, που αν αναπαρασταθούν σε ένα κοινό γράφημα, η εκτίμησή μας δείχνει σχεδόν σταθερή στο 0.

Για το επόμενο παράδειγμα θα χρειαστούμε μια πολυδιάστατη γενικευση της κατανομής Student. Υπενθυμίζουμε ότι μία τ.μ. \(X\sim t_n\) ανν μπορεί να αναπαρασταθεί στην μορφή

\[\begin{equation*} X = \frac{Z}{\sqrt{Q/n}}, \end{equation*}\]

όπου \(Z, Q\) ανεξάρτητες τ.μ. με \(Z\sim \mathcal{N}(0,1)\) και \(Q\sim\mathcal{X}^2_n\).

Υπάρχουν πολλοί διαφορετικοί τρόποι γενίκευσης της κατανομής Student. Περιγράφουμε έναν από αυτούς που χρησιμοποιείται συχνά.

Ορισμός 3.14 (Multivariate Student) Ένα τ.δ. \(X=(X_1, X_2, ..., X_d)\) ακολουθεί την πολυδιάστατη κατανομή Student \(\mathcal{T}_n(\mu, \Sigma)\) ανν μπορεί να αναπαρασταθεί στην μορφή

\[\begin{equation*} X = \mu +\frac{W}{\sqrt{Q/n}}, \end{equation*}\]

όπου \(W\sim \mathcal{N}_d(0,\Sigma)\), \(Q\sim\mathcal{X}^2_n\) και \(W, Q\) ανεξάρτητα.

Η συνάρτηση πυκνότητας πιθανότητας του \(X\) είναι

\[\begin{equation*} f(x) = \frac{\Gamma[(n+d)/2]}{\Gamma(n/2)n^{d/2}\pi^{d/2}|\Sigma|^{1/2}} \left[ 1 +\frac{1}{n} (x-\mu)^\top \Sigma^{-1} (x-\mu) \right]^{-(n+d)/2}. \end{equation*}\]

Θα θέλαμε να τονίσουμε ότι η μέθοδος δειγματοληψίας σπουδαιότητας εφαρμόζεται και σε περιπτώσεις που οι σταθερές κανονικοποίησης είναι άγνωστες, κάτι το οποίο επεκτείνει κατά πολύ το πεδίο εφαρμογών της μεθόδου. Σε αυτές τις περιπτώσεις η εκτίμηση της μέσης τιμής μπορεί να δοθεί πάλι από τη σχέση

\[\begin{equation*} \frac{\sum_{i=1}^n w(X_i)h(X_i)}{\sum_{i=1}^n w(X_i)}, \end{equation*}\]

όπου η κανονικοποίηση ως προς το άθροισμα των βαρών απλοποιεί άγνωστες σταθερές. Εύκολα παρατηρούμε ότι

\[\begin{equation*} \frac{\sum_{i=1}^n w(X_i)h(X_i)}{\sum_{i=1}^n w(X_i)} = \frac{\sum_{i=1}^n w(X_i)h(X_i)/n}{\sum_{i=1}^n w(X_i)/n}\overset{a.s.}{\longrightarrow} \frac{\mathbf{E}_g\left[w(X)h(X)\right]}{\underbrace{\mathbf{E}_g\left[w(X)\right]}_{=1}} = \mathbf{E}_f\left[h(X)\right]. \end{equation*}\]

Στην περίπτωση που υπάρχει άγνωστη σταθερά κανονικοποίησης, τότε η παραπάνω σύγκλιση ισχύει πάλι, με μόνη διαφορά ότι

\[\begin{equation*} \frac{\mathbf{E}_g\left[w(X)h(X)\right]}{\mathbf{E}_g\left[w(X)\right]} = \frac{c\mathbf{E}_f\left[h(X)\right]}{c} \mathbf{E}_f\left[h(X)\right]. \end{equation*}\]

Χρησιμοποιώντας την παραπάνω σχέση, μπορούμε να εκτιμήσουμε τη σταθερά \(c\) μέσα από το \(\sum_{i=1}^n w(X_i)/n\).

Παράδειγμα 3.10 (Robert & Casella 3.6) Ας μελετήσουμε μία εφαρμογή της δειγματοληψίας σπουδαιότητας στην Μπεϋζιανή Στατιστική. Αν \(x\) είναι μία παρατήρηση από την \(B(a, \beta)\), με σ.π.π.

\[\begin{equation*} f(x|α, \beta) = \frac{\Gamma(a+\beta)}{\Gamma(a)\Gamma(\beta)} x^{a-1} (1-x)^{\beta-1} \mathbb{I}_{[0,1]}(x), \end{equation*}\]

τότε υπάρχει μία οικογένεια συζυγών prior κατανομών για τα \((a, \beta)\) της μορφής

\[\begin{equation*} \pi(a, \beta) \propto \left\{\frac{\Gamma(a+\beta)}{\Gamma(a)\Gamma(\beta)}\right\}^\lambda x_0^{a} y_0^{\beta}, \end{equation*}\]

όπου \(\lambda, x_0, y_0\) είναι υπερπαράμετροι, οδηγώντας στην posterior κατανομή

\[\begin{equation*} \pi(a, \beta|x) \propto \left\{\frac{\Gamma(a+\beta)}{\Gamma(a)\Gamma(\beta)}\right\}^{\lambda+1} [xx_0]^{a} [(1-x)y_0]^{\beta}. \end{equation*}\]

Αυτή η οικογένεια κατανομών είναι δύσχρηστη εξαιτίας της δυσκολίας των συναρτήσεων \(\Gamma\). Ως αποτέλεσμα, η άμεση προσομοίωση από την \(\pi(a, \beta|x)\) είναι αδύνατη. Χρειαζόμαστε λοιπόν μία κατανομή \(g(a, \beta)\) η οποία θα λειτουργήσει ως συνάρτηση σπουδαιότητας. Κοιτώντας το γράφημα της \(\pi(a, \beta|x)\), για \(\lambda=1, x_0=y_0=0.5\) και \(x=0.6\), έχουμε:

f <- function(a, b){
  exp(2 * (lgamma(a + b) - lgamma(a) - lgamma(b)) + a * log(.3) + b * log(.2))
}

aa <- 1:150 # alpha grid for image
bb <- 1:100 # beta grid for image
post <- outer(aa, bb, f)

image(aa, bb, post, xlab = expression(alpha), ylab=" ")
contour(aa, bb, post, add = TRUE)

x <- matrix(rt(2 * 10 ^ 4, 3), ncol = 2) # T sample
E <- matrix(c(220, 190, 190, 180), ncol = 2) # Scale matrix
image(aa, bb, post, xlab = expression(alpha), ylab = " ")
y <- t(t(chol(E)) %*% t(x) + c(50, 45))
points(y, cex = .6, pch = 19)

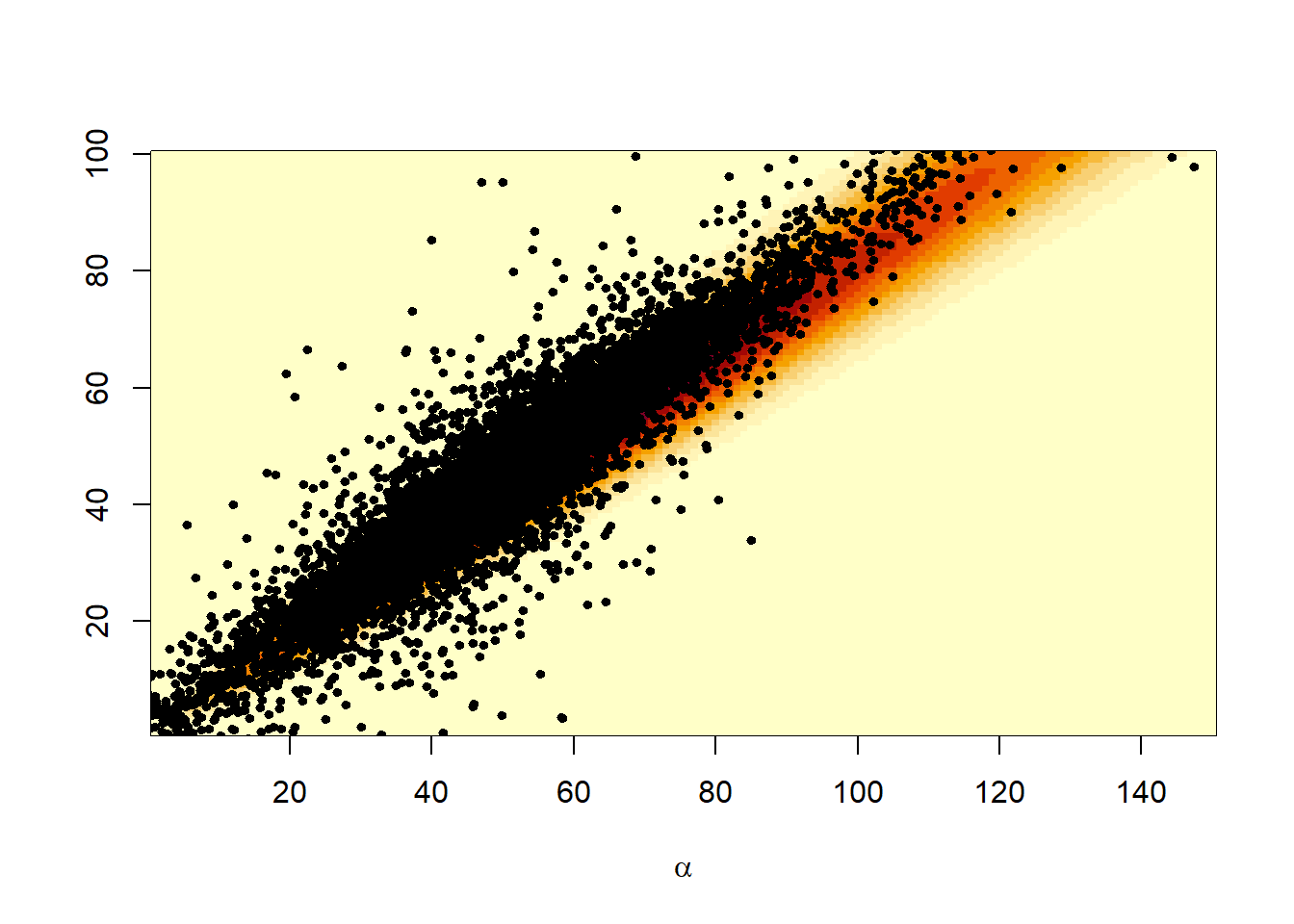
Εξετάζοντας το αριστερό γράφημα παρατηρούμε ότι μία κανονική ή Student’s \(t\) κατανομή ίσως είναι κατάλληλη για το ζεύγος \((a, \beta)\). Επιλέγουμε την κατανομή \(\mathcal{T}_3(\mu, \Sigma)\) με \(\mu = (50, 45)^\top\) και \(\Sigma= \left(\begin{array}{cc} 220 & 190 \\ 190 & 180 \end{array} \right)\). Στο γράφημα δεξιά βλέπουμε ένα προσομοιωμένο δείγμα από την συγκεκριμένη κατανομή πάνω στην επιφάνεια της posterior κατανομής. Οι τιμές των \(\mu, \Sigma\) επιλέχθηκαν με trial-and-error, προκειμένου να ταιριάζουν στην posterior κατανομή.

Αν η ποσότητα που μας ενδιαφέρει είναι η περιθώρια πιθανοφάνεια (marginal likelihood),

\[\begin{equation*} m(x)=\int_{\mathbb{R}^2_+} f(x|a, \beta) \pi(a, \beta) da d\beta = \frac{\int_{\mathbb{R}^2_+}\left\{\frac{\Gamma(a+\beta)}{\Gamma(a)\Gamma(\beta)} \right\}^{\lambda+1} [xx_0]^a[(1-x)y_0]^\beta da d\beta}{x(1-x)\int_{\mathbb{R}^2_+}\left\{\frac{\Gamma(a+\beta)}{\Gamma(a)\Gamma(\beta)} \right\}^{\lambda} x_0^ay_0^\beta da d\beta}, \end{equation*}\]

χρειάζεται να προσεγγίσουμε και τα δύο ολοκληρώματα. Μπορούμε να χρησιμοποιήσουμε το δείγμα που προσομοιώσαμε από την παραπάνω κατανομή student και για τα δύο, αφού η επιλογή της κατανομής αυτής στέκει τόσο για την prior όσο και για την posterior. Η προσέγγισή μας είναι η

\[\begin{equation*} \widehat{m}(x) = \frac{\sum_{i=1}^n \left\{\frac{\Gamma(a_i+\beta_i)}{\Gamma(a_i)\Gamma(\beta_i)} \right\}^{\lambda+1} [xx_0]^{a_i} [(1-x)y_0]^{\beta_i} / g(a_i, \beta_i)}{\sum_{i=1}^n \left\{\frac{\Gamma(a_i+\beta_i)}{\Gamma(a_i)\Gamma(\beta_i)} \right\}^{\lambda} x_0^{a_i} y_0^{\beta_i} / g(a_i, \beta_i)}, \end{equation*}\]

όπου τα \((a_i, \beta_i)_{1\leq i \leq n}\) είναι ανεξάρτητες και ισόνομες παρατηρήσεις από την \(g\), μπορεί να πραγματοποιηθεί άμεσα στην R:

ine <- apply(y, 1, min)
y <- y[ine > 0, ]
x <- x[ine > 0, ]
normx <- sqrt(x[ , 1] ^ 2 + x[ , 2] ^ 2)

f <- function(a) {
  exp(2 * (lgamma(a[ , 1] + a[ , 2]) - lgamma(a[ , 1]) - lgamma(a[ , 2])) + a[ , 1] * log(.3) + a[ , 2] * log(.2))
}

h <- function(a) {
  exp(1 * (lgamma(a[ , 1] + a[ , 2]) - lgamma(a[ , 1]) - lgamma(a[ , 2])) + a[ , 1] * log(.5) + a[ , 2] * log(.5))
}

den <- dt(normx, 3)
m <- mean(f(y) / den) / mean(h(y) / den)
m
## [1] 0.244607

Η προσέγγιση της περιθώριας πιθανοφάνειας, βασισμένη σε αυτό το προσομοιωμένο δείγμα, είναι 0.2446. Ομοίως, οι posterior μέσες τιμές των παραμέτρων \(a\) και \(\beta\) εκτιμούνται ως

a <- mean(y[ , 1] * f(y) / den) / mean(h(y) / den)
b <- mean(y[ , 2] * f(y) / den) / mean(h(y) / den)
a ; b
## [1] 23.99874
## [1] 20.35882

3.7 Δειγματοληψία Σπουδαιότητας με Επαναδειγματοληψία

Στην προηγούμενη παράγραφο αναφέραμε ότι η δειγματοληψία σπουδαιότητας μπορεί να χρησιμοποιηθεί γενικότερα για την εναλλακτική προσέγγιση μίας κατανομής από κάποια άλλη με τη βοήθεια του σταθμισμένου δείγματος. Στην περίπτωση της εμπειρικής κατανομής, τα σταθμισμένα βάρη είναι ίσα για όλες τις παρατηρήσεις και έτσι αν κάνουμε επαναδειγματοληψία από τις παρατηρήσεις \((X_1, X_2, ..., X_n)\), η προκύπτουσα κατανομή παραμένει η ίδια. Θα μπορούσαμε λοιπόν να περιγράψουμε την επαναδειγματοληψία μέσω μίας τ.μ.

\[\begin{equation*} X_n^\star = \left\{ \begin{array}{ccc} X_1 & \text{με πιθ.} & 1/n \\ X_2 & \text{με πιθ.} & 1/n \\ \vdots & \vdots & \vdots \\ X_n & \text{με πιθ.} & 1/n \end{array} \right. . \end{equation*}\]

Στην περίπτωση του σταθμισμένου δείγματος, η επαναδειγματοληψία περιγράφεται μέσω μίας τ.μ.

\[\begin{equation*} X_n^\star = \left\{ \begin{array}{ccc} X_1 & \text{με πιθ.} & w_{1,n}(X_1) \\ X_2 & \text{με πιθ.} & w_{2,n}(X_2) \\ \vdots & \vdots & \vdots \\ X_n & \text{με πιθ.} & w_{n,n}(X_n) \end{array} \right. , \end{equation*}\]

όπου

\[\begin{equation*} w_{i,n}(X_i) = \frac{w(X_i)}{\sum_{j=1}^n w(X_j)}. \end{equation*}\]

Υπενθυμίζουμε ότι \(w(x)=f(x)/g(x)\).

Είναι σημαντικό να κατανοηθεί ότι με τη δειγματοληψία σπουδαιότητας από ένα σταθμισμένο δείγμα και την επακόλουθη δειγματοληψία, δεν έχουμε γενικά προσομοίωση ακριβώς από την \(f\), αλλά μόνο προσεγγιστικά. Η προσέγγιση αυτή γίνεται όλο και καλύτερη όσο μεγαλώνει το μέγεθος δείγματος. Επιπλέον, με την επαναδειγματοληψία το καινούριο δείγμα αντιστοιχεί σε δεσμευμένα ανεξάρτητες τ.μ. και όχι γενικά σε ανεξάρτητες τ.μ.. Αυτό μπορεί μπορεί να γίνει εμφανές με το παρακάτω απλό παράδειγμα.

Παράδειγμα 3.11 Θέλουμε να προσομοιώσουμε από την κατανομή \(Be(p)\) για κάποιο \(p \in (0, 1)\) χρησιμοποιώντας δειγματοληψία σπουδαιότητας με επαναδειγματοληψία, έχοντας ως συνάρτηση σπουδαιότητας την \(g\), την σ.π. της \(Be(1/2)\). Τότε τα βάρη \(w(X)\) παίρνουν την μορφή

\[\begin{equation*} w(X) = \frac{f(X)}{g(X)} = \frac{p^X(1-p)^{1-X}}{1/2} = 2p^X(1-p)^{1-X}, \end{equation*}\]

δηλαδή έχουμε \(w(1)=2p\) και \(w(0)=2(1-p)\). Θεωρούμε λοιπόν ότι έχουμε δύο παρατηρήσεις \(X_1, X_2\) από την \(Be(1/2)\). Τότε η \(X_2^\star\) έχει την μορφή

\[\begin{equation*} X_2^\star = \left\{ \begin{array}{ccc} X_1 & \text{με πιθ.} & w_{1,2}(X_1) \\ X_2 & \text{με πιθ.} & w_{2,2}(X_2) \end{array} \right. , \end{equation*}\]

όπου

\[\begin{equation*} w_{i,2}(X_i) = \frac{w(X_i)}{w(X_1)+w(X_2)}, \ i=1,2. \end{equation*}\]

Εύκολα προκύπτει ότι \[\begin{align*} X_1=1, X_2=1 &\Rightarrow w_{1,2}(X_1)=1/2,\ \ w_{2,2}(X_2)=1/2, \\ X_1=1, X_2=0 &\Rightarrow w_{1,2}(X_1)=p, \ \ \ \ w_{2,2}(X_2)=1-p, \\ X_1=0, X_2=1 &\Rightarrow w_{1,2}(X_1)=1-p, w_{2,2}(X_2)=p, \\ X_1=0, X_2=0 &\Rightarrow w_{1,2}(X_1)=1/2, \ \ w_{2,2}(X_2)=1/2. \end{align*}\]

Επομένως για την δεσμευμένη κατανομή της \(X_2^\star\), δεδομένων των \(X_1, X_2\), έχουμε

\[\begin{align*} \mathbf{P}(X_2^\star=1|X_1=1, X_2=1)&=1 \\ \mathbf{P}(X_2^\star=1|X_1=1, X_2=0)&=p \\ \mathbf{P}(X_2^\star=1|X_1=0, X_2=1)&=p \\ \mathbf{P}(X_2^\star=1|X_1=0, X_2=0)&=0 \end{align*}\]

Άμεσα συμπεραίνουμε τις συμπληρωματικές πιθανότητες των παραπάνω ενδεχομένων. Επομένως έχουμε ότι

\[\begin{align*} \mathbf{P}(X_2^\star=1)&=\sum_{i_1=0}^1\sum_{i_2=0}^1 \mathbf{P}(X_2^\star=1, X_1=i_1, X_2=i_2) =\sum_{i_1=0}^1\sum_{i_2=0}^1 \mathbf{P}(X_2^\star=1| X_1=i_1, X_2=i_2) \cdot \mathbf{P}(X_1=i_1, X_2=i_2) \\ &=\frac{1}{4} \sum_{i_1=0}^1\sum_{i_2=0}^1 \mathbf{P}(X_2^\star=1| X_1=i_1, X_2=i_2) = \frac{1}{4} \cdot (1 + p + p) = \frac{1+2p}{4}, \end{align*}\]

δηλαδή \(X_2^\star \sim Be(\frac{1+2p}{4})\). Επισημαίνουμε ότι για \(p\neq 1/2\), έχουμε \(\frac{1+2p}{4}\neq p\) δηλαδή η κατανομή που παίρνουμε διαφέρει από την επιθυμητή. Από αυτό παρατηρούμε ότι δεν μπορούμε γενικά με το σταθμισμένο δείγμα να πετύχουμε την ακριβή κατανομή. Επιπλέον, αν κάνουμε επαναδειγματοληψία και σχηματίσουμε δείγμα μεγέθους 2 από αυτή την κατανομή, παρατηρούμε ότι η από κοινού συνάρτηση πιθανότητας των δύο δεν αντιστοιχεί σε ανεξάρτητες Bernoulli. Πράγματι, ομοίως με παραπάνω προκύπτει ότι

\[\begin{align*} \mathbf{P}(X_2^{\star(1)}=1, X_2^{\star(2)}=1)&=\sum_{i_1=0}^1\sum_{i_2=0}^1 \mathbf{P}(X_2^{\star(1)}=1, X_2^{\star(2)}=1, X_1=i_1, X_2=i_2) \\ &= \sum_{i_1=0}^1\sum_{i_2=0}^1 \mathbf{P}(X_2^{\star(1)}=1, X_2^{\star(2)}=1 | X_1=i_1, X_2=i_2) \cdot \mathbf{P}(X_1=i_1, X_2=i_2) \\ &= \frac{1}{4} \sum_{i_1=0}^1\sum_{i_2=0}^1 \mathbf{P}(X_2^{\star(1)}=1, X_2^{\star(2)}=1 | X_1=i_1, X_2=i_2) \\ &=\frac{1}{4} (1\cdot 1 + p\cdot p +p\cdot p +0\cdot 0) = \frac{1+2p^2}{4}, \end{align*}\]

και όχι \(\left(\frac{1+2p}{4}\right)^2\) που θα είχαμε αν οι \(X_2^{\star(1)}, X_2^{\star(2)}\) ήταν ανεξάρτητες Bernoulli με παράμετρο \(\frac{1+2p}{4}\). Για λόγους πληρότητας παραθέτουμε ακόμη ότι

\[\begin{align*} \mathbf{P}(X_2^{\star(1)}=1, X_2^{\star(2)}=0)&= \frac{2p(1-p)}{4}, \\ \mathbf{P}(X_2^{\star(1)}=0, X_2^{\star(2)}=1)&= \frac{2p(1-p)}{4}, \\ \mathbf{P}(X_2^{\star(1)}=0, X_2^{\star(2)}=0)&= \frac{1+2(1-p)^2}{4}. \end{align*}\]

Φυσικά, η παραπάνω αδυναμία της επαναδειγματοληψίας δεν εμφανίζεται μόνο στις διακριτές κατανομές, όπως δείχνει το επόμενο παράδειγμα.

Παράδειγμα 3.12 Θέλουμε να προσομοιώσουμε από την κατανομή \(\mathcal{N}(1,1)\) χρησιμοποιώντας δειγματοληψία σπουδαιότητας με επαναδειγματοληψία, έχοντας ως συνάρτηση σπουδαιότητας την \(g\), την σ.π.π. της \(\mathcal{N}(0,1)\). Σε αυτή την περίπτωση, τα βάρη σπουδαιότητας παίρνουν την μορφή:

\[\begin{equation*} w(X)=\frac{f(X)}{g(X)} = \frac{1/\sqrt{2\pi}e^{-\frac{1}{2}(X-1)^2}}{1/\sqrt{2\pi}e^{-\frac{1}{2}X^2}}=e^{-\frac{1}{2}\left[(X-1)^2-X^2\right]}=e^{-\frac{1}{2}(-2X+1)}. \end{equation*}\]

Θεωρούμε λοιπόν ότι έχουμε δύο παρατηρήσεις \(X_1, X_2\) από την \(\mathcal{N}(0,1)\). Τότε η \(X_2^\star\) έχει την μορφή

\[\begin{equation*} X_2^\star = \left\{ \begin{array}{ccc} X_1 & \text{με πιθ.} & w_{1,2}(X_1) \\ X_2 & \text{με πιθ.} & w_{2,2}(X_2) \end{array} \right. , \end{equation*}\]

όπου

\[\begin{equation*} w_{i,2}(X_i) = \frac{w(X_i)}{w(X_1)+w(X_2)}, \ i=1,2. \end{equation*}\]

Θέλουμε να δούμε μέσα από προσομοίωση την κατανομή της \(X_2^\star\). Για τον λόγο αυτό, προσομοιώνουμε δύο παρατηρήσεις από την \(\mathcal{N}(0,1)\) και χρησιμοποιώντας δειγματοληψία σπουδαιότητας, επιλέγουμε μία παρατήρηση για την \(X_2^\star\). Επαναλαμβάνουμε αυτή τη διαδικασία \(n=10^4\) φορές και δημιουργούμε το ιστόγραμμα.

## Warning: The dot-dot notation (`..density..`) was deprecated in ggplot2 3.4.0.
## ℹ Please use `after_stat(density)` instead.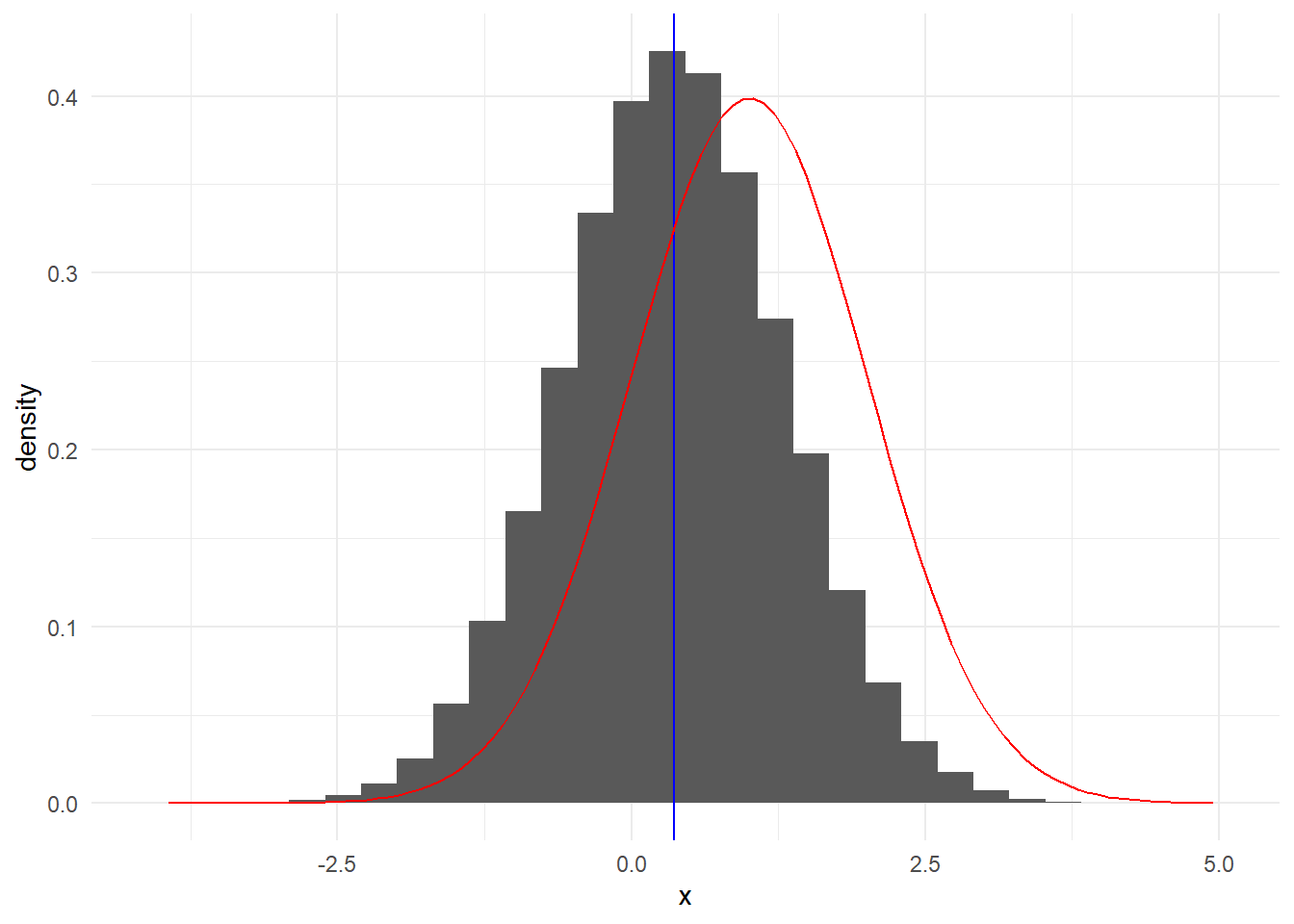

Το δείγμα μας έχει δειγματικό μέσο 0.3628, αρκετά μακριά από το επιθυμητό \(1\). Επαναλαμβάνουμε την διαδικασία, αυτή τη φορά όμως προσομοιώνουμε \(100\) παρατηρήσεις \(X_1, X_2, ..., X_{100}\) για κάθε πραγματοποίηση της \(X_{100}^\star\).

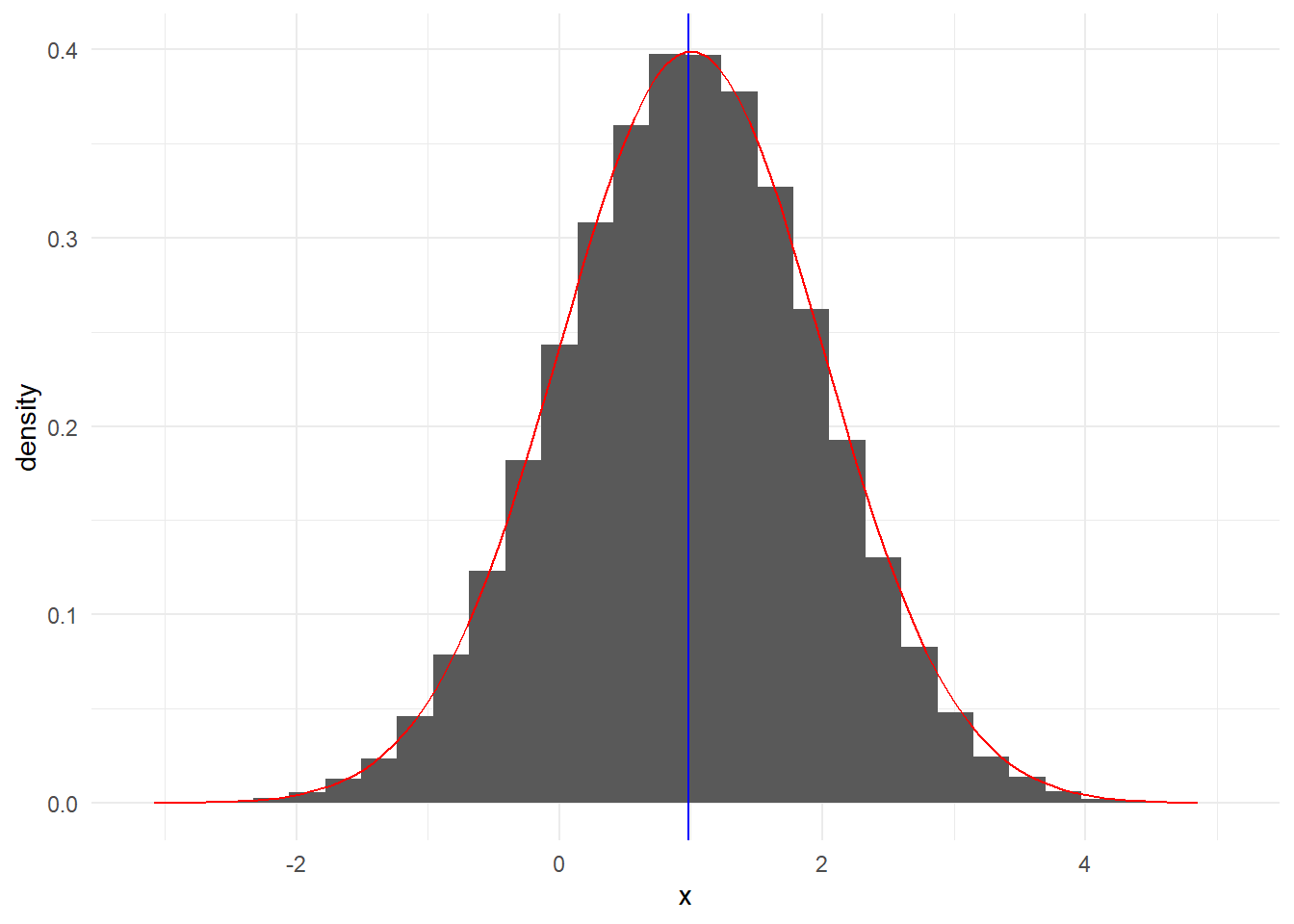
Πράγματι, αυτή τη φορά το δείγμα μας έχει δειγματικό μέσο 0.9797, αρκετά κοντά στο \(1\).

Παράδειγμα 3.13 (Robert & Casella 3.7) Συνεχίζοντας το προηγούμενο παράδειγμα, η εγκυρότητα των προσεγγίσεων της περιθώριας πιθανοφάνειας μπορεί να ελεγχθεί γραφικά ως εξής

weit <- (f(y) / den) / mean(h(y) / den)
image(aa, bb, post, xlab = expression(alpha), ylab = expression(beta))
points(y[sample(1:length(weit), 10 ^ 3, replace = TRUE, prob = weit), ], cex = .6, pch = 19)
boxplot(weit, ylab = "importance weight")
plot(cumsum(weit) / (1:length(weit)), type = "l", xlab = "simulations", ylab = "marginal likelihood")

boot <- matrix(0, ncol = length(weit), nrow = 500)
for (t in 1:500)
  boot[t, ] <- cumsum(sample(weit)) / (1:length(weit))
uppa <- apply(boot, 2, quantile, .95)
lowa <- apply(boot, 2, quantile, .05)
polygon(c(1:length(weit), length(weit):1), c(uppa, rev(lowa)), col = "gold")
lines(cumsum(weit) / (1:length(weit)), lwd = 2)
plot(cumsum(weit) ^ 2 / cumsum(weit ^ 2), type = "l", xlab = "simulations", ylab = "Effective sample size", lwd = 2)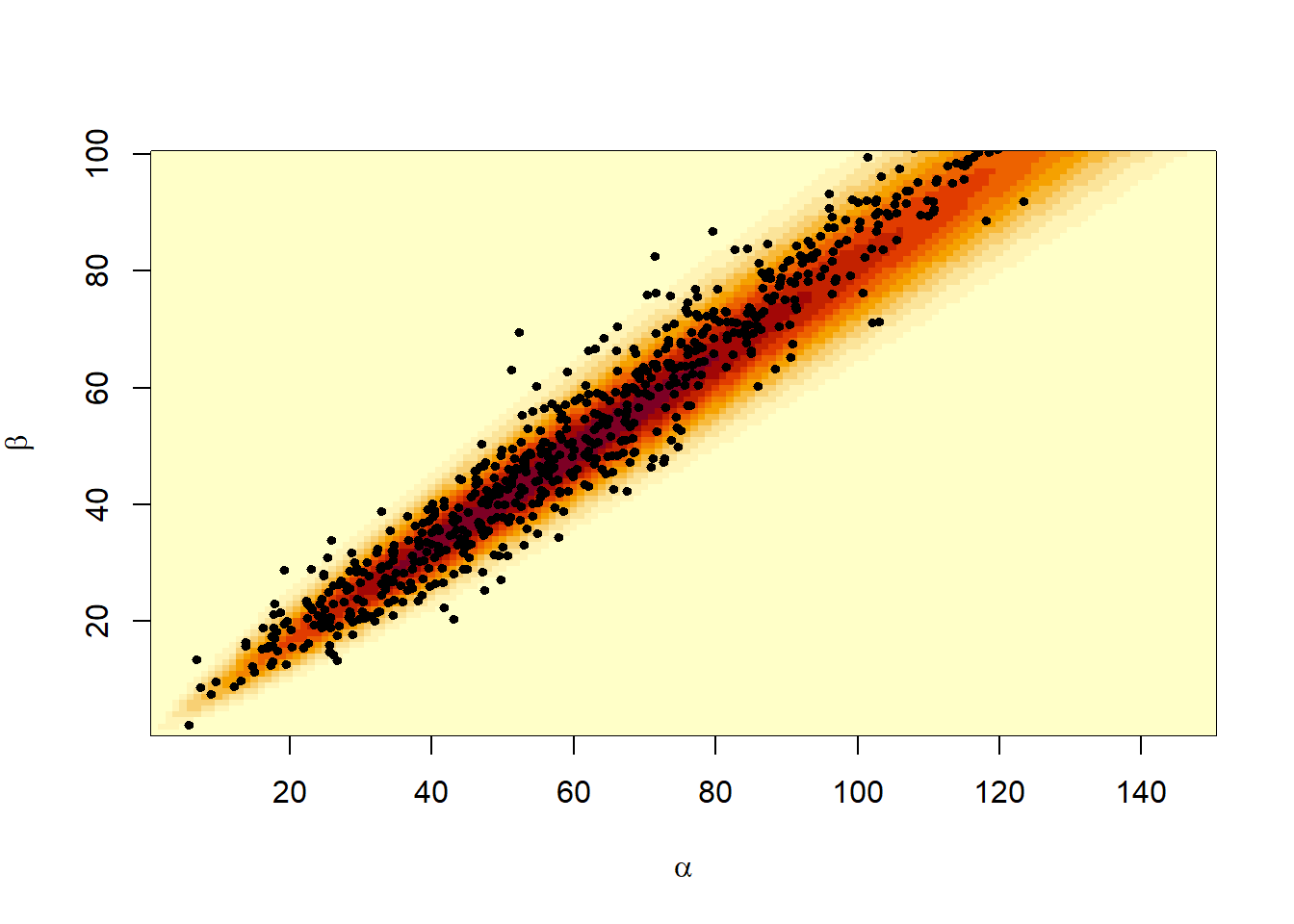

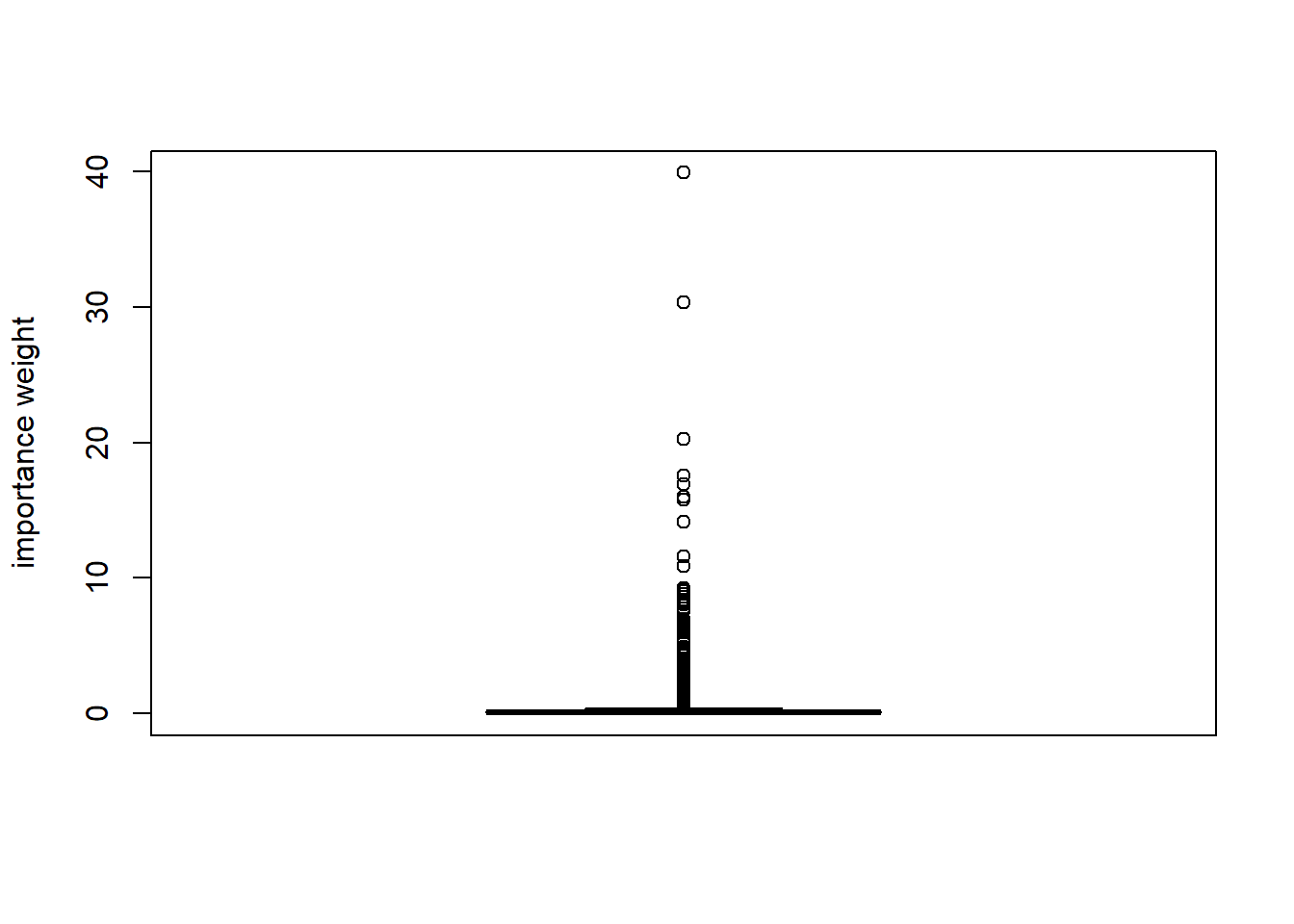
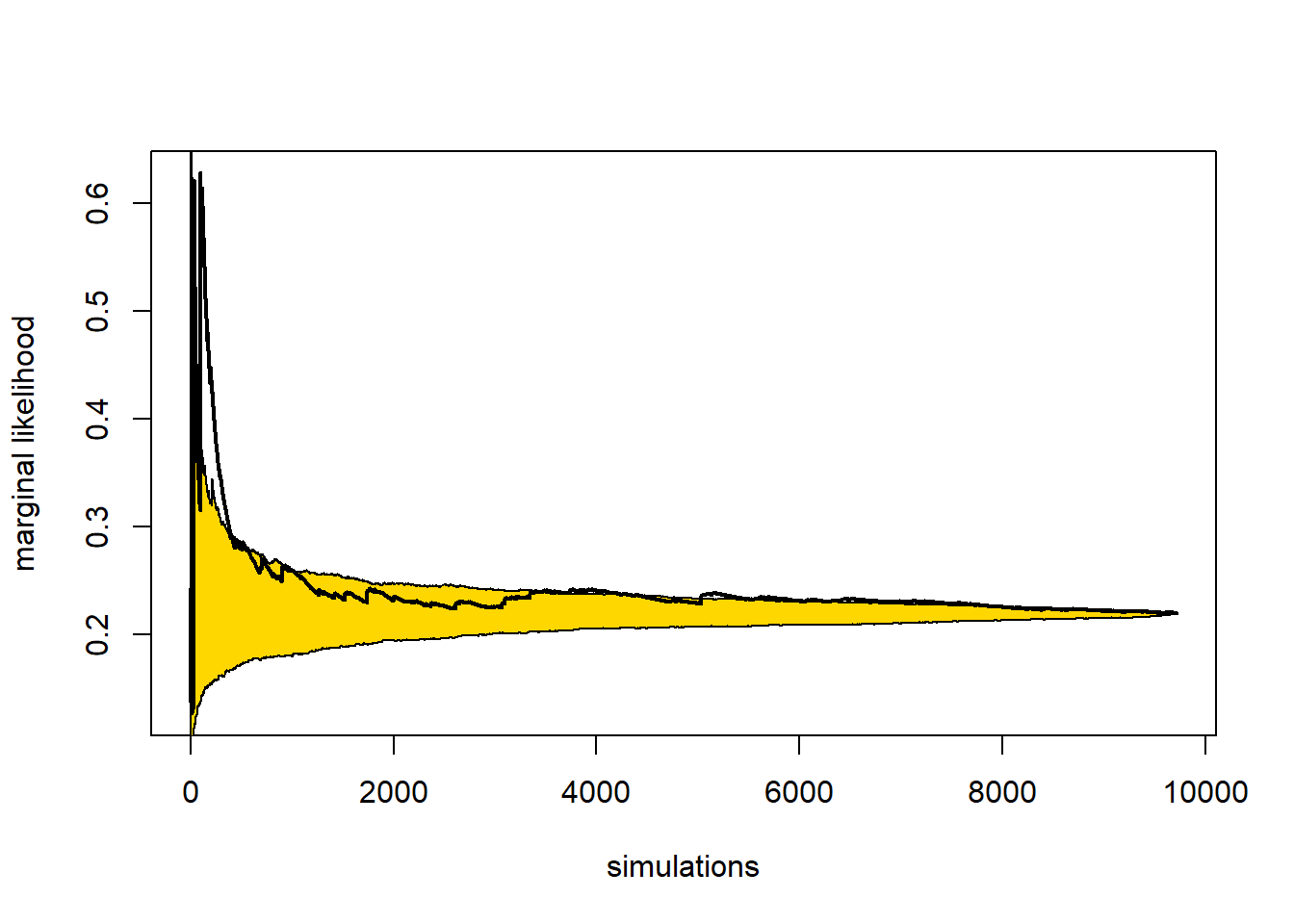
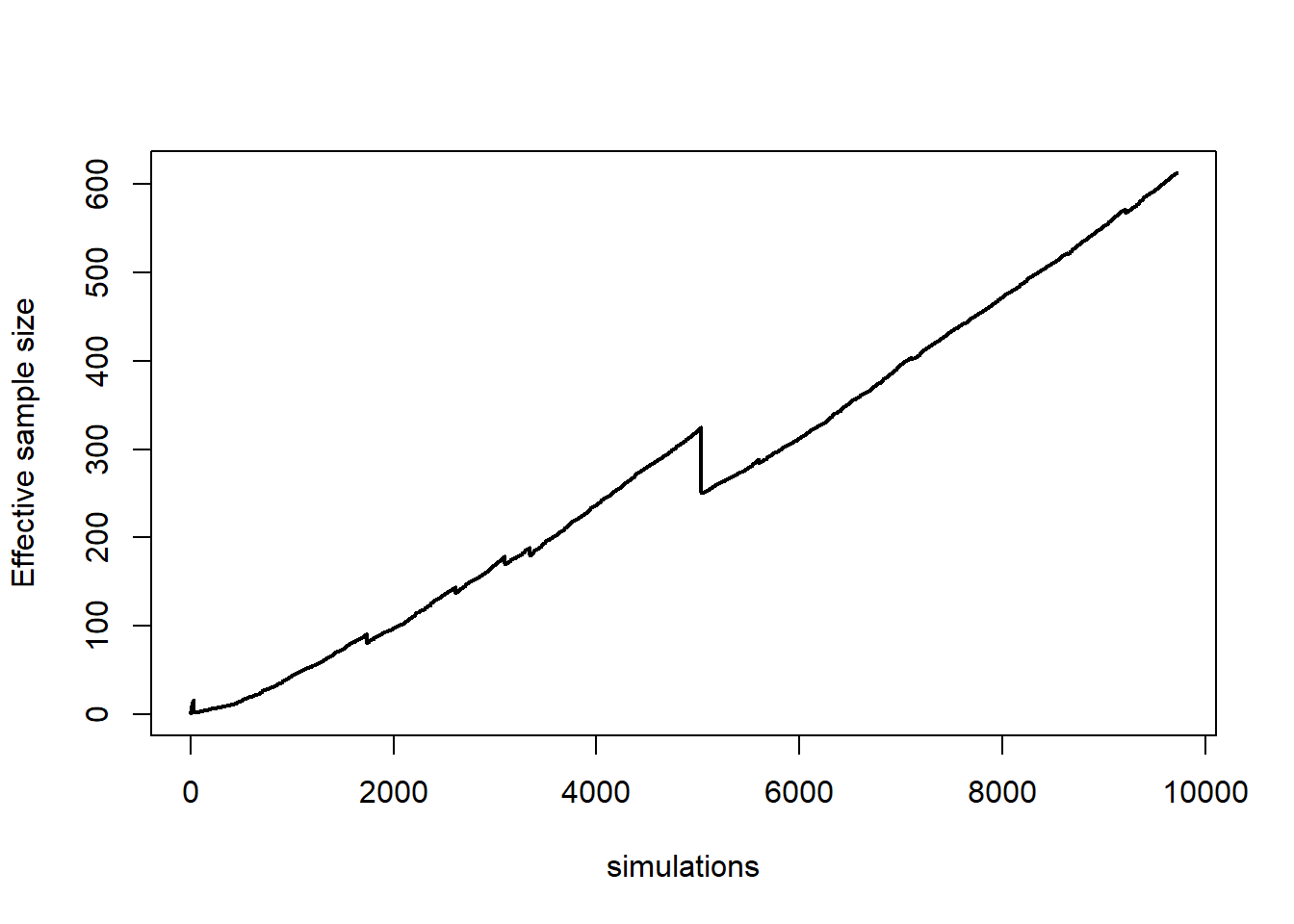
Το γράφημα πάνω αριστερά δείχνει ότι το σταθμισμένο δείγμα με τα βάρη σπουδαιότητας \(\pi(a_i, \beta_i|x)/g(a_i, \beta_i)\) παράγει μία δίκαιη εικόνα ενός δείγματος από την \(\pi(a, \beta|x)\). Οι επανεκλεγμένες παρατηρήσεις δεν συγκεντρώνονται σε λίγα σημεία, αντίθετα καλύπτουν με υψηλή πυκνότητα την ορθή περιοχή της κατανομής στόχου. Το γράφημα πάνω δεξιά δίνει μία απεικόνιση της έκτασης των βαρών σπουδαιότητας. Παρότι υπάρχουν προσομοιωμένες παρατηρήσεις με πολύ μεγαλύτερα βάρη από άλλες, οι διαφορές τους δεν είναι τόσο μεγάλες ώστε να υποδηλώσουν εκφυλισμό της μεθόδου. Για παράδειγμα, το σημείο με το μεγαλύτερο βάρος αντιπροσωπεύει μόλις το \(1\%\) του συνολικού δείγματος. Το γράφημα κάτω αριστερά αναπαριστά την σύγκλιση της εκτιμήτριας \(\widehat{m}(x)\) καθώς το \(n\) αυξάνει. Η χρωματισμένη λωρίδα που παρουσιάζεται έχει δημιουργηθεί με bootstrap και μιμείται την λωρίδα εμπιστοσύνης. Η καμπύλη κάτω δεξιά αναπαριστά την αποδοτικότητα της δειγματοληψίας σπουδαιότητας ως προς το αποτελεσματικό μέγεθος δείγματος (effective sample size),

\[\begin{equation*} \frac{\left\{\sum_{i=1}^n \pi(a_i, \beta_i|x)/g(a_i, \beta_i) \right\}^2}{\sum_{i=1}^n \left\{\pi(a_i, \beta_i|x)/g(a_i, \beta_i)\right\}^2}, \end{equation*}\]

το οποίο θα ήταν ίσο με \(n\), αν τα \((a_i, \beta_i)\) είχαν παραχθεί από την posterior. Το συγκεκριμένο γράφημα δείχνει απόδοσης περίπου \(6\%\).

Παρατήρηση:.

1. Ο τρόπος αυτός κανονικοποίησης των βαρών γίνεται έτσι ώστε να αποτελούν συνάρτηση πιθανότητας.

2. Υπολογίζοντας την μέση τιμή \[\begin{equation*} \mathbf{E}_g\left[\sum_{i=1}^n w(X_j)\right] = \sum_{i=1}^n \mathbf{E}_g\left[w(X_j)\right] = n \cdot \mathbf{E}_g\left[w(X_1)\right] = n \int_{-\infty}^{+\infty} \frac{f(x)}{g(x)} \cdot g(x) dx = n \int_{-\infty}^{+\infty} f(x) dx = n, \end{equation*}\] παρατηρούμε ότι συμπίπτει με το συνολικό μέγεθος του δείγματος. Αυτό είναι το καλύτερο που μπορούμε να εξασφαλίσουμε, αφού βέβαια οι πραγματοποιήσεις τους δεν αθροίζουν γενικά στο \(n\).

3. Η επαναδειγματοληψία μας επιτρέπει να φτιάξουμε ένα καινούριο δείγμα από μία κατανομή που προσεγγίζει την \(f\) για μεγάλο μέγεθος δείγματος. Παρ’ όλα αυτά εισάγεται μία μεροληψία μέσα από τη διαδικασία της κανονικοποίησης. Όταν το μέγεθος του δείγματος γίνει αρκετά μεγάλο, τότε η αμεροληψία γίνεται αμελητέα. Επομένως μπορούμε να χρησιμοποιήσουμε την πολυωνυμική κατανομή για να εξάγουμε τιμές από αυτήν.

Δίνουμε τώρα κάποια βασικά στοιχεία για την πολυωνυμική κατανομή.

3.8 Πολυωνυμική Κατανομή

3.8.1 Βασικές Ιδιότητες

Η πολυωνυμική κατανομή γενικεύει τη διωνυμική κατανομή. Είναι γνωστό ότι μία τ.μ. που ακολουθεί τη διωνυμική κατανομή ερμηνεύεται ως το πλήθος των επιτυχιών σε ένα δεδομένο αριθμό ανεξάρτητων δοκιμών Bernoulli με σταθερή πιθανότητα επιτυχίας σε κάθε δοκιμή. Αν η επιτυχία δεν είναι μονοσήμαντα ορισμένη, αλλά θεωρήσουμε για παράδειγμα ότι υπάρχουν \(d\) είδη επιτυχιών, τότε είναι φυσιολογικό να αναζητήσουμε την κατανομή της δ.τ.μ. που εκφράζει την από κοινού καταγραφή του πλήθους των επιτυχιών \(i-\)είδους σε ένα δεδομένο αριθμό ανεξάρτητων δοκιμών, όπου σε κάθε δοκιμή έχουμε το πολύ μία επιτυχία \(i-\)είδους με σταθερή πιθανότητα. Για παράδειγμα, σε \(20\) ρίψεις ενός ζαριού μπορεί κάποιος να ενδιαφέρεται για την απο κοινού κατανομή του πλήθους των ρίψεων που ήρθαν \(1\) μαζί με αυτές που ήρθαν \(6\). Εδώ, σε κάθε ρίψη μπορούμε να θεωρήσουμε την ένδειξη \(1\) ως επιτυχία πρώτου είδους και την ένδειξη \(6\) ως επιτυχία δεύτερου είδους. Αν το ζάρι είναι δίκαιο τότε και τα δύο είδη επιτυχιών έχουν σταθερή πιθανότητα \(1/6\) σε κάθε δοκιμή. Αν στο ίδιο τυχαίο πείραμα σε κάθε δοκιμή αντιστοιχίσουμε την αποτυχία, δηλαδή την εμφάνιση κάποιας από τις έδρες \(2\), \(3\), \(4\) ή \(5\), σε επιτυχία τρίτου είδους και συμπεριλάβουμε την τ.μ. που καταγράφει το πλήθος των επιτυχιών τρίτου είδους στις δύο προηγούμενες, τότε είναι φανερό ότι δεν κερδίζουμε παραπάνω πληροφορία αφού η τελευταία καθορίζεται πλήρως ως η διαφορά του πλήθους των συνολικών δοκιμών από το άθροισμα των επιτυχιών πρώτου και δεύτερου είδους. Παρ όλα αυτά συναντάμε στη βιβλιογραφία και τις δύο αυτές ισοδύναμες μορφές της πολυωνυμικής κατανομής. Πριν δώσουμε τον τυπικό ορισμό τους, ας δούμε μία χρήσιμη επέκταση του διωνυμικού συντελεστή.

Υπενθυμίζουμε ότι ο διωνυμικός συντελεστής \(\binom{n}{k}\) φέρει το όνομα αυτό λόγω του ότι προκύπτει ως συντελεστής στο διωνυμικό ανάπτυγμα. Συγκεκριμένα,

\[\begin{equation*} (x+y)^n = \sum_{k=0}^{n}\,\binom{n}{k}\,x^{k}y^{n-k}, \quad \textrm{όπου}\ \ \binom{n}{k}=\frac{n!}{k!(n-k)!}. \end{equation*}\]

Εύκολα δείχνεται (με επαγωγή στο \(n\)) η ισχύς του πολυωνυμικού θεωρήματος, το οποίο μας επιτρέπει να γενικεύσουμε το διωνυμικό ανάπτυγμα από πολυώνυμα \(2\) μεταβλητών σε πολυώνυμα \(d\) μεταβλητών:

\[\begin{equation} (x_1+x_2+\ldots + x_d)^n = \sum_{k=0}^{n}\,\frac{n!}{n_1!n_2!\ldots n_d!}\,x_1^{n_1}x_2^{n_2}\ldots x_d^{n_d}, \quad \textrm{όπου} \ \ n_1+n_2+\ldots n_d =n. \tag{3.5} \end{equation}\]

Αν κάνουμε μία αρίθμηση (διάκριση) των \(n\) παραγόντων που εμφανίζονται στο αριστερό μέλος:

\[\begin{equation*} \underbrace{(x_1+x_2+\ldots + x_d)}_{1}\cdot\underbrace{(x_1+x_2+\ldots + x_d)}_{2}\cdot\ldots \cdot\underbrace{(x_1+x_2+\ldots + x_d)}_{n}, \end{equation*}\]

τότε είναι φανερό ότι το ανάπτυγμα συνίσταται σε ένα άθροισμα διακεκριμένων μονωνύμων βαθμού \(n\) (επιλέγοντας μία μεταβλητή από κάθε παράγοντα) της μορφής \(x_1^{n_1}x_2^{n_2}\ldots x_d^{n_d}\), όπου κάθε εκθέτης αντιστοιχεί στο πλήθος των φορών που επιλέχθηκε η αντίστοιχη μεταβλητή, και σε κάθε μονώνυμο αντιστοιχεί ένας συντελεστής που εκφράζει το πλήθος των διαφορετικών τρόπων με τους οποίους μπορούμε να επιλέξουμε μέσα από το σύνολο των \(n\) διακεκριμένων παραγόντων (θέσεων), τις \(n_1\) θέσεις για την επιλογή του \(x_1\), τις \(n_2\) θέσεις για την επιλογή του \(x_2\) και τις υπολοιπόμενες \(n_d\) θέσεις για την επιλογή του \(x_d\). Η σκέψη αυτή μας οδηγεί σε μία δεύτερη συνδιαστική απόδειξη (χωρίς επαγωγή) του πολυωνυμικού αναπτύγματος (3.5) κάνοντας χρήση της πολλαπλασιαστικής αρχής (ολοκληρώστε την απόδειξη).

Ορισμός 3.15 Έστω \(n, n_i \in \mathbb{N}\), \(i=1,2,\ldots,d\) με \(n_1+n_2+\ldots n_{d}=n\). Λέμε πολυωνυμικό συντελεστή τον αριθμό

\[\begin{equation}\label{multi-coeff-1} \binom{n}{n_1,n_2,\ldots,n_d}:=\frac{n!}{n_1!n_2!\ldots n_d!}, \end{equation}\]

που εμφανίζεται ως συντελεστής στο πολυωνυμικό ανάπτυγμα (3.5).

Παρατήρηση:.

1. Στην ειδική περίπτωση που \(d=2\), ο πολυωνυμικός συντελεστής αντιστοιχεί στο διωνυμικό συντελεστή, έτσι έχουμε \(\binom{n}{k,n-k}=\binom{n}{k}\). Παραδοσιακά προτιμάται ο τελευταίος συμβολισμός που είναι και ο πιο σύντομος.

2. Κάποιες φορές ο πολυωνυμικός συντελεστής εμφανίζεται στη μορφή \[\begin{equation}\label{multi-coeff-4} \binom{n}{n_1,n_2,\ldots,n_{d-1}}:=\frac{n!}{n_1!\ldots n_{d-1}! (n-n_1-\ldots-n_{d-1})!}. \end{equation}\] Αυτό δεν θα πρέπει να προκαλεί σύγχυση αφού οι 2 εκφράσεις διακρίνονται από το αν οι δείκτες που εκφράζουν το πλήθος των επιλογών αθροίζουν ή όχι στο συνολικό πλήθος των στοιχείων \(n\).

3. Είναι φανερό από τα σχόλια που ακολουθούν το πολυωνυμικό ανάπτυγμα ότι ο πολυωνυμικός συντελεστής εκφράζει το πλήθος των διαφορετικών τρόπων με τους οποίους μπορούμε να διαμερίσουμε ένα σύνολο \(n\) στοιχείων σε \(d\) υποσύνολα με \(n_i\) στοιχεία το καθένα, \(1\leq i \leq d\).

Είμαστε τώρα σε θέση να ορίσουμε την πολυωνυμική κατανομή που αντιπροσωπεύει την κατανομή ενός τυχαίου διανύσματος που καταγράφει το πλήθος των επιτυχιών όλων των ειδών σε \(n\) ανεξάρτητες δοκιμές με σταθερές πιθανότητες επιτυχίας κάθε είδους σε κάθε δοκιμή, όταν σε κάθε μία από αυτές έχουμε επιτυχία μόνο ενός είδους ή το πολύ ενός. Για να αποφύγουμε ενδεχόμενη σύγχυση θα διακρίνουμε αυτές τις δύο ισοδύναμες μορφές, οι οποίες διαφέρουν μόνο στο αν θα ονομάσουμε την αποτυχία ως επιτυχία ενός επιπρόσθετου είδους με ταυτόχρονη καταγραφή του πλήθους τους ή απλά θα τις εξαιρέσουμε από την ανάλυσή μας. Πρακτικά, αυτό φαίνεται από το αν τα σημεία που έχουν θετική πιθανότητα έχουν σταθερό άθροισμα ή όχι αντίστοιχα.

Ορισμός 3.16 Έστω \(X=(X_1,\ldots,X_d)\) ένα τ.δ. με \(d\geq 2\). Θα λέμε ότι το \(X\) ακολουθεί την πολυωνυμική κατανομή \(\mathcal{M}(n,p_1,\ldots,p_d)\) με παραμέτρους \(n\geq 1\) και \(p_1,\ldots,p_d > 0\), όπου \(\sum_{i=1}^{d}{p_i}=1\), αν

\[\begin{equation}\label{multi-coeff-5} \mathbf{P}(X_1=x_1,\ldots,X_d=x_d) = \binom{n}{x_1,\ldots,x_d}p_{1}^{x_1}\ldots p_{d}^{x_d}, \ \ \textrm{όπου} \ x_i\in \mathbb{N}, \ 1\leq i \leq d,\ \textrm{και} \ \sum_{i=1}^{d}{x_i}=n. \end{equation}\]

Αν όμως \(d\geq 1\) και \(S_{X}=\left\{x\in \mathbb{N}^{d} : 0 \leq \sum_{i=1}^{d}{x_i}\leq n \right\}\), τότε θα λέμε ότι το \(X\) ακολουθεί την πολυωνυμική κατανομή \(\mathcal{M}^{*}(n,p_1,\ldots,p_d)\) με παραμέτρους \(n\geq 1\), \(p_i>0\) που ικανοποιούν \(0<\sum_{i=1}^{d}{p_i}<1\) και

\[\begin{equation}\label{multi-coeff-6} \mathbf{P}(X_1=x_1,\ldots, X_d=x_d) = \binom{n}{x_1,\ldots,x_d} p_{1}^{x_1}\ldots p_{d}^{x_d} (1-p_1 - \ldots - p_{d})^{n-x_1 - \ldots - x_{d} }, \ \ \textrm{όπου } x \in S_{X}. \end{equation}\]

Παρατήρηση:.

1. Με τον παραπάνω ορισμό είναι φανερό ότι η διωνυμική κατανομή \(Bin(n,p)\) ταυτίζεται με την \(\mathcal{M}^{*}(n,p)\)

2. Για \(n=1\), η πολυωνυμική κατανομή \(\mathcal{M}(1,p_1,\ldots,p_d)\) ή \(\mathcal{M}^{*}(1,p_1,\ldots,p_d)\), αναφέρεται ως κατηγορική και θα λέμε ότι το τ.δ. \(C \sim Cat(p_1,\ldots,p_d)\) (\(d \geq 2\)) ή \(C \sim Cat{}^{*}(p_1,\ldots,p_d)\) (\(d \geq 1\)) αντίστοιχα. Η κατηγορική κατανομή γενικεύει την κατανομή Bernoulli, όπου αντί για τον καθορισμό μόνο μιας πιθανότητας επιτυχίας, προσδιορίζει τις πιθανότητες όλων των επιτυχιών \(i\)-είδους. Ένα τ.δ. \(C \sim Cat(p_1,\ldots,p_d)\) παίρνει τιμές στο σύνολο \(\{e_1,\ldots,e_d\}\), δηλαδή στα διανύσματα της ορθοκανονικής βάσης του \(\mathbb{R}^d\) και \(\mathbf{P}(C=e_i)=p_i\) για κάθε \(i=1,\ldots,d\).

3. Είναι φανερό από τον ορισμό και την ερμηνεία της πολυωνυμικής κατανομής ότι αν \(X\sim \mathcal{M}(n,p_1,\ldots,p_d)\), τότε μπορούμε να έχουμε την εξής χρήσιμη αναπαράσταση \[\begin{equation} X = \sum_{i=1}^{n} C_i, \tag{3.6} \end{equation}\] όπου \(C_i \sim Cat(p_1,\ldots,p_d)\), \(i=1,2,\ldots, n\), και είναι μεταξύ τους ανεξάρτητα τ.δ.. Η έκφραση αυτή του \(X\) που ακολουθεί πολυωνυμική κατανομή ως άθροισμα ανεξάρτητων και ισόνομων κατηγορικών τ.δ. είναι η γενίκευση στα πολυδιάστατα της αντίστοιχης αναπαράστασης μιας τυχαίας μεταβλητής που ακολουθεί τη διωνυμική κατανομή ως άθροισμα ανεξάρτητων και ισόνομων τ.μ. που ακολουθούν κατανομή Bernoulli. Οι αναπαραστάσεις αυτές είναι χρήσιμες, όπως γνωρίζουμε και από τις Πιθανότητες I, για τον υπολογισμό μέσων τιμών και διασπορών.

Πρόταση 3.13 Αν ένα τ.δ. \(X\sim \mathcal{M}(n,p)\) με \(p=(p_1,\ldots,p_d)\), τότε η μέση τιμή του είναι

\[\begin{equation*} \mathbf{E}(X) = np = n\,(p_1,\ldots, p_d) \end{equation*}\]

και η διασπορά του (ο πίνακας διασποράς) είναι

\[\begin{equation*} \mathbf{V}(X) = n\,[\,\text{dg}(p) - p p^{\top}] = n\, \begin{pmatrix} p_1(1-p_1) & -p_1 p_2 & \ldots & -p_1 p_d \\ -p_1 p_2 & p_2(1-p_2) & \ldots & -p_2 p_d \\ \vdots & \vdots & \ddots & \vdots \\ -p_1 p_d & - p_2 p_d= & \ldots & p_d(1-p_d) \end{pmatrix}. \end{equation*}\]

Απόδειξη:. Χρησιμοποιώντας την αναπαράσταση (3.6) έχουμε

\[\begin{equation*} \mathbf{E}(X) = \mathbf{E}\left(\sum_{i=1}^{n} C_i\right) = \sum_{i=1}^{n} \mathbf{E}(C_i) = n\,\mathbf{E}(C), \end{equation*}\]

όπου \(C\sim Cat(p)\). Όμως \(C\in \{e_1,\ldots,e_d\}\) και \(\mathbf{P}(C=e_i)=p_i\), \(1\leq i \leq d\). Επειδή \(\{C_i = 1\}=\{C=e_i\}\) συμπεραίνουμε ότι

\[\begin{equation*} \mathbf{E}(C)=\big(\!\mathbf{E}(C_1),\ldots,\mathbf{E}(C_d)\big)=\big(\!\mathbf{P}(C_1=1),\ldots,\mathbf{P}(C_d=1)\big)=(p_1,\ldots,p_d)=p. \end{equation*}\]

Επίσης, λόγω της ανεξαρτησίας, για τον υπολογισμό της διασποράς έχουμε

\[\begin{equation*} \mathbf{V}(X) = \mathbf{V}\left(\sum_{i=1}^{n} C_i\right) = \sum_{i=1}^{n} \mathbf{V}(C_i) = n\mathbf{V}(C). \end{equation*}\]

Για τον τελευταίο πίνακα έχουμε

\[\begin{equation*} \mathbf{V}(C) = \mathbf{E}(CC^{\top}) - \mathbf{E}(C)\mathbf{E}(C^{\top}) =\text{dg}(p) - p p^{\top}, \end{equation*}\]

χρησιμοποιώντας ότι \(C_i \sim Be(p_i)\), ότι \(C_iC_j=0\) για \(i \neq j\), και άρα

\[\begin{equation*} \mathbf{E}(CC^{\top}) = \begin{pmatrix} \mathbf{E}(C_1^2) & \mathbf{E}(C_1C_2) & \ldots & \mathbf{E}(C_1C_d) \\ \mathbf{E}(C_2C_1) & \mathbf{E}(C_2^2) &\ldots & \mathbf{E}(C_2C_d) \\ \vdots & \vdots & \ddots & \vdots \\ \mathbf{E}(C_dC_1) & \mathbf{E}(C_dC_2) & \ldots & \mathbf{E}(C_d^2) \end{pmatrix} = \begin{pmatrix} p_1 & 0 & \ldots & 0 \\ 0 & p_2 & \ldots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & p_d \end{pmatrix}. \end{equation*}\]

3.8.2 Εφαρμογές

Μια εφαρμογή της πολυωνυμικής κατανομής βρίσκουμε στην επαναδειγματοληψία με τη βοήθεια του σταθμισμένου δείγματος. Συγκεκριμένα, ας υποθέσουμε ότι έχουμε σχηματίσει ένα σταθμισμένο δείγμα \(\{(X_i,w(X_i))\}_{i=1}^{n}\) με στόχο να παράγουμε από την \(f\). Όπως αναφέραμε ήδη η επαναδειγματοληψία μας δίνει τη δυνατότητα προσέγγισης της \(f\), σχηματίζοντας ένα καινούριο δείγμα \(\{X_n^{*(i)}\}_{i=1}^{R}\) από τα \(\{X_i\}_{i=1}^{n}\). Ο τρόπος επιλογής του δείγματος γίνεται με \(R\) ανεξάρτητες κατηγορικές δοκιμές, όπου κάθε παρατήρηση \(X_i\) επιλέγεται με πιθανότητα ανάλογη του βάρους της \(w(X_i)\). Ο τρόπος αυτός επαναδειγματοληψίας μπορεί να περιγραφεί με τη βοήθεια ενός τυχαίου διανύσματος \(Ν=(Ν_1,\ldots,N_n)\sim \mathcal{M}_{n}(R,w_{1,n},\ldots,w_{n,n})\), όπου θέτουμε για συντομία \(w_{i,n}\) το κανονικοποιημένο βάρος πιθανότητας που αντιστοιχεί στην επιλογή της παρατήρησης \(X_i\) που έχει προκύψει από το αρχικό δείγμα μεγέθους \(n\).

Μια παρόμοια εφαρμογή μπορούμε να βρούμε και στον σχηματισμό Bootstrap δειγμάτων. Συγκεκριμένα, αν υποθέσουμε ότι έχουν εξαχθεί \(n\) παρατηρήσεις \(X_1, X_2, ..., X_n\), τότε μπορούμε να χρησιμοποιήσουμε το Bootstrap για την εκτίμηση της μεροληψίας ή/και της μεταβλητότητας κάποιου χαρακτηριστικού που εξαρτάται από το παραπάνω τυχαίο δείγμα. Σε αυτή την περίπτωση τα βάρη που χρησιμοποιούνται είναι ίσα, δηλαδή \(1/n\) για κάθε παρατήρηση. Με τη βοήθεια του Bootstrap δείγματος δημιουργείται ένα καινούριο δείγμα τιμών για κάποιο στατιστικό ενδιαφέροντος και με τη βοήθεια αυτού γίνεται προσέγγιση της θεωρητικής κατανομής του στατιστικού. Στην πλεοψηφία των περιπτώσεων το Bootstrap δείγμα χρησιμοποιείται για εκτίμηση μεροληψίας, διασποράς και κατασκευή διαστημάτων εμπιστοσύνης.

3.8.3 Επιλογή συνάρτησης σημαντικότητας

Η ευελιξία της δειγματοληψίας σπουδαιότητας είναι μεγάλη, αλλά ένα μειονέκτημα που μπορεί να προκύψει, συνδέεται με μία κακή επιλογή της συνάρτησης σπουδαιότητας \(g\). Παρότι η επιλογή της βέλτιστης \(g\) αποτελεί θεωρητική άσκηση (βλ. Rubinstein, 1981, ή Robert and Casella, 2004, Θεώρημα 3.12), μπορούμε να αξιολογήσουμε τη συνάρτηση σπουδαιότητας μελετόντας τη διασπορά της παραγόμενης εκτιμήτριας. Πράγματι, γνωρίζουμε ότι

\[\begin{equation*} \frac{1}{n}\sum_{j=1}^n \frac{f(X_j)}{g(X_j)}h(X_j)\rightarrow \mathbf{E}_f\left[h(X)\right], \end{equation*}\]

όταν η μέση τιμή υπάρχει, η διασπορά αυτής της εκτιμήτριας είναι πεπερασμένη μόνο όταν η μέση τιμή

\[\begin{equation*} \mathbf{E}_g\left[h^2(X)\frac{f^2(X)}{g^2(X)}\right]=\mathbf{E}_f\left[h^2(X)\frac{f(X)}{g(X)}\right]=\int_\mathcal{X}h^2(x)\frac{f^2(x)}{g(x)}dx, \end{equation*}\]

είναι πεπερασμένη. Επισημαίνουμε εδώ ότι η χρήση συναρτήσεων σπουδαιότητας \(g\) με ουρές ελαφρύτερες από εκείνες της \(f\) δεν είναι απαγορευτική, αλλά οδηγεί σε μη φραγμένους λόγους \(f/g\), που με τη σειρά τους οδηγούν σε εκτιμήτριες άπειρης διασποράς.

Παράδειγμα 3.14 (Robert & Casella 3.8) Θέλουμε να εφαρμόσουμε δειγματοληψία σπουδαιότητας με στόχο την προσομοίωση από την κατανομή Cauchy \(\mathcal{C}(0,1)\), χρησιμοποιώντας ως συνάρτηση σπουδαιότητας την κανονική \(\mathcal{N}(0,1)\).

Σε αυτή την περίπτωση, ο λόγος

\[\begin{equation*} \frac{f(x)}{g(x)}\propto \frac{e^{\frac{x^2}{2}}}{1+x^2} \end{equation*}\]

εκρήγνυται, δίνοντας πολύ μεγάλα βάρη σπουδαιότητας για σχετικά υψηλές τιμές του \(x\). Τρέχοντας τον κώδικα

set.seed(10)
x <- rnorm(10 ^ 6)
wein <- dcauchy(x) / dnorm(x)
boxplot(wein / sum(wein))
plot(cumsum(wein * (x > 2) * (x < 6)) / cumsum(wein), type = "l")
abline(a = pcauchy(6) - pcauchy(2), b = 0, col = "sienna")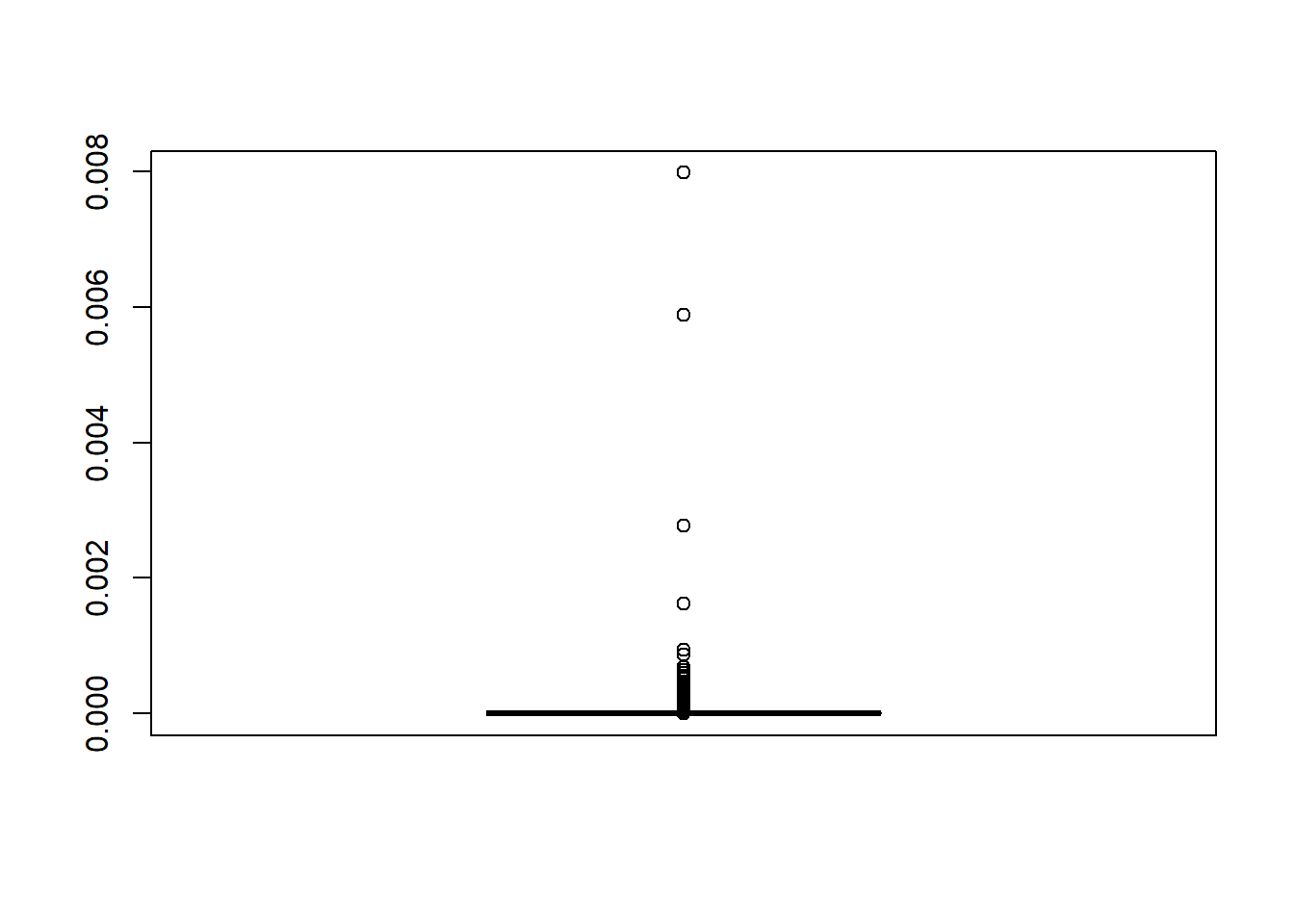

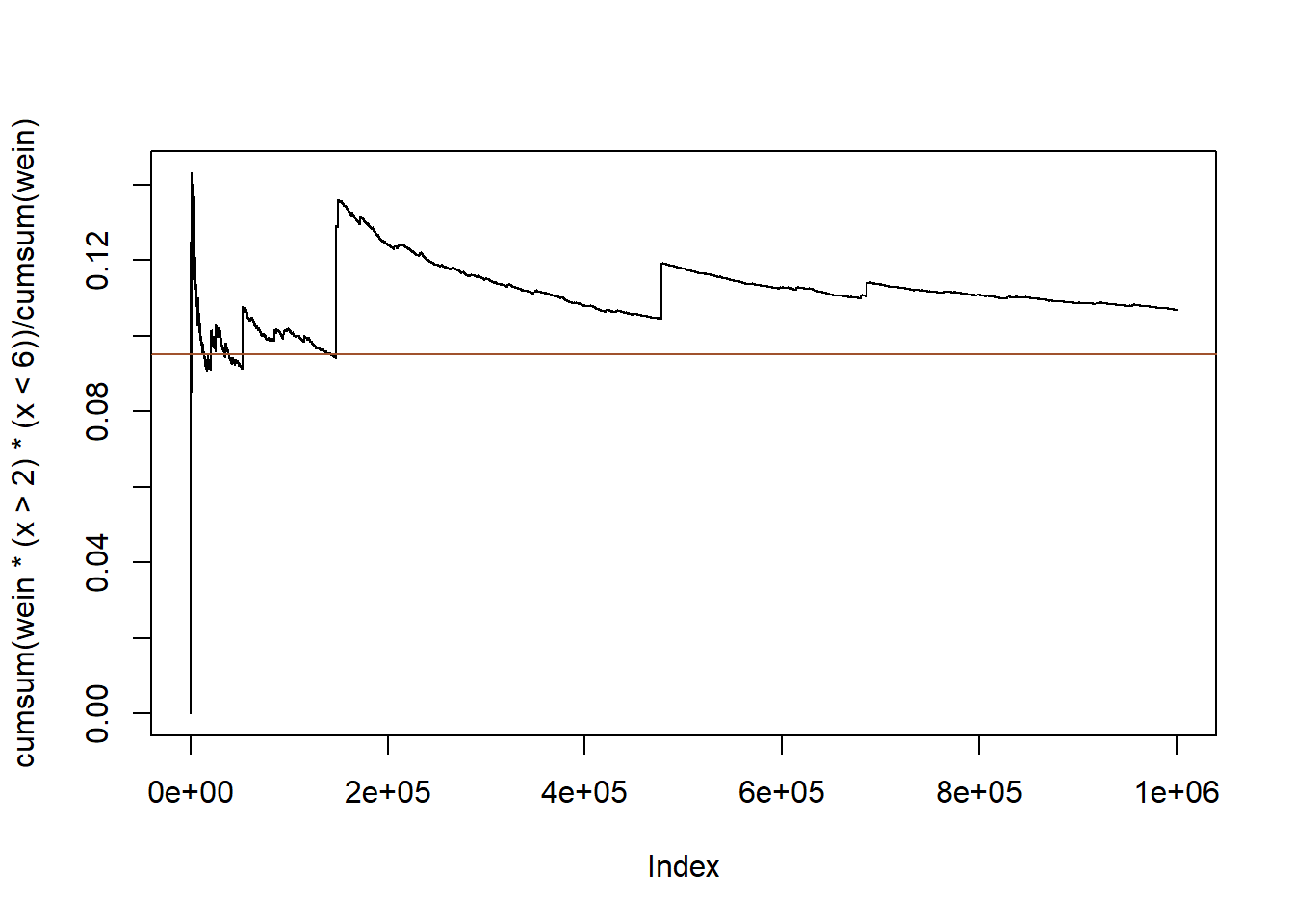
παρατηρούμε ότι ο δειγματικός μέσος εμφανίζει μεγάλα άλματα, ακόμα και για μεγάλες τιμές του \(n\). Τα άλματα αυτά παρατηρούνται σε τιμές για τις οποίες το \(exp(x^2/2)/(1+x^2)\) είναι μεγάλο, δηλαδή το \(x\) είναι μεγάλο. Ο λόγος πίσω από αυτό το φαινόμενο είναι πως τέτοιες τιμές σπανίζουν στην κανονική κατανομή (περισσότερο απ’ ότι στην Cauchy), κάτι που διορθώνουν λαμβάνοντας μεγάλες τιμές στα βάρη τους. Φυσικά, είναι αδύνατο να εμπιστευτούμε τα αποτελέσματα αυτής της προσομοίωσης, καθώς οι λίγες τιμές με μεγάλα βάρη καθιστούν τα βάρη των υπολοίπων αμελητέα.

Το θέμα της σύγκρισης διαφορετικών συναρτήσεων σημαντικότητας με τη βοήθεια κατάλληλων κριτηρίων θα εξεταστεί στο επόμενο κεφάλαιο.