5 Βελτιστοποίηση Monte Carlo

5.1 Εισαγωγή

Τα προβλήματα βελτιστοποίησης μπορούν να χωριστούν σε δύο μεγάλες κατηγορίες, την αναζήτηση των ακροτάτων μίας συνάρτησης \(h(\theta)\) και την αναζήτηση των λύσεων της εξίσωσης \(g(\theta)=0\), σε ένα χώρο \(\Theta\). Ένα πρόβλημα της μίας κατηγορίας μπορεί, υπό συγκεκριμένες συνθήκες, να εκφραστεί ως ένα ισοδύναμο πρόβλημα της άλλης, αφού η εύρεση ακροτάτων μίας διαφορίσιμης συνάρτησης \(h\) ισοδυναμεί με την επίλυση της εξίσωσης \(\nabla h(\theta)=0\), ενώ η επίλυση της εξίσωσης \(g(\theta)=0\) μπορεί να εκφραστεί ως πρόβλημα ελαχιστοποίησης της συνάρτησης \(h(\theta)=g^2 (\theta)\). Επιπλέον, κάθε πρόβλημα μεγιστοποίησης της συνάρτησης \(h(\theta)\) μπορεί να εκφραστεί ισοδύναμα ως πρόβλημα ελαχιστοποίησης της συνάρτησης \(-h(\theta)\) (ή της \(1/h(\theta)\), αν η \(h\) είναι μονίμως θετική ή αρνητική στο χώρο \(\Theta\)).

Στη μελέτη αυτή θα συμπεριλάβουμε δύο διαφορετικές προσεγγίσεις, την αριθμητική και τη στοχαστική. Από την πλευρά της αριθμητικής βελτιστοποίησης, η αποδοτικότητα των μεθόδων εξαρτάται σημαντικά από τις αναλυτικές ιδιότητες της υπό ελαχιστοποίηση/μεγιστοποίηση συνάρτησης (συνέχεια, διαφορισιμότητα, κυρτότητα, μελέτη φραγμάτων, …), ενώ οι ιδιότητες αυτές παίζουν δευτερεύοντα ρόλο στις προσεγγίσεις που βασίζονται σε προσομοίωση. Συμπεραίνουμε πως, για τη μεγιστοποίηση μίας απλής συνάρτησης \(h\) με καλές ιδιότητες συμφέρει να χρησιμοποιήσουμε αριθμητικές μεθόδους, ενώ για τη μεγιστοποίηση μίας περίπλοκης συνάρτησης ορισμένη ίσως και σε έναν περίπλοκο χώρο \(\Theta\), προτιμάμε να καταφύγουμε σε στοχαστικές προσεγγίσεις.

Σε αυτό το σημείο, αξίζει να αναφέρουμε ότι γενικά, τα προβλήματα βελτιστοποίησης είναι δυσκολότερα από τα προβλήματα ολοκλήρωσης (τουλάχιστον από πρακτικής πλευράς), καθώς απαιτούν τοπική μελέτη της συνάρτησης σε όλο το χώρο που είναι ορισμένη. Με άλλα λόγια, είναι πολύ πιο δύσκολο να εντοπίσουμε ένα συγκεκριμένο σημείο του χώρου στο οποίο επιτυγχάνεται το μέγιστο μιας συνάρτησης, από το να προσεγγίσουμε τη μέση τιμή της συνάρτησης σε όλο το χώρο.

Προτού αναλύσουμε τις στοχαστικές μεθόδους βελτιστοποίησης, παρουσιάζουμε κάποιες από τις σημαντικότερες μεθόδους αριθμητικής βελτιστοποίησης και αναλύουμε κάποιες σημαντικές ιδιότητές τους.

5.2 Μέθοδοι Αριθμητικής Βελτιστοποίησης

Όλοι οι αλγόριθμοι αριθμητικής βελτιστοποίησης που θα μελετήσουμε βασίζονται στην ίδια δομή. Ξεκινούν από ένα αρχικό σημείο \(x_0\), επιλέγουν μία κατεύθυνση κίνησης \(d_0\) και κινούνται σε αυτή σε ένα σημείο \(x_1\), πραγματοποιώντας ένα μήκος βήματος \(a_0\). Στο νέο αυτό σημείο \(x_1\), επιλέγεται μία νέα κατεύθυνση \(d_1\) και ένα μήκος βήματος \(a_1\), και η διαδικασία επαναλαμβάνεται μέχρι να ικανοποιηθεί κάποιο κριτήριο τερματισμού. Η σχηματιζόμενη ακολουθία \((x_k)\) ικανοποιεί λοιπόν την αναδρομική σχέση:

\[\begin{equation*} x_{k+1} = x_k + a_k d_k, \qquad k\geq 0. \end{equation*}\]

Οι αλγόριθμοι που θα εξετάσουμε διακρίνονται από τους κανόνες σύμφωνα με τους οποίους επιλέγεται η κατεύθυνση κίνησης \(d_k\) και καθορίζεται το μήκος βήματος \(a_k\). Οι αλγόριθμοι αυτής της μορφής είναι γνωστοί και με το όνομα Αλγόριθμοι Γραμμικής Αναζήτησης (Line Search Algorithms) και αποτελούν μαζί με τους αλγορίθμους που χρησιμοποιούν περιοχές εμπιστοσύνης (Trust Regions), τις 2 βασικές στρατηγικές βελτιστοποίησης. Περιγράφουμε τώρα κάποιους από αυτούς τους αλγορίθμους κατάβασης (descent algorithms) που έχουν ως στόχο με σχετικά απλό, αλλά αποτελεσματικό τρόπο να οδηγήσουν σε μονοπάτια ελάττωσης των τιμών της υπό μελέτη συνάρτησης.

5.2.1 Μέθοδος Απότομης Κατάβασης

Μία από τις πιο παλιές και ταυτόχρονα πιο διαδεδομένες μεθόδους ελαχιστοποίησης μιας συνάρτησης είναι η μέθοδος απότομης κατάβασης (steepest descent method).

Θα λέγαμε πως η μέθοδος απότομης κατάβασης είναι η καθιερωμένη μέθοδος αριθμητικής βελτιστοποίησης, πάνω στην οποία έχουν βασιστεί πολλές παραλλαγές, ενώ παράλληλα αποτελεί το κύριο μέτρο σύγκρισης για όλες τις άλλες αριθμητικές μεθόδους. Ο αλγόριθμος απότομης κατάβασης μπορεί να οριστεί ως ειδική περίπτωση του αλγορίθμου γραμμικής αναζήτησης, όπου η κατεύθυνση αναζήτησης \(d_k = \nabla f(x_k)\) και το μήκος βήματος \(a_k\) επιλέγεται έτσι ώστε η συνάρτηση \(f\) να ελαχιστοποιείται στην αντίστοιχη γραμμή αναζήτησης. Δίνουμε λοιπόν ένα γενικό ορισμό ενός αλγορίθμου γραμμικής αναζήτησης, τον οποίο θα εξειδικεύσουμε στη συνέχεια.

Ορισμός 5.1 (Line Search Algorithm) Ένας αλγόριθμος γραμμικής αναζήτησης, είναι μία απεικόνιση \(S: E^{2n}\rightarrow \mathcal{P}(E^n)\), που ορίζεται ως \[\begin{equation*} S(x, d)=\{y: y=x+ad,\ a\geq 0\ \textrm{και}\ f(y)=\min_{0\leq a< +\infty} f(x+ad)\}. \end{equation*}\]

Ο αλγόριθμος γραμμικής αναζήτησης, για δεδομένο σημείο \(x_0\in E^n\) και δεδομένη κατεύθυνση \(d_0\in E^n\), βρίσκει όλα τα σημεία ελαχίστου πάνω στην ημιευθεία που ξεκινά από το \(x_0\) και είναι παράλληλη στην κατεύθυνση του \(d_0\). Εάν προσδιοριστεί με κάποιο τρόπο μία ακολουθία κατευθύνσεων αναζήτησης \(\{d_k\}_{k=0}^{+\infty}\), μπορούμε να επαναλάβουμε την παραπάνω διαδικασία, ορίζοντας αναδρομικά μία ακολουθία σημείων ελαχίστου \(\{x_k\}_{k=0}^{+\infty}\) της \(f\) περιορισμένης στην αντίστοιχη ημιευθεία. Είναι φανερό ότι η ακολουθία των κατευθύνσεων θα πρέπει να επιλέγεται με τέτοιο τρόπο που να εξασφαλίζει την καθοδική πορεία της \(f\). Ο αλγόριθμος απότομης κατάβασης το επιτυγχάνει επιλέγοντας ως διάνυσμα κατεύθυνσης, σταθερά σε κάθε επανάληψη, το αντίθετο της κλίσης της \(f\) στο εκάστοτε σημείο. Ο επόμενος ορισμός δίνει μία τυπική περιγραφή του αλγορίθμου αυτού.

Ορισμός 5.2 (Steepest Descent Method) Έστω \(f\in C^{1}(E^n,\mathbb{R})\) μία συνάρτηση με συνεχείς μερικές παραγώγους πρώτης τάξης στο \(E^n\) και \(g(x)=\nabla f(x)^\top\) το n-διάστατο διάνυσμα στήλη των πρώτων μερικών παραγώγων. Αν \(S\) είναι ο αλγόριθμος γραμμικής αναζήτησης που δίνεται στον Ορισμό 5.1 και \(G: E^{n}\rightarrow E^{2n}\) με \(G(x)=(x,-g(x))\), τότε η συνάρτηση \[\begin{equation*} A:E^{n}\rightarrow\mathcal{P}(E^{2n}),\ \ \textrm{με}\ \ A=S\circ G, \end{equation*}\] λέγεται αλγόριθμος απότομης κατάβασης και αποτελεί ειδική περίπτωση του αλγορίθμου γραμμικής αναζήτησης αν επιλέξουμε ως κατεύθυνση αναζήτησης \(d=-g(x)\). Κατά συνέπεια, η μέθοδος απότομης κατάβασης περιγράφεται από την αναδρομική σχέση \[\begin{equation*} x_{k+1} = x_k - a_k g_k = x_k - a_k\nabla f(x_k), \qquad k\geq 0, \tag{5.1} \end{equation*}\]

Ποιός είναι όμως ο λόγος που επιλέγεται η αντίθετη φορά του \(\nabla\) ; Ας δούμε πρώτα το απλούστερο παράδειγμα μίας μεταβλητής. Στο παράδειγμα αυτό, όπως φαίνεται στο παρακάτω σχήμα, είναι φανερό ότι για να κινηθούμε προς τη θέση ελαχίστου πρέπει να κινηθούμε αντίθετα από το πρόσημο της παραγώγου. Αν αυτό είναι αρνητικό, κινούμαστε δεξιά (θετική μετατόπιση) και αν αυτό είναι θετικό, κινούμαστε αριστερά (αρνητική μετατόπιση), καθώς και στις 2 περιπτώσεις, έτσι μόνο θα εξασφαλίσουμε ελάττωση της τιμής της συνάρτησης. Αν λοιπόν υπάρχει ένα μοναδικό τοπικό ελάχιστο (άρα και ολικό), τότε είμαστε στη σωστή κατεύθυνση, και μία ελαχιστοποίηση της συνάρτησης στην αντίστοιχη ημιευθεία, όπως προτείνεται από τον αλγόριθμο απότομης κατάβασης, θα εντοπίσει με σιγουριά το ολικό ελάχιστο.

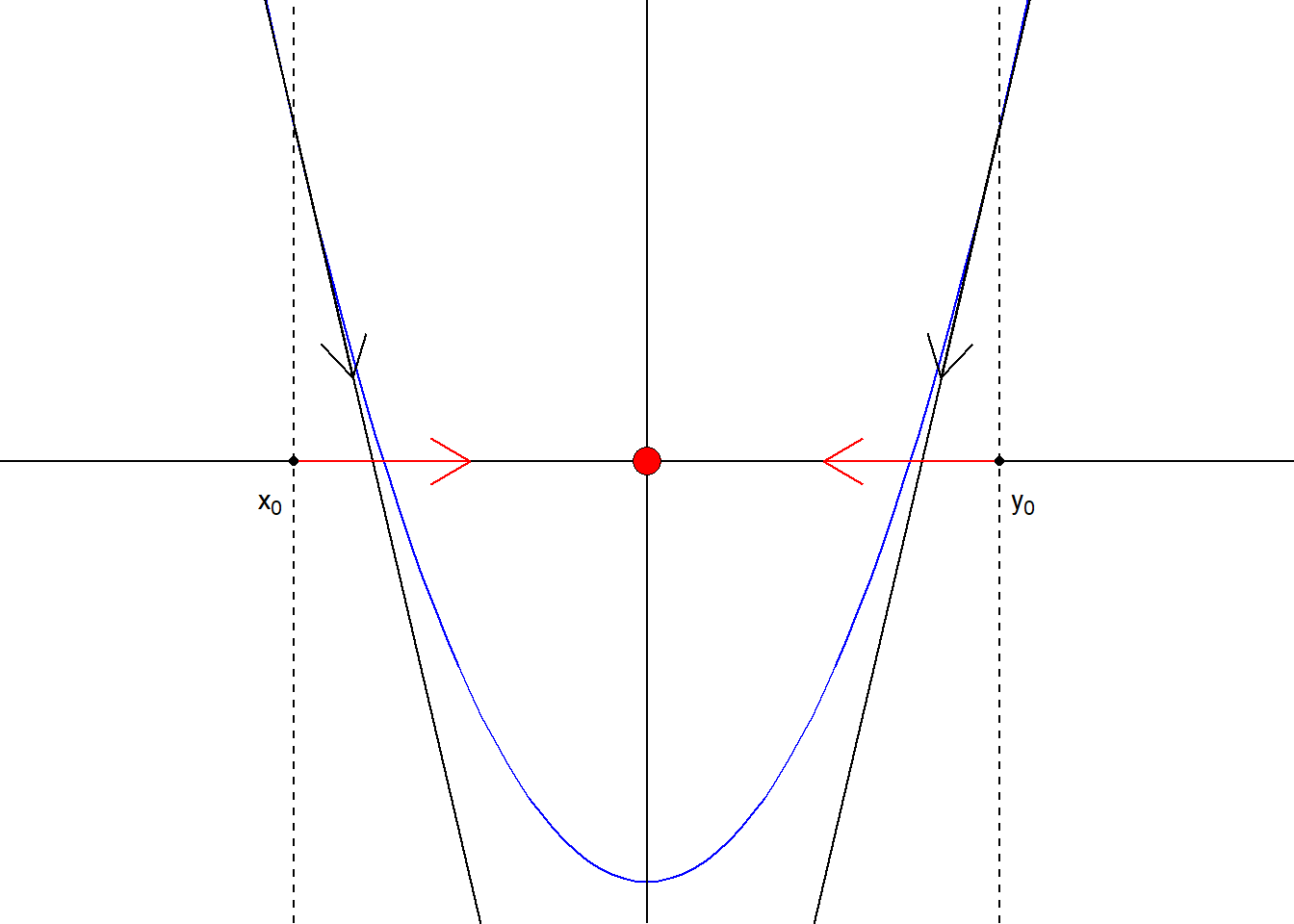
Εικόνα 5.1: A representation of the Steepest Descent movement for two different initial points \(x_0, y_0\), for a unimodal function \(f\).

Η κατάσταση γίνεται πιο περίπλοκη στην περίπτωση περισσότερων μεταβλητών. Ενώ στη μία μεταβλητή, αν το σημείο δεν είναι στάσιμο, τότε έχει μία μοναδική καθοδική κατεύθυνση, σε περισσότερες μεταβλητές έχουμε συνήθως άπειρες επιλογές. Εδώ λοιπόν τίθεται ένα θέμα βελτιστότητας. Ποιά είναι η κατεύθυνση στην οποία θα πρέπει να κινηθούμε ώστε να εξασφαλίσουμε τη μεγαλύτερη δυνατή ελάττωση, τουλάχιστον τοπικά; Για καλή μας τύχη η απάντηση είναι εύκολη. Πρέπει να κινηθούμε αντίθετα από την κλίση της συνάρτησης σε αυτό το σημείο. Η κλίση καθορίζει την κατεύθυνση της μέγιστης τοπικής ανόδου, άρα η αντίθετη κίνηση καθορίζει την κατεύθυνση της μέγιστης τοπικής ελάττωσης. Αυτή η παρατήρηση εξηγεί και το όνομα της μεθόδου απότομης κατάβασης. Πράγματι, το \(\nabla f(x)\), όπως γνωρίζουμε, μας δίνει την τοπική γραμμική προσέγγιση της \(f\). Αναζητούμε λοιπόν \(h^{*}\) στα \(h\) με \(\|h\|= 1\) (\(h\in S^{n-1}\)): \[\begin{equation*} f(x+h^{*})=\min_{h\in S^{n-1}} f(x+h) \approx f(x) + \min_{h\in S^{n-1}} \langle \nabla f(x), h \rangle \end{equation*}\] Από την ανισότητα Cauchy-Schwarz, έχουμε ότι το εσωτερικό γινόμενο έχει κάτω φράγμα \(-\|\nabla f(x)\|\) και έτσι \[\begin{equation*} h^{*}=\arg\min_{h\in S^{n-1}} f(x+h) \approx -\, \frac{\nabla f(x)}{\|\nabla f(x)\|} \propto - \nabla f(x) \end{equation*}\]

Οι αλγόριθμοι αριθμητικής βελτιστοποίησης δοκιμάζονται πάντα στις τετραγωνικές συναρτήσεις, από τις οποίες εμπνέονται για παραπέρα βελτιώσεις, έτσι ώστε να μπορούν να ανταπεξέρθουν καλύτερα σε πιο δύσκολες συναρτήσεις. Στο παρακάτω παράδειγμα θα δούμε πώς λειτουργεί η μέθοδος αυτή σε μία τέτοια συνάρτηση.

Παράδειγμα 5.1 Έστω ότι θέλουμε να ελαχιστοποιήσουμε τη συνάρτηση \(f: \mathbb{R}^2\rightarrow \mathbb{R}\) με τύπο \[\begin{equation*} f(x,y) = x^2 +2y^2 +2xy -6x -10y +13. \end{equation*}\] Αρχικά, παρατηρούμε ότι \(f\in C^{1}(\mathbb{R}^2, \mathbb{R})\) και οι πρώτες μερικές παράγωγοι είναι \[\begin{align*} \frac{\partial f}{\partial x}(x,y) &= 2x + 2y -6, \\ \frac{\partial f}{\partial y}(x,y) &= 4y +2x -10, \end{align*}\] επομένως έχουμε \[\begin{equation*} \nabla f(x,y) = (2x + 2y -6, 4y +2x -10). \end{equation*}\] Η λύση του συστήματος των εξισώσεων μας οδηγεί σε μοναδικό στάσιμο σημείο \((x^{*},y^{*})=(1,2)\), το οποίο είναι και ολικό ελάχιστο, όπως εύκολα επαληθεύεται. Θα δούμε τώρα πώς λειτουργεί η μέθοδος της απότομης κατάβασης σε μία επανάληψη του αλγορίθμου με σημεία εκκίνησης τα \((x_0^{(1)},y_0^{(1)})=(0,0)\) και \((x_{0}^{(2)},y_{0}^{(2)})=(3,1)\). Υπολογίζουμε την κλίση σε κάθε σημείο ως \(\nabla f(0,0)=(-6,-10)\) και \(\nabla f(3,1)=(2, 0)\). Σε κάθε περίπτωση, τα σημεία (x_1^{(1)},y_1{(1)}) και \((x_1^{(2)},y_1^{(2)})\) θα προσδιοριστούν σε ένα βήμα του αλγορίθμου απότομης κατάβασης, ως τα σημεία εκείνα που ελαχιστοποιούν τη συνάρτηση \(f\) στις ημιευθείες με αρχή τα σημεία \((0,0)\) και \((3,1)\), και κατευθύνσεις \((6,10)\) και \((-2,0)\) αντίστοιχα (που είναι αντίθετα της κλίσης της \(f\) στα εν λόγω σημεία). Οι ημιευθείες αυτές περιγράφονται από τις εξισώσεις: \[\begin{align*} y&=\frac{10}{6}x, \ x>0, \\ y&=1, \ x<3, \end{align*}\] στην πρώτη και τη δεύτερη περίπτωση αντίστοιχα. Είτε αντικαθιστώντας τους παραπάνω περιορισμούς στον τύπο της \(f\), είτε χρησιμοποιώντας την παραμετρική μορφή (ως προς \(a\)) των καμπυλών που υποδεικνύονται από τον αλγόριθμο, βρίσκουμε άμεσα ότι τα σημεία ελαχίστου επιτυγχάνονται στα σημεία \((51/40, 51/24)\) και \((2, 1)\) αντίστοιχα. Είναι φανερό ότι παρόλο που η πρώτη αρχικοποίηση ήταν σε τιμή της \(f\) αρκετά πιο μεγάλη από τη δεύτερη, η κλίση της \(f\) στο πρώτο σημείο την οδήγησε τελικά πιο κοντά στη θέση ελαχίστου.

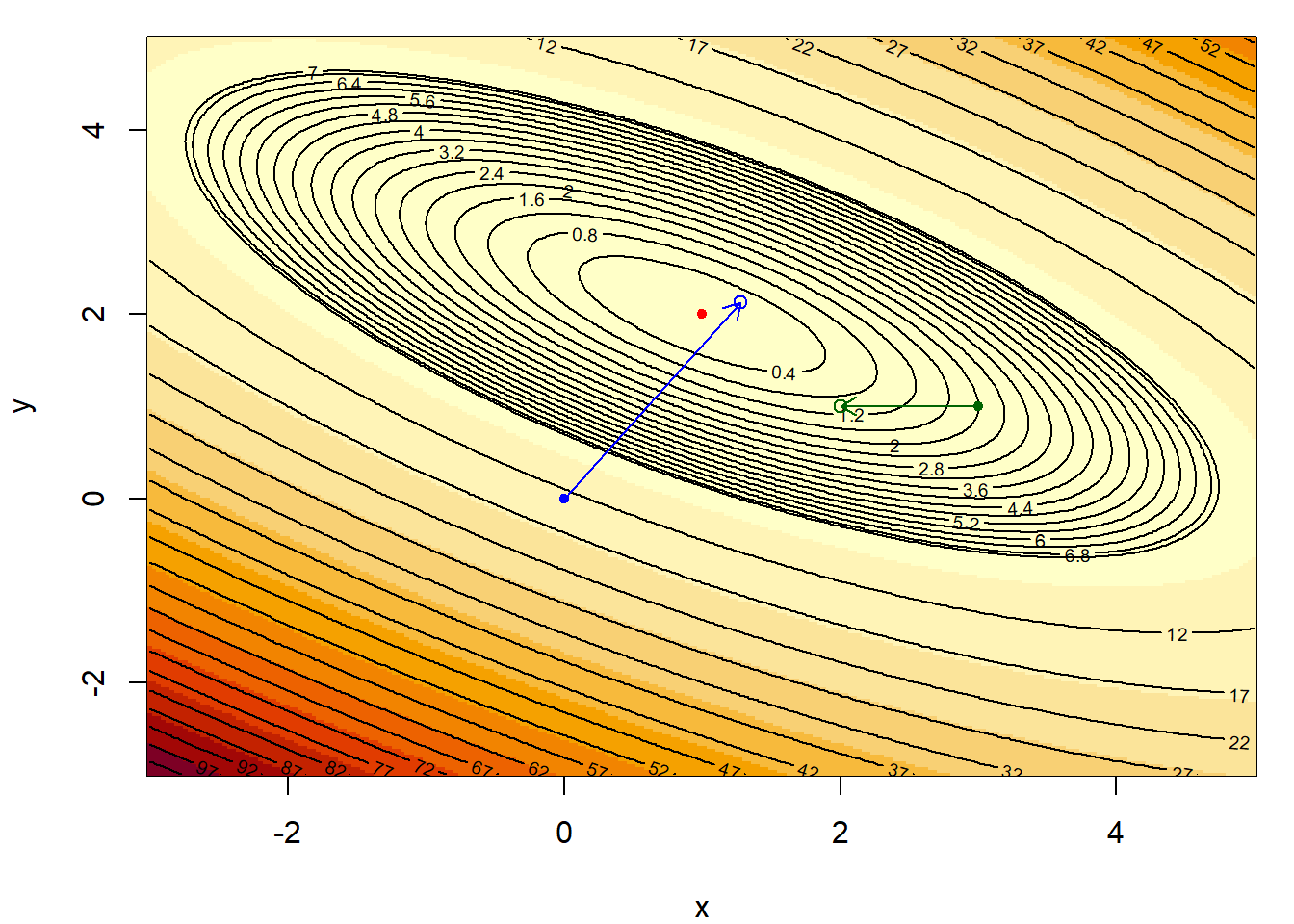
Εικόνα 5.2: One steepest descent step with two different initializations for the problem of \(f\) minimization, with starting points \((0,0)\) (blue) and \((3,1)\) (green). The argmin of the function is \((1,2)\) (red dot), with \(f(1,2)=0\).

Ας δούμε τώρα και την εξέλιξη διάφορων μονοπατιών, με διαφορετική αρχικοποίηση, μέχρι να ικανοποιηθεί το κριτήριο τερματισμού.

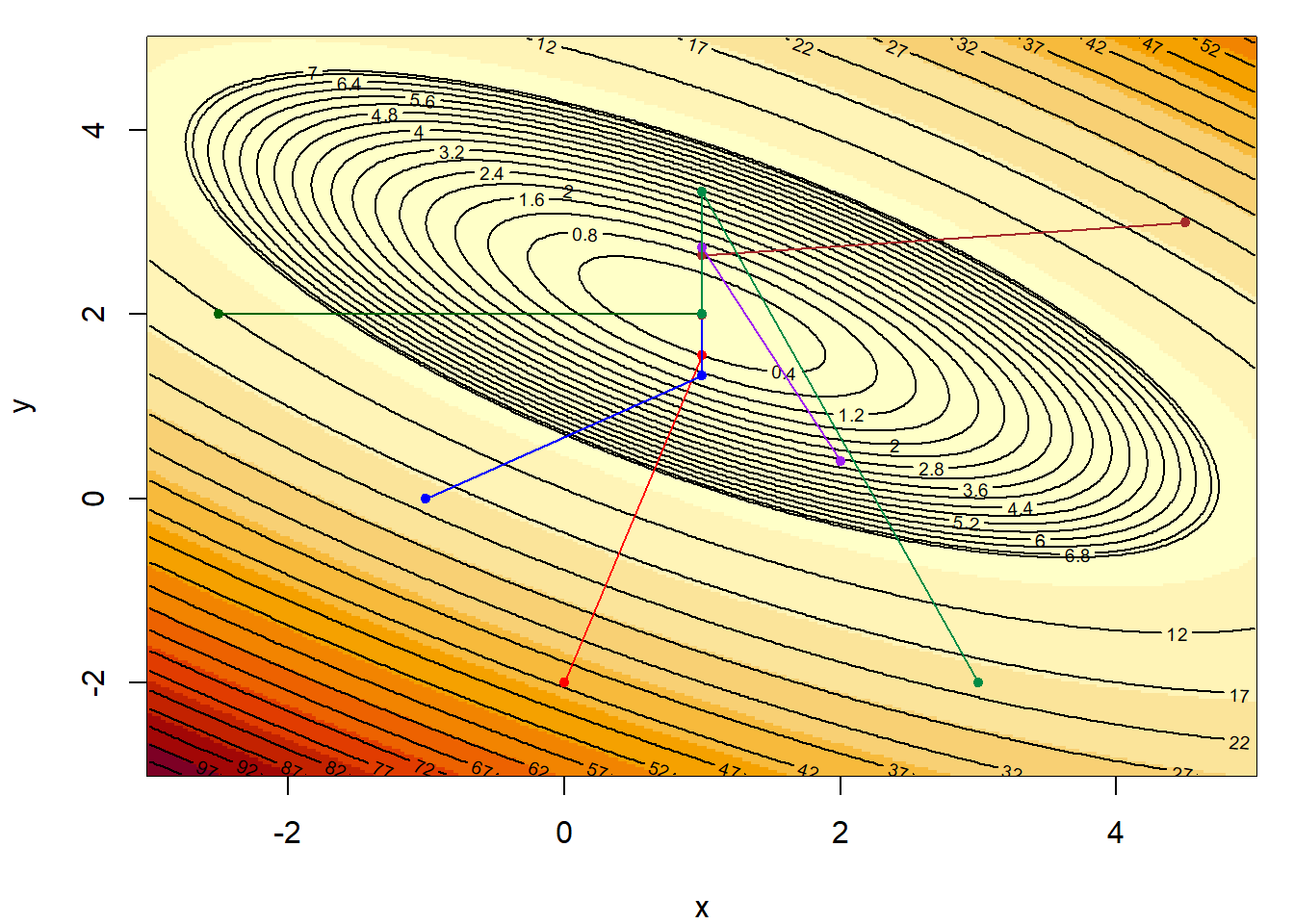
Εικόνα 5.3: Steepest Descent algorithm for 6 different initializations.

Το πρώτο, και σημαντικότερο, ερώτημα που γεννάται, είναι αν η ακολουθία που ορίσαμε συγκλίνει στο σημείο ολικού ελαχίστου της \(f\) στο σύνολο \(E^n\). Καθώς το σημείο αυτό δεν είναι απαραίτητα μοναδικό, ορίζουμε ως σύνολο λύσεων \(\Gamma = \{x^\star\in E^n : f(x^\star)=\min_{x\in E^n} f(x) \}\). Η ερώτηση που θέσαμε λοιπόν αναδιαμορφώνεται ως εξής: Συγκλίνει η αναδρομική ακολουθία (5.1) σε σημείο \(x\in \Gamma\); Για να το αποδείξουμε, θα χρειαστούμε το Θεώρημα Ολικής Σύγκλισης.

Θεώρημα 5.1 (Global Convergence Theorem) Έστω \(A: E^n\rightarrow \mathcal{P}(E^n)\) ένας αλγόριθμος, ένα σύνολο λύσεων \(\Gamma\subset X\) και μία ακολουθία \(\{x_k\}_{k=0}^{+\infty}\) η οποία για δεδομένο αρχικό σημείο \(x_0\) ορίζεται αναδρομικά ως \(x_{k+1}\in A(x_k)\). Εάν

1. υπάρχει συμπαγές σύνολο \(S\subset X\) τέτοιο ώστε \(x_k\in S, \forall k\in \mathbb{N}\),
2. υπάρχει μία συνεχής συνάρτηση \(Z:X\rightarrow \mathbb{R}\) ώστε,
   • Αν \(x\notin \Gamma\), τότε \(Z(y)<Z(x), \ \forall y \in A(x)\),
   • Αν \(x\in \Gamma\), τότε \(Z(y)\leq Z(x), \ \forall y \in A(x)\),
3. η απεικόνιση \(A\) είναι κλειστή στα σημεία εκτός του \(\Gamma\),

τότε το όριο κάθε συγκλίνουσας υπακολουθίας της \(x_k\) είναι λύση, δηλαδή για το σημείο σύγκλισης \(x\) ισχύει ότι \(x\in \Gamma\).

Απόδειξη:.

Από την υπόθεση (i), η ακολουθία \(\{x_k\}_{k=0}^{+\infty}\) βρίσκεται μέσα σε ένα συμπαγές σύνολο \(S\), επομένως υπάρχει υπακολουθία \(\{x_k\}_\mathcal{Κ}\) (όπου \(\mathcal{K}\) το σύνολο των δεικτών της υπακολουθίας, \(\mathcal{K}\subset \mathbb{N}\)), η οποία συγκλίνει στο σημείο \(x\in S\), δηλαδή \(x_k\rightarrow x, k\in \mathcal{K}\). Η συνάρτηση \(Z\) είναι συνεχής (υπόθεση ii), επομένως \(Z(x_k)\rightarrow Z(x), k\in \mathcal{K}\). Σύμφωνα με τον ορισμό της σύγκλισης,

\[\begin{equation*} \forall \epsilon>0 \exists K\in \mathcal{K}: Z(x_k)-Z(x)<\epsilon, \ \ \forall k>K, k\in \mathcal{K}. \end{equation*}\]

Δείξαμε ότι η \(Z\) συγκλίνει ως προς την υπακολουθία. Θα δείξουμε ότι συγκλίνει ως προς ολόκληρη την ακολουθία, δηλαδή ότι η παραπάνω σύγκλιση ισχύει για όλα τα \(k>K\), όχι μόνο για αυτά του συνόλου \(\mathcal{K}\). Από την μονοτονία της \(Z\) (υπόθεση ii), έχουμε \(i<j \Rightarrow Z(x_i)>Z(x_j)>Z(x), i,j\in \mathbb{N}\). Έστω λοιπόν \(k>K\), τότε

\[\begin{equation*} Z(x_k) - Z(x) = \underbrace{Z(x_k) - Z(x_K)}_{<0} + \underbrace{Z(x_K) - Z(x)}_{<\epsilon} < \epsilon, \end{equation*}\]

επομένως \(Z(x_k)\rightarrow Z(x)\). Είμαστε έτοιμοι να δείξουμε ότι \(x\in \Gamma\). Έστω ότι \(x\notin \Gamma\). Τότε ορίζουμε την ακολουθία \(y_k:=x_{k+1}, k\in \mathcal {K}\). Η \(\{y_k\}_{\mathcal{K}}\) βρίσκεται μέσα στο \(S\), επομένως έχει συγκλίνουσα υπακολουθία \(\{y_k\}_{\mathcal{L}}, \mathcal{L}\subset \mathcal{K}\), η οποία συγκλίνει στο \(y\). Επομένως έχουμε \(x_k \rightarrow x, k\in \mathcal{L}\subset \mathcal{K}\), \(y_k\rightarrow y, k\in \mathcal{L}\) και \(y_k\in A(x_k), k\in \mathcal {L}\). Από την υπόθεση (iii), η \(A\) είναι κλειστή στο \(x\notin\Gamma\), επομένως \(y\in A(x)\). Αφού \(x\notin \Gamma, Z(y)<Z(x)\). Όμως δείξαμε ότι \(Z(x_k)\rightarrow Z(x)\) για ολόκληρη την ακολουθία \(\{x_k\}_{k=0}^{+\infty}\), επομένως και για τις υπακολουθίες \(\{x_k\}_\mathcal{K}, \{y_k\}_\mathcal{L}\), οπότε από την μοναδικότητα του ορίου \(Z(x)=Z(y)\), άτοπο. Επομένως \(x\in \Gamma\), δηλαδή κάθε συγκλίνουσα υπακολουθία συγκλίνει σε λύση.

Επιστρέφοντας στη μέθοδο ελάχιστης κλίσης, θέλουμε να δείξουμε ότι οι τρεις υποθέσεις του Θεωρήματος Ολικής Σύγκλισης ικανοποιούνται. Αρχικά, ορίζουμε το σύνολο λύσεων \(\Gamma = \{x\in E^n: \nabla f(x)=0\}\).

2. Ως συνάρτηση \(Z\), επιλέγουμε την ίδια την \(f\) που επιθυμούμε να ελαχιστοποιήσουμε, η οποία είναι συνεχής εξ ορισμού. Εύκολα βλέπουμε ότι
   • Αν \(x\notin \Gamma\), τότε \(g(x)=\nabla f(x)\neq 0\), άρα \(\min_{0\leq a <+\infty}f(x-ag(x))<f(x)\)
   • Αν \(x\in \Gamma\), τότε \(g(x)=\nabla f(x)= 0\), άρα \(f(x-ag(x))=f(x), \ \forall y \in A(x)\)
3. Η \(A(x)\) είναι κλειστή,

Επομένως, εάν η ακολουθία \(\{x_k\}_{k=0}^{+\infty}\) είναι φραγμένη, τότε ικανοποιούνται και οι τρεις υποθέσεις του Θεωρήματος Ολικής Σύγκλισης, επομένως θα έχει υπακολουθία που θα συγκλίνει μέσα στο σύνολο των λύσεων.

5.2.1.1 Τετραγωνική Συνάρτηση

Θα εξετάσουμε θεωρητικά τη σύγκλιση του αλγορίθμου στις τετραγωνικές συναρτήσεις

\[\begin{equation*} f(x) = \frac{1}{2}x^\top Q x - x^\top b, \end{equation*}\]

όπου \(Q\) ένας θετικά ορισμένος και συμμετρικός \(n\times n\) πίνακας. Παραγωγίζοντας τη συνάρτηση παίρνουμε \[\begin{equation*} g(x)=\nabla f(x) = \frac{1}{2} 2 Qx - b = Qx - b. \end{equation*}\]

Στην συγκεκριμένη περίπτωση, μπορούμε να βρούμε ότι το μοναδικό σημείο ελαχίστου \(x^\star\) της \(f(x)\) ικανοποιεί τη σχέση \(Qx^\star = b\). Θα προσεγγίσουμε το σημείο με τη μέθοδο σύγκλισης, μέσω της αναδρομικής ακολουθίας

\[\begin{equation*} x_{k+1}=x_k-a_k g_k, \end{equation*}\]

όπου \(g_k=Qx_k - b\) και το \(a_k\) ελαχιστοποιεί την \(f(x_k-a_k g_k)\). Το \(a_k\) μπορεί να υπολογιστεί αναλυτικά, παραγωγίζοντας την

\[\begin{equation*} f(x_k-ag_k) = \frac{1}{2}(x_k-ag_k)^\top Q (x_k-ag_k) - (x_k-ag_k)^\top b, \end{equation*}\]

ως προς \(a\), κάτι που δίνει την λύση

\[\begin{equation*} a_k = \frac{g_k^\top g_k}{g_k^\top Q g_k}. \end{equation*}\]

Τελικά, η αναδρομική ακολουθία παίρνει τη μορφή

\[\begin{equation*} x_{k+1}=x_k-\frac{g_k^\top g_k}{g_k^\top Q g_k} g_k, \end{equation*}\]

όπου \(g_k=Qx_k - b\).

Παρουσιάζουμε τώρα δύο αποτελέσματα χωρίς απόδειξη, τα οποία θα μας βοηθήσουν να μελετήσουμε την ταχύτητα σύγκλισης της μεθόδου ελάχιστης κλίσης.

Λήμμα 5.1 Ορίζουμε τη συνάρτηση \[\begin{equation*} E(x)=f(x)+\frac{1}{2}{x^\star}^\top Q x^\star =\frac{1}{2}(x-x^\star)^\top Q (x-x^\star), \end{equation*}\] όπου \(x^\star\) το σημείο ολικού ελαχίστου της \(f\). Για την αναδρομική ακολουθία \(\{x_k\}_{k=0}^{+\infty}\) της μεθόδου σύγκλισης ισχύει \[\begin{equation*} E(x_{k+1} = \left\{1-\frac{\left(g_k^\top g_k\right)^2}{\left(g_k^\top Q g_k\right) \left(g_k^\top Q^{-1} g_k\right)} \right\} E(x_k). \end{equation*}\]

Πρόταση 5.1 (Kantorovich Inequality) Έστω \(Q\) ένας θετικά ορισμένος και συμμετρικός \(n\times n\) πίνακας. Για κάθε n-διάστατο διάνυσμα \(x\) ισχύει \[\begin{equation*} \frac{\left(x^\top x\right)^2}{\left(x^\top Q x\right) \left(x^\top Q^{-1} x\right)}\geq \frac{4aA}{(a+A)^2}, \end{equation*}\] όπου \(a, A\) είναι η μικρότερη και η μεγαλύτερη ιδιοτιμή του \(Q\), αντίστοιχα.

Από τα παραπάνω προκύπτει άμεσα το ακόλουθο θεώρημα.

Θεώρημα 5.2 (Steepest Descent - Quadratic Case) Για κάθε \(x_0\in E^n\), η μέθοδος ελάχιστης κλίσης συγκλίνει στο μοναδικό σημείο ελαχίστου \(x^\star\) της \(f\). Επιπλέον, για την συνάρτηση \(E(x)=\frac{1}{2}(x-x^\star)^ \top Q (x-x^\star)\) ισχύει \[\begin{equation*} E(x_{k+1} \leq \left( \frac{A-a}{A+a} \right)^2 E(x_k), \end{equation*}\] ή θέτοντας \(r=A/a\), \[\begin{equation*} E(x_{k+1} \leq \left( \frac{r-1}{r+1} \right)^2 E(x_k), \end{equation*}\]

Απόδειξη:.

Από το λήμμα 5.1 και την ανισότητα του Kantorovich προκύπτει άμεσα ότι

\[\begin{equation*} E(x_{k+1} \leq \left\{1-\frac{4aA}{(A+a)^2} \right\} E(x_k) = \left( \frac{A-a}{A+a} \right)^2 E(x_k). \end{equation*}\]

Επομένως, \(E(x_k)\rightarrow 0\) και καθώς ο \(Q\) είναι θετικά ορισμένος, \(x_k\rightarrow x^\star\).

Αδρά μιλώντας, το παραπάνω θεώρημα δηλώνει πως ο ρυθμός σύγκλισης της μεθόδου ελάχιστης κλίσης μειώνεται καθώς ο λόγος \(r=A/a\) μεγαλώνει. Επομένως, ακόμα και αν έχουμε \(n-1\) από τις \(n\) ιδιοτιμές να είναι ίσες με \(a\), με την τελευταία ιδιοτιμή να είναι πολύ μεγαλύτερη, ο λόγος αυτός είναι κοντά στο 1 και η σύγκλιση του αλγορίθμου είναι αργή. Αντίθετα, στην ακραία περίπτωση που όλες οι ιδιοτιμές είναι ίσες (οπότε \(a=A\)), ο αλγόριθμος συγκλίνει σε ένα μόλις βήμα. Ο λόγος \(r\) ονομάζεται δεσμευμένος αριθμός (conditional number) του πίνακα \(Q\).

Αξίζει εδώ να παρατηρήσουμε ότι ο λόγος \(\left[ (A-a)/(A+a) \right]^2\) δεν είναι ο πραγματικός ρυθμός σύγκλισης της μεθόδου, αλλά ένα άνω φράγμα αυτού (το χειρότερο δυνατό σενάριο). Παρ’ όλα αυτά, συχνά δηλώνουμε ότι ο ρυθμός σύγκλισης του αλγορίθμου ελάχιστης κλίσης είναι \(\left( (A-a)/(A+a) \right)^2\).

5.2.2 Μέθοδος Newton - Raphson

Αρχικά, ας μελετήσουμε τον αλγόριθμο για την περίπτωση της μίας μεταβλητής, δηλαδή την ελαχιστοποίηση μίας συνάρτησης \(f: \mathbb{R}\rightarrow \mathbb{R}\), όπως αυτή της εικόνας 5.4. Η βασική ιδέα στηρίζεται στο να κινηθούμε αντίθετα από το πρόσημο που μας καθορίζει η κλίση της συνάρτησης στο σημείο αυτό (αντίστοιχα, σύμφωνα με το πρόσημο σε προβλήματα μεγιστοποίησης). Είναι φανερό ότι \(f'(x_0)<0\), ενώ \(f'(y_0)>0\) και άρα επιλέγοντας κατάλληλα \(x_1>x_0\) και \(y_1<y_0\), θα παίρναμε μικρότερες τιμές για την \(f\). Αλγεβρικά έχουμε γενικά ότι \(\nabla f(x_0) (x-x_0)<0\), έτσι ώστε

\[\begin{equation*} f(x) \approx f(x_0) +\nabla f(x_0) (x-x_0) < f(x_0), \end{equation*}\]

για αρκούντως μικρή μετακίνηση \(x-x_0\).

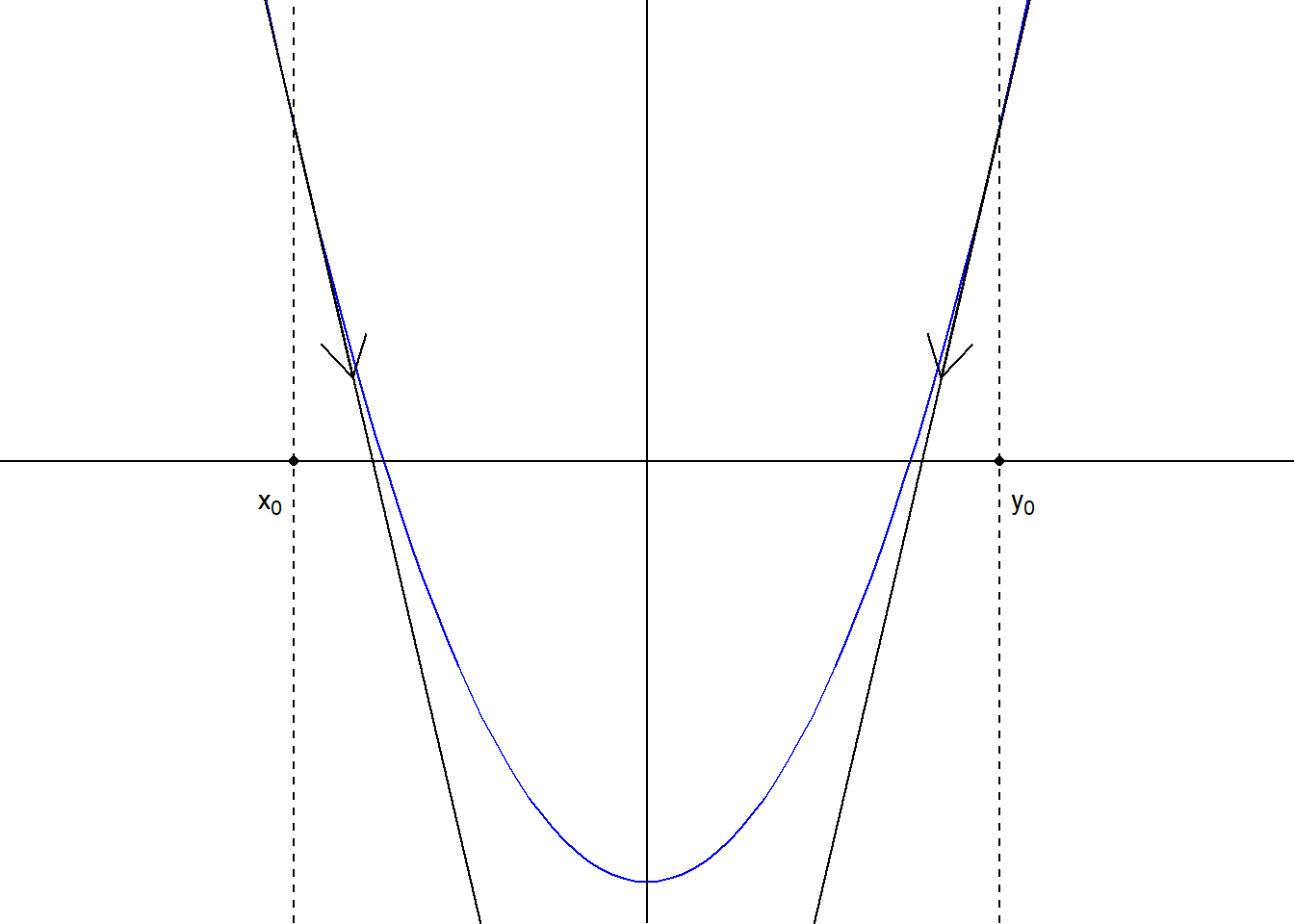
Εικόνα 5.4: A representation of the moving direction of the Newton-Raphson algorithm for two different initial points \(x_0, y_0\), for a unimodal function \(f\).

Γενικότερα, η ιδέα πίσω από τη μέθοδο Newton - Raphson είναι ότι η υπό ελαχιστοποίηση συνάρτηση \(f\) μπορεί να προσεγγιστεί τοπικά από μία τετραγωνική συνάρτηση, την οποία μπορούμε να ελαχιστοποιήσουμε αναλυτικά. Επομένως, σε μία περιοχή γύρω από το σημείο \(x_k\), η \(f\) προσεγγίζεται από την περικεκκομένη σειρά Taylor

\[\begin{equation*} f(x) \approx f(x_k) + \nabla f(x_k) (x-x_k) +\frac{1}{2} (x-x_k)^\top H(x_k) (x-x_k). \end{equation*}\]

Το δεξί μέλος ελαχιστοποιείται στο σημείο

\[\begin{equation*} x_{k+1} = x_k - H(x_k)^{-1} \nabla f(x_k)^\top, \end{equation*}\]

όπου \(H(x_k)\) ο Εσσιανός πίνακας της \(f\) υπολογισμένος στο σημείο \(x_k\). Παρατηρούμε λοιπόν ότι η μέθοδος Newton - Raphson είναι μία παραλλαγή της μεθόδου κλίσης, με \(a_k=H(x_k)^{-1}\). Για τη σύγκλιση του αλγορίθμου ισχύει το παρακάτω θεώρημα:

Θεώρημα 5.3 (Newton - Raphson Method) Έστω \(f\in C^3(E^n, \mathbb{R})\) (συνάρτηση από το \(E^n\) στο \(\mathbb{R}\) με συνεχείς τρίτες μερικές παραγώγους) και τοπικό σημείο ελαχίστου \(x^\star\) με τον εσσιανό πίνακα \(H(x^\star)\) να είναι θετικά ορισμένος. Τότε, υπάρχει σφαίρα \(S\subset E^n\) γύρω από το \(x^\star\) τέτοια ώστε, αν η αναδρομική ακολουθία του αλγορίθμου ξεκινήσει με αρχικό όρο \(x_0\in S\), τότε η ακολουθία συγκλίνει το \(x^\star\). Η τάξη σύγκλισης είναι τουλάχιστον 2, δηλαδή \(||x_{k+1}-x^\star||\leq c \cdot ||x_{k}-x^\star||\), για κάποια θετική σταθερά \(c\).

Απόδειξη:.

Έστω \(p>0, \beta_1>0, \beta_2>0\), τέτοια ώστε για όλα τα \(x: |x-x^\star|<p\) να ισχύει \(|H(x)^{-1}|<\beta_1\) (όπου \(|\cdot |\) νόρμα) και \(|\nabla f(x^\star)^\top-\nabla f(x)^\top -H(x)(x^\star -x)|\leq \beta_2 |x-x^\star|^2\). Υποθέτουμε ότι το \(x_k\) επιλέγεται έτσι ώστε \(\beta_1\beta_2|x_k-x^\star|<1\) και \(|x_k-x^\star|<p\). Τότε

\[\begin{align*} |x_{k+1}-x^\star| &= |x_k -x^\star - H(x_k)^{-1} \nabla f(x_k)^\top | \\ &= |H(x_k)^{-1} \left[\nabla f(x^\star)^\top-\nabla f(x_k)^\top -H(x_k)(x^\star -x_k) \right]| \\ &\leq |H(x_k)^{-1}| \beta_2 |x_k-x^\star|^2 \leq \beta_1 \beta_2 |x_k-x^\star|^2 < |x_k-x^\star|. \end{align*}\]

Η τελευταία ανισότητα δείχνει πως το νέο σημείο είναι πιο κοντά στο \(x^\star\), ενώ η προτελευταία ανισότητα δείχνει ότι σύγκλιση είναι δεύτερης τάξης.

Βλέπουμε επομένως πως η μέθοδος Newton - Raphson είναι ιδιαίτερα αποδοτική όταν η υπό ελαχιστοποίηση (ή μεγιστοποίηση) συνάρτηση \(f\) έχει καλές ιδιότητες, εγκυμονεί όμως ο κίνδυνος να μας οδηγήσει σε ένα τοπικό ελάχιστο και όχι το ολικό ελάχιστο που επιθυμούμε. Επομένως, μία συχνή παραλλαγή είναι να επαναλαμβάνουμε τη μέθοδο πολλές φορές, με διαφορετικά σημεία εκκίνησης.

5.2.3 Εφαρμογές

Θα μελετήσουμε δύο βασικές συναρτήσεις της R, την optimise, που χρησιμοποιεί μία μίξη των αλγορίθμων αναζήτησης της χρυσής τομής και παραβολικής παρεμβολής, και την nlm, η οποία υλοποιεί τον αλγόριθμο Newton - Raphson. Δίνουμε ένα παράδειγμα από την κάθε μία

Παράδειγμα 5.2 (Cauchy MLE Approximation) Έστω η συνάρτηση πιθανοφάνειας ενός δείγματος από την κατανομή \(\mathcal{C}(\theta, 1)\)

\[\begin{equation*} L(\theta) = \prod_{i=1}^n \frac{1}{1+(x_i-\theta)^2}, \end{equation*}\]

και η λογαριθμοπιθανοφάνεια \[\begin{equation*} \ell(\theta) = -\sum_{i=1}^n \log (1+(x_i-\theta)^2). \end{equation*}\]

Γνωρίζουμε πως η ακολουθία των ε.μ.π. συγκλίνει στο \(\theta^\star=0\), καθώς \(n\rightarrow +\infty\). Παίρνουμε ένα δείγμα μεγέθους \(n=400\) από την \(\mathcal{C}(0, 1)\) και υπολογίζουμε αναδρομικά τις ε.μ.π. με τη συνάρτηση optimise, καθώς το μέγεθος του δείγματος αυξάνεται χρησιμοποιώντας την πιθανοφάνεια και την λογαριθμοπιθανοφάνεια. Όπως φαίνεται στην εικόνα 5.5 (αριστερά), για τις πρώτες περίπου 300 παρατηρήσεις, οι δύο συναρτήσεις \(L, \ell\) δίνουν το ίδιο σημείο μεγίστου, ενώ μετά η συνάρτηση πιθανοφάνειας φτάνει σε τόσο μικρές τιμές, που τα αριθμητικά σφάλματα γιγαντώνονται και η ακολουθία αποκλίνει. Αυτό είναι ένα χαρακτηριστικό παράδειγμα αστάθειας, που μπορεί εύκολα να διορθωθεί μετασχηματίζοντας σε \(\ell=\log L\).

Εάν αντικαταστήσουμε την πιθανοφάνεια με μία διαταραγμένη (perturbed) μορφή

\[\begin{equation*} L_p(\theta) = \prod_{i=1}^n \frac{e^{-\sin(100\theta)^2}}{1+(x_i-\theta)^2}, \end{equation*}\] και αντίστοιχα \[\begin{equation*} \ell_p(\theta) = -\sin(100\theta)^2-\sum_{i=1}^n \log (1+(x_i-\theta)^2), \end{equation*}\]

βλέπουμε (εικόνα 5.5, δεξιά) ότι η συνάρτηση optimise γίνεται ιδιαίτερα ασταθής, καθώς οι \(L, \ell\) δίνουν διαφορετικές ακολουθίες σημείων μεγίστου.

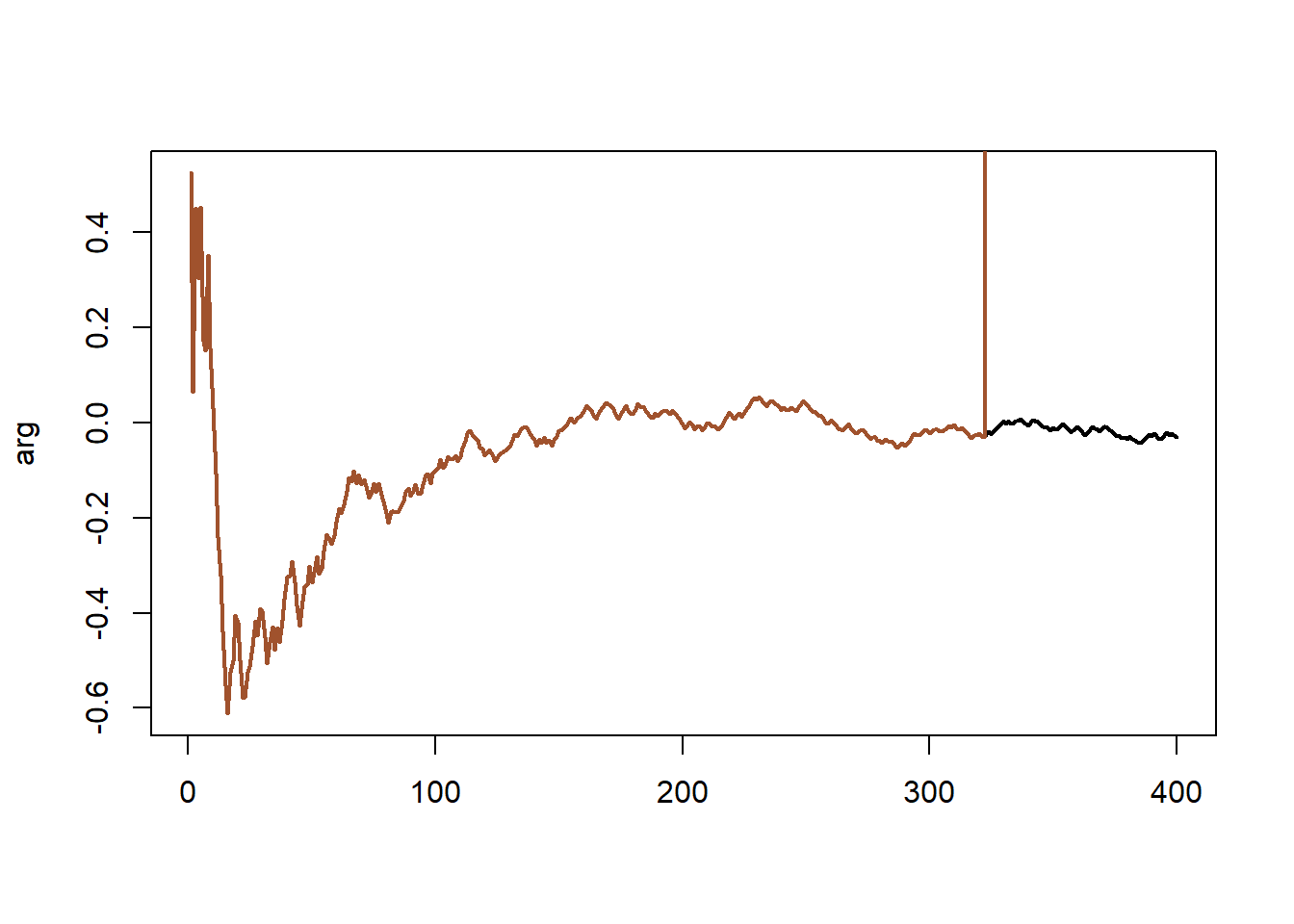
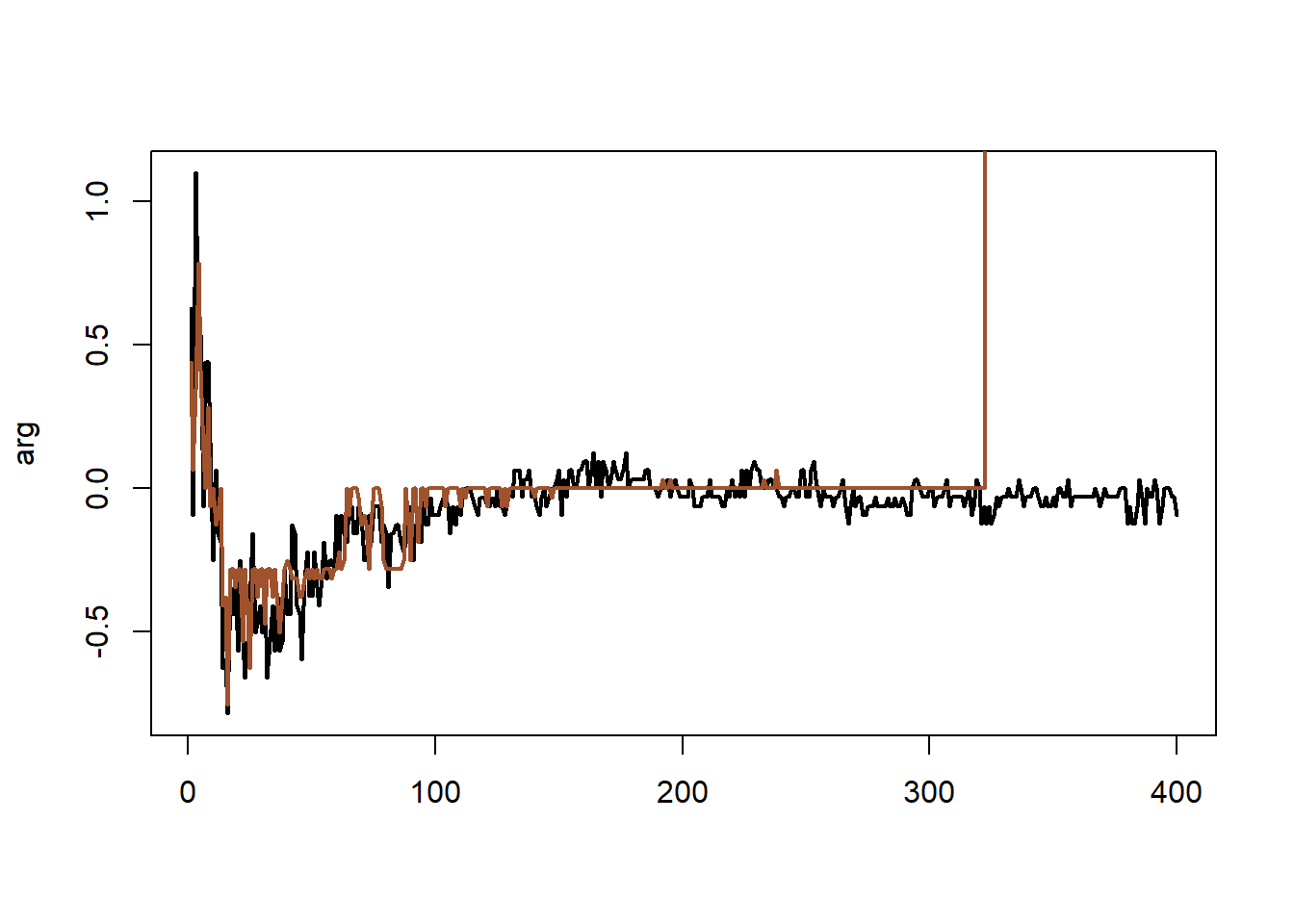
Εικόνα 5.5: (Left) Sequence of MLEs corresponding to 400 simulations from a Cauchy \(\mathcal{C}(0, 1)\) distribution obtained by applying optimise to the log-likelihood and the likelihood (in lighter colors). (Right) the same sequences when using a perturbed likelihood.

5.3 Στοχαστική Βελτιστοποίηση

5.3.1 Εισαγωγή

Μία πρώτη σκέψη στο πρόβλημα προσέγγισης του \(\max_{\theta\in\Theta} h(\theta)\) μέσω προσομοίωσης είναι να προσομοιώσουμε ένα μεγάλο αριθμό σημείων από όλο το \(\Theta\) σύμφωνα με μία αυθαίρετη κατανομή \(f\), έως ότου παρατηρηθεί μία “πολύ μεγάλη” τιμή της \(h\). Όπως είναι εμφανές, αυτός ο τρόπος δεν είναι καθόλου αποδοτικός εάν η \(f\) δεν έχει επιλεχθεί βάση της \(h\), αλλά κάτω από συγκεκριμένες υποθέσεις (όπως τη συμπάγεια του \(\Theta\)) συγκλίνει στο \(\max_{\theta\in\Theta} h(\theta)\) καθώς ο αριθμός των προσομοιώσεων τείνει στο άπειρο.

Παράδειγμα 5.3 (Robert & Casella 5.3.) Έστω η συνάρτηση \[\begin{equation*} h(x) = \left[ \cos(50x) + \sin(20x) \right]^2, \ x\in [0,1], \end{equation*}\] η οποία, παρότι παρουσιάζει καλές ιδιότητες (είναι ορισμένη σε φραγμένο διάστημα, συνεχής και άπειρες φορές παραγωγίσιμη), έχει ιδιαίτερα μεγάλη μεταβλητότητα, κάτι που περιπλέκει το πρόβλημα εύρεσης των ακροτάτων της (Σχήμα 5.6 ).

Εικόνα 5.6: Plot of \(h(x)=\left[ \cos(50x) + \sin(20x) \right]^2\) defined over \([0,1]\).

Η optimise μας πληροφορεί ότι το σημείο μεγίστου είναι το \(x^\star=\) 0.379 με τιμή \(h(x^\star)=\) 3.833.

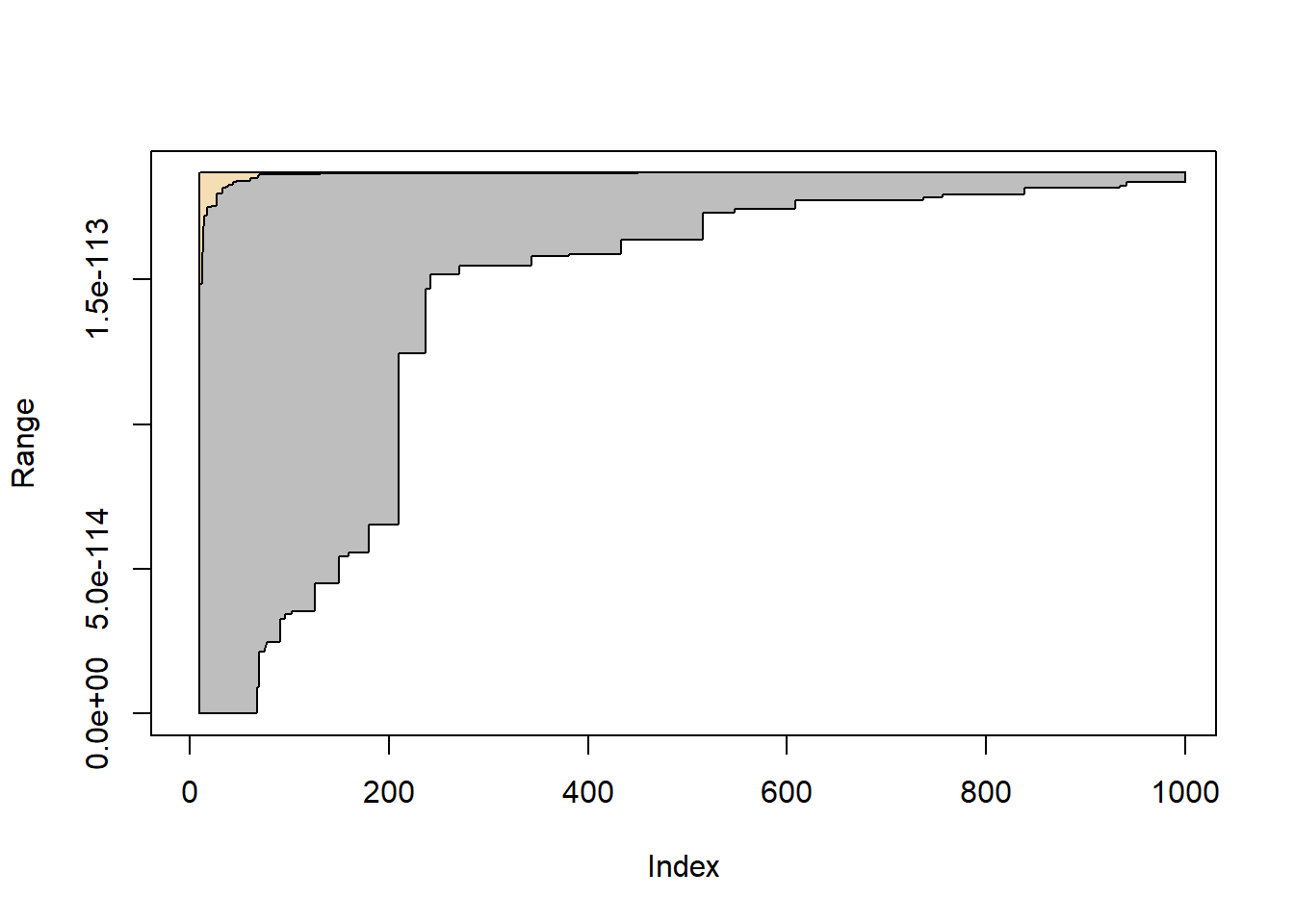
Θα προσομοιώσουμε \(M=10^3\) φορές, ένα μέγεθος δείγματος \(10^3\) από την \(Unif(0,1)\) και μέσα από το δείγμα \(\{\widehat{\theta}_{n}^{(i)}\}_{i=1}^{M}\) θα μελετήσουμε πώς μεταβάλλεται το \(\widehat{\theta}_{n}\) και το \(\widehat{h}_n:= h(\widehat{\theta}_{n})\), δηλαδή η εκτίμηση της θέσης και της τιμής του μεγίστου. Στο σχήμα 5.7 παρουσιάζεται το γράφημα του εύρους των τιμών που κινείτει η προσέγγιση του μεγίστου της \(h\), με ανώτερο όριο το \(max_{1\leq i \leq M}\widehat{h}_n^{(i)}\) και κατώτερο όριο το \(min_{1\leq i \leq M}\widehat{h}_n^{(i)}\) της \(h(\widehat{\theta}_{n})\), καθώς το \(n\) αυξάνει μέχρι τη μέγιστο διαθέσιμο δείγμα \(10^3\). Βλέπουμε πως η \(h(U_1)\) παρουσιάζει πολύ μεγάλη μεταβλητότητα, αφού δεν είναι παρά η τιμή της \(h\) σε ένα τυχαίο σημείο του διαστήματος \([0,1]\). Η μεταβλητότητα των εκτιμήσεων όμως γρήγορα ελαττώνεται και μετά από \(10^3\) βήματα, η μεγαλύτερη απόσταση από την τιμή που υπέδειξε η optimise είναι 0.017 .

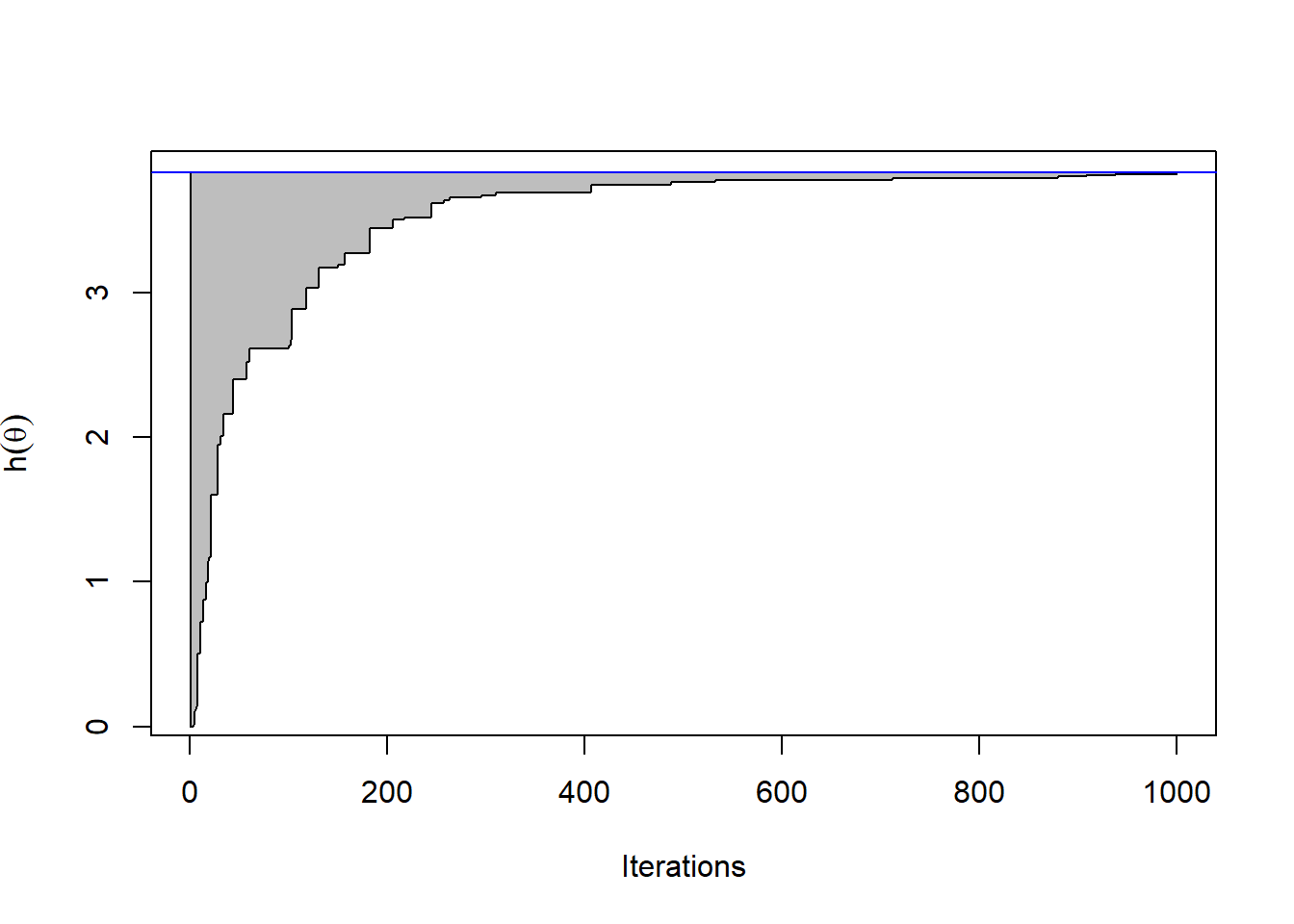
Εικόνα 5.7: Range of \(10^3\) sequences of successive maxima found by random uniform sampling over \(10^3\) iterations. The true maximum value is identified by the blue line on top of the graph.

Στο σημείο αυτό αξίζει να παρατηρήσουμε ότι η παραπάνω διαδικασία μπορεί να εφαρμοστεί άμεσα μόνο όταν το σύνολο \(\Theta\) έχει επαρκώς απλή δομή. Διαφορετικά, καλούμαστε να προσομοιώσουμε ομοιόμορφα από ένα υπερσύνολο του \(\Theta\) με απλή δομή και να απορρίψουμε όσα σημεία πέφτουν εκτός του \(\Theta\).

Παράδειγμα 5.4 Υποθέτουμε ότι έχουμε μία συνάρτηση \(h(x,y)\) την οποία επιθυμούμε να μεγιστοποιήσουμε στο διάστημα \[\begin{equation*} \Theta=\{(x,y)\in \mathbb{R}^2: x^2(1+\sin(3y)\cos(8x))+y^2(2+\cos(5x)\cos(8y))\leq 1\}. \end{equation*}\]

Για να εφαρμόσουμε στοχαστική βελτιστοποίηση μέσω ομοιόμορφης δειγματοληψίας, πρέπει πρώτα να βρούμε ένα βολικό υπερσύνολο του \(\Theta\).

Φυσικά, αυτή η μέθοδος αγνοεί τελείως τη συνάρτηση \(h\) και γρήγορα σταματά να είναι αποδοτική καθώς η διάσταση του προβλήματος μεγαλώνει. Για παράδειγμα, σε ένα Μπεϋζιανό περιβάλλον, όταν το μέγεθος \(n\) ενός αν.ισ. δείγματος \(x_1, \dots, x_n\) από την \(f(x|\theta)\) αυξάνεται, η posterior σ.π. / σ.π.π. \(\pi(\theta|x_1, \dots, x_n)\) συγκεντρώνεται όλο και περισσότερο γύρω από την επικρατούσα τιμή, επομένως η περιοχή που συγκεντρώνονται οι μεγάλες τιμές στενεύει, και η στοχαστική εκτίμηση μέσω ομοιόμορφης δειγματοληψίας γίνεται όλο και πιο δύσκολη. Αυτό φυσικά δεν ισχύει πάντα, όπως φαίνεται στο παρακάτω παράδειγμα.

Παράδειγμα 5.5 (Robert & Casella 5.4.) Συνεχίζοντας το παράδειγμα 5.1, μπορούμε να παρακολουθήσουμε τη διαφορά ανάμεσα στην αριθμητική βελτιστοποίηση της optimise και τη στοχαστική βελτιστοποίηση της ομοιόμορφης δειγματοληψίας στο \([-5, 5]\), καθώς το δείγμα \(x_1, x_2, \dots, x_n\) της κατανομής Cauchy αυξάνεται από \(n=1\) έως \(n=5001\). Στην εικόνα 5.8 (πάνω) έχουμε στον οριζόντιο άξονα τις τιμές \(\theta^\star\) της optimise και στον κάθετο τις στοχαστικές εκτιμήσεις. Παρότι φαίνεται να έχουμε μεγάλα σφάλματα γύρω από το 0, συγκριτικά με άλλες περιοχές, πρέπει να λάβουμε υπ’ όψιν το μεγάλο πλήθος παρατηρήσεων σε εκείνη την περιοχή. Στην εικόνα 5.8 (κάτω), παρουσιάζονται τα σχετικά σφάλματα \(e=(h(\theta^\star) - h(\widehat{\theta}))/|h(\theta^\star)|\), τα οποία δεν δείχνουν αυξητική τάση καθώς το δείγμα αυξάνεται.

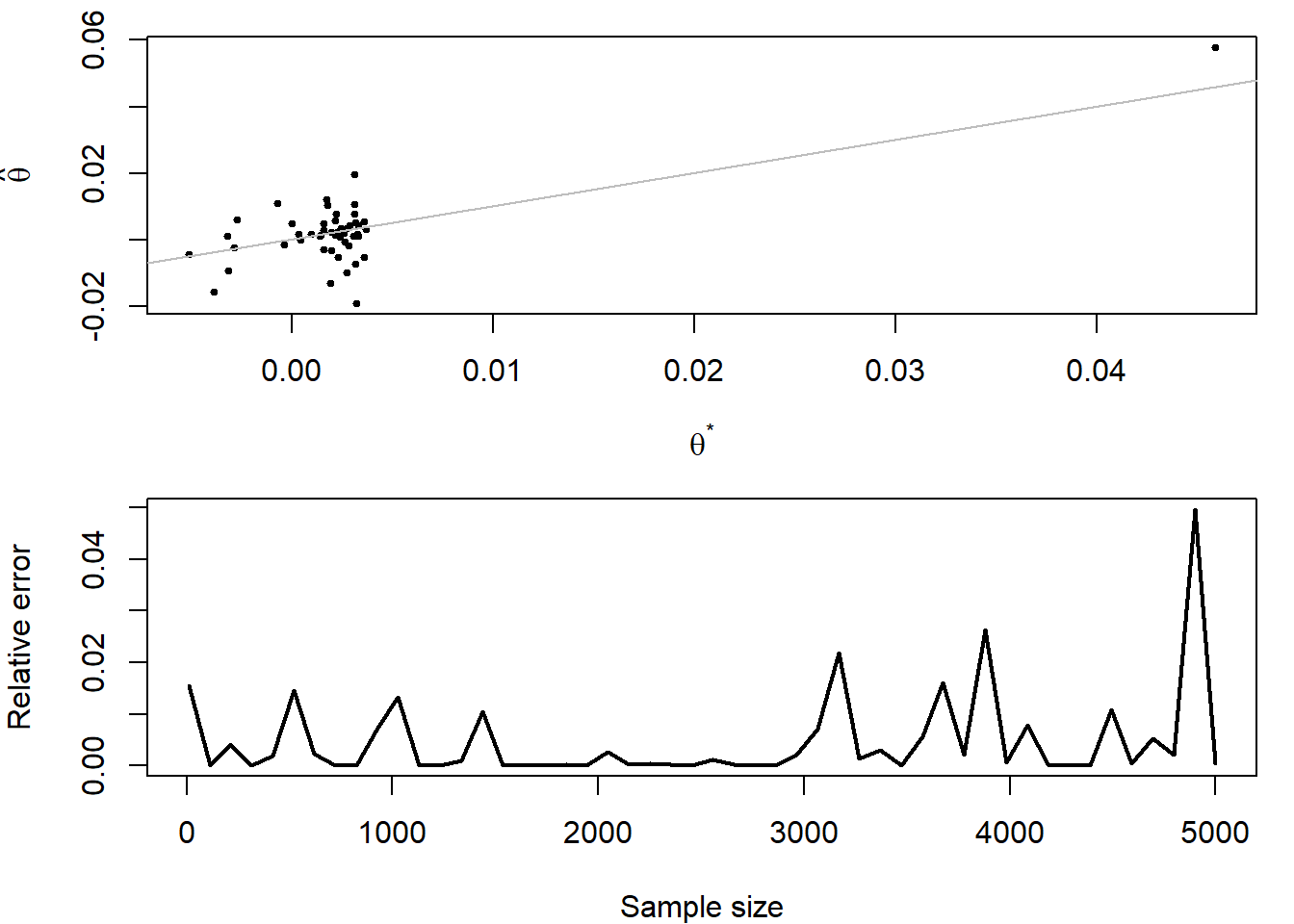
Εικόνα 5.8: Comparison of a numerical and a stochastic maximization of a Cauchy likelihood in terms of the sample size via (top) respective locations of the numerical and stochastic evaluations of the arguments, plotted along the diagonal; (bottom) relative error of the stochastic evaluation against the numerical evaluation as a function of the sample size.

Είναι επομένως ιδιαίτερα σημαντικό να σχεδιάζουμε πειράματα προσομοίωσης άμεσα συσχετισμένα με την υπό βελτιστοποίηση συνάρτηση \(h\), όπως και με τον χώρο \(\Theta\). Ενστικτωδώς, θέλουμε να προσομοιώνουμε με μεγάλη πιθανότητα από περιοχές όπου η \(h\) παίρνει μεγάλες τιμές και με μικρή πιθανότητα από περιοχές όπου η \(h\) παίρνει μικρές τιμές. Στην περίπτωση που η \(h\) είναι θετική και ολοκληρώσιμη, δηλαδή

\[\begin{equation*} \int_{\Theta} h(\theta) d\theta <+\infty, \end{equation*}\]

στόχος μας είναι να βρούμε τη συνάρτηση πυκνότητας \(f\) η οποία είναι ανάλογη ως προς την \(h\), δηλαδή \(f=c\cdot h\), όπου \(c\) η σταθερά κανονικοποίησης. Γενικότερα, κάθε σ.π.π. \(H\) η οποία έχει τα ίδια ολικά μέγιστα με την \(h\) αποτελεί μια ενδιαφέρουσα επιλογή, όπως για παράδειγμα η

\[\begin{equation*} H(\theta) \propto e^{h(\theta)/T}, \end{equation*}\]

για θετική σταθερά \(Τ\), τέτοια ώστε η \(H\) να είναι ολοκληρώσιμη. Η παράμετρος \(T\) ονομάζεται θερμοκρασία (temperature) και είναι ελεύθερη να επιλεγεί έτσι ώστε να επιταχύνουμε τη σύγκλιση ή να αποφύγουμε τα τοπικά μέγιστα, όπως θα συζητήσουμε στην πορεία. Για να επιλύσουμε λοιπόν το πρόβλημα μεγιστοποίησης της \(h\), θα προσομοιώσουμε ένα δείγμα \(\theta_1, \dots, \theta_m\) από την \(H\) και θα εκτιμήσουμε την κορυφή της \(h\). Σε μερικές περιπτώσεις θα είναι πιο πρακτικό να αναλύσουμε την \(H\) σε \(H(\theta)=H_1(\theta)\cdot H_2(\theta)\) και να προσομοιώσουμε μόνο από την \(H_1\). Σε στατιστικά προβλήματα, η \(h\) είναι συνήθως συνάρτηση πιθανοφάνειας και έτσι, η προσομοίωση από την \(h\) ταυτίζεται με την προσομοίωση από μία posterior κατανομή, όταν έχουμε μία επίπεδη prior.

Παράδειγμα 5.6 (Robert & Casella 5.5.) Συνεχίζοντας το παράδειγμα 5.1, θεωρώντας ομοιόμορφη prior στο διάστημα \([-5, 5]\), η συνάρτηση πιθανοφάνειας που θέλουμε να μεγιστοποιήσουμε μπορεί να ερμηνευθεί και ως posterior κατανομή του \(\theta\) (η posterior είναι ανάλογη της πιθανοφάνειας). Όμως, δεν μπορούμε να προσομοιώσουμε από αυτή την κατανομή, επομένως χρειαζόμαστε ένα υποκατάστατο. Καθώς το γινόμενο των σ.π.π. της Cauchy είναι το αντίστροφο ενός πολυωνύμου βαθμού \(2n\) (ως προς \(\theta\)), μπορούμε να επιλέξουμε την κατανομή Student με \((n-1)/2\) βαθμούς ελευθερίας με μέση τιμή την εμπειρική διάμεσο (καθώς η μέση τιμή της Cauchy δεν ορίζεται και ο δειγματικός μέσος της είναι ιδιαίτερα ασταθής) και παράμετρο κλίμακας κατάλληλη σταθερά. Όπως φαίνεται στο σχήμα 5.9, η κατανομή Student παρέχει μία πολύ ικανοποιητική προσέγγιση της posterior κατανομής γύρω από την κορυφή της.

Εικόνα 5.9: Comparison of the posterior density (in black) of a Cauchy location parameter based on 101 observations and a t approximation (dotted lines).

Όπως είναι αναμενόμενο, η στοχαστική εκτίμηση μέσω της Student συγκλίνει ταχύτερα από την αντίστοιχη μέσω ομοιόμορφης, όπως φαίνεται και στην εικόνα 5.10, όπου συγκρίνονται τα εύρη των δύο προσεγγίσεων, κατασκευασμένα από 100 μονοπατια κάθε μεθόδου.

Εικόνα 5.10: Comparison of the Cauchy mle stochastic estimation based on 500 independent paths of the uniform sampler and the Student sampler. The grey area is the range of the uniform estimator and the wheat area is the range of the student estimator.

Παράδειγμα 5.7 (Robert & Casella 5.6.) Επιθυμούμε να ελαχιστοποιήσουμε τη συνάρτηση \[\begin{equation*} h(x,y) = (x\sin(20y) +y\sin(20x))^2cosh(sin(10x)x) + (x\cos(10y)-y\sin(10x))^2cosh(cos(20y)y), \end{equation*}\] στο \(\mathbb{R}\), η οποία έχει ολικό μέγιστο \(h(0,0)=0\). Όπως φαίνεται στην εικόνα 5.11, η συνάρτηση αυτή δεν πληροί τις προϋποθέσεις των αριθμητικών μεθόδων που εξετάσαμε. Μπορούμε όμως να προσομοιώσουμε από την σ.π.π. που είναι ανάλογη της \(e^{-h(x,y)}\), με τον αλγόριθμο αποδοχής - απόρριψης προτείνοντας από την ομοιόμορφη κατανομή. Κάτι τέτοιο όμως, έρχεται σε αντιπαράθεση με το να επιδιώξουμε προσομοίωση από την \(h\) για να αποφύγουμε την ομοιόμορφη κατανομή. Θα δούμε στη συνέχεια πιο εξειδικευμένες μεθόδους MCMC που επιλύουν αυτό το πρόβλημα.

Εικόνα 5.11: Representation via persp of the highly multimodal function \(h(x,y), [-3, 3]^2\).

5.4 Στοχαστική Μέθοδος Κλίσης

Σε πολλές περιπτώσεις η άμεση προσομοίωση από την \(H\) είναι ιδιαίτερα δύσκολη, κάτι που μας οδηγεί στην ανάγκη να εξερευνήσουμε τον χώρο \(\Theta\) όχι τυχαία, αλλά με εξαρτημένα βήματα, ορίζοντας δηλαδή μία ακολουθία \(\{\theta_j\}_{j\in\mathbb{N}}\) και κινούμενοι από το \(\theta_j\) στο \(\theta_{j+1}\). Η εξάρτηση του \(\theta_{j+1}\) στο \(\theta_{j}\) συχνά επιλέγεται να είναι γραμμική, κάτι που μας δίνει την αναπαράσταση \[\begin{equation*} \theta_{j+1}=\theta_{j}+\epsilon_j, \end{equation*}\] όπου το \(\epsilon_j\) είναι ένας (μικρός) θόρυβος της παρούσας τιμής (τα \(\epsilon_i, \epsilon_j\) είναι ανεξάρτητες τ.μ. για \(i\neq j\)). Από την παραπάνω σχέση μπορούμε άμεσα να επαληθεύσουμε ότι η \(\{\theta_j\}_{j\in\mathbb{N}}\) είναι μία μαρκοβιανή αλυσίδα. Η κατανομή των \(\epsilon_j\) μπορεί να προσομοιωθεί από οποιαδήποτε κατανομή, όπως η \(\mathcal{N}_p(\sigma^2 I_p)\) αν \(\Theta\subset \mathbb{R}^p\). Παρ’ όλα αυτά, καθώς αναζητούμε το μέγιστο της \(h\), η χρήση κάποιας πληροφορίας σχετικής με την \(h\) στην επιλογή της κατανομής των \(\epsilon_j\), αναμένεται να αυξήσει την αποδοτικότητα του αλγορίθμου. Συγκεκριμένα, είναι λογικό να προτιμάμε κατευθύνσεις στις οποίες η \(h\) αυξάνεται και να αποφεύγουμε κατευθύνσεις στις οποίες η \(h\) μειώνεται (χωρίς τέτοιες κινήσεις να είναι αδύνατες, ώστε να μην παγιδευτούμε σε τοπικά μέγιστα). Μια λογική επιλογή είναι να χρησιμοποιήσουμε την κλίση \(\nabla h\), εάν αυτό είναι διαθέσιμο. Οι στοχαστικές μέθοδοι κλίσης εκμεταλλεύονται τη ντετερμινιστική μέθοδο κλίσης για να χτίσουν τον θόρυβο \(\epsilon_j\).

Η παραλλαγή της πεπερασμένης διαφοράς προτείνει να αντικαταστήσουμε την κλίση με το \[\begin{equation*} \nabla h(\theta_j) \approx \frac{h(\theta_j+\beta_j\zeta_j)-h(\theta_j-\beta_j\zeta_j)}{2\beta_j}\zeta_j = \frac{\Delta h(\theta_j, \beta_j \zeta_j)}{2\beta_j}\zeta_j, \end{equation*}\] όπου η \((\beta_j)\) είναι μία φθίνουσα ακολουθία και η \(\zeta_j\) είναι ομοιόμορφα κατανεμημένη στην μοναδιαία σφαίρα (\(||\zeta||=1\)). Σε αντίθεση με τη ντετερμινιστική προσέγγιση, η ανανέωση του \(\theta\) \[\begin{equation*} \theta_{j+1}=\theta_j +\frac{a_j}{2\beta_j}\Delta h(\theta_j, \beta_j, \zeta_j) \zeta_j, \tag{5.2} \end{equation*}\]

δεν προχωράει πάνω στην πιο απότομη κατεύθυνση της \(h\) στο \(\theta_j\) αφού κάθε φορά η κατεύθυνση τυχαία, αλλά αυτή η ιδιότητα μπορεί δυνητικά να λειτουργήσει θετικά, καθώς αποφεύγουμε να παγιδευτούμε σε τοπικά μέγιστα ή σαγματικά σημεία. Το αν η \(\{\theta_j\}_{j\in\mathbb{N}}\) συγκλίνει στο σημείο ολικού μεγίστου \(\theta^\star\) εξαρτάται από την επιλογή των ακολουθιών \(\{a_j\}_{j\in\mathbb{N}}\) και \(\{\beta_j\}_{j\in\mathbb{N}}\). Τα \(a_j\) πρέπει να φθίνουν αρκετά αργά στο 0 ώστε η σειρά \(\sum_j a_j\) να αποκλίνει, ενώ τα \(\beta_j\) πρέπει να φθίνουν ακόμα πιο αργά ώστε η σειρά \(\sum_k (a_j/\beta_j)^2\) να συγκλίνει (Spall, 2003, Chapter 6).

Παράδειγμα 5.8 (Robert & Casella 5.7.) Εφαρμόζουμε τη μέθοδο (5.2) στη συνάρτηση \(h(x,y)\) με διαφορετικές ακολουθίες \(\{a_j\}_{j\in\mathbb{N}}\) και \(\{\beta_j\}_{j\in\mathbb{N}}\). Ένας λογικός κανόνας τερματισμού του αλγορίθμου είναι να ελέγχουμε τη σταθεροποίηση της ακολουθίας \(\theta_j\). Οι τέσσερεις διαφορετικές ακολουθίες που επιλέχθηκαν ήταν:

1. \(a_j=1/\log (j+1), \beta_j=1/\log (j+1)^{0.1}\),
2. \(a_j=1/100\log (j+1), \beta_j=1/\log (j+1)^{0.1}\),
3. \(a_j=1/(j+1), \beta_j=1/(j+1)^{0.5}\),
4. \(a_j=1/(j+1), \beta_j=1/(j+1)^{0.1}\).

Σε αυτό το σημείο, παρατηρούμε ότι η ακολουθία των \(b_j\) φθίνει πολύ πιο αργά από την ακολουθία των \(a_j\) σε όλα τα σενάρια. Για ακολουθίες \(\{\beta_j\}_{j\in\mathbb{N}}\) που φθίνουν ταχύτερα, η μέθοδος δεν συγκλίνει απαραίτητα στο ολικό ελάχιστο. Η εικόνα 5.12 παρουσιάζει μία πραγματοποίηση κάθε σεναρίου. Στην περίπτωση του σεναρίου 1, τα \(\theta_j\) δε σταθεροποιούνται αρκετά γρήγορα ώστε να παραμείνουν στο ολικό ελάχιστο, ενώ διαιρώντας την \(a_j\) με το 100 (οπότε τα \(a_j\) και τα \(b_j\) φθίνουν πολύ αργά) οδηγεί σε μία ακολουθία \(\{\theta_j\}_{j\in\mathbb{N}}\) που αδυνατεί να φτάσει το ολικό ελάχιστο. Για τα σενάρια 3 και 4 παρατηρούμε ότι εντοπίζουν το ολικό ελάχιστο και η διαφορά στον εκθέτη των \(b_j\) δεν επηρεάζει σημαντικά το αποτέλεσμα.

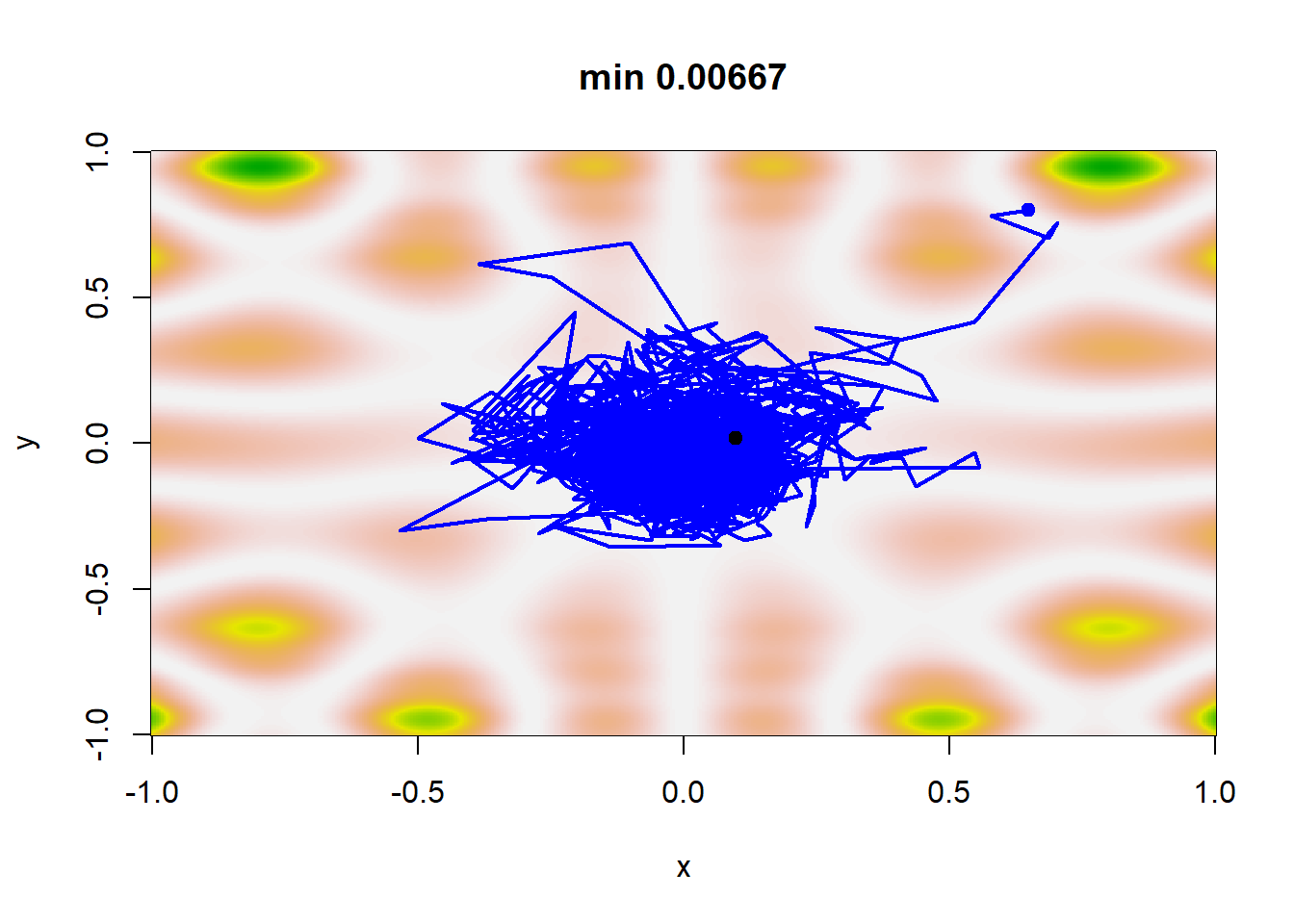
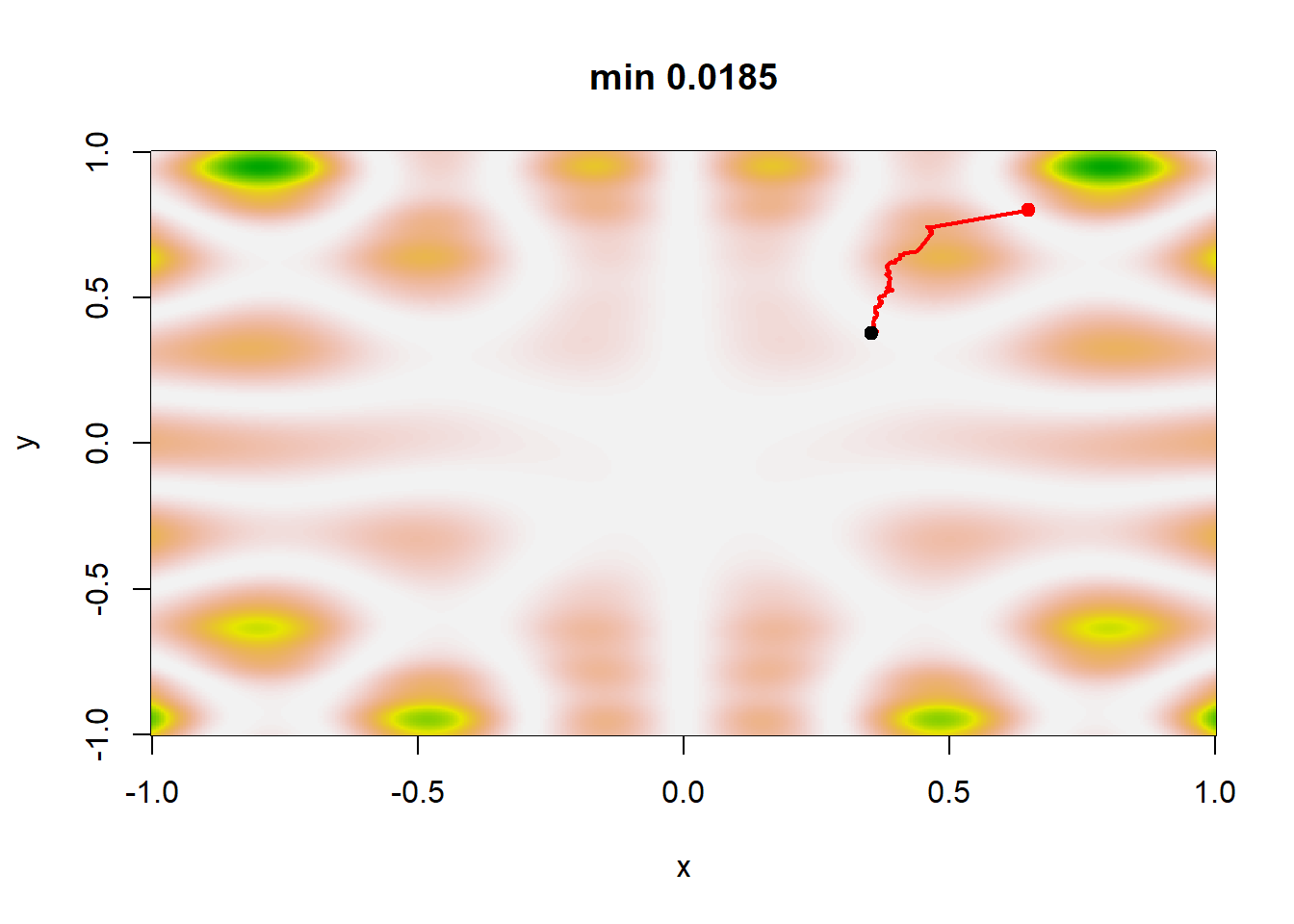
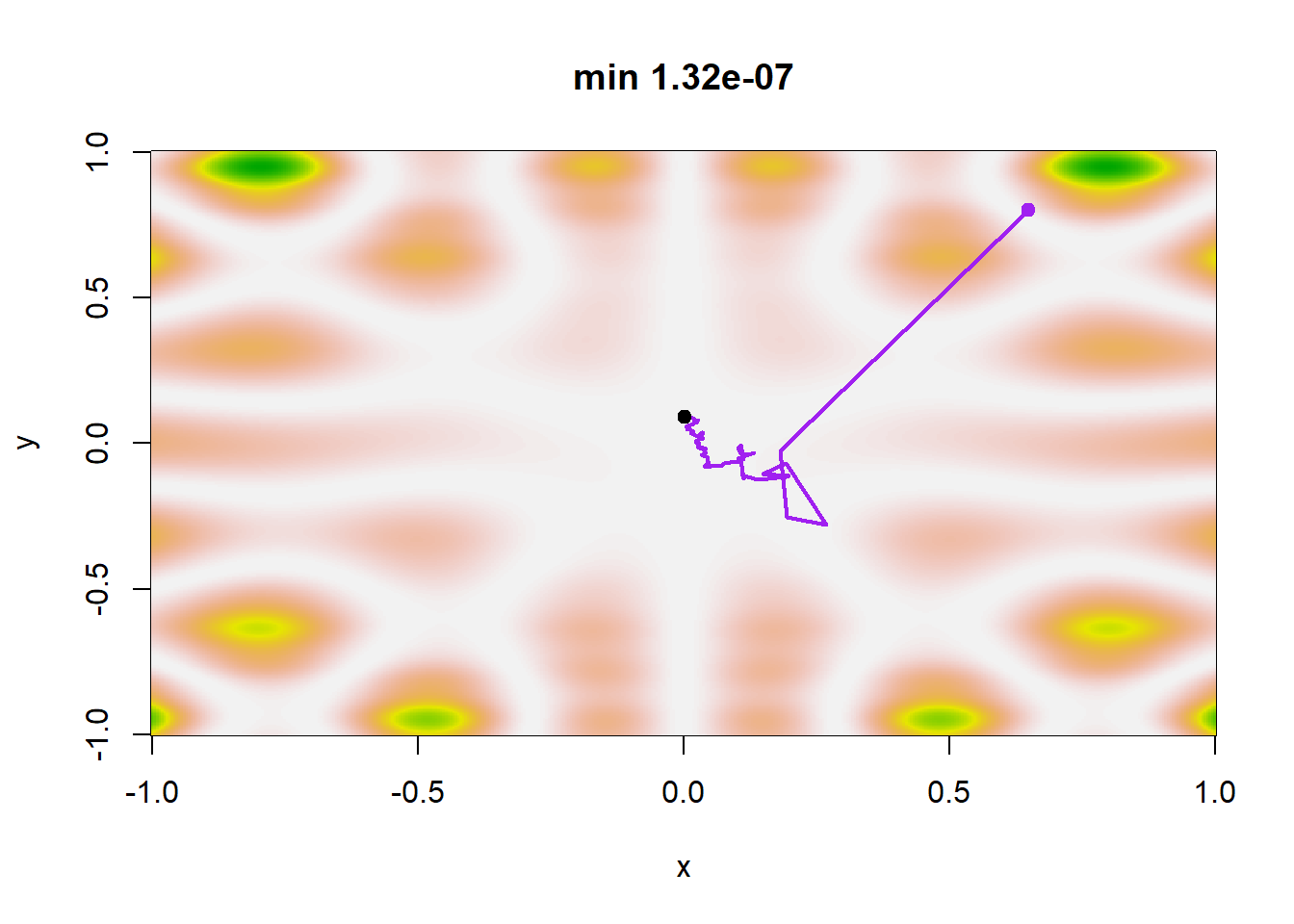
Εικόνα 5.12: Single realizations of stochastic gradient paths for four different choices of the sequences \(a_j\) and \(\beta_j\) with the same starting point (0.65, 0.8): Scenario 1 corresponds to \((a_j, \beta_j) = (1/100 log(j + 1), 1/ log(j + 1)^{0.1})\), scenario 2 corresponds to \(a_j=1/100log (j+1), \beta_j=1/log (j+1)^{0.1}\), scenario 3 corresponds to \(a_j=1/(j+1), \beta_j=1/(j+1)^{0.5}\), and scenario 4 corresponds to \(a_j=1/(j+1), \beta_j=1/(j+1)^{0.1}\). The function h to be minimized is defined in Example 5.6 and the minimum of h is achieved at the central point (0, 0).

5.5 Simulated Annealing

---

Αλγόριθμος: Simulated Annealing

Στην επανάληψη \(t\),

1. Προσομοιώνουμε \(\zeta\sim g(\zeta)\);
2. Δεχόμαστε \(\theta_{t+1}=\theta_t+\zeta\) με πιθανότητα \(p_t=min\{e^{\Delta h_t/T_t}, 1\}\), αλλιώς παίρνουμε \(\theta_{t+1}=\theta_t\).

---

Άσκηση 5.1 (Robert & Casella 5.6.) Για την πιθανοφάνεια της Cauchy που μελετήθηκε στο παράδειγμα 5.1., δείξτε ότι η ψευδο-posterior κατανομή \[\begin{equation*} \pi_m(\theta|x) \propto \ell(\theta|x)^m, \end{equation*}\] συγκεντρώνεται γύρω από ένα σημείο καθώς το \(m\) αυξάνεται.

theta <- rep(theta0, Nsim)
hcur <- h(theta0)
xis <- randg(Nsim)
for (t in 2:Nsim) {
    prop <- theta[t - 1] + xis[t]
    hprop <- h(prop)
    if (Temp[t] * log(runif(1)) < hprop - hcur) {
        theta[t] <- prop
        hcur <- hprop
    } else {
        theta[t] <- theta[t - 1]
    }
}

Παράδειγμα 5.9 (Robert & Casella 5.8.) Για τη συνάρτηση \(h(x)=[\cos(50x)+\sin(20x)]^2, x\in[0,1]\), μπορούμε να συγκρίνουμε την επίδραση των διαφορετικών θερμοκρασιών \(T_t\) στις προσομοιωμένες ακολουθίες. Σημειώνουμε εδώ ότι πέρα από την ακολουθία των \(T_t\), πρέπει να ορίσουμε την κατανομή \(g\) και ένα κανόνα τερματισμού. Καθώς εδώ το πεδίο ορισμού της \(h\) είναι το διάστημα \([0,1]\), χρησιμοποιούμε την κατανομη \(Unif(-p, p)\), ενώ ο αλγόριθμος τερματίζει όταν το παρατηρήσιμο μέγιστο της \(h\) δεν έχει αλλάξει για το τελευταίο μισό της ακολουθίας \(\{x_t\}\). Ο αλγόριθμος αυτός στην R μπορεί να υλοποιηθεί ως εξής:

x <- runif(1)
hval <- hcur <- h(x)
diff <- iter <- 1

while (diff > 10 ^ (-4)) {
    prop <- x[iter] + runif(1, -1, 1) * scale
    if ((prop > 1) || (prop < 0) || (log(runif(1)) * temp[iter] > h(prop) - hcur)) {
      prop <- x[iter]
    }
    x <- c(x, prop)
    hcur <- h(prop)
    hval <- c(hval, hcur)
    if ((iter > 10) && (length(unique(x[(iter / 2):iter])) > 1))
    diff <- max(hval) - max(hval[1:(iter / 2)])
    iter <- iter + 1
}

Παρατηρούμε εδώ ότι ο περιορισμός που θέλει το unique ακυρώνει τον κανόνα τερματισμού όταν καμία τιμή διαφορετική της παρούσης δεν έχει γίνει αποδεκτή για το δεύτερο μισό των επαναλήψεων, κάτι που υποδεικνύει ότι η scale μπορεί είναι ακατάλληλη. Επιπλέον, παρατηρούμε ότι η ανανέωση των temp και scale πρέπει να συμπεριλαμβάνονται μέσα στο επαναληπτικό κομμάτι του κώδικα (loop).

Για κλίμακα (scale) \(\sqrt{T_t}\) και μείωση θερμοκρασίας \(1/\log(1+t)\), η ακολουθία σχεδόν πάντα καταλήγει σε μία τιμή κοντά στο πραγματικό μέγιστο. Παρόμοια αποτελέσματα ισχύουν για κλίμακα \(5\sqrt{T_t}\) και μείωση θερμοκρασίας \(1/(1+t)^2\), όπως φαίνεται στην εικόνα 5.13. Η μείωση της κλίμακας κατά παράγοντα του 10 έχει καθαρά αρνητική επίδραση στην αποτελεσματικότητα του αλγορίθμου.

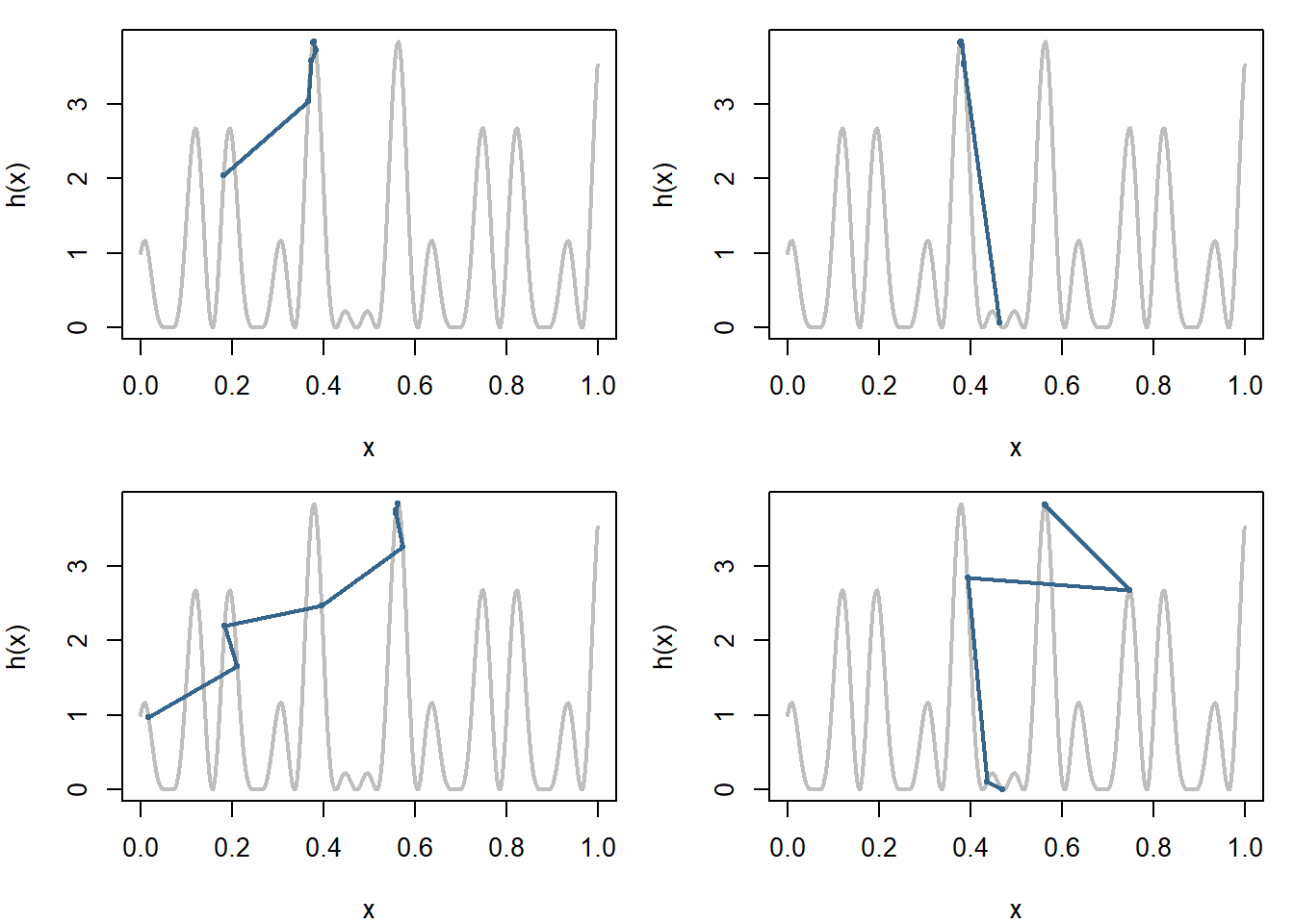
Εικόνα 5.13: Realizations of four simulated annealing sequences for \(T_t=1/(t+1)^2\) and \(p=5\sqrt{T_t}\) over the graph of the function \(h\) (grey). Note that the points represented on the graph of h correspond to successive accepted values in Algorithm 2 and do not reflect the number of iterations.

Παράδειγμα 5.10 (Robert & Casella 5.9.) Χρησιμοποιώντας την ίδια μίξη κανονικών κατανομών με το παράδειγμα 5.2., μπορούμε να υλοποιήσουμε τον αλγόριθμο simulated annealing στην R, όπως φαίνεται παρακάτω:

SA <- function(x) {
  temp <- scale <- iter <- dif <- factor <- 1
  the <- matrix(x, ncol = 2)
  curlike <- hval <- like(x)
  while (dif > 10 ^ (-4)) {
    prop <- the[iter, ] + rnorm(2) * scale[iter]
    if ((max(-prop) > 2) || (max(prop) > 5) || (temp[iter] * log(runif(1)) > - like(prop) + curlike)) {
      prop <- the[iter, ]
    }
    curlike <- like(prop)
    hval <- c(hval, curlike)
    the <- rbind(the, prop)
    iter <- iter + 1
    temp <- c(temp, 1 / 10 * log(iter + 1))
    ace <- length(unique(the[(iter / 2):iter, 1]))
    if (ace==1) {
      factor <- factor / 10
    }
    if (2 * ace > iter) {
      factor <- factor * 10
    }
    scale <- c(scale, max(2, factor * sqrt(temp[iter])))
    dif <- (iter < 100) + (ace < 2) + (max(hval) - max(hval[1:(iter / 2)]))
    }
    list(theta = the, like = hval, ite = iter)
}

Όπως φαίνεται στην εικόνα 5.14, το αποτέλεσμα είναι ιδιαίτερα ικανοποιητικό. Οι περισσότερες ακολουθίες καταλήγουν σε μία κοντινή γειτονιά του σημείου μεγίστου. Ενδιαφέρον παρουσιάζει η φαινομενική αδιαφορία των ακολουθιών ως προς την εγκύτητα ενός τοπικού μεγίστου, υπό την έννοια ότι συχνά επισκέπτονται πρώτα το άλλο ακρότατο προτού συγκλίνουν.

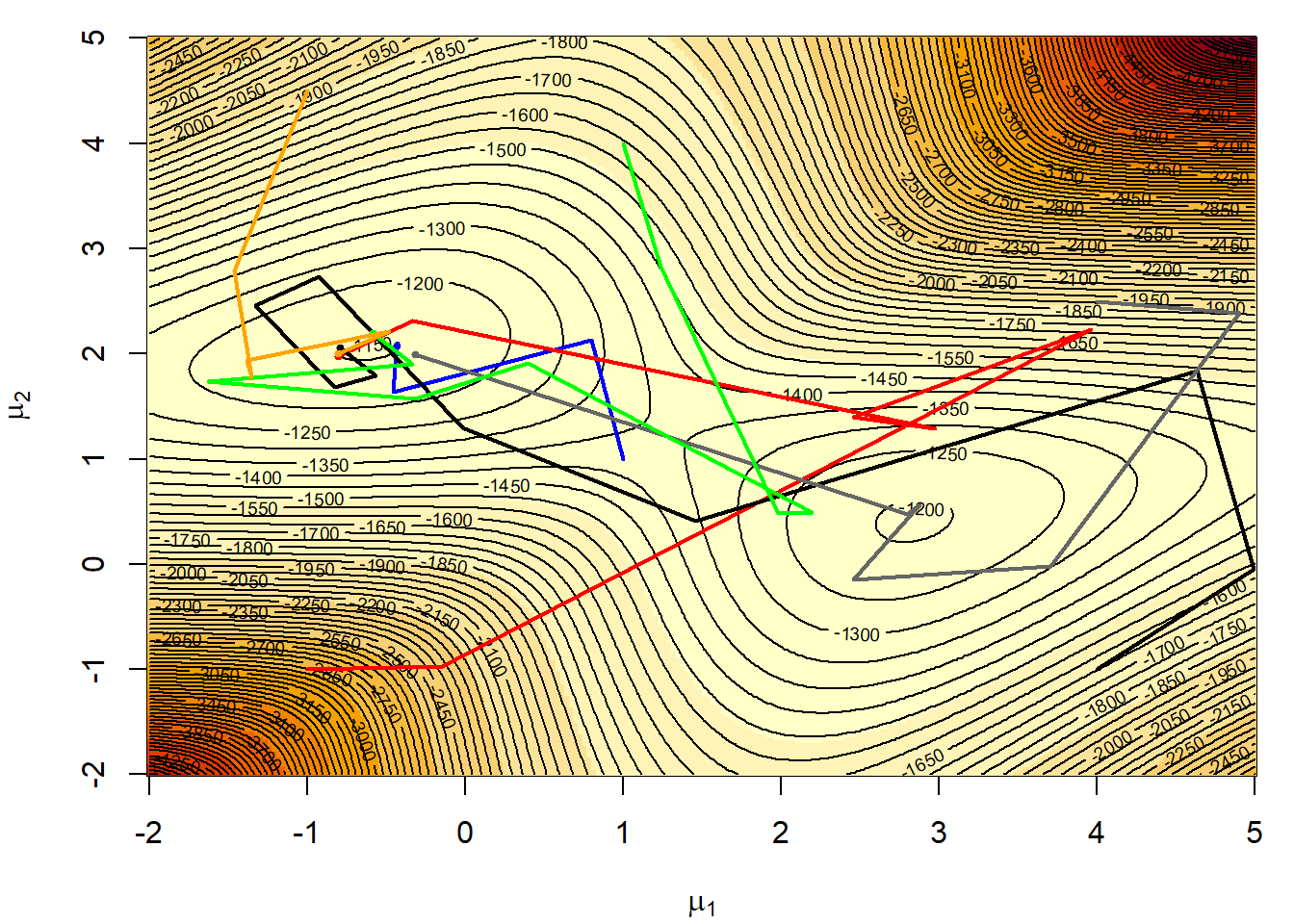
Εικόνα 5.14: Six simulated annealing sequences for a temperature schedule \(T_t=1/\log(1+t)\) based on a sample of 400 observations from the normal mixture (5.2) with \(\mu_1=0\) and \(\mu_2=2.5\).

Παράδειγμα 5.11 (Robert & Casella 5.10.) Μπορούμε να εφαρμόσουμε τον ίδιο αλγόριθμο και στη συνάρτηση \(h\) του παραδείγματος 5.6., επιλέγοντας την τ.μ. θορύβου να είναι κανονική και την κλίμακα να βασίζεται στην παρούσα θερμοκρασία (όπου η μεταβλητή factor εξαρτάται από το ποσοστό αποδοχής του αλγορίθμου.

prop <- the[iter, ] + scale[iter] * rnorm(2)
scale <- min(.1, 5 * factor * sqrt(temp[iter]))

Όπως φαίνεται στην εικόνα 5.15, τα αποτελέσματα αλλάζουν με το ρυθμό μείωσης της θερμοκρασίας \(Τ\), τόσο ως προς το ελάχιστο, όσο και ως προς το μοτίβο εξερεύνησης των κοιλάδων της \(h\).

# highly multimodal function to maximise
h <- function(x) {
  - (x[1] * sin(20 * x[2]) + x[2] * sin(20 * x[1])) ^ 2 * cosh(sin(10 * x[1]) * x[1])
  - (x[1] * cos(10 * x[2]) - x[2] * sin(10 * x[1])) ^ 2 * cosh(cos(20 * x[2]) * x[2])
}

ha <- function(x, y){
  - (x * sin(20 * y) + y * sin(20 * x)) ^ 2 * cosh(sin(10 * x) * x)
  - (x * cos(10 * y) - y * sin(10 * x)) ^ 2 * cosh(cos(20 * y) * y)
}

# Simulated Annealing
annealing <- function(temper) {
  temper <- match.fun(temper)

  #SA version
  start <- c(.65,.8)
  the <- matrix(start,ncol = 2)
  temp <- scale <- dif <- iter <- factor <- 1
  hcur <- hval <- h(start)
  
  while (dif > 10 ^ -5) {
    prop <- the[iter, ] + scale[iter] * rnorm(2)
    while (max(abs(prop)) > 1) {
      prop <- the[iter, ] + scale[iter] * rnorm(2) 
    }
    
    if (temp[iter] * log(runif(1)) > h(prop) - hcur) {
      prop <- the[iter, ]
    }
    
    hcur <- h(prop)
    the <- rbind(the, prop)
    hval <- c(hval, hcur)
    iter <- iter + 1
    temp <- c(temp, temper(iter))
    ace <- length(unique(the[(iter / 2):iter, 1]))
    
    if (iter > 100){
      if (ace == 1) {
        factor <- factor / 10
      }
      if (2.5 * ace > iter) {
        factor <- min(.1, factor * 10)
      }
    }
    scale <- c(scale, min(.1, 5 * factor * sqrt(temp[iter])))
    dif <- (iter < 10 ^ 3) + (ace < 2) + (max(hval) - max(hval[1:(iter / 2)]))
  }
  
  the
}

# Plots
set.seed(141)
x <- y <- seq(-1, 1, le = 435)
z <- outer(x, y, ha)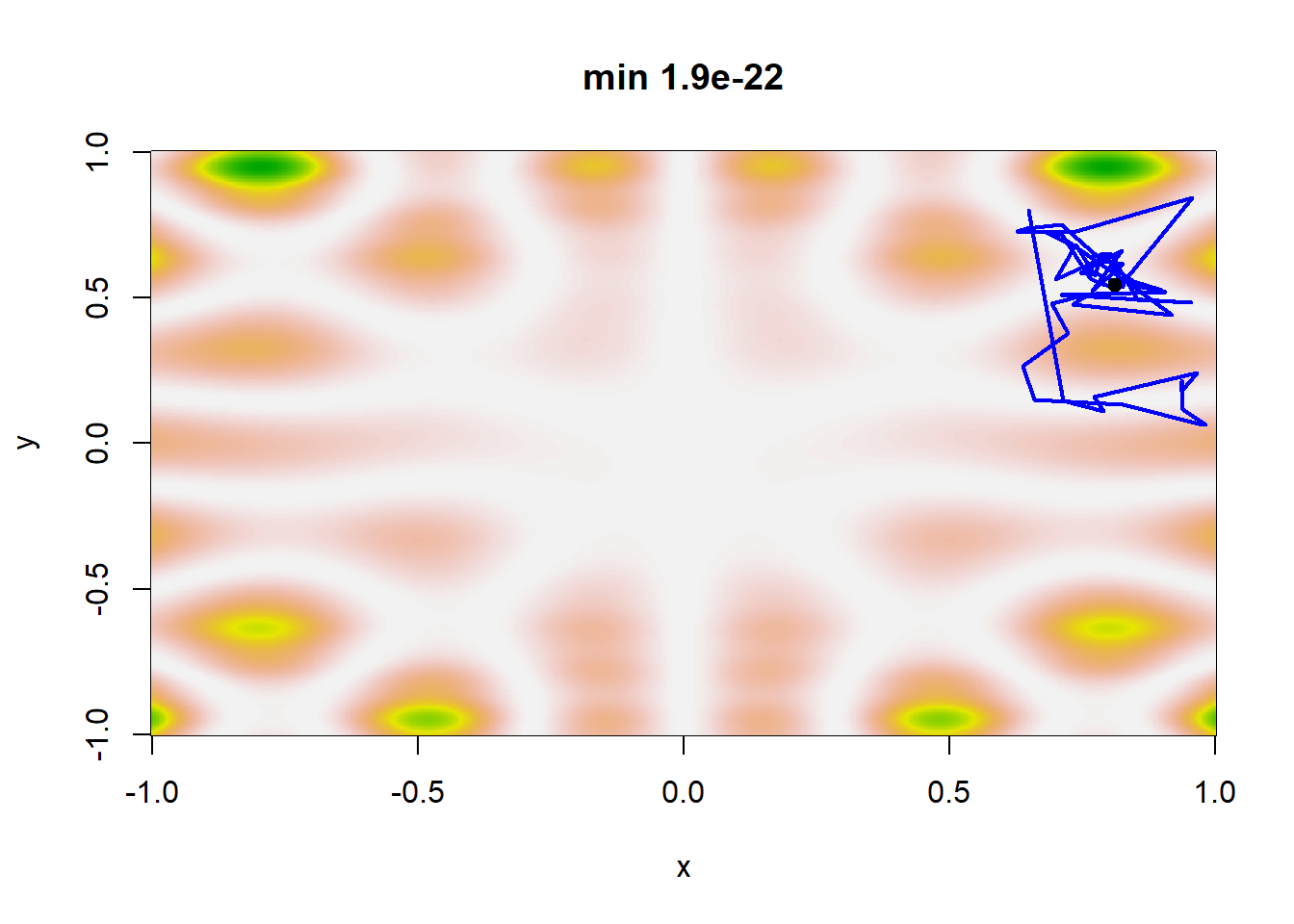

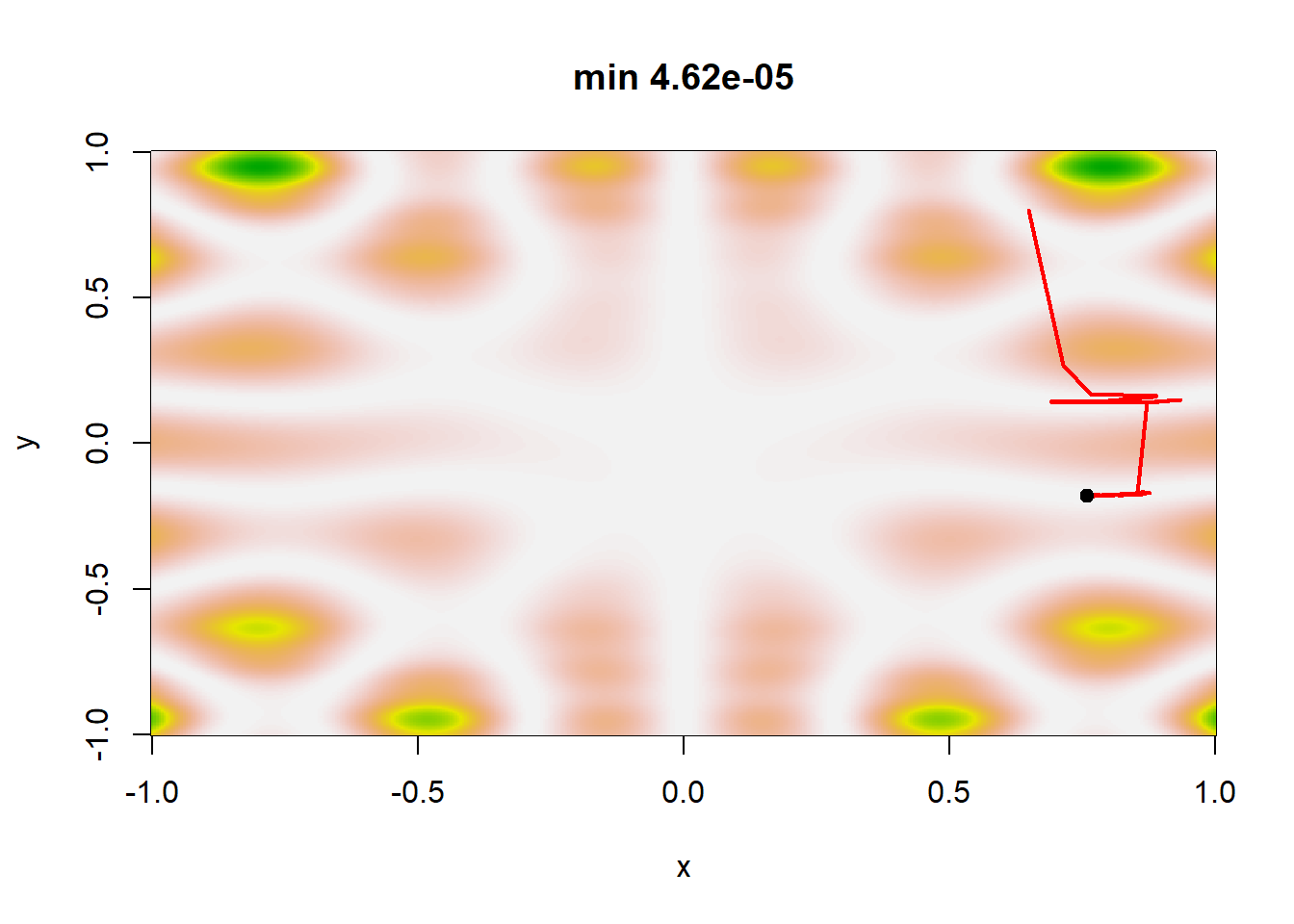
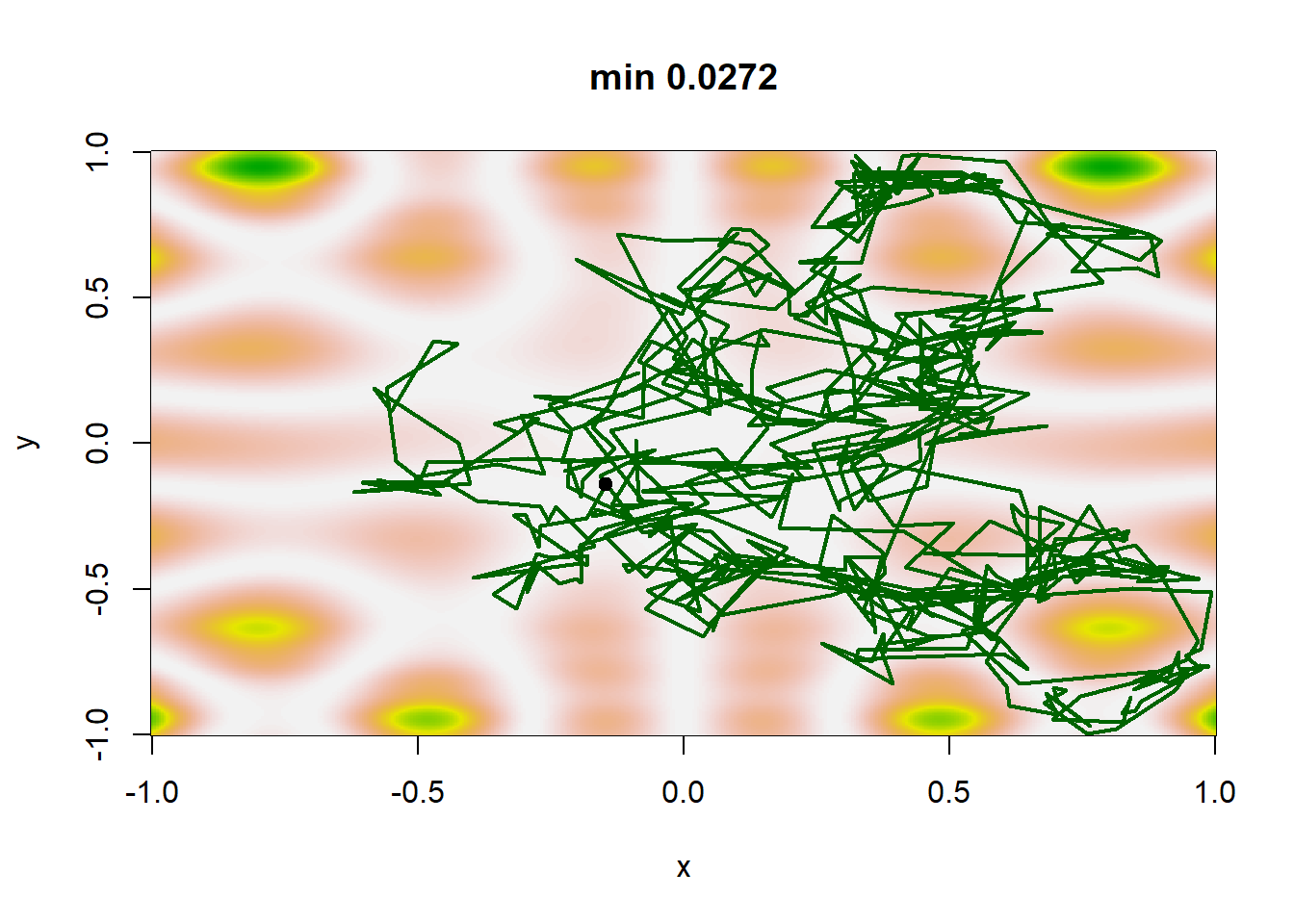
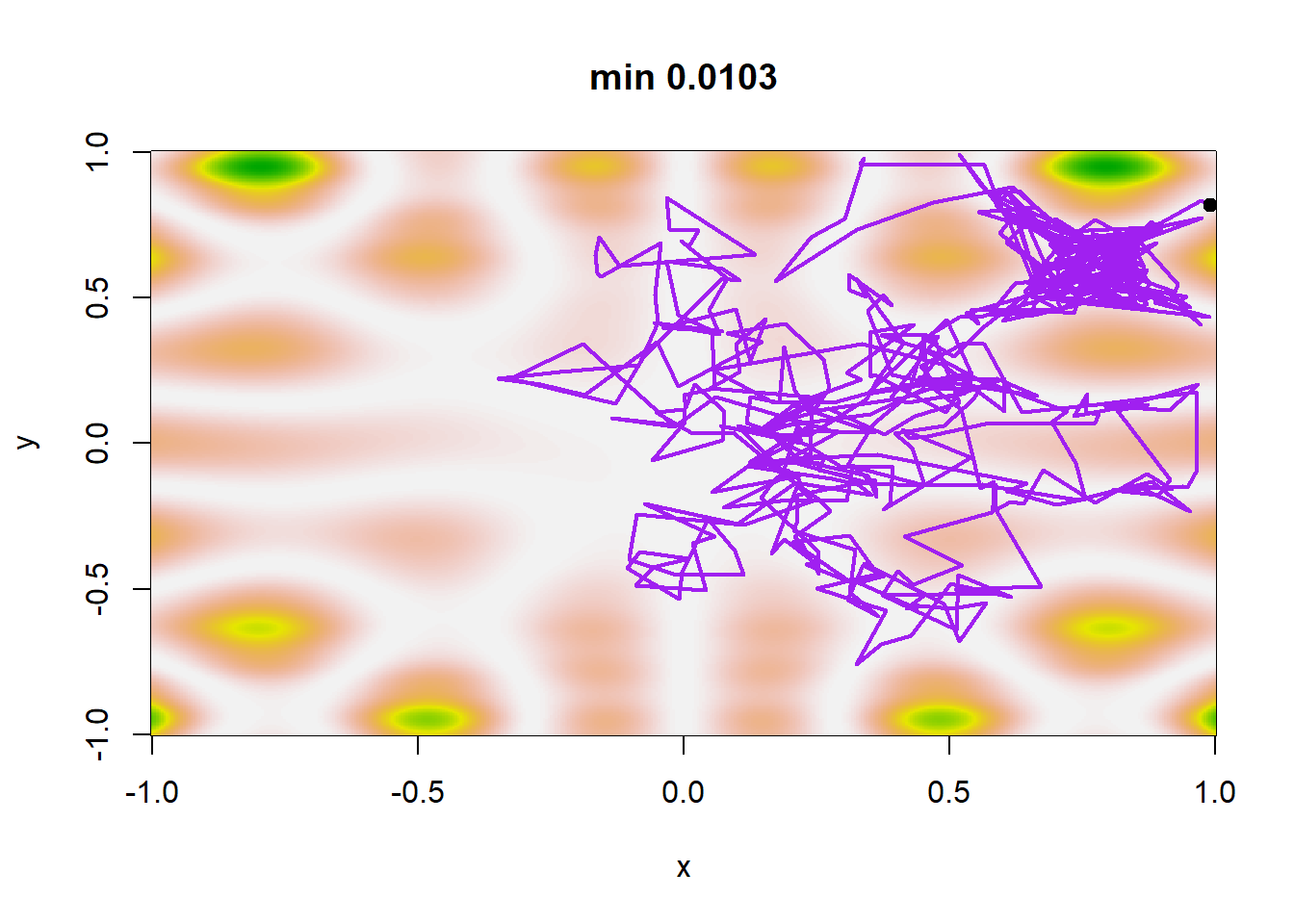
Εικόνα 5.15: Simulated annealing sequences for four temperature schedules: \(T_t=0.95^t\), \(T_t=1/10(t+1)\), \(T_t=1/\log(1+t)\) and \(T_t=1/10\sqrt{\log(1+t)}\) and starting point \((0.65, 0.8)\), aimed at minimizing the function \(h\) of Example 5.6. The light dot on top of the sequence corresponds to the final stage of the sequence \(\{\theta_t\}\) and not necessarily the minimizer of \(h\).

5.6 Στοχαστική Προσέγγιση

Στην ενότητα αυτή θα κάνουμε μία εισαγωγή σε μεθόδους που επικεντρώνονται στη συνάρτηση ενδιαφέροντος \(h\) και όχι στην εξερεύνηση του χώρου \(\Theta\). Μιλώντας ελεύθερα, οι μέθοδοι αυτοί εκμεταλλεύονται την προσομοίωση για να προσεγγίσουν τη συνάρτηση \(h\), κάτι που όμως εισάγει ένα επιπλέον είδος σφάλματος που οφείλεται στην προσέγγιση της \(h\). Σε πολλά στατιστικά προβλήματα μπορούμε να εκφράσουμε την υπό βελτιστοποίηση συνάρτηση \(h\) στη μορφή

\[\begin{equation*} h(x)=\mathbf{E}\left(H(x,Z)\right). \end{equation*}\]

Σε αυτό το πλαίσιο ανήκουν τα μοντέλα ελλιπών δεδομένων (missing-data models) στα οποία η πιθανοφάνεια μπορεί να εκφραστεί ως

\[\begin{equation*} g(x|\theta) = \int_{\mathcal{Z}} f(x,z|\theta) dz. \end{equation*}\]

Η παραπάνω αναπαράσταση της \(g\) ως το ολοκλήρωμα μιας πιο εύκολα διαχειρίσιμης \(f\) συχνά ονομάζεται αποπεριθωριοποίηση (demarginalization) και αποτελεί ένα χρήσιμο υπολογιστικό εργαλείο. Προτού προχωρήσουμε, ας μελετήσουμε το πρόβλημα της μεγιστοποίησης μιας προσέγγισης της \(h\).

5.6.1 Βελτιστοποίηση Monte Carlo Προσεγγίσεων

Αν η \(h(x)\) μπορεί να γραφεί ως \(\mathbf{E}\left(H(x,Z)\right)\), αλλά δεν είναι δυνατόν να την υπολογίσουμε άμεσα, μία φυσική monte carlo προσέγγιση είναι η

\[\begin{equation*} \widehat{h}(x) = \frac{1}{m} \sum_{i=1}^m H(x, z_i), \end{equation*}\]

όπους τα \(Z_i\) προσομοιώνονται από τη δεσμευμένη κατανομή \(f(z|x)\). Η εκτιμήτρια αυτή συγκλίνει στην \(h(x)\) για κάθε \(x\) με πιθανότητα 1, δεν είναι όμως μία εκτιμήτρια που προτείνεται στα πλαίσια της βελτιστοποίησης, καθώς δεν μπορούμε να χρήσιμοποιήσουμε ένα κοινό δείγμα \(Z_i\) για την προσέγγιση διαφορετικών τιμών \(x\). Τα \(Z_i\) προκύπτουν από την κατανομή \(f(z|x)\), επομένως για διαφορετικές τιμές του \(x\) χρειαζόμαστε διαφορετικά δείγματα από τις \(Z_i\), με αποτέλεσμα να εισάγεται επιπλέον θόρυβος στην εκτίμηση των τιμών της \(h\).

Παράδειγμα 5.12 (Robert & Casella 5.11.) Θα μελετήσουμε ένα σετ δεδομένων που αφορά την φυλή Ινδιάνων Akimel O’odham (“River People”), γνωστοί και ως Pima. Συγκεκριμένα, θα προβλέψουμε την πιθανότητα εμφάνισης διαβήτη σε ένα άτομο με βάση το BMI του (Body Mass Index), το οποίο για βάρος \(w\) μετρημένο σε κιλά και ύψος \(h\) μετρημένο σε μέτρα υπολογίζεται ως

\[\begin{equation*} BMI=\frac{w}{h^2}. \end{equation*}\]

Για να μελετήσουμε τη σύνδεση των δύο αυτών μεταβλητών θα χρησιμοποιήσουμε το μοντέλο probit. Για το άτομο \(i\), θέτουμε \(y_i\) την τ.μ. που υποδηλώνει την παρουσία (\(y_i=1\)) ή απουσία (\(y_i=0\)) διαβήτη και \(x_i\) το BMI του. Έπομένως έχουμε \(y_i|x_i\sim Bin(1, p_i)\) και το γενικευμένο μοντέλο μας παίρνει τη μορφή

\[\begin{equation*} p_i = \mathbf{Ε}\left(y_i|x_i\right) = \Phi(\beta_0+\beta_1 x_i), i=1, 2, \dots, n. \end{equation*}\]

Πίνακας 5.1: Table 1: Part of the Pima Indians dataset.

bmi	type
30.2	No
25.1	Yes
35.8	No
47.9	No
26.4	No
35.6	Yes

Τρέχουμε στην R το μοντέλο και παίρνουμε τα αποτελέσματα:

# Probit GLM
model <- glm(type ~ bmi, data = Pima.tr, family = binomial(link = "probit"))

# Results
summary(model)
## 
## Call:
## glm(formula = type ~ bmi, family = binomial(link = "probit"), 
##     data = Pima.tr)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -1.5788  -0.9242  -0.6442   1.2506   1.9661  
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)    
## (Intercept) -2.54303    0.54211  -4.691 2.72e-06 ***
## bmi          0.06479    0.01615   4.011 6.05e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 256.41  on 199  degrees of freedom
## Residual deviance: 239.55  on 198  degrees of freedom
## AIC: 243.55
## 
## Number of Fisher Scoring iterations: 4

Παρατηρούμε ότι τόσο ο σταθερός όρος (intercept) \(\beta_0\), όσο και ο συντελεστής \(\beta_1\) του BMI είναι στατιστικά σημαντικοί (διάφοροι του μηδενός), μπορούμε επομένως να δηλώσουμε ότι προσφέρουν ουσιαστική πληροφορία στο μοντέλο μας. Αποθηκεύουμε σε μεταβλητές τις εκτιμήσεις \(\widehat{\beta_0}, \widehat{\beta_1}\), καθώς και τα εκτιμημένα τυπικά σφάλματα \(s_{\beta_0}, s_{\beta_1}\).

m0 <- -4.1 ; sd0 <- 0.93
m1 <- +0.1 ; sd1 <- 0.03

Υπό το πρίσμα της Μπεϋζιανής στατιστικής, οι παράμετροι \(\beta_0, \beta_1\) είναι τυχαίες μεταβλητές και το ενδιαφέρον στρέφεται στον προσδιορισμό της κατανομής τους. Θεωρούμε λοιπόν τις prior κατανομές \(f(\beta_0), f(\beta_1)\), με \(\beta_0, \beta_1\) ανεξάρτητα. Η επιλογή μίας επίπεδης prior κατανομής είναι κλασική όταν δεν έχουμε πραγματικά γνώση για την κατανομή των μεταβλητών. Έχοντας ορίσει \(y_i|x_i\sim Bin(1, p_i)\), ο υπολογισμός της συνάρτησης πιθανοφάνειας γίνεται άμεσα

\[\begin{align*} L(\beta_0, \beta_1) &= f(y_1, y_2,\dots, y_n|x_1, x_2,\dots, x_n, \beta_0, \beta_1) = \prod_{i=1}^n f(y_i|x_i, \beta_0, \beta_1) = \prod_{i=1}^n \Phi(\beta_0+\beta_1 x_i)^{y_i} \cdot (1-\Phi(\beta_0+\beta_1 x_i))^{1-y_i} \\ &= \prod_{i=1}^n \Phi(\beta_0+\beta_1 x_i)^{y_i} \cdot \Phi(-\beta_0-\beta_1 x_i)^{1-y_i} \end{align*}\]

Τέλος, μπορούμε να υπολογίσουμε, μέχρι μίας σταθεράς κανονικοποίησης, την posterior κατανομή των \(\beta_0, \beta_1\)

\[\begin{equation*} f(\beta_0, \beta_1 | y_{1:n}, x_{1:n}) = \frac{f(y_{1:n} | x_{1:n}, \beta_0, \beta_1) \cdot f(\beta_0, \beta_1)}{f( y_{1:n}| x_{1:n})} = c \cdot L(\beta_0, \beta_1). \end{equation*}\]

Ας υποθέσουμε ότι μας ενδιαφέρει η περιθώρια posterior κατανομή του \(\beta_0\) και συγκεκριμένα το μέγιστο αυτής. Έχουμε λοιπόν

\[\begin{equation*} f(\beta_0 | y_{1:n}, x_{1:n}) = \int_\mathbb{R} f(\beta_0, \beta_1 | y_{1:n}, x_{1:n}) d\beta_1 = \int_\mathbb{R} c\cdot L(\beta_0, \beta_1) d\beta_1 = c \int_\mathbb{R} \frac{L(\beta_0, \beta_1)}{f(\beta_1|\beta_0, y_{1:n}, x_{1:n})} f(\beta_1|\beta_0, y_{1:n}, x_{1:n}) d\beta_1, \end{equation*}\]

και άρα

\[\begin{equation*} f(\beta_0 | y_{1:n}, x_{1:n}) = c \cdot \mathbf{E}_{\beta_1|\beta_0}\left(H(\beta_0, \beta_1)\right), \end{equation*}\]

όπου

\[\begin{equation*} H(\beta_0, \beta_1) = \frac{L(\beta_0, \beta_1)}{f(\beta_1|\beta_0, y_{1:n}, x_{1:n})}. \end{equation*}\]

Θέτοντας λοιπόν

\[\begin{equation*} h(\beta_0)=f(\beta_0 | y_{1:n}, x_{1:n})= c \cdot \mathbf{E}_{\beta_1|\beta_0}\left(H(\beta_0, \beta_1)\right), \end{equation*}\]

παρατηρούμε ότι είμαστε στο πλαίσιο που συζητήσαμε παραπάνω. Η \(h\) δεν μπορεί να γραφεί αναλυτικά, όπως δεν μπορεί ούτε η δεσμευμένη κατανομή του \(\beta_1|\beta_0\). Επομένως θα χρησιμοποιήσουμε δειγματοληψία σπουδαιότητας, προτείνοντας από την \(\mathcal{T}_5(0.1, 0.03^2)\), όπου \(\mu_1=0.1, s_1=0.03\) οι εκτιμήσεις που προέκυψαν από το glm. Έτσι, θέτοντας \(t_5\) την σ.π.π. της κατανομής Student, έχουμε

\[\begin{equation*} \mathbf{E}_{\beta_1|\beta_0}\left(H(\beta_0, \beta_1)\right) = \mathbf{E}_{t_5}\left(w(\beta_1) H(\beta_0, \beta_1)\right) = \mathbf{E}_{t_5}\left( \frac{f(\beta_1|\beta_0, y_{1:n}, x_{1:n})}{t_5(\beta_1)} \frac{L(\beta_0, \beta_1)}{f(\beta_1|\beta_0, y_{1:n}, x_{1:n})} \right) = \mathbf{E}_{t_5}\left( \frac{L(\beta_0, \beta_1)}{t_5(\beta_1)} \right). \end{equation*}\]

Επομένως, για κάθε τιμή του \(\beta_0\), μπορούμε να παράγουμε ένα δείγμα \(\beta_1^m, m=1, \dots, M\) από την \(t_5\) και να εκτιμήσουμε το το \(h(\beta_0)\) ως

\[\begin{equation*} \widehat{h}(\beta_0) = \frac{1}{M} \sum_{m=1}^M \prod_{i=1}^n \Phi(\beta_0+\beta_1^m x_i)^{y_i} \cdot \Phi(-\beta_0-\beta_1^m x_i)^{1-y_i} \cdot t_5(\beta_1^m)^{-1}. \end{equation*}\]

Αφού όμως η κατανομή από την οποία προσομοιώνουμε τα \(\beta_1\) είναι η ίδια για όλες τις τιμές του \(\beta_0\), θα μπορούσαμε να χρησιμοποιήσουμε το ίδιο δείγμα για όλες, απαλείφοντας τον επιπλέον θόρυβο στην εκτίμηση των τιμών της \(h\). Στην εικόνα 5.16 (πάνω) μπορούμε να δούμε τη μεταβλητότητα που προκαλεί η εκτίμηση \(\widehat{h}(\beta_0)\) χρησιμοποιώντας διαφορετικό δείγμα για κάθε τιμή του \(\beta_0\) καθώς και το εύρος αυτής της μεταβλητότητας βασισμένο σε 100 δείγματα μεγέθους 200 για κάθε τιμή του \(\beta_0\). Είναι εμφανές ότι η εκτίμηση που δημιουργείται με τη χρήση ενός δείγματος για όλες τις τιμές του \(\beta_0\), παρότι παρουσιάζει το ίδιο εύρος, παράγει μία πολύ πιο λεία και αξιόπιστη καμπύλη (Εικόνα 5.16, μέση). Τέλος, παίρνοντας τη μέση εκτίμηση \(\widehat{h}(\beta_0)\) ως προς τις 100 επαναλήψεις, μπορούμε να δούμε ότι και δύο μέθοδοι δεν παρουσιάζουν διαφορά, κάτι που υποδεικνύει πως το μέγεθος δείγματος 200 είναι επαρκές για να παράγει μία σταθερή προσέγγιση της \(h\).

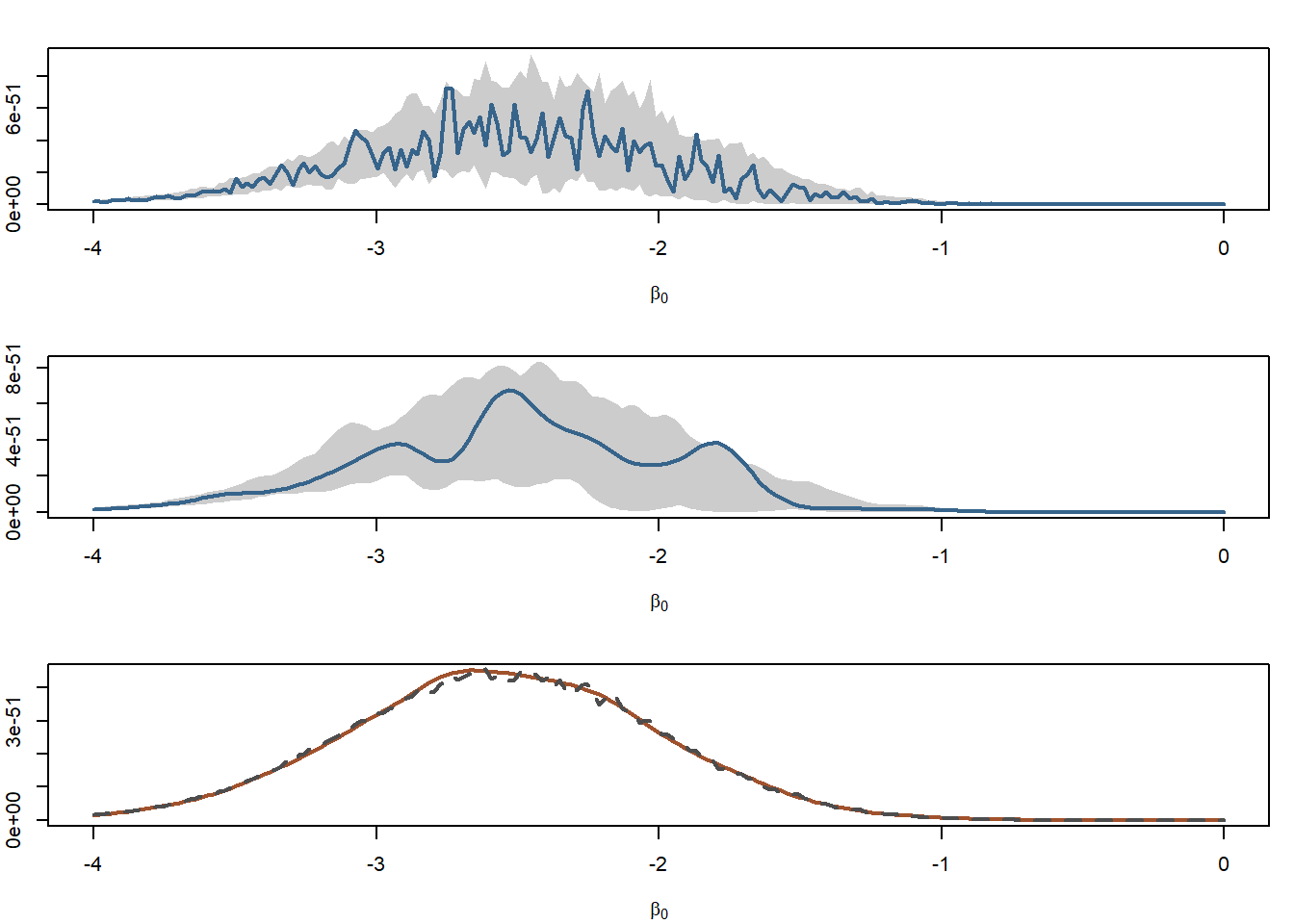
Εικόνα 5.16: Monte Carlo approximations of the marginal posterior of the probit posterior distribution associated with the Pima.tr dataset based on \(200\) simulations from a \(\mathcal{T}_5(0.1, 0.03^2)\) distribution. (top) Range of 100 replications of the approximation \(\widehat{h}\) when simulating a different t sample for each value of \(\beta_0\) and overlay of one replication; (middle) range of 100 replications of the approximation \(\widehat{h}\) when simulating the same t sample for each value of \(\beta_0\) and overlay of one replication; (bottom) comparison of the averages of both experiments (the dotted graph corresponding to the top experiment is not distinguishable from the other graph).

Σε αυτό το σημείο, αξίζει να παρατηρήσουμε ότι αυτό που επιθυμούμε από την προσέγγισή μας δεν είναι η κατά σημείο σύγκλιση, αλλά η ομοιόμορφη σύγκλιση, προκειμένου να μπορούμε να εμπιστευτούμε την \(\widehat{h}(x)\). Επομένως η χρήση ενός δείγματος σπουδαιότητας για όλες τις τιμές του \(x\), όπως παραπάνω, είναι μία λογική προσέγγιση του προβλήματος. Φυσικά, η ακρίβεια της εκτίμησης \(\widehat{h}(x)\) δεν είναι απαραίτητα ανεξάρτητη του \(x\). Επομένως, πρέπει να λάβουμε υπ’ όψιν το χειρότερο δυνατό σενάριο όταν επιλέγουμε το μέγεθος του δείγματος που θα προσομοιώσουμε. Επιπλέον, σημαντικό ρόλο παίζει η συνάρτηση σημαντικότητας \(g\) την οποία επιλέγουμε, όπως έχουμε ήδη δει στη δειγματοληψία σπουδαιότητας. ### Μοντέλα με Ελλιπή Δεδομένα

Μια ειδική περίπτωση των συναρτήσεων της μορφής \(h(x)=\mathbf{E}\left(H(x,Z)\right)\) που μελετάμε είναι αυτή των μοντέλων με ελλειπή δεδομένα (missing-data models) στα οποία η πιθανοφάνεια μπορεί να εκφραστεί ως

\[\begin{equation*} g(x|\theta) = \int_{\mathcal{Z}} f(x,z|\theta) dz. \end{equation*}\]

Η παραπάνω αναπαράσταση προκύπτει σε πολλά στατιστικά πλαίσια. Ένα τέτοιο πλαίσιο είναι τα δείγματα από μίξεις κατανομών, όπου η κάθε παρατήρηση δεν είναι γνωστό σε ποιο πληθυσμό ανήκει. Για παράδειγμα μπορεί να γνωρίζουμε ότι το ύψος ενός ανθρώπου είναι μίξη δύο κανονικών κατανομών, μία για τις γυναίκες και μία για τους άνδρες, και να έχουμε ένα δείγμα με τα ύψη \(X_1, X_2, \dots X_n\) ανθρώπων, αλλά να μη γνωρίζουμε το φύλο της κάθε παρατήρησης.

Παράδειγμα 5.13 (Robert & Casella 5.12) Στο παράδειγμα είδαμε ένα δείγμα 400 παρατηρήσεων από μίξη κατανομών \(\mathcal{N}(1, 1)\) και \(\mathcal{N}(2.5, 1)\), με αντίστοιχες πιθανότητες \(1/4\) και \(3/4\) με πιθανοφάνεια

\[\begin{equation*} L(\mu_1, \mu_2) = \prod_{i=1}^n \frac{1}{4} f(x_i;\mu_1) + \frac{3}{4} f(x_i;\mu_2). \end{equation*}\]

Σε αυτό το σημείο, εισάγουμε τις τ.μ. \(Z_i\sim Ber(1/4)\), έτσι ώστε \(X_i|Z_i=z\sim\mathcal{N}(\mu_z, 1)\). Έτσι, μπορούμε να γράψουμε την πιθανοφάνεια στη μορφή \(\mathbf{E}\left(H(x,Z)\right)\), όπου

\[\begin{equation*} H(x, z) \propto \prod_{i:z_i=1} \frac{1}{4} e^{-\frac{1}{2}(x_i-\mu_1)^2} \prod_{i:z_i=0} \frac{3}{4} e^{-\frac{1}{2}(x_i-\mu_2)^2} \end{equation*}\]

Ένα άλλο ενδιαφέρον πλαίσιο αποτελούν τα “λογοκριμένα” δεδομένα (censored data). Για παράδειγμα, αν μελετάμε την ηλικία θνησιμότητας ασθενών με μία συγκεκριμένη πάθηση, και την παρούσα στιγμή ο ασθενής \(i\) είναι ζωντανός σε ηλικία 60 ετών, δεν γνωρίζουμε την παρατήρηση \(X_i\) (ηλικία θανάτου), παρά μόνο ότι \(X_i\geq 60\).

Παράδειγμα 5.14 (Robert & Casella 5.13) Ας υποθέσουμε ότι έχουμε \(Y_1, Y_2, \dots, Y_m\) ανεξάρτητες και ισόνομες παρατηρήσεις από την κατανομή \(F\) με συνάρτηση πυκνότητας \(f(y-\theta)\) και ότι οι εναπομείνουσες \((n-m)\) παρατηρήσεις \(Y_{m+1}, Y_{m+2}, \dots, Y_n\) είναι censored με κατώφλι \(a\) (γνωρίζουμε δηλαδή ότι είναι \(\geq a\)). Τότε, η παρατηρούμενη πιθανοφάνεια είναι ίση με

\[\begin{equation*} L(\theta|y) = \left[ 1 - F(a-\theta)\right]^{n-m} \prod_{i=1}^m f(y_i-\theta). \end{equation*}\]

Αν είχαμε παρατηρήσει τα censored δεδομένα, έστω \(z_{m+1}, z_{m+2}, \dots, z_n\) με \(z_i\geq a\), θα μπορούσαμε να είχαμε την πλήρη πιθανοφάνεια

\[\begin{equation*} L(\theta|y) = \prod_{i=m+1}^n f(z_i-\theta) \prod_{i=1}^m f(y_i-\theta). \end{equation*}\]

Παρατηρούμε ότι

\[\begin{equation*} L(\theta|y) = \mathbb{E}\left(L^c(\theta|y, Z)\right) = \int_{\mathcal{Z}}L^c(\theta|y, z) f(z|y,\theta) dz, \end{equation*}\]

όπου

\[\begin{equation*} f(z|y,\theta) = \prod_{i=m+1}^n f(z_i|y,\theta) = \prod_{i=m+1}^n \frac{f(z_i-\theta)}{[1-F(a-\theta)]}. \end{equation*}\]

Σε όλα τα προβλήματα που συζητήθηκαν, οι τ.μ. \(Z\) εξυπηρετούν στην απλοποίηση των υπολογισμών, χωρίς απαραίτητα να έχουν φυσική ερμηνεία στο στατιστικό πρόβλημα. Γενικά αναφερόμαστε στα \(z\) ως ελλειπή δεδομενα, στα \(x\) ως παρατηρούμενα δεδομένα, και στα \((x,z)\) πλήρη δεδομένα. Αντίστοιχα κάνουμε λόγο για παρατηρούμενη πιθανοφάνεια \(L(\theta|x)\) και πλήρη πιθανοφάνεια \(L^c(\theta|x, z)\).

Στις επόμενες ενότητες θα μελετήσουμε υβριδικές μεθόδους, όπου η προσέγγιση της συνάρτησης ενδιαφέροντος \(h\) και η μεγιστοποίησή της συνδιάζονται σε μία διαδικασία. Η απλούστερη περίπτωση τέτοιων μεθόδων είναι ο αλγόριθμος EM (Expectation - Maximization).

5.7 Ο Αλγόριθμος EM

Ο αλγόριθμος EM είναι ένας επαναληπτικός αλγόριθμος που μας επιτρέπει να προσεγγίσουμε την ε.μ.π. σε περιπτώσεις που στο εν λόγω στατιστικό μοντέλο υπεισέρχονται μη παρατηρήσιμες ή κρυμμένες μεταβλητές. Αυτό θα μπορούσε να συνδέεται άμεσα με τον τρόπο περιγραφής του μοντέλου ή να εισάγονται τέτοιες μεταβλητές ως τεχνική ομαλοποίησης της συνάρτησης πιθανοφάνειας του μοντέλου. Η χρήση του αλγορίθμου EM είναι περισσότερο ελκυστική σε προβλήματα που η συνάρτηση πιθανοφάνειας των πλήρων δεδομένων (με ενσωμάτωση των κρυμμένων μεταβλητών ως παρατηρήσιμων) οδηγεί σε ένα πολύ ευκολότερο πρόβλημα μεγιστοποίησης.

Έστω λοιπόν \(X\) ένα παρατηρήσιμο διάνυσμα, το οποίο εξαρτάται από κάποιο άλλο μη παρατηρήσιμο διάνυσμα \(Z\), και από μία παράμετρο \(\theta \in \Theta\) για την εκτίμηση της οποίας απαιτούνται παρατηρήσεις από τις μεταβλητές \(X\) και \(Z\). Καθώς το \(Z\) είναι μη παρατηρήσιμο, η \(L_{X,Z}(\theta)\) δε μπορεί να χρησιμοποιηθεί άμεσα για την εύρεση της ε.μ.π.. Η απευθείας μεγιστοποίηση της \(L_{X}(\theta)\) είναι αρκετά δύσκολη και τις περισσότερες φορές αδύνατη, άρα η ιδέα του αλγορίθμου EM είναι να αντικαταστήσει τη μεγιστοποίηση αυτή απόμία ευκολότερη διαδικασία που να βασίζεται στην πιθανοφάνεια των πλήρων δεδομένων. Υπό κάποιες συνθήκες κανονικότητας, ο αλγόριθμος αυτός οδηγεί σε μία ακολουθία \(\theta^{(m)}\rightarrow \theta^\star\) που είναι ένα στάσιμο σημείο της \(l(\theta)=\log L_Y(\theta)\) και πολλές φορές το σημείο στο οποίο συγκλίνει είναι πράγματι η ε.μ.π..

Συμβολίζοντας \(f(x, z|\theta)\) την από κοινού συνάρτηση πυκνότητας των \(x\) και \(z\), \(g(x|\theta)\) την περιθώρια συνάρτηση πυκνότητας των \(x\) και \(k(z| \theta, x)\) τη δεσμευμένη πυκνότητα των \(z\) δεδομένων των \(x\), έχουμε τη σχέση

\[\begin{equation*} k(z| \theta, x)=\frac{f(x, z|\theta)}{g(x|\theta)}, \ x\in S_x, z \in S_z. \end{equation*}\]

Βλέποντας τη σχέση αυτή ως συνάρτηση του \(\theta\) και λογαριθμίζοντας παίρνουμε

\[\begin{equation*} \log L(\theta|z) = \mathbf{E}_{\theta_0}\left(\log L^c (\theta|x, Z) \right) - \mathbf{E}_{\theta_0}\left(\log k(Z|\theta, x) \right), \end{equation*}\]

όπου η μέση τιμή είναι ως προς τη \(k(Z|\theta_0, x)\). Καθώς επιθυμούμε να μεγιστοποιήσουμε την $ L(|z)$, μας ενδιαφέρει ο πρώτος όρος στο δεύτερο μέρος, \(\mathbf{E}_{\theta_0}\left(\log L^c (\theta|x, Z) \right)\). Θέτουμε

\[\begin{equation*} Q(\theta|\theta_0, x) = \mathbf{E}_{\theta_0}\left(\log L^c (\theta|x, Z) \right). \end{equation*}\]

Ο αλγόριθμος EM κινείται αναδρομικά ως εξής:

---

Ο αλγόριθμος EM

Επιλέγουμε μία αρχική τιμή \(\theta_{(0)}\). Επαναλαμβάνουμε:

1. E-step: Υπολογίζουμε την \[\begin{equation*} Q(\theta|\theta_{(m)}, x) = \mathbf{E}_{\theta_{(m)}}\left(\log L^c (\theta|x, Z) \right), \end{equation*}\] όπου η μέση τιμή παίρνεται ως προς την \(k(z|\theta_{(m)}, x)\).

2. M-step: Μεγιστοποιούμε τη \(Q(\theta|\theta_{(m)}, x)\) στο \(\theta\) και παίρνουμε \[\begin{equation*} \theta_{(m+1)} = arg\max_{\theta\in\Theta} Q(\theta|\theta_{(m)}, x). \end{equation*}\]

μέχρι ο αλγόριθμος να συγκλίνει σε ένα σημείο, δηλαδή \(\theta_{(m+1)}=\theta_{(m)}\).

Ορισμός 5.3 Η \(Q\)-συνάρτηση που αντιστοιχεί στον αλγόριθμο EM, είναι η οικογένεια των συναρτήσεων \(\{Q(\cdot \ ; \theta')\}_{\theta'\in\Theta}\), που ορίζεται από τη σχέση \[\begin{equation*} Q(\theta ; \theta')=\int \log p(x,y ; \theta) p(x|y ; \theta') \lambda(dx) = E_{\theta'} \left[\ell_{y,X}(\theta)| Y=y \right]. \end{equation*}\]

1. \(\Theta \subset \mathbb{R}^{d_\theta}, d_\theta \geq 1\) είναι ανοικτό υποσύνολο,
2. \(\forall \theta \in \Theta\), η \(L_y(\theta)\) είναι θετική και πεπερασμένη,
3. \(\forall (\theta, \theta') \in \Theta\times\Theta, \int \lVert \nabla _\theta \log p(x|y ; \theta)\rVert\, p(x|y;\theta') \lambda(dx) = E_{\theta'}\left[ \lVert \nabla _\theta \log p(X|y ; \theta)\lVert \, \mid y \right] < +\infty\).

Λήμμα 5.2 \(Q(\theta ; \theta')=\ell_y(\theta) - H(\theta ; \theta')\) όπου \[\begin{equation*} H(\theta ; \theta')= E_{\theta'} \big[ \underbrace{-\log p(X|y ; \theta)}_{g(X)}\mid y \big] =-\int \log p(x|y; \theta) \cdot p(x|y ; \theta') \lambda(dx) \end{equation*}\]

Παρατήρηση:. Η \(H(\theta' ; \theta') = E_{\theta'}\left[ -\log p(X|y ; \theta') \mid y \right]\) αντιστοιχεί στην εντροπία της δεσμευμένης συνάρτησης πυκνότητας της \(X\) δοθείσης της \(Y=y\), όταν αυτή υπολογίζεται κάτω από το \(\theta'\) .

Απόδειξη:. \[\begin{align*} p(y ; \theta) = \frac{p(x,y ; \theta)}{p(x|y ; \theta)}, \forall \text{εφικτό} \ x \end{align*}\]

Επομένως \[\begin{align*} p(y ; \theta) = \frac{p(X,y ; \theta)}{p(X|y ; \theta)}. \end{align*}\]

Άρα \[\begin{align*} Q(\theta ; \theta') &= E_{\theta'}\left[ \log p(X, y ; \theta) \mid y \right] = E_{\theta'}\left[ \log p(y ; \theta) + \log p(X | y ; \theta) \mid y \right] \\ &=\ell_y(\theta) - E_{\theta'}\left[ - \log p(X | y ; \theta) \mid y \right] = \ell_y(\theta) - H(\theta ; \theta') \end{align*}\]

Πρόταση 5.2 Κάτω από τις υποθέσεις \((i)-(iii), \forall (\theta, \theta') \in \Theta \times \Theta\), έχουμε ότι: \[\begin{equation*} \ell_y(\theta) - \ell_y(\theta') \geq Q(\theta ; \theta') - Q(\theta' ; \theta') \end{equation*}\] Προφανώς, λοιπόν, αν \(\theta^\star = \arg\max_\theta Q(\theta ; \theta')\), τότε \(\ell_y(\theta^\star) \geq \ell_y(\theta')\), το οποίο δείχνει ότι σε κάθε επανάληψη του EM, έχουμε βελτίωση του \(\ell_y(\theta)\).

Απόδειξη:. Θέλουμε νδο: \[\begin{align*} \ell_y(\theta)-\ell_y(\theta') &\geq Q(\theta ; \theta') - Q(\theta' ; \theta') \\ \ell_y(\theta)- Q(\theta ; \theta') &\geq \ell_y(\theta') - Q(\theta' ; \theta') \\ H(\theta ; \theta') &\geq H(\theta' ; \theta') \\ H(\theta ; \theta') - H(\theta' ; \theta') &\geq 0 \end{align*}\]

Πρέπει νδο ισχύει \(H(\theta ; \theta') - H(\theta' ; \theta') \geq 0\). Όμως, \[\begin{align*} H(\theta ; \theta') &= E_{\theta'}\left[- \log p(X |y ; \theta) \mid y \right] \\ H(\theta' ; \theta') &= E_{\theta'}\left[ -\log p(X) \right], \text{όταν} X \thicksim p(x)=p(x|y ; \theta') \end{align*}\]

Παίρνουμε τη διαφορά: \[\begin{align*} H(\theta ; \theta') - H(\theta' ; \theta') = E_{\theta'}\left[ -\log \frac{p(X|y; \theta)}{p(X|y; \theta')} \mid y \right] \text{(κυρτή συνάρτηση)} \end{align*}\]

Λόγω Jensen, \[\begin{align*} H(\theta ; \theta') - H(\theta' ; \theta') \geq -\log \left( E_{\theta'}\left[\frac{p(X|y; \theta)}{p(X|y; \theta')} \mid y \right] \right). \end{align*}\]

Όμως, \[\begin{align*} E_{\theta'}\left[\frac{p(X|y; \theta)}{p(X|y; \theta')} \mid y \right] = \int \frac{p(x|y; \theta)}{p(x|y; \theta')} \cdot p(x|y; \theta') \lambda(dx) = \int p(x|y; \theta) \lambda(dx) = 1 \end{align*}\]

Τελικά \[\begin{align*} H(\theta ; \theta') - H(\theta' ; \theta') \geq 0. \end{align*}\]

Παράδειγμα 5.15 (Robert & Casella 5.14) Συνεχίζοντας το παράδειγμα 5.14, αν η κατανομή \(f(x-\theta)\) αντιστοιχεί στην κανονική κατανομή \(\mathcal{N}(\theta, 1)\), η πλήρης πιθανοφάνεια γράφεται

\[\begin{equation*} L^c (\theta|y,z) \propto \prod_{i=1}^m e^{-\frac{1}{2} (y_i-\theta)^2} \prod_{i=m+1}^n e^{-\frac{1}{2} (z_i-\theta)^2}, \end{equation*}\]

επομένως

\[\begin{align*} Q(\theta|\theta_0, y) &= -\frac{1}{2} \sum_{i=1}^m (y_i-\theta)^2 -\frac{1}{2} \sum_{i=m+1}^n \mathbf{E}_{\theta_0} \left((Z_i - \theta)^2 \right) \\ &= -\frac{1}{2} \sum_{i=1}^m (y_i-\theta)^2 -\frac{1}{2} \sum_{i=m+1}^n \mathbf{V}_{\theta_0}(Z_i-\theta) + \mathbf{E}^2_{\theta_0} \left((Z_i - \theta) \right) \end{align*}\]

όπου τα \(Z_i\) ακολουθούν κανονική κατανομή \(\mathcal{N}_a(\theta, 1)\) περικεκκομένη στο \(a\). Παραγωγίζοντας την \(Q(\theta|\theta_0, y)\) ως προς \(\theta\) και κάνοντας πράξεις βρίσκουμε το σημείο μεγίστου

\[\begin{equation*} \theta=\frac{m\overline{y} +(n-m)\mathbf{E}_{\theta_0}(Z_1)}{n}. \end{equation*}\]

Καθώς \[\begin{equation*} \mathbf{E}_{\theta}(Z_1) = \theta + \frac{\phi(a-\theta)}{1-\Phi(a-\theta)}, \end{equation*}\]

όπου τα \(\phi, \Phi\) συμβολίζουν τη σ.π.π. και σ.κ. της κανονικής κατανομής, ο αλγόριθμος EM παράγει την αναδρομική ακολουθία

\[\begin{equation*} \theta_{(j+1)} = \frac{m}{n} \overline{y} +\frac{n-m}{n} \left[\theta_{(j)} +\frac{\phi(a-\theta_{(j)})}{1-\Phi(a-\theta_{(j)})} \right]. \end{equation*}\]

Όπως μπορούμε να δούμε στην εικόνα 5.17, για \(\overline{y}=0, a=1, n=30, m=20\), ο αλγόριθμος συγκλίνει αρκετά γρήγορα.

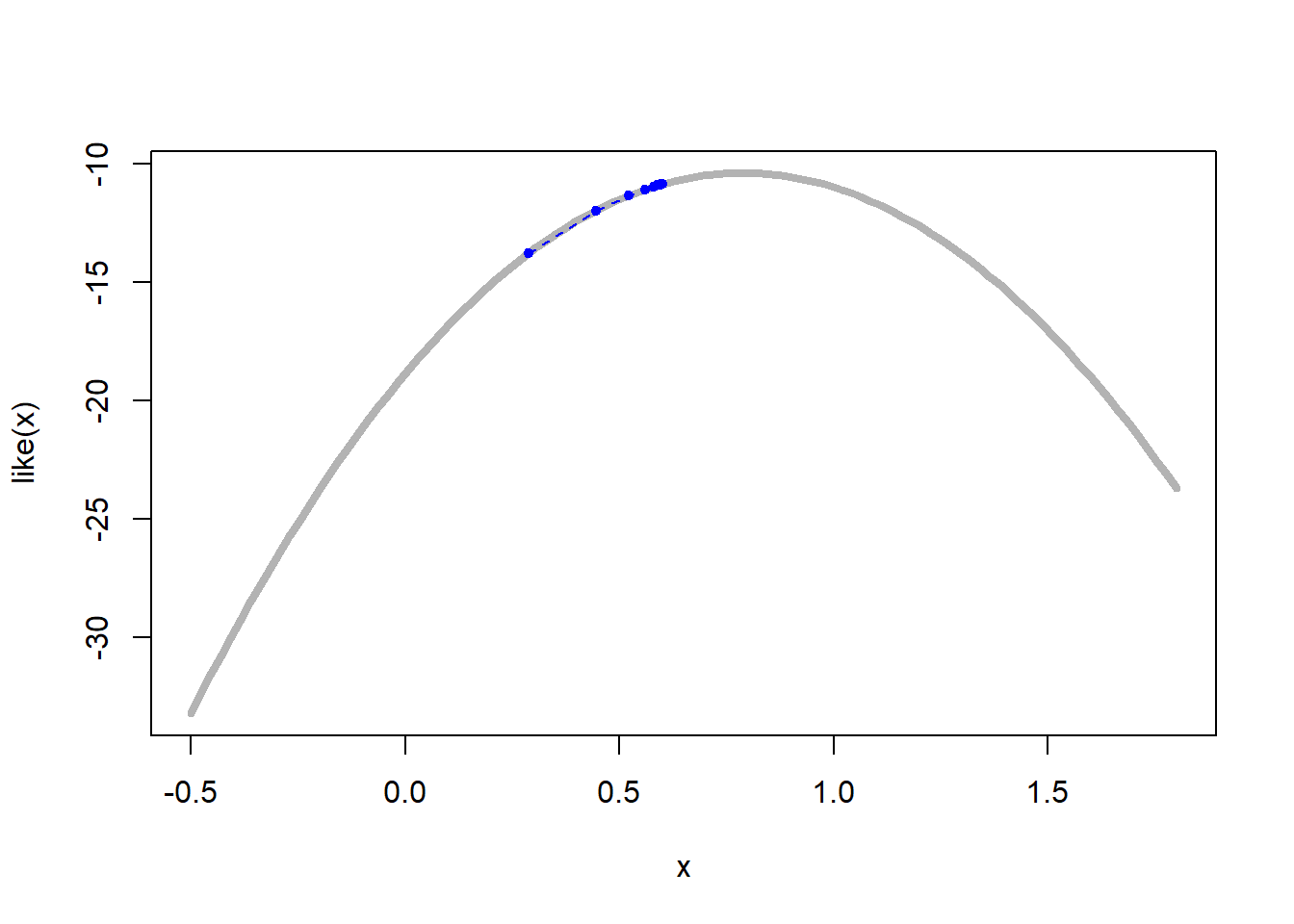
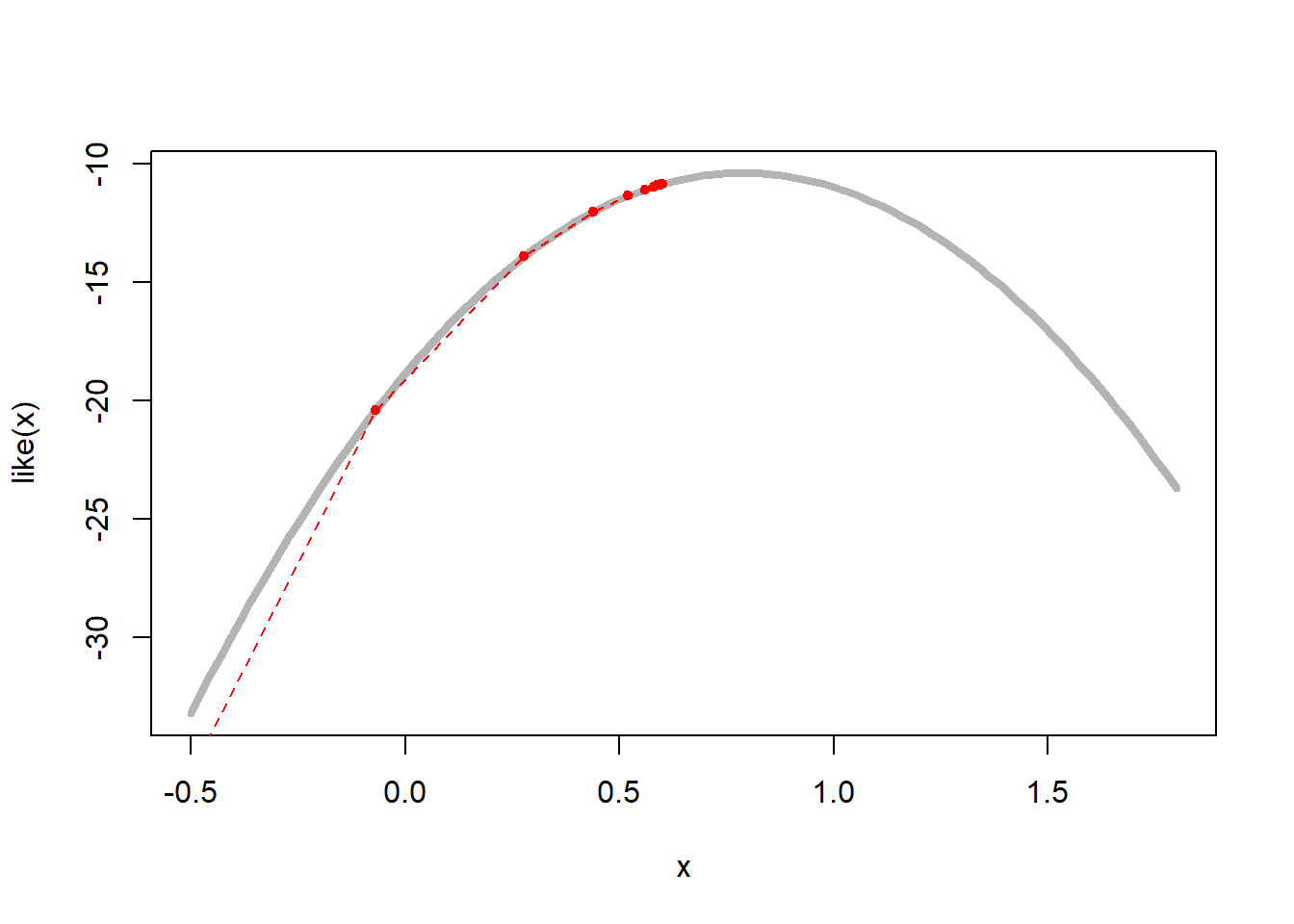
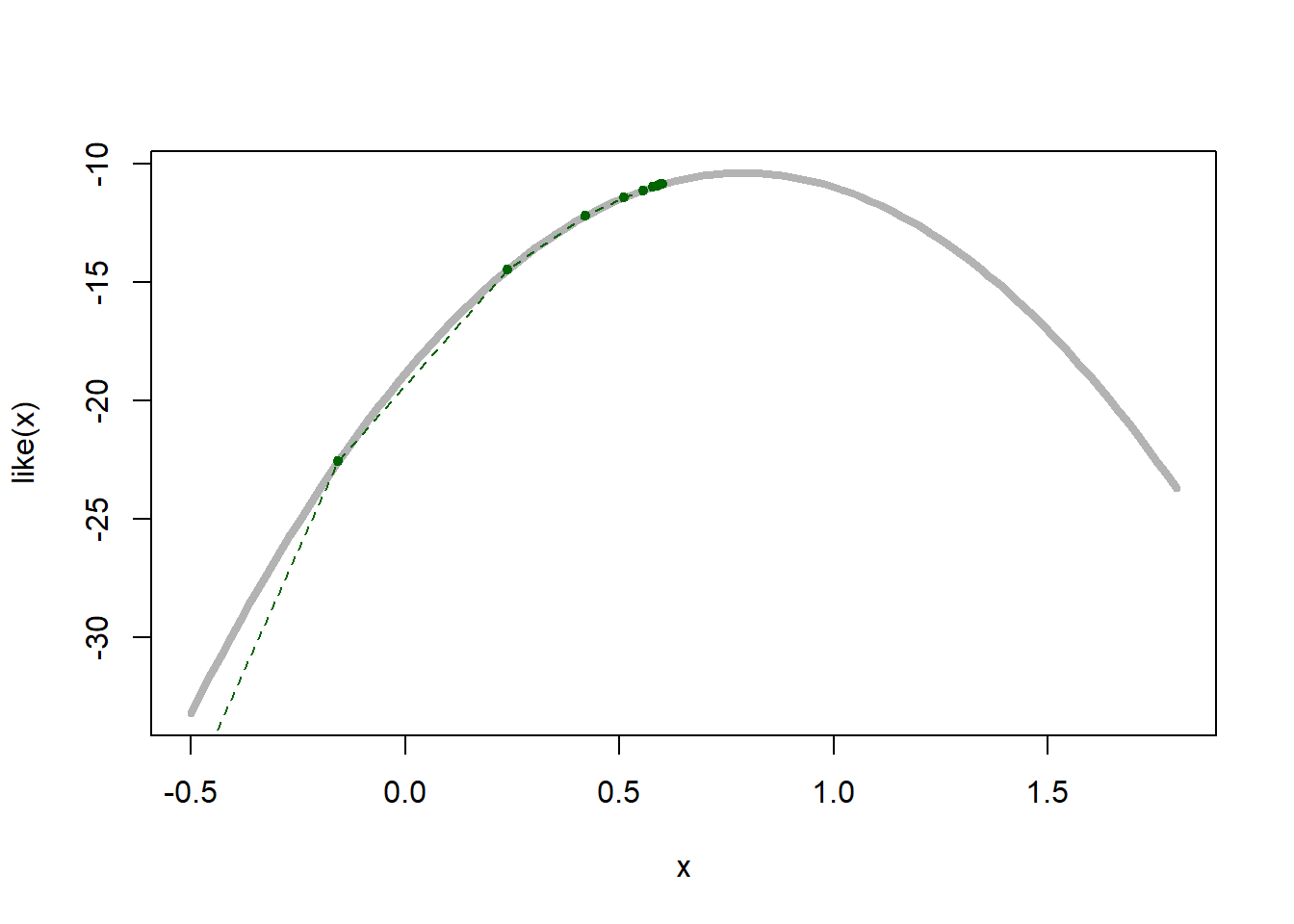
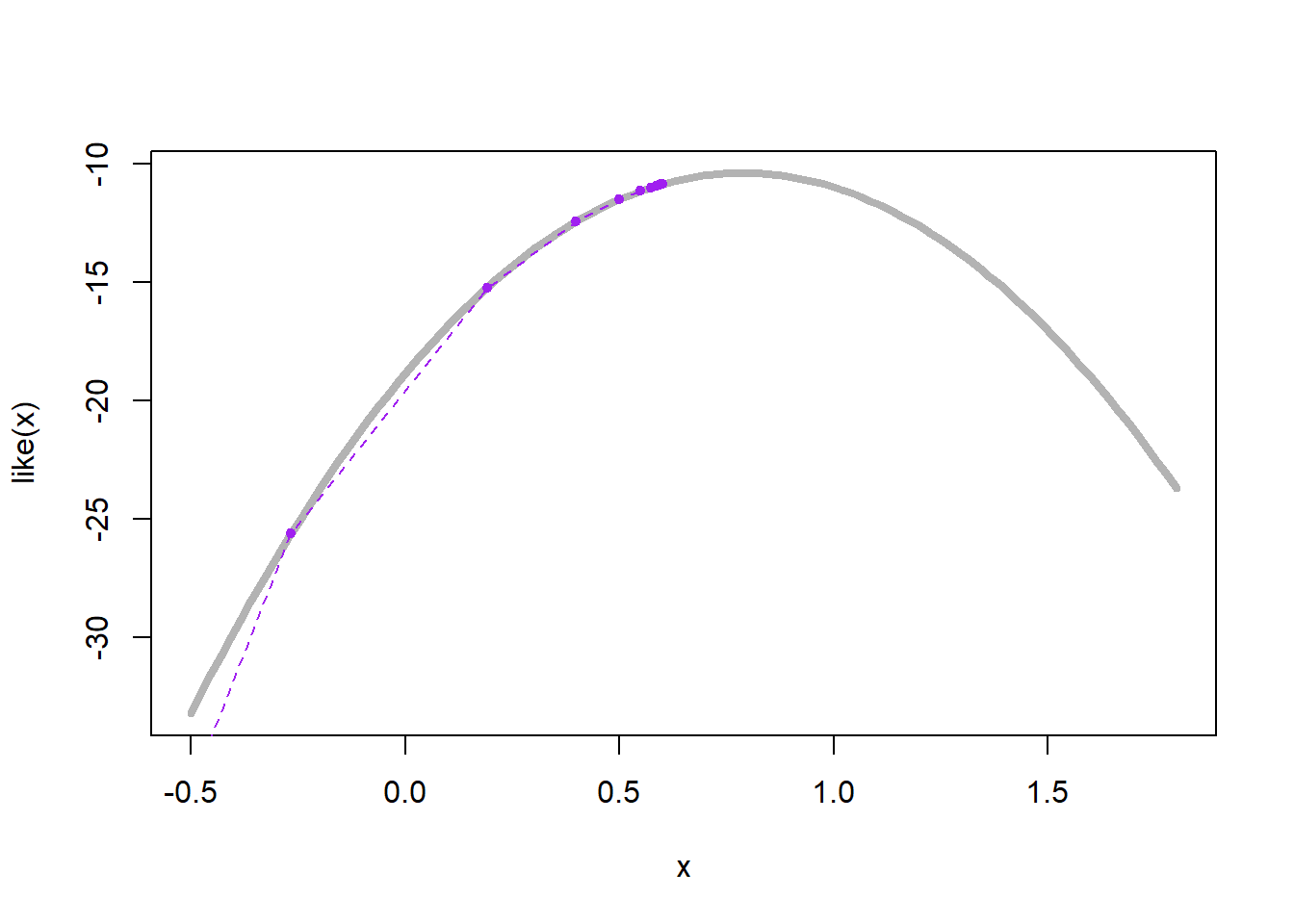
Εικόνα 5.17: Representation by 4 EM sequences started at random for the censored likelihood when the data is normal, \(\overline{y}=0, a=1, n=30, m=20\), on top of the true log-likelihood (grey curve).

Παράδειγμα 5.16 (Robert & Casella 5.15) Συνεχίζουμε το παράδειγμα 5.13 με τη δικόρυφη πιθανοφάνεια της μίξης κανονικών. Όπως είδαμε, η χρήση των ψευδομεταβλητών \(Z_i\) οδηγεί στη συνάρτηση

\[\begin{equation*} Q(\theta^{'}|theta, x) = -\frac{1}{2} \sum_{i=1}^m \mathbf{E}_{\theta} \left[ Z_i (x_i-\mu_1)^2 +(1-Z_i)(x_i-\mu_2)^2 |x \right], \end{equation*}\]

όπου \(\theta=(\mu_1, \mu_2)\). Εκτελώντας το βήμα M του αλγορίθμου παίρνουμε τις λύσεις

\[\begin{equation*} \mu_1^{'} = \frac{\mathbf{E}_\theta \left[\sum_{i=1}^n Z_i x_i |x \right]}{\mathbf{E}_\theta \left[\sum_{i=1}^n Z_i |x \right]}, \mu_2^{'} = \frac{\mathbf{E}_\theta \left[\sum_{i=1}^n (1-Z_i) x_i |x \right]}{\mathbf{E}_\theta \left[\sum_{i=1}^n (1-Z_i) |x \right]}. \end{equation*}\]

Καθώς έχουμε γνωστή μέση τιμή

\[\begin{equation*} \mathbf{E}_\theta \left[Z_i|x\right] = \frac{\phi(x_i-\mu_1)}{\phi(x_i-\mu_1)+3\phi(x_i-\mu_2)}, \end{equation*}\]

ο αλγόριθμος EM μπορεί εύκολα να υλοποιηθεί στο συγκεκριμένο πρόβλημα. Στην εικόνα 5.18 παρατηρούμε ότι από τις 6 ακολουθίες EM, δύο συγκλίνουν στο πραγματικό ολικό μέγιστο, δύο συγκλίνουν στο τοπικό, μη ολικό μέγιστο, και δύο συγκλίνουν στο σαγματικό σημείο της πιθανοφάνειας. Αξίζει να παράτηρήσουμε ότι στα αρχικά βήματα του αλγορίθμου η σύγκλιση είναι πολύ γρήγορη και μέσα σε 2-3 βήματα έχουμε φτάσει σε μία “μικρή” περιοχή γύρω από το σημείο σύγκλισης, ενώ στα επόμενα βήματα η σύγκλιση είναι σημαντικά πιο αργή. Αυτό το παράδειγμα κάνει εμφανή την ανάγκη να επαναλάβουμε τον αλγόριθμο αρκετές φορές, ξεκινώντας από τυχαία αρχικά σημεία, ώστε να εντοπίσουμε τα διαφορετικά ακρότατα της συνάρτησης που θέλουμε να βελτιστοποιήσουμε.

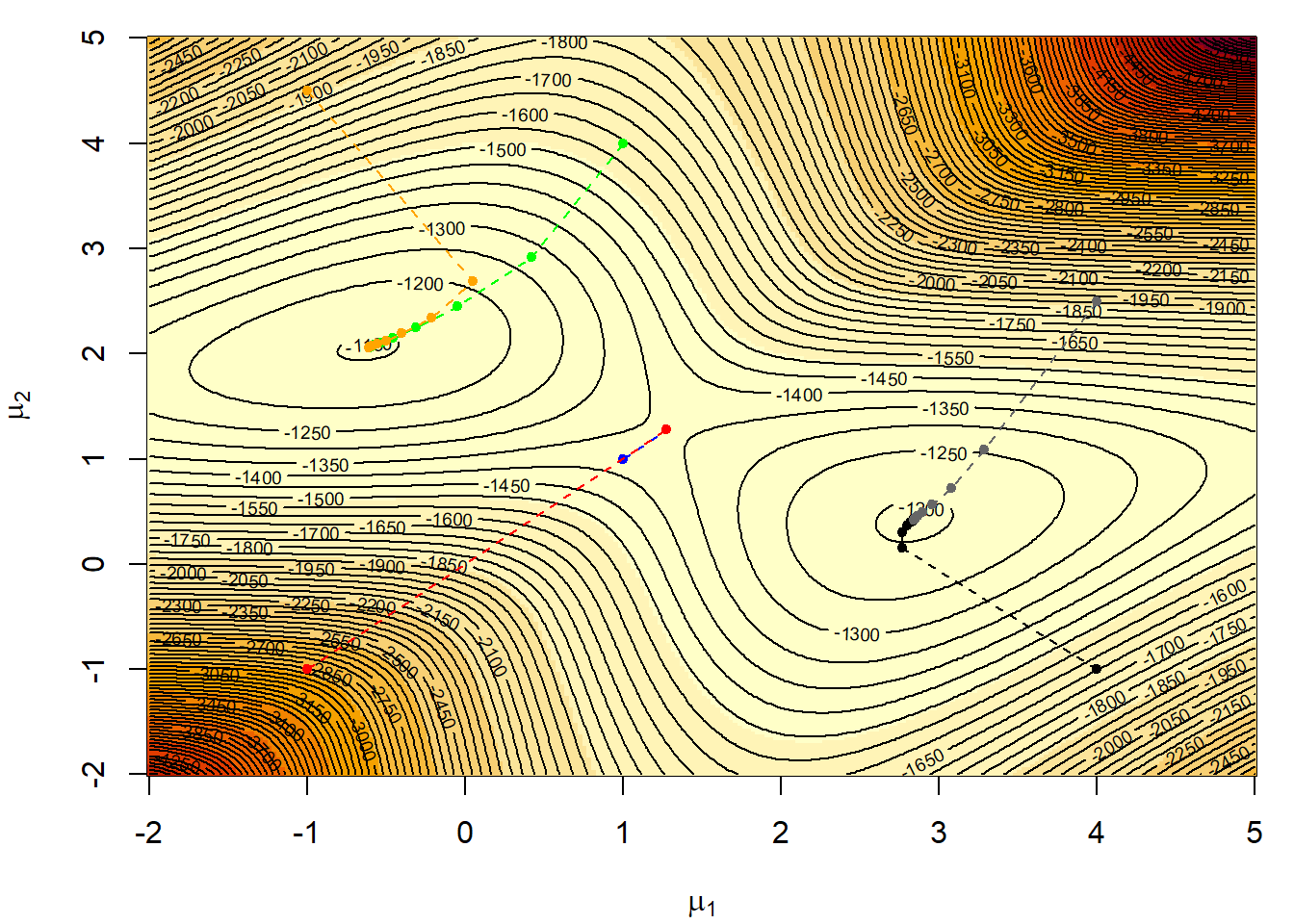
Εικόνα 5.18: Six EM sequences for a mixture likelihood ending in one of two modes depending on the starting point based on a sample of 400 observations from the normal mixture with \(\mu_1 = 0\) and \(\mu_2 = 2.5\)

5.7.1 Monte Carlo EM

Μία δυσκολία στην εφαρμογή του αλγορίθμου EM είναι ότι κάθε βήμα E απαιτεί τον υπολογισμό της μέσης τιμής της λογαριθμοπιθανοφάνειας, δηλαδή της \(Q(\theta|\theta_{(m)}, x)\). Πέρα από πολύ συγκεκριμένα παραδείγματα όπου η συνάρτηση \(Q\) γράφεται σε κλειστή μορφή, πρέπει να την εκτιμήσουμε. Καθώς η \(Q\) είναι μία μέση τιμή, είναι φυσικό να χρησιμοποιήσουμε μεθόδους Monte Carlo. Όπως είδαμε, μπορούμε να προσομοιώσουμε παρατηρήσεις \(Z_1, ..., Z_T\) από τη κατανομή \(k(z|x, \theta_{(m)})\) και να εκτιμήσουμε τη πλήρη λογαριθμοπιθανοφάνεια ως

\[\begin{equation*} Q(\theta|\theta_{(m)}, x) = \frac{1}{T} \sum_{i=1}^T \log L^c (\theta|x, z_i), \end{equation*}\]

μία μέθοδος που ονομάζεται Monte Carlo EM (Wei & Tanner, 1990). Σύμφωνα με τα παραπάνω, σε κάθε βήμα του αλγορίθμου πρέπει να προσομοιώνουμε ένα καινούριο δείγμα \(Z_i\) από την \(k(z|x, \theta_{(m)})\). Όπως είδαμε όμως, μία πιο σταθερή εκτίμηση βασίζεται στη δειγματοληψία σπουδαιότητας ώστε να μην απαιτείται η παραγωγή διαφορετικού δείγματος για κάθε τιμή της \(\theta_{(m)}\). Βασιζόμενοι στη σχέση των πυκνοτήτων

\[\begin{equation*} g(x|\theta)=\frac{f(x, z|\theta)}{k(z| \theta, x)}, \ x\in S_x, z \in S_z, \end{equation*}\]

παίρνουμε

\[\begin{equation*} \frac{g(x|\theta)}{g(x|\theta_{(0)})}=\frac{f(x, z|\theta)}{f(x, z|\theta_{(0)})} \frac{k(z| \theta_{(0)}, x)}{k(z| \theta, x)}, \ x\in S_x, z \in S_z. \end{equation*}\]

Παίρνοντας μέσες τιμές ως προς την κατανομή \(k(z|x, \theta)\), καταλήγουμε στη σχέση

\[\begin{equation*} \frac{g(x|\theta)}{g(x|\theta_{(0)})}=\mathbf{E}_{\theta} \left( \frac{f(x, z|\theta)}{f(x, z|\theta_{(0)})} \frac{k(z| \theta_{(0)}, x)}{k(z| \theta, x)}\right) =\mathbf{E}_{\theta_{(0)}} \left( \frac{f(x, z|\theta)}{f(x, z|\theta_{(0)})}\right) =\mathbf{E}_{\theta_{(0)}} \left( \frac{L^c(\theta|x, z)}{L^c(\theta_{(0)}|x, z)}\right), \end{equation*}\]

επομένως, αγνοώντας τον σταθερό ως προς το \(\theta\) όρο \(g(x|\theta_{(0)})\) βλέπουμε ότι για να μεγιστοποιήσουμε την πιθανοφάνεια \(L(\theta|x)=g(x|\theta)\) μπορούμε να χρησιμοποιήσουμε την Monte Carlo εκτιμήτρια

\[\begin{equation*} \frac{1}{T} \sum_{i=1}^T \frac{L^c(\theta|x, z_i)}{L^c(\theta_{(0)}|x, z_i}. \end{equation*}\]

Η επιλογή της \(\theta_{(0)}\) είναι ιδιαίτερα σημαντική για να εξασφαλιστεί η πεπερασμένη διασπορά της εκτιμήτριας.

Παράδειγμα 5.17 (Robert & Casella 5.16) Μία κλασική εφαρμογή του EM είναι στο ακόλουθο πρόβλημα βιολογίας (Dempster et al., 1977). Θεωρούμε παρατηρήσεις

\[\begin{equation*} (x_1, x_2, x_3, x_4)\sim\mathcal{M}\left(n ; \frac{1}{2} + \frac{\theta}{4}, \frac{1}{4} (1-\theta), \frac{1}{4} (1-\theta), \frac{\theta}{4} \right). \end{equation*}\]

Η εκτίμηση του \(\theta\) γίνεται πολύ πιο εύκολα αν οι παρατηρήσεις \(x_1\) διαιρεθούν σε δύο τμήματα, έτσι ώστε

\[\begin{equation*} (z_1, z_2, x_2, x_3, x_4)\sim\mathcal{M}\left(n ; \frac{1}{2}, \frac{\theta}{4}, \frac{1}{4} (1-\theta), \frac{1}{4} (1-\theta), \frac{\theta}{4} \right), \end{equation*}\]

όπου \(x_1=z_1+z_2\). Η πλήρης και η παρατηρούμενη πιθανοφάνεια γράφονται ως:

\[\begin{align*} L^c(\theta|z, x) & \propto \theta^{z_2+x_4} (1-\theta)^{x_2+x_3}, \\ L(\theta|x) & \propto (2+\theta)^{x_1} \theta^{x_4} (1-\theta)^{x_2+x_3}. \end{align*}\]

Στο παρόν παράδειγμα, δεν υπάρχει λόγος να χρησιμοποιήσουμε MCEM, αφού η αναμενόμενη τιμή της πλήρους λογαριθμοπιθανοφάνειας είναι

\[\begin{equation*} \mathbf{E}_{\theta_0}\left(\ell^c(\theta|Z, x)\right) = \mathbf{E}_{\theta_0}\left( (Z_2 +x_4) \log \theta + (x_2 +x_3) \log (1-\theta) \right) = \left( \frac{\theta_0}{2+\theta_0}x_1 +x_4 \right) \log \theta + (x_2 + x_3) \log (1-\theta), \end{equation*}\]

η οποία εύκολα μεγιστοποιείται ως προς \(\theta\), με σημείο μεγίστου

\[\begin{equation*} \theta_1 = \frac{ \frac{\theta_0 x_1}{2+\theta_0+x_4} }{ \frac{\theta_0 x_1}{2+\theta_0} +x_2 + x_3 + x_4 }. \end{equation*}\]

Εναλλακτικά, εάν χρησιμοποιούσαμε Monte Carlo EM, θα αντικαθιστούσαμε τη \(\mathbf{E}_{\theta_0}(Z_2) = \theta_0 x_1 / (2+\theta_0)\) με τον εμπειρικό μέσο

\[\begin{equation*} \overline{z}_m = \frac{1}{m} \sum_{i=1}^m z_i, \end{equation*}\]

όπου τα \(z_i\) προσομοιώνονται από τη διωνυμική κατανομή \(Bin(x_1, \theta_0/(2+\theta_0) )\). Σε αυτή την περίπτωση θα είχαμε

\[\begin{equation*} \widehat{\theta}_1 = \frac{ \overline{z}_m + x_4 }{ \overline{z}_m + x_2 + x_3 + x_4 }, \end{equation*}\]

η οποία συγκλίνει στη \(\theta_1\) καθώς το \(m\) πάει στο άπειρο.