6 Αλγόριθμοι Metropolis-Hastings

6.1 Εισαγωγή

Μέχρι τώρα στηριχθήκαμε σε ανεξάρτητες προσομοιώσεις, είτε αυτό αφορούσε απευθείας προσομοίωση από μία κατανομή στόχο $f$, είτε με τη βοήθεια του αλγορίθμου αποδοχής-απόρριψης, είτε έμμεσα μέσω του δειγματολήπτη σπουδαιότητας. Σε αυτό το κεφάλαιο και στα επόμενα θα μας απασχολήσουν τρόποι δειγματοληψίας που στηρίζονται στην παραγωγή εξαρτημένων τυχαίων μεταβλητών. Η εξάρτηση αυτή μετατοπίζει σημαντικά τη θεωρητική θεμελίωση αυτών των μεθόδων σε περιοχές που δεν θα μπορούσαν να καλυφθούν επαρκώς σε ένα εισαγωγικό μάθημα. Παρ’όλα αυτά είναι δυνατή η κατανόηση της μεθοδολογίας για την πρακτική εφαρμογή των μεθόδων αυτών και η ανάπτυξη της διαίσθησης με επιλεγμένα παραδείγματα και κατάλληλη ερμηνεία των αποτελεσμάτων. Τα εξαρτημένα δείγματα παράγονται με τη βοήθεια κατάλληλων μαρκοβιανών αλυσίδων και έτσι δίνουμε εδώ κάποια απαραίτητα στοιχεία της αντίστοιχης θεωρίας. Τα στοιχεία αυτά χρειάζονται για να κατανοηθούν οι βασικότερες μέθοδοι Markov Chain Monte Carlo (MCMC).

6.2 Στοιχεία Μαρκοβιανών Αλυσίδων

Ορισμός 6.1 Έστω $(X_n)_{n\geq 0}$ μία ακολουθία τυχαίων μεταβλητών, ορισμένων σε κοινό χώρο πιθανότητας με τιμές στο μετρήσιμο χώρο $(S, \mathcal{A})$. Θα λέμε ότι η $(X_n)$ είναι μαρκοβιανή αλυσίδα (μ.α.), αν \[\begin{equation*}\label{eqn:MCgeneralcasedefn} \mathbb{P}(X_{n+1}\in A\mid Χ_{0:n})\stackrel{a.s.}{=}\mathbb{P}(X_{n+1}\in A\mid X_n), \end{equation*}\] για κάθε $n\geq 0$ και $A\in \mathcal{A}$. Η μ.α. θα λέγεται (χρονικά) ομογενής, αν η παραπάνω ισότητα είναι ανεξάρτητη του $n$ (με πιθανότητα 1).

Είναι φανερό ότι η χαρακτηριστική ιδιότητα μιας μ.α. είναι ότι μας “απαλλάσσει” από την απαίτηση να γνωρίζουμε όλο το μονοπάτι $x_{0:n}$ για να καθορίσουμε την κατανομή της επόμενης κατάστασης $X_{n+1}$. Η κατανομή αυτή εξαρτάται μόνο από την “παρούσα” κατάσταση $x_n$ (ανεξάρτητη και του $n$ για χρονικά ομογενείς) και μάλιστα επιτρέπεται να αλλάζει ανάλογα με την τιμή του $x_n$. Η δυναμική λοιπόν μιας μ.α. καθορίζεται πλήρως από τη γνώση αυτής της οικογένειας κατανομών, μία για κάθε τιμή του $x_n$. Να σημειωθεί επίσης ότι ο παραπάνω ορισμός τίθεται με όρους ισότητας (με πιθανότητα 1) τυχαίων μεταβλητών, καθώς στη δέσμευση υπεισέρχονται τυχαίες μεταβλητές, χωρίς να καθορίζουμε συγκεκριμένες τιμές τους.

Το μαθηματικό αντικείμενο που μας επιτρέπει να φιλοξενούμε μία τέτοια οικογένεια κατανομών, δηλ., μία οικογένεια μέτρων πιθανότητας που με φυσιολογικό τρόπο καθορίζουν τη δυναμική της αλυσίδας, είναι γνωστό με το όνομα πυρήνας (kernel) και γενικεύει την έννοια του πίνακα πιθανοτήτων μετάβασης, από έναν αριθμήσιμο χώρο καταστάσεων σε ένα γενικό χώρο καταστάσεων.

Ορισμός 6.2 Έστω $(X, \mathcal{X})$ και $(Y, \mathcal{Y})$ δύο μετρήσιμοι χώροι. Μία απεικόνιση $P: X\times \mathcal{Y}\rightarrow \mathbb{R}_{+}$ λέγεται πυρήνας μετάβασης (ή μαρκοβιανός πυρήνας) (kernel) στο $X\times \mathcal{Y}$ αν ικανοποιεί:

για κάθε $x\in X$, η απεικόνιση $P(x,\cdot): \mathcal{Y}\rightarrow \mathbb{R}_{+}$, όπου $A\mapsto P(x, A)$, είναι μέτρο πιθανότητας στον $(Y, \mathcal{Y})$;
για κάθε $A\in\mathcal{Y}$, η απεικόνιση $P(\cdot, A):(X,\mathcal{X})\rightarrow (\mathbb{R}_{+},\mathcal{B}(\mathbb{R}_{+}))$, όπου $x\mapsto P(x, A)$, είναι Borel-μετρήσιμη συνάρτηση.

Στο σημείο αυτό, μετά το τέλος του σεμιναρίου, θα προστεθεί ένα σύντομο κομμάτι που αναφέρεται σε διαχωρίσιμες μαρκοβιανές αλυσίδες, την έννοια των $\phi$ και $\psi$-διαχωρίσιμων μ.α., την έννοια της επαναληπτικότητας (απλής ή κατά Harris), μηδενικά και θετικά επαναληπτικών μ.α., καθώς και την έννοια της στάσιμης κατανομής και της αντιστρεψιμότητας μιας μ.α.. Οι έννοιες αυτές αναφέρθηκαν σύντομα και σχετίζονται με το εργοδικό θεώρημα των μ.α., που μας επιτρέπει να έχουμε σύγκλιση (με πιθανότητα 1) του εργοδικού μέσου μιας συνάρτησης $f(X_n)$ μιας μ.α. στη θεωρητική μέση τιμή $E_{\pi}(f(X_{0}))$, που προκύπτει κάτω από τη στάσιμη κατανομή.
::: {.exercise #unnamed-chunk-3 name=“Robert & Casella 6.1.”} Έστω η μαρκοβιανή αλυσίδα που ορίζεται από την αναδρομική σχέση \[\begin{equation*} X_{t+1} = p X_t + \epsilon_t, \ \ \epsilon_t\sim \mathcal{N}(0,1). \end{equation*}\] Προσομοιώστε $X^{(0)}\sim\mathcal{N}(0,1)$, σχεδιάστε το ιστόγραμμα του δείγματος $X_t$ για $t\leq 10^4$ και $p=0.9$. Ελέγξτε αν η κατανομή $\mathcal{N}(0,1/(1-p^2))$ ταιριάζει να είναι η στάσιμη κατανομή της μαρκοβιανής αλυσίδας. :::

set.seed(1194)
n <- 10 ^ 4
p <- 0.9
x <- c(rnorm(1), rep(NULL, n))

for (i in 2:(n + 1)) {
  x[i] <- p * x[i - 1] + rnorm(1)
}

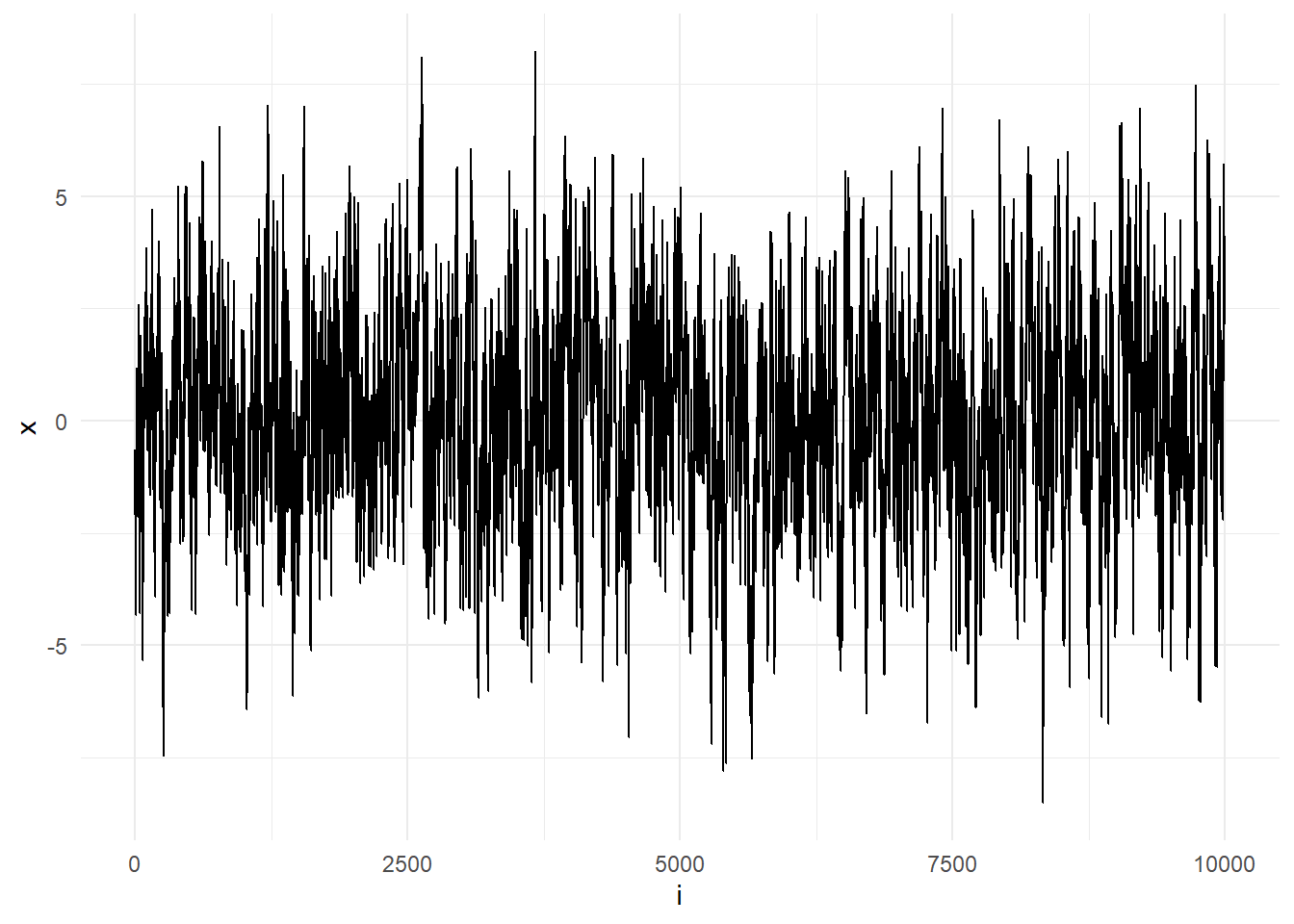
$Sequence $X_t$ when simulated using the formula $X_{t+1} = p X_t + \epsilon_t, \epsilon_t\sim \mathcal{N}(0,1).$.$

Εικόνα 6.1: Sequence $X_t$ when simulated using the formula $X_{t+1} = p X_t + \epsilon_t, \epsilon_t\sim \mathcal{N}(0,1).$.

ks.test(x = x, y = pnorm, mean = 0, sd = sqrt(1 / (1 - p ^ 2)))
## 
##  Asymptotic one-sample Kolmogorov-Smirnov test
## 
## data:  x
## D = 0.025758, p-value = 3.45e-06
## alternative hypothesis: two-sided
ks.test(x = x[5000:n], y = pnorm, mean = 0, sd = sqrt(1 / (1 - p ^ 2)))
## 
##  Asymptotic one-sample Kolmogorov-Smirnov test
## 
## data:  x[5000:n]
## D = 0.01814, p-value = 0.07442
## alternative hypothesis: two-sided

Παρατηρούμε λοιπόν, ότι ενώ η χρήση όλου του δείγματος μας οδηγεί σε μεγάλη απόκλιση από την υποψήφια στάσιμη κατανομή, η απομάκρυνση του πρώτου μισού μας οδηγεί σε ένα δείγμα που φαίνεται να παράγεται από αυτήν. Επίσης, θα πρέπει να τονιστεί εδώ ότι η χρήση του ελέγχου Kolmogorov-Smirnov δεν είναι αυστηρή, αλλά ενδεικτική. Η αυτοσυσχέτιση που παρουσιάζεται στις μαρκοβιανές αλυσίδες θέλει ιδιαίτερη προσοχή, αφού η ασυμπτωτική κατανομή του KS-στατιστικού κάτω από τη μηδενική υπόθεση που χρησιμοποιείται για τον υπολογισμό των p-value είναι έγκυρη κάτω από την υπόθεση της ανεξαρτησίας. Η εξάρτηση που υπάρχει σε ένα δείγμα που αποτελεί μ.α. δημιουργεί αποκλίσεις από αυτές τις θεωρητικές p-value και έτσι τα αποτελέσματα θα πρέπει να ερμηνεύονται με προσοχή.

6.3 Αλγόριθμοι Metropolis-Hastings

Η αρχή λειτουργίας των μεθόδων MCMC είναι αρκετά άμεση. Για δεδομένη συνάρτηση πυκνότητας $f$, κατασκευάζουμε ένα μαρκοβιανό πυρήνα $K$ με στάσιμη κατανομή την $f$ και προσομοιώνουμε μία μαρκοβιανή αλυσίδα $\left(X_t\right)$ χρησιμοποιώντας τον πυρήνα, έτσι ώστε η οριακή κατανομή της μ.α. να είναι η $f$ και να κάνουμε προσεγγίσεις βασιζόμενοι στο εργοδικό θεώρημα. Η δυσκολία που θα αναμέναμε να προκύψει αφορά την κατασκευή ενός τέτοιου πυρήνα $K$. Θα δούμε όμως ότι υπάρχουν γενικές μέθοδοι κατασκευής τέτοιων πυρήνων για κάθε πυκνότητα $f$.

Ένα παράδειγμα τέτοιων μεθόδων είναι ο αλγόριθμος Metropolis-Hastings. Δεδομένης μίας πυκνότητας $f$, η μέθοδος στηρίζεται σε μία δεσμευμένη πυκνότητα $q(y|x)$ από την οποία μπορούμε εύκολα να προσομοιώσουμε. Η πυκνότητα αυτή μπορεί πρέπει να είναι τέτοια ώστε ο λόγος $f(y)/q(y|x)$ να είναι γνωστός μέχρι μίας σταθεράς ανεξάρτητης από το $x$ και επιπλέον η διασπορά της $q(\cdot|x)$ να είναι αρκετά μεγάλη ώστε να οδηγήσει στην εξερεύνηση όλου του στηρίγματος της $f$. Το ιδιαίτερο χαρακτηριστικού του αλγορίθμου Metropolis-Hastings είναι η δυνατότητα κατασκευής ένος πυρήνα με στάσιμη κατανομή την $f$, για οποιαδήποτε πυκνότητα $q$ όπως παραπάνω.

Αλγόριθμος Metropolis - Hastings

Για δεδομένο $x_t$,

Προσομοιώνουμε $Y_t\sim q\left(y|X_t\right)$
Επιλέγουμε \[\begin{equation*} X_{t+1} = \left\{ \begin{array}{ccl} Y_t & \text{με πιθ.} & p\left(x_t, Y_t\right) \\ x_t & \text{με πιθ.} & 1-p\left(x_t, Y_t\right) \end{array}\right. \end{equation*}\] όπου \[\begin{equation*} p(x,y) = \min \left\{ \frac{f(y)}{f(x)} \frac{q(x|y)}{q(y|x)}, 1 \right\}. \end{equation*}\]

Μία γενική υλοποίηση του αλγορίθμου είναι η ακόλουθη, όπου θεωρούμε πως η συνάρτηση geneq(x) παίζει τον ρόλο της $q(y|x)$.

y <- geneq(x[t])
if (runif(1) < f(y) * q(y, x[t]) / (f(x[t]) * q(x[t], y))) {
  x[t + 1] <- y
} else {
  x[t + 1] <- x[t]
}

Η κατανομή $q$ ονομάζεται υποψήφια κατανομή (instrumental, proposal, candidate) και η πιθανότητα $p(x,y)$ ονομάζεται πιθανότητα αποδοχής Metropolis-Hastings. Προσέχουμε πώς η πιθανότητα αποδοχής διαφέρει από το ρυθμό αποδοχής, το οποίο ορίζεται ως

\[\begin{equation*} \overline{p} = \lim_{T\rightarrow +\infty} \frac{1}{T} \sum_{t=0}^T p\left( X_t, Y_t \right) = \iint p(x,y) f(x) q(y|x) dydx. \end{equation*}\]

Η παραπάνω ποσότητα μας επιτρέπει να αξιολογήσουμε την αποδοτικότητα του αλγορίθμου, όπως θα συζητήσουμε στην πορεία. Παρότι ο αλγόριθμος Metropolis-Hastings σε πρώτη ματιά δεν δείχνει να διαφέρει από τη στοχαστική βελτιστοποίηση, υπάρχουν δύο θεμελιώδεις διαφορές. Η πρώτη διαφορά είναι ότι ο αλγόριθμος Metropolis-Hastings στοχεύει στην εξερεύνηση του στηρίγματος της $f$ σύμφωνα με την κατανομή της, ενώ η στοχαστική βελτιστοποίηση στη μεγιστοποίηση της συνάρτησης $h$. Η δεύτερη διαφορά είναι στις ιδιότητες σύγκλισης. Ο αλγόριθμος Metropolis-Hastings συγκλίνει στην κατανομή της $f$, ενώ ο αλγόριθμος simulated annealing, υπό κατάλληλη θερμοκρασία $T_t$, συγκλίνει στο μέγιστο της $h$. Τέλος, η αλλαγή της υποψήφιας $q$ από επανάληψη σε επανάληψη μπορεί να έχει δραστικές επιδράσεις στην σύγκλιση του Metropolis-Hastings.

Ο αλγόριθμος Metropolis-Hastings ικανοποιεί τις εξισώσεις λεπτομερούς ισορροπίας \[\begin{equation*} f(x) K(y|x) = f(y) K(x|y), \end{equation*}\]

από την οποία μπορούμε να συμπεράνουμε ότι η $f$ είναι η στάσιμη κατανομή της μ.α. $\left\{ X_t \right\}$, ολοκληρώνοντας τα δύο μέρη της εξίσωσης ως προς $x$. Στη θεωρία, η στάσιμη κατανομή θα είναι πράγματι η ζητούμενη $f$, αλλά στις εφαρμογές η αποδοτικότητα του αλγορίθμου εξαρτάται από την επιλογή της $q$. Ας δούμε ένα παράδειγμα όπου ο αλγόριθμος Metropolis-Hastings μπορεί να συγκριθεί με μεθόδους προσομοίωσης ανεξάρτητων και ισόνομων μεταβλητών.

Παράδειγμα 6.1 (Robert & Casella, 6.1.) Στο παράδειγμα 2.7. είχαμε δει πως μπορούμε να προσομοιώσουμε από την $B(a,b), a,b>1$ με τον αλγόριθμο αποδοχής - απόρριψης, χρησιμοποιώντας την $Unif(0,1)$ ως υποψήφια. Ας υλοποιήσουμε επιπλέον ένα αλγόριθμο Metropolis - Hastings με την ίδια υποψήφια πυκνότητα. Προσομοιώνουμε $5000$ παρατηρήσεις, από τις οποίες οι πρώτες $1000$ θεωρούνται burn-in period και δε λαμβάνονται υπ’ όψιν.

# Initial Values
Nsim <- 5000
a <- 2.7 ; b <- 6.3
M <- 2.67

# Accept - Reject
x <- NULL
while (length(x) < Nsim) {
  y <- runif(Nsim * M)
  x <- c(x, y[runif(Nsim * M) * M < dbeta(y, a, b)])
}
x <- x[1:Nsim]

# Metropolis - Hastings
X <- rep(runif(1), Nsim) # initialize the chain
for (i in 2:Nsim) {
  Y <- runif(1)
  rho <- dbeta(Y, a, b) / dbeta(X[i - 1], a, b)
  X[i] <- X[i - 1] + (Y - X[i - 1]) * (runif(1) < rho)
}

Στην εικόνα 6.2 βλέπουμε τα ιστογράμματα των δύο δειγμάτων με την πυκνότητα της κατανομής και παρατηρούμε ότι οι δύο αλγόριθμοι προσομοιώνουν ικανοποιητικά δείγματα, κάτι που μπορεί να επαληθευτεί με ένα έλεγχο Kolmogorov-Smirnov. Καθώς στον έλεγχο Kolmogorov - Smirnov δεν μπορούμε να έχουμε ίσες παρατηρήσεις, εδώ προσθέτουμε ένα τεχνικό θόρυβο στις παρατηρήσεις με τη συνάρτηση jitter(). Ακόμα μπορούμε να συγκρίνουμε τη θεωρητική μέση τιμή $a/(a+b)=0.3$ και τη θεωρητική διασπορά $ab/(a+b)^2(a+b+1)=0.205$ με τις αντίστοιχες δειγματικές.

ks.test(jitter(X[1001:Nsim]), rbeta(4000, a, b))
## 
##  Asymptotic two-sample Kolmogorov-Smirnov test
## 
## data:  jitter(X[1001:Nsim]) and rbeta(4000, a, b)
## D = 0.02525, p-value = 0.1561
## alternative hypothesis: two-sided
mean(X)
## [1] 0.2976115
var(X)
## [1] 0.02095261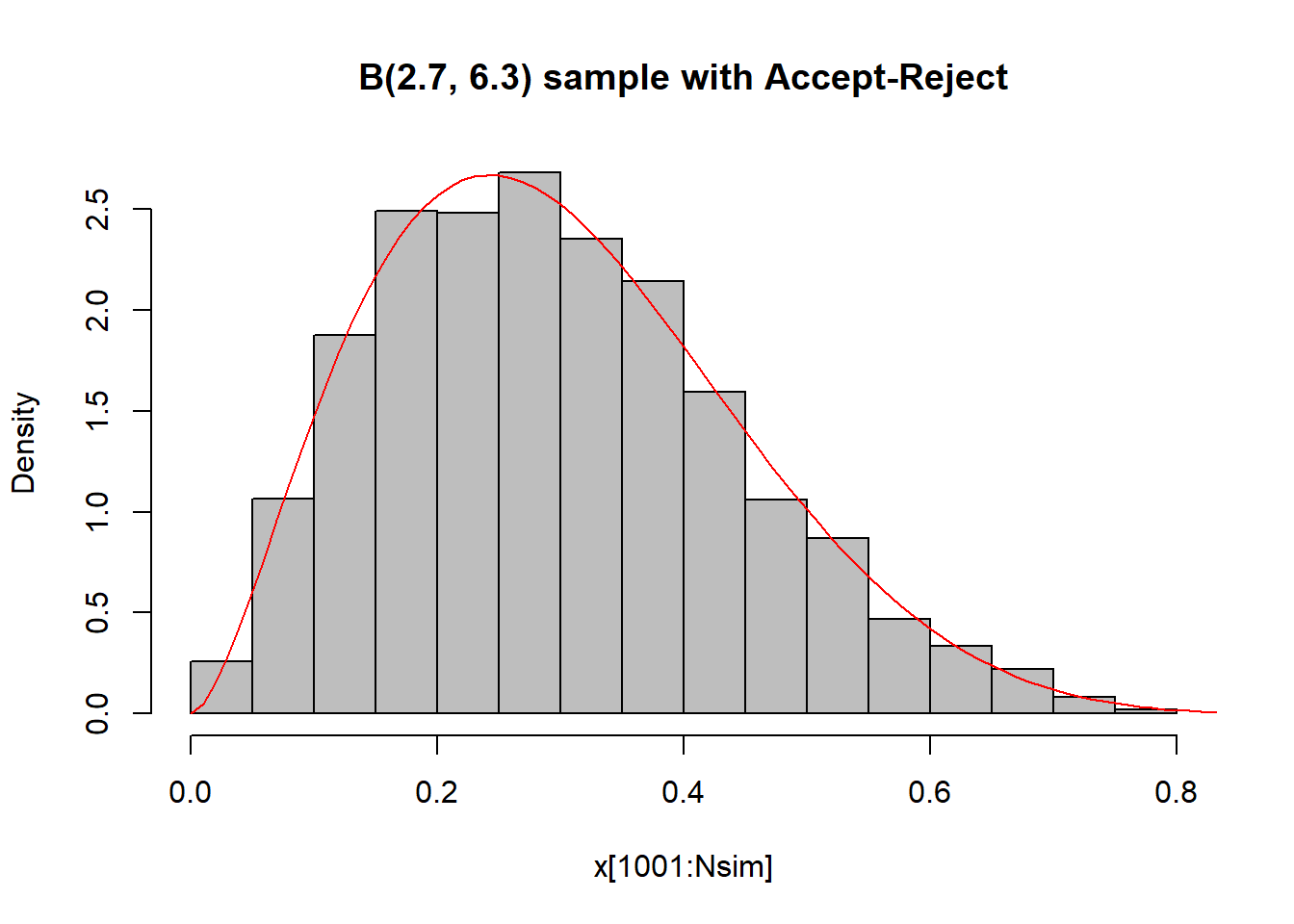

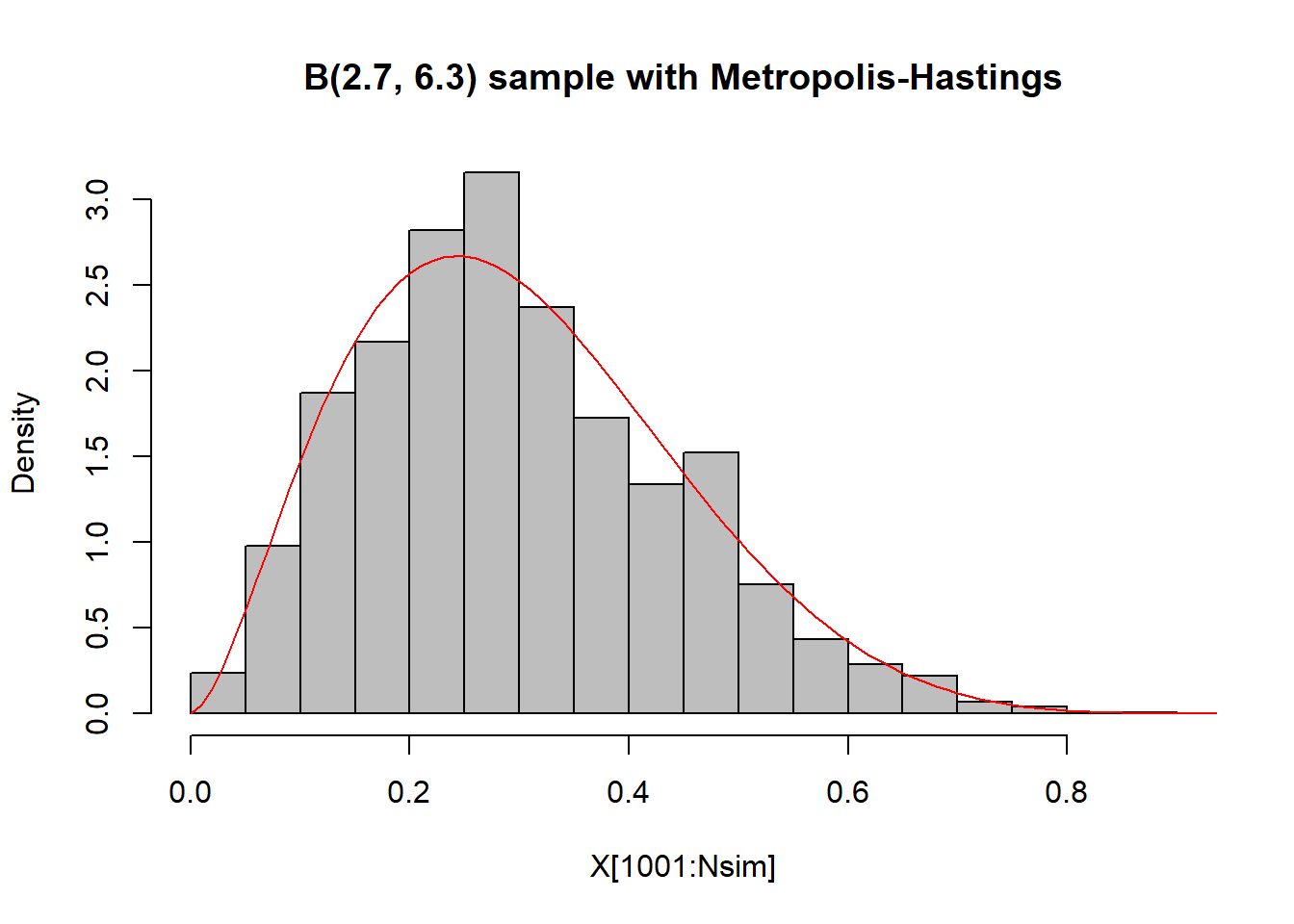
Histograms of $B(2.7, 6.3)$ random variables with density function overlaid. In the left panel, the variables were generated from an accept-reject algorithm with a uniform candidate, and in the right panel the random variables were generated from a Metropolis–Hastings algorithm.

Εικόνα 6.2: Histograms of $B(2.7, 6.3)$ random variables with density function overlaid. In the left panel, the variables were generated from an accept-reject algorithm with a uniform candidate, and in the right panel the random variables were generated from a Metropolis–Hastings algorithm.

Ας εστιάσουμε στην προσομοιωμένη ακολουθία του αλγορίθμου Metropolis-Hastings, για τις τιμές $4500 \leq t \leq 4800$, (εικόνα 6.3) παρατηρούμε ένα χαρακτηριστικό μοτίβο του αλγορίθμου, όπου η ακολουθία $X_t$ μένει σταθερή για κάποια βήματα καθώς οι αντίστοιχες παρατηρήσεις $Y_i$ απορρίπτονται.

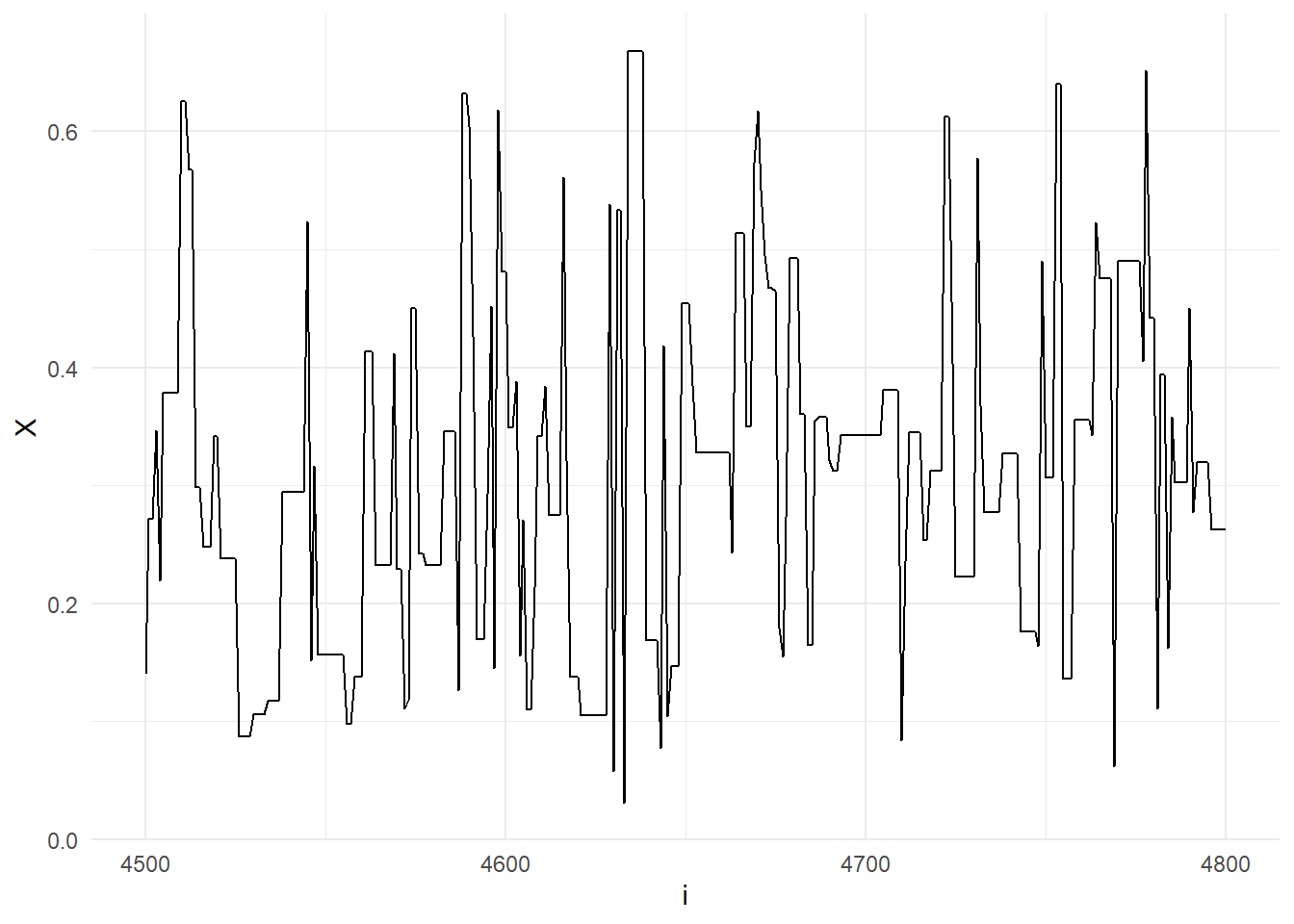
$Sequence $X_t$ for $t=4500, \dots, 4800$, when simulated from the Metropolis-Hastings algorithm with uniform proposal and $B(2.7, 6.3)$ target.$

Εικόνα 6.3: Sequence $X_t$ for $t=4500, \dots, 4800$, when simulated from the Metropolis-Hastings algorithm with uniform proposal and $B(2.7, 6.3)$ target.

Παρότι τα αποτελέσματα των δύο μεθόδων δείχνουν πανομοιότυπα, είναι σημαντικό να θυμόμαστε ότι οι παρατηρήσεις του δείγματος MCMC είναι συσχετισμένες, ενώ του αλγορίθμου αποδοχής-απόρριψης όχι. Αυτό σημαίνει πως οι MCMC μέθοδοι απαιτούν μεγαλύτερο αριθμό προσομοιώσεων για να πετύχουν την ίδια ακρίβεια.

Επανερχόμαστε στην μελέτη του αλγορίθμου Metropolis-Hastings. Στην συμμετρική περίπτωση (όπου $q(x|y)=q(y|x)$), η πιθανότητα αποδοχής $p(x_t,y_t)$ καθορίζεται από τον λόγο $f(y_t)/q(y_t|x_t)$ με αποτέλεσμα να είναι ανεξάρτητη της $q$. Γενικά, ο αλγόριθμος δέχεται πάντα τιμές $y_t$ που αυξάνουν το λόγο $f(y_t)/q(y_t|x_t)$ σε σχέση με την τιμή $f(x_t)/q(x_t|y_t)$. Παρ’ όλα αυτά, μερικές τιμές $y_t$ που ελαττώνουν το συγκεκριμένο λόγο μπορεί να γίνουν αποδεκτές, αλλά αν η μείωση είναι πολύ μεγάλη, είναι σχεδόν σίγουρο ότι η $y_t$ θα απορριφθεί. Η ιδιότητα αυτή υποδεικνύει πώς η επιλογή της $q$ επηρεάζει την αποδοτικότητα του αλγορίθμου Metropolis-Hastings. Αν ο χώρος που εξερευνά η $q$ (το στήριγμά της) είναι πολύ μικρός σε σύγκριση με της $f$, η μαρκοβιανή αλυσίδα είτε θα συγκλίνει πολύ αργά (στην πράξη πιθανώς να μην συγκλίνει καθόλου).

Μία ακόμα ενδιαφέρουσα ιδιότητα του αλγορίθμου Metropolis-Hastings που ενισχύει την απήχησή του είναι ότι εξαρτάται μόνο από τους λόγους $f(y_t)/f(x_t)$ και $q(x_t|y_t)/q(y_t)|x_t)$, επομένως δεν επηρεάζεται από άγνωστες σταθερές κανονικοποίησης. Επιπλέον, καθώς τα μόνα βήματα αφορούν (α) την προσομοίωση από την $q$ και (β) τον υπολογισμό του λόγου $f(y_t)/q(y_t|x_t)$, η $q$ μπορεί να επιλεγεί με τρόπο τέτοιο ώστε τα μη-υπολογίσιμα κομμάτια της $f$ να διαγραφούν από τον λόγο. Φυσικά, όταν αναφερόμαστε σε σταθερές κανονικοποίησης της $q(y|x)$, δεν εννοούμε σταθερές $c(x)$ που εξαρτώνται από την τιμή $x$ της δέσμευσης, καθώς αυτές δεν μπορούν να απλοποιηθούν.

6.3.1 Ο Ανεξάρτητος Αλγόριθμος Metropolis - Hastings

Ο αλγόριθμος Metropolis - Hastings που αναλύσαμε παραπάνω κάνει χρήση μίας πυκνότητας $q(y|x)$ που εξαρτάται από την παρούσα κατάσταση της αλυσίδας. Εάν επιλέξουμε μία πυκνότητα $g(y)$ ανεξάρτητη της παρούσας κατάστασης, έχουμε μία ειδική περίπτωση του αλγορίθμου Metropolis - Hastings.

Αλγόριθμος Metropolis - Hastings

Για δεδομένο $x_t$,

Προσομοιώνουμε $Y_t\sim g\left(y\right)$
Επιλέγουμε \[\begin{equation*} X_{t+1} = \left\{ \begin{array}{ccl} Y_t & \text{με πιθ.} & p\left(x_t, Y_t\right) \\ x_t & \text{με πιθ.} & 1-p\left(x_t, Y_t\right) \end{array}\right. \end{equation*}\] όπου \[\begin{equation*} p(x,y) = \min \left\{ \frac{f(y)}{f(x)} \frac{g(x)}{g(y)}, 1 \right\}. \end{equation*}\]

Αυτή η ειδική περίπτωση του αλγορίθμου Metropolis-Hastings μπορεί να θεωρηθεί γενίκευση του αλγορίθμου αποδοχής - απόρριψης. Οι δύο αλγόριθμοι παρουσιάζουν πολλές ομοιότητες οι οποίες επιτρέπουν τη σύγκρισή τους, αν και σπάνια θα χρησιμοποιούσαμε Metropolis-Hastings σε ένα πρόβλημα που μπορεί να λυθεί με αλγόριθμο αποδοχής - απόρριψης. Μερικές σημαντικές διαφορές των δύο αλγορίθμων είναι:

Ο αλγόριθμος αποδοχής - απόρριψης δημιουργεί ένα δείγμα ανεξάρτητων παρατηρήσεων, ενώ ο αλγόριθμος Metropolis - Hastings όχι. Παρότι τα $Y_t$ προσομοιώνονται ανεξάρτητα, το τελικό δείγμα δεν αποτελείται από ανεξάρτητες παρατηρήσεις, αφού η πιθανότητα αποδοχής της $Y_t$ εξαρτάται από την $X_t$ (εκτός από την τετριμμένη περίπτωση $f=g$).
Το δείγμα του Metropolis - Hastings περιέχει επαναλήψεις των ίδιων τιμών, καθώς αν η $Y_t$ απορριφθεί, θα έχουμε $X_{t+1}=X_t$. Αυτό κάνει απαγορευτική τη χρήση ελέγχων που δεν δέχονται επαναλήψεις τιμών, όπως το Kolmogorov-Smirnov.
Ο αλγόριθμος αποδοχής - απόρριψης προϋποθέτει τον υπολογισμό της σταθεράς $M\geq \sup_x f(x)/g(x)$, ενώ ο Metropolis - Hastings όχι. Αυτό είναι ένα από τα χαρακτηριστικά που ενισχύουν την απήχηση του Metropolis - Hastings σε περιπτώσεις που ο υπολογισμός της $M$ είναι αδύνατος ή μη-αποδοτικός.

Άσκηση 6.1 (Robert & Casella 6.4.) Έστω ότι θέλουμε να προσομοιώσουμε από την κατανομή $\Gamma(a,\beta)$ με υποψήφια πυκνότητα από την $\Gamma([a],\lambda)$, όπου με $[a]$ συμβολίζουμε το ακέραιο μέρος του $a$.

Δημιουργήστε ένα αλγόριθμο αποδοχής - απόρριψης και δείξτε ότι, όταν $\beta=1$, η βέλτιστη επιλογή του $\lambda$ είναι $\lambda=[a]/a$.
Προσομοιώστε $5000$ παρατηρήσεις από την $\Gamma(4, 4/4.85)$ και δημιουργήστε ένα δείγμα από την $\Gamma(4.85, 1)$ (κρατώντας μόνο τις αποδεκτές παρατηρήσεις του αλγορίθμου αποδοχής - απόρριψης).
Επαναλάβετε τη διαδικασία του ερωτήματος b. με τον αλγόριθμο Metropolis - Hastings.
Συγκρίνετε (i) τους ρυθμούς αποδοχής και (ii) τις εκτιμήσεις της μέσης τιμής και της διασποράς, καθώς και τα τυπικά σφάλματα των δύο αλγορίθμων.

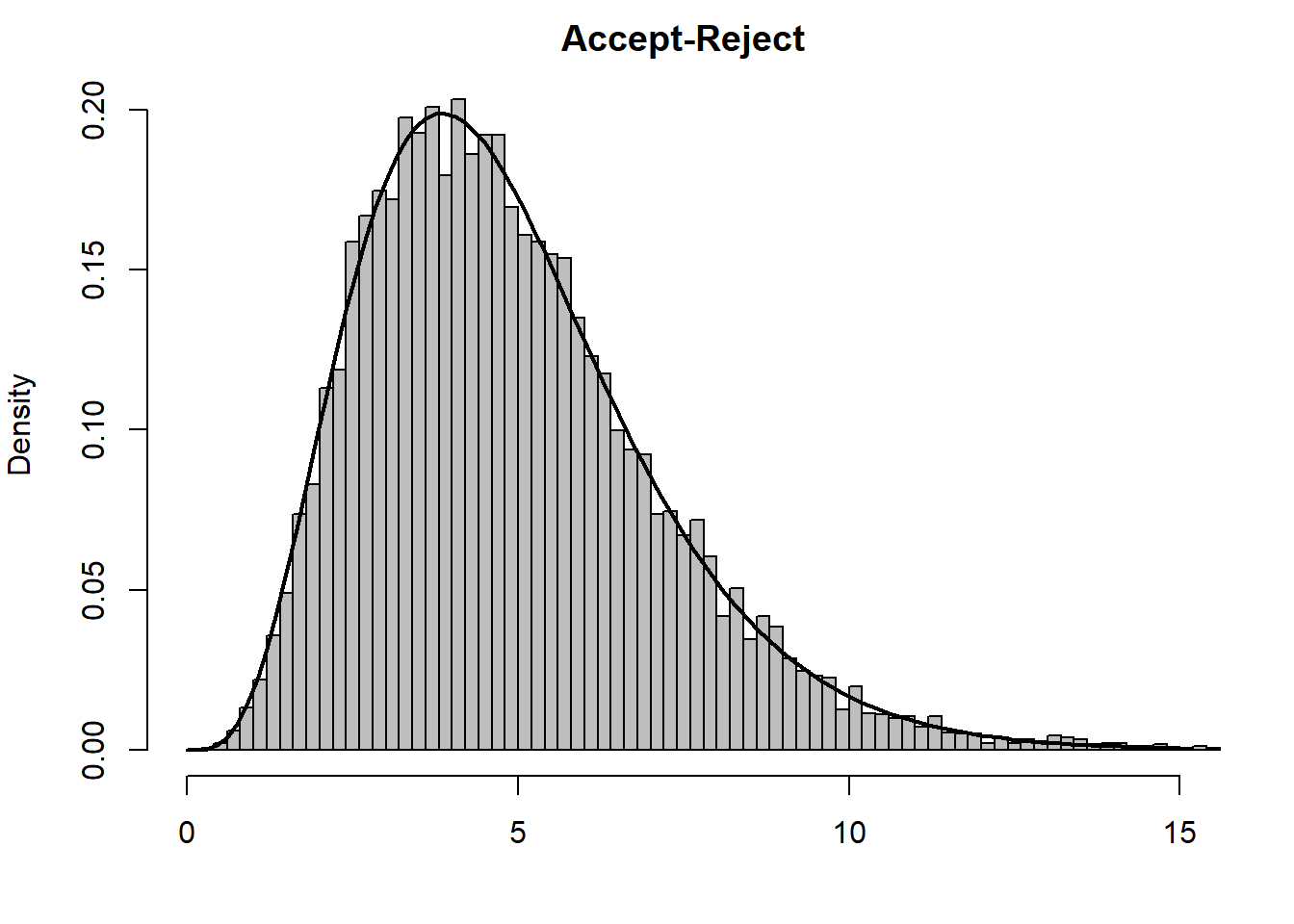
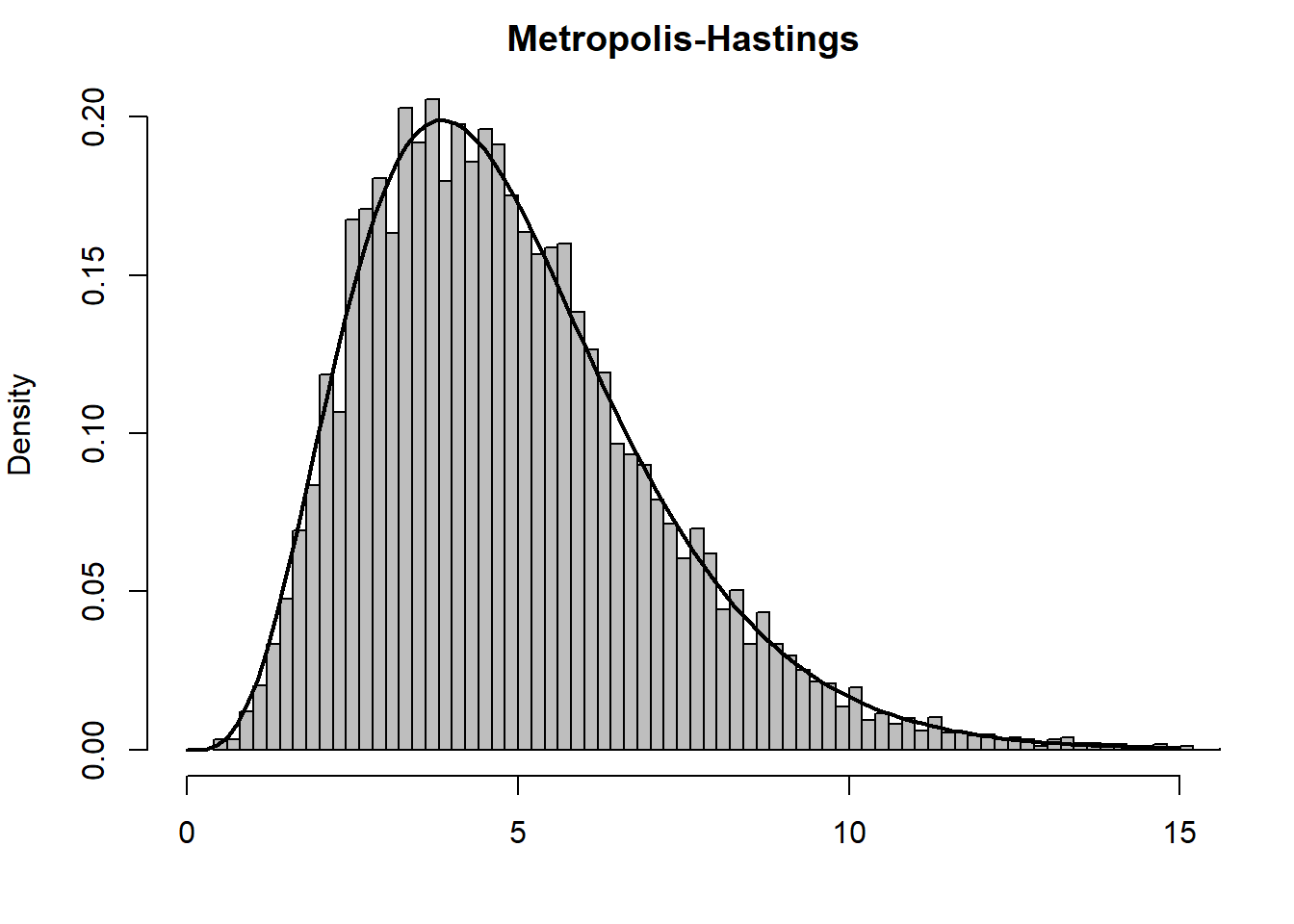
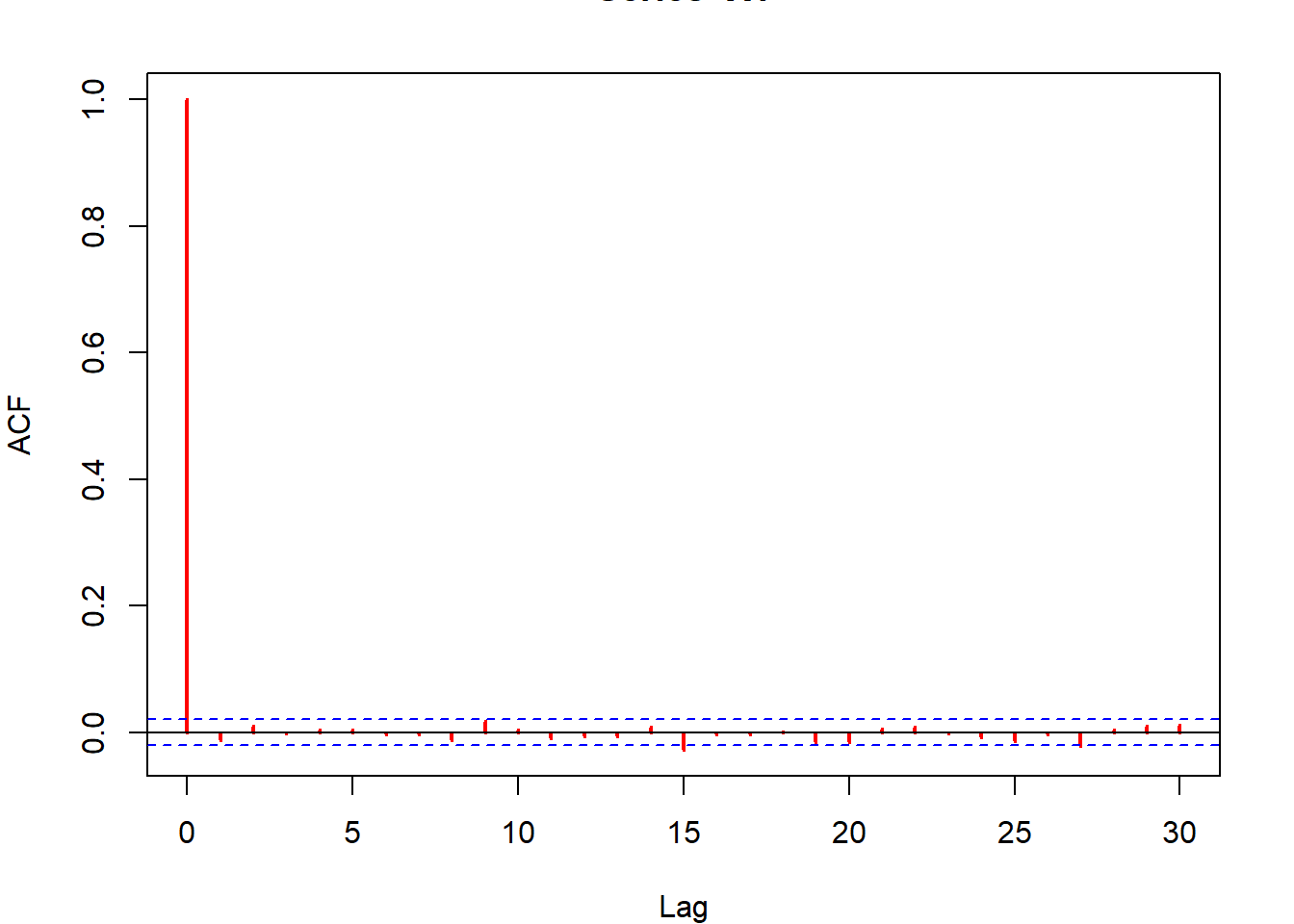
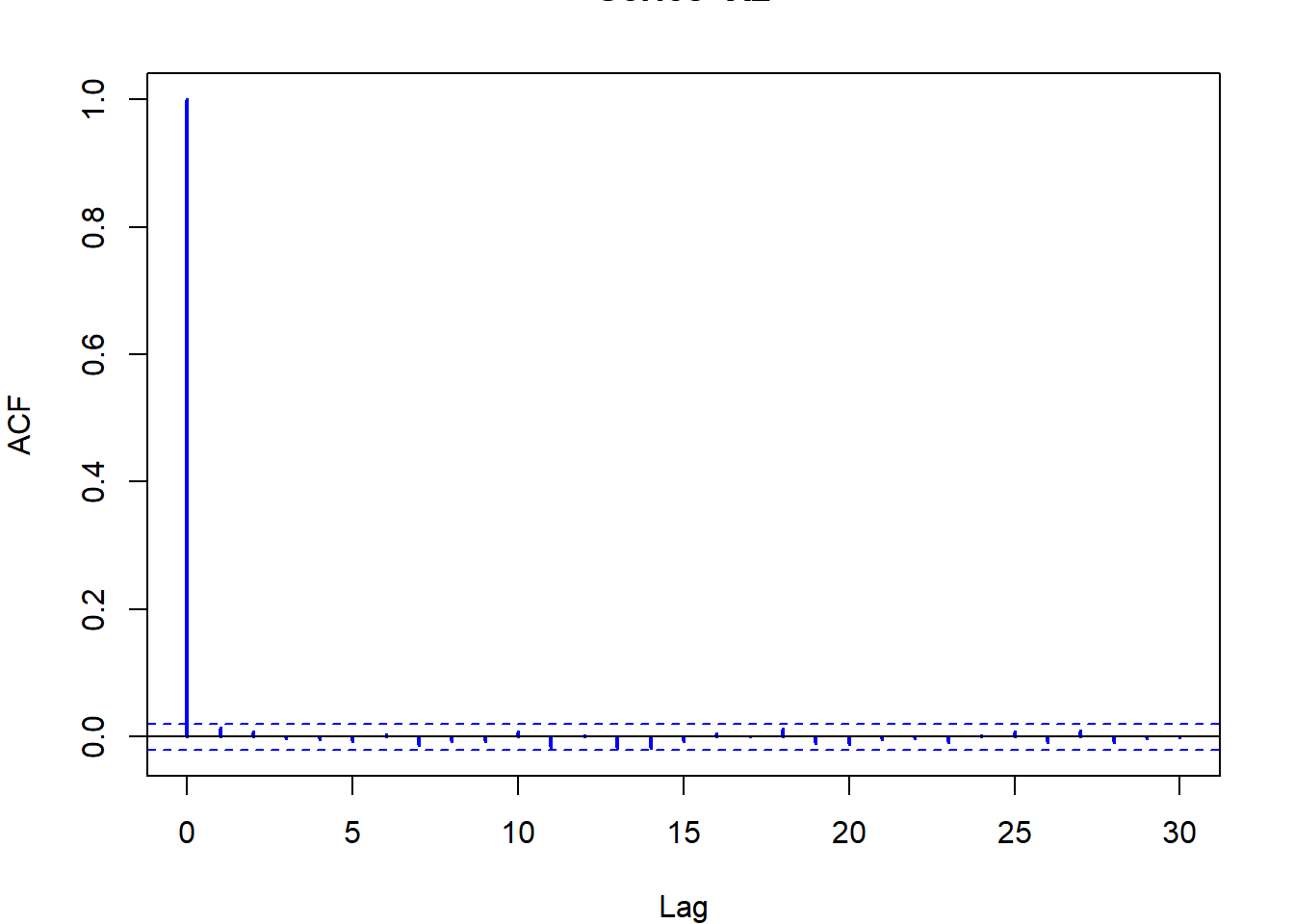
$Histograms and autocovariance functions from a gamma Accept–Reject algorithm (left panels) and a gamma Metropolis–Hastings algorithm (right panels). The target is a $\Gamma(4.85, 1)$ distribution and the candidate is a $\Gamma(4, 4/4.85)$ distribution. The autocovariance function is calculated with the R function acf.$ $Histograms and autocovariance functions from a gamma Accept–Reject algorithm (left panels) and a gamma Metropolis–Hastings algorithm (right panels). The target is a $\Gamma(4.85, 1)$ distribution and the candidate is a $\Gamma(4, 4/4.85)$ distribution. The autocovariance function is calculated with the R function acf.$ $Histograms and autocovariance functions from a gamma Accept–Reject algorithm (left panels) and a gamma Metropolis–Hastings algorithm (right panels). The target is a $\Gamma(4.85, 1)$ distribution and the candidate is a $\Gamma(4, 4/4.85)$ distribution. The autocovariance function is calculated with the R function acf.$ $Histograms and autocovariance functions from a gamma Accept–Reject algorithm (left panels) and a gamma Metropolis–Hastings algorithm (right panels). The target is a $\Gamma(4.85, 1)$ distribution and the candidate is a $\Gamma(4, 4/4.85)$ distribution. The autocovariance function is calculated with the R function acf.$

Εικόνα 6.4: Histograms and autocovariance functions from a gamma Accept–Reject algorithm (left panels) and a gamma Metropolis–Hastings algorithm (right panels). The target is a $\Gamma(4.85, 1)$ distribution and the candidate is a $\Gamma(4, 4/4.85)$ distribution. The autocovariance function is calculated with the R function acf.

# Accept - Reject
mean(X1) ; var(X1) 
## [1] 4.898297
## [1] 5.093071

# Metropolis - Hastings
mean(X2[2500:nsim]) ; var(X2[2500:nsim])
## [1] NA
## [1] NA

Παράδειγμα 6.2 (Robert & Casella 6.2.) Θα χρησιμοποιήσουμε τον αλγόριθμο Metropolis - Hastings για να δημιουργήσουμε παρατηρήσεις από την κατανομή Cauchy $\mathcal{C}(0,1)$, έχοντας την $\mathcal{N}(0,1)$ ως υποψήφια πυκνότητα. Αυτό μπορεί να επιτευχθεί με τον ακόλουθο κώδικα:

nsim <- 10 ^ 4
X <- Z <- c(rt(1, 1))  # initialize the chain from the stationary
for (t in 2:nsim){
  Y <- rnorm(1) # candidate normal
  rho <- min(1, dt(Y, 1) * dnorm(X[t - 1]) / (dt(X[t - 1], 1) * dnorm(Y)))
  X[t] <- X[t - 1] + (Y - X[t - 1]) * (runif(1) < rho)
}

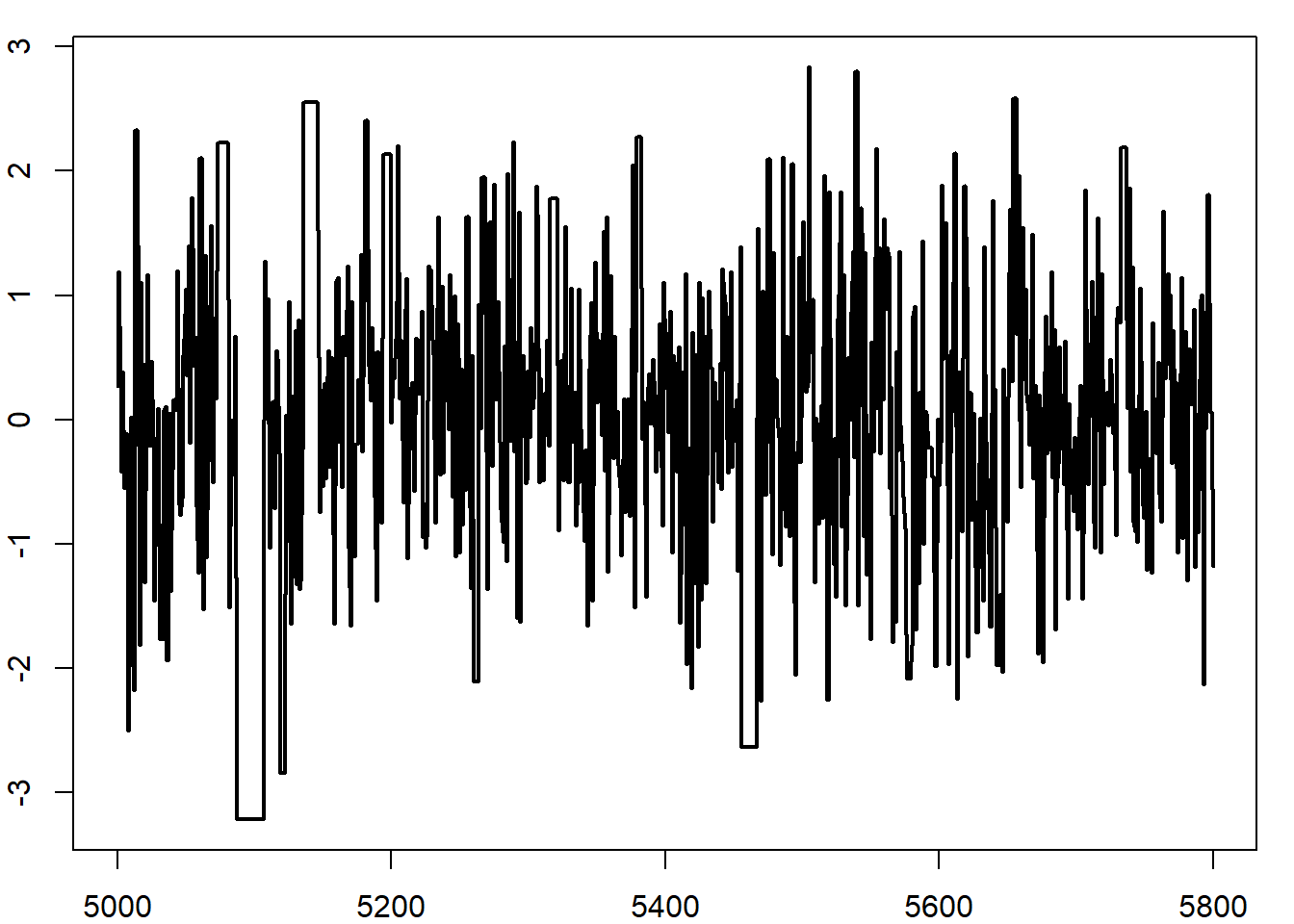
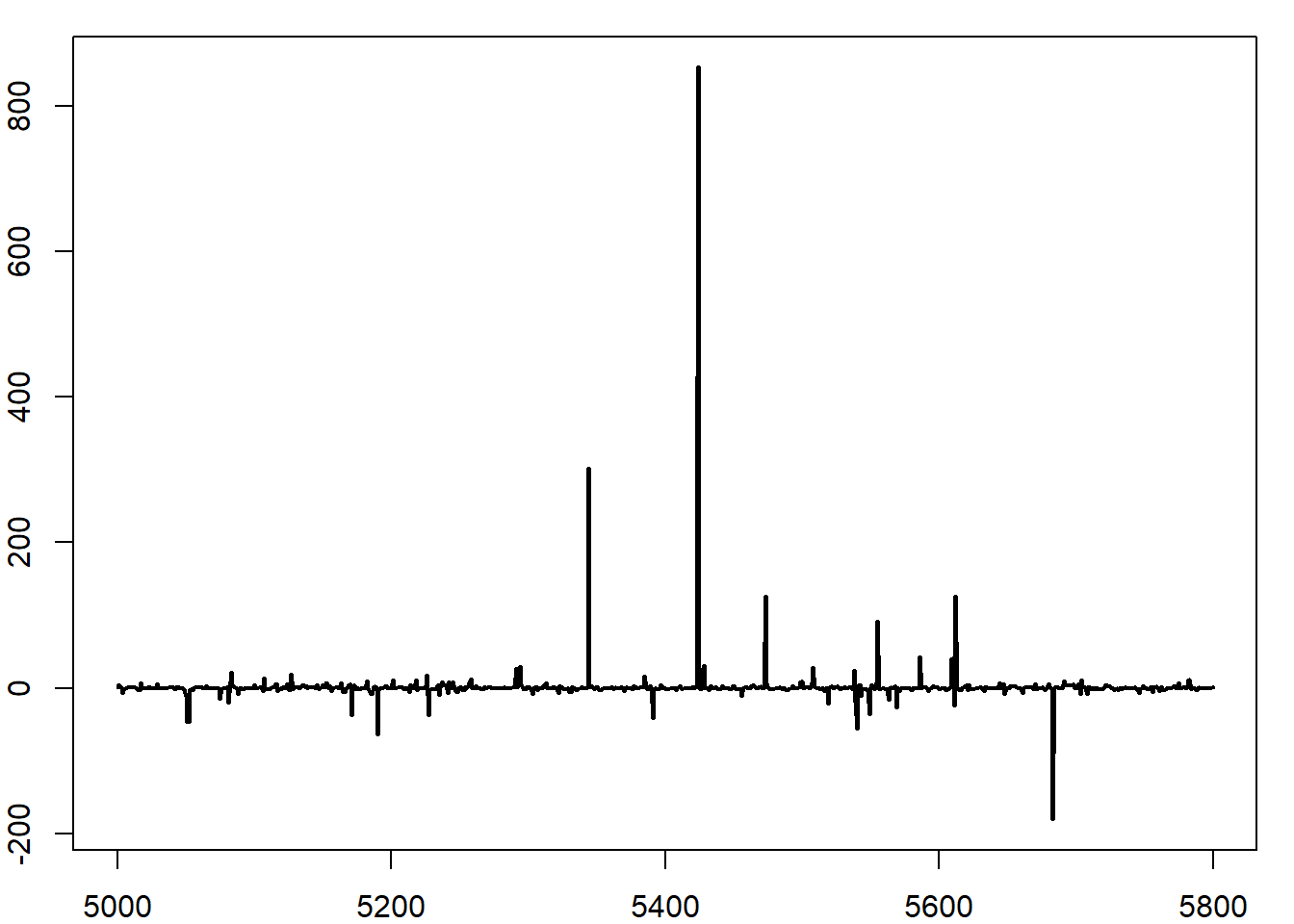
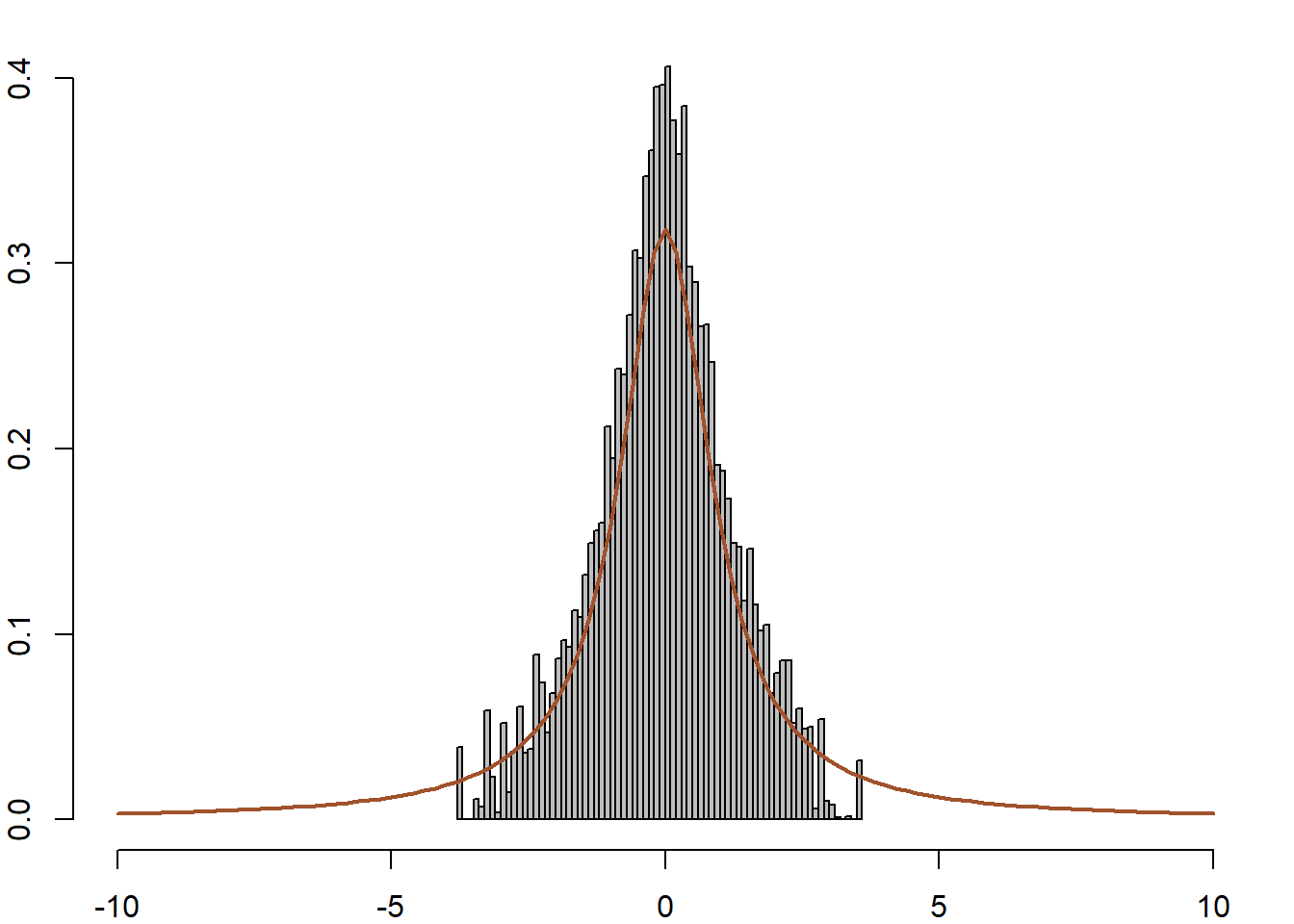
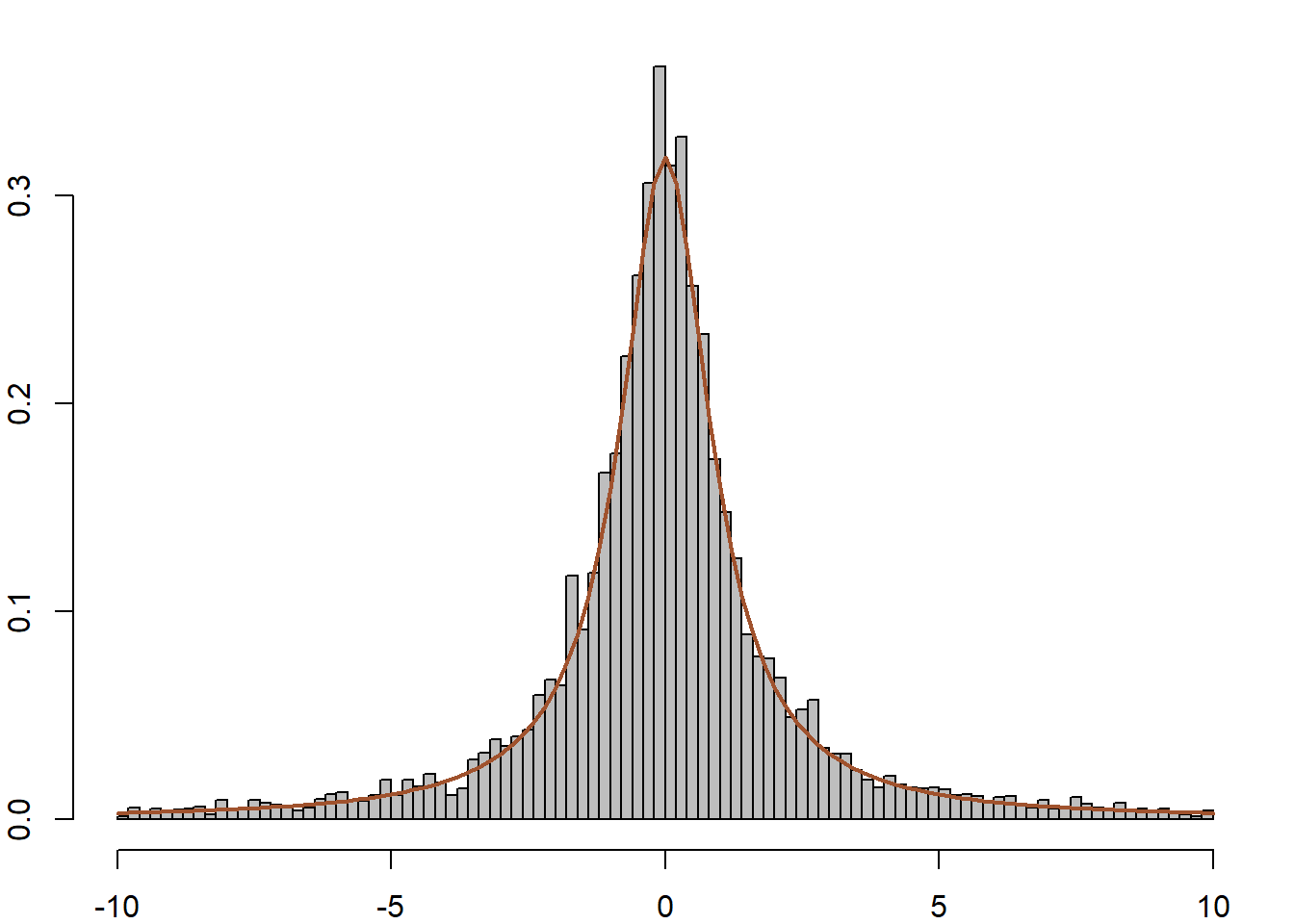
Το πρώτο σημείο που χρειάζεται προσοχή, είναι ότι αν ξεκινήσουμε με μία μεγάλη τιμή, όπως $x_0=12.788$. Σε αυτή την περίπτωση, έχουμε $f(x_0)$ πρακτικά ίση με 0, κάτι που οδηγεί σε σίγουρη απόρριψη, με αποτέλεσμα η αλυσίδα να μείνει σταθερή για όλες τις $10^4$ επαναλήψεις. Αν η αλυσίδα ξεκινήσει από ένα κεντρικό σημείο, το αποτέλεσμα θυμίζει πολύ περισσότερο την κανονική κατανομή απ’ ότι την Cauchy, όπως φαίνεται στην εικόνα 6.5 (κέντρο δεξιά). Επιπλέον, πολύ μεγάλες τιμές της ακολουθίας θα έχουν μεγάλα βάρη, με αποτέλεσμα η αλυσίδα να μείνει σταθερή για μεγάλο χρονικό διάστημα ( εικόνα 6.5 πάνω αριστερά, κέντρο αριστερά).

Αντίθετα, αν χρησιμοποιήσουμε ανεξάρτητο Metropolis - Hastings προτείνοντας από τη κατανομή Student με $0.5$ βαθμούς ελευθερίας, η συμπεριφορά της αλυσίδας είναι τελείως διαφορετική. Η $Y_t$ παίρνει πιο συχνά μεγάλες τιμές, (εικόνα 6.5 πάνω δεξιά), το ιστόγραμμα προσαρμόζεται αρκετά καλά (κέντρο δεξιά) και η αλυσίδα δεν παρουσιάζει ορατή συσχέτιση (κάτω δεξιά).

set.seed(1)

#Section 6.2.2, Cauchy generator of example 6.2
nsim <- 10 ^ 4
X <- Z <- c(rt(1, 1))  # initialize the chain from the stationary
for (t in 2:nsim){
  Y <- rnorm(1) # candidate normal
  rho <- min(1, dt(Y, 1) * dnorm(X[t - 1]) / (dt(X[t - 1], 1) * dnorm(Y)))
  X[t] <- X[t - 1] + (Y - X[t - 1]) * (runif(1) < rho)
  Y <- rt(1, .5)  # candidate t
  rho <- min(1, dt(Y, 1) * dt(Z[t - 1], .5) / (dt(Z[t - 1], 1) * dt(Y, .5)))
  Z[t] <- Z[t - 1] + (Y - Z[t - 1]) * (runif(1) < rho)
}

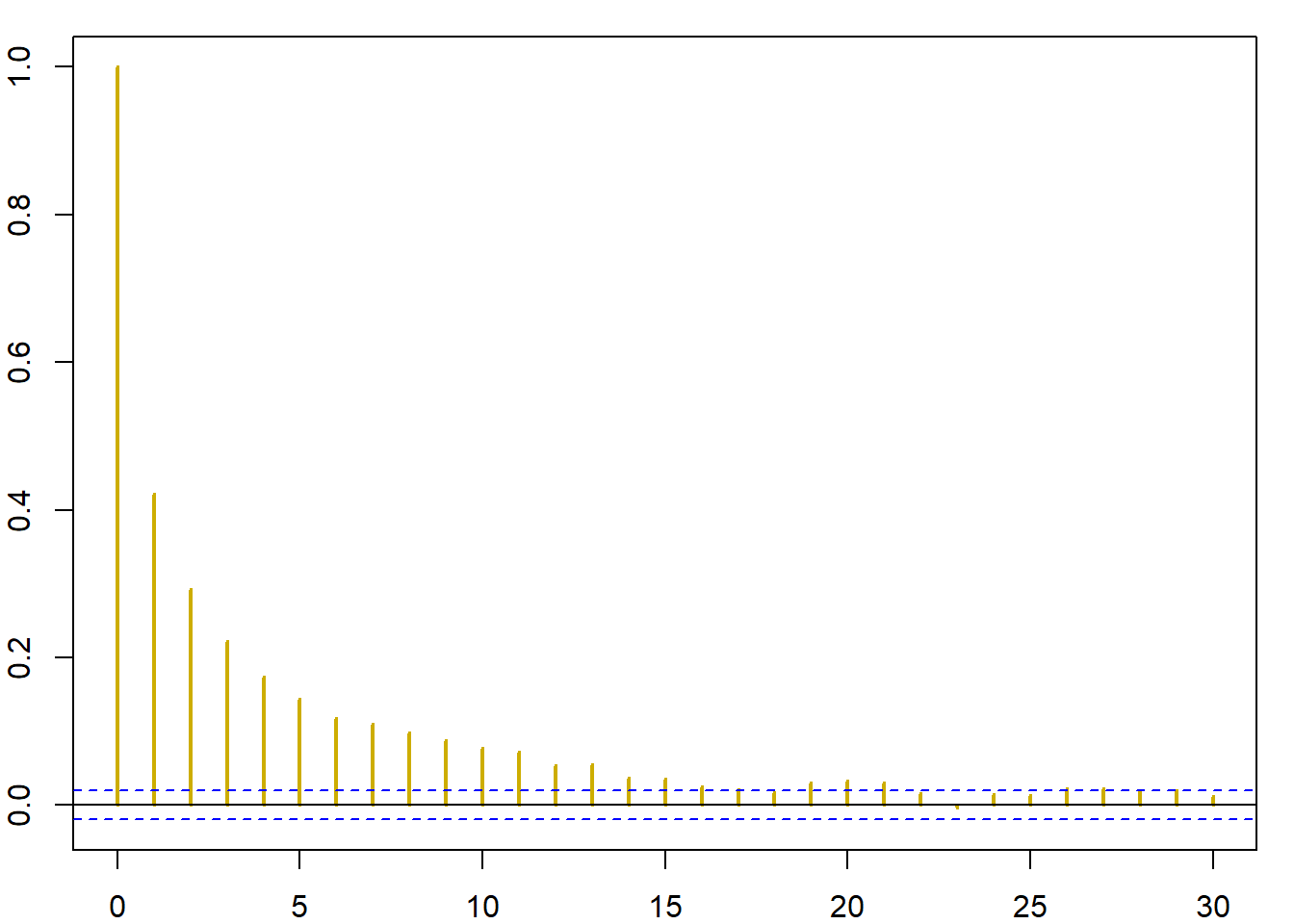
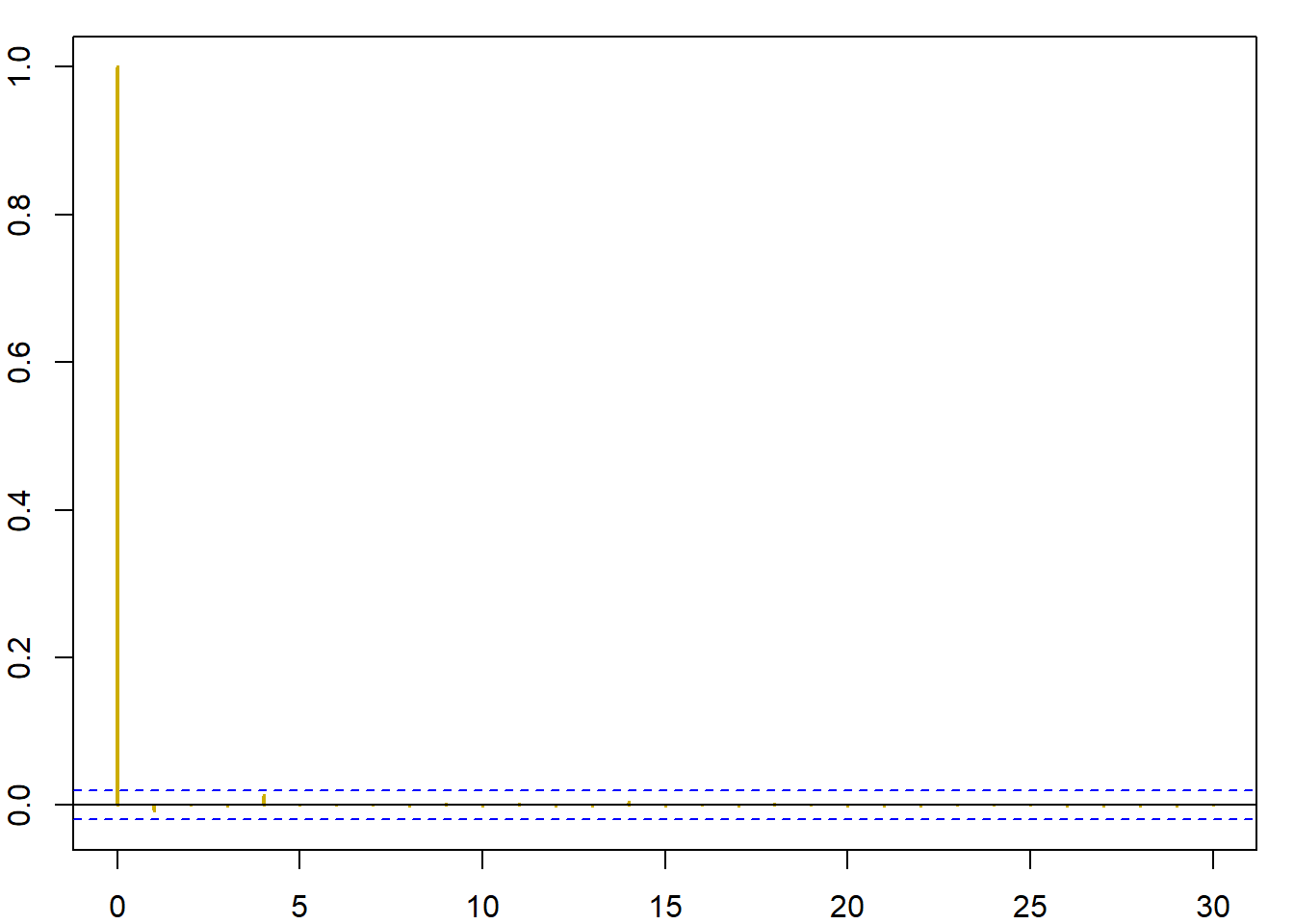
$Comparison of two Metropolis–Hastings schemes for a Cauchy target when generating (left) from a $\mathcal{N}(0,1)$ proposal and (right) from a $T_{1/2}$ proposal based on 105 simulations. (top) Excerpt from the chains $X_t$ ; (center) histograms of the samples; (bottom) autocorrelation graphs obtained by acf.$ $Comparison of two Metropolis–Hastings schemes for a Cauchy target when generating (left) from a $\mathcal{N}(0,1)$ proposal and (right) from a $T_{1/2}$ proposal based on 105 simulations. (top) Excerpt from the chains $X_t$ ; (center) histograms of the samples; (bottom) autocorrelation graphs obtained by acf.$ $Comparison of two Metropolis–Hastings schemes for a Cauchy target when generating (left) from a $\mathcal{N}(0,1)$ proposal and (right) from a $T_{1/2}$ proposal based on 105 simulations. (top) Excerpt from the chains $X_t$ ; (center) histograms of the samples; (bottom) autocorrelation graphs obtained by acf.$ $Comparison of two Metropolis–Hastings schemes for a Cauchy target when generating (left) from a $\mathcal{N}(0,1)$ proposal and (right) from a $T_{1/2}$ proposal based on 105 simulations. (top) Excerpt from the chains $X_t$ ; (center) histograms of the samples; (bottom) autocorrelation graphs obtained by acf.$ $Comparison of two Metropolis–Hastings schemes for a Cauchy target when generating (left) from a $\mathcal{N}(0,1)$ proposal and (right) from a $T_{1/2}$ proposal based on 105 simulations. (top) Excerpt from the chains $X_t$ ; (center) histograms of the samples; (bottom) autocorrelation graphs obtained by acf.$ $Comparison of two Metropolis–Hastings schemes for a Cauchy target when generating (left) from a $\mathcal{N}(0,1)$ proposal and (right) from a $T_{1/2}$ proposal based on 105 simulations. (top) Excerpt from the chains $X_t$ ; (center) histograms of the samples; (bottom) autocorrelation graphs obtained by acf.$

Εικόνα 6.5: Comparison of two Metropolis–Hastings schemes for a Cauchy target when generating (left) from a $\mathcal{N}(0,1)$ proposal and (right) from a $T_{1/2}$ proposal based on 105 simulations. (top) Excerpt from the chains $X_t$ ; (center) histograms of the samples; (bottom) autocorrelation graphs obtained by acf.

Αν μας ενδιαφέρει η προσέγγιση της πιθανότητας $\mathbf{P}(X<3)=$ 0.898, η διαφορά ανάμεσα στις δύο επιλογές υποψήφιας πυκνότητας είναι ξεκάθαρη (εικόνα 6.6). Παρότι θεωρητικά και οι δύο αλυσίδες συγκλίνουν, η αλυσίδα με υποψήφια πυκνότητα την κανονική συγκλίνει τόσο αργά που πρακτικά στο μέγεθος δείγματος $n=10^4$ που χρησιμοποιήσαμε δεν πλησιάζει καν την πραγματική τιμή.

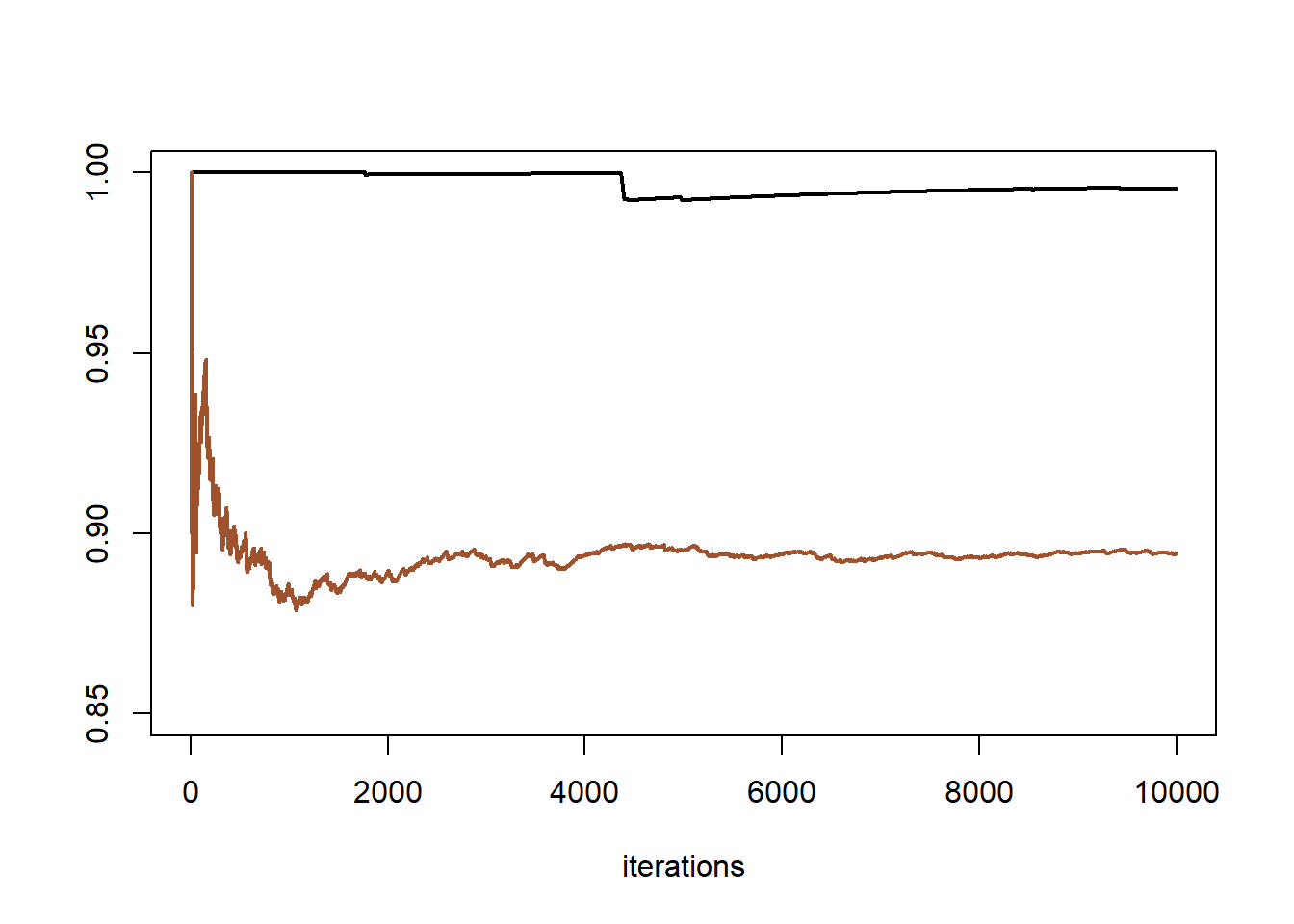
$Cumulative coverage plot of a Cauchy sequence generated by a Metropolis–Hastings algorithm based on a $\mathcal{N}(0,1)$ proposal (upper lines) and one generated by a Metropolis–Hastings algorithm based on a $T_{1/2}$ proposal (lower lines). After 105 iterations, the Metropolis–Hastings algorithm based on the normal proposal has not yet converged.$

Εικόνα 6.6: Cumulative coverage plot of a Cauchy sequence generated by a Metropolis–Hastings algorithm based on a $\mathcal{N}(0,1)$ proposal (upper lines) and one generated by a Metropolis–Hastings algorithm based on a $T_{1/2}$ proposal (lower lines). After 105 iterations, the Metropolis–Hastings algorithm based on the normal proposal has not yet converged.

Κοιτάμε τώρα ένα πιο ρεαλιστικό παράδειγμα που ανταποκρίνεται στο γενικότερο πλαίσιο όπου η ανεξάρτητη υποψήφια προκύπτει από μία αρχική εκτίμηση των παραμέτρων του μοντέλου. Για παράδειγμα, όταν προσομοιώνουμε από την posterior κατανομή $\pi(\theta|x) \propto \pi(\theta) f(x|\theta)$, αυτή η ανεξάρτηση υποψήφια πυκνότητα θα μπορούσε να είναι της κανονικής ή της Student, κεντραρισμένη στην ε.μ.π. $\widehat{\theta}$ και με πίνακα διασπορών-συνδιασπορών ίσο με τον αντίστροφο του πίνακα πληροφορίας του Fisher.

Παράδειγμα 6.3 (Robert & Casella 6.3.) Το σετ δεδομένων cars περιλαμβάνει ένα δείγμα αυτοκινήτων για τα οποία έχουν μετρηθεί η απόσταση πεδήσεως $y$ για ταχύτητα $x$. Η εικόνα 6.7 δείχνει μία προσαρμοσμένη τετραγωνική καμπύλη στα δεδομένα χρησιμοποιώντας τη συνάρτηση lm της R. Το μοντέλο περιγράφεται ως \[\begin{equation*} y_{ij} = a+bx_i +cx_i^2 +e_{ij}, \ i=1,\dots, k, j=1, \dots, n_i, \end{equation*}\] όπου υποθέτουμε ότι $e_{ij}\sim \mathcal{N}(0,\sigma^2)$, ανεξάρτητα. Η συνάρτηση πιθανοφάνειας είναι τότε ανάλογη της ποσότητας \[\begin{equation*} L(\theta) \propto \left(\frac{1}{\sigma^2}\right)^{N/2} e^{-\frac{1}{2\sigma^2} \sum_{ij} (y_{ij} -a -bx_i -cx_i^2 )^2}, \end{equation*}\] όπου $N=\sum_i n_i$ είναι ο συνολικός αριθμός παρατηρήσεων. Μπορούμε να δούμε αυτή τη συνάρτηση πιθανοφάνειας ως posterior κατανομή των $a,b,c,\sigma^2$ (έχοντας μία σταθερή prior) και, ως απλό παράδειγμα, μπορούμε να δοκιμάσουμε να προσομοιώσουμε από την κατανομή αυτή με ένα αλγόριθμο Metropolis-Hastings. Για αρχή, χρειαζόμαστε τις ε.μ.π. που προκύπτουν από το γραμμικό μοντέλο.

data <- cars
x <- data[, 1]
y <- data[, 2]
x2 <- x ^ 2
summary(lm(y ~ x + x2))
## 
## Call:
## lm(formula = y ~ x + x2)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -28.720  -9.184  -3.188   4.628  45.152 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)
## (Intercept)  2.47014   14.81716   0.167    0.868
## x            0.91329    2.03422   0.449    0.656
## x2           0.09996    0.06597   1.515    0.136
## 
## Residual standard error: 15.18 on 47 degrees of freedom
## Multiple R-squared:  0.6673, Adjusted R-squared:  0.6532 
## F-statistic: 47.14 on 2 and 47 DF,  p-value: 5.852e-12

Επιλέγουμε λοιπόν υποψήφιες κατανομές \[\begin{align*} a &\sim\mathcal{N}\left(2.63, 14.8^2\right), \\ b &\sim\mathcal{N}\left(0.887, 2.03^2\right), \\ c &\sim\mathcal{N}\left(0.100, 0.065^2\right), \\ \sigma^{-2} &\sim \Gamma\left(n/2, (n-3)(15.17)^2\right) \end{align*}\] με τις οποίες προσομοιώνουμε παρατηρήσεις $(a(i), b(i), c(i))$. Η εικόνα 6.7 αποτυπώνει τη μεταβλητότητα των παραγόμενων καμπυλών.

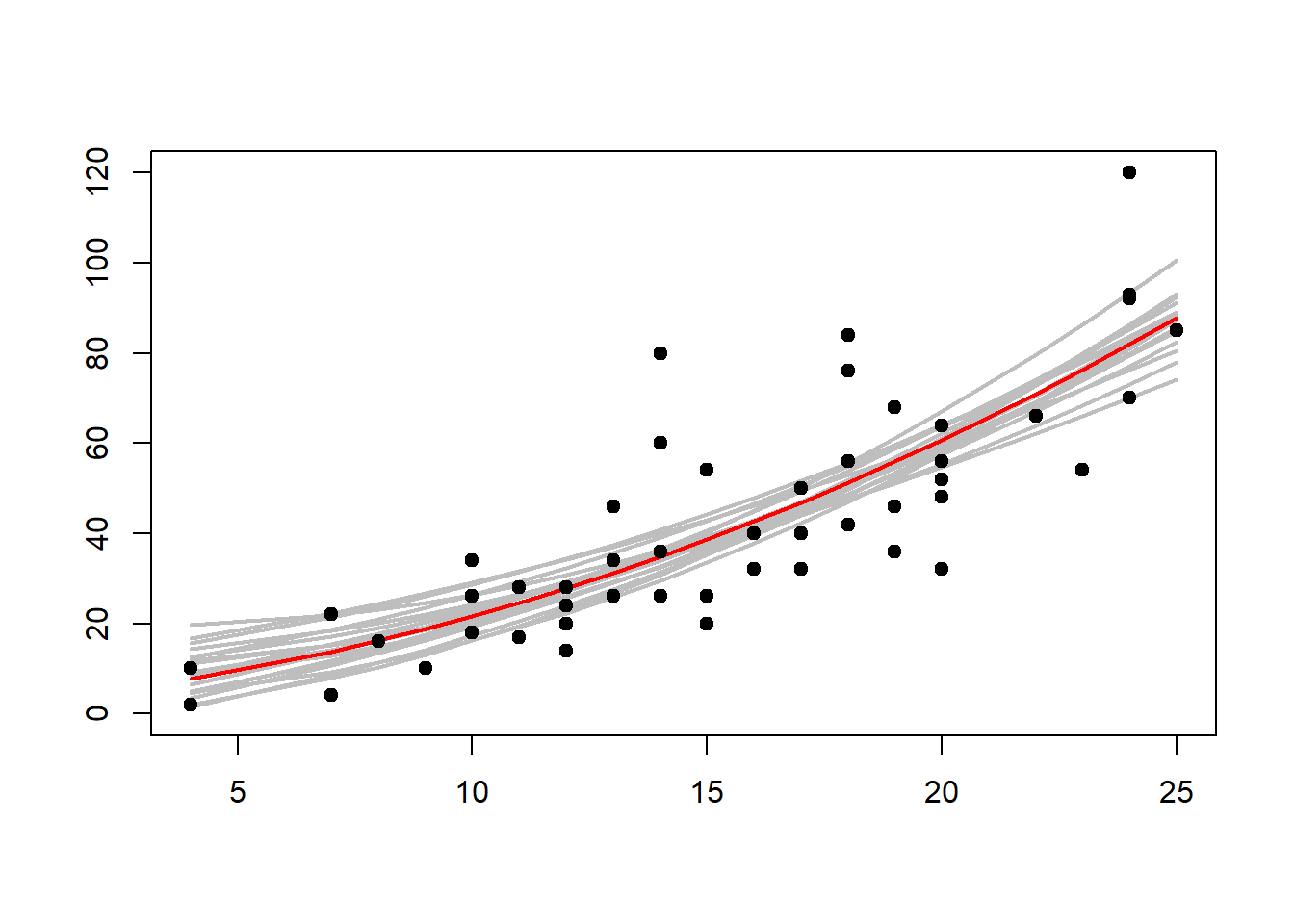
Braking data with quadratic curve (red) fitted with the least squares / mle function lm. The grey curves represent the Monte Carlo sample $(a(i), b(i), c(i))$ and show the variability in the fitted lines based on the last $500$ iterations of $4000$ simulations.

Εικόνα 6.7: Braking data with quadratic curve (red) fitted with the least squares / mle function lm. The grey curves represent the Monte Carlo sample $(a(i), b(i), c(i))$ and show the variability in the fitted lines based on the last $500$ iterations of $4000$ simulations.