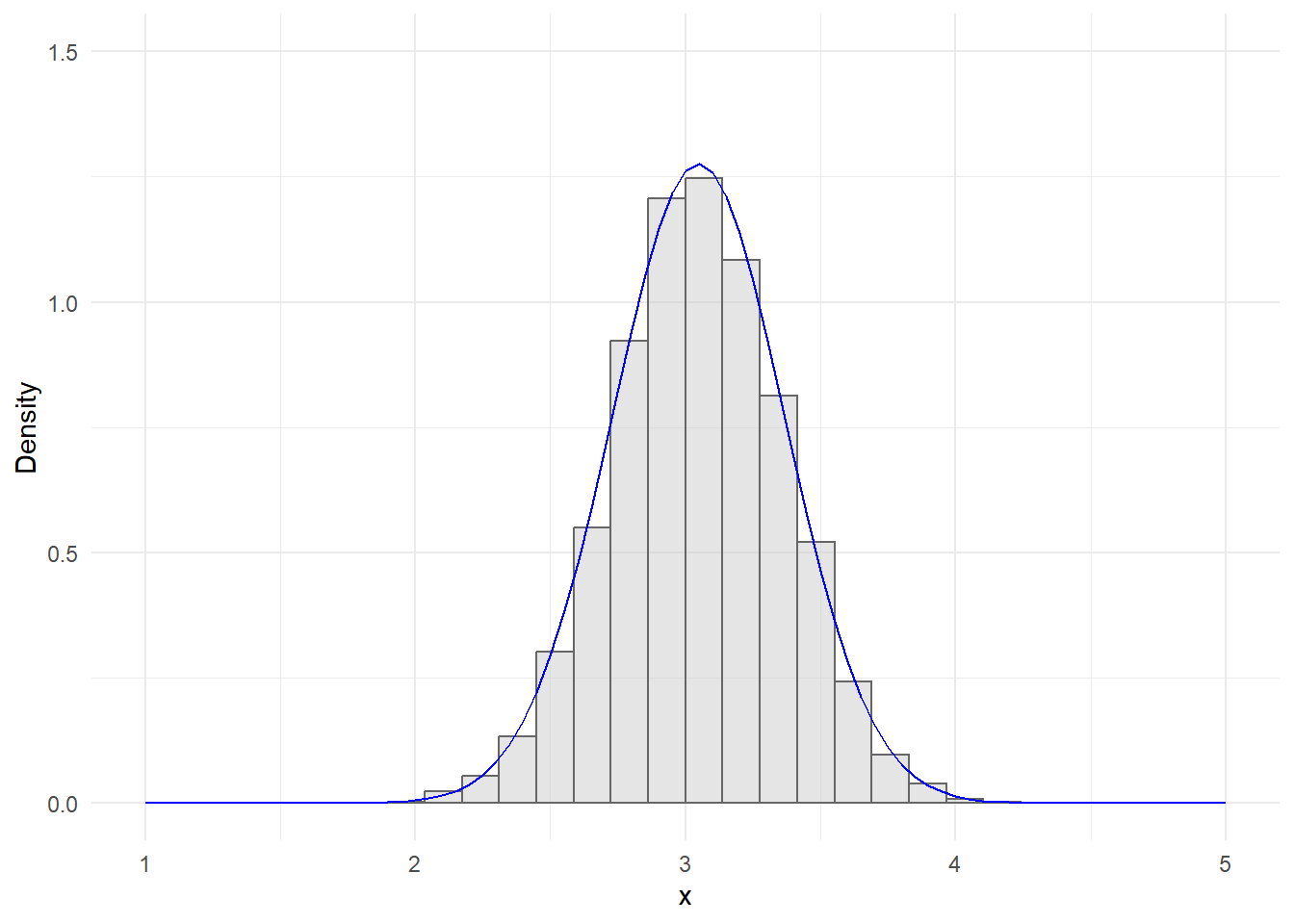
3 Προσομοίωση Τυχαίων Μεταβλητών

Όλα τα προβλήματα στατιστικής ξεκινούν με την φράση “Έστω δείγμα \(X_1, \dots, X_n\) από την κανονική κατανομή \(\mathcal{N}(\mu,\sigma^2)\)”. Πώς όμως μπορούμε να φτιάξουμε ένα τέτοιο δείγμα στην πράξη; Η δυνατότητα προσομοίωσης δεδομένων σύμφωνα με κάποιο υποτιθέμενο στοχαστικό πρότυπο επιτυγχάνεται πολύ εύκολα με τη βοήθεια των ηλεκτρονικών υπολογιστών. Καθώς οι αριθμοί αυτοί δεν είναι πραγματικά “τυχαίοι”, αλλά παράγονται ντετερμινιστικά από τον υπολογιστή με σκοπό να μιμούνται τις ιδιότητες τυχαίων αριθμών, ονομάζονται “ψευδοτυχαίοι” αριθμοί.

3.1 Ψευδοτυχαίοι Αριθμοί

Το πρώτο σημαντικό βήμα για την παραγωγή ανεξάρτητων και ισόμορφων (αν.ισ.) παρατηρήσεων από οποιαδήποτε κατανομή πιθανότητας, είναι η παραγωγή αν.ισ. παρατηρήσεων από την ομοιόμορφη κατανομή \(\mathcal{U}(0,1)\).

Κάθε στατιστικό λογισμικό είναι εφοδιασμένο με γεννήτορες ψευδοτυχαίων αριθμών. Ο προκαθορισμένος αλγόριθμος στην R είναι ο Mersenne-Twister που βασίζεται στους πρώτους αριθμούς του Mersenne. Οι πρώτοι αριθμοί του Mersenne είναι της μορφής \(n=2^p-1\), όπου \(p\) κατάλληλος πρώτος αριθμός ώστε ο \(n\) να βγαίνει πρώτος. Η πιο διαδεδομένη μορφή του αλγορίθμου Mersenne Twister είναι η MT19337 που βασίζεται στον πρώτο \(n=2^{19337}-1\). Αυτό σημαίνει ότι η ακολουθία που παράγει επαναλαμβάνεται μόνο μετά από έναν (αστρονομικά) μεγάλο αριθμό βημάτων, γεγονός που τον καθιστά κατάλληλο για στατιστικές προσομοιώσεις και υπολογιστικές εφαρμογές. Η μελέτη αυτού του αλγορίθμου αποτελεί αντικείμενο ενός μαθήματος προσομοίωσης.

Η R έχει έτοιμη συνάρτηση για την παραγωγή τιμών από την \(Unif(0,1)\). Κάθε φορά που ζητάμε μία τιμή της, η R μας δίνει μία διαφορετική παρατήρηση, υλοποιώντας τον Mersenne-Twister. H αρχικοποίηση \(x_0\), χωρίς άλλη παρέμβαση, γίνεται αρκετά “τυχαία” καθώς υπεισέρχεται ο χρόνος που πατήσαμε την εντολή:

runif(1)
## [1] 0.2655087
runif(1)
## [1] 0.3721239

Στην R μπορούμε να ορίσουμε έναν σπόρο με την εντολή set.seed(\(k\)), αρχικοποιώντας έτσι τον MT19337 σε συγκεκριμένη θέση της ακολουθίας που καθορίζεται από την επιλογή ενός θετικού ακεραίου \(k\). Με αυτόν τον τρόπο, αν επαναλάβουμε τις προσομοιώσεις με την ίδια τιμή του \(k\), θα παίρνουμε τις ίδιες παρατηρήσεις:

set.seed(1465)
runif(1)
## [1] 0.7645799
runif(1)
## [1] 0.9772592

set.seed(1465)
runif(1)
## [1] 0.7645799
runif(1)
## [1] 0.9772592

3.2 Μέθοδος Αντιστροφής

Η σημασία προσομοίωσης τιμών από την ομοιόμορφη κατανομή βρίσκεται στο γεγονός ότι οι προσομοιώσεις άλλων κατανομών βασίζονται είτε άμεσα, είτε έμμεσα στην ομοιόμορφη. Η μέθοδος της αντιστροφής μας επιτρέπει να “μετασχηματίζουμε” τιμές που προσομοιώθηκαν από την \(Unif(0,1)\) σε τιμές που προσομοιώθηκαν από την \(F\). Το μόνο που χρειάζεται να διαθέτουμε είναι μία τιμή που έχει παραχθεί από την \(Unif(0,1)\) και έναν τρόπο αντιστροφής της \(F\).

3.2.1 Συνεχείς και Γνησίως Αύξουσες Συναρτήσεις Κατανομής

Πρόταση 3.1 Έστω \(F:\mathbb{R}\rightarrow [0,1]\) συνάρτηση κατανομής που είναι συνεχής και γνησίως αύξουσα στο \(I=\{x\in \mathbb{R}:F(x)\in (0,1)\}.\) Αν \(U\thicksim Unif(0,1)\), τότε \(X=F^{-1}(U) \thicksim F\).

Απόδειξη:. Με τις υποθέσεις της Πρότασης έχουμε ότι η \(F:I\rightarrow (0,1)\) έχει συνήθη αντίστροφη. Θα δείξουμε λοιπόν ότι η \(X=F^{-1}(U)\thicksim F\) με τη βοήθεια συναρτήσεων κατανομών.

Έστω \(x \in I\). Θέτουμε \(F_X\) τη συνάρτηση κατανομής της \(X=F^{-1}(U)\) και έχουμε

\[\begin{equation*} F_X(x) = \mathbf{P}(F^{-1}(U) \leq x) = \mathbf{P}(F\left(F^{-1}(U)\right) \leq F(x)) = \mathbf{P}(U \leq F(x)) = F_U\left( F(x) \right) = F(x). \end{equation*}\]

Από το παραπάνω συμπεραίνουμε ότι \(F_X=F\) και άρα \(X\thicksim F\).

Παράδειγμα 3.1 Προσομοιώστε παρατηρήσεις από την \(Exp(1)\) χρησιμοποιώντας τη μέθοδο αντιστροφής.

Λύση:

Υπενθυμίζουμε ότι:

\[\begin{equation*} F(x) = 1-e^{-x}, \ \ x>0, \end{equation*}\]

και εύκολα βλέπουμε ότι η \(F\) είναι συνεχής και γνησίως αύξουσα στο \((0,+\infty)\). Έτσι μπορούμε να ορίσουμε τη συνήθη αντίστροφη της \(F\) στο \((0,1)\). Συγκεκριμένα, έχουμε

\[\begin{equation*} u = 1-e^{-x} \Leftrightarrow e^{-x} = 1-u \Leftrightarrow -x = \log(1-u) \Leftrightarrow x=-\log(1-u). \end{equation*}\]

Συμπεραίνουμε ότι \(F^{-1}(u)=-\log(1-u)\) και από τη μέθοδο της αντιστροφής έχουμε ότι αν \(U\thicksim Unif(0,1)\), τότε η \(X=-\log(1-U) \thicksim Exp(1)\).

Στην περίπτωση της ομοιόμορφης κατανομής παρατηρούμε ότι \(U\overset{d}{=} 1-U\) και έτσι μπορούμε να απλοποιήσουμε ακόμα πιο πολύ στη μορφή \(X=-\log(U) \thicksim Exp(1)\).

Στην R το παραπάνω μπορεί να υλοποιηθεί ως εξής:

set.seed(123)

Nsim <- 10 ^ 4 
U <- runif(Nsim)
X <- - log(U) 
Y <- rexp(Nsim)

hist(X, freq = FALSE, main = "Exp from Uniform", breaks = seq(0, 12, 0.5))
curve(dexp, from = 0, to = 10, lty = 1, lwd = 1, col = "red", add = TRUE)

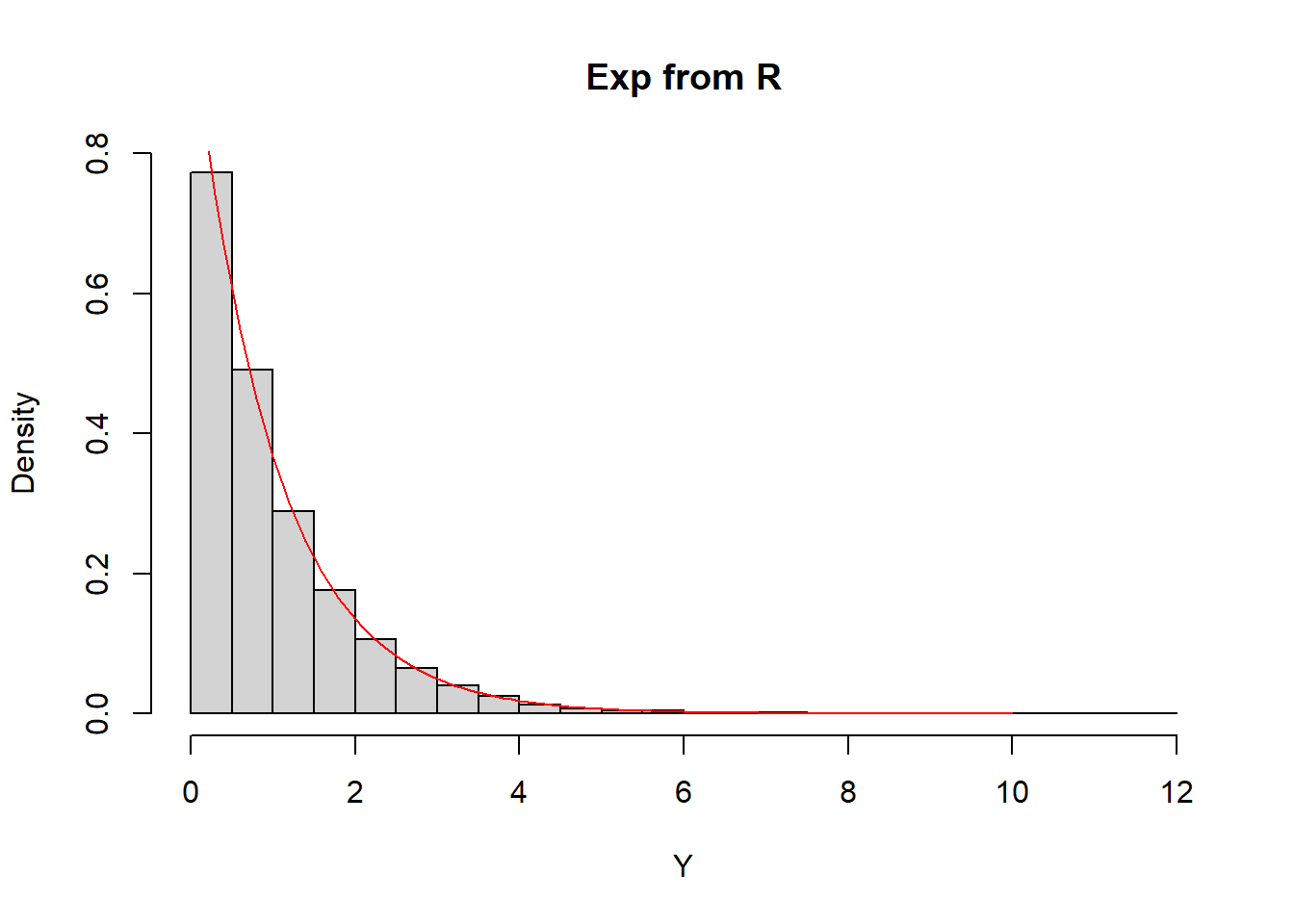
hist(Y, freq = FALSE, main = "Exp from R", breaks = seq(0, 12, 0.5))
curve(dexp, from = 0, to = 10, lty = 1, lwd = 1, col = "red", add = TRUE)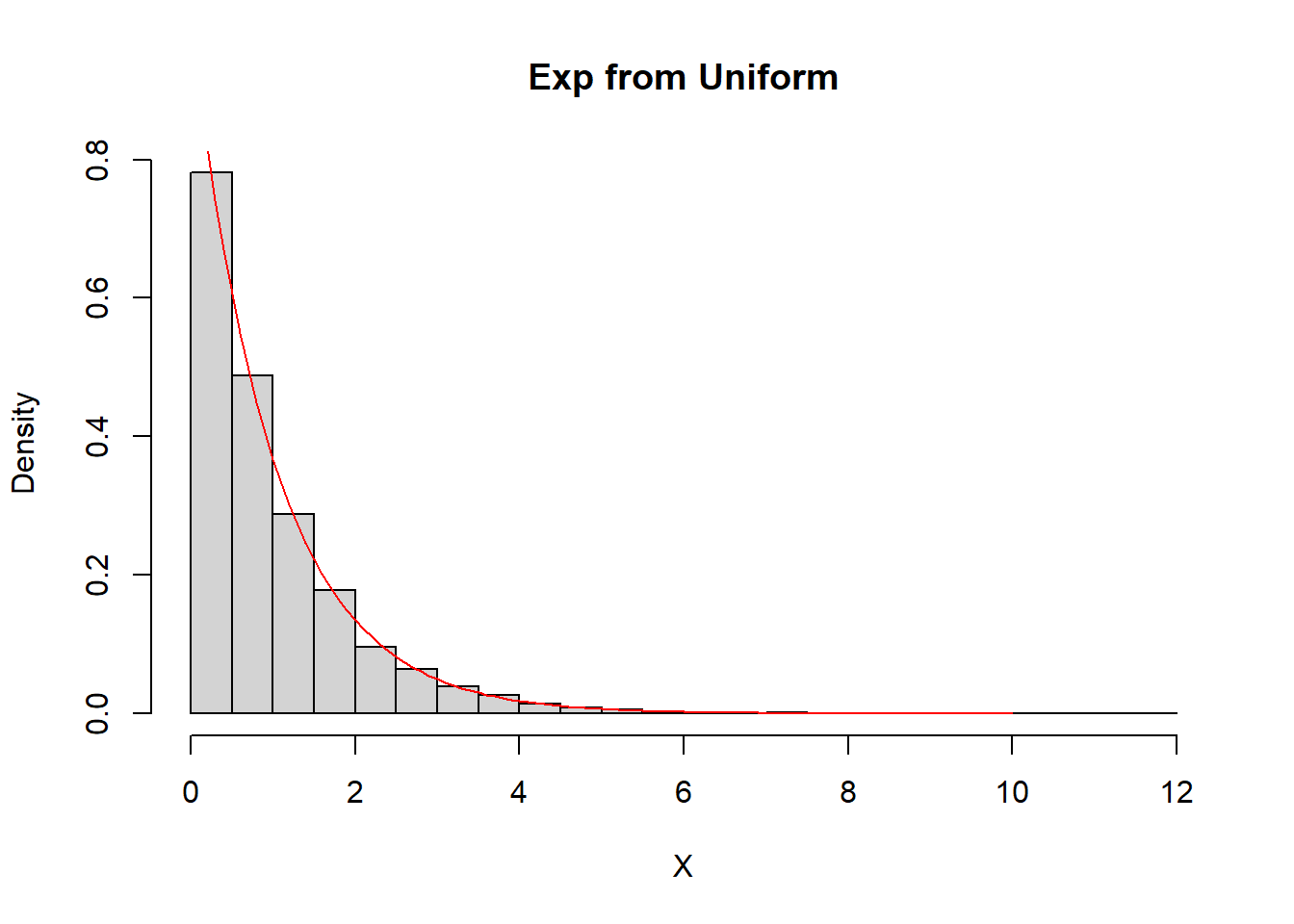

Παράδειγμα 3.2 Προσομοιώστε παρατηρήσεις από τη λογιστική κατανομή \(L(0,1)\) χρησιμοποιώντας τη μέθοδο αντιστροφής.

Λύση:

Υπενθυμίζουμε ότι αν \(L\thicksim L(0,1)\), τότε:

\[\begin{equation*} F_L(x)=\frac{1}{1+e^{-x}}, \quad x\in \mathbb{R}. \end{equation*}\]

Θα χρησιμοποιήσουμε τη μέθοδο αντιστροφής:

\[\begin{equation*} F_L(x)=\frac{1}{1+e^{-x}} \Rightarrow u = \frac{1}{1+e^{-x}} \Leftrightarrow u+ue^{-x}=1 \Leftrightarrow e^{-x} = \frac{1-u}{u} \Leftrightarrow -x = \log \frac{1-u}{u} \Leftrightarrow x = \log \frac{u}{1-u}. \end{equation*}\]

Τελικά,

\[\begin{equation*} X_i = \log \frac{U_i}{1-U_i}. \end{equation*}\]

Παράδειγμα 3.3 Προσομοιώστε παρατηρήσεις από την κανονική κατανομή \(\mathcal{N}(0, 1)\) χρησιμοποιώντας τη μέθοδο αντιστροφής.

Λύση:

Η σ.κ. της τυπικής κανονικής \(\Phi\) είναι συνεχής και γνησίως αύξουσα σε όλο το \(\mathbb{R}\). Έτσι η εξίσωση \(F(x)=u\) έχει μοναδική λύση για \(u\in (0,1)\) και καθορίζει μονοσήμαντα τα κάτω ποσοστημόρια \(q_u:=F^{-1}(u)\) της κατανομής, τα οποία ικανοποιούν τη σχέση \(F(q_u)=F\left(F^{-1}(u)\right)=u\).

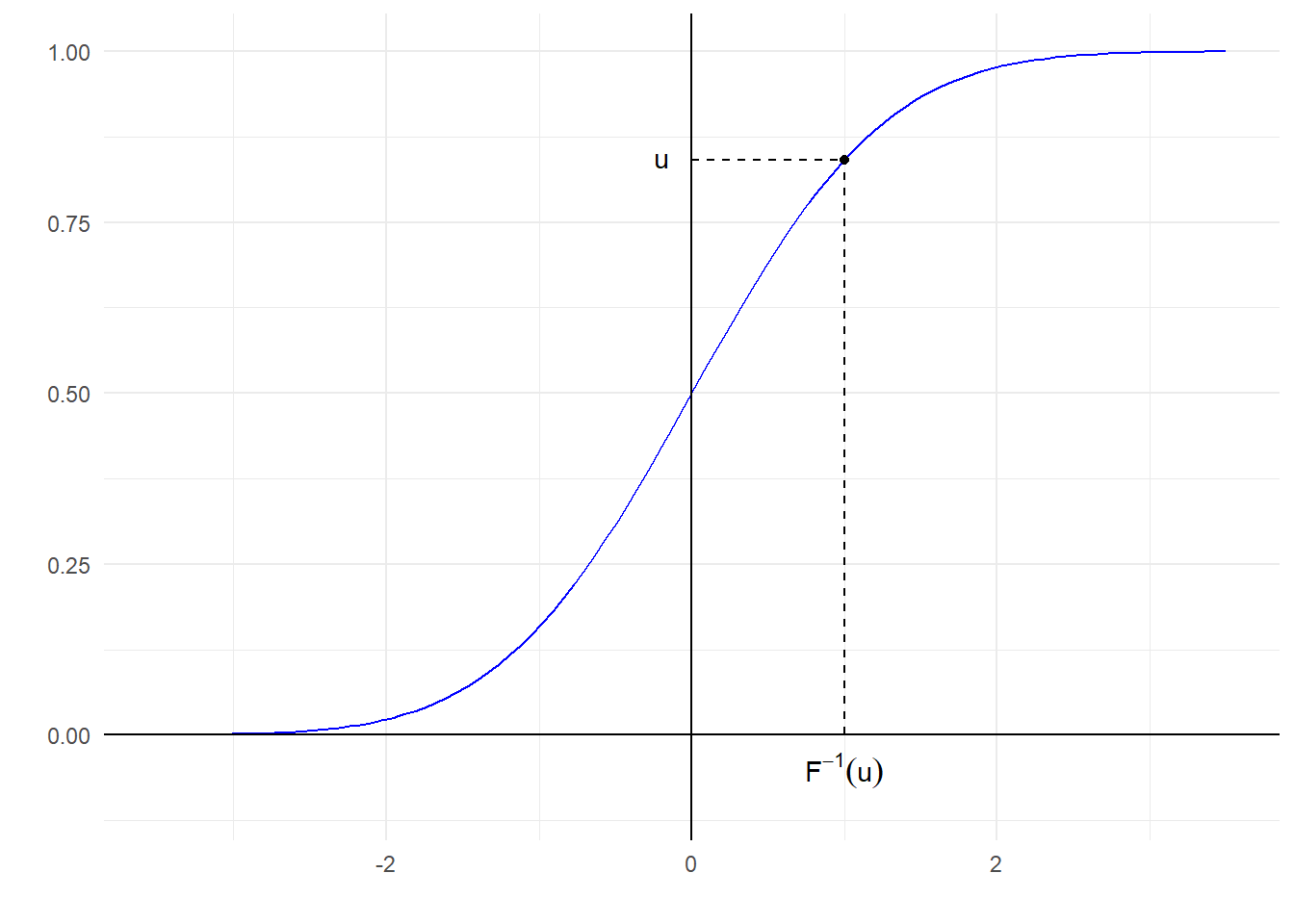
Τελικά, ο τρόπος παραγωγής ενός τυχαίου δείγματος από την \(F\) είναι πολύ απλός. Αν \(\{U_i\}_{i=1}^{n}\) είναι ένα τυχαίο δείγμα από την \(Unif(0,1)\), τότε οι \(\{X_i\}_{i=1}^{n}\) με \(X_i = F^{-1}(U_i)\) αποτελούν ένα τυχαίο δείγμα από την \(F\).

3.2.2 Γενικευμένη Αντίστροφη

Η χρήση της γενικευμένης αντίστροφης μας δίνει τη δυνατότητα να κάνουμε αντιστροφή σ.κ. που δεν είναι αντιστρέψιμες με τη συνήθη έννοια.

Ορισμός 3.1 Έστω \(F: \mathbb{R}\rightarrow [0,1]\) μία συνάρτηση κατανομής. Γενικευμένη αντίστροφη ονομάζουμε τη συνάρτηση \(F^{-}:(0,1)\rightarrow \mathbb{R}\) με

\[\begin{equation*} F^-(u) = \inf \left\{ x \in \mathbb{R}: F(x) \geq u \right\}. \end{equation*}\]

Η παρακάτω πρόταση γενικεύει τη δυνατότητα χρήσης της μεθόδου αντιστροφής για την προσομοίωση τιμών από κατανομές με γνωστή συνάρτηση κατανομής \(F\).

Πρόταση 3.2 Έστω \(F:\mathbb{R}\rightarrow [0,1]\) συνάρτηση κατανομής. Αν \(U\thicksim Unif(0,1)\), τότε \(X=F^-(U) \thicksim F\).

Η απόδειξη της παραπάνω πρότασης γίνεται στο μάθημα της Μη-Παραμετρικής Στατιστικής.

Η γενικευμένη αντίστροφη \(F^-\) λύνει το πρόβλημα αντιστροφής σε 2 “προβληματικές” περιπτώσεις. Η μία αφορά τις περιοχές σταθεροποίησης της \(F\) και η άλλη των σημείων που παρουσιάζονται άλματα ασυνέχειας της \(F\). Ισοδύναμα, από αλγεβρική σκοπιά, οι παραπάνω περιπτώσεις αναφέρονται στις περιπτώσεις που η εξίσωση \(F(x)=u\) έχει άπειρες λύσεις ή είναι αδύνατη αντίστοιχα.

Παράδειγμα 3.4 Θεωρούμε την παρακάτω συνάρτηση κατανομής με περιοχή σταθεροποίησης το \([x_a, x_b]\):

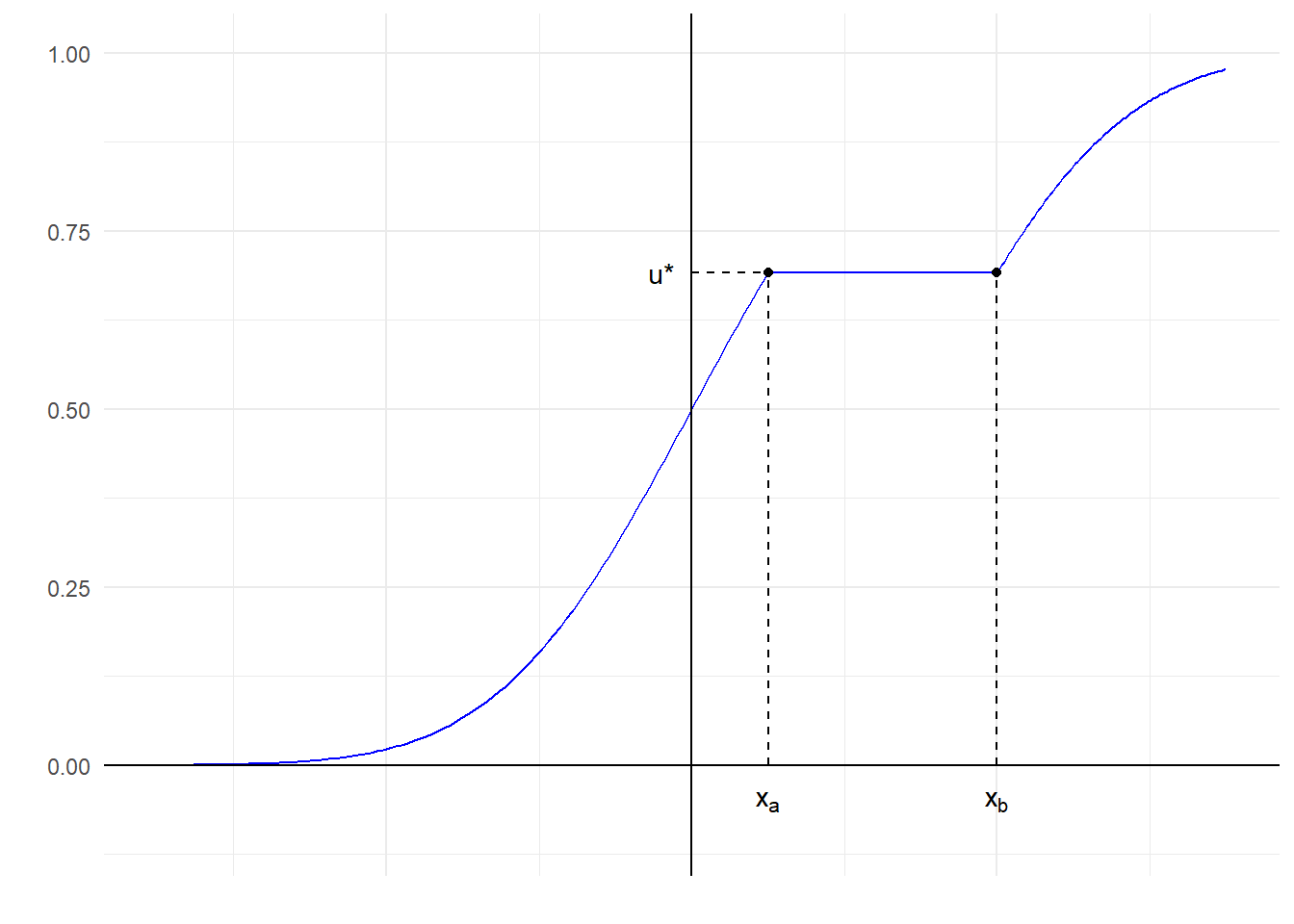
Στο παραπάνω γράφημα βλέπουμε πως για \(u^\star\) όλα τα \(x\) στο διάστημα \(I=[x_a, x_b]\) ικανοποιούν την σχέση \(F(x)=u^\star\). Επομένως, η συνάρτηση \(F\) δεν είναι 1-1, άρα ούτε και αντιστρέψιμη. Παρότι η \(F\) δεν έχει συνήθη αντίστροφη, έχει γενικευμένη αντίστροφη, σύμφωνα με τον ορισμό της οποίας:

\[\begin{equation*} F^{-}(u^\star)=\inf\{x: F(x)\geq u^\star\}=\inf\{x:F(x)=u^\star\}=x_a. \end{equation*}\]

Παράδειγμα 3.5 Θεωρούμε την παρακάτω συνάρτηση κατανομής με άλμα ασυνέχειας \([u_a, u_b)\) στο \(x_0\):

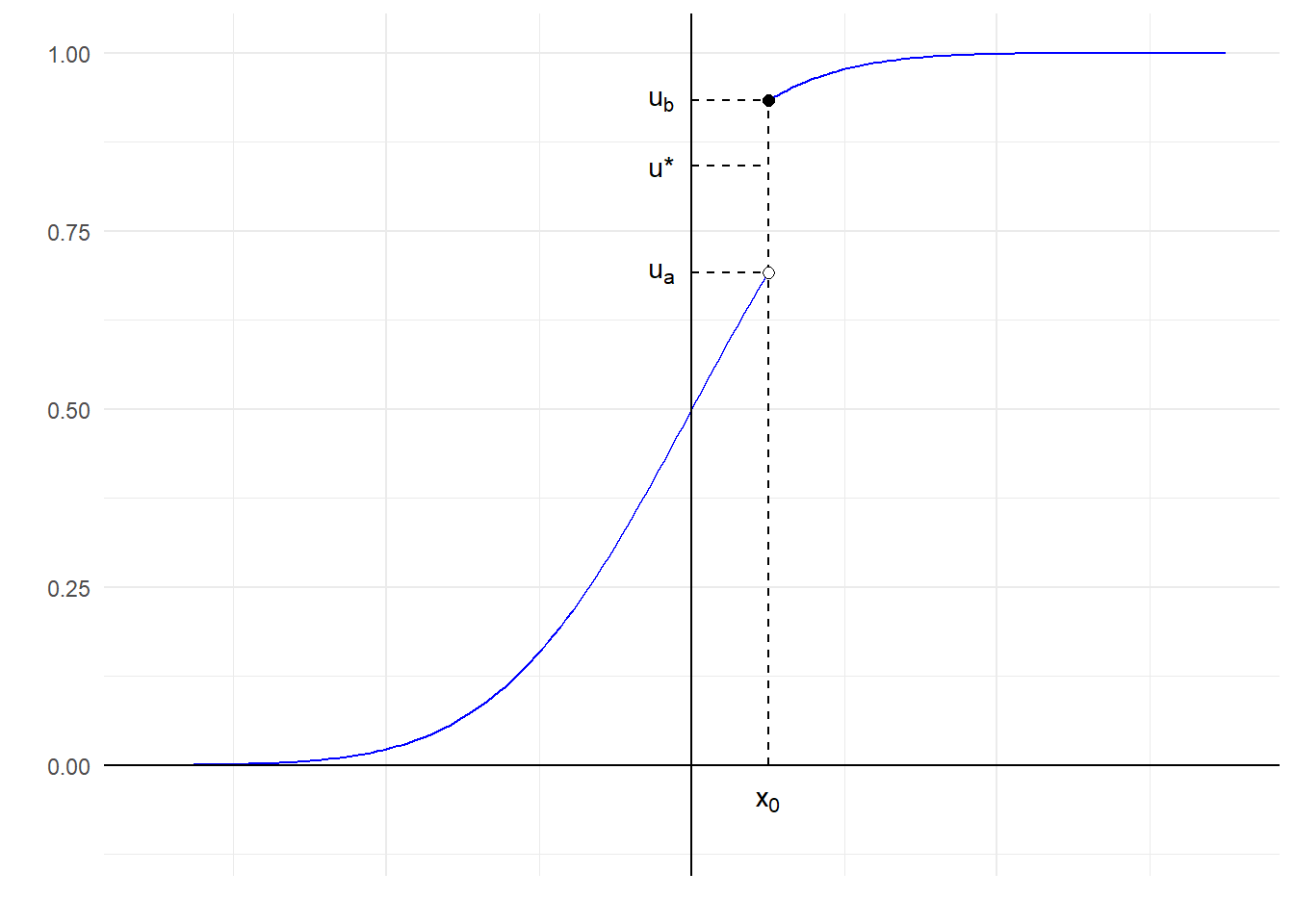
Στο παραπάνω γράφημα βλέπουμε πως για \(u^\star \in [u_a, u_b)\) δεν υπάρχει κανένα \(x \in \mathbb{R}\) που να ικανοποιεί την σχέση \(F(x)=u^\star\). Επομένως, η συνάρτηση \(F\) δεν είναι επί του \((0,1)\), άρα δεν υπάρχει αντίστροφη της \(F\) με πεδίο ορισμού το \((0,1)\). Υπάρχει όμως η γενικευμένη αντίστροφη, σύμφωνα με τον ορισμό της οποίας:

\[\begin{equation*} F^{-}(u^\star)=\inf\{x: F(x)\geq u^\star\}=\inf\{x:F(x)=u_b\}=x_0. \end{equation*}\]

Η μέθοδος της αντιστροφής μας επιτρέπει να παράγουμε παρατηρήσεις διακριτών κατανομών χρησιμοποιώντας την ομοιόμορφη κατανομή.

Παράδειγμα 3.6 Προσομοιώστε παρατηρήσεις από τη διωνυμική κατανομή \(Bin(10, 0.3)\) χρησιμοποιώντας τη μέθοδο αντιστροφής.

Λύση:

set.seed(2184)
Nsim <- 10 ;  N <- 10 ; p <- 0.3
prob <- pbinom((-1):(N - 1), N, p)
X <- rep(10, Nsim)
for (i in 1:Nsim){
  u <- runif(1)
  while(prob[X[i] + 1] >= u){
   X[i] <- X[i] - 1 
  }
}
X
##  [1] 3 3 2 3 0 3 1 0 1 3

Συγκρίνετε με τον παρακάτω τρόπο παραγωγής.

set.seed(2184)
Nsim <- 10 ;  N <- 10 ; p <- 0.3
prob <- pbinom(0:9, N, p)
X <- rep(0, Nsim)
for (i in 1:Nsim){
   u <- runif(1)
   X[i] <- sum(prob < u) 
}
X
##  [1] 3 3 2 3 0 3 1 0 1 3

Είναι φανερό ότι οδηγούμαστε στις ίδιες τιμές. Ο πρώτος τρόπος χρησιμοποιεί τον ορισμό της γενικευμένης αντίστροφης. Ο δεύτερος τρόπος είναι ισοδύναμος, αλλά αποδοτικότερος. Για να δούμε πώς προσομοιώνει και η R:

set.seed(2184)
rbinom(10, N, p)
##  [1] 3 3 2 3 0 3 1 0 1 3

Παράδειγμα 3.7 Προσομοιώστε παρατηρήσεις από την κατανομή \(Poisson(100)\) χρησιμοποιώντας τη μέθοδο αντιστροφής.

Λύση:

set.seed(2544)
Nsim <- 10 ^ 4 ; lambda <- 100
lmax <- 300 
prob <- ppois(0:lmax, lambda)

X <- rep(0, Nsim)
for (i in 1:Nsim) {
  u <- runif(1)
  X[i] <- sum(prob < u) 
}
X[1:10]
##  [1] 101  84 112 108 102 105 120 107  97  98

Συγκρίνετε με τον παρακάτω τρόπο προσομοίωσης:

set.seed(2544)
Nsim <- 10 ^ 4 ; lambda <- 100
spread <- 3 * sqrt(lambda)  # var(Poisson(lambda)) = lambda
t <- round(seq(max(0, lambda - spread), lambda + spread, 1))
prob <- ppois(t, lambda)

Y <- rep(0,Nsim)
for (i in 1:Nsim){
  u <- runif(1)
  Y[i] <- t[1] + sum(prob < u)  # Υποθέτουμε ότι X[1] >= t[1]
}
Y[1:10]
##  [1] 101  84 112 108 102 105 120 107  97  98

Ίσως φαίνεται να μην υπάρχουν διαφορές. Όμως, υπάρχουν κάποιες παρατηρήσεις που διαφέρουν στα 2 δείγματα. Μπορούμε λοιπόν να υπολογίσουμε, όπως παρακάτω, την πιθανότητα μία παρατήρηση να βρεθεί εντός του διαστήματος που καθορίσαμε \([\lambda -3\sqrt{\lambda},\lambda+3\sqrt{\lambda}]\) και άρα και το αναμενόμενο πλήθος των παρατηρήσεων που θα διαφέρουν. Στο συγκεκριμένο πρόβλημα μπορούμε να το ελέγξουμε κατάλληλα.

sum(X != Y)
## [1] 15
proba.in <- ppois(lambda + spread, lambda) - ppois(lambda - spread - 1, lambda)
proba.in
## [1] 0.9976323
1 - proba.in
## [1] 0.002367724
expected.out <- Nsim * (1 - proba.in)
expected.out
## [1] 23.67724

Τέλος, ας δούμε και η R πώς παράγει από την παραπάνω Poisson.

set.seed(2544)
rpois(10, 100)
##  [1] 100 112 102 119  97  82 102  83  98  99

3.3 Μετασχηματισμοί Κατανομών

Έστω ότι έχουμε μία πραγματική τ.μ. \(X\) με συνάρτηση πυκνότητας πιθανότητας \(f_X\) και θέλουμε να κάνουμε το μετασχηματισμό \(Y=g(X)\), με \(g\) 1-1 και αμφιδιαφορίσιμη (\(g,g^{-1}\) διαφορίσιμες). Τότε:

\[\begin{equation*} f_Y(y)=f_X\left(g^{-1}(y)\right) \cdot \left| \frac{dg^{-1}(y)}{dy}\right| , \ \ \forall y\in g(S_X). \end{equation*}\]

Θα είναι χρήσιμο στα επόμενα να επεκτείνουμε τη μέθοδο εύρεσης της συνάρτησης πυκνότητας πιθανότητας αντιστρέψιμων μετασχηματισμών για διανυσματικές τυχαίες μεταβλητές. Για παράδειγμα, αν \(X=(X_1, X_2)\), \(Y=(Y_1, Y_2)\) και

\[\begin{equation*} Y=(Y_1,Y_2)=(g_1(X),g_2(X))=g(X), \end{equation*}\]

όπου \(g\) κατάλληλος μετασχηματισμός. Τότε, αν η \(g\) είναι 1-1, διαφορίσιμη και συμβολίζοντας με \(J_g(x)\) τον Ιακωβιανό πίνακα της \(g\) υπολογισμένο στο \(x\):

\[\begin{equation*} J_g(x) = \left(\begin{array}{cc} \frac{\partial g_1(x)}{\partial x_1} & \frac{\partial g_1(x)}{\partial x_2} \\ \frac{\partial g_2(x)}{\partial x_1} & \frac{\partial g_2(x)}{\partial x_2} \end{array} \right) \end{equation*}\]

Αν υποθέσουμε επιπλέον ότι \(det J_g(x) \neq 0, \ \forall x \in S_x\), μπορεί να δειχθεί ότι η \(Y\) έχει σ.π.π. που δίνεται από τη σχέση

\[\begin{equation*} f_Y(y)=f_X\left(g^{-1}(y)\right) \cdot \left| detJ_{g^{-1}}(y) \right| , \ \ \forall y\in g(S_X). \end{equation*}\]

Η παραπάνω σχέση ισχύει γενικότερα για διανυσματικές τυχαίες μεταβλητές.

3.3.1 Οικογένειες Κατανομών Θέσης - Κλίμακας

Μας ενδιαφέρει η προσομοίωση τιμών από οικογένειες κατανομών θέσης - κλίμακας, δηλ τ.μ. της μορφής \(X=\mu +\sigma Z\), όπου \(\mu \in \mathbb{R}\) και \(\sigma >0\). Το \(\mu\) ονομάζεται παράμετρος θέσης (location) ενώ το \(\sigma\) παράμετρος κλίμακας (scale). Για να μην τα μπερδεύουμε με τη μέση τιμή και την τυπική απόκλιση μίας τυχαίας μεταβλητής, πολλές φορές θα χρησιμοποιούμε διαφορετικά σύμβολα.

Παρατήρηση:. Συνήθως το \(\theta=1/\sigma\) ονομάζεται παράμετρος ρυθμού (rate). Για παράδειγμα, η εκθετική κατανομή μπορεί να εκφραστεί είτε ως \(Exp(rate)\), είτε ως \(Exp(scale)\). Χρησιμοποιώντας τα σύμβολα \(\theta, \lambda\) αντίστοιχα, η σ.π.π. γράφεται

\[\begin{align*} f(x) &= \theta e^{-\theta x}, \quad x>0, \\ f(x) &= \frac{1}{\lambda} e^{-\frac{x}{\lambda}}, \quad x>0, \end{align*}\]

Είναι φανερό ότι οι μετασχηματισμοί θέσης - κλίμακας αποτελούν ειδική κατηγορία μετασχηματισμών, για τους οποίους έχουμε \(g(x)=\mu+\sigma x\). Επομένως:

\[\begin{equation*} F_Y(y)=\mathbf{P}(Y\leq y) = \mathbf{P}(\mu+\sigma X \leq y)= \mathbf{P}(X\leq \frac{y-\mu}{\sigma}) = F_X\left(\frac{y-\mu}{\sigma}\right), \end{equation*}\]

και

\[\begin{equation*} f_Y(y) = \frac{1}{\sigma} \cdot f_X\left( \frac{y-\mu}{\sigma} \right). \end{equation*}\]

Γενικότερα, σε μετασχηματισμούς θέσης - κλίμακας (ή μόνο θέσης αν \(\sigma=0\), ή μόνο κλίμακας αν \(\mu=0\)) αρκεί να βρούμε την αντίστροφη για την “τυπική” κατανομή αυτής της οικογένειας.

Παράδειγμα 3.8 Υποθέτοντας ότι μπορείτε να παράγετε παρατηρήσεις από την \(Exp(1)\), πώς μπορείτε να παράγετε από την \(Exp(\theta)\), όπου \(θ\) παράμετρος ρυθμού;

Λύση:

Ισχύει ότι

\[\begin{equation*} X \thicksim Exp(1) \Rightarrow Y=\frac{1}{\theta} X \thicksim Exp(\theta). \end{equation*}\]

Επομένως, από το παράδειγμα 3.1 παίρνουμε ότι \(Y=-\frac{1}{\theta}\log U \thicksim Exp(\theta).\)

Παράδειγμα 3.9 (Παραγωγή Βήτα από Γάμμα) Υποθέτουμε ότι ένας ασθενής φτάνει στο νοσοκομείο και πρέπει να κάνει 2 εξετάσεις, μία εξέταση αίματος και μία ακτινογραφία θώρακος. Ο χρόνος που θα χρειαστεί για να πραγματοποιήσει διαδοχικά αυτές τις 2 εξετάσεις υποθέτουμε ότι είναι \(X, Y\) αντίστοιχα, όπου \(X\thicksim G(a, \theta), Y\thicksim G(\beta, \theta)\) και \(X \perp \!\!\! \perp Y\). Ποια είναι η κατανομή του ποσοστού του χρόνου \(W\) που καταλαμβάνει η 1η δραστηριότητα;

Λύση:

Ορίζουμε \(Z:=X+Y\) τον συνολικό χρόνο και για τις δύο εξετάσεις. Για το ποσοστό \(W\) ισχύει \(W=\frac{X}{X+Y}\). Παρατηρούμε ότι:

\[\begin{equation*} (Z, W) = g(X, Y) , (z,w) = (g_1(x,y), g_2(x,y))=\left(x+y, \frac{x}{x+y}\right). \end{equation*}\]

Επομένως:

\[\begin{equation*} \begin{array}{c} z=x+y \\ w=\frac{x}{x+y} \end{array} \Leftrightarrow \begin{array}{c} zw=x \\ y=z-x \end{array} \Leftrightarrow \begin{array}{c} x=zw \\ y=z(1-w) \end{array} \end{equation*}\]

H \(g\) είναι 1-1, διαφορίσιμη με \(det J_g(x) \neq 0\).

\[\begin{equation*} detJ_{g^{-1}}(z,w) = \left|\begin{array}{cc} w & z \\ 1-w & -z \end{array} \right| = -wz-z+zw=-z\neq 0. \end{equation*}\]

Τελικά,

\[\begin{align*} f_{Z,W}(z,w) & = f_{X,Y}(g^{-1}(z,w)) \cdot \left| detJ_{g^{-1}}(z,w) \right| \\ & \propto (zw)^{a-1} e^{-\theta zw} z^{\beta-1} (1-w)^{\beta-1} e^{-\theta z (1-w)}) \\ & = z^{a+\beta-1} e^{-\theta z} w^{a-1} (1-w)^{\beta-1} \\ & = h_1(z) \cdot h_2(w), \end{align*}\]

όπου

\[\begin{align*} h_1(z) &= z^{a+\beta-1} e^{-\theta z}, \ \ 0<z<+\infty, \\ h_2(w) &= w^{a-1} (1-w)^{\beta-1}, \ \ 0<w<1. \end{align*}\]

Επομένως \(Z\thicksim G(a+\beta, \theta)\), \(W\thicksim Beta(a, \beta)\) και \(Z \perp \!\!\! \perp W\).

Έστω \(X\thicksim G(a, \theta), Y \thicksim G(\beta, \theta)\) και \(X'\thicksim G(a, 1), Y' \thicksim G(\beta, 1)\). Τότε:

\[\begin{equation*} W = \frac{X}{X+Y} = \frac{\frac{1}{\theta}X'}{\frac{1}{\theta}X'+\frac{1}{\theta}Y'} = \frac{X'}{X'+Y'}. \end{equation*}\]

Άρα

\[\begin{equation*} W_i = \frac{X'_i}{X'_i+Y'_i}. \end{equation*}\]

Άρα η \(Beta(a, \beta)\) μπορεί να παραχθεί από 2 ανεξάρτητες \(G(a, 1)\), \(G(\beta, 1)\).

a <- 3
b <- 7
G1 <- rgamma(10 ^ 4, shape = a, rate = 1)
G2 <-  rgamma(10 ^ 4, shape = b, rate = 1)
B <- G1 / (G1 + G2)

hist(B, freq = FALSE, main = "Beta from Gamma", xlab = "x")
curve(dbeta(x, shape1 = a, shape2 = b), from = 0, to = 1, lty = 1, lwd = 1, col = "red", add = TRUE)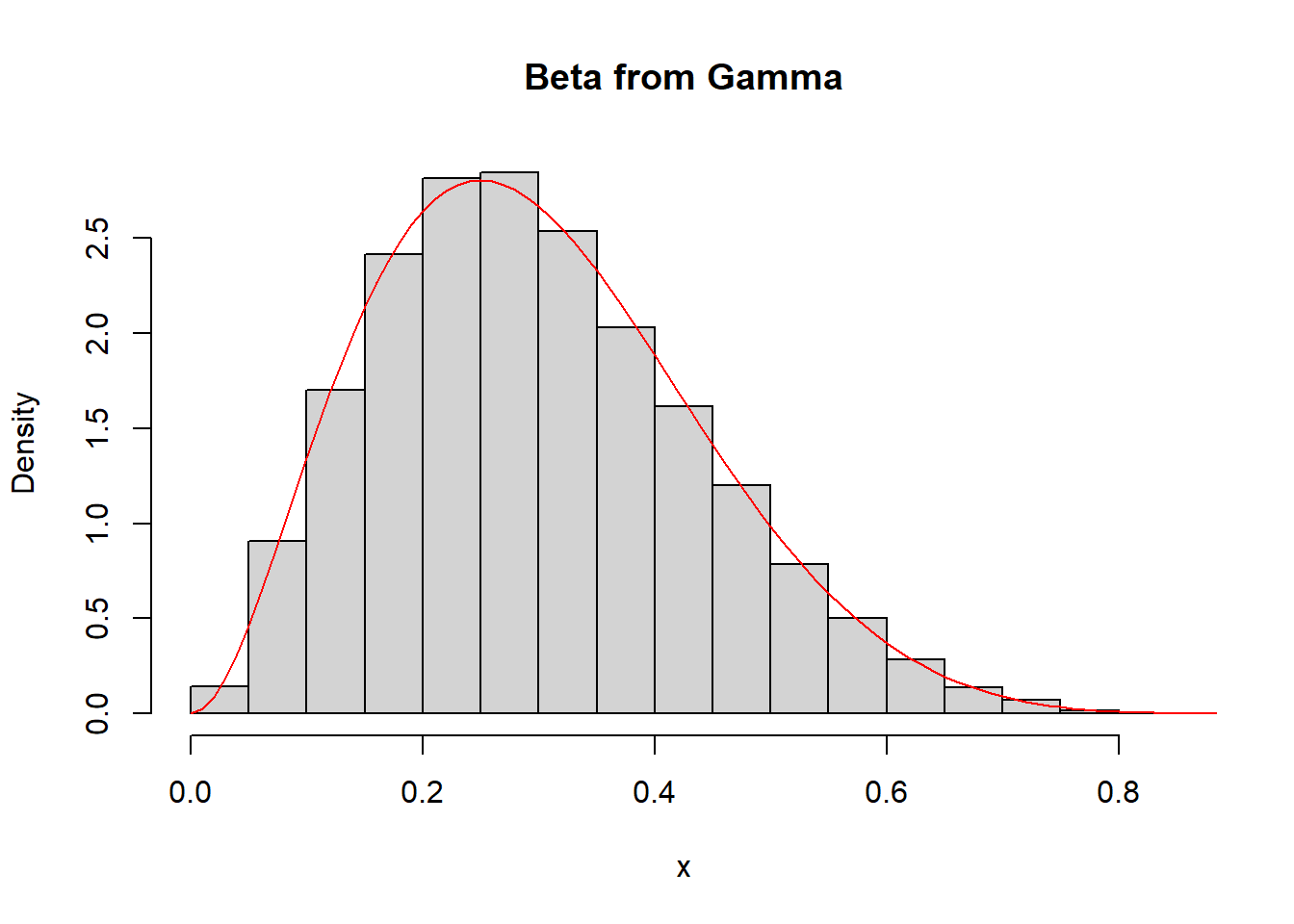

Παράδειγμα 3.10 (Λογιστική Οικογένεια Κατανομών) Προσομοιώστε παρατηρήσεις από τη λογιστική κατανομή \(Logistic(\mu, \beta), \mu \in \mathbb{R}, \beta >0\).

Λύση:

Έστω ότι η \(X\thicksim Logistic(\mu, \beta), \mu \in \mathbb{R}, \beta >0\). Τότε \(X=\mu +\beta L, \ L \thicksim Logistic(0,1)\) και

\[\begin{equation*} F_L(x) = \frac{1}{1+e^{-x}}, \ \ f_L(x) = \frac{e^{-x}}{\left( 1+ e^{-x} \right)^2}, \ \ \forall x\in \mathbb{R}. \end{equation*}\]

Χρησιμοποιώντας ότι έχουμε οικογένεια θέσης-κλίμακας για την \(X\) ισχύει ότι:

\[\begin{equation*} F_X(x) = F_L\left(\frac{x-\mu}{\beta}\right) \Rightarrow f_X(x) = \frac{1}{\beta} f_L\left(\frac{x-\mu}{\beta}\right), \ \ \forall x\in \mathbb{R}. \end{equation*}\]

Ας υλοποιήσουμε το παραπάνω στην R:

set.seed(467)
mu <- 0
beta <- 1
U <- runif(10 ^ 4)
L1 <- mu + beta * log(U / (1 - U))

set.seed(467)
L2 <- rlogis(10 ^ 4)

hist(L1, freq = FALSE, main = "Logistic(0,1) from Uniform", breaks = 50, ylim = c(0, 0.3))
curve(dlogis, from = -10, to = 10, lty = 1, lwd = 1, col = "red", add = TRUE)

hist(L2, freq = FALSE, main = "Logistic(0,1) from R", breaks = 50, ylim = c(0, 0.3))
curve(dlogis,  from = -10, to = 10, lty= 1, lwd = 1, col = "red", add = TRUE)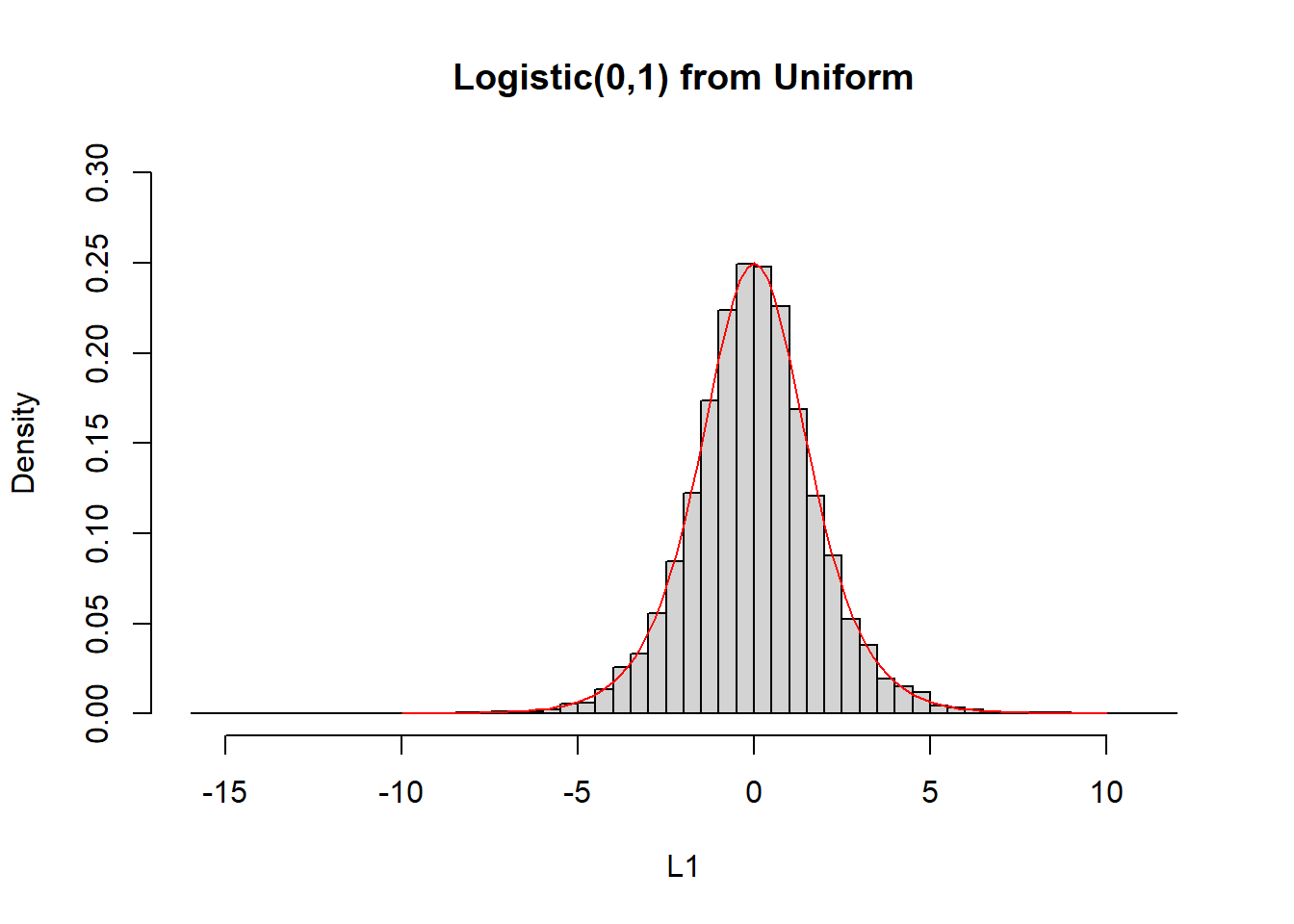

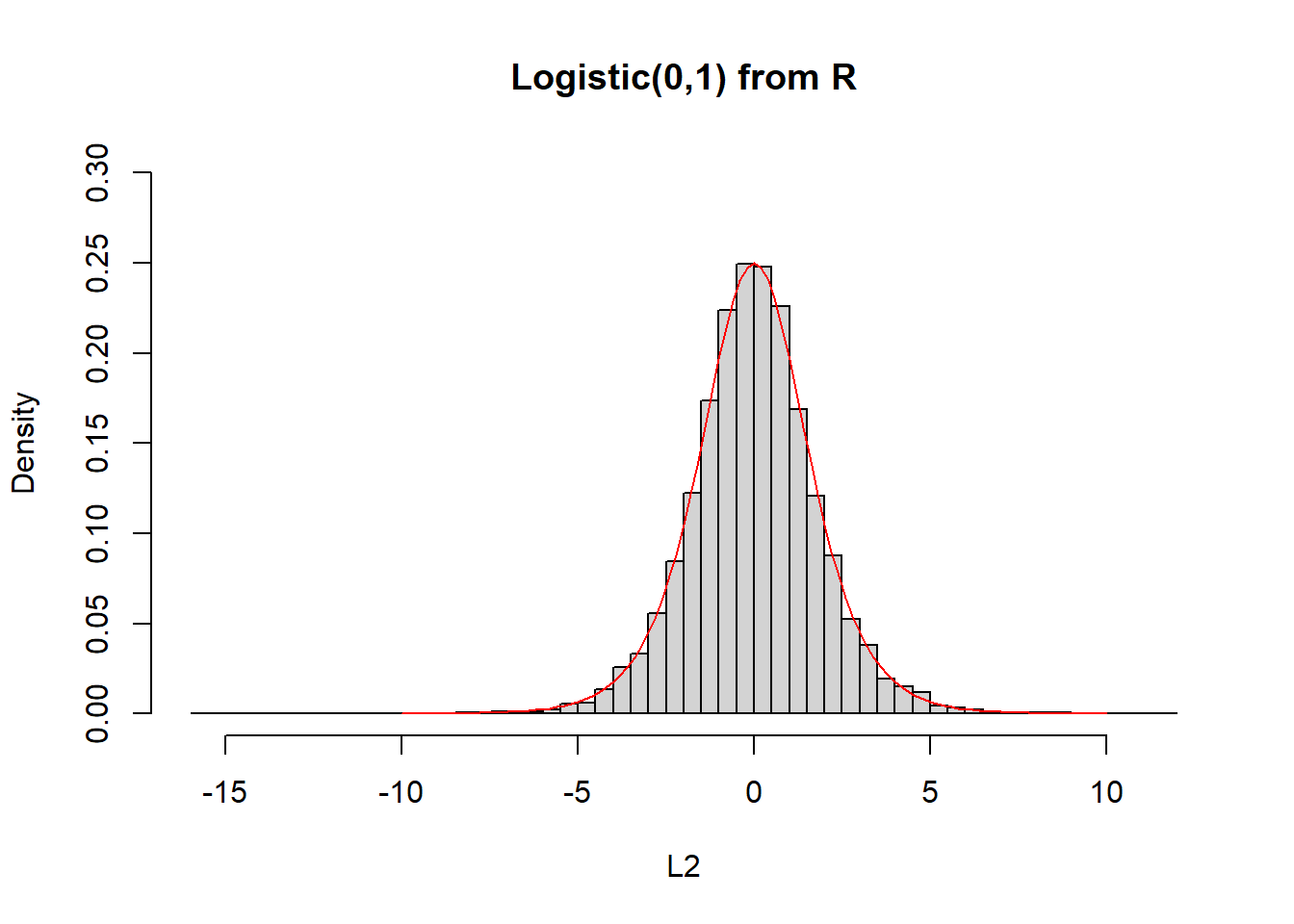
Το παραπάνω δείγμα είναι από την “τυπική” λογιστική κατανομή. Θα μπορούσαμε να επιλέξουμε και \((\mu,\beta)\neq (0,1)\), π.χ.,

set.seed(467)
mu <- 1
beta <- 2
U <- runif(10 ^ 4)
L1 <- mu + beta * log(U / (1 - U))
set.seed(467)
L2 <- rlogis(10 ^ 4, mu, beta)
identical(L1, L2)
## [1] TRUE

Το παραπάνω αποτέλεσμα δείχνει ότι έχουμε αναπαράγει με ακρίβεια τον τρόπο που η R προσομοιώνει τιμές από την οικογένεια θέσης - κλίμακας της λογιστικής κατανομής.

Παράδειγμα 3.11 (Οικογένεια Κατανομών Cauchy) Προσομοιώστε παρατηρήσεις από την κατανομή \(Cauchy(\mu, \sigma)\), χρησιμοποιώντας την ακόλουθη σχέση:

\[\begin{equation*} U\thicksim \mathcal{U}(0,1) \Longrightarrow X := \tan\left[\pi (U-0.5)\right]\thicksim Cauchy(0, 1), \end{equation*}\]

και το γεγονός ότι η οικογένεια των κατανομών Cauchy αποτελεί οικογένεια θέσης - κλίμακας.

Λύση:

Η τυπική Cauchy έχει συνάρτηση κατανομής:

\[\begin{equation*} F_{C}(x) = \frac{1}{\pi}\arctan(x) + 1/2=\int_{-\infty}^{x}\frac{1}{\pi}\frac{1}{1+t^2}dt. \end{equation*}\]

και άρα αντίστροφη συνάρτηση κατανομής που βρίσκεται από τη σχέση \(u=1/\pi\, \arctan(x) + 1/2\), δίνοντας

\[\begin{equation*} F_{C}^{-1}(u) = tan\big(\pi(u-1/2)\big), \quad 0<u<1. \end{equation*}\]

mu <- 0
sigma <- 1
ssize <- 10 ^ 4
U <- runif(ssize)
C1 <- mu + sigma * tan(pi * (U - 0.5))
C2 <- rcauchy(ssize)
C3 <- rt(ssize, df = 1)
N <- rnorm(ssize)

hist(C1[abs(C1) < 10], freq = FALSE, ylim = c(0, 0.45), main = "Cauchy(0,1) from Uniform", xlab = "x")
curve(dcauchy, from = -10, to = 10, lty= 1, lwd = 1, col = "red", add = TRUE)

hist(C2[abs(C2) < 10], freq = FALSE, ylim = c(0, 0.45), main = "Cauchy(0,1) from R", xlab = "x")
curve(dcauchy, from = -10, to = 10, lty = 1, lwd = 1, col = "red", add = TRUE)

hist(C3[abs(C3) < 10], freq = FALSE, ylim = c(0, 0.45), main = "Cauchy(0,1) as t1", xlab = "x")
curve(dcauchy, from = -10, to = 10, lty = 1, lwd = 1, col = "red", add = TRUE)

hist(N, freq = FALSE, ylim = c(0, 0.45), main = "N(0,1) vs Cauchy(0,1)", xlab = "x")
curve(dcauchy, from = -5, to = 5, lty = 1, lwd = 1, col = "red", add = TRUE)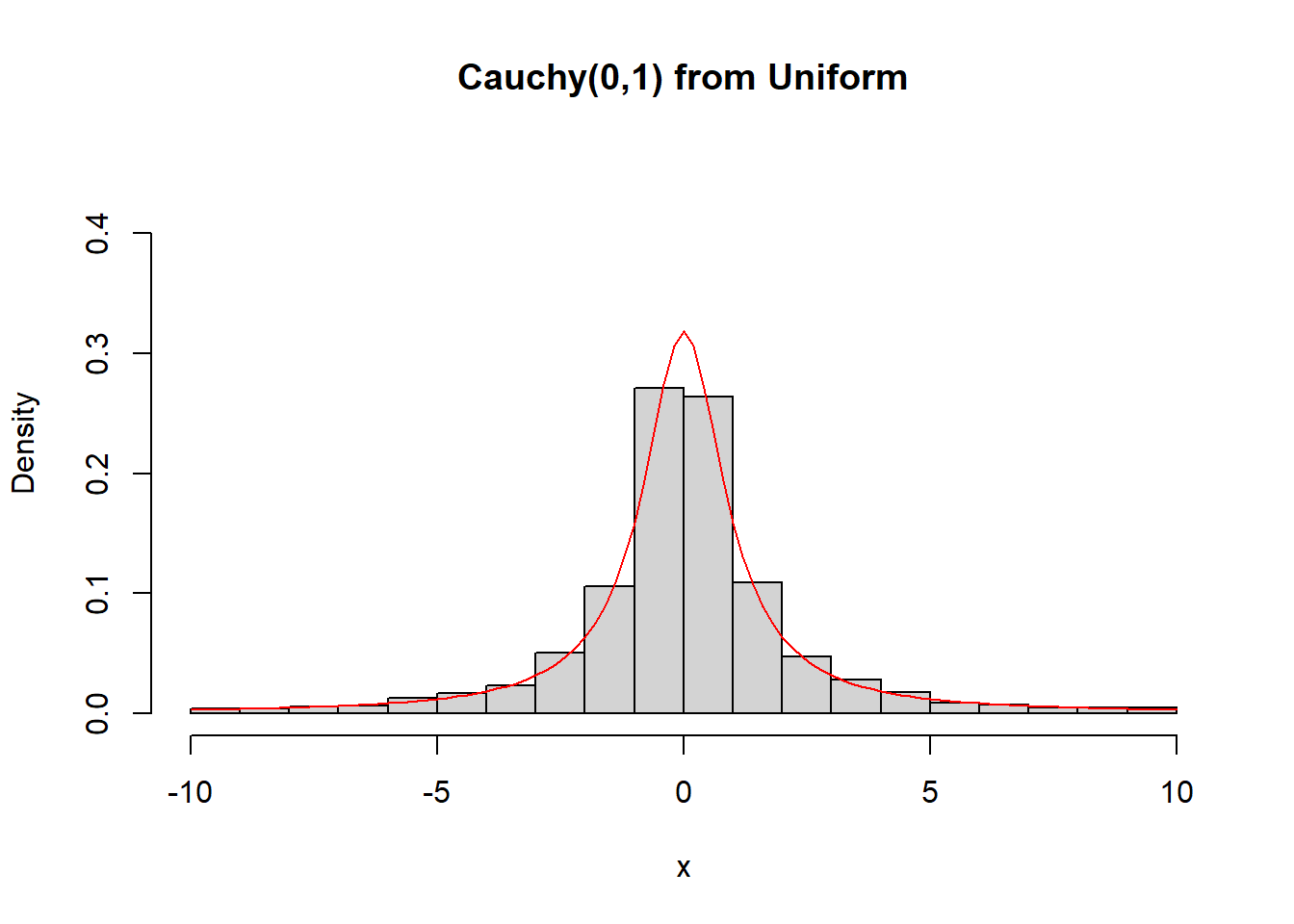

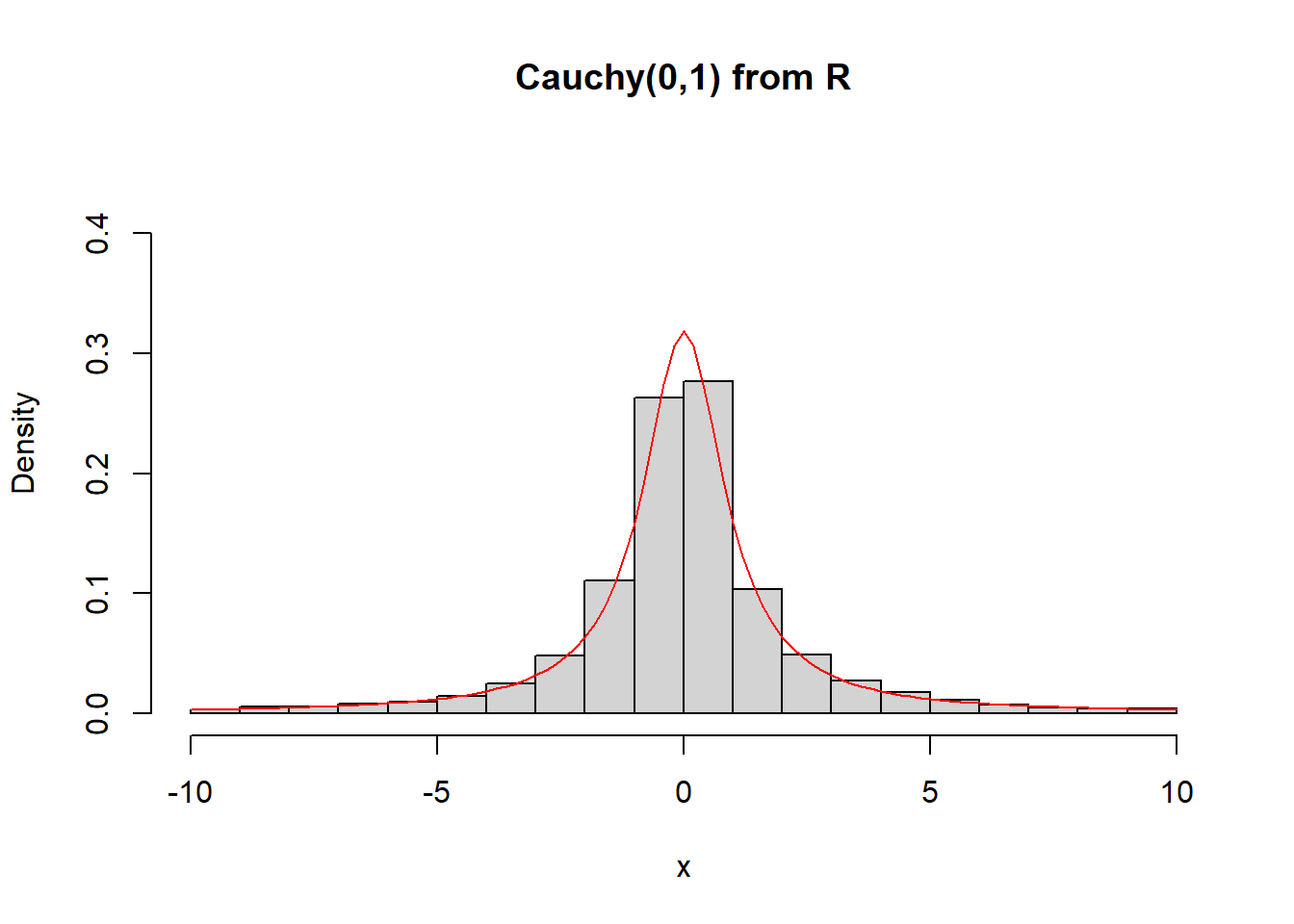
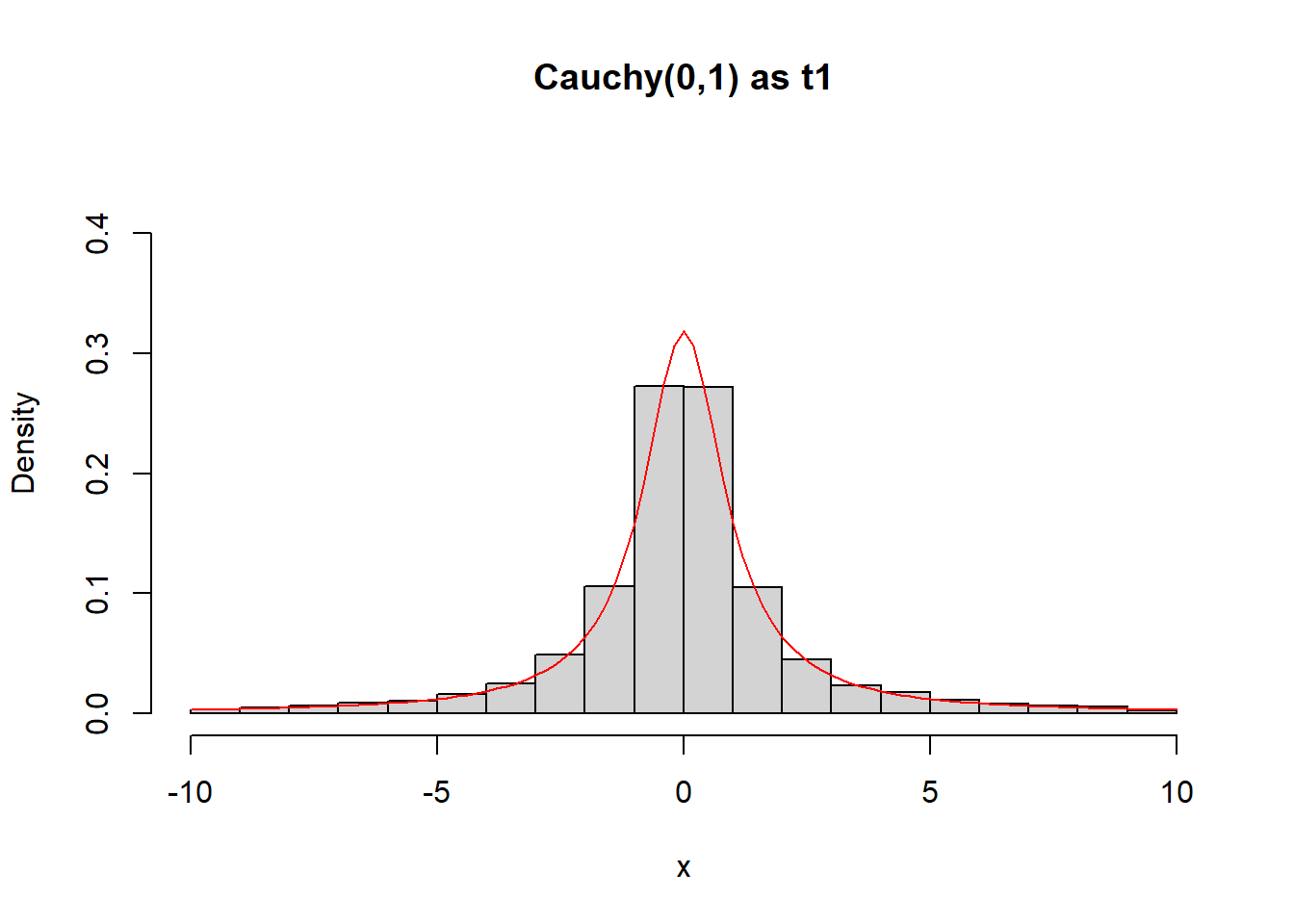
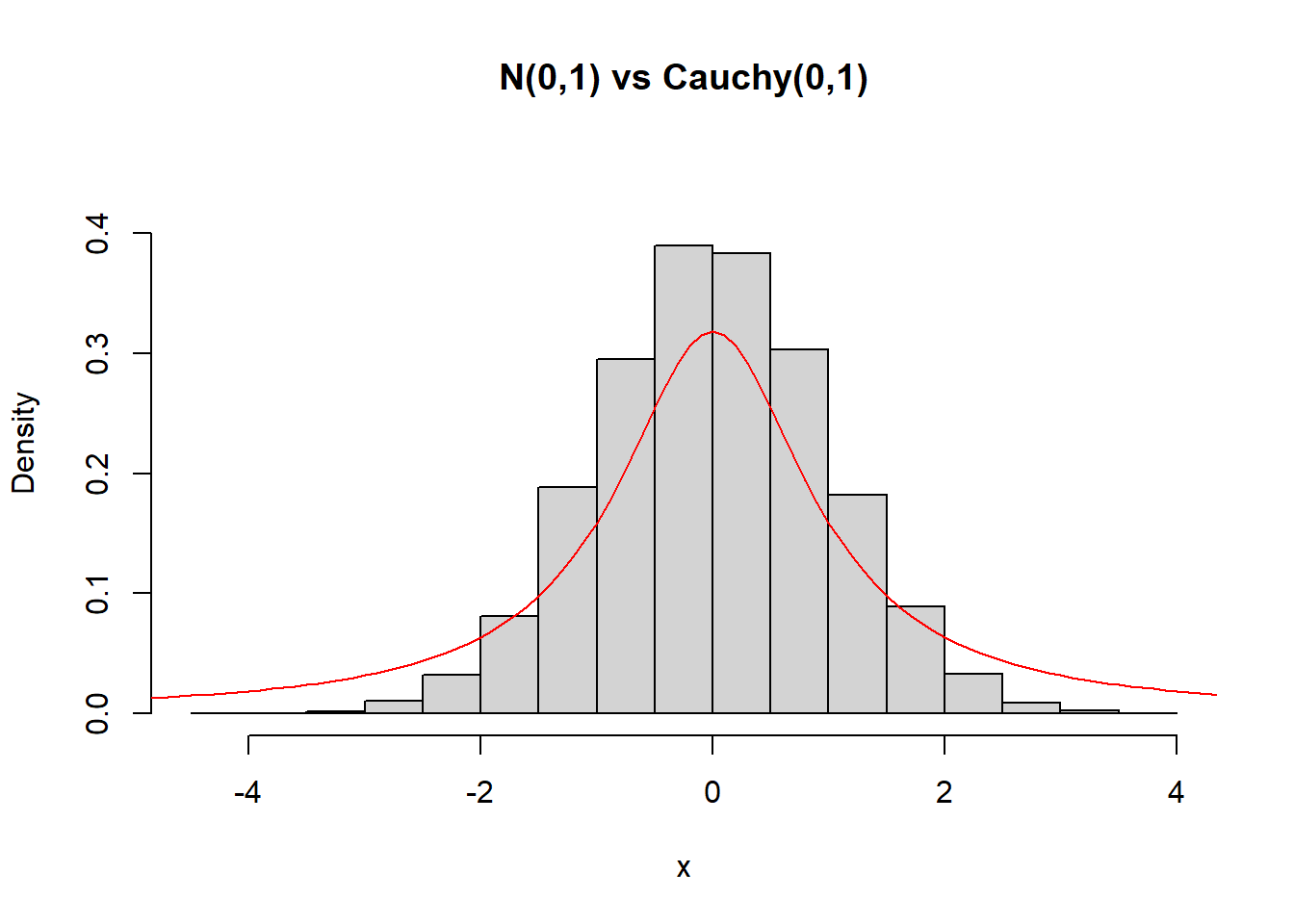
3.4 Προσομοίωση από την Κανονική Κατανομή

3.4.1 Μετασχηματισμός Box-Muller

Θα δείξουμε ότι αν \((U_1, U_2)\) ανεξάρτητες τ.μ. από την \(Unif(0,1)\) και

\[\begin{align*} X_1 &= \sqrt{-2\log U_1} \cdot \cos(2\pi U_2), \\ X_2 &= \sqrt{-2\log U_1} \cdot \sin(2\pi U_2), \end{align*}\]

τότε \(X_1 \thicksim N(0,1), X_2 \thicksim N(0,1)\) και \(X_1 \perp \!\!\! \perp Χ_2\).

Έστω ότι έχουμε \(Χ_1, Χ_2 \thicksim N(0,1)\) και \(X_1 \perp \!\!\! \perp Χ_2\). Θα μελετήσουμε το ζεύγος τ.μ.

\[\begin{equation*} (R, \Theta) = (\sqrt{X_1^2 +X_2^2}, \arctan\frac{X_2}{X_1}). \end{equation*}\]

Ισχύει ότι

\[\begin{equation*} \begin{array}{c} x_1 = r \cos\theta \\ x_2 = r \sin\theta\end{array} \Leftrightarrow \begin{array}{c} r=\sqrt{x_1^2+x_2^2} \\ \theta=\arctan\frac{x_2}{x_1} \end{array}. \end{equation*}\] \[\begin{equation*} detJ_g(x) = \left|\begin{array}{cc} \frac{\partial g_1(x)}{\partial x_1} & \frac{\partial g_1(x)}{\partial x_2} \\ \frac{\partial g_2(x)}{\partial x_1} & \frac{\partial g_2(x)}{\partial x_2} \end{array} \right| = ... = r \end{equation*}\]

Επομένως για \(r \neq 0\) έχουμε τον μετασχηματισμό:

\[\begin{align*} f_{R, \Theta}(R, \theta) &= f_{X_1, X_2}(r\cos\theta, r\sin\theta) \cdot r \\ &= \frac{1}{\sqrt{2\pi}} e^{-r^2\cos^2\theta} \cdot \frac{1}{\sqrt{2\pi}} e^{-r^2\sin^2\theta} \cdot r \\ &= \frac{1}{2\pi} r e^{-r^2} \\ &= f_\Theta (\theta) \cdot f_R (r). \end{align*}\]

όπου

\[\begin{align*} f_\Theta (\theta) &= \frac{1}{2\pi}, \ 0<\theta<2\pi, \\ f_R (r) &= r e^{-r^2} \ 0<r<+\infty. \end{align*}\]

Επομένως \(\Theta \perp \!\!\! \perp R\). Επιπλέον:

\[\begin{equation*} X_1, X_2 \thicksim N(0,1) \Rightarrow X_1^2+X_2^2 \thicksim \mathcal{X}_2^2 \equiv G\left(1,\frac{1}{2}\right) \equiv Exp\left(\frac{1}{2}\right). \end{equation*}\]

Άρα

\[\begin{align*} R^2 &= X_1^2+X_2^2 \thicksim Exp\left(\frac{1}{2}\right) = 2 \cdot Exp(1) \\ \Theta &= \frac{1}{2\pi} \thicksim Unif(0, 2\pi)= 2\pi \cdot Unif(0,1). \end{align*}\]

Παρατήρηση:. Θα μπορούσαμε να παράγουμε παρατηρήσεις και με την αντίστροφη \(\Phi^{-1}\). Σε αυτή την περίπτωση όμως δεν θα ήταν ακριβής προσομοίωση, αλλά προσεγγιστική, αφού θα χρησιμοποιούσαμε αριθμητικές μεθόδους για τους υπολογισμούς μας (με μεγάλη ακρίβεια).

boxmuller <- function(size, nb) {
  theta <- runif(size, 0, 2 * pi) 
  U1 <- runif(size)
  samples <- matrix(ncol = 2, nrow = size)
  R <- sqrt(-2 * log(U1))
  # alternative transformation
  # R <- sqrt(rchisq(size,df=2)) [why this is equivalent ?] 
  X <- R * cos(theta)
  Y <- R * sin(theta)
  normal <- rnorm(size)
  label <- rep(c("x", "y", "normal"), size)
  value <- c(X, Y, normal)
  df <- data.frame(value, label)
  plt <- ggplot(df, aes(x = value, color = label, fill = label)) + 
     geom_histogram(aes(y = ..density..), bins = nb, position = "identity", alpha = 0.3) +
     labs(x = "Value", y = "Density") + theme_bw() +
      stat_function(fun = dnorm, colour = "red")
  print(plt)
}

boxmuller(size = 10^4, nb = 60)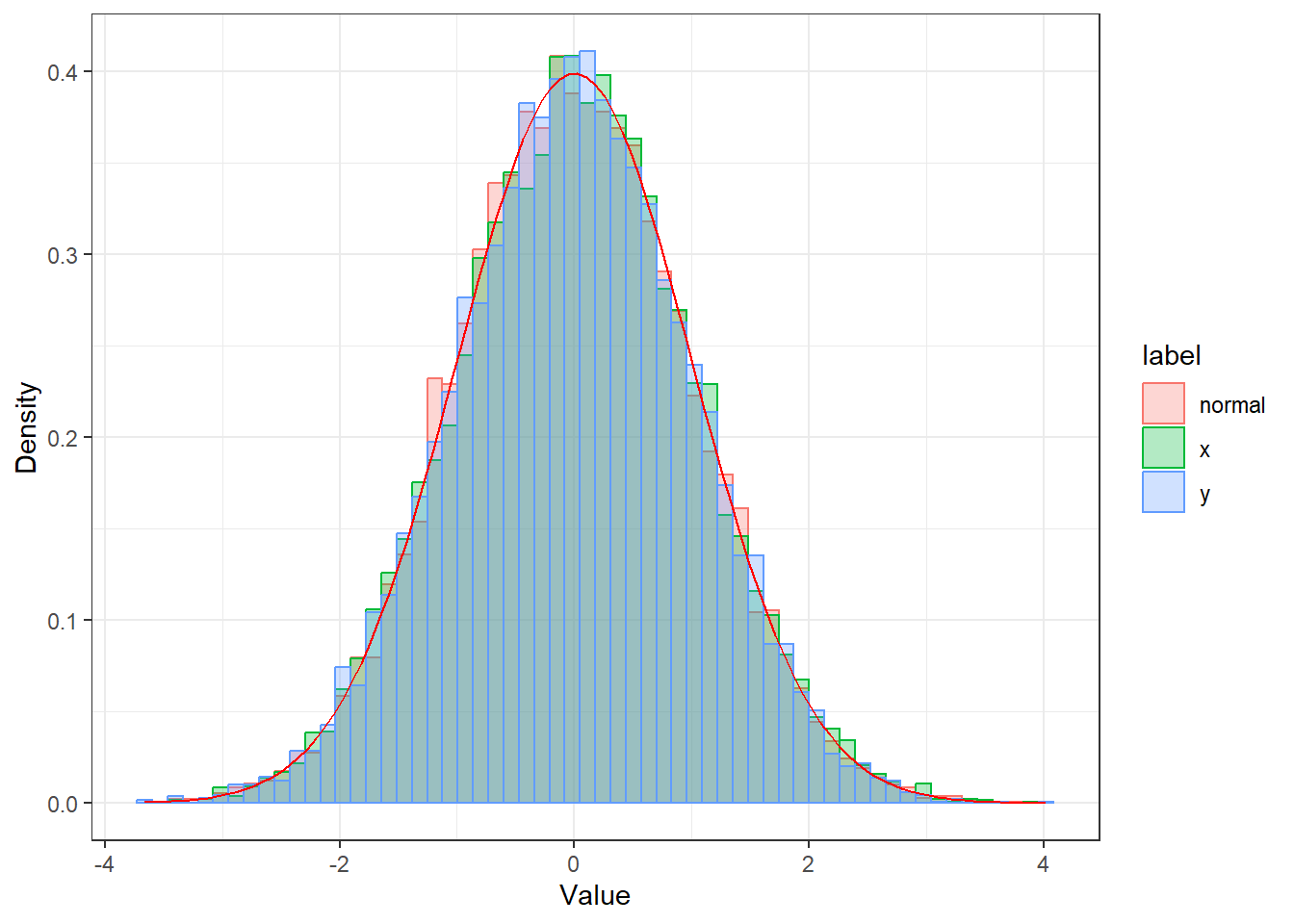

3.4.2 Προσομοίωση από την Πολυδιάστατη Κανονική

Η κατανομή μίας p-διάστατης τ.μ. \(X = (X_1, X_2, ..., X_p)^\top\) περιγράφεται πλήρως από τις κατανομές όλων των γραμμικών συνδυασμών \(u^\top X= \sum_{i=1}^p u_i X_i\).

Ορισμός 3.2 Έστω \(\mu=(\mu_1, \mu_2, ..., \mu_p)^\top\) και \(\Sigma = \left(\sigma_{ij}\right)_{p\times p}\) με \(\Sigma\) συμμετρικό και θετικά ημιορισμένο. Θα λέμε ότι η \(X\) ακολουθεί p-διάστατη κανονική, με διάνυσμα μέσων τιμών \(\mu\) και πίνακα διασπορών-συνδιασπορών ή συνδιακύμανσης \(\Sigma\) και θα γράφουμε \(X\thicksim N_p(\mu, \Sigma)\), αν \(u^\top X\thicksim N_1(u^\top \mu, u^\top \Sigma u), \ \forall u \in \mathbb{R}^p\).

Παρατήρηση:. Εάν υπάρχουν οι μέσες τιμές και οι διασπορές, ισχύουν οι παρακάτω σχέσεις:

\[\begin{align*} \mathbf{E}(u^\top X) &= u^\top \mathbf{E}(X)=u^\top \mu \\ \mathbf{V}(u^\top X) &= u^\top \mathbf{V}(X) u = u^\top \Sigma u \end{align*}\]

Το γεγονός ότι ο \(\Sigma\) είναι θετικά ημιορισμένος εξασφαλίζει ότι \(u^\top \Sigma u \geq 0, \ \forall u \in \mathbb{R}^p\), ώστε να ισχύει \(\mathbf{V}(u^\top X) \geq 0\) (ως διασπορά). Η διασπορά επιτρέπεται να είναι μηδενική για \(u \neq 0\), σε περιπτώσεις που έχουμε εκφυλισμούς κάποιων γραμμικών συνδυασμών.

Για παράδειγμα, αν \(X=(Z, Z)^\top, Z\thicksim N(0,1)\), τότε:

\[\begin{equation*} X\thicksim N_2(\mathbf{0}, \Sigma), \ \mathbf{0}=\left(\begin{array}{c} 0 \\ 0 \end{array}\right), \ \Sigma =\left(\begin{array}{cc} 1 & 1 \\ 1 & 1 \end{array}\right). \end{equation*}\]

Για \(u=(1, -1)^\top\) παίρνουμε:

\[\begin{equation*} u^\top X = \left(\begin{array}{cc} 1 & -1 \end{array}\right) \cdot \left(\begin{array}{c} Z \\ Z \end{array}\right) = Z-Z=0. \end{equation*}\]

Σε μονοδιάστατη γνωρίζουμε ότι:

\[\begin{equation*} X\thicksim N(\mu, \sigma^2) \Leftrightarrow X=\mu +\sigma Z, Z\thicksim N(0,1), \mu \in \mathbb{R}, \sigma>0. \end{equation*}\]

Για τις p-διάστατες χρησιμοποιούμε την σχέση:

\[\begin{equation*} Z\thicksim N_p(O_p, I_p) \Leftrightarrow Z=(Z_1, Z_2, ..., Z_p)^\top, Z_i\thicksim N(0,1), i=1,2,...,p \end{equation*}\]

όπου \(Z_i, Z_j\) ανεξάρτητες για \(i\neq j\).

Άρα

\[\begin{equation*} \mathbf{E}(Z)=\left(\begin{array}{c} \mathbf{E}(Z_1) \\ ... \\ \mathbf{E}(Z_p) \end{array}\right) = \left(\begin{array}{c} 0 \\ ... \\ 0 \end{array}\right) = O_p. \end{equation*}\] \[\begin{equation*} \mathbf{V}(Z)=\left(\begin{array}{cccc} \mathbf{V}(Z_1) & \mathbf{C}(Z_1, Z_2) & \ldots & \mathbf{C}(Z_1, Z_p)\\ \mathbf{C}(Z_2, Z_1) & \mathbf{V}(Z_2) & \ldots & \mathbf{C}(Z_2, Z_p) \\ \vdots & \vdots & \ddots & \vdots \\ \mathbf{C}(Z_p, Z_1) & \mathbf{C}(Z_p, Z_2) & \ldots & \mathbf{V}(Z_p) \end{array}\right) = \left(\begin{array}{cccc} 1 & 0 & \ldots & 0 \\ 0 & 1 & \ldots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & 1 \end{array}\right) = I_p. \end{equation*}\]

Για μία μονοδιάστατη κατανομή, έχουμε ότι \(\sigma=\sqrt{\sigma^2}\). Για μία πολυδιάστατη πώς μπορεί να γενικευθεί αυτό;

Πρόταση 3.3 Αν \(\Sigma\) συμμετρικός και θετικά ημιορισμένος, τότε γράφεται στην μορφή \(\Sigma = A A^\top\), με γενικά πολλές επιλογές για τον Α. Από όλες τις επιλογές, υπάρχει “βολική” αναπαράσταση με Α κάτω τριγωνικό (παράγοντας ανάλυση Choleski). Είναι μοναδική αν ο \(\Sigma\) είναι θετικά ορισμένος, δηλ \(x^\top \Sigma x>0, \ \forall x\neq 0\).

Πόρισμα 3.1 \[\begin{equation*} X\thicksim N_p(\mu, \Sigma) \Leftrightarrow X= \mu +A Z, Z\thicksim N_p(O_p, I_p), \mu \in \mathbb{R}, \Sigma=AA^\top, A \ \text{κάτω τριγωνικός}. \end{equation*}\]

Παράδειγμα 3.12 Προσομοιώστε παρατηρήσεις από την δι-διάσταση κανονική κατανομή.

Λύση:

Θέλουμε

\[\begin{equation*} X\thicksim N_2(\mu, \Sigma), \mu=\left(\begin{array}{c} \mu_1 \\ \mu_2 \end{array}\right), \Sigma=\left(\begin{array}{cc} \sigma_1^2 & p \sigma_1 \sigma_2 \\ p \sigma_1 \sigma_2 & \sigma_2^2 \end{array}\right), \end{equation*}\]

όπου

\[\begin{equation*} p=\frac{Cov(X_1, X_2)}{\sqrt{\mathbf{V}(X_1)\mathbf{V}(X_2)}}=\frac{\sigma_{1,2}}{\sigma_1 \sigma_2} \end{equation*}\]

Επιλέγουμε τον πίνακα

\[\begin{equation*} Α=\left(\begin{array}{cc} \sigma_1 & 0 \\ p \sigma_2 & \sqrt{1-p^2}\sigma_2 \end{array}\right). \end{equation*}\]

Εύκολα βλέπουμε ότι

\[\begin{equation*} X= \mu + AZ, Z=\left(\begin{array}{c} Z_1 \\ Z_2 \end{array}\right). \end{equation*}\]

Το παραπάνω γράφεται ως σύστημα:

\[\begin{align*} X_1 &= \mu_1 +\sigma_1 Z_1 \\ X_2 &= \mu_2 + p \sigma_2 Z_1 +\sqrt{1-p^2} \sigma_2 Z_2 = \mu_2 + \sigma_2 (pZ_1 + \sqrt{1-p^2}) Z_2 \end{align*}\]

Τελικά έχουμε:

\[\begin{equation*} \left(\begin{array}{c} Z_1 \\ Z_2 \end{array}\right) \rightarrow \left(\begin{array}{cc} 1 & 0 \\ p & \sqrt{1-p^2} \end{array}\right) \cdot \left(\begin{array}{c} Z_1 \\ Z_2 \end{array}\right) \equiv \left(\begin{array}{c} Z_1' \\ Z_2' \end{array}\right) \rightarrow \left(\begin{array}{cc} \sigma_1 & 0 \\ 0 & \sigma_2 \end{array}\right) \left(\begin{array}{c} Z_1' \\ Z_2' \end{array}\right) \rightarrow \mu + \left(\begin{array}{cc} \sigma_1 & 0 \\ 0 & \sigma_2 \end{array}\right) \left(\begin{array}{c} Z_1' \\ Z_2' \end{array}\right). \end{equation*}\] Ας μελετήσουμε ένα παράδειγμα στην R

set.seed(2184)

Sigma <- cov(matrix(rnorm(30), nrow = 10))

# compare times for generating 1 vector
system.time(for(i in 1:10000) { t(chol(Sigma)) %*% rnorm(3) })
##    user  system elapsed 
##    0.28    0.02    0.31
system.time(for(i in 1:10000) { rmnorm(1, varcov = Sigma) })
##    user  system elapsed 
##    0.44    0.11    0.56

# compare times for generating a sample of 100 vectors
test_1 <- function(Nsim = 10 ^ 4) {
  for(i in 1:Nsim){
    A <- t(chol(Sigma))
    for(j in 1:100) {
      A %*% rnorm(3)
    }
  }
}

test_2 <- function(Nsim = 10 ^ 4) {
  for(i in 1:Nsim) {
    rmnorm(100, varcov = Sigma)
  }
}
system.time(test_1())
##    user  system elapsed 
##    2.66    0.08    2.80
system.time(test_2())
##    user  system elapsed 
##    0.84    0.06    0.91

Θα προσομοιώσουμε με Monte Carlo από την δισδιάστατη κανονική κατανομή. Εύκολα μπορεί κάποιος να παρατηρήσει την μεταβολή των προσομοιωμένων τιμών καθώς η τιμή του \(p\) μεταβάλλεται από το \(-1\) στο \(1\). Η προσομοίωση των ανεξάρτητων τ.μ. \((Ζ_1, Ζ_2)\) έγινε με τον μετασχηματισμό Box-Muller, όπου για μηδενικές μέσες τιμές και μοναδιαίες τυπικές αποκλίσεις οι εξαρτημένες \((Χ_1, Χ_2)\) δίνονται από τις σχέσεις:

\[\begin{align*} X_1 &= Z_1, \\ X_2 &= pZ_1 +\sqrt{1-p^2} Z_2 \end{align*}\]

boxmuller <- function(n, p){
  
  theta <- runif(n, min = 0, max = 2 * pi) 
  U <- runif(n)
  R <- sqrt( - 2 * log(U))
  
  Z1 <- R * cos(theta)
  Z2 <- R * sin(theta)
  
  X1 <- Z1
  X2 <- p * Z1 + sqrt(1 - p ^ 2) * Z2
  
  data.frame(x = X1, y = X2)
}

3.5 Μέθοδος Αποδοχής-Απόρριψης

Μέχρι τώρα, είτε μέσω του αντίστροφου μετασχηματισμού, είτε με κατάλληλους γενικούς μετασχηματισμούς παράγουμε άμεσα τιμές από μία τ.μ. \(X\). Οι μέθοδοι αποδοχής-απόρριψης μας προσφέρουν έναν πολύ γενικό τρόπο να παράγουμε έμμεσα από μία τ.μ. \(X\). Προϋπόθεση είναι να γνωρίζουμε τη συναρτησιακή μορφή της σ.π.π. / σ.π. της \(X\).

Για τη μέθοδο αποδοχής-απόρριψης χρειαζόμαστε:

Μία πυκνότητα στόχο (target density) \(f\), γνωστή μέχρι κάποια πολλαπλασιαστική σταθερά (π.χ. \(f(x)=cx^3e^{-2x}, x>0\)),
Μία υποψήφια (προτεινόμενη) πυκνότητα (instrumental / candidate density) \(g\), από την οποία μπορούμε να προσομοιώσουμε απ’ ευθείας.

Οι υποθέσεις του αλγορίθμου είναι:

\[\begin{align*} & S_f \subset S_g, \ \text{δηλ} \ f(x)>0 \Rightarrow g(x) >0 \\ & \exists M>0: f(x)\leq M\cdot g(x), \ \forall x \in S_g \Leftrightarrow \sup_{x\in S_g}\frac{f(x)}{g(x)}<+\infty. \end{align*}\]

Πρόταση 3.4 Γενικός Αλγόριθμος Αποδοχής-Απόρριψης

Προσομοιώνουμε \(Y\thicksim g\).
Προσομοιώνουμε ανεξάρτητα \(U\thicksim Unif(0,1)\).
Αν \(U\leq \frac{1}{M} \frac{f(Y)}{g(Y)}\), τότε αποδεχόμαστε την \(Y\), δηλ. \(X=Y\), διαφορετικά επιστρέφουμε στο Βήμα 1.

Ο αλγόριθμος τερματίζει όταν για 1η φορά γίνει αποδοχή κάποιας \(Y\). Οι παρατηρήσεις που παράγονται από τον αλγόριθμο ακολουθούν την \(f\).

Απόδειξη:. Η τελική αποδοχή της \(Y\) συμβαίνει όταν ικανοποιηθεί ο περιορισμός \(U\leq \frac{1}{M} \frac{f(Y)}{g(Y)}\). Επομένως, η κατανομή της αποδεκτής τιμής του αλγορίθμου εκφράζεται μέσα από την κατανομή της τ.μ. \(X=\left[Y\ \middle\vert \ U\leq \frac{1}{M} \frac{f(Y)}{g(Y)}\right]\). Υπολογίζουμε τη σ.κ. της \(X\). Συγκεκριμένα, έστω \(x\in \mathbb{R}\).

\[\begin{align*} \mathbf{P}(X\leq x) &= \mathbf{P}\left(Y\leq x \ \middle\vert \ U\leq \frac{1}{M} \frac{f(Y)}{g(Y)}\right) =\frac{\mathbf{P}\left(Y\leq x , U\leq \frac{1}{M} \frac{f(Y)}{g(Y)}\right)}{\mathbf{P}\left(U\leq \frac{1}{M} \frac{f(Y)}{g(Y)}\right)} =\frac{\mathbf{E}\left(\mathbf{1}_{ Y\leq x} \cdot \mathbf{1}_{U\leq \frac{1}{M} \frac{f(Y)}{g(Y)}}\right)}{\mathbf{E}\left(\mathbf{1}_{U\leq \frac{1}{M} \frac{f(Y)}{g(Y)}}\right)}\\ &=\frac{\mathbf{E}\left(\mathbf{1}_{Y\leq x} \cdot \mathbf{E}\left(\mathbf{1}_{U\leq \frac{1}{M} \frac{f(Y)}{g(Y)}}\ \middle \vert\ Y\right)\right)}{\mathbf{E}\left(\mathbf{E}\left(\mathbf{1}_{U\leq \frac{1}{M} \frac{f(Y)}{g(Y)}}\ \middle \vert \ Y\right)\right)} = \frac{\mathbf{E}\left(\mathbf{1}_{Y\leq x} \cdot \mathbf{P}\left(U\leq \frac{1}{M} \frac{f(Y)}{g(Y)}\ \middle \vert\ Y\right)\right)}{\mathbf{E}\left(\mathbf{E}\left(\mathbf{1}_{U\leq \frac{1}{M} \frac{f(Y)}{g(Y)}}\ \middle \vert \ Y\right)\right)} =\frac{\mathbf{E}\left(\mathbf{1}_{Y\leq x} \cdot \frac{1}{M} \frac{f(Y)}{g(Y)}\right)}{\mathbf{E}\left(\frac{1}{M} \frac{f(Y)}{g(Y)}\right)} \\ & = \frac{\int_{y\leq x}\frac{f(y)}{g(y)}\cdot g(y) dy}{\int_{y \in S_f}\frac{f(y)}{g(y)}\cdot g(y) dy} = F(x) \end{align*}\]

Γενικότερα,

\[\begin{equation*} \mathbf{E}\left[h(X)\right]=\mathbf{E}_f\left[ h(Y) \right]=\mathbf{E}_g\left[h(Y) \cdot \frac{f(Y)}{g(Y)} \right]. \end{equation*}\]

Άρα,

\[\begin{equation*} \mathbf{P}(X\leq x) = \mathbf{E}\left(\mathbf{1}_{X\leq x}\right) = \mathbf{E}_g\left( \mathbf{1}_{Y\leq x} \cdot \frac{f(Y)}{g(Y)} \right). \end{equation*}\]

Παρατήρηση:. Σημαντικό στην αποδοτικότητα ενός αλγορίθμου αποδοχής-απόρριψης είναι η πιθανότητα αποδοχής, όπου το ενδεχόμενο αποδοχής είναι το \(A=\left\{U \leq \frac{1}{M} \frac{f(Y)}{g(Y)} \right\}\).

\[\begin{equation*} \mathbf{P}(A) = \mathbf{P}\left( U \leq \frac{1}{M} \frac{f(Y)}{g(Y)} \right) = \mathbf{E}\left[ \mathbf{P}\left( U \leq \frac{1}{M} \frac{f(Y)}{g(Y)} \ \middle \vert \ Y \right) \right] = \mathbf{E}_g\left[ \frac{1}{M} \frac{f(Y)}{g(Y)} \right] = \frac{1}{M} \mathbf{E}_g\left[ \frac{f(Y)}{g(Y)} \right] = \frac{1}{M} \mathbf{E}_f\left[ 1 \right]=\frac{1}{M}. \end{equation*}\]

Παρατήρηση:. Στα προηγούμενα υποθέτουμε ότι οι σταθερές κανονικοποίησης είναι γνωστές και τότε η πιθανότητα αποδοχής είναι \(1/M\). Όμως ο αλγόριθμος εφαρμόζεται ακόμα και αν οι σταθερές είναι άγνωστες (τόσο για την \(f\) όσο και για την \(g\)). Έστω \(f=c_f \widetilde{f}, g=c_g \widetilde{g}\). Τότε:

\[\begin{equation*} \sup_{x\in S_{\widetilde{g}}}\frac{\widetilde{f}(x)}{\widetilde{g}(x)}= \frac{c_g}{c_f} \sup_{x\in S_g}\frac{f(x)}{g(x)}. \end{equation*}\]

Επομένως:

\[\begin{equation*} \sup_{x\in S_{\widetilde{g}}}\frac{\widetilde{f}(x)}{\widetilde{g}(x)} \leq M'\ \Longrightarrow \ \sup_{x\in S_g}\frac{f(x)}{g(x)} \leq \frac{c_f}{c_g} \cdot M'. \end{equation*}\]

Αν γνωρίζουμε ένα τέτοιο \(M'\), τότε ο αλγόριθμος αποδοχής-απόρριψης αποδέχεται την παραγόμενη παρατήρηση \(Y\) όταν \(U<\frac{1}{M'} \cdot \frac{\widetilde{f}(Y)}{\widetilde{g}(Y)}\).

Σε αυτή την περίπτωση, η πιθανότητα αποδοχής μεταβάλλεται:

\[\begin{equation*} \mathbf{P}(A) = \mathbf{P}\left( U \leq \frac{1}{M'} \frac{\widetilde{f}(Y)}{\widetilde{g}(Y)} \right) = \mathbf{E}_g\left[ \frac{1}{M'} \frac{\tilde{f}(Y)}{\tilde{g}(Y)} \right] = \frac{1}{M'} \frac{c_g}{c_f} \mathbf{E}_g\left[ \frac{f(Y)}{g(Y)} \right] = \frac{1}{M'} \cdot \frac{c_g}{c_f}. \end{equation*}\]

Πολλές φορές είναι άγνωστο μόνο το \(c_f\), και έτσι μπορούμε να εκτιμήσουμε τη σταθερά ολοκλήρωσης μέσα από μία σειρά διαδοχικών προσομοιώσεων. Αν είναι άγνωστος ο λόγος, τότε αντί για το \(c_f\), εκτιμάται ο λόγος \(c_f/c_g\) (ή \(c_g/c_f\)). Εφ’ όσον έχουμε πιθανότητα αποδοχής \(p=\frac{1}{M'} \cdot \frac{c_g}{c_f}\), αν σε ένα δείγμα \(n\) ανεξάρτητων προσομοιώσεων έχουμε ποσοστό αποδοχών \(\widehat{p}_n\), τότε:

\[\begin{equation*} \widehat{\left(\frac{c_g}{c_f}\right)}=M'\, \hat{p}_n. \end{equation*}\]

Παράδειγμα 3.13 Προσομοιώστε παρατηρήσεις από την \(Beta(a,b), a,b>1\), με τον αλγόριθμο αποδοχής-απόρριψης, χρησιμοποιώντας την \(Unif(0,1)\) ως υποψήφια.

Λύση:

f <- function(x){
  dbeta(x, 2.7, 6.3)
}
optimize(f, interval = c(0, 1), maximum = TRUE)$objective
## [1] 2.669744

Nsim <- 2500
a <- 2.7
b <- 6.3
M <- 2.67
u <- runif(Nsim, max = M) # uniform over (0, M)
y <- runif(Nsim) # generation from g
x <- y[u < dbeta(y, a, b)] # accepted subsample

hist(x, main = "Beta(2.7, 6.3) sample with Accept-Reject", freq = FALSE, col = "grey")
curve(dbeta(x, 2.7, 6.3),  from = 0, to = 1, lty= 1, lwd = 1, col = "red", add = TRUE)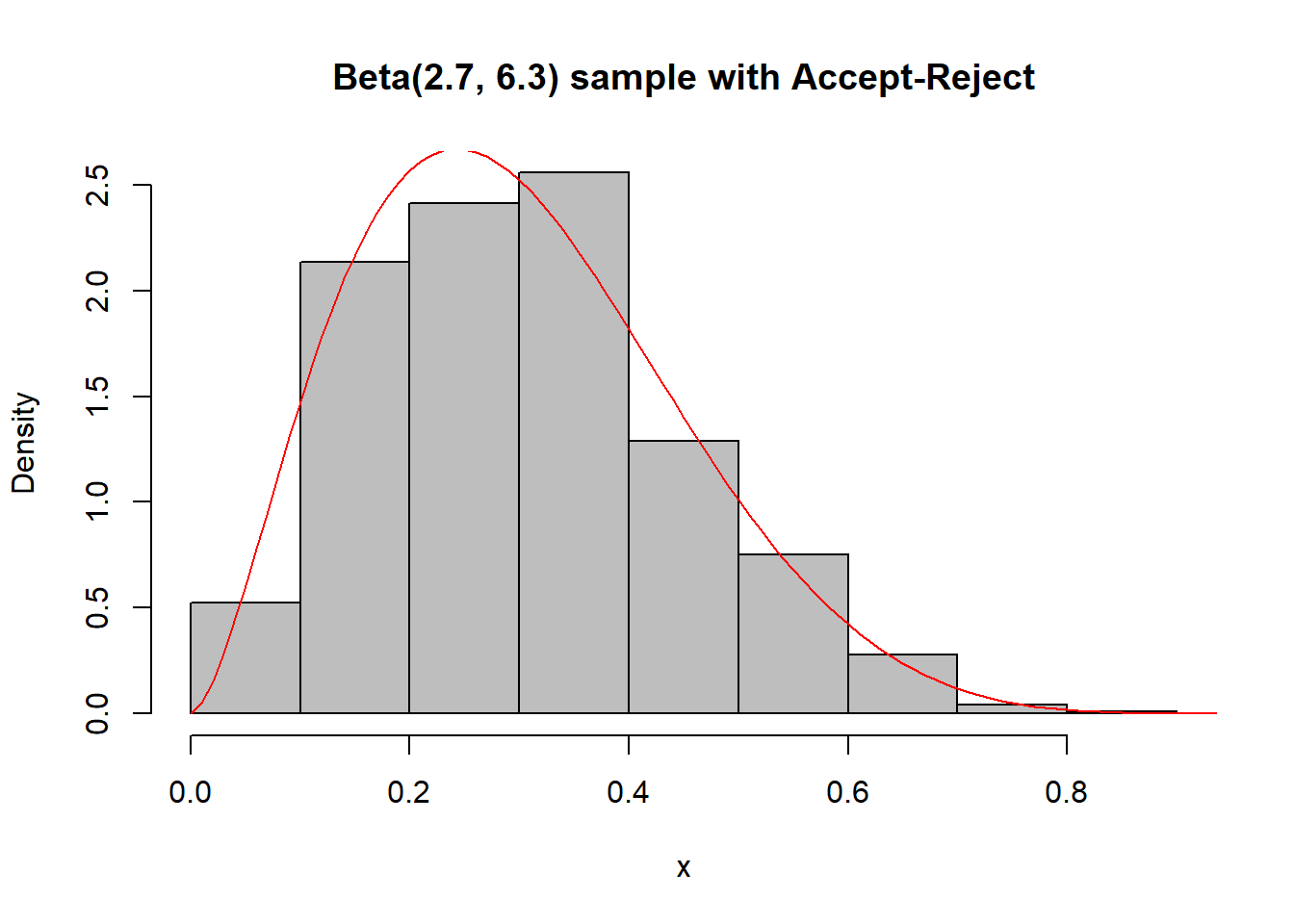

Στον παραπάνω κώδικα παράγουμε πολλές παρατηρήσεις από τις οποίες δεχόμαστε μόνο μερικές. Ένας πιο αποδοτικός τρόπος είναι ρυθμίζοντας τον αριθμό προσομοιώσεων να είναι τέτοιος ώστε ο μέσος αριθμός αποδεκτών καταστάσεων να συμπίπτει με το μέγεθος του δείγματος που θέλουμε να πάρουμε, όπως φαίνεται παρακάτω:

x <- NULL
while (length(x) < Nsim) {
y <- runif(Nsim * M)
x <- c(x, y[runif(Nsim * M) * M < dbeta(y, a, b)])}
x <- x[1:Nsim]

hist(x, main = "Beta(2.7, 6.3) sample with Accept-Reject", freq = FALSE, col = "grey")
curve(dbeta(x, 2.7, 6.3), from = 0, to = 1, lty= 1, lwd = 1, col = "red", add = TRUE)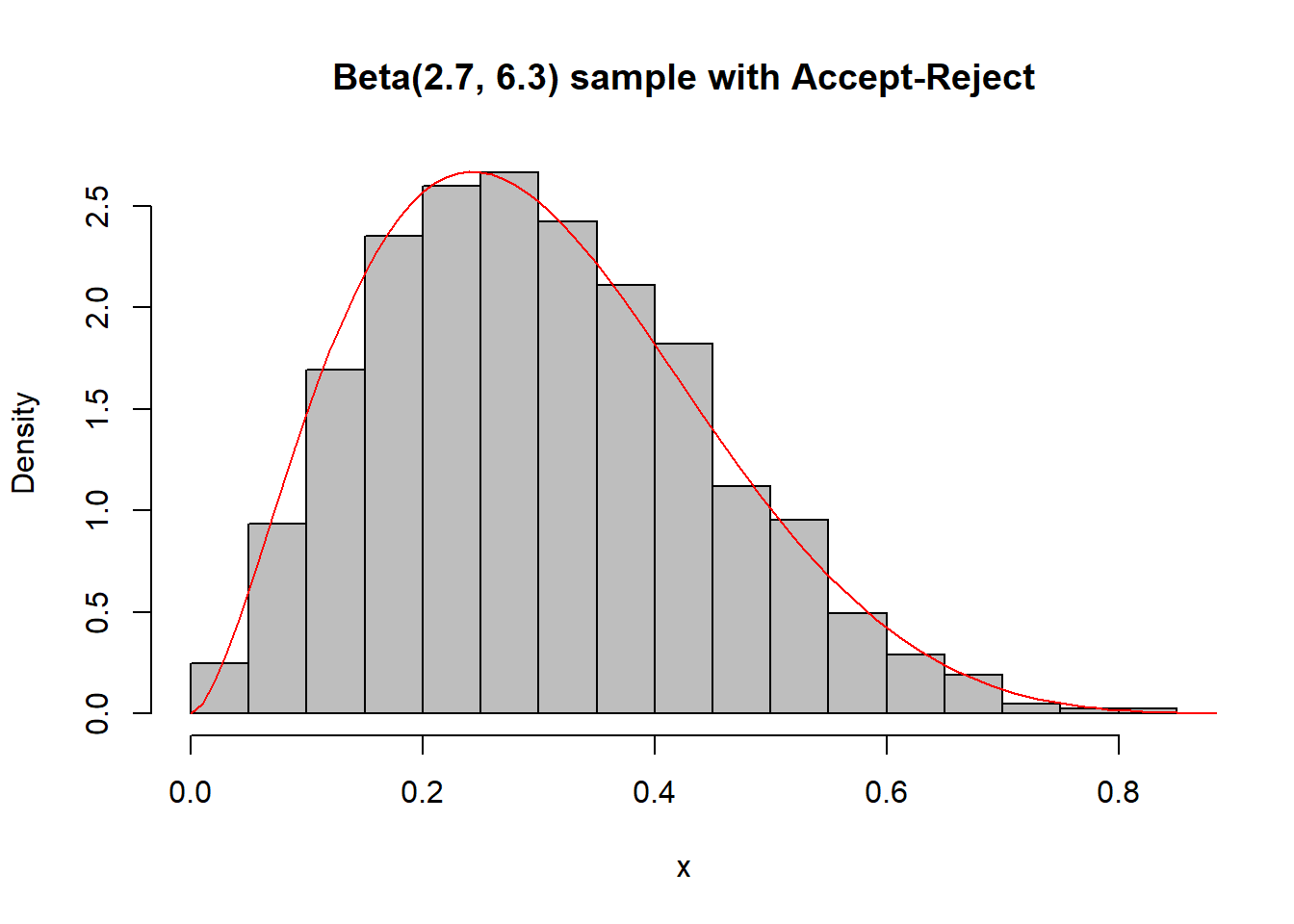

Παράδειγμα 3.14 (Προσομοίωση από την Κανονική Κατανομή) Ας υποθέσουμε ότι θέλουμε να παράγουμε από \(N(0,1)\) με τον αλγόριθμο αποδοχής-απόρριψης και χρησιμοποιούμε κατανομή πρότασης τη διπλή εκθετική (Laplace) \(\mathcal{L}(a)\), με πυκνότητα

\[\begin{equation} g(x|a) = \frac{a}{2} \, e^{-a\,|x|}, \quad x\in \mathbb{R},\ a>0, \end{equation}\]

Να δειχθεί ότι

\[\begin{equation} \frac{f(x)}{g(x|a)}\leq \sqrt{\frac{2}{\pi}}a^{-1}e^{\frac{a^2}{2}} \end{equation}\]

και ότι το ελάχιστο του παραπάνω φράγματος (στο \(a\)) επιτυγχάνεται στο \(a=1\).

Να δειχθεί ότι η πιθανότητα αποδοχής γίνεται τότε \(\sqrt{\pi/2e}=0.76\) και συμπεράνετε ότι για να παραχθεί μία \(N(0,1)\) απαιτούνται κατά μέσο όρο \(1/0.76 \approx 1.3\) ομοιόμορφες τυχαίες μεταβλητές.
Να δειχθεί ότι η διπλή εκθετική \(\mathcal{L}(a)\) μπορεί να παραχθεί από τον αντίστροφο μετασχηματισμό πιθανότητας και συγκρίνετε αυτόν τον αλγόριθμο με τον αλγόριθμο Box-Muller του Παραδείγματος 2.3 ως προς το χρόνο εκτέλεσης.

Λύση:

Ερώτημα a

Σε πρώτη φάση υπολογίζουμε τον λόγο:

\[\begin{equation*} \frac{f(x)}{g(x|a)}=\frac{\frac{1}{\sqrt{2\pi}}e^{-x^2/2}}{\frac{a}{2} e^{-a|x|}}= \sqrt{\frac{2}{\pi}}a^{-1}e^{-\frac{x^2}{2}+a |x|} \end{equation*}\]

Όμως

\[\begin{equation*} e^{-\frac{x^2}{2}+a |x|}=e^{\frac{a^2}{2}}\cdot e^{-\frac{(|x|-a)^2}{2}}, \ \ \forall x \in \mathbb{R}, \end{equation*}\]

και

\[\begin{equation*} \sup_{x\in \mathbb{R}} e^{-\frac{(|x|-a)^2}{2}}=1, \end{equation*}\]

το οποίο επιτυγχάνεται για \(|x|=a.\) Συμπεραίνουμε ότι:

\[\begin{equation*} \sup_{x\in\mathbb{R}}\frac{f(x)}{g(x|a)}= \sqrt{\frac{2}{\pi}}a^{-1}e^{\frac{a^2}{2}}. \end{equation*}\]

Η χρήση μιας παραμετρικής οικογένειας \(g(x|a)\) αντί μιας συγκεκριμένης πυκνότητας μας επιτρέπει την περαιτέρω βελτίωση της σταθεράς \(M\) που παίζει σημαντικό ρόλο στην απόδοση του αλγορίθμου αποδοχής - απόρριψης.

Εδώ

\[\begin{equation*} M(a)=\sqrt{\frac{2}{\pi}} \frac{e^{\frac{a^2}{2}}}{a}, \end{equation*}\]

και έτσι ελαχιστοποιούμε την \(M(a)\) ως προς \(a>0\).

Παραγωγίζοντας την \(M(a)\) έχουμε

\[\begin{equation*} M'(a)=\sqrt{\frac{2}{\pi}} \frac{(a^2-1)e^{\frac{a^2}{2}}}{a^2}, \ \ a>0 \end{equation*}\]

και άρα

\[\begin{equation*} M'(a)=0 \Leftrightarrow a=1. \end{equation*}\]

Παρατηρούμε επίσης ότι \(M'(a)<0\), για \(a<1\) και \(M'(a)>0\), για \(a>1\). Συμπεραίνουμε λοιπόν ότι

\[\begin{equation*} \min_{a>0} M(a) = M(1) = \sqrt{\frac{2e}{\pi}} \cong 1.315 \end{equation*}\]

Ερώτημα b

Έχουμε δείξει ότι η πιθανότητα αποδοχής ενός αλγορίθμου αποδοχής - απόρριψης είναι

\[\begin{equation*} p = P\left[ U<\frac{1}{M} \cdot \frac{f(Y)}{g(Y)}\right]=\frac{1}{M}, \end{equation*}\]

και άρα εδώ

\[\begin{equation*} p=\frac{1}{M(1)}=\sqrt{\frac{\pi}{2e}}\cong 0.76 \ . \end{equation*}\]

Επίσης, αν \(N\) είναι το πλήθος των ανεξάρτητων ομοιόμορφων τ.μ. που παράγονται μέχρι να ικανοποιηθεί το κριτήριο και να γίνει για πρώτη φορά δεκτή, τότε

\[\begin{equation*} N\thicksim Geo(p), \quad N\in \mathbb{N}^{*}. \end{equation*}\]

Συμπεραίνουμε ότι

\[\begin{equation*} E(N)=\frac{1}{p}=M(1) \cong 1.315. \end{equation*}\]

Γενικότερα, ο μέσος αριθμός προσομοιώσεων ομοιόμορφων τ.μ. που χρειάζονται για να παραχθεί μία τιμή μίας τ.μ. \(X\) μέσω του αλγορίθμου αποδοχής - απόρριψης είναι \(M\). Θυμίζουμε βέβαια εδώ ότι αυτό ισχύει όταν οι σταθερές κανονικοποίησης των \(f,g\) είναι γνωστές.

Ερώτημα c

Η μέθοδος αντίστροφου μετασχηματισμού πιθανότητας για την προσομοίωση τυχαίων μεταβλητών στηρίζεται στη δυνατότητα υπολογισμού και αντιστροφής της σ.κ. της εν λόγω τ.μ..

Αν

\[\begin{equation*} X\thicksim \mathcal{L}(a), \ \ a>0, \end{equation*}\]

τότε

\[\begin{equation*} X=\frac{1}{a} \cdot Z, \ \text{όπου} \ \ Z\thicksim \mathcal{L}(1), \end{equation*}\]

άρα αρκεί να “αντιστρέψουμε” για \(a=1\).

Αν \(z<0,\) τότε

\[\begin{equation*} F_Z(z)=P(Z\leq z)=\int_{-\infty}^z\frac{1}{2}e^{-|u|}du=\frac{1}{2}\int_{-\infty}^ze^{u}du=\frac{1}{2}e^z. \end{equation*}\]

Για \(z\geq 0,\) έχουμε

\[\begin{align*} F_Z(z)=P(Z\leq z) &=P(Z \leq 0)+ P (0 \leq Z \leq z) \\ &= \frac{1}{2}+\frac{1}{2}\int_{0}^ze^{-u}du \\ &=\frac{1}{2}+\frac{1}{2}\left(1 - e^{-z}\right) \\ &= 1-\frac{1}{2} e^{-z}. \end{align*}\]

Τελικά,

\[\begin{equation*} F_Z(z)=\left\{\begin{array}{lcc} \frac{1}{2}e^z & , & z<0 \\ 1-\frac{1}{2}e^{-z} & , & z \geq 0 \end{array}\right. \ \ . \end{equation*}\]

Θέτοντας \(u=F_Z(z),\) έχουμε

\[\begin{equation*} z=F^{-1}_Z(u)=\left\{\begin{array}{lcc} \log(2u) & , & 0<u<\frac{1}{2} \\ -\log[2(1-u)] & , & \frac{1}{2} \leq u < 1 \end{array}\right. \ \ . \end{equation*}\]

Η παραπάνω σχέση μας οδηγεί στο συμπέρασμα ότι

\[\begin{equation*} Z=F^{-1}_Z(U)=\log(2u) \cdot 1_{\left(0, \frac{1}{2}\right)}(u)-\log[2(1-u)] \cdot 1_{\left[ \frac{1}{2}, 1\right)}(u), \end{equation*}\]

και άρα \(X=\frac{1}{a}F^{-1}_Z(U)\).

Σύγκριση Αλγορίθμων

Υλοποιούμε τον αλγόριθμο παραγωγής παρατηρήσεων από την τυπική κανονική μέσω της κατανομής Laplace.

Αρχικά, δημιουργούμε μία συνάρτηση για την πυκνότητα της Laplace:

dlaplace <- function(x) {
  exp( - abs(x)) / 2
}

Έπειτα, δημιουργούμε μία συνάρτηση για την παραγωγή τυχαίων παρατηρήσεων από την Laplace (μέσω αντίστροφου μετασχηματισμού):

rlaplace <- function(size) {
  u <- runif(size)
  log(2 * u) * I((0 < u) & (u < 1 / 2)) - log(2 * (1 - u)) * I((1 / 2 <= u) & (u < 1))
}

Τέλος, δημιουργούμε τη συνάρτηση που υλοποιεί τον αλγόριθμο αποδοχής - απόρριψης:

acc.rej <- function(size, plot = TRUE, report = TRUE) {
  
  # Αρχικοποιούμε τα διανύσματα και το M
  u <- x <- y <- NULL
  M <- sqrt(2 * exp(1) / pi)
  
  while (length(x) < size) {
    
    # Δημιουργούμε τον αναμενόμενο αριθμό παρατηρήσεων που θα
    # χρειαστούμε, δηλαδή (size-length(x))*M και εξετάζουμε
    # πόσα θα γίνουν δεκτά
    if (report) {
      cat(paste0("Number of trials: ", floor((size - length(x)) * M), "\n"))
    }
    
    u <- c(u, runif((size - length(x)) * M))
    y <- c(y, rlaplace((size - length(x)) * M))
    x <- y[u * M * dlaplace(y) < dnorm(y)]
    
    if (report) {
      cat(paste0("Total Accepted: ", length(x), "\n"))
    }
    
  }  
  
  # Κρατάμε μόνο όσες παρατηρήσεις μας ζητούνται
  u<-u[1:size]
  x<-x[1:size]
  y<-y[1:size]
  
  # Κάνουμε το γράφημα
  if (plot) { 
    data<-data.frame(pointx = y,
                     pointy = u * M * dlaplace(y), 
                     accept = (u * M * dlaplace(y) < dnorm(y)))
    
    a <- ggplot(data) +
      stat_function(fun = function(x) { dlaplace(x) * M }, xlim = c(-8,8)) +
      stat_function(fun = dnorm, xlim = c(-8,8)) +
      geom_point(aes(x = pointx, y = pointy, col = accept), size = 0.4) +
      xlab("x") + ylab("y") +
      theme_minimal()
    print(a)
  }
  
  x
}

x <- acc.rej(1000)
## Number of trials: 1315
## Total Accepted: 1027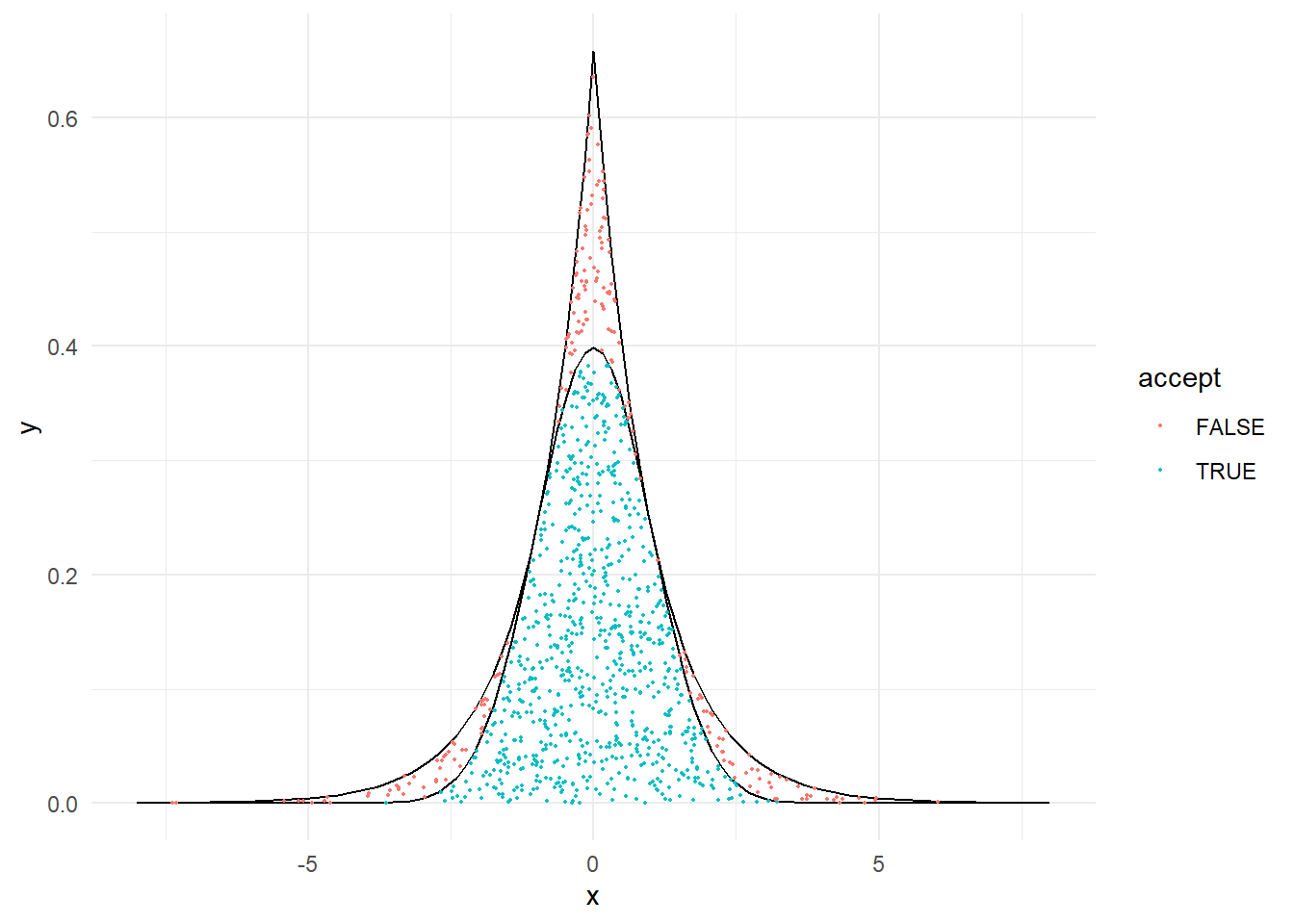

H παραπάνω συνάρτηση δημιουργεί τον αναμενόμενο αριθμό παρατηρήσεων που θα χρειαστούμε. Έτσι, γλυτώνει αρκετό χρόνο σε σύγκριση με την αντίστοιχη συνάρτηση που δημιουργεί τις παρατηρήσεις μία-μία:

acc.rej.1 <- function(size, plot = TRUE){
  
  # Αρχικοποιούμε τα διανύσματα και το M
  u <- x <- y <- NULL
  M <- sqrt(2 * exp(1) / pi)
  
  # Δημιουργούμε μία νέα παρατήρηση και εξετάζουμε εάν θα γίνει δεκτή
  while (length(x)<size) {
    unew <- runif(1)
    ynew <- rlaplace(1)
    u <- c(u, unew)
    y <- c(y, ynew)
    x <- c(x, ynew[unew * M * dlaplace(ynew) < dnorm(ynew)])
  }  
  
  # Κάνουμε το γράφημα
  if (plot) { 
    data<-data.frame(pointx = y,
                     pointy = u * M * dlaplace(y), 
                     accept = (u * M * dlaplace(y) < dnorm(y)))
    
    a <- ggplot(data) +
      stat_function(fun = function(x){ dlaplace(x) * M }, xlim = c(-8,8)) +
      stat_function(fun = dnorm, xlim = c(-8,8)) +
      geom_point(aes(x = pointx, y = pointy, col = accept), size = 0.4) +
      xlab("x") + ylab("y") +
      theme_minimal()
    print(a)
  }
  
  x
}

x <- acc.rej.1(1000)

Ο αλγόριθμος Box-Muller μπορεί να εκτελεστεί στην R ως εξής:

boxmuller <- function(size) {
  
  if(size %% 2 == 1){
    size <- size + 1
  }
  
  theta <- runif(size / 2, 0, 2 * pi) 
  U1 <- runif(size / 2)
  R <- sqrt(-2 * log(U1))
  Z <- c(R * cos(theta), R * sin(theta))
  if(size %% 2 == 1){
    Z <- Z[-1]
  }
  Z
}

Συγκρίνουμε την ταχύτητα των τριών αλγορίθμων με το πακέτο microbenchmark:

microbenchmark(acc.rej(1000, plot = FALSE, report = FALSE), times = 100, unit = "us")
## Unit: microseconds
##                                         expr   min       lq     mean  median
##  acc.rej(1000, plot = FALSE, report = FALSE) 402.8 429.5005 722.4291 617.401
##     uq   max neval
##  657.8 10040   100
microbenchmark(acc.rej.1(1000, plot = FALSE), times = 100, unit = "us")
## Unit: microseconds
##                           expr     min      lq     mean  median      uq
##  acc.rej.1(1000, plot = FALSE) 32524.9 36417.7 40236.81 38151.4 43555.5
##       max neval
##  106611.3   100
microbenchmark(boxmuller(1000), times = 100, unit = "us")
## Unit: microseconds
##             expr    min     lq     mean median     uq      max neval
##  boxmuller(1000) 80.801 81.501 159.0149 83.701 89.401 7370.701   100

Παράδειγμα 3.15 Η παρακάτω “περίεργη” συνάρτηση πυκνότητας

\[\begin{equation*} f(x)\propto e^{-x^2/2} \cdot \left(\sin(6x)^2 +3 \cos(x)^2 sin(4x)^2 +1 \right), \end{equation*}\]

μπορεί να προσομοιωθεί χρησιμοποιώντας τον αλγόριθμο Αποδοχής - Απόρριψης.

Σχεδιάστε την \(f(x)\) και δείξτε ότι μπορούμε να τη φράξουμε από τη \(M g(x)\), όπου \(g\) είναι η σ.π.π. της τυπικής κανονικής \(g(x)=e^{-x^2/2}/\sqrt{2\pi}\). Βρείτε μία αποδεκτή, αν όχι βέλτιστη, τιμή για το \(M\) (Υπόδειξη: Χρησιμοποιήστε τη συνάρτηση optimise).
Προσομοιώστε 2500 τυχαίες παρατηρήσεις από την \(f\) χρησιμοποιώντας τον αλγόριθμο Αποδοχής - Απόρριψης.
Από το ποσοστό αποδοχής του αλγορίθμου εκτιμήστε τη σταθερά κανονικοποίησης της \(f\) και συγκρίνετε το ιστόγραμμα του τυχαίου δείγματος με την κανονικοποιημένη καμπύλη \(f\).

Λύση:

Θα σχεδιάσουμε τις συναρτήσεις \(c\cdot f\) και \(M\cdot g\), δίνοντας τη δυνατότητα στα \(c\) και \(M\) να μεταβάλλονται.

Παρατηρούμε ότι η \(f\) είναι δικόρυφη (το μέγιστο επιτυγχάνεται σε 2 διαφορετικές θέσεις) και για \(c=1\) βρίσκεται γενικά πάνω από τη \(g\). Επομένως, προκειμένου η \(f\) να ολοκληρώνει στη μονάδα, έχουμε ότι \(c<1\). Για \(c=1\) μπορούμε να βρούμε κατάλληλο \(M>1\) ώστε \(f<=M\cdot g\). Μπορούμε να βρούμε ένα τέτοιο \(M\) με τον παρακάτω κώδικα:

# target density
f <- function(x, c = 1) {
  c * exp(- x ^ 2 / 2) * (sin(6 * x) ^ 2 + 3 * cos(x) ^ 2 * sin(4 * x) ^ 2 + 1)
}

# candidate density N(0,1)
g <- function(x, M = 1) {
  M * exp(- x ^ 2 / 2) / sqrt( 2 * pi)
}

# ratio f/g
ratio <- function(x) {
  f(x) / g(x)
}

opt <- optimize(ratio, interval = c(-5, 5), maximum = TRUE)
M <- opt$objective
M
## [1] 10.94031

Σύμφωνα με τα παραπάνω, εργαζόμαστε με \(M=\) 10.9403062. Προσέχουμε ότι το \(M\) αυτό θα ήταν βέλτιστο αν η πραγματική τιμή της σταθεράς ήταν \(c=1\). Γνωρίζοντας όμως ότι είναι μικρότερη, το ίδιο ισχύει και για το βέλτιστο \(Μ\).

Είμαστε τώρα έτοιμοι να υλοποιήσουμε τον αλγόριθμο Αποδοχής - Απόρριψης.

y <- NULL
n <- 2500
trials <- 0

while (length(y) < n) {
  x <- rnorm(1)
  u <- runif(1)
  y <- c(y, x[u < f(x) / (M * g(x))])
  trials <- trials + 1
}

Έχοντας παράγει το δείγμα, θα εκτιμήσουμε τη σταθερά κανονικοποίησης

\[\begin{equation*} \hat{c}=\frac{1}{\hat{p}M}, \end{equation*}\]

όπου \(\hat{p}\) το ποσοστό αποδοχών.

acc <- n / trials
chat <- 1 / (acc * M)
acc ; chat
## [1] 0.5318017
## [1] 0.1718782

Επομένως η κανονικοποιημένη f και το ιστόγραμμά της έχουν τη μορφή:

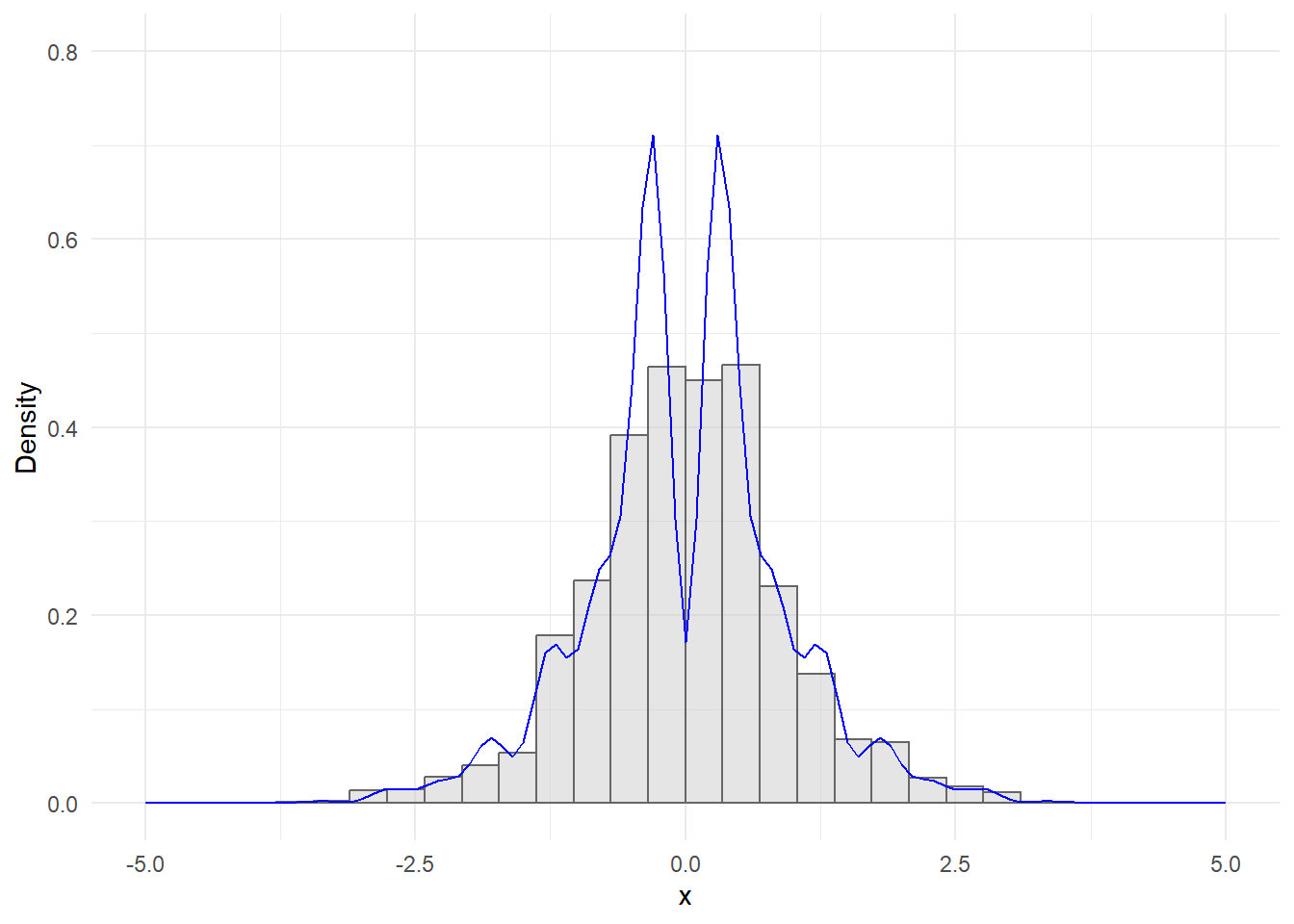
3.6 Ειδικά Θέματα

3.6.1 Προσομοίωση με αναπαράσταση ως μίξη

Ας υποθέσουμε ότι θέλουμε να προσομοιώσουμε τιμές από κάποια τ.μ. \(X\). Υποθέτουμε ότι εξαρτάται από κάποια τ.μ. \(Y\) και μπορούμε να προσομοιώσουμε ευκολότερα τιμές τις \(Y\), αλλά και από την \(\left[X|Y=y\right]\). Τότε:

\[\begin{align*} f_X(x) &= \sum_{i=1}^k f_Y(y_i) f_{X|Y}(x|y_i),\ Y \ \text{διακριτή}, \\ f_X(x) &= \int_{\mathbb{R}} f_Y(y) f_{X|Y}(x|y),\ Y \ \text{συνεχής}. \end{align*}\]

Επειδή είναι δύσκολο να προσομοιώσουμε απ’ ευθείας από κατανομές αυτής της μορφής, αντί να προσομοιώσουμε τιμές της \(X\), προσομοιώνουμε από το ζεύγος \((Y,X)\) ξεκινώντας από την \(Y\) και μετά την \(\left[X|Y=y\right]\). Η διαδικασία αυτή αιτιολογείται μέσω της σχέσης:

\[\begin{equation*} f_{X,Y}(x,y)=f_Y(y) f_{X|Y}(x|y). \end{equation*}\]

Έτσι, η τιμή \(x\) της \(X\) έχει παραχθεί ισοδύναμα από την περιθώρια \(f_X\) της \(X\), με ‘κόστος’ την προσομοίωση μίας επιπλέον τιμής, της \(y\).

Παράδειγμα 3.16 Προσομοιώστε παρατηρήσεις από την κατανομή Student \(t_n\).

Λύση:

\[\begin{equation*} T=\frac{Z}{\sqrt{Q/n}},\ Z\thicksim N(0,1),\ Q\thicksim \mathcal{X}^2_n,. \end{equation*}\]

Επομένως, \(\left[ T\mid Q=q\right]\thicksim N(0, n/q)\).

Nsim <- 10 ^ 4
n <- 10
q <- rchisq(Nsim, df = n)
t <- rnorm(Nsim, rep(0, Nsim), sqrt(n / q))

hist(t, main = "Student with df=10 as a mixture", freq = FALSE, col = "grey", breaks = 50)
curve(dt(x, df = n), from = -5, to = 5, lty = 1, lwd = 1, col = "red", add = TRUE)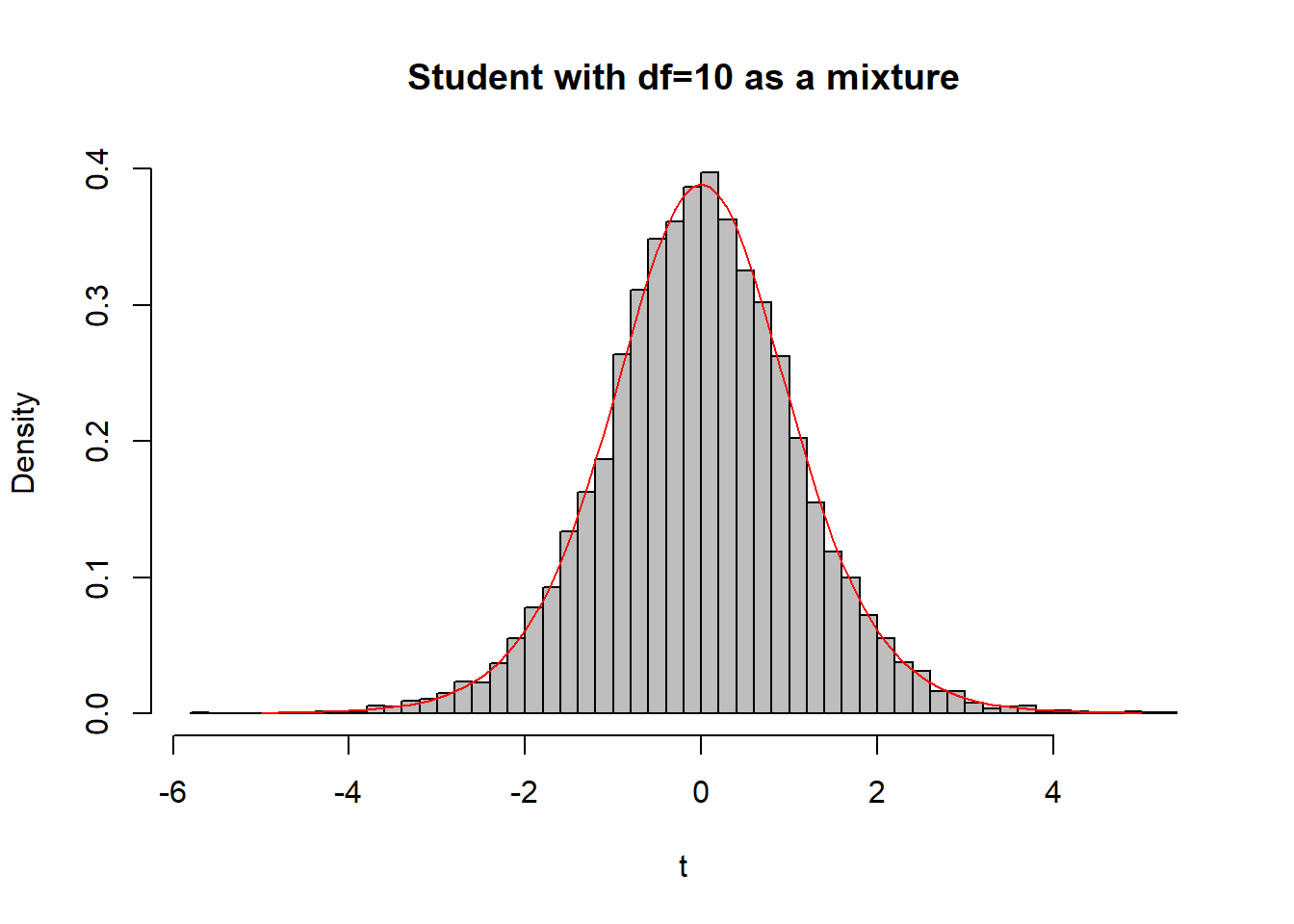

Παράδειγμα 3.17 Προσομοιώστε παρατηρήσεις από την αρνητική διωνυμική \(NegBin(r,p)\)

Λύση:

Ισχύει ότι:

\[\begin{equation*} [X|Y=y]\thicksim Poisson(y), \ Y\thicksim Gamma\left(r, \frac{p}{1-p}\right) \Rightarrow \ X \thicksim NegBin(r,p). \end{equation*}\]

Επομένως, μπορούμε να παράγουμε τιμές από την αρνητική διωνυμική ως μίξη Poisson με βάρη από κατανομή Gamma.

Nsim <- 10 ^ 4
r <- 6 ; p <- 0.3
y <- rgamma(Nsim, r, rate = p / (1 - p))
x <- rpois(Nsim, y)

hist(x, main = "", freq = FALSE, col = "grey", breaks = 40)
lines(1:50, dnbinom(1:50, r, p), lwd = 2, col = "sienna")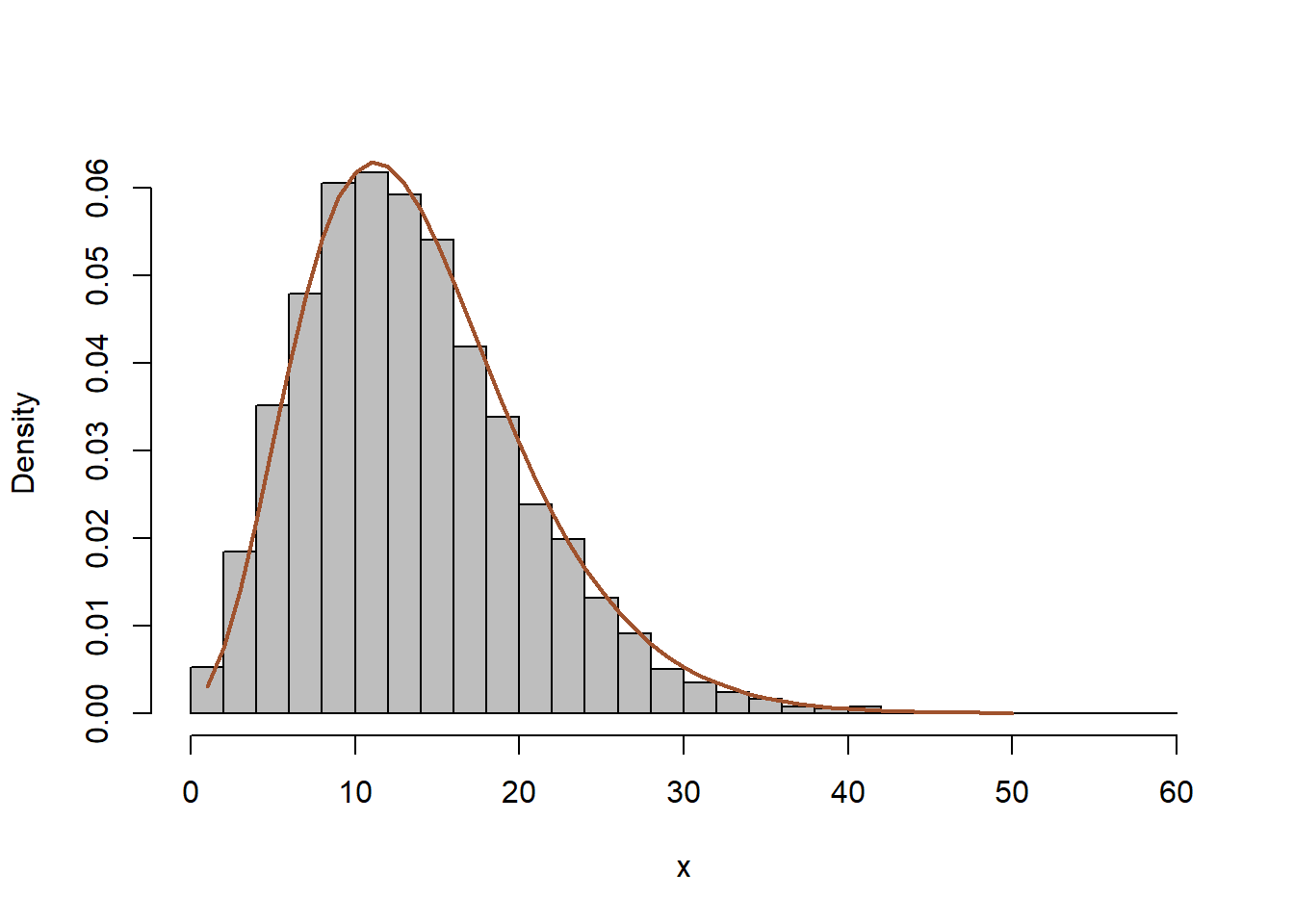

3.6.2 Εφαρμογές στη Μπεϋζιανή Στατιστική

Στη Μπεϋζιανή Στατιστική η παράμετρος \({\theta}\), που στην κλασική Στατιστική είναι άγνωστη σταθερά, θεωρείται τυχαία μεταβλητή με μία εκ των προτέρων (prior) κατανομή \(f(\theta)\). Μόλις τα δεδομένα γίνουν διαθέσιμα, τότε η κατανομή της \(\Theta\) μεταβάλλεται φυσιολογικά σε \(f(\theta|x)\). Η κατανομή της \(\left[\Theta|X=x\right]\) λέγεται εκ των υστέρων (posterior) κατανομή της \(\Theta\) (δεδομένου του \(X=x\)), και η εύρεση αυτής της κατανομής αποτελεί το διακαή πόθο μίας μπεϋζιανής προσέγγισης.

Με τη βοήθεια της εκ των υστέρων κατανομής μπορούμε να απαντήσουμε στα ίδια ερωτήματα που θέτει η κλασική στατιστική, εφαρμόζοντας όμως τώρα τη μπεϋζιανή προσέγγιση.

Ένα από τα “μειονεκτήματα” της μπεϋζιανής προσέγγισης αποτελεί η αυθαιρεσία στην επιλογή της prior \(f(\theta)\), κάτι όμως που μπορεί να αποδειχθεί ένα από τα μεγαλύτερα “πλεονεκτήματά” της, καθώς μπορεί να αποτυπώσει με τη μορφή μιας κατανομής, εκ των προτέρων πληροφορία που μπορεί ένας ειδικός να διαθέτει για τις πιο πιθανές τιμές που μπορεί να πάρει το άγνωστο \(\theta\), πριν ακόμα τα δεδομένα γίνουν διαθέσιμα. Τελικά, η \(\Theta\) με prior \(f(\theta)\) αλληλεπιδρά με τα δεδομένα \(x\) και μέσω του Bayes καταλήγουμε στην εκ των υστέρων σ.π. / σ.π.π. της \(\Theta\) δοθείσης της \(X=x\)

\[\begin{equation} f(\theta|x)=\frac{f(\theta)\cdot f(x|\theta)}{f(x)}, \tag{3.1} \end{equation}\]

όπου

\[\begin{equation} f(x)=\int_{\theta} f(\theta) f(x|\theta) d\theta. \tag{3.2} \end{equation}\]

Η γνώση της \(f(\theta|x)\) είναι ό,τι χρειάζεται να γνωρίζουμε για να εφαρμόσουμε μπεϋζιανή συμπερασματολογία σε κάποιο στατιστικό πρόβλημα. Να σημειώσουμε εδώ ότι η \(f(x|\theta)\) παίζει το ρόλο που έπαιζε η συνάρτηση πιθανοφάνειας στην κλασική στατιστική. Οι πιο συχνά χρησιμοποιούμενες σημειακές εκτιμήτριες της μπεϋζιανής προσέγγισης προκύπτουν από την εκ των υστέρων μέση τιμή \(E\left[\theta|x\right]\) και το εκ των υστέρων μέγιστο \(\arg\max_{\theta}f(\theta|x)\).

Με γνώση / καθορισμό της prior \(f(\theta)\) και της \(f(x|\theta)\), είναι φανερό ότι ο υπολογισμός της posterior \(f(\theta|x)\) είναι στενά συνδεδεμένος με τη δυνατότητα υπολογισμού της (3.2), που παίζει το ρόλο της σταθεράς κανονικοποίησης, εφ’όσον

\[\begin{equation*} f(\theta|x)\overset{\theta}{\propto} f(\theta)\cdot f(x|\theta). \end{equation*}\]

Χωρίς να μπούμε σε λεπτομέρειες για τον τρόπο επιλογής της prior και και καλές πρακτικές μπεϋζιανής μεθοδολογίας, δίνουμε τώρα ένα πολύ απλό παράδειγμα εφαρμογής της στην περίπτωση ενός τυχαίου δείγματος \(Χ=(Χ_1,\ldots,X_n)\) που προέρχεται από την κατανομή \(Bernoulli(\theta)\), \(\theta\in (0,1)\).

Θυμίζουμε ότι αν \(x=(x_1,\ldots,x_n)\in \{0,1\}^{n}\) είναι οι παρατηρούμενες τιμές, τότε η συνάρτηση πιθανοφάνειας που αντιστοιχεί στο \(x\) δίνεται από τη σχέση:

\[\begin{equation*} f(x|\theta) = \theta^{s_n}(1-\theta)^{s_n},\qquad \theta \in (0,1), \end{equation*}\]

όπου \(s_n = x_1+x_2 +\ldots x_n,\) και έτσι η εκτιμήτρια μέγιστης πιθανοφάνειας \(\widehat{\theta}_n\) του \(\theta\) που προκύπτει με μεγιστοποίηση της παραπάνω είναι

\[\begin{equation*} \widehat{\theta}_n = \frac{S_n}{n}= \overline{X}_n, \end{equation*}\]

επιτρέποντας και τις οριακές τιμές \(\theta\in \{0,1\}\) με συμπαγοποίηση του παραμετρικού χώρου. Η μέθοδος της μέγιστης πιθανοφάνειας είναι αρκετά δημοφιλής λόγω των καλών ασυμπτωτικών ιδιοτήτων των εκτιμητριών που προκύπτουν με τη μέθοδο αυτή. Σε πολλές περιπτώσεις λοιπόν, αργεί να φανεί η δύναμή της, καθώς το δείγμα μπορεί να είναι σχετικά μικρό. Ως ακραία περίπτωση, σκεφτείτε την περίπτωση που διαθέτουμε μία μόνο παρατήρηση \(X_1\sim Bernoulli(\theta)\). Τότε, αν γνωρίζαμε ότι \(\theta \in (0,1)\), η ε.μ.π. δεν θα μπορούσε καν να δώσει τιμή στο \((0,1)\), καθώς \(\widehat{\theta}_1=X_1\in \{0,1\}\). Η μπεϋζιανή προσέγγιση μπορεί λοιπόν πολλές φορές να μας εξασφαλίσει εκτιμήτριες που έχουν καλύτερη συμπεριφορά, ιδιαιτέρως σε περιπτώσεις που το δείγμα είναι σχετικά μικρό.

Από την άλλη μεριά, λόγω της ποικιλίας των διαφορετικών prior που μπορούν να επιλεγούν είναι πολλές φορές εφικτό να πλησιάσουμε πάρα πολύ τη συμπεριφορά της ε.μ.π., επιλέγοντας κατάλληλη prior και κατάλληλη σημειακή εκτιμήτρια μέσα από την posterior κατανομή. Στο συγκεκριμένο παράδειγμα έχουμε

\[\begin{equation*} f(\theta|x)\propto f(\theta)\cdot f(x|\theta)=f(\theta)\cdot \theta^{s_n}(1-\theta)^{n-s_n}. \end{equation*}\]

Είναι λοιπόν φανερό ότι με την επιλογή της ομοιόμορφης κατανομής \(Unif(0,1)\) ως prior κατανομής της παραμέτρου \(\theta\), η posterior κατανομή γίνεται ανάλογη της συνάρτησης πιθανοφάνειας. Έτσι αν χρησιμοποιηθεί το εκ των υστέρων μέγιστο (posterior max ή MAP) \(\arg \max_{\theta} f(\theta|x)\) ως σημειακή εκτιμήτρια του \(\theta\), έχουμε

\[\begin{equation*} \arg \max_{\theta} f(\theta|x) = \arg \max_{\theta} f(x|\theta), \end{equation*}\]

και άρα

\[\begin{equation*} \widehat{\theta}^{mle}_{n}=\widehat{\theta}^{map}_n=\overline{X}_n. \end{equation*}\]

Η επιλογή αυτή μας οδηγεί ακριβώς στην ε.μ.π. και έτσι παρουσιάζει τα ίδια προβλήματα. Από την άλλη μεριά η χρήση του posterior mean μας οδηγεί σε διαφορετική εκτιμήτρια. Για την εύρεση του μέσου, παρατηρούμε κατ’αρχήν ότι αν \(\Theta \sim Unif(0,1)\), τότε

\[\begin{equation*} f(\theta|x)\propto \theta^{s_n}(1-\theta)^{n-s_n}, \end{equation*}\]

από το οποίο συμπεραίνουμε ότι

\[\begin{equation*} \big[\Theta\,|\,\underbrace{X_1=x_1,\ldots,X_n=x_n}_{X=x}\big]\sim Beta\big(\,\underbrace{s_n+1}_{=\alpha},\ \underbrace{n-s_n+1}_{=\beta}\big), \end{equation*}\]

και άρα

\[\begin{equation*} \widehat{\theta}^{bayes}_{n} = E[\Theta|X]= \frac{\alpha}{\alpha+\beta}=\frac{S_n+1}{n+2}= \frac{n}{n+2}\widehat{\theta}^{mle}_{n}+\frac{2}{n+2}E(\Theta), \end{equation*}\]

που είναι η ζητούμενη σημειακή εκτιμήτρια.

Υποθέτουμε λοιπόν τώρα ότι στο παραπάνω πρόβλημα πήραμε τις εξής παρατηρήσεις:

##  [1] 1 1 0 1 1 1 0 0 1 0

Έχουμε \(n=10\), \(s_{10}=6\) και άρα \(f(\theta|x)\propto \theta^6 (1-\theta)^4, \qquad \theta \in (0,1)\). Σε αυτό το παράδειγμα υποθέτουμε λοιπόν ότι η σταθερά κανονικοποίησης είναι άγνωστη, αλλά εμείς παρ’όλα αυτά θέλουμε να προσομοιώσουμε από την \(f(\theta|x)\). Όπως έχει ήδη ειπωθεί ο αλγόριθμος Accept-Reject μπορεί να εφαρμοστεί και σε τέτοιες περιπτώσεις.

f_tilde <- function(x) {
  x ^ 6 * (1 - x) ^ 4 * I((x > 0) & (x < 1))
}

Μετά σταθμίζουμε κατάλληλα τη συνάρτηση διαιρώντας με τη μέγιστη τιμή της:

f_tilde_max <- optimize(f_tilde, interval = c(0, 1), maximum = TRUE)$objective
f_tilde_max
## [1] 0.001194394

και άρα

fb_tilde <- function(x) {
  f_tilde(x) / optimize(f_tilde, interval = c(0, 1), maximum = TRUE)$objective 
}

Τέλος, δημιουργούμε τη συνάρτηση που υλοποιεί τον αλγόριθμο αποδοχής - απόρριψης με κατανομή πρότασης την Unif(0,1)

acc.rej.beta <- function(size, plot = TRUE, report = TRUE){
  
  # Αρχικοποιούμε τα διανύσματα και το M
  u <- x <- y <- NULL
  M_pr <- 1 + 0.00000001
  
  while (length(x) < size) {
    
    # Δημιουργούμε τον αναμενόμενο αριθμό παρατηρήσεων που θα
    # χρειαστούμε, δηλαδή (size-length(x))*M και εξετάζουμε
    # πόσα θα γίνουν δεκτά
    M <- M_pr
    c <- f_tilde_max/beta(7, 5)
    if (report) {
      cat(paste0("Number of trials: ", floor((size - length(x)) * M * c), "\n"))
    }
    
    u <- c(u, runif((size - length(x)) * M * c))
    y <- c(y, runif((size - length(x)) * M * c))
    x <- y[u * M < fb_tilde(y)]
    beta_est <- (length(x) * f_tilde_max) / length(y)
    
    if (report) {
      cat(paste0("Total Accepted: ", length(x), "\n"))
    }
    
  }  
  
  # Κρατάμε μόνο όσες παρατηρήσεις μας ζητούνται
  u <- u[1:size]
  x <- x[1:size]
  y <- y[1:size]
  
  # Κάνουμε το γράφημα  
  if (plot) { 
    
    data <- data.frame(pointx = y,
                     pointy = u * M, 
                     accept = (u * M < fb_tilde(y)))
    
    a <- ggplot(data) +
      stat_function(fun = function(x) { dunif(x) * M }, xlim = c(0,1)) +
      stat_function(fun = fb_tilde, xlim = c(0, 1)) +
      geom_point(aes(x = pointx, y = pointy, col = accept), size = 0.4) +
      xlab("x") + ylab("y") +
      theme_minimal()
    print(a)
  }
  
  list(x, beta_est)
}

AR <- acc.rej.beta(10000)
## Number of trials: 27590
## Total Accepted: 9913
## Number of trials: 240
## Total Accepted: 10000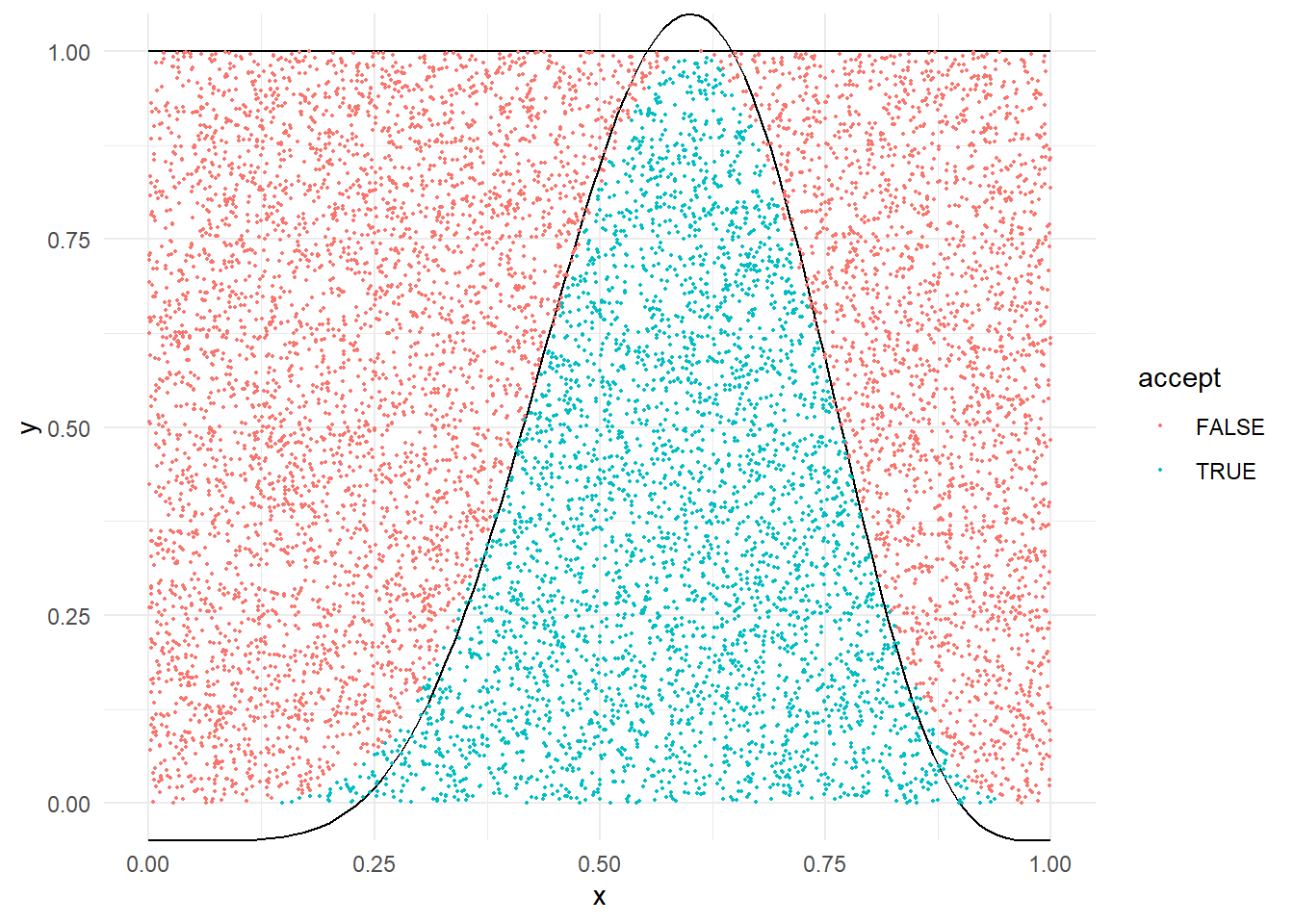

H εκτίμηση του \(B(7,5)\approx 0.0004329\) είναι εφικτή (όπως είδαμε) από το ποσοστό αποδοχής του Accept-Reject και ο αλγόριθμος έδωσε

AR[[2]]
## [1] 0.0004291748

Μπορεί να θεωρηθεί το παραγόμενο δείγμα ότι προέρχεται από την αντίστοιχη κατανομή Βήτα;

hist(AR[[1]], main = "Beta(7, 5) sample with Accept-Reject", freq = FALSE, col = "grey", breaks = 20)
curve(dbeta(x, 7, 5),  from = 0, to = 1, lty= 1, lwd = 1, col = "red", add = TRUE)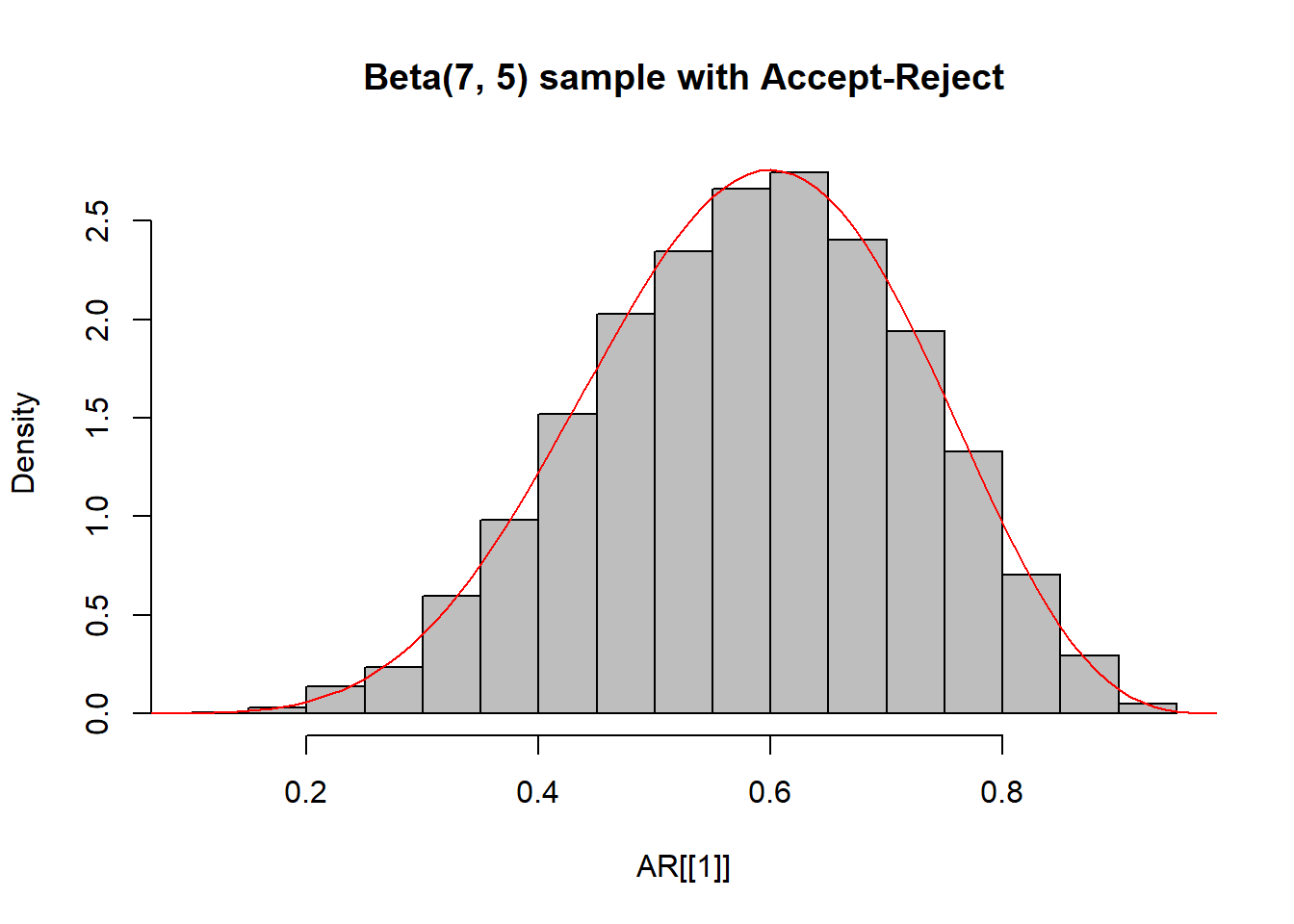

Παράδειγμα 3.18 Έστω ότι έχουμε μία πυκνότητα \(f(x|\theta)\), όπου το \(\theta\) είναι η υπό εκτίμηση παράμετρος, και μία prior \(\pi(\theta)\). Αν παρατηρήσουμε \(x=(x_1, x_2, ..., x_n)\), τότε η posterior του \(\theta\) είναι:

\[\begin{equation*} \pi(\theta|x)=\pi(\theta|x_1, x_2, ..., x_n) \propto \prod_{i} f(x_i|\theta) \pi(\theta), \end{equation*}\]

όπου \(\prod_{i} f(x_i|\theta) = L(\theta|x_1, x_2, ..., x_n)\) είναι η συνάρτηση πιθανοφάνειας.

Αν \(\pi(\theta|x)\) είναι η πυκνότητα στόχος σε ένα αλγόριθμο Αποδοχής - Απόρριψης και αν \(\pi(\theta)\) είναι η υποψήφια πυκνότητα, δείξτε ότι το βέλτιστο φράγμα \(M\) είναι η συνάρτηση πιθανοφάνειας στο σημείο μέγιστης πιθανοφάνειας.
Για την εκτίμηση του \(\mu\) σε μία κανονική κατανομή, μία καλή prior (ανθεκτική στις ακραίες παρατηρήσεις) είναι η Cauchy. Για \(X_i \thicksim N(\theta, 1), \theta \thicksim C(0,1)\), η posterior είναι η

\[\begin{equation*} \pi(\theta|x)=\propto \frac{1}{\pi} \frac{1}{1+\theta^2} \prod_{i=1}^n e^{-(x_i-\theta)^2/2}. \end{equation*}\]

Θέστε \(\theta_0=3, n=10\) και προσομοιώστε \(X_1, X_2, ..., X_n \thicksim Ν(\theta_0, 1)\). Χρησιμοποιήστε τον αλγόριθμο Αποδοχής - Απόρριψης με την Cauchy \(C(0,1)\) ως υποψήφια πυκνότητα και προσομοιώστε ένα δείγμα από την posterior. Αξιολογήστε πόσο καλά εκτιμάται το \(\theta_0\). Πόσο βελτιώνεται η εκτίμηση καθώς το \(n\) αυξάνεται;

Λύση:

Αρχικά, ας γράψουμε την posterior στην πλήρη της μορφή:

\[\begin{equation*} \pi(\theta|x)= \frac{\prod_{i} f(x_i|\theta) \pi(\theta)}{\prod_{i} f(x_i)} = c_{post} \prod_{i} f(x_i|\theta) \pi(\theta) = c_{post} L(\theta| x) \pi(\theta), \ \theta \in S_\theta, \end{equation*}\]

θέτοντας \(c_{post}=\frac{1}{\prod_{i} f(x_i)}\).

Μας ενδιαφέρει να βρούμε ένα άνω φράγμα για το λόγο

\[\begin{equation*} \frac{\pi(\theta|x)}{\pi(\theta)} = c_{post} L(\theta| x), \ \theta \in S_\theta. \end{equation*}\]

Επομένως το βέλτιστο φράγμα επιτυγχάνεται για \(\theta=\arg\max_\theta L(\theta|x)\), δηλαδή για την ΕΜΠ \(\widehat{\theta}\).

Ας εφαρμόσουμε το παραπάνω στην εκτίμηση του \(\theta_0=3\) στο τυχαίο δείγμα κανονικών όταν προτείνουμε με prior κατανομή την Cauchy. Εδώ πρέπει να προσέξουμε ότι η ε.μ.π. \(\widehat{\theta}=\overline{x}\) είναι γνωστή και άρα \[\begin{equation*} M = L(\widehat{\theta})= (2\pi)^{-n/2} e^{-0.5\sum_{i=1}^{n}(x_i-\overline{x})^2} \end{equation*}\] Δημιουργούμε στην R όλα τα απαραίτητα στοιχεία:

# sample and mle
theta0 <- 3
n <- 10
x0 <- rnorm(n, mean = theta0, sd = 1)
mle <- mean(x0)
M <- prod(dnorm(x0, mean = mle, sd = 1))

Για να απαλλαγούμε προσωρινά από το \(c_{post}\) ορίζουμε την \(\widetilde{\pi}(\theta|x):\)

\[\begin{equation*} \pi(\theta|x)=c_{post}\widetilde{\pi}(\theta|x). \end{equation*}\]

Δημιουργούμε στην R την μη κανονικοποιημένη posterior της \(\pi(\theta|x)\), με αρχική τιμή \(c_{post}=1\) (δηλαδή \(\widetilde{\pi}(\theta|x)\)):

# posterior
post <- function(theta, x0, c = 1) {
  c * sapply(theta, function(theta) prod(dnorm(x0, mean = theta, sd = 1))) * dcauchy(theta) 
}

Είμαστε έτοιμοι να τρέξουμε τον αλγόριθμο:

# Accept - Reject
theta <- NULL
trials <- 0
size <- 5000

while(length(theta) < size){
  cand <- rcauchy(1, 0, 1)
  u <- runif(1)
  theta <- c(theta, cand[u < (post(cand, x0) / (M * dcauchy(cand)))])
  trials <- trials + 1
}

Μέσα από το ποσοστό αποδοχής εκτιμούμε τη σταθερά κανονικοποίησης

acc <- size / trials
chat <- 1 / (acc * M)
acc ; chat
## [1] 0.02383086
## [1] 251474854

Δημιουργούμε το γράφημα: