4 Βελτιστοποίηση Monte Carlo

4.1 Εισαγωγή

Τα προβλήματα βελτιστοποίησης μπορούν να χωριστούν σε δύο μεγάλες κατηγορίες, την αναζήτηση των ακροτάτων μίας συνάρτησης \(h(\theta)\) και την αναζήτηση των λύσεων της εξίσωσης \(g(\theta)=0\), σε ένα χώρο \(\Theta\). Ένα πρόβλημα της μίας κατηγορίας μπορεί, υπό συγκεκριμένες συνθήκες, να εκφραστεί ως ένα ισοδύναμο πρόβλημα της άλλης, αφού η εύρεση ακροτάτων μίας διαφορίσιμης συνάρτησης \(h\) ισοδυναμεί με την επίλυση της εξίσωσης \(\nabla h(\theta)=0\), ενώ η επίλυση της εξίσωσης \(g(\theta)=0\) μπορεί να εκφραστεί ως πρόβλημα ελαχιστοποίησης της συνάρτησης \(h(\theta)=g^2 (\theta)\). Επιπλέον, κάθε πρόβλημα μεγιστοποίησης της συνάρτησης \(h(\theta)\) μπορεί να εκφραστεί ισοδύναμα ως πρόβλημα ελαχιστοποίησης της συνάρτησης \(-h(\theta)\) (ή της \(1/h(\theta)\), αν η \(h\) είναι μονίμως θετική ή αρνητική στο χώρο \(\Theta\)).

Στη μελέτη αυτή θα συμπεριλάβουμε δύο διαφορετικές προσεγγίσεις, την αριθμητική και τη στοχαστική. Από την πλευρά της αριθμητικής βελτιστοποίησης, η αποδοτικότητα των μεθόδων εξαρτάται σημαντικά από τις αναλυτικές ιδιότητες της υπό ελαχιστοποίηση/μεγιστοποίηση συνάρτησης (συνέχεια, διαφορισιμότητα, κυρτότητα, μελέτη φραγμάτων, κ.ά.), ενώ οι ιδιότητες αυτές παίζουν δευτερεύοντα ρόλο στις προσεγγίσεις που βασίζονται σε προσομοίωση. Συμπεραίνουμε πως, για τη μεγιστοποίηση μίας απλής συνάρτησης \(h\) με καλές ιδιότητες συμφέρει να χρησιμοποιήσουμε αριθμητικές μεθόδους, ενώ για τη μεγιστοποίηση μίας περίπλοκης συνάρτησης ορισμένη ίσως και σε έναν περίπλοκο χώρο \(\Theta\), προτιμάμε να καταφύγουμε σε στοχαστικές προσεγγίσεις.

Σε αυτό το σημείο, αξίζει να αναφέρουμε ότι γενικά, τα προβλήματα βελτιστοποίησης είναι δυσκολότερα από τα προβλήματα ολοκλήρωσης (τουλάχιστον από πρακτικής πλευράς), καθώς απαιτούν τοπική μελέτη της συνάρτησης σε όλο το χώρο που είναι ορισμένη. Με άλλα λόγια, είναι πολύ πιο δύσκολο να εντοπίσουμε ένα συγκεκριμένο σημείο του χώρου στο οποίο επιτυγχάνεται το μέγιστο μιας συνάρτησης, από το να προσεγγίσουμε τη μέση τιμή της συνάρτησης σε όλο το χώρο.

Προτού αναλύσουμε τις στοχαστικές μεθόδους βελτιστοποίησης, παρουσιάζουμε κάποιες από τις σημαντικότερες μεθόδους αριθμητικής βελτιστοποίησης και αναλύουμε κάποιες σημαντικές ιδιότητές τους.

4.2 Μέθοδοι Αριθμητικής Βελτιστοποίησης

Όλοι οι αλγόριθμοι αριθμητικής βελτιστοποίησης που θα μελετήσουμε βασίζονται στην ίδια δομή. Ξεκινούν από ένα αρχικό σημείο \(x_0\), επιλέγουν μία κατεύθυνση κίνησης \(d_0\) και κινούνται σε αυτή σε ένα σημείο \(x_1\), πραγματοποιώντας ένα μήκος βήματος \(a_0\). Στο νέο αυτό σημείο \(x_1\), επιλέγεται μία νέα κατεύθυνση \(d_1\) και ένα μήκος βήματος \(a_1\), και η διαδικασία επαναλαμβάνεται μέχρι να ικανοποιηθεί κάποιο κριτήριο τερματισμού. Η σχηματιζόμενη ακολουθία \((x_k)\) ικανοποιεί λοιπόν την αναδρομική σχέση:

\[\begin{equation*} x_{k+1} = x_k + a_k d_k, \qquad k\geq 0. \end{equation*}\]

Οι αλγόριθμοι που θα εξετάσουμε διακρίνονται από τους κανόνες σύμφωνα με τους οποίους επιλέγεται η κατεύθυνση κίνησης \(d_k\) και καθορίζεται το μήκος βήματος \(a_k\). Οι αλγόριθμοι αυτής της μορφής είναι γνωστοί και με το όνομα Αλγόριθμοι Γραμμικής Αναζήτησης (Line Search Algorithms) και αποτελούν μαζί με τους αλγορίθμους που χρησιμοποιούν περιοχές εμπιστοσύνης (Trust Regions), τις 2 βασικές στρατηγικές βελτιστοποίησης. Περιγράφουμε τώρα κάποιους από αυτούς τους αλγορίθμους κατάβασης (descent algorithms) που έχουν ως στόχο με σχετικά απλό, αλλά αποτελεσματικό τρόπο να οδηγήσουν σε μονοπάτια ελάττωσης των τιμών της υπό μελέτη συνάρτησης.

4.2.1 Μέθοδος Απότομης Κατάβασης

Μία από τις πιο παλιές και ταυτόχρονα πιο διαδεδομένες μεθόδους ελαχιστοποίησης μιας συνάρτησης είναι η μέθοδος απότομης κατάβασης (steepest descent method).

Θα λέγαμε πως η μέθοδος απότομης κατάβασης είναι η καθιερωμένη μέθοδος αριθμητικής βελτιστοποίησης, πάνω στην οποία έχουν βασιστεί πολλές παραλλαγές, ενώ παράλληλα αποτελεί το κύριο μέτρο σύγκρισης για όλες τις άλλες αριθμητικές μεθόδους. Ο αλγόριθμος απότομης κατάβασης μπορεί να οριστεί ως ειδική περίπτωση του αλγορίθμου γραμμικής αναζήτησης, όπου η κατεύθυνση αναζήτησης \(d_k = \nabla f(x_k)\) και το μήκος βήματος \(a_k\) επιλέγεται έτσι ώστε η συνάρτηση \(f\) να ελαχιστοποιείται στην αντίστοιχη γραμμή αναζήτησης. Δίνουμε λοιπόν ένα γενικό ορισμό ενός αλγορίθμου γραμμικής αναζήτησης, τον οποίο θα εξειδικεύσουμε στη συνέχεια.

Ορισμός 4.1 (Line Search Algorithm) Ένας αλγόριθμος γραμμικής αναζήτησης, είναι μία απεικόνιση \(S: E^{2n}\rightarrow \mathcal{P}(E^n)\), που ορίζεται ως \[\begin{equation*} S(x, d)=\{y: y=x+ad,\ a\geq 0\ \textrm{και}\ f(y)=\min_{0\leq a< +\infty} f(x+ad)\}. \end{equation*}\]

Ο αλγόριθμος γραμμικής αναζήτησης, για δεδομένο σημείο \(x_0\in E^n\) και δεδομένη κατεύθυνση \(d_0\in E^n\), βρίσκει όλα τα σημεία ελαχίστου πάνω στην ημιευθεία που ξεκινά από το \(x_0\) και είναι παράλληλη στην κατεύθυνση του \(d_0\). Εάν προσδιοριστεί με κάποιο τρόπο μία ακολουθία κατευθύνσεων αναζήτησης \(\{d_k\}_{k=0}^{+\infty}\), μπορούμε να επαναλάβουμε την παραπάνω διαδικασία, ορίζοντας αναδρομικά μία ακολουθία σημείων ελαχίστου \(\{x_k\}_{k=0}^{+\infty}\) της \(f\) περιορισμένης στην αντίστοιχη ημιευθεία. Είναι φανερό ότι η ακολουθία των κατευθύνσεων θα πρέπει να επιλέγεται με τέτοιο τρόπο που να εξασφαλίζει την καθοδική πορεία της \(f\). Ο αλγόριθμος απότομης κατάβασης το επιτυγχάνει επιλέγοντας ως διάνυσμα κατεύθυνσης, σταθερά σε κάθε επανάληψη, το αντίθετο της κλίσης της \(f\) στο εκάστοτε σημείο. Ο επόμενος ορισμός δίνει μία τυπική περιγραφή του αλγορίθμου αυτού.

Ορισμός 4.2 (Steepest Descent Method) Έστω \(f\in C^{1}(E^n,\mathbb{R})\) μία συνάρτηση με συνεχείς μερικές παραγώγους πρώτης τάξης στο \(E^n\) και \(g(x)=\nabla f(x)^\top\) το n-διάστατο διάνυσμα στήλη των πρώτων μερικών παραγώγων. Αν \(S\) είναι ο αλγόριθμος γραμμικής αναζήτησης που δίνεται στον Ορισμό 4.1 και \(G: E^{n}\rightarrow E^{2n}\) με \(G(x)=(x,-g(x))\), τότε η συνάρτηση \[\begin{equation*} A:E^{n}\rightarrow\mathcal{P}(E^{2n}),\ \ \textrm{με}\ \ A=S\circ G, \end{equation*}\] λέγεται αλγόριθμος απότομης κατάβασης και αποτελεί ειδική περίπτωση του αλγορίθμου γραμμικής αναζήτησης αν επιλέξουμε ως κατεύθυνση αναζήτησης \(d=-g(x)\). Κατά συνέπεια, η μέθοδος απότομης κατάβασης περιγράφεται από την αναδρομική σχέση \[\begin{equation*} x_{k+1} = x_k - a_k g_k = x_k - a_k\nabla f(x_k), \qquad k\geq 0, \tag{4.1} \end{equation*}\]

Ποιός είναι όμως ο λόγος που επιλέγεται η αντίθετη φορά του \(\nabla\) ; Ας δούμε πρώτα το απλούστερο παράδειγμα μίας μεταβλητής. Στο παράδειγμα αυτό, όπως φαίνεται στο παρακάτω σχήμα, είναι φανερό ότι για να κινηθούμε προς τη θέση ελαχίστου πρέπει να κινηθούμε αντίθετα από το πρόσημο της παραγώγου. Αν αυτό είναι αρνητικό, κινούμαστε δεξιά (θετική μετατόπιση) και αν αυτό είναι θετικό, κινούμαστε αριστερά (αρνητική μετατόπιση), καθώς και στις 2 περιπτώσεις, έτσι μόνο θα εξασφαλίσουμε ελάττωση της τιμής της συνάρτησης. Αν λοιπόν υπάρχει ένα μοναδικό τοπικό ελάχιστο (άρα και ολικό), τότε είμαστε στη σωστή κατεύθυνση, και μία ελαχιστοποίηση της συνάρτησης στην αντίστοιχη ημιευθεία, όπως προτείνεται από τον αλγόριθμο απότομης κατάβασης, θα εντοπίσει με σιγουριά το ολικό ελάχιστο.

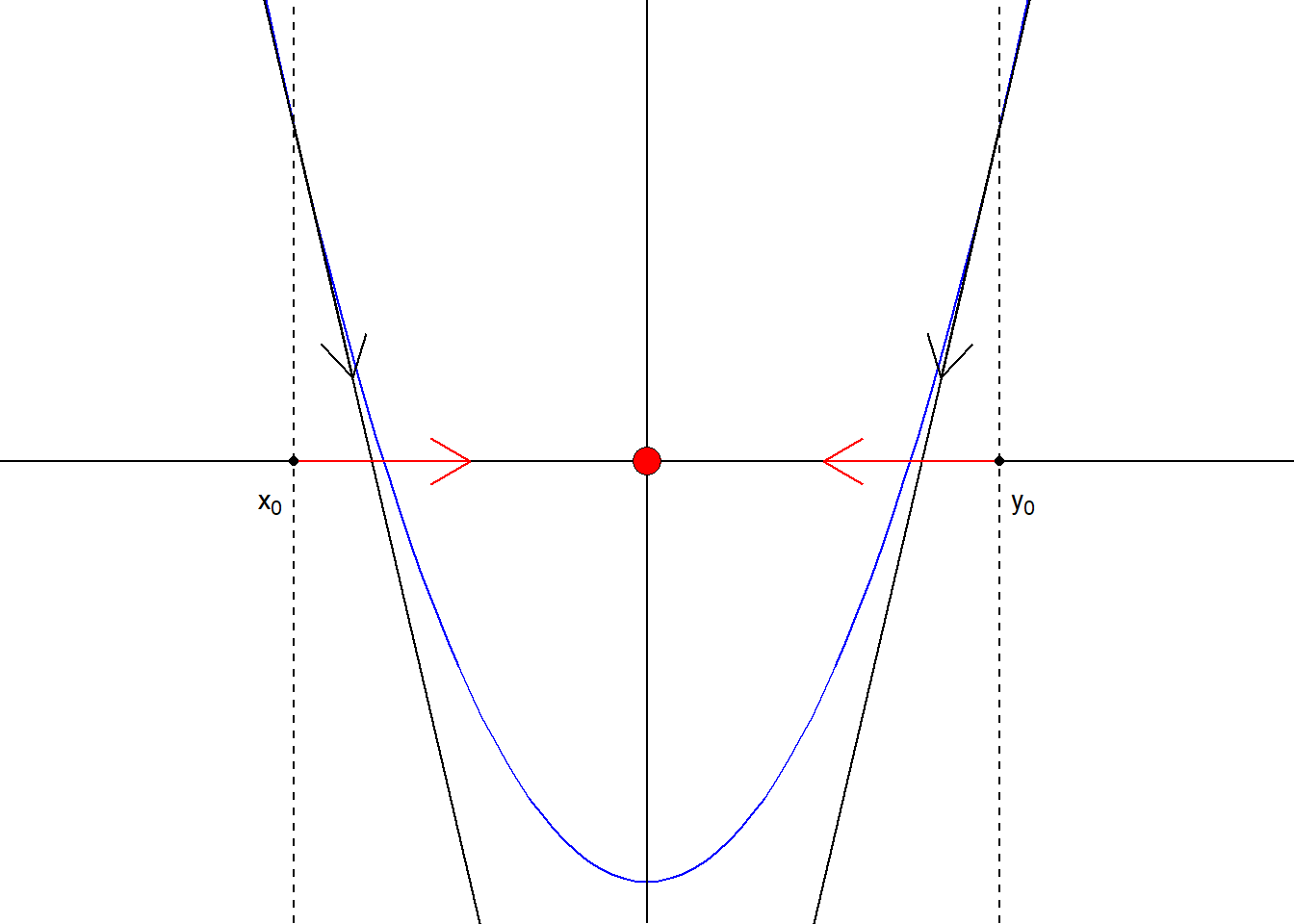
Εικόνα 4.1: A representation of the Steepest Descent movement for two different initial points \(x_0, y_0\), for a unimodal function \(f\).

Η κατάσταση γίνεται πιο περίπλοκη στην περίπτωση περισσότερων μεταβλητών. Ενώ στη μία μεταβλητή, αν το σημείο δεν είναι στάσιμο, τότε έχει μία μοναδική καθοδική κατεύθυνση, σε περισσότερες μεταβλητές έχουμε συνήθως άπειρες επιλογές. Εδώ λοιπόν τίθεται ένα θέμα βελτιστότητας. Ποιά είναι η κατεύθυνση στην οποία θα πρέπει να κινηθούμε ώστε να εξασφαλίσουμε τη μεγαλύτερη δυνατή ελάττωση, τουλάχιστον τοπικά; Για καλή μας τύχη η απάντηση είναι εύκολη. Πρέπει να κινηθούμε αντίθετα από την κλίση της συνάρτησης σε αυτό το σημείο. Η κλίση καθορίζει την κατεύθυνση της μέγιστης τοπικής ανόδου, άρα η αντίθετη κίνηση καθορίζει την κατεύθυνση της μέγιστης τοπικής ελάττωσης. Αυτή η παρατήρηση εξηγεί και το όνομα της μεθόδου απότομης κατάβασης. Πράγματι, το \(\nabla f(x)\), όπως γνωρίζουμε, μας δίνει την τοπική γραμμική προσέγγιση της \(f\). Αναζητούμε λοιπόν \(h^{*}\) στα \(h\) με \(\|h\|= 1\) (\(h\in S^{n-1}\)): \[\begin{equation*} f(x+h^{*})=\min_{h\in S^{n-1}} f(x+h) \approx f(x) + \min_{h\in S^{n-1}} \langle \nabla f(x), h \rangle \end{equation*}\] Από την ανισότητα Cauchy-Schwarz, έχουμε ότι το εσωτερικό γινόμενο έχει κάτω φράγμα \(-\|\nabla f(x)\|\) και έτσι \[\begin{equation*} h^{*}=\arg\min_{h\in S^{n-1}} f(x+h) \approx -\, \frac{\nabla f(x)}{\|\nabla f(x)\|} \propto - \nabla f(x) \end{equation*}\]

Οι αλγόριθμοι αριθμητικής βελτιστοποίησης δοκιμάζονται πάντα στις τετραγωνικές συναρτήσεις, από τις οποίες εμπνέονται για παραπέρα βελτιώσεις, έτσι ώστε να μπορούν να ανταπεξέρθουν καλύτερα σε πιο δύσκολες συναρτήσεις. Στο παρακάτω παράδειγμα θα δούμε πώς λειτουργεί η μέθοδος αυτή σε μία τέτοια συνάρτηση.

Παράδειγμα 4.1 Ελαχιστοποιήστε τη συνάρτηση \(f: \mathbb{R}^2\rightarrow \mathbb{R}\) με τύπο \[\begin{equation*} f(x,y) = x^2 +2y^2 +2xy -6x -10y +13, \end{equation*}\] χρησιμοποιώντας τη μέθοδο απότομης κατάβασης.

Λύση:

Αρχικά, παρατηρούμε ότι \(f\in C^{1}(\mathbb{R}^2, \mathbb{R})\) και οι πρώτες μερικές παράγωγοι είναι \[\begin{align*} \frac{\partial f}{\partial x}(x,y) &= 2x + 2y -6, \\ \frac{\partial f}{\partial y}(x,y) &= 4y +2x -10, \end{align*}\] επομένως έχουμε \[\begin{equation*} \nabla f(x,y) = (2x + 2y -6, 4y +2x -10). \end{equation*}\] Η λύση του συστήματος των εξισώσεων μας οδηγεί σε μοναδικό στάσιμο σημείο \((x^{*},y^{*})=(1,2)\), το οποίο είναι και ολικό ελάχιστο, όπως εύκολα επαληθεύεται. Θα δούμε τώρα πώς λειτουργεί η μέθοδος της απότομης κατάβασης σε μία επανάληψη του αλγορίθμου με σημεία εκκίνησης τα \((x_0^{(1)},y_0^{(1)})=(0,0)\) και \((x_{0}^{(2)},y_{0}^{(2)})=(3,1)\). Υπολογίζουμε την κλίση σε κάθε σημείο ως \(\nabla f(0,0)=(-6,-10)\) και \(\nabla f(3,1)=(2, 0)\). Σε κάθε περίπτωση, τα σημεία \((x_1^{(1)},y_1^{(1)})\) και \((x_1^{(2)},y_1^{(2)})\) θα προσδιοριστούν σε ένα βήμα του αλγορίθμου απότομης κατάβασης, ως τα σημεία εκείνα που ελαχιστοποιούν τη συνάρτηση \(f\) στις ημιευθείες με αρχή τα σημεία \((0,0)\) και \((3,1)\), και κατευθύνσεις \((6,10)\) και \((-2,0)\) αντίστοιχα (που είναι αντίθετα της κλίσης της \(f\) στα εν λόγω σημεία). Οι ημιευθείες αυτές περιγράφονται από τις εξισώσεις: \[\begin{align*} y&=\frac{10}{6}x, \ x>0, \\ y&=1, \ x<3, \end{align*}\] στην πρώτη και τη δεύτερη περίπτωση αντίστοιχα. Είτε αντικαθιστώντας τους παραπάνω περιορισμούς στον τύπο της \(f\), είτε χρησιμοποιώντας την παραμετρική μορφή (ως προς \(a\)) των καμπυλών που υποδεικνύονται από τον αλγόριθμο, βρίσκουμε άμεσα ότι τα σημεία ελαχίστου επιτυγχάνονται στα σημεία \((51/40, 51/24)\) και \((2, 1)\) αντίστοιχα. Είναι φανερό ότι παρόλο που η πρώτη αρχικοποίηση ήταν σε τιμή της \(f\) αρκετά πιο μεγάλη από τη δεύτερη, η κλίση της \(f\) στο πρώτο σημείο την οδήγησε τελικά πιο κοντά στη θέση ελαχίστου.

set.seed(1193)
# h function
h <- function(x,y) {
  x ^ 2 + 2 * (y ^ 2) + 2 * x * y - 6 * x - 10 * y + 13
}

# h surface
n <- 250
x <- y <- seq(-3, 5, length = 250)
hmat <- matrix(0, ncol = n, nrow = n)

for (i in 1:n) {
  for (j in 1:n) {
    hmat[i, j] <- h(x[i], y[j])
  }
}
ax0 <- 0 ; ay0 <- 0; ax1 <- 51 / 40; ay1 <- 51 / 24 ; cola = "blue"
bx0 <- 3 ; by0 <- 1; bx1 <- 2; by1 <- 1 ; colb = "darkgreen"

par(mar = c(4, 4, 1, 1))
image(x, y, hmat)
contour(x, y, hmat, levels = c(seq(0,7, by = 0.4), seq(2, 400, by = 5)), add = TRUE)
points(x = 1, y = 2, col = "red", pch = 20)
points(x = ax0, y = ay0, col = cola, pch = 20)
points(x = ax1, y = ay1, col = cola)
arrows(x0 = ax0, y0 = ay0, x1 = ax1, y1 = ay1, length = 0.1, col = cola)
points(x = bx0, y = by0, col = colb, pch = 20)
points(x = bx1, y = by1, col = colb)
arrows(x0 = bx0, y0 = by0, x1 = bx1, y1 = by1, length = 0.1, col = colb)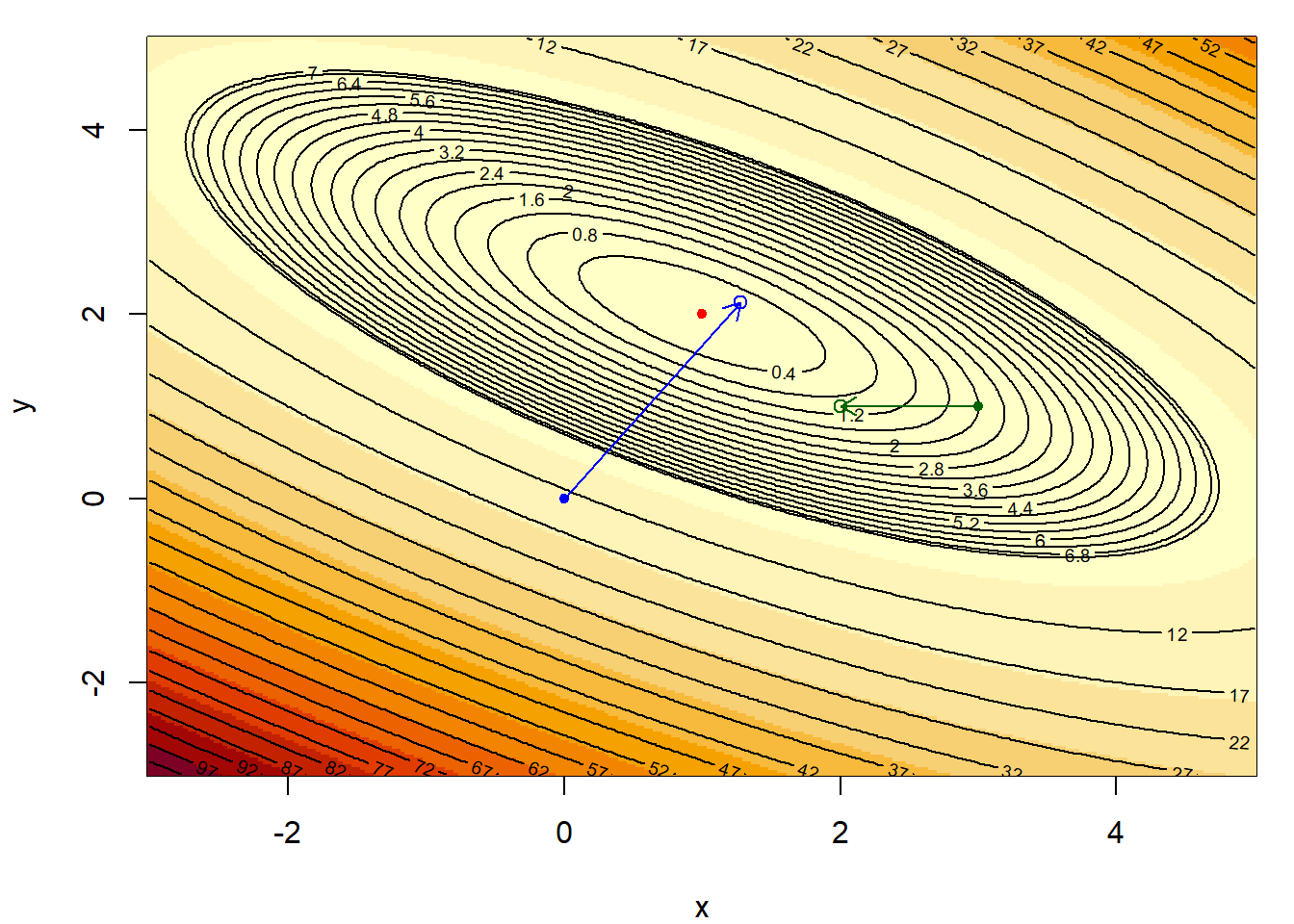

Εικόνα 4.2: One steepest descent step with two different initializations for the problem of \(f\) minimization, with starting points \((0,0)\) (blue) and \((3,1)\) (green). The argmin of the function is \((1,2)\) (red dot), with \(f(1,2)=0\).

Ας δούμε τώρα και την εξέλιξη διάφορων μονοπατιών, με διαφορετική αρχικοποίηση, μέχρι να ικανοποιηθεί το κριτήριο τερματισμού.

# gradient 
dh <- function(x, y) {
  dx <- 2 * x + 2 * y - 6
  dy <- 4 * y + 2 * x - 10
  c(dx, dy)
}

# line search
f <- function(a, x, y){
  h(x - a[1] * dh(x, y)[1], y - a[2] * dh(x, y)[2])
}

# Steepest Descent Algorithm
st.descent <- function(x, y, tol = 1e-10){
  
  # keep record
  path <- matrix(c(x, y), ncol = 2, nrow = 1)
  
  while (sum(dh(x, y) ^ 2) > tol) {
    a <- optim(par = c(1, 1), fn = f, x = x, y = y)$par # min in line
    x <- x - a[1] * dh(x, y)[1]
    y <- y - a[2] * dh(x, y)[2]
    path <- rbind(path, c(x, y))
  }
  
  path
}

# Starting points
x0 <- c(0, -2.5, -1, 4.5, 2)
y0 <- c(-2, 2, 0, 3, 0.4)
col <- c("red", "darkgreen", "blue", "brown", "purple")

# h surface
n <- 250
x <- y <- seq(-3, 5, length = 250)
hmat <- matrix(0, ncol = n, nrow = n)

for (i in 1:n) {
  for (j in 1:n) {
    hmat[i,j] <- h(x[i], y[j])
  }
}

# Contour
par(mar = c(4, 4, 1, 1))
image(x, y , hmat)
contour(x, y, hmat, levels = c(seq(0, 7, by = 0.4), seq(2, 400, by = 5)), add = TRUE)

# Add the sequences
for (i in 1:length(x0)) {
  x <- st.descent(x0[i], y0[i])[ , 1]
  y <- st.descent(x0[i], y0[i])[ , 2]
  points(x, y, col = col[i], pch = 20)
  lines(x, y, col = col[i], pch = 20)
}

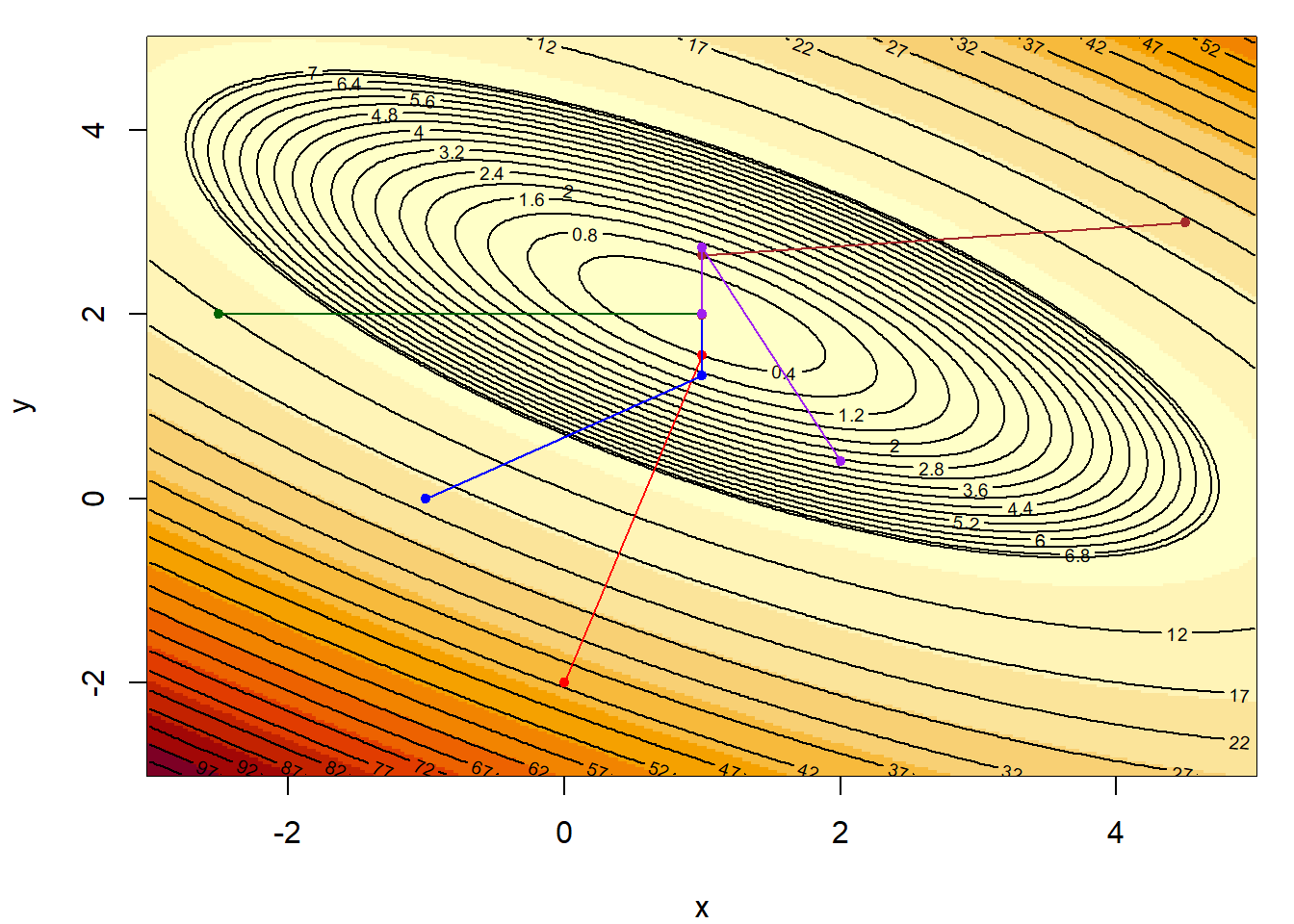
Εικόνα 4.3: Steepest Descent algorithm for 6 different initializations.

Το πρώτο, και σημαντικότερο, ερώτημα που γεννάται, είναι αν η ακολουθία που ορίσαμε συγκλίνει στο σημείο ολικού ελαχίστου της \(f\) στο σύνολο \(E^n\). Καθώς το σημείο αυτό δεν είναι απαραίτητα μοναδικό, ορίζουμε ως σύνολο λύσεων \(\Gamma = \{x^\star\in E^n : f(x^\star)=\min_{x\in E^n} f(x) \}\). Η ερώτηση που θέσαμε λοιπόν αναδιαμορφώνεται ως εξής: Συγκλίνει η αναδρομική ακολουθία (4.1) σε σημείο \(x\in \Gamma\); Για να το αποδείξουμε, θα χρειαστούμε το Θεώρημα Ολικής Σύγκλισης.

Θεώρημα 4.1 (Global Convergence Theorem) Έστω \(A: E^n\rightarrow \mathcal{P}(E^n)\) ένας αλγόριθμος, ένα σύνολο λύσεων \(\Gamma\subset X\) και μία ακολουθία \(\{x_k\}_{k=0}^{+\infty}\) η οποία για δεδομένο αρχικό σημείο \(x_0\) ορίζεται αναδρομικά ως \(x_{k+1}\in A(x_k)\). Εάν

1. υπάρχει συμπαγές σύνολο \(S\subset X\) τέτοιο ώστε \(x_k\in S, \forall k\in \mathbb{N}\),
2. υπάρχει μία συνεχής συνάρτηση \(Z:X\rightarrow \mathbb{R}\) ώστε,
   • Αν \(x\notin \Gamma\), τότε \(Z(y)<Z(x), \ \forall y \in A(x)\),
   • Αν \(x\in \Gamma\), τότε \(Z(y)\leq Z(x), \ \forall y \in A(x)\),
3. η απεικόνιση \(A\) είναι κλειστή στα σημεία εκτός του \(\Gamma\),

τότε το όριο κάθε συγκλίνουσας υπακολουθίας της \(x_k\) είναι λύση, δηλαδή για το σημείο σύγκλισης \(x\) ισχύει ότι \(x\in \Gamma\).

Απόδειξη:. Από την υπόθεση (i), η ακολουθία \(\{x_k\}_{k=0}^{+\infty}\) βρίσκεται μέσα σε ένα συμπαγές σύνολο \(S\), επομένως υπάρχει υπακολουθία \(\{x_k\}_{k\in\mathcal{Κ}}\) (όπου \(\mathcal{K}\) το σύνολο των δεικτών της υπακολουθίας, \(\mathcal{K}\subset \mathbb{N}\)), η οποία συγκλίνει στο σημείο \(x\in S\), δηλαδή \(x_k\rightarrow x, k\in \mathcal{K}\). Η συνάρτηση \(Z\) είναι συνεχής (υπόθεση ii), επομένως \(Z(x_k)\rightarrow Z(x), k\in \mathcal{K}\). Σύμφωνα με τον ορισμό της σύγκλισης,

\[\begin{equation*} \forall \epsilon>0 \,\exists K\in \mathcal{K}: Z(x_k)-Z(x)<\epsilon, \ \ \forall k>K, k\in \mathcal{K}. \end{equation*}\]

Δείξαμε ότι η \(Z\) συγκλίνει ως προς την υπακολουθία. Θα δείξουμε ότι συγκλίνει ως προς ολόκληρη την ακολουθία, δηλαδή ότι η παραπάνω σύγκλιση ισχύει για όλα τα \(k>K\), όχι μόνο για αυτά του συνόλου \(\mathcal{K}\). Από την μονοτονία της \(Z\) (υπόθεση ii), έχουμε \(i<j \Rightarrow Z(x_i)>Z(x_j)>Z(x), i,j\in \mathbb{N}\). Έστω λοιπόν \(k>K\), τότε

\[\begin{equation*} Z(x_k) - Z(x) = \underbrace{Z(x_k) - Z(x_K)}_{<0} + \underbrace{Z(x_K) - Z(x)}_{<\epsilon} < \epsilon, \end{equation*}\]

επομένως \(Z(x_k)\rightarrow Z(x)\). Είμαστε έτοιμοι να δείξουμε ότι \(x\in \Gamma\). Έστω ότι \(x\notin \Gamma\). Τότε ορίζουμε την ακολουθία \(y_k:=x_{k+1}, k\in \mathcal {K}\). Η \(\{y_k\}_{\mathcal{K}}\) βρίσκεται μέσα στο \(S\), επομένως έχει συγκλίνουσα υπακολουθία \(\{y_k\}_{\mathcal{L}}, \mathcal{L}\subset \mathcal{K}\), η οποία συγκλίνει στο \(y\). Επομένως έχουμε \(x_k \rightarrow x, k\in \mathcal{L}\subset \mathcal{K}\), \(y_k\rightarrow y, k\in \mathcal{L}\) και \(y_k\in A(x_k), k\in \mathcal {L}\). Από την υπόθεση (iii), η \(A\) είναι κλειστή στο \(x\notin\Gamma\), επομένως \(y\in A(x)\). Αφού \(x\notin \Gamma, Z(y)<Z(x)\). Όμως δείξαμε ότι \(Z(x_k)\rightarrow Z(x)\) για ολόκληρη την ακολουθία \(\{x_k\}_{k=0}^{+\infty}\), επομένως και για τις υπακολουθίες \(\{x_k\}_\mathcal{K}, \{y_k\}_\mathcal{L}\), οπότε από την μοναδικότητα του ορίου \(Z(x)=Z(y)\), άτοπο. Επομένως \(x\in \Gamma\), δηλαδή κάθε συγκλίνουσα υπακολουθία συγκλίνει σε λύση.

Επιστρέφοντας στη μέθοδο απότομης κατάβασης, θέλουμε να δείξουμε ότι οι τρεις υποθέσεις του Θεωρήματος Ολικής Σύγκλισης ικανοποιούνται. Αρχικά, ορίζουμε το σύνολο λύσεων \(\Gamma = \{x\in E^n: \nabla f(x)=0\}\).

2. Ως συνάρτηση \(Z\), επιλέγουμε την ίδια την \(f\) που επιθυμούμε να ελαχιστοποιήσουμε, η οποία είναι συνεχής εξ ορισμού. Εύκολα βλέπουμε ότι
   • Αν \(x\notin \Gamma\), τότε \(g(x)=\nabla f(x)\neq 0\), άρα \(\min_{0\leq a <+\infty}f(x-ag(x))<f(x)\)
   • Αν \(x\in \Gamma\), τότε \(g(x)=\nabla f(x)= 0\), άρα \(f(x-ag(x))=f(x), \ \forall y \in A(x)\)
3. Η \(A(x)\) είναι κλειστή,

Επομένως, εάν η ακολουθία \(\{x_k\}_{k=0}^{+\infty}\) είναι φραγμένη, τότε ικανοποιούνται και οι τρεις υποθέσεις του Θεωρήματος Ολικής Σύγκλισης, επομένως θα έχει υπακολουθία που θα συγκλίνει μέσα στο σύνολο των λύσεων.

4.2.2 Σύγκλιση Μεθόδου για τις Τετραγωνικές Συναρτήσεις

Θα εξετάσουμε θεωρητικά τη σύγκλιση του αλγορίθμου στις τετραγωνικές συναρτήσεις

\[\begin{equation*} f(x) = \frac{1}{2}x^\top Q x - x^\top b, \end{equation*}\]

όπου \(Q\) ένας θετικά ορισμένος και συμμετρικός \(n\times n\) πίνακας.

Παραγωγίζοντας τη συνάρτηση παίρνουμε \[\begin{equation*} g(x)=\nabla f(x) = \frac{1}{2} 2 Qx - b = Qx - b. \end{equation*}\]

Στην συγκεκριμένη περίπτωση, μπορούμε να βρούμε ότι το μοναδικό σημείο ελαχίστου \(x^\star\) της \(f(x)\) ικανοποιεί τη σχέση \(Qx^\star = b\). Θα προσεγγίσουμε το σημείο με τη μέθοδο σύγκλισης, μέσω της αναδρομικής ακολουθίας

\[\begin{equation*} x_{k+1}=x_k-a_k g_k, \end{equation*}\]

όπου \(g_k=Qx_k - b\) και το \(a_k\) ελαχιστοποιεί την \(f(x_k-a_k g_k)\). Το \(a_k\) μπορεί να υπολογιστεί αναλυτικά, παραγωγίζοντας την

\[\begin{equation*} f(x_k-ag_k) = \frac{1}{2}(x_k-ag_k)^\top Q (x_k-ag_k) - (x_k-ag_k)^\top b, \end{equation*}\]

ως προς \(a\), κάτι που δίνει την λύση

\[\begin{equation*} a_k = \frac{g_k^\top g_k}{g_k^\top Q g_k}. \end{equation*}\]

Τελικά, η αναδρομική ακολουθία παίρνει τη μορφή

\[\begin{equation*} x_{k+1}=x_k-\frac{g_k^\top g_k}{g_k^\top Q g_k} g_k, \end{equation*}\]

όπου \(g_k=Qx_k - b\).

Παρουσιάζουμε τώρα δύο αποτελέσματα χωρίς απόδειξη, τα οποία θα μας βοηθήσουν να μελετήσουμε την ταχύτητα σύγκλισης της μεθόδου απότομης κατάβασης.

Λήμμα 4.1 Ορίζουμε τη συνάρτηση \[\begin{equation*} E(x)=f(x)+\frac{1}{2}{x^\star}^\top Q x^\star =\frac{1}{2}(x-x^\star)^\top Q (x-x^\star), \end{equation*}\] όπου \(x^\star\) το σημείο ολικού ελαχίστου της \(f\). Για την αναδρομική ακολουθία \(\{x_k\}_{k=0}^{+\infty}\) της μεθόδου σύγκλισης ισχύει \[\begin{equation*} E(x_{k+1} = \left\{1-\frac{\left(g_k^\top g_k\right)^2}{\left(g_k^\top Q g_k\right) \left(g_k^\top Q^{-1} g_k\right)} \right\} E(x_k). \end{equation*}\]

Πρόταση 4.1 (Kantorovich Inequality) Έστω \(Q\) ένας θετικά ορισμένος και συμμετρικός \(n\times n\) πίνακας. Για κάθε n-διάστατο διάνυσμα \(x\) ισχύει \[\begin{equation*} \frac{\left(x^\top x\right)^2}{\left(x^\top Q x\right) \left(x^\top Q^{-1} x\right)}\geq \frac{4aA}{(a+A)^2}, \end{equation*}\] όπου \(a, A\) είναι η μικρότερη και η μεγαλύτερη ιδιοτιμή του \(Q\), αντίστοιχα.

Από τα παραπάνω προκύπτει άμεσα το ακόλουθο θεώρημα.

Θεώρημα 4.2 (Steepest Descent - Quadratic Case) Για κάθε \(x_0\in E^n\), η μέθοδος απότομης κατάβασης συγκλίνει στο μοναδικό σημείο ελαχίστου \(x^\star\) της \(f\). Επιπλέον, για την συνάρτηση \(E(x)=\frac{1}{2}(x-x^\star)^ \top Q (x-x^\star)\) ισχύει \[\begin{equation*} E(x_{k+1} \leq \left( \frac{A-a}{A+a} \right)^2 E(x_k), \end{equation*}\] ή θέτοντας \(r=A/a\), \[\begin{equation*} E(x_{k+1} \leq \left( \frac{r-1}{r+1} \right)^2 E(x_k), \end{equation*}\]

Απόδειξη:. Από το λήμμα 4.1 και την ανισότητα του Kantorovich προκύπτει άμεσα ότι

\[\begin{equation*} E(x_{k+1} \leq \left\{1-\frac{4aA}{(A+a)^2} \right\} E(x_k) = \left( \frac{A-a}{A+a} \right)^2 E(x_k). \end{equation*}\]

Επομένως, \(E(x_k)\rightarrow 0\) και καθώς ο \(Q\) είναι θετικά ορισμένος, \(x_k\rightarrow x^\star\).

Αδρά μιλώντας, το παραπάνω θεώρημα δηλώνει πως ο ρυθμός σύγκλισης της μεθόδου απότομης κατάβασης μειώνεται καθώς ο λόγος \(r=A/a\) μεγαλώνει. Επομένως, ακόμα και αν έχουμε \(n-1\) από τις \(n\) ιδιοτιμές να είναι ίσες με \(a\), με την τελευταία ιδιοτιμή να είναι πολύ μεγαλύτερη, ο λόγος αυτός είναι κοντά στο 1 και η σύγκλιση του αλγορίθμου είναι αργή. Αντίθετα, στην ακραία περίπτωση που όλες οι ιδιοτιμές είναι ίσες (οπότε \(a=A\)), ο αλγόριθμος συγκλίνει σε ένα μόλις βήμα. Ο λόγος \(r\) ονομάζεται δεσμευμένος αριθμός (conditional number) του πίνακα \(Q\).

Αξίζει εδώ να παρατηρήσουμε ότι ο λόγος \(\left[ (A-a)/(A+a) \right]^2\) δεν είναι ο πραγματικός ρυθμός σύγκλισης της μεθόδου, αλλά ένα άνω φράγμα αυτού (το χειρότερο δυνατό σενάριο). Παρ’ όλα αυτά, συχνά δηλώνουμε ότι ο ρυθμός σύγκλισης του αλγορίθμου απότομης κατάβασης είναι \(\left( (A-a)/(A+a) \right)^2\).

4.2.3 Μέθοδος Newton - Raphson

Αρχικά, ας μελετήσουμε τον αλγόριθμο για την περίπτωση της μίας μεταβλητής, δηλαδή την ελαχιστοποίηση μίας συνάρτησης \(f: \mathbb{R}\rightarrow \mathbb{R}\), όπως αυτή της εικόνας 4.4. Η βασική ιδέα στηρίζεται στο να κινηθούμε αντίθετα από το πρόσημο που μας καθορίζει η κλίση της συνάρτησης στο σημείο αυτό (αντίστοιχα, σύμφωνα με το πρόσημο σε προβλήματα μεγιστοποίησης). Είναι φανερό ότι \(f'(x_0)<0\), ενώ \(f'(y_0)>0\) και άρα επιλέγοντας κατάλληλα \(x_1>x_0\) και \(y_1<y_0\), θα παίρναμε μικρότερες τιμές για την \(f\). Αλγεβρικά έχουμε γενικά ότι \(\nabla f(x_0) (x-x_0)<0\), έτσι ώστε

\[\begin{equation*} f(x) \approx f(x_0) +\nabla f(x_0) (x-x_0) < f(x_0), \end{equation*}\]

για αρκούντως μικρή μετακίνηση \(x-x_0\).

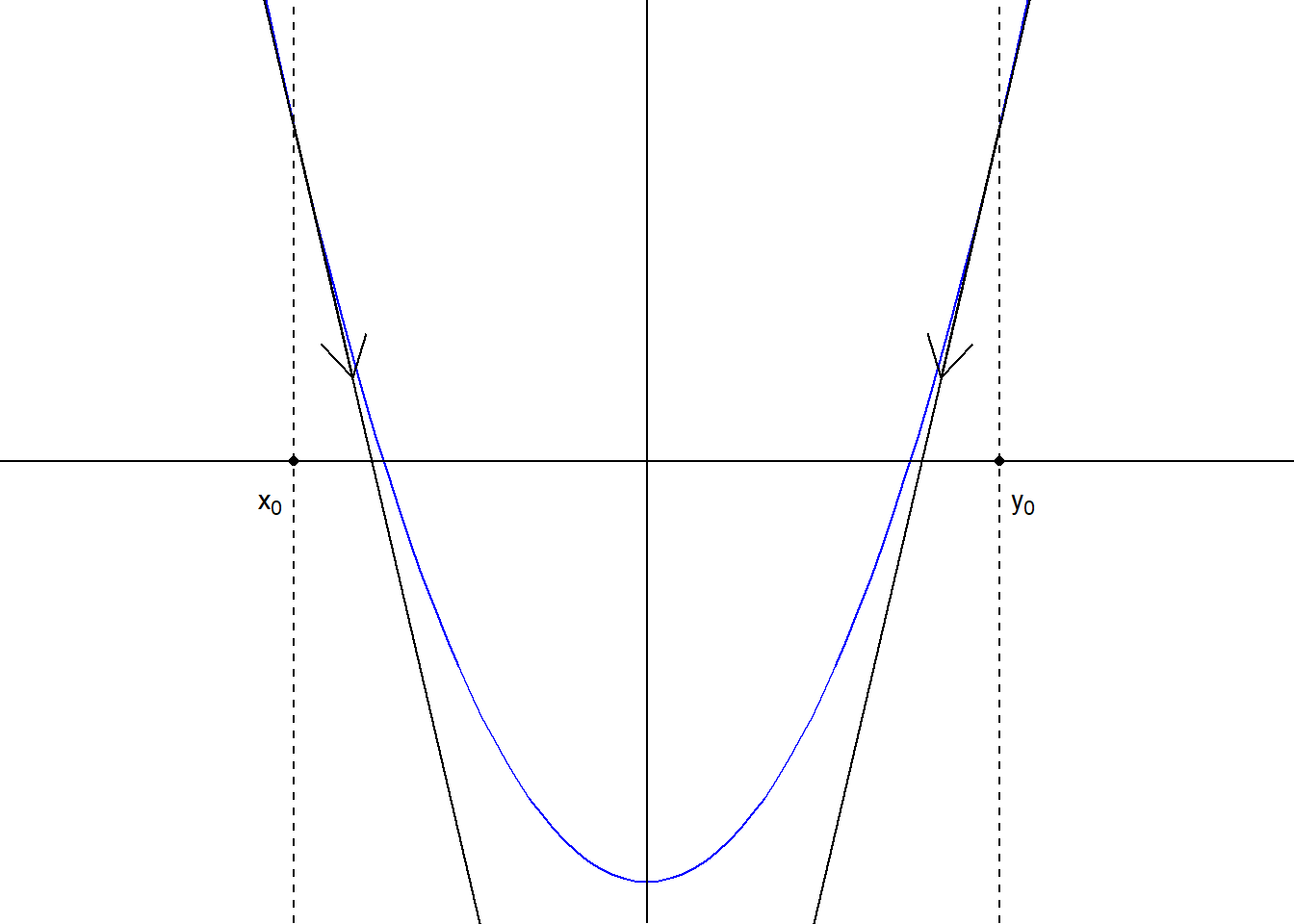
Εικόνα 4.4: A representation of the moving direction of the Newton-Raphson algorithm for two different initial points \(x_0, y_0\), for a unimodal function \(f\).

Γενικότερα, η ιδέα πίσω από τη μέθοδο Newton - Raphson είναι ότι η υπό ελαχιστοποίηση συνάρτηση \(f\) μπορεί να προσεγγιστεί τοπικά από μία τετραγωνική συνάρτηση, την οποία μπορούμε να ελαχιστοποιήσουμε αναλυτικά. Επομένως, σε μία περιοχή γύρω από το σημείο \(x_k\), η \(f\) προσεγγίζεται από την περικεκκομένη σειρά Taylor

\[\begin{equation*} f(x) \approx f(x_k) + \nabla f(x_k) (x-x_k) +\frac{1}{2} (x-x_k)^\top H(x_k) (x-x_k). \end{equation*}\]

Το δεξί μέλος ελαχιστοποιείται στο σημείο

\[\begin{equation*} x_{k+1} = x_k - H(x_k)^{-1} \nabla f(x_k)^\top, \end{equation*}\]

όπου \(H(x_k)\) ο Εσσιανός πίνακας της \(f\) υπολογισμένος στο σημείο \(x_k\). Παρατηρούμε λοιπόν ότι η μέθοδος Newton - Raphson είναι μία παραλλαγή της μεθόδου κλίσης, με \(a_k=H(x_k)^{-1}\). Για τη σύγκλιση του αλγορίθμου ισχύει το παρακάτω θεώρημα:

Θεώρημα 4.3 (Newton - Raphson Method) Έστω \(f\in C^3(E^n, \mathbb{R})\) (συνάρτηση από το \(E^n\) στο \(\mathbb{R}\) με συνεχείς τρίτες μερικές παραγώγους) και τοπικό σημείο ελαχίστου \(x^\star\) με τον εσσιανό πίνακα \(H(x^\star)\) να είναι θετικά ορισμένος. Τότε, υπάρχει σφαίρα \(S\subset E^n\) γύρω από το \(x^\star\) τέτοια ώστε, αν η αναδρομική ακολουθία του αλγορίθμου ξεκινήσει με αρχικό όρο \(x_0\in S\), τότε η ακολουθία συγκλίνει το \(x^\star\). Η τάξη σύγκλισης είναι τουλάχιστον 2, δηλαδή \(||x_{k+1}-x^\star||\leq c \cdot ||x_{k}-x^\star||\), για κάποια θετική σταθερά \(c\).

Απόδειξη:. Έστω \(p>0, \beta_1>0, \beta_2>0\), τέτοια ώστε για όλα τα \(x: |x-x^\star|<p\) να ισχύει \(|H(x)^{-1}|<\beta_1\) (όπου \(|\cdot |\) νόρμα) και \(|\nabla f(x^\star)^\top-\nabla f(x)^\top -H(x)(x^\star -x)|\leq \beta_2 |x-x^\star|^2\). Υποθέτουμε ότι το \(x_k\) επιλέγεται έτσι ώστε \(\beta_1\beta_2|x_k-x^\star|<1\) και \(|x_k-x^\star|<p\). Τότε

\[\begin{align*} |x_{k+1}-x^\star| &= |x_k -x^\star - H(x_k)^{-1} \nabla f(x_k)^\top | \\ &= |H(x_k)^{-1} \left[\nabla f(x^\star)^\top-\nabla f(x_k)^\top -H(x_k)(x^\star -x_k) \right]| \\ &\leq |H(x_k)^{-1}| \beta_2 |x_k-x^\star|^2 \leq \beta_1 \beta_2 |x_k-x^\star|^2 < |x_k-x^\star|. \end{align*}\]

Η τελευταία ανισότητα δείχνει πως το νέο σημείο είναι πιο κοντά στο \(x^\star\), ενώ η προτελευταία ανισότητα δείχνει ότι σύγκλιση είναι δεύτερης τάξης.

Βλέπουμε επομένως πως η μέθοδος Newton - Raphson είναι ιδιαίτερα αποδοτική όταν η υπό ελαχιστοποίηση (ή μεγιστοποίηση) συνάρτηση \(f\) έχει καλές ιδιότητες, εγκυμονεί όμως ο κίνδυνος να μας οδηγήσει σε ένα τοπικό ελάχιστο και όχι το ολικό ελάχιστο που επιθυμούμε. Επομένως, μία συχνή παραλλαγή είναι να επαναλαμβάνουμε τη μέθοδο πολλές φορές, με διαφορετικά σημεία εκκίνησης.

Παράδειγμα 4.2 Θέλουμε να υπολογίσουμε την τετραγωνική ρίζα ενός θετικού αριθμού \(p\). Αναζητούμε δηλαδή τη θετική λύση της εξίσωσης \(x ^ 2 = p\). Μία μέθοδος γενικού σκοπού για την εύρεση ριζών μίας συνάρτησης είναι η μέθοδος του Νεύτωνα, γνωστή και ως μέθοδος Newton-Raphson. Η μετατροπή του αρχικού προβλήματος, σε ένα πρόβλημα εύρεσης ριζών κατάλληλης συνάρτησης γίνεται άμεσα. Θέτουμε

\[\begin{equation} f(x)=x^2-p, \end{equation}\]

και η λύση του αρχικού προβλήματος μετατρέπεται σε ένα πρόβλημα εύρεσης της θετικής λύσης της εξίσωσης \(f(x)=0\).

Λύση:

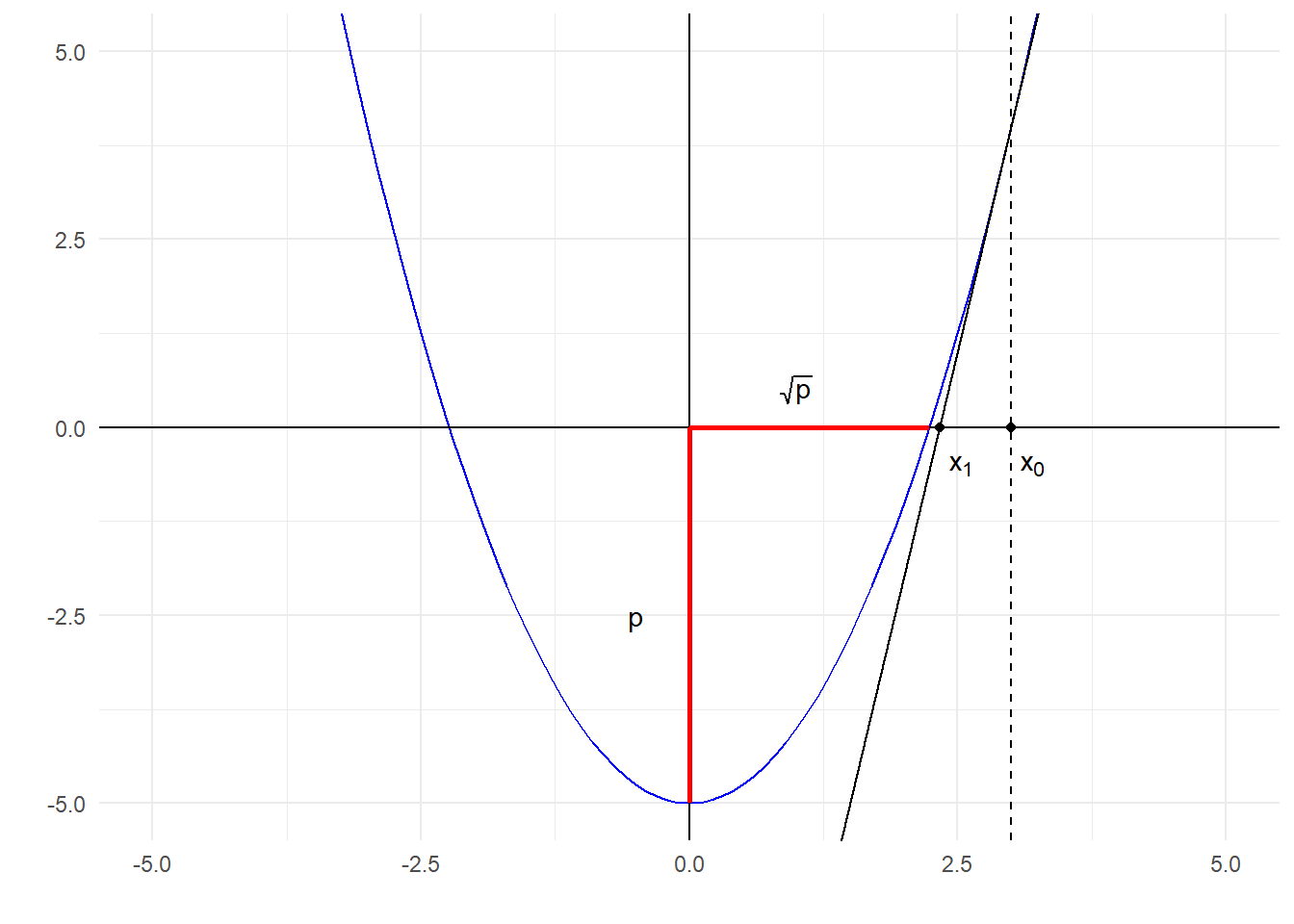
Η ιδέα που βρίσκεται στη βάση κατασκευής του αλγορίθμου Newton-Raphson είναι η δυνατότητα ικανοποιητικής γραμμικής προσέγγισης της εν λόγω συνάρτησης σε μία περιοχή που περιλαμβάνει τη ρίζα της.

Αν \(x_0\) είναι ένα αρχικό σημείο εντός αυτής της περιοχής, τότε

\[\begin{equation} f(x)\cong f(x_0) +f'(x_0)(x-x_0). \end{equation}\]

Επομένως, αντί να λύσουμε την εξίσωση \(f(x)=0\), λύνουμε την:

\[\begin{equation*} f(x_0) +f'(x_0)(x-x_0) = 0. \end{equation*}\]

Yποθέτοντας λοιπόν ότι \(f'(x_0)\neq 0\), επιλέγουμε ως επόμενο σημείο το

\[\begin{equation} x_1 = x_0 - \frac{f(x_0)}{f'(x_0)}, \end{equation}\]

και επαναλαμβάνοντας τη διαδικασία γραμμικών προσεγγίσεων της \(f\) στα σημεία που παίρνουμε κάθε φορά, καταληγούμε στον εξής αναδρομικό ορισμό της ακολουθίας:

\[\begin{equation} x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}, \quad \forall n\geq 0. \end{equation}\]

Αν εφαρμόσουμε τον αλγόριθμο αυτό στο παράδειγμα εύρεσης της τετραγωνικής ρίζας, τότε με \(f'(x)=2x\), καταλήγουμε στην αναδρομή:

\[\begin{equation} x_{n+1} = x_n - \frac{x^2_n-p}{2x_n} = \frac{x_n+\frac{p}{x_n}}{2}. \end{equation}\]

Μπορούμε τώρα να δημιουργήσουμε μία συνάρτηση στην R, η οποία υλοποιεί τη μέθοδο του Νεύτωνα και υπολογίζει την τετραγωνική ρίζα ενός θετικού αριθμού με συγκεκριμένη ακρίβεια.

sqrnt <- function(p, tol = 1e-5){
  x <- p / 2
  y <- (x + p / x) / 2
  while (abs(y - x) > tol) {
    x <- y
    y <- (x + p / x) / 2
  }
  y
}
sqrnt(2)
## [1] 1.414214

Το κριτήριο τερματισμού που αντιστοιχεί στον παραπάνω αλγόριθμο αφορά την απόσταση μεταξύ δύο διαδοχικών όρων της ακολουθίας. Στην περίπτωση που ο αλγόριθμος συγκλίνει, τότε και η απόσταση των διαδοχικών όρων \(|x_{n+1}-x_n|\) συγκλίνει στο \(0\). Είναι επίσης δυνατό να χρησιμοποιηθεί ένα κριτήριο τερματισμού που στηρίζεται στις τιμές της αρχικής συνάρτησης \(f(x)\).

sqrnt2 <- function(p, tol = 1e-5){
  x <- p / 2
  while (abs(x * x - p) > tol) {
    x <- (x + p / x) / 2
  }
  x
}
sqrnt2(2)
## [1] 1.414216

Θα πρέπει βέβαια να σημειωθεί ότι γενικότερα σε κάποιον αλγόριθμο μπορούμε να συνδυάζουμε και τα 2 κριτήρια, απαιτώντας ο αλγόριθμος να σταματά όταν και οι 2 συνθήκες παύουν να ισχύουν. Αυτό θα δίνει μία περαιτέρω εγγύηση στο ότι μικρές αποστάσεις διαδοχικών όρων, δε σημαίνει κατ’ανάγκη ότι έχουμε καλή προσέγγιση της λύσης.

Στο σημείο αυτό αξίζει να σημειώσουμε την ανταλλαγή ακρίβειας-ταχύτητας που αποτελεί γενικό χαρακτηριστικό των υπολογιστικών μεθόδων. Καθώς αυξάνεται η ακρίβεια της προσέγγισης που απαιτούμε από τον αλγόριθμο, ελαττώνεται η ταχύτητα διεκπεραίωσης της εργασίας που έχει αναλάβει το πρόγραμμα, αυξάνοντας έτσι το συνολικό χρόνο ολοκλήρωσης του προγράμματος.

Στη συνάρτηση που κατασκευάσαμε έχουμε επιτρέψει τον έλεγχο της ακρίβειας του αλγορίθμου Newton-Raphson μέσα από το όρισμα tol, με αρχική τιμή \(10^{-5}\). Ας ζητήσουμε από την R να τρέξει τη συνάρτηση με διαφορετικές ακρίβειες και να τις χρονομετρήσει. Σε αυτό θα μας βοηθήσει το πακέτο microbenchmark, που τρέχει μία συνάρτηση πολλές φορές και υπολογίζει βασικά στατιστικά όπως ο μέσος χρόνος εκτέλεσης.

library(microbenchmark)
microbenchmark(sqrnt(2, tol = 1e-1), times = 10000, unit = 'ns')
## Unit: nanoseconds
##                 expr min  lq   mean median  uq  max neval
##  sqrnt(2, tol = 0.1) 600 600 717.45    700 700 8700 10000
microbenchmark(sqrnt(2, tol = 1e-3), times = 10000, unit = 'ns')
## Unit: nanoseconds
##                   expr min  lq  mean median  uq   max neval
##  sqrnt(2, tol = 0.001) 800 800 908.1    900 900 30700 10000
microbenchmark(sqrnt(2, tol = 1e-10), times = 10000, unit = 'ns')
## Unit: nanoseconds
##                   expr min   lq    mean median   uq   max neval
##  sqrnt(2, tol = 1e-10) 900 1000 1032.81   1000 1000 29700 10000
#print.microbenchmark to display and boxplot.microbenchmark or autoplot.microbenchmark to plot the results.

Πράγματι, καθώς αυξάνουμε την επιθυμητή ακρίβεια, αυξάνεται και ο χρόνος εκτέλεσης. Οι διαφορές βέβαια εδώ είναι πολύ μικρές, καθώς ο αλγόριθμος αυτός έχει μεγάλη ταχύτητα σύγκλισης. Θα επανέλθουμε στο σημείο αυτό αργότερα.

Έχοντας δημιουργήσει τη συνάρτηση, είμαστε έτοιμοι να κάνουμε τη σύγκριση με την έτοιμη εντολή της R για τον υπολογισμό της τετραγωνικής ρίζας.

sqrnt(2) # our function
## [1] 1.414214
sqrt(2)  # base R function
## [1] 1.414214

Οι δύο συναρτήσεις φαίνεται να παράγουν το ίδιο αποτέλεσμα. Αυτό είναι σωστό, μέχρι την ακρίβεια που καθορίσαμε. Για να συγκρίνουμε τις δύο προσεγγίσεις, μπορούμε να εμφανίσουμε περισσότερα ψηφία από τα 6 που εμφανίζει by default η R και να εμφανίσουμε και τα 20 πραγματικά δεκαδικά ψηφία του \(\sqrt{2}\)

format(sqrnt(2),nsmall = 20)
## [1] "1.41421356237468986983"
format(sqrt(2),nsmall = 20)
## [1] "1.41421356237309514547"
1.41421356237309504880
## [1] 1.414214

H προσέγγιση της R είναι σωστή μέχρι και το 15ο ψηφίο και βλέπουμε ότι ο αλγόριθμος πέτυχε σωστά τα 11 πρώτα. Αυτό δεν είναι περίεργο, καθώς η προσέγγιση στα 5 που ζητήσαμε αποτελεί την ελάχιστη ακρίβεια που εμείς επιζητάμε. Η τελευταία επανάληψη του αλγορίθμου που προκύπτει όταν για πρώτη φορά θα ικανοποιηθεί το κριτήριο τερματισμού (της ζητούμενης ακρίβειας), μπορεί να οδηγήσει σε αριθμό που έχει αρκετά καλύτερη ακρίβεια από αυτήν που θέσαμε. Αυτό είναι εμφανές σε αυτό το παράδειγμα. Αν από την άλλη, αυξήσουμε την ακρίβεια, π.χ., στα 18 ψηφία, τότε έχουμε αντίστοιχα

format(sqrnt(2, tol = 1e-18), nsmall = 20)
## [1] "1.41421356237309492343"
format(sqrt(2), nsmall = 20)
## [1] "1.41421356237309514547"
1.41421356237309504880
## [1] 1.414214

φτάνοντας στο όριο των 15 ψηφίων, όσο μπορεί δηλ. και η R. Ας συγκρίνουμε τώρα τους χρόνους εκτέλεσης των δύο αλγορίθμων:

microbenchmark(sqrnt(2, tol = 1e-12), unit = "ns")
## Unit: nanoseconds
##                   expr  min   lq mean median   uq  max neval
##  sqrnt(2, tol = 1e-12) 1000 1000 1206   1100 1150 9200   100
microbenchmark(sqrt(2), unit = "ns")
## Unit: nanoseconds
##     expr min lq mean median  uq  max neval
##  sqrt(2)   0  0   73      0 100 2800   100

Βλέπουμε πως η συνάρτηση που φτιάξαμε είναι πιο αργή στο μέσο χρόνο εκτέλεσης από την έτοιμη συνάρτηση της R. Επιπλέον, προγραμματιστικά δεν είναι πλήρης, αφού είναι πολύ πιθανό να μην λειτουργήσει με τον επιθυμητό τρόπο σε όλα τα σενάρια που μπορεί να προκύψουν. Για παράδειγμα, αν τρέξουμε τις παρακάτω γραμμές κώδικα, θα δούμε πως η συνάρτησή μας παγιδεύεται μέσα στο while και δε σταματά ποτέ.

sqrnt(-1)     
sqrt(-1)

Μπορούμε βέβαια να τροποποιήσουμε τη συνάρτηση για να χειριστούμε κάποια σημεία που είναι προβληματικά.

4.2.4 Εφαρμογές

Θα μελετήσουμε δύο βασικές συναρτήσεις της R, την nlm, η οποία υλοποιεί τον αλγόριθμο Newton - Raphson, και την optim(), την κύρια συνάρτηση βελτιστοποίησης στην R που υλοποιεί πολλές μεθόδους. Δίνουμε ένα παράδειγμα από την κάθε μία.

Παράδειγμα 4.3 (Cauchy MLE Approximation) Έστω η συνάρτηση πιθανοφάνειας ενός δείγματος από την κατανομή \(\mathcal{C}(\theta, 1)\)

\[\begin{equation*} L(\theta) = \prod_{i=1}^n \frac{1}{1+(x_i-\theta)^2}, \end{equation*}\]

και η λογαριθμοπιθανοφάνεια \[\begin{equation*} \ell(\theta) = -\sum_{i=1}^n \log (1+(x_i-\theta)^2). \end{equation*}\]

Προσομοιώστε ένα δείγμα μεγέθους \(n = 1000\) από την \(\mathcal{C}(0, 1)\) και υπολογίστε την εκτιμήτρια μέγιστης πιθανοφάνειας με τη συνάρτηση optim().

Λύση:

Γνωρίζουμε πως η ακολουθία των ε.μ.π. συγκλίνει στο \(\theta^\star=0\), καθώς \(n\rightarrow +\infty\). Παίρνουμε ένα δείγμα μεγέθους \(n = 1000\) από την \(\mathcal{C}(0, 1)\) και υπολογίζουμε αναδρομικά τις ε.μ.π. με τη συνάρτηση optim(), καθώς το μέγεθος του δείγματος αυξάνεται χρησιμοποιώντας την πιθανοφάνεια και την λογαριθμοπιθανοφάνεια.

Όπως φαίνεται στην εικόνα 4.5 (αριστερά), η μεγιστοποίηση της συνάρτησης πιθανοφάνειας \(L\) αποτυγχάνει. Αυτό είναι ένα χαρακτηριστικό παράδειγμα αστάθειας, που μπορεί εύκολα να διορθωθεί μετασχηματίζοντας σε \(\ell=\log L\).

Εάν αντικαταστήσουμε την πιθανοφάνεια με μία διαταραγμένη (perturbed) μορφή

\[\begin{equation*} L_p(\theta) = \prod_{i=1}^n \frac{e^{-\sin(100\theta)^2}}{1+(x_i-\theta)^2}, \end{equation*}\] και αντίστοιχα \[\begin{equation*} \ell_p(\theta) = -\sin(100\theta)^2-\sum_{i=1}^n \log (1+(x_i-\theta)^2), \end{equation*}\]

παίρνουμε τα αντίστοιχα αποτελέσματα.

set.seed(283)
n <- 1000
sam <- rcauchy(n)

loglike <- function(y, sam){ 
  -sum(log(1 + (x - y) ^ 2))
}
like <- function(y, sam) {
  1 / prod((1 + (x - y) ^ 2))
}
ploglike <- function(y, sam) {
  -sin(y * 100) ^ 2 - sum(log(1 + (x - y) ^ 2))
}
plike <- function(y, sam) {
  exp(-sin(y * 100) ^ 2) / prod((1 + (x - y) ^ 2))
}

lmax <- Lmax <- plmax <- pLmax <- NULL
for (i in 1:n) {
  x <- sam[1:i]
  opt_loglike <- optim(par = -1, sam = x, fn = loglike, method = "L-BFGS-B",
                       lower = -10, upper = 10, control = list(fnscale = -1))
  opt_like <- optim(par = -1, sam = x, fn = like, method = "L-BFGS-B",
                    lower = -10, upper = 10, control = list(fnscale = -1))
  opt_ploglike <- optim(par = -1, sam = x, fn = ploglike, method = "L-BFGS-B",
                        lower = -10, upper = 10, control = list(fnscale = -1))
  opt_plike <- optim(par = -1, sam = x, fn = plike, method = "L-BFGS-B",
                     lower = -10, upper = 10, control = list(fnscale = -1))
  lmax <- c(lmax, opt_loglike$par)
  Lmax <- c(Lmax, opt_like$par)
  plmax <- c(plmax, opt_ploglike$par)
  pLmax <- c(pLmax, opt_plike$par)
}


plot(lmax, ty = "l", lwd = 2, xlab = "", ylab = "arg")
lines(Lmax, col = "sienna", lwd = 2)

plot(plmax, ty = "l", lwd = 2, xlab = "", ylab = "arg")
lines(pLmax, col = "sienna", lwd = 2)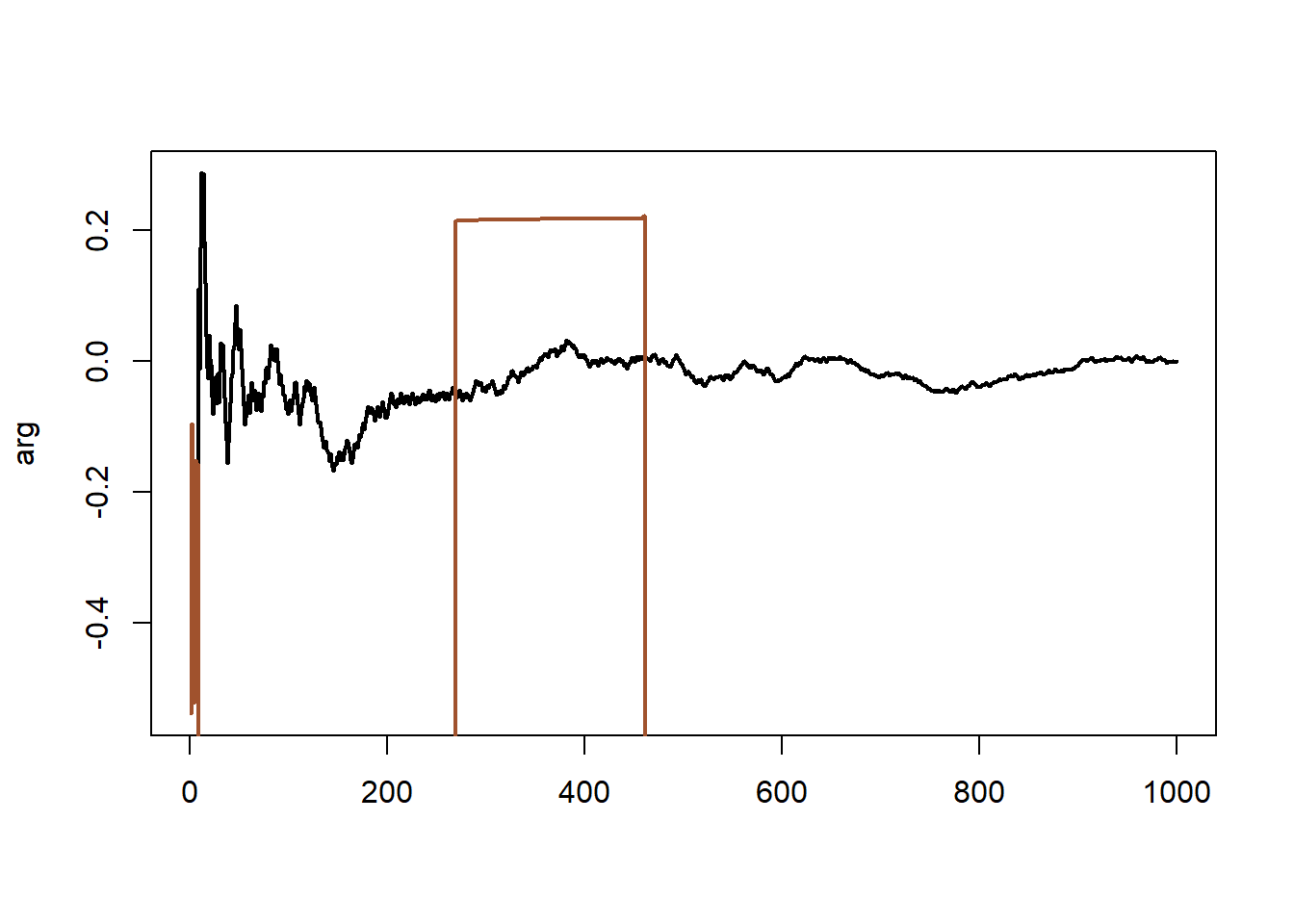

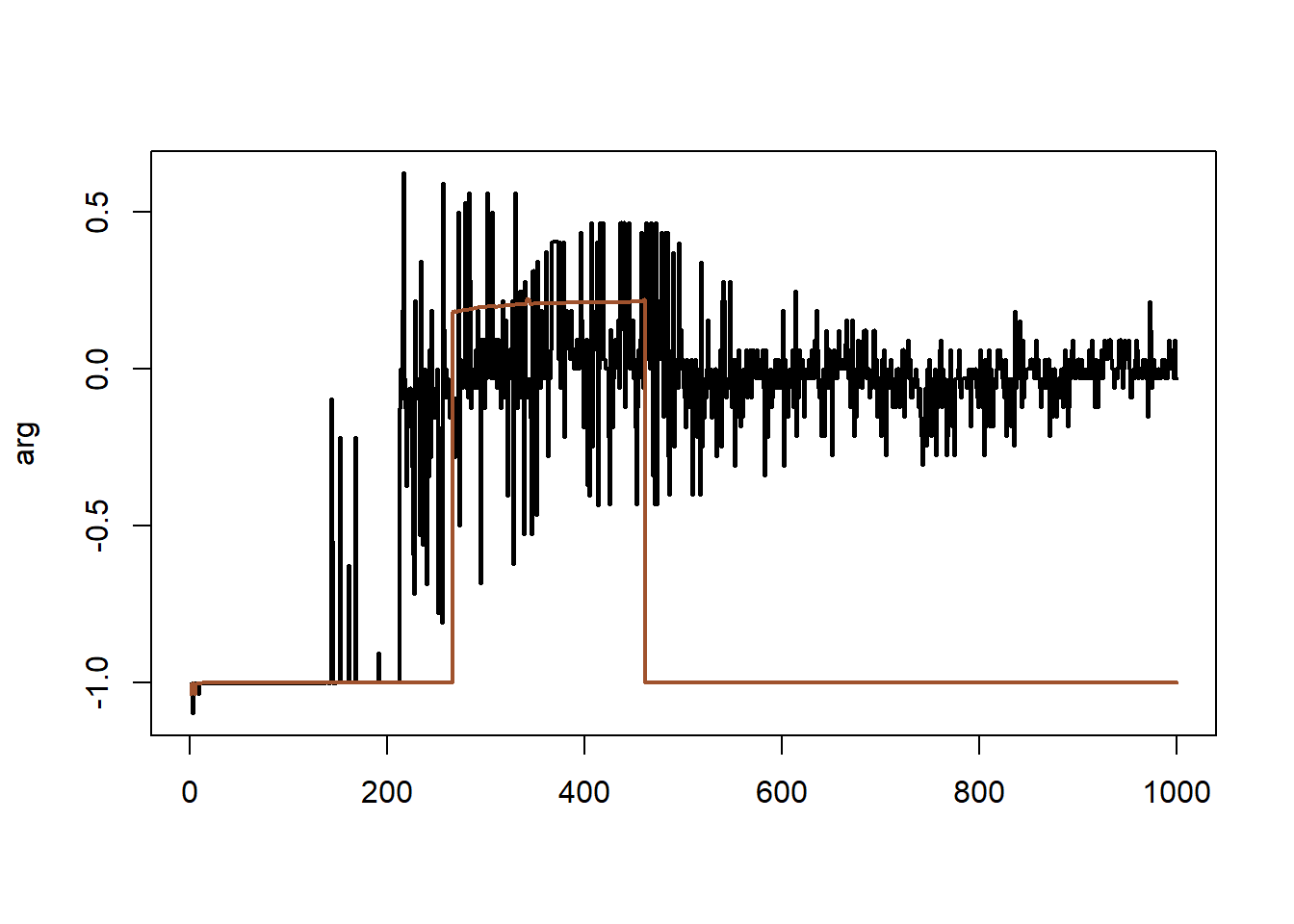
Εικόνα 4.5: (Left) Sequence of MLEs corresponding to 400 simulations from a Cauchy \(\mathcal{C}(0, 1)\) distribution obtained by applying optimize to the log-likelihood and the likelihood (in lighter colors). (Right) the same sequences when using a perturbed likelihood.

Παράδειγμα 4.4 (Normal Mixture Model) Υποθέτουμε πως έχουμε ένα δείγμα 400 παρατηρήσεων από μίξη κατανομών \(\mathcal{N}(1, 1)\) και \(\mathcal{N}(2.5, 1)\), με αντίστοιχες πιθανότητες \(1/4\) και \(3/4\). Όπως φαίνεται στην εικόνα 4.6, η λογαριθμοπιθανοφάνεια \(\ell(\mu_1, \mu_2)\) της παραπάνω κατανομής είναι δικόρυφη. Η ε.μ.π. δεν μπορεί να υπολογιστεί αναλυτικά, αφού η πιθανοφάνεια είναι ένα γινόμενο αθροισμάτων

\[\begin{equation*} L(\mu_1, \mu_2) = \prod_{i=1}^n \left[\frac{1}{4} f(x_i;\mu_1) + \frac{3}{4} f(x_i;\mu_2)\right], \end{equation*}\]

και ως αποτέλεσμα η λογαριθμοπιθανοφάνεια παίρνει τη μορφή

\[\begin{equation*} \ell(\mu_1, \mu_2) = \sum_{i=1}^n \log \left(\frac{1}{4} f(x_i;\mu_1) + \frac{3}{4} f(x_i;\mu_2)\right). \end{equation*}\]

Επαληθεύστε τη σύγκλιση του αλγορίθμου Newton - Raphson μέσα από 6 ακολουθίες, με αντίστοιχα αρχικά σημεία \((x_0, y_0)=(1, 1), (-1, -1), (4, -1), (4, 2.5), (1, 4)\) και \((-1, 4.5)\), χρησιμοποιώντας τη συνάρτηση nlm().

Λύση:

Η πορεία κάθε ακολουθίας σημειώνεται πάνω στην εικόνα 4.6. Παρατηρούμε ότι 4 από τις ακολουθίες συγκλίνουν στο ολικό μέγιστο (-0.68, 1.98), ενώ οι άλλες δύο συγκλίνουν στο τοπικό, αλλά όχι ολικό μέγιστο. Επιπλέον, ακολουθίες που ξεκινάνε πολύ μακριά από τα σημεία μεγίστου είναι πιθανό να αποκλίνουν.

set.seed(1028)
da <- sample(rbind(rnorm(10 ^ 2), 2 + rnorm(3 * 10 ^ 2)))

# minus the log-likelihood function
like <- function(mu) {
  - sum(log((0.25 * dnorm(da - mu[1]) + 0.75 * dnorm(da - mu[2]))))
}

# log-likelihood surface
mu1 <- mu2 <- seq(-2, 5, length = 250)
lli <- matrix(0, ncol = 250, nrow = 250)

for (i in 1:250) {
  for (j in 1:250) {
    lli[i,j] <- like(c(mu1[i], mu2[j]))
  }
}

par(mar = c(4, 4, 1, 1))
image(mu1, mu2, -lli, xlab = expression(mu[1]), ylab = expression(mu[2]),
      col = hcl.colors(12, "YlOrRd", rev = FALSE))
contour(mu1, mu2, -lli, nle = 100, add = TRUE)

# sequence of NR maxima
starts <- matrix(c(1, 1, -1, -1, 4, -1, 4, 2.5, 1, 4, -1, 4.5), nrow = 2)
colours <- c("blue", "red", "black", "grey40", "green", "orange")
for (j in 1:dim(starts)[2]) {
  sta <- starts[, j]
  mmu <- starts[, j]
  for (i in 1:(nlm(like, sta)$it)) {
    mmu <- rbind(mmu, nlm(like, starts[, j], iterlim = i)$est)
  }
  points(starts[1, j], starts[2, j], size = 3, pch = 20, col = colours[j])
  lines(mmu[, 1], mmu[, 2], lwd = 2, col = colours[j])
}

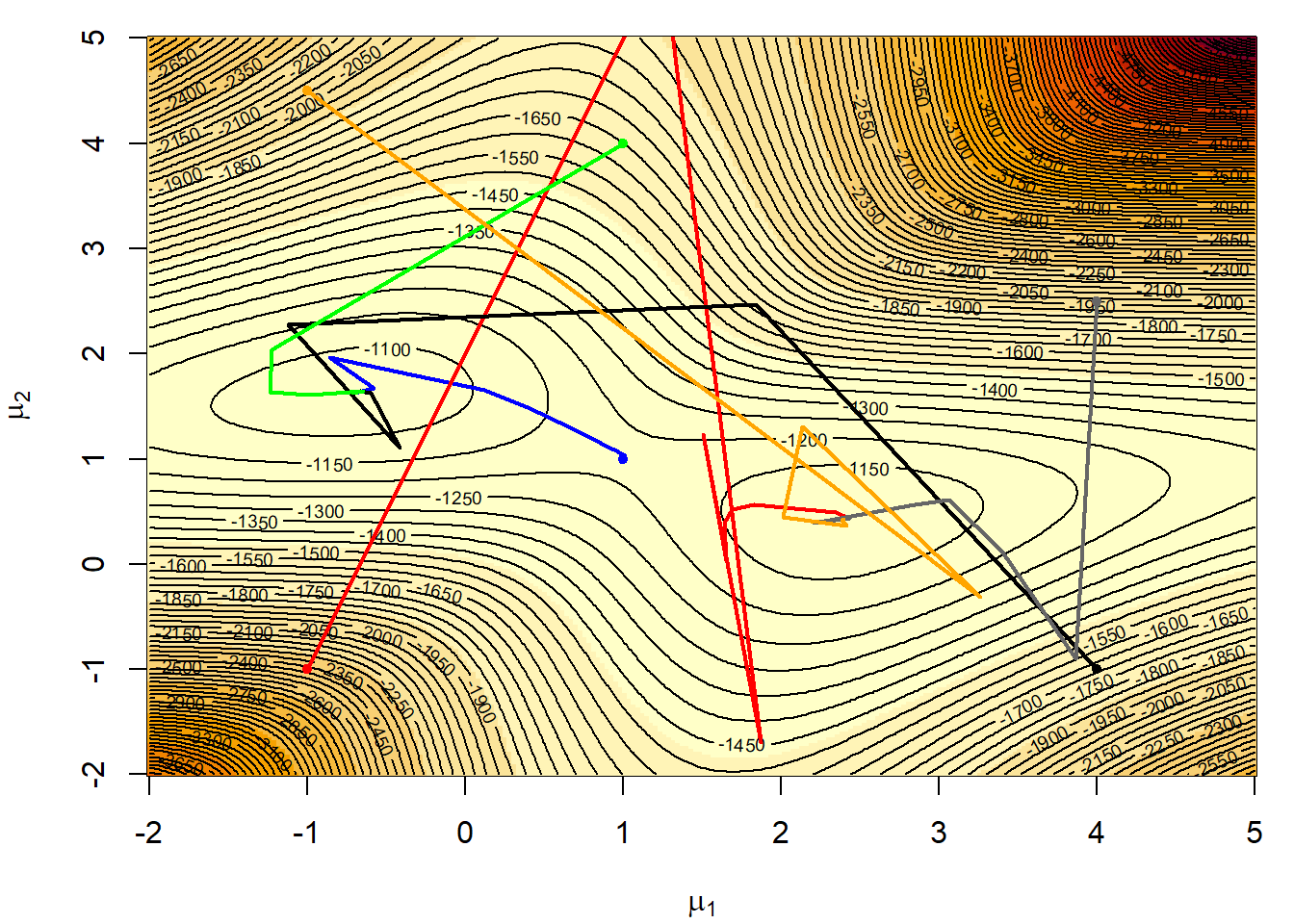
Εικόνα 4.6: Six Newton–Raphson sequences for a mixture likelihood ending in one of two modes depending on the starting point based on a sample of 400 observations from the normal mixture with \(\mu_1 = 0\) and \(\mu_2 = 2.5\)

4.3 Στοχαστική Βελτιστοποίηση

4.3.1 Εισαγωγή

Μία πρώτη σκέψη στο πρόβλημα προσέγγισης του \(\max_{\theta\in\Theta} h(\theta)\) μέσω προσομοίωσης είναι να προσομοιώσουμε ένα μεγάλο αριθμό σημείων από όλο το \(\Theta\) σύμφωνα με μία αυθαίρετη κατανομή \(f\), έως ότου παρατηρηθεί μία “πολύ μεγάλη” τιμή της \(h\). Όπως είναι εμφανές, αυτός ο τρόπος δεν είναι καθόλου αποδοτικός εάν η \(f\) δεν έχει επιλεχθεί βάση της \(h\). Παρ’ όλα αυτά, κάτω από συγκεκριμένες υποθέσεις (όπως τη συμπάγεια του \(\Theta\)), συγκλίνει στο \(\max_{\theta\in\Theta} h(\theta)\) καθώς ο αριθμός των προσομοιώσεων τείνει στο άπειρο.

Παράδειγμα 4.5 Έστω η συνάρτηση \[\begin{equation*} h(x) = \left[ \cos(50x) + \sin(20x) \right]^2, \ x\in [0,1]. \end{equation*}\] Εφαρμόστε στοχαστική βελτιστοποίηση μέσω ομοιόμορφης δειγματοληψίας στο \([0, 1]\).

Λύση:

Η \(h\), παρότι παρουσιάζει καλές ιδιότητες (είναι ορισμένη σε φραγμένο διάστημα, συνεχής και άπειρες φορές παραγωγίσιμη), έχει ιδιαίτερα μεγάλη μεταβλητότητα, κάτι που περιπλέκει το πρόβλημα εύρεσης των ακροτάτων της (Σχήμα 4.7).

h <- function(x) {
  (cos(50 * x) + sin(20 * x)) ^ 2
}

ggplot() +
stat_function(fun = h, xlim = c(0, 1)) +
theme_minimal()

Εικόνα 4.7: Γράφημα της \(h(x)=\left[ \cos(50x) + \sin(20x) \right]^2\) ορισμένη στο \([0,1]\).

Η optimize() μας πληροφορεί ότι το σημείο μεγίστου είναι το \(x^\star=\) 0.379 με τιμή \(h(x^\star)=\) 3.833.

rangom <- h(matrix(runif(10 ^ 6), ncol = 10 ^ 3))
monitor <- t(apply(rangom, 1, cummax))
hmax <- optimize(h, int = c(0, 1), maximum = TRUE)$ob

Θα προσομοιώσουμε \(M=10^3\) φορές, ένα μέγεθος δείγματος \(10^3\) από την \(Unif(0,1)\) και μέσα από το δείγμα \(\{\widehat{\theta}_{n}^{(i)}\}_{i=1}^{M}\) θα μελετήσουμε πώς μεταβάλλεται το \(\widehat{\theta}_{n}\) και το \(\widehat{h}_n:= h(\widehat{\theta}_{n})\), δηλαδή η εκτίμηση της θέσης και της τιμής του μεγίστου. Στο σχήμα 4.8 παρουσιάζεται το γράφημα του εύρους των τιμών που κινείται η προσέγγιση του μεγίστου της \(h\), με ανώτερο όριο το \(max_{1\leq i \leq M}\widehat{h}_n^{(i)}\) και κατώτερο όριο το \(min_{1\leq i \leq M}\widehat{h}_n^{(i)}\) της \(h(\widehat{\theta}_{n})\), καθώς το \(n\) αυξάνει μέχρι τη μέγιστο διαθέσιμο δείγμα \(10^3\). Βλέπουμε πως η \(h(U_1)\) παρουσιάζει πολύ μεγάλη μεταβλητότητα, αφού δεν είναι παρά η τιμή της \(h\) σε ένα τυχαίο σημείο του διαστήματος \([0,1]\). Η μεταβλητότητα των εκτιμήσεων όμως γρήγορα ελαττώνεται και μετά από \(10^3\) βήματα, η μεγαλύτερη απόσταση από την τιμή που υπέδειξε η optimize() είναι 2996.181 .

plot(monitor[1, ],type = "l", col = "white", xlab = "Iterations", ylab = expression(h(theta)))
polygon(c(1:10 ^ 3, 10 ^ 3:1), c(apply(monitor, 2, max), rev(apply(monitor, 2, min))), col = "grey")
abline(h = hmax, col = "blue")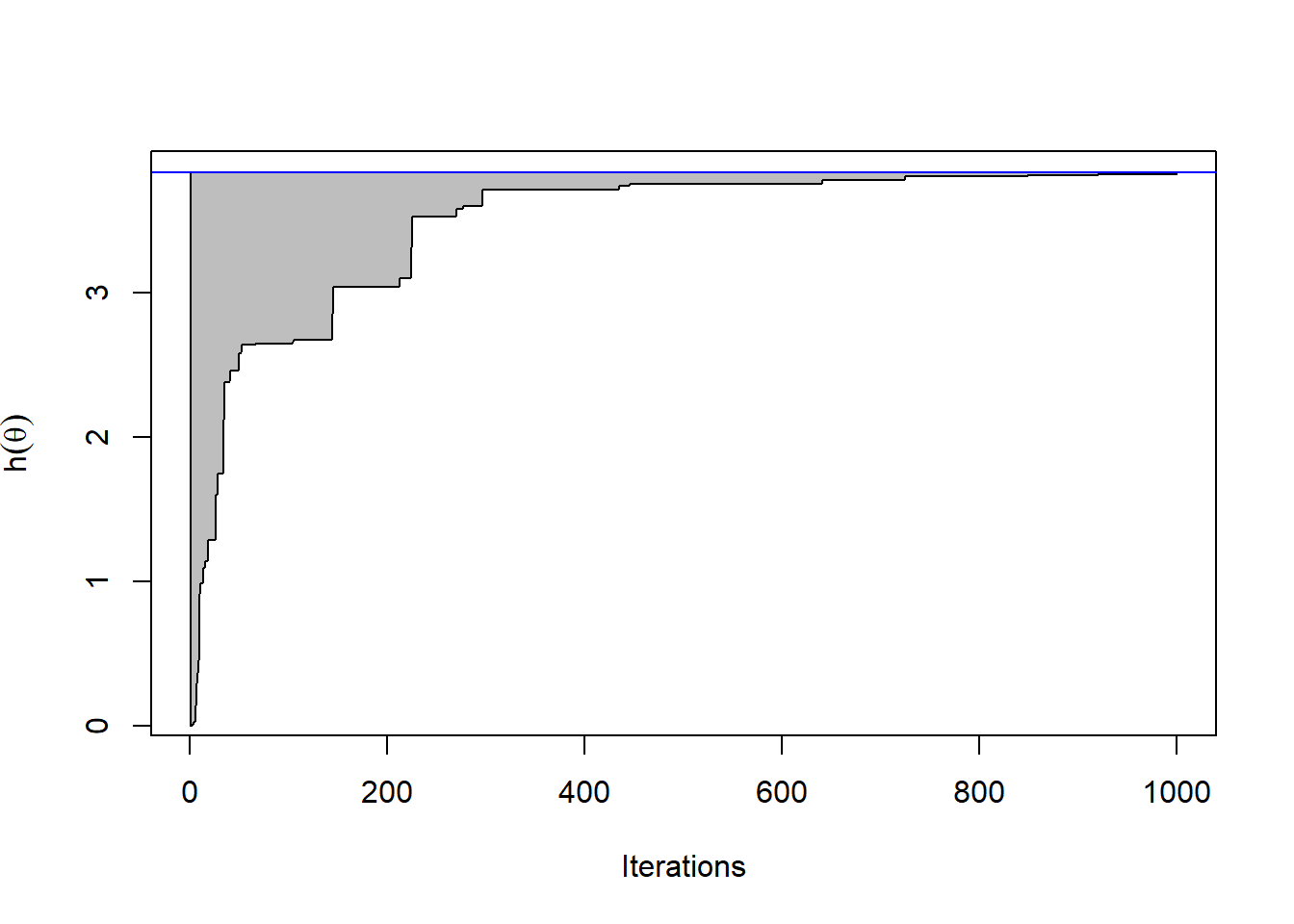

Εικόνα 4.8: Εύρος των \(10^3\) ακολουθιών από το μέγιστο που προέκυψε από ομοιόμορφη δειγματοληψία με \(10^3\) επαναλήψεις. Το πραγματικό μέγιστο παρουσιάζεται με μία μπλε γραμμή.

Μπορούμε να παρακολουθήσουμε τη διαφορά ανάμεσα στην αριθμητική βελτιστοποίηση της optimize() και τη στοχαστική βελτιστοποίηση της ομοιόμορφης δειγματοληψίας στο \([-5, 5]\), καθώς το δείγμα \(x_1, x_2, \dots, x_n\) της κατανομής Cauchy αυξάνεται από \(n=1\) έως \(n=5001\). Στην Εικόνα 4.9 (πάνω) έχουμε στον οριζόντιο άξονα τις τιμές \(\theta^\star\) της optimize και στον κάθετο τις στοχαστικές εκτιμήσεις. Παρότι φαίνεται να έχουμε μεγάλα σφάλματα γύρω από το 0, συγκριτικά με άλλες περιοχές, πρέπει να λάβουμε υπ’ όψιν το μεγάλο πλήθος παρατηρήσεων σε εκείνη την περιοχή. Στην Εικόνα 4.9 (κάτω), παρουσιάζονται τα σχετικά σφάλματα \(e=(h(\theta^\star) - h(\widehat{\theta}))/|h(\theta^\star)|\), τα οποία δεν δείχνουν αυξητική τάση καθώς το δείγμα αυξάνεται.

ref <- .1 * rnorm(5001)
f <- function(y) {
  -y ^ 2 * .1 - sum(log(1 + (x - y) ^ 2))
}

maxv <- loc <- truv <- trul <- NULL

for (i in seq(10, length(ref), le = 50)) {
  prop <- runif(10^3,-5,5)
  x <- ref[1:i]
  tru <- optimize(f, c(-5,5), maximum = TRUE)
  trul <- c(trul,tru$max)
  truv <- c(truv,tru$ob)
  vale <- apply(as.matrix(prop), 1, f)
  loc <- c(loc, prop[order(-vale)[1]])
  maxv <- c(maxv, max(vale))
}

par(mar = c(4, 4, 1, 1), mfrow = c(2,1))
plot(trul, loc, cex = .5, pch = 19, xlab = expression(theta^"*"), ylab = expression(hat(theta)))
abline(a = 0, b = 1, col = "grey")
plot(seq(10, length(ref), le = 50), (truv - maxv) / abs(truv), type = "l", lwd = 2, xlab = "Sample size", ylab = "Relative error")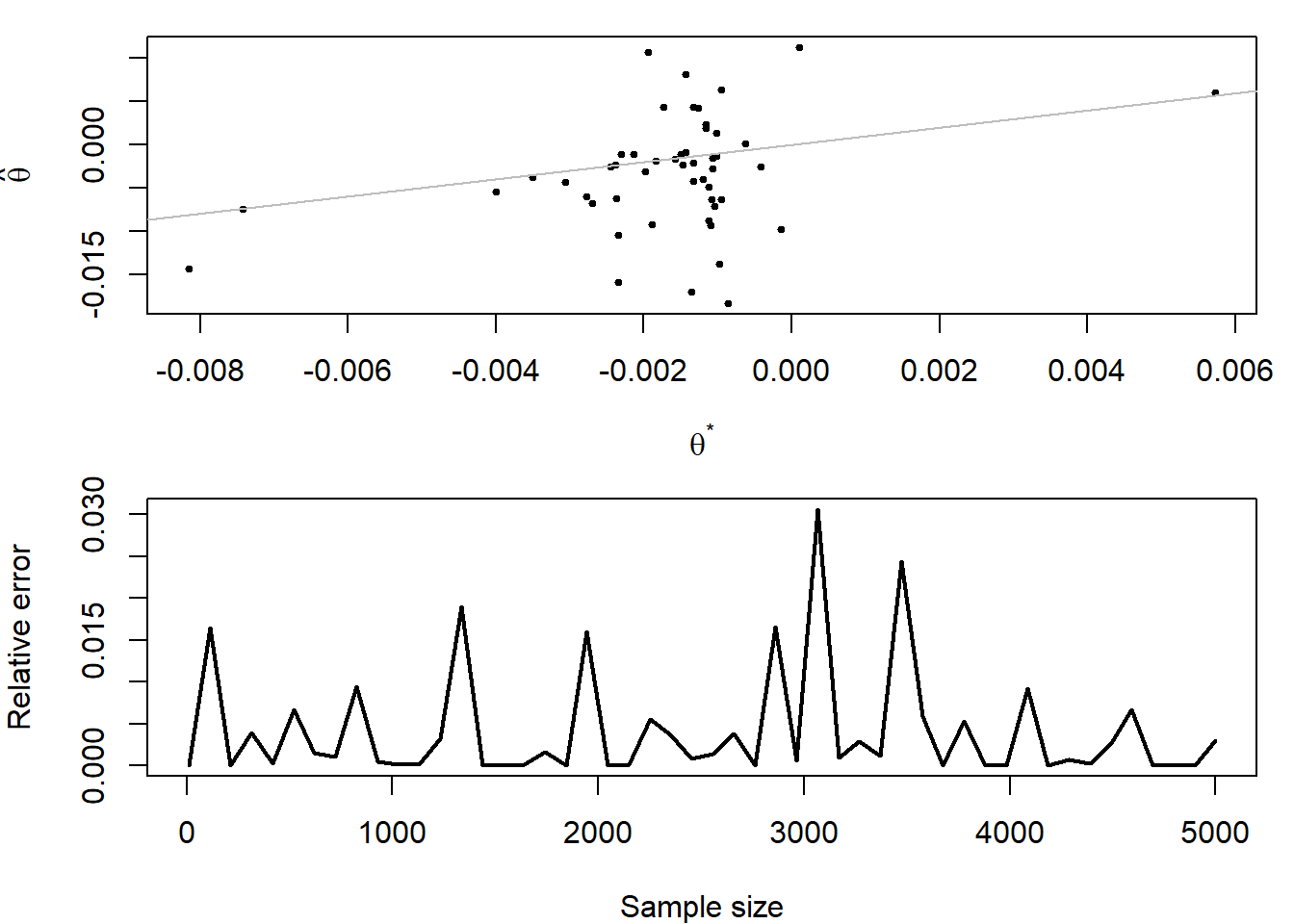

Εικόνα 4.9: Σύγκριση της αριθμητικής και στοχαστικής μεγιστοποίησης της πιθανοφάνειας της Cauchy. Πάνω: Σημειόγραμμα σύγκρισης εκτιμήσεων. Κάτω: Σχετικό σφάλμα ως συνάρτηση του μεγέθους δείγματος.

Στο σημείο αυτό αξίζει να παρατηρήσουμε ότι η παραπάνω διαδικασία μπορεί να εφαρμοστεί άμεσα μόνο όταν το σύνολο \(\Theta\) έχει επαρκώς απλή δομή. Διαφορετικά, καλούμαστε να προσομοιώσουμε ομοιόμορφα από ένα υπερσύνολο του \(\Theta\) με απλή δομή και να απορρίψουμε όσα σημεία πέφτουν εκτός του \(\Theta\).

Υποθέτουμε ότι έχουμε μία συνάρτηση \(h(x,y)\) την οποία επιθυμούμε να μεγιστοποιήσουμε στο διάστημα \[\begin{equation*} \Theta=\{(x,y)\in \mathbb{R}^2: x^2(1+\sin(3y)\cos(8x))+y^2(2+\cos(5x)\cos(8y))\leq 1\}. \end{equation*}\]

Για να εφαρμόσουμε στοχαστική βελτιστοποίηση μέσω ομοιόμορφης δειγματοληψίας, πρέπει πρώτα να βρούμε ένα βολικό υπερσύνολο του \(\Theta\).

Φυσικά, αυτή η μέθοδος αγνοεί τελείως τη συνάρτηση \(h\) και γρήγορα σταματά να είναι αποδοτική καθώς η διάσταση του προβλήματος μεγαλώνει. Για παράδειγμα, σε ένα Μπεϋζιανό περιβάλλον, όταν το μέγεθος \(n\) ενός αν.ισ. δείγματος \(x_1, \dots, x_n\) από την \(f(x|\theta)\) αυξάνεται, η posterior σ.π. / σ.π.π. \(\pi(\theta|x_1, \dots, x_n)\) συγκεντρώνεται όλο και περισσότερο γύρω από την επικρατούσα τιμή, επομένως η περιοχή που συγκεντρώνονται οι μεγάλες τιμές στενεύει, και η στοχαστική εκτίμηση μέσω ομοιόμορφης δειγματοληψίας γίνεται όλο και πιο δύσκολη.

Είναι επομένως ιδιαίτερα σημαντικό να σχεδιάζουμε πειράματα προσομοίωσης άμεσα συσχετισμένα με την υπό βελτιστοποίηση συνάρτηση \(h\), όπως και με τον χώρο \(\Theta\). Ενστικτωδώς, θέλουμε να προσομοιώνουμε με μεγάλη πιθανότητα από περιοχές όπου η \(h\) παίρνει μεγάλες τιμές και με μικρή πιθανότητα από περιοχές όπου η \(h\) παίρνει μικρές τιμές. Στην περίπτωση που η \(h\) είναι θετική και ολοκληρώσιμη, δηλαδή

\[\begin{equation*} \int_{\Theta} h(\theta) d\theta <+\infty, \end{equation*}\]

στόχος μας είναι να βρούμε τη συνάρτηση πυκνότητας \(f\) η οποία είναι ανάλογη ως προς την \(h\), δηλαδή \(f=c\cdot h\), όπου \(c\) η σταθερά κανονικοποίησης. Γενικότερα, κάθε σ.π.π. \(H\) η οποία έχει τα ίδια ολικά μέγιστα με την \(h\) αποτελεί μια ενδιαφέρουσα επιλογή, όπως για παράδειγμα η

\[\begin{equation*} H(\theta) \propto e^{h(\theta)/T}, \end{equation*}\]

για θετική σταθερά \(Τ\), τέτοια ώστε η \(H\) να είναι ολοκληρώσιμη. Η παράμετρος \(T\) ονομάζεται θερμοκρασία (temperature) και είναι ελεύθερη να επιλεγεί έτσι ώστε να επιταχύνουμε τη σύγκλιση ή να αποφύγουμε τα τοπικά μέγιστα, όπως θα συζητήσουμε στην πορεία. Για να επιλύσουμε λοιπόν το πρόβλημα μεγιστοποίησης της \(h\), θα προσομοιώσουμε ένα δείγμα \(\theta_1, \dots, \theta_m\) από την \(H\) και θα εκτιμήσουμε την κορυφή της \(h\). Σε μερικές περιπτώσεις θα είναι πιο πρακτικό να αναλύσουμε την \(H\) σε \(H(\theta)=H_1(\theta)\cdot H_2(\theta)\) και να προσομοιώσουμε μόνο από την \(H_1\). Σε στατιστικά προβλήματα, η \(h\) είναι συνήθως συνάρτηση πιθανοφάνειας και έτσι, η προσομοίωση από την \(h\) ταυτίζεται με την προσομοίωση από μία posterior κατανομή, όταν έχουμε μία επίπεδη prior.

Παράδειγμα 4.6 Θέλουμε να μεγιστοποιήσουμε τη συνάρτηση πιθανοφάνειας της Cauchy \(\mathcal{C}(\theta, 1)\), έχοντας ένα δείγμα \(X_1,\dots,X_n\). Εφαρμόστε στοχαστική βελτιστοποίηση προσομοιώνοντας από την κατανομή Student με \((n-1)/2\) βαθμούς ελευθερίας με μέση τιμή την εμπειρική διάμεσο (καθώς η μέση τιμή της Cauchy δεν ορίζεται και ο δειγματικός μέσος της είναι ιδιαίτερα ασταθής) και παράμετρο κλίμακας κατάλληλη σταθερά.

Λύση:

Θεωρώντας ομοιόμορφη prior στο διάστημα \([-5, 5]\), η συνάρτηση πιθανοφάνειας που θέλουμε να μεγιστοποιήσουμε μπορεί να ερμηνευθεί και ως posterior κατανομή του \(\theta\) (η posterior είναι ανάλογη της πιθανοφάνειας). Όμως, δεν μπορούμε να προσομοιώσουμε από αυτή την κατανομή, επομένως χρειαζόμαστε ένα υποκατάστατο. Καθώς το γινόμενο των σ.π.π. της Cauchy είναι το αντίστροφο ενός πολυωνύμου βαθμού \(2n\) (ως προς \(\theta\)), η κατανομή Student παρέχει μία πολύ ικανοποιητική προσέγγιση της posterior κατανομής γύρω από την κορυφή της, όπως φαίνεται στο σχήμα 3.1.

set.seed(13)
N <- 1 + 10 ^ 2
cau <- rcauchy(N)

# cauchy likelihood
f <- function(x) {
  z <- dcauchy(outer(x, cau, FUN = "-"))
  exp(apply(log(z), 1, sum))
}
# normalization constant
fcst <- integrate(f, low = -3, up = 3)$va
# posterior
ft <- function(x) {
  f(x) / fcst
}

# Student
dft <- (N - 1) / 2
mcau <- median(cau)
rcau <- 0.14 # diff(quantile(cau,c(.25,.75)))
g <- function(x) {
  dt((x - mcau) / rcau, df = dft) / rcau
}

par(mar = c(2, 2, 1, 1))
curve(g, from = -3, to = 3, xlab = "", ylab = "", col = "steelblue", lwd = 2, lty = 2, n = 10 ^ 3)
curve(ft, lwd = 2, n = 10 ^ 3, add = TRUE)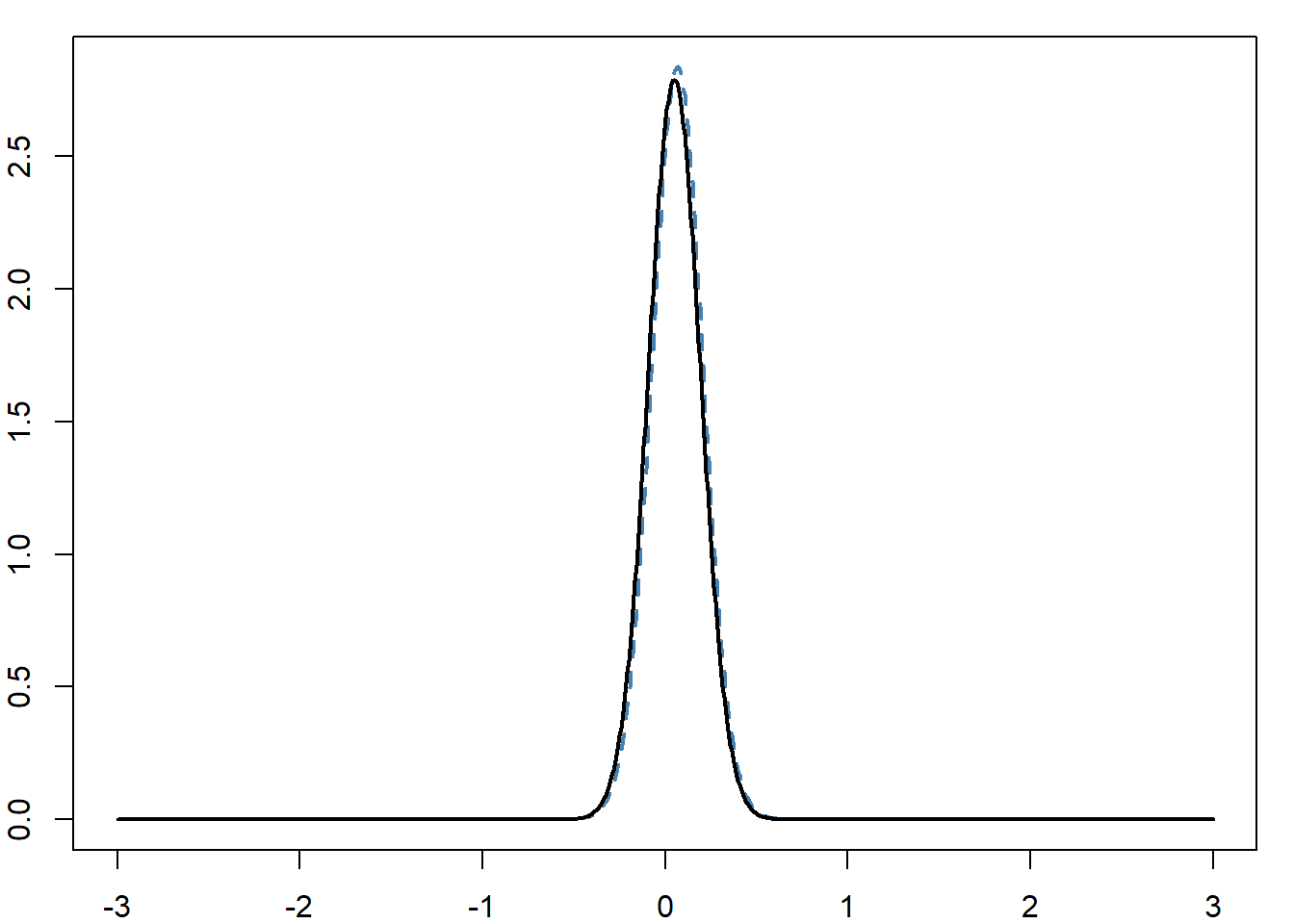

Εικόνα 4.10: Σύγκριση της posterior πυκνότητας (μαύρη συνεχής καμπύλη) της παραμέτρου θέσης της Cauchy βασισμένη σε 101 παρατηρήσεις και μία προσέγγιση της t (μπλε διακεκομμένη καμπύλη).

Όπως είναι αναμενόμενο, η στοχαστική εκτίμηση μέσω της Student συγκλίνει ταχύτερα από την αντίστοιχη μέσω ομοιόμορφης, όπως φαίνεται και στην εικόνα 4.11, όπου συγκρίνονται τα εύρη των δύο προσεγγίσεων, κατασκευασμένα από 100 μονοπατια κάθε μεθόδου.

m <- 10 ^ 3
unisan <- matrix(f(runif(500 * m, -5, 5)), ncol = 500)
causan <- matrix(f(rt(500 * m, df = dft) * rcau + mcau), ncol = 500)
unimax <- apply(unisan, 2, cummax)[10:m, ]
caumax <- apply(causan, 2, cummax)[10:m, ]
plot(caumax[ , 1], col = "white", ylim = c(0, max(unimax)), ylab = "Range")
polygon(c(10:m, m:10), c(apply(unimax, 1, max), rev(apply(unimax, 1, min))), col = "grey")
polygon(c(10:m, m:10), c(apply(caumax, 1, max), rev(apply(caumax, 1, min))), col = "wheat")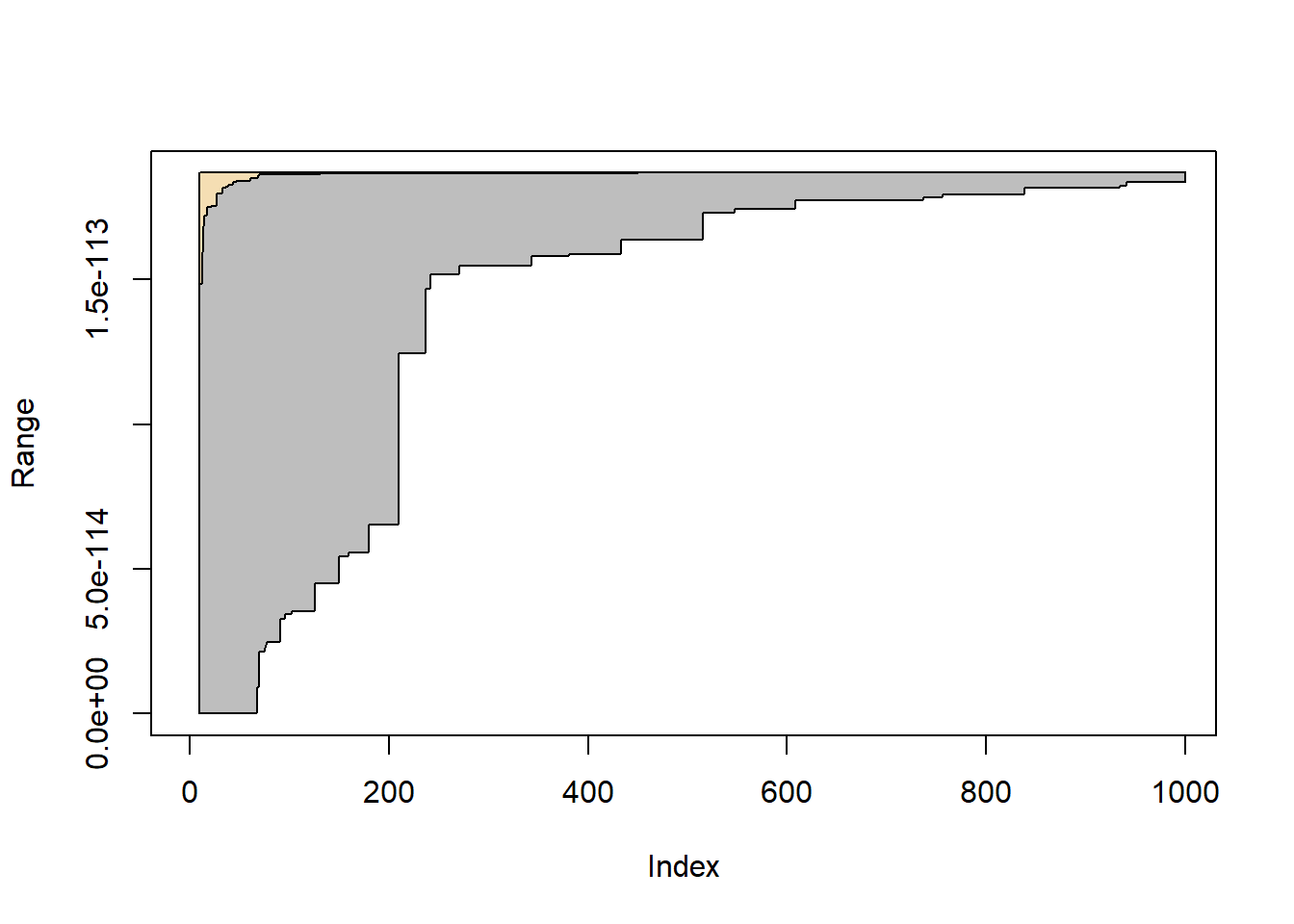

Εικόνα 4.11: Σύγκριση της στοχαστικής βελτιστοποίησης της ΕΜΠ της Cauchy βασισμένη σε 500 ανεξάρτητα μονοπάτια της ομοιόμορφης και της Student. Η γκρι περιοχή είναι το εύρος της ομοιόμορφης εκτιμήτριας και η πορτοκαλί περιοχή είναι το εύρος της εκτιμήτριας Student.

Παράδειγμα 4.7 Ελαχιστοποιήστε τη συνάρτηση \[\begin{equation*} f(x,y) = (x\sin(20y) +y\sin(20x))^2cosh(sin(10x)x) + (x\cos(10y)-y\sin(10x))^2cosh(cos(20y)y), \end{equation*}\] στο \(\mathbb{R}\), η οποία έχει ολικό μέγιστο \(f(0,0)=0\).

Λύση:

Όπως φαίνεται στην εικόνα 4.12, η συνάρτηση αυτή δεν πληροί τις προϋποθέσεις των αριθμητικών μεθόδων που εξετάσαμε. Μπορούμε όμως να προσομοιώσουμε από την σ.π.π. που είναι ανάλογη της \(e^{-f(x,y)}\), με τον αλγόριθμο αποδοχής - απόρριψης προτείνοντας από την ομοιόμορφη κατανομή. Κάτι τέτοιο όμως, έρχεται σε αντιπαράθεση με το να επιδιώξουμε προσομοίωση από την \(f\) για να αποφύγουμε την ομοιόμορφη κατανομή. Θα δούμε στη συνέχεια πιο εξειδικευμένες μεθόδους MCMC που επιλύουν αυτό το πρόβλημα.

f <- function(x){
  - (x[1] * sin(20 * x[2]) + x[2] * sin(20 * x[1])) ^ 2 * cosh(sin(10 * x[1]) * x[1])
  - (x[1] * cos(10 * x[2]) - x[2] * sin(10 * x[1])) ^ 2 * cosh(cos(20 * x[2]) * x[2])
}

x <- y <- seq(-3, 3, le = 435)
z <- - outer(x, y, function(x, y){ apply(X = cbind(x, y), 1, FUN = f) })
par(bg = "wheat", mar = c(1, 1, 1, 1))
persp(x, y, z, theta = 155, phi = 30, col = "green4", ltheta = -120, shade = 0.75, border = NA, box = FALSE)

Εικόνα 4.12: Τρισδιάστατο Γράφημα της \(f(x,y)\) στο \([-3, 3]^2\).

4.4 Stochastic Gradient Descent / Ascent

Σε πολλές περιπτώσεις η άμεση προσομοίωση από την \(H\) είναι ιδιαίτερα δύσκολη, κάτι που μας οδηγεί στην ανάγκη να εξερευνήσουμε τον χώρο \(\Theta\) όχι τυχαία, αλλά με εξαρτημένα βήματα, ορίζοντας δηλαδή μία ακολουθία \(\{\theta_j\}_{j\in\mathbb{N}}\) και κινούμενοι από το \(\theta_j\) στο \(\theta_{j+1}\). Η εξάρτηση του \(\theta_{j+1}\) στο \(\theta_{j}\) συχνά επιλέγεται να είναι γραμμική, κάτι που μας δίνει την αναπαράσταση \[\begin{equation*} \theta_{j+1}=\theta_{j}+\epsilon_j, \end{equation*}\] όπου το \(\epsilon_j\) είναι ένας (μικρός) θόρυβος της παρούσας τιμής (τα \(\epsilon_i, \epsilon_j\) είναι ανεξάρτητες τ.μ. για \(i\neq j\)). Από την παραπάνω σχέση μπορούμε άμεσα να επαληθεύσουμε ότι η \(\{\theta_j\}_{j\in\mathbb{N}}\) είναι μία μαρκοβιανή αλυσίδα. Η κατανομή των \(\epsilon_j\) μπορεί να προσομοιωθεί από οποιαδήποτε κατανομή, όπως η \(\mathcal{N}_p(0_p, \sigma^2 I_p)\) αν \(\Theta\subset \mathbb{R}^p\). Παρ’ όλα αυτά, καθώς αναζητούμε το μέγιστο της \(h\), η χρήση κάποιας πληροφορίας σχετικής με την \(h\) στην επιλογή της κατανομής των \(\epsilon_j\), αναμένεται να αυξήσει την αποδοτικότητα του αλγορίθμου. Συγκεκριμένα, είναι λογικό να προτιμάμε κατευθύνσεις στις οποίες η \(h\) αυξάνεται και να αποφεύγουμε κατευθύνσεις στις οποίες η \(h\) μειώνεται (χωρίς τέτοιες κινήσεις να είναι αδύνατες, ώστε να μην παγιδευτούμε σε τοπικά μέγιστα). Μια λογική επιλογή είναι να χρησιμοποιήσουμε την κλίση \(\nabla h\), εάν αυτό είναι διαθέσιμο. Οι στοχαστικές μέθοδοι απότομης κατάβασης/ανάβασης (stochastic gradient descent/ascent) εκμεταλλεύονται τη ντετερμινιστική εκδοχή των μεθόδων για να χτίσουν τον θόρυβο \(\epsilon_j\).

Η παραλλαγή της πεπερασμένης διαφοράς προτείνει να αντικαταστήσουμε την κλίση με το \[\begin{equation*} \nabla h(\theta_j) \approx \frac{h(\theta_j+\beta_j\zeta_j)-h(\theta_j-\beta_j\zeta_j)}{2\beta_j}\zeta_j = \frac{\Delta h(\theta_j, \beta_j \zeta_j)}{2\beta_j}\zeta_j, \end{equation*}\] όπου η \((\beta_j)\) είναι μία φθίνουσα ακολουθία και η \(\zeta_j\) είναι ομοιόμορφα κατανεμημένη στην μοναδιαία σφαίρα (\(||\zeta||=1\)). Σε αντίθεση με τη ντετερμινιστική προσέγγιση, η ανανέωση του \(\theta\) \[\begin{equation*} \theta_{j+1}=\theta_j + a_j\nabla h(\theta_j)\approx\theta_j +\frac{a_j}{2\beta_j}\Delta h(\theta_j, \beta_j, \zeta_j) \zeta_j \end{equation*}\]

δεν προχωράει πάνω στην πιο απότομη κατεύθυνση της \(h\) στο \(\theta_j\) αφού κάθε φορά η κατεύθυνση τυχαία, αλλά αυτή η ιδιότητα μπορεί δυνητικά να λειτουργήσει θετικά, καθώς αποφεύγουμε να παγιδευτούμε σε τοπικά μέγιστα ή σαγματικά σημεία. Το αν η \(\{\theta_j\}_{j\in\mathbb{N}}\) συγκλίνει στο σημείο ολικού μεγίστου \(\theta^\star\) εξαρτάται από την επιλογή των ακολουθιών \(\{a_j\}_{j\in\mathbb{N}}\) και \(\{\beta_j\}_{j\in\mathbb{N}}\). Τα \(a_j\) πρέπει να φθίνουν αρκετά αργά στο 0 ώστε η σειρά \(\sum_j a_j\) να αποκλίνει, ενώ τα \(\beta_j\) πρέπει να φθίνουν ακόμα πιο αργά ώστε η σειρά \(\sum_k (a_j/\beta_j)^2\) να συγκλίνει (Spall, 2003, Chapter 6).

Ο παρακάτω κώδικας αποτελεί μία υλοποίηση της μεθόδου:

# Stochastic Gradient Descent
sgd <- function(f, a, b, x0 = c(0, 0), descent = TRUE, maxdiff = 1, tol = 1e-7) {
  
  # Initialize
  x <- matrix(NA, ncol = length(x0))
  x[1, ] <- x0
  fx <- f(x0)
  dif <- k <- alpha <- beta <- 1
  
  while (dif > tol) {
    
    # Random Direction
    zeta <- rnorm(length(x0))
    zeta <- zeta / sqrt(sum(zeta ^ 2))
    
    # Gradient
    grad <- alpha * zeta * (f(x[k, ] + beta * zeta) - f(x[k, ] - beta * zeta)) / (2 * beta)
    
    # Safety condition
    dif <- sqrt(sum(grad ^ 2))
    if (dif < maxdiff) {
      # Update
      if (descent) {
        x <- rbind(x, x[k, ] - grad)
      } else {
        x <- rbind(x, x[k, ] + grad)
      }
      fx <- c(fx, f(x[k, ]))
      k <- k + 1
      alpha <- a(k)
      beta <- b(k) 
    }
  }
  cbind(x, fx)
}

# Plot Stochastic Gradient Descent
plot_sgd <- function(a, b, labs = c(-1, 1), col = "blue", nlevels = 10, ...) {
  
  # Execute the algorithm
  path <- sgd(f, a, b, ...)
  nmax <- nrow(path)
  
  # Create a plot
  set.seed(141)
  x <- y <- seq(labs[1], labs[2], le = 435)
  z <- outer(x, y, function(x, y){ apply(X = cbind(x, y), 1, FUN = f) })
  image(x, y, z)
  contour(x, y, z, nlevels = nlevels, add = TRUE)

  # Add the trajectory
  lines(path[, 1:2], lwd = 2, col = col)
  points(path[1, 1], path[1, 2], col = col, pch = 19)
  points(path[nmax, 1], path[nmax, 2], col = "black", pch = 19)
  title(main = paste0("f(", format(path[nmax, 1], dig = 4), ", ", format(path[nmax, 2], dig = 4), ") = ", format(f(path[nmax, 1:2]), dig = 4)))  
}

Παράδειγμα 4.8 Θεωρούμε τα σημεία στο επίπεδο \[ (a_1,b_1) = (1,2),\quad (a_2,b_2) = (2,1),\quad (a_3,b_3) = (3,4),\quad (a_4,b_4) = (4,3). \]

και ορίζουμε τη συνάρτηση \[ f(x,y) = \frac{1}{4} \sum_{i=1}^4 f_i(x,y), \quad \text{όπου} \quad f_i(x,y) = -\big[(x-a_i)^2 + (y-b_i)^2\big]. \]

Δείξτε ότι η \(f(x,y)\) είναι κοίλη και βρείτε αναλυτικά το σημείο \((x^\ast,y^\ast)\) που μεγιστοποιεί την \(f\).Υπολογίστε το ανάδελτα (gradient) της \(f_i(x,y)\), δηλαδή το διάνυσμα \(\nabla f_i(x,y)\), και γράψτε τον τύπο ενημέρωσης της στοχαστικής μεθόδου απότομης ανάβασης (stochastic gradient ascent) πεπερασμένης διαφοράς για τη μεγιστοποίηση της \(f\). Τέλος, υλοποιήστε τη μεγιστοποίηση στην R, με αρχικό σημείο \((x_0,y_0)=(0,0)\) και διαφορετικές ακολουθίες \(\{a_j\}_{j\in\mathbb{N}}\) και \(\{\beta_j\}_{j\in\mathbb{N}}\):

1. \(a_j=1/\log (j+1), \beta_j=1/\log (j+1)^{0.1}\),
2. \(a_j=1/100\log (j+1), \beta_j=1/\log (j+1)^{0.1}\),
3. \(a_j=1/(j+1), \beta_j=1/(j+1)^{0.5}\),
4. \(a_j=1/(j+1), \beta_j=1/(j+1)^{0.1}\).

Λύση:

Γράφουμε τη συνάρτηση \[ f(x,y) = \frac{1}{4}\sum_{i=1}^4 -\big[(x-a_i)^2 + (y-b_i)^2\big] = -\frac{1}{4}\sum_{i=1}^4 (x-a_i)^2 - \frac{1}{4}\sum_{i=1}^4 (y-b_i)^2. \]

Κάθε όρος \((x-a_i)^2\) είναι κυρτή συνάρτηση του \(x\), άρα ο όρος \(-(x-a_i)^2\) είναι κοίλη. Το άθροισμα κοίλων συναρτήσεων είναι κοίλο, και ο πολλαπλασιασμός με θετική σταθερά \(\frac{1}{4}\) διατηρεί την κοίλη μορφή. Άρα \(f(x,y)\) είναι κοίλη συνάρτηση ως προς \((x,y)\), δηλαδή έχει μοναδικό ολικό μέγιστο.

Υπολογίζουμε το ανάδελτα της \(f\): \[ \nabla f(x,y) = \begin{pmatrix} \frac{\partial f}{\partial x} \\ \frac{\partial f}{\partial y} \end{pmatrix}. \]

Αρχικά, \[ f_i(x,y) = -\big[(x-a_i)^2 + (y-b_i)^2\big], \] άρα \[ \frac{\partial f_i}{\partial x} = -2(x-a_i), \qquad \frac{\partial f_i}{\partial y} = -2(y-b_i). \] Επομένως \[ \frac{\partial f}{\partial x} = \frac{1}{4}\sum_{i=1}^4 \frac{\partial f_i}{\partial x} = \frac{1}{4}\sum_{i=1}^4 -2(x-a_i) = -\frac{1}{2}\left(4x - \sum_{i=1}^4 a_i \right), \] \[ \frac{\partial f}{\partial y} = \frac{1}{4}\sum_{i=1}^4 \frac{\partial f_i}{\partial y} = \frac{1}{4}\sum_{i=1}^4 -2(y-b_i) = -\frac{1}{2}\left(4y - \sum_{i=1}^4 b_i \right). \]

Για το μέγιστο θέτουμε το ανάδελτα ίσο με μηδέν: \[ \frac{\partial f}{\partial x} = 0 \;\Rightarrow\; -\frac{1}{2}\left(4x - \sum_{i=1}^4 a_i \right) = 0 \;\Rightarrow\; x = \frac{1}{4}\sum_{i=1}^4 a_i, \] \[ \frac{\partial f}{\partial y} = 0 \;\Rightarrow\; -\frac{1}{2}\left(4y - \sum_{i=1}^4 b_i \right) = 0 \;\Rightarrow\; y = \frac{1}{4}\sum_{i=1}^4 b_i. \]

Στο συγκεκριμένο αριθμητικό παράδειγμα: \[ \sum_{i=1}^4 a_i = 1+2+3+4 = 10 \quad \Rightarrow \quad x^\ast = \frac{10}{4} = 2.5, \] \[ \sum_{i=1}^4 b_i = 2+1+4+3 = 10 \quad \Rightarrow \quad y^\ast = \frac{10}{4} = 2.5. \]

Άρα το μοναδικό παγκόσμιο μέγιστο είναι \[ (x^\ast, y^\ast) = (2.5,\; 2.5). \]

Για κάθε \(i\) έχουμε \[ \nabla f_i(x,y) = \begin{pmatrix} \frac{\partial f_i}{\partial x} \\ \frac{\partial f_i}{\partial y} \end{pmatrix} = \begin{pmatrix} -2(x-a_i) \\ -2(y-b_i) \end{pmatrix}. \]

Στη στοχαστική μέθοδο απότομης ανάβασης (stochastic gradient ascent), σε κάθε επανάληψη \(k\) βρισκόμαστε στο \(\theta_j = (x_j, y_j)\), επιλέγουμε τυχαία μία κατεύθυνση \(\zeta_j\) και ενημερώνουμε:

\[\begin{equation*} \theta_{j+1}=\theta_j + a_j\nabla h(\theta_j)\approx\theta_j +\frac{a_j}{2\beta_j}\Delta h(\theta_j, \beta_j, \zeta_j) \zeta_j. \end{equation*}\]

Προκύπτει ότι: \[ x_{k+1} = x_k + \alpha_k\big[-2(x_k - a_{i_k})\big] = x_k - 2\alpha_k(x_k - a_{i_k}), \] \[ y_{k+1} = y_k + \alpha_k\big[-2(y_k - b_{i_k})\big] = y_k - 2\alpha_k(y_k - b_{i_k}). \]

Παρακάτω δίνεται κώδικας για τη στοχαστική μέθοδο με αρχικό σημείο \((x_0,y_0)=(0,0)\) για τις διαφορετικές ακολουθίες.

f <- function(x) {
  - ((x[1] - 1) ^ 2 + (x[2] - 2) ^ 2 + (x[1] - 2) ^ 2 + (x[2] - 1) ^ 2 +
    (x[1] - 3) ^ 2 + (x[2] - 4) ^ 2 + (x[1] - 4) ^ 2 + (x[2] - 3) ^ 2 )
}

# Plot 1
a <- function(iter) { 1 / log(iter + 1) }
b <- function(iter) { 1 / log(iter + 1) ^ 0.1 }
plot_sgd(a, b, x0 = c(0, 0), labs = c(-2, 6), col = "blue", descent = FALSE)

# Plot 2
a <- function(iter) { 1 / (100 * log(iter + 1)) }
b <- function(iter) { 1 / log(iter + 1) ^ 0.1 }
plot_sgd(a, b, x0 = c(0, 0), labs = c(-2, 6), col = "red", descent = FALSE)

# Plot 3
a <- function(iter) { 1 / (iter + 1) }
b <- function(iter) { 1 / (iter + 1) ^ 0.5 }
plot_sgd(a, b, x0 = c(0, 0), labs = c(-2, 6), col = "brown", descent = FALSE)

# Plot 4
a <- function(iter) { 1 / (iter + 1) }
b <- function(iter) { 1 / (iter + 1) ^ 0.1 }
plot_sgd(a, b, x0 = c(0, 0), labs = c(-2, 6), col = "purple", descent = FALSE)

Εικόνα 4.13: Πραγματοποιήσεις της στοχαστικής μεθόδου απότομης κατάβασης με τέσσερις διαφορετικές επιλογές ακολουθιών \(a_j\) και \(\beta_j\), έχοντας το ίδιο σημείο εκκίνησης (0, 0): Το ελάχιστο της \(f\) επιτυγχάνεται στο σημείο (2.5, 2.5).

Παράδειγμα 4.9 Εφαρμόστε τη στοχαστική μέθοδο απότομης κατάβασης στη συνάρτηση \[\begin{equation*} f(x,y) = (x\sin(20y) +y\sin(20x))^2cosh(sin(10x)x) + (x\cos(10y)-y\sin(10x))^2cosh(cos(20y)y), \end{equation*}\] με διαφορετικές ακολουθίες \(\{a_j\}_{j\in\mathbb{N}}\) και \(\{\beta_j\}_{j\in\mathbb{N}}\):

1. \(a_j=1/\log (j+1), \beta_j=1/\log (j+1)^{0.1}\),
2. \(a_j=1/100\log (j+1), \beta_j=1/\log (j+1)^{0.1}\),
3. \(a_j=1/(j+1), \beta_j=1/(j+1)^{0.5}\),
4. \(a_j=1/(j+1), \beta_j=1/(j+1)^{0.1}\).

Λύση:

Ένας λογικός κανόνας τερματισμού του αλγορίθμου είναι να ελέγχουμε τη σταθεροποίηση της ακολουθίας \(\theta_j\). Σε αυτό το σημείο, παρατηρούμε ότι η ακολουθία των \(b_j\) φθίνει πολύ πιο αργά από την ακολουθία των \(a_j\) σε όλα τα σενάρια. Για ακολουθίες \(\{\beta_j\}_{j\in\mathbb{N}}\) που φθίνουν ταχύτερα, η μέθοδος δεν συγκλίνει απαραίτητα στο ολικό ελάχιστο. Η εικόνα 4.14 παρουσιάζει μία πραγματοποίηση κάθε σεναρίου. Στην περίπτωση του σεναρίου 1, τα \(\theta_j\) δε σταθεροποιούνται αρκετά γρήγορα ώστε να παραμείνουν στο ολικό ελάχιστο, ενώ διαιρώντας την \(a_j\) με το 100 (οπότε τα \(a_j\) και τα \(b_j\) φθίνουν πολύ αργά) οδηγεί σε μία ακολουθία \(\{\theta_j\}_{j\in\mathbb{N}}\) που αδυνατεί να φτάσει το ολικό ελάχιστο. Για τα σενάρια 3 και 4 παρατηρούμε ότι εντοπίζουν το ολικό ελάχιστο και η διαφορά στον εκθέτη των \(b_j\) δεν επηρεάζει σημαντικά το αποτέλεσμα.

f <- function(x){
  (x[1] * sin(20 * x[2]) + x[2] * sin(20 * x[1])) ^ 2 * cosh(sin(10 * x[1]) * x[1])
  + (x[1] * cos(10 * x[2]) - x[2] * sin(10 * x[1])) ^ 2 * cosh(cos(20 * x[2]) * x[2])
}

# Plot 1
a <- function(iter) { 1 / log(iter + 1) }
b <- function(iter) { 1 / log(iter + 1) ^ 0.1 }
plot_sgd(a, b, x0 = c(0.65, 0.8), col = "blue")

# Plot 2
a <- function(iter) { 1 / (100 * log(iter + 1)) }
b <- function(iter) { 1 / log(iter + 1) ^ 0.1 }
plot_sgd(a, b, x0 = c(0.65, 0.8), col = "red")

# Plot 3
a <- function(iter) { 1 / (iter + 1) }
b <- function(iter) { 1 / (iter + 1) ^ 0.5 }
plot_sgd(a, b, x0 = c(0.65, 0.8), col = "brown")

# Plot 4
a <- function(iter) { 1 / (iter + 1) }
b <- function(iter) { 1 / (iter + 1) ^ 0.1 }
plot_sgd(a, b, x0 = c(0.65, 0.8), col = "purple")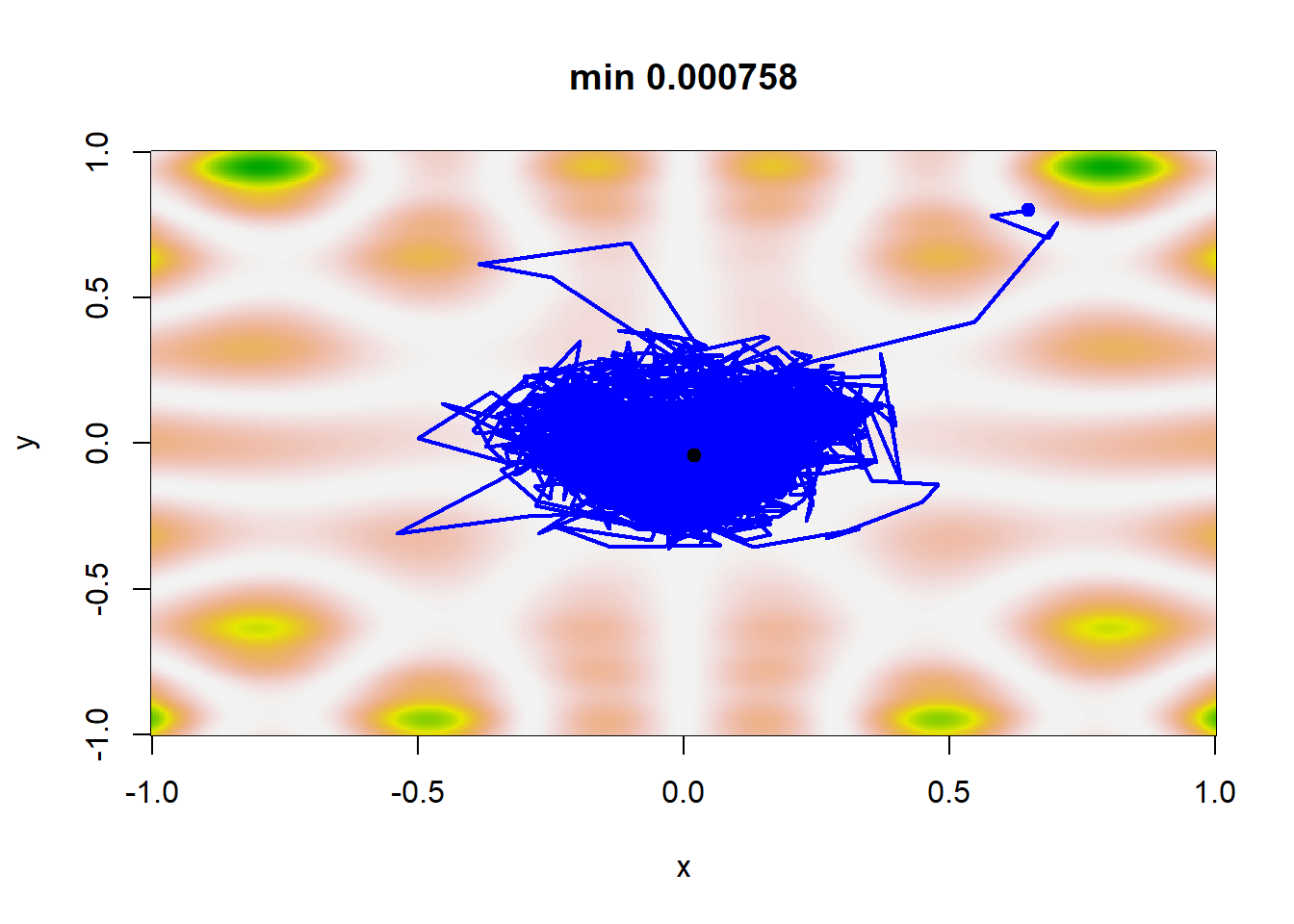

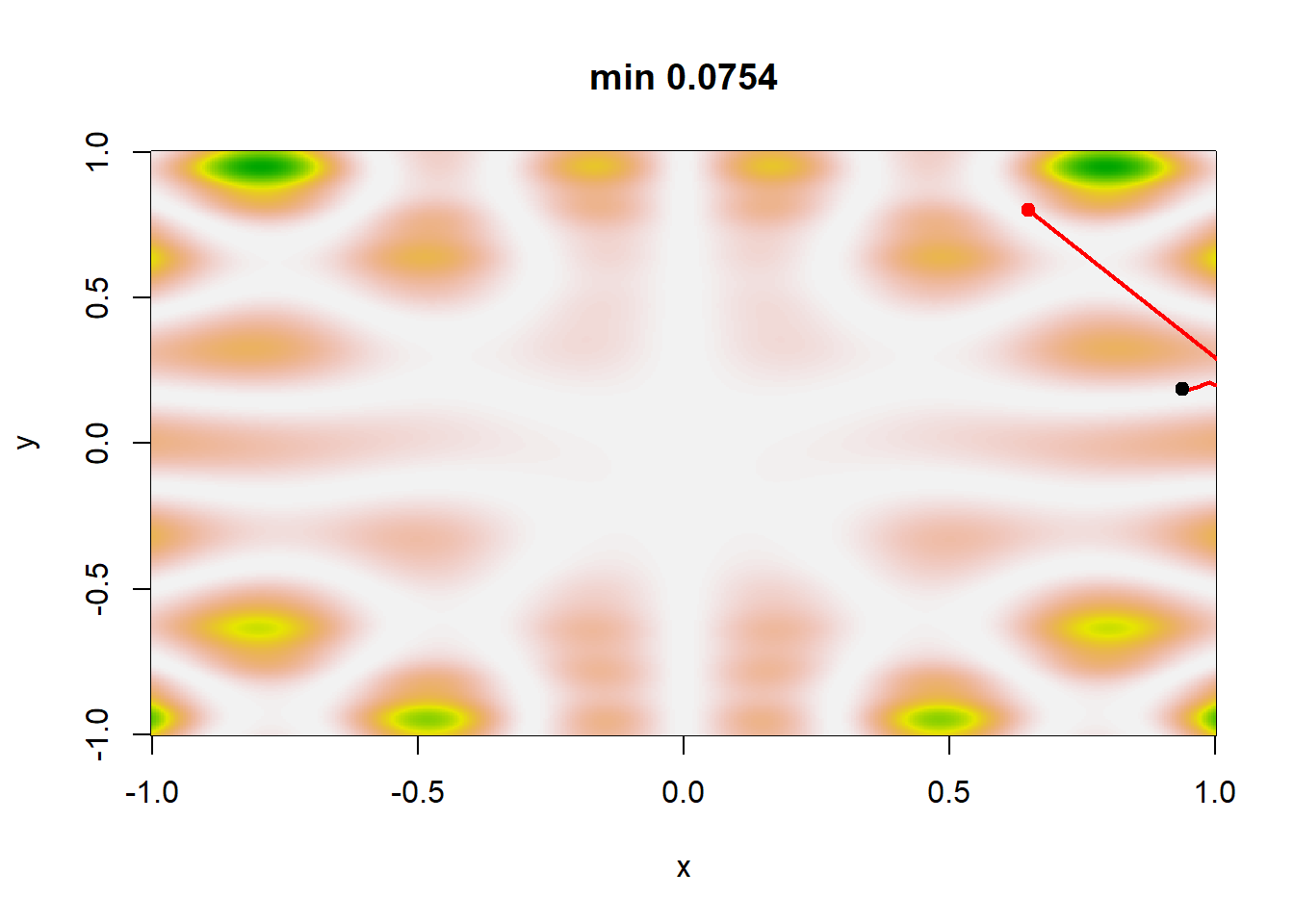
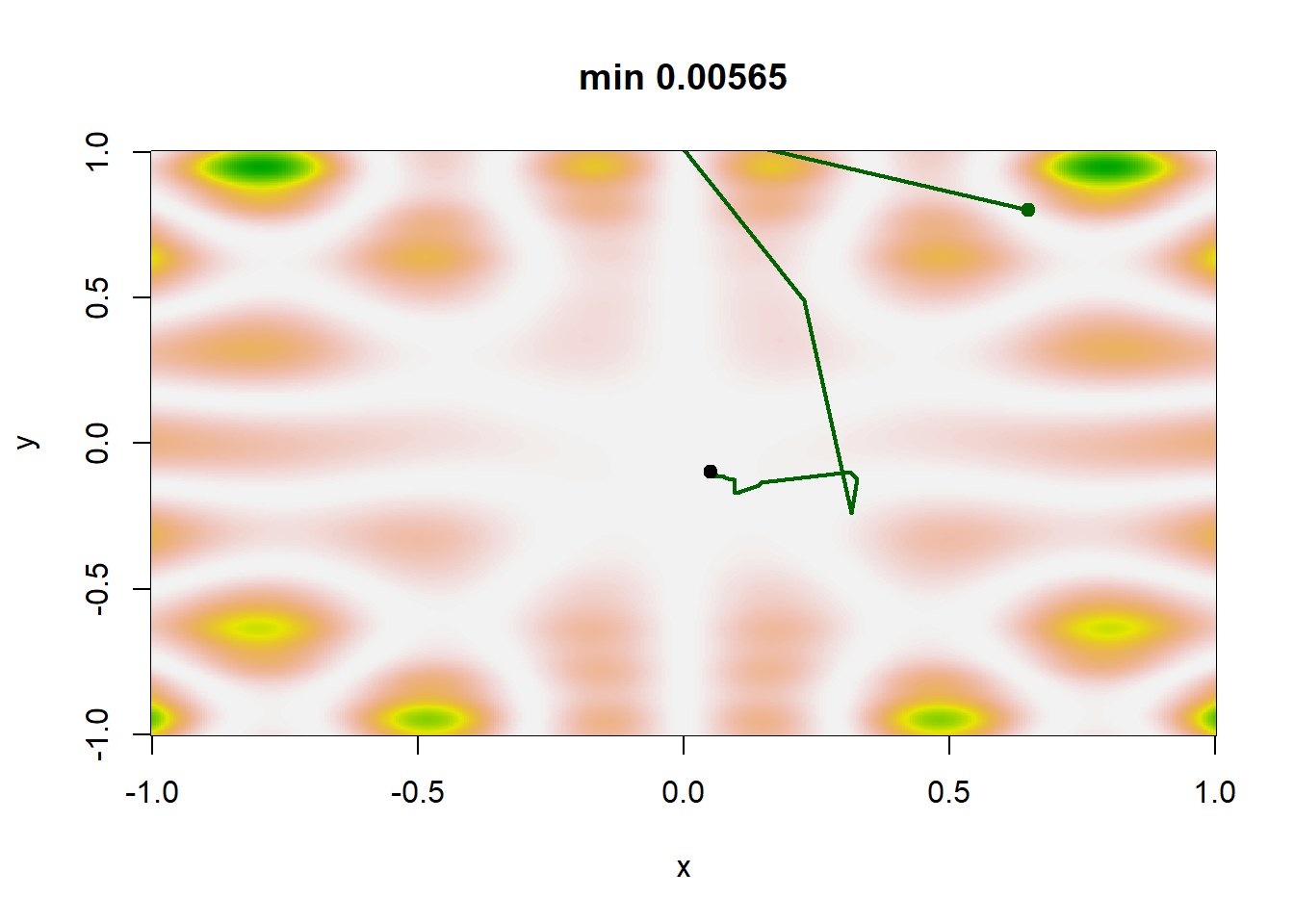
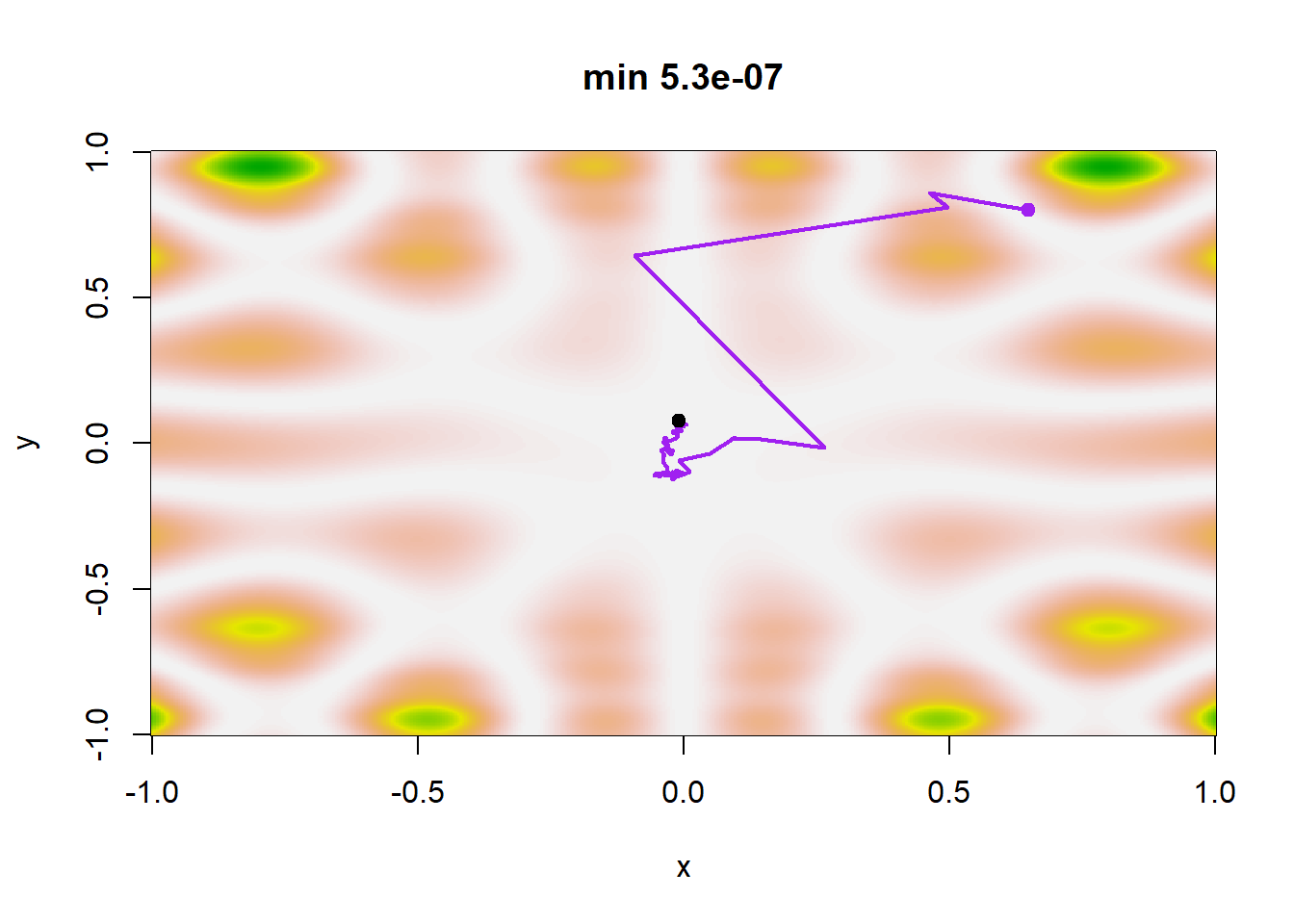
Εικόνα 4.14: Πραγματοποιήσεις της στοχαστικής μεθόδου απότομης κατάβασης με τέσσερις διαφορετικές επιλογές ακολουθιών \(a_j\) και \(\beta_j\), έχοντας το ίδιο σημείο εκκίνησης (0.65, 0.8): Το ελάχιστο της \(f\) επιτυγχάνεται στο σημείο (0, 0).

4.5 Simulated Annealing

Ο αλγόριθμος Simulated Annealing (προσομοιωμένη ανόπτηση) είναι μία στοχαστική μέθοδος βελτιστοποίησης, εμπνευσμένη από τη φυσική διεργασία της ανόπτησης μετάλλων. Η βασική ιδέα είναι ότι, όπως ένα υλικό θερμαίνεται και στη συνέχεια ψύχεται αργά ώστε να αποφύγει «κακές» κρυσταλλικές δομές και να καταλήξει σε μια σχεδόν ιδανική διάταξη χαμηλής ενέργειας, έτσι και ο αλγόριθμος επιτρέπει τυχαίες μετακινήσεις στη χωρική περιοχή των παραμέτρων, αποδεχόμενος κάποιες χειρότερες λύσεις με ελεγχόμενο τρόπο, ώστε να αποφύγει τοπικά ελάχιστα.

Έστω ότι θέλουμε να μεγιστοποιήσουμε μια συνάρτηση \(h(\theta)\). Στο βήμα \(t\) βρισκόμαστε σε μία τρέχουσα λύση \(\theta_t\) και εξετάζουμε μια νέα υποψήφια λύση προσθέτοντας ένα τυχαίο διάνυσμα μεταβολής \(\zeta\), το οποίο ακολουθεί κάποια κατανομή πρότασης \(F\). Η αποδοχή ή απόρριψη αυτής της νέας λύσης ελέγχεται από μία θερμοκρασία \(T_t\), η οποία φθίνει με τον χρόνο και ρυθμίζει το πόσο “τολμηρές” είναι οι τυχαίες μεταβάσεις.

Συνοπτικά, ο αλγόριθμος μπορεί να περιγραφεί ως εξής:

1. Ξεκινάμε με ένα αρχικό σημείο \(\theta_0\).
2. Προσομοιώνουμε \(\zeta\sim F\);
3. Δεχόμαστε \(\theta_{t+1}=\theta_t+\zeta\) με πιθανότητα \(p_t=min\{e^{\Delta h_t/T_t}, 1\}\), αλλιώς παίρνουμε \(\theta_{t+1}=\theta_t\).
4. Επαναλαμβάνουμε τα βήματα 2. και 3. μέχρι να εκπληρωθεί κάποιο κριτήριο τερματισμού.

Εδώ το \(\Delta h_t\) συμβολίζει τη μεταβολή της συνάρτησης \(h\) κατά τη μετάβαση από \(\theta_t\) σε \(\theta_t + \zeta\). Όταν η νέα λύση είναι καλύτερη, (\(\Delta h_t > 0\)), γίνεται πάντα δεκτή. Όταν είναι χειρότερη (\(\Delta h_t < 0\)), γίνεται δεκτή μόνο με μια πιθανότητα που μειώνεται εκθετικά ως προς τη διαφορά και την τρέχουσα θερμοκρασία \(T_t\). Καθώς η θερμοκρασία μειώνεται, ο αλγόριθμος γίνεται πιο “συντηρητικός” και τελικά σταθεροποιείται κοντά σε μία βέλτιστη λύση.

Ο παρακάτω κώδικας αποτελεί μία υλοποίηση του αλγορίθμου στην R:

sa <- function(f, # objective function
               x0, # starting point (numeric vector)
               T0 = 1, # initial temperature
               max_k = 1000, # max iterations
               g = function(x) {rnorm(length(x), mean = 0, sd = 0.1)}, # simulation function
               cooling = function(k, T0) {T0 * 0.99 ^ k}, # geometric cooling factor
               minimize = TRUE, 
               show_progress = TRUE) { # show progress bar
  
  # Initialize
  x <- matrix(NA, nrow = max_k + 1, ncol = length(x0))
  y <- numeric(length = max_k + 1)
  x_best <- x[1, ] <- x0
  y_best <- y[1] <- f(x0)
  
  Tk <- T0
  
  # create progress bar
  if (show_progress) {
    pb <- txtProgressBar(min = 0, max = max_k, style = 3)
  }
  
  for (k in 1:max_k) {
    # Propose a new point: Gaussian perturbation
    x_new <- x[k, ] + g(x[k, ])
    y_new <- f(x_new)
    
    # Change in objective
    if (minimize) {
      delta <- y_new - y[k]
    } else {
      delta <- y[k] - y_new
    }
    
    # Acceptance probability
    accept <- (runif(1) < exp(- delta / Tk))
    
    if (accept) {
      x[k + 1, ] <- x_new
      y[k + 1] <- y_new
      
      # Track best solution
      if ((y_new < y_best & minimize) || (y_new > y_best & !minimize)) {
        x_best <- x_new
        y_best <- y_new
      }
    } else {
      x[k + 1, ] <- x[k, ]
      y[k + 1] <- y[k]
    }
    
    # update progress bar
    if (show_progress) {
      setTxtProgressBar(pb, k)
    }
    
    # Cool down
    Tk <- cooling(k, T0)
    
  }
  
  # ensure bar ends and gets closed
  if (show_progress) {
    setTxtProgressBar(pb, max_k)
    close(pb)
  }
  
  list(x_best = x_best, y_best = y_best, x = x, y = y)
}

# Plot Simulated Annealing
plot_sa <- function(f, labs = c(-1, 1), col = "blue", nlevels = 10, ...) {
  
  # Execute the algorithm
  res <- sa(f, ...)
  path <- cbind(res$x, res$y)
  nmax <- nrow(path)
  
  # Create a plot
  set.seed(141)
  x <- y <- seq(labs[1], labs[2], le = 200)
  z <- outer(x, y, function(x, y){ apply(X = cbind(x, y), 1, FUN = f) })
  image(x, y, z)
  contour(x, y, z, nlevels = nlevels, add = TRUE)
  
  # Add the trajectory
  lines(path[, 1:2], lwd = 2, col = col)
  points(path[1, 1], path[1, 2], col = col, pch = 19)
  points(path[nmax, 1], path[nmax, 2], col = col, pch = 2)
  points(res$x_best[1], res$x_best[2], col = "black", pch = 19)
  title(main = paste0("f(", format(res$x_best[1], dig = 4), ", ", format(res$x_best[2], dig = 4), ") = ", format(res$y_best, dig = 4)))  
}

Παράδειγμα 4.10 Ελαχιστοποιήστε τη συνάρτηση \[ f(x, y)= (1 - x) ^ 2 + 100 (y - x ^ 2) ^ 2, \] χρησιμοποιώντας τον αλγόριθμο simulated annealing.

Λύση:

Μπορούμε εύκολα να επαληθεύσουμε ότι η συνάρτηση παρουσιάζει ολικό ελάχιστο το \(0\) στο σημείο \((1, 1)\).

f <- function(x) {
  x <- as.numeric(x)
  (1 - x[1]) ^ 2 + 100 * (x[2] - x[1] ^ 2) ^ 2
}

set.seed(123)
res <- sa(
  f = f,
  x0 = c(-2, -2),
  T0 = 1,
  max_k = 5000,
  show_progress = FALSE
)

res$x_best # estimated argmin - should be near (1, 1)
## [1] 1.001109 1.001898
res$y_best # estimated min
## [1] 1.155375e-05

# Run the SA and plot
set.seed(292)
plot_sa(f = f,
        x0 = c(-2, -2),
        T0 = 1,
        labs = c(-3, 3),
        g = function(x) {rnorm(length(x), mean = 0, sd = 0.1)},
               cooling = function(k, T0) {T0 * 0.99 ^ k},
        max_k = 5000)
##   |                                                                              |                                                                      |   0%  |                                                                              |                                                                      |   1%  |                                                                              |=                                                                     |   1%  |                                                                              |=                                                                     |   2%  |                                                                              |==                                                                    |   2%  |                                                                              |==                                                                    |   3%  |                                                                              |==                                                                    |   4%  |                                                                              |===                                                                   |   4%  |                                                                              |===                                                                   |   5%  |                                                                              |====                                                                  |   5%  |                                                                              |====                                                                  |   6%  |                                                                              |=====                                                                 |   6%  |                                                                              |=====                                                                 |   7%  |                                                                              |=====                                                                 |   8%  |                                                                              |======                                                                |   8%  |                                                                              |======                                                                |   9%  |                                                                              |=======                                                               |   9%  |                                                                              |=======                                                               |  10%  |                                                                              |=======                                                               |  11%  |                                                                              |========                                                              |  11%  |                                                                              |========                                                              |  12%  |                                                                              |=========                                                             |  12%  |                                                                              |=========                                                             |  13%  |                                                                              |=========                                                             |  14%  |                                                                              |==========                                                            |  14%  |                                                                              |==========                                                            |  15%  |                                                                              |===========                                                           |  15%  |                                                                              |===========                                                           |  16%  |                                                                              |============                                                          |  16%  |                                                                              |============                                                          |  17%  |                                                                              |============                                                          |  18%  |                                                                              |=============                                                         |  18%  |                                                                              |=============                                                         |  19%  |                                                                              |==============                                                        |  19%  |                                                                              |==============                                                        |  20%  |                                                                              |==============                                                        |  21%  |                                                                              |===============                                                       |  21%  |                                                                              |===============                                                       |  22%  |                                                                              |================                                                      |  22%  |                                                                              |================                                                      |  23%  |                                                                              |================                                                      |  24%  |                                                                              |=================                                                     |  24%  |                                                                              |=================                                                     |  25%  |                                                                              |==================                                                    |  25%  |                                                                              |==================                                                    |  26%  |                                                                              |===================                                                   |  26%  |                                                                              |===================                                                   |  27%  |                                                                              |===================                                                   |  28%  |                                                                              |====================                                                  |  28%  |                                                                              |====================                                                  |  29%  |                                                                              |=====================                                                 |  29%  |                                                                              |=====================                                                 |  30%  |                                                                              |=====================                                                 |  31%  |                                                                              |======================                                                |  31%  |                                                                              |======================                                                |  32%  |                                                                              |=======================                                               |  32%  |                                                                              |=======================                                               |  33%  |                                                                              |=======================                                               |  34%  |                                                                              |========================                                              |  34%  |                                                                              |========================                                              |  35%  |                                                                              |=========================                                             |  35%  |                                                                              |=========================                                             |  36%  |                                                                              |==========================                                            |  36%  |                                                                              |==========================                                            |  37%  |                                                                              |==========================                                            |  38%  |                                                                              |===========================                                           |  38%  |                                                                              |===========================                                           |  39%  |                                                                              |============================                                          |  39%  |                                                                              |============================                                          |  40%  |                                                                              |============================                                          |  41%  |                                                                              |=============================                                         |  41%  |                                                                              |=============================                                         |  42%  |                                                                              |==============================                                        |  42%  |                                                                              |==============================                                        |  43%  |                                                                              |==============================                                        |  44%  |                                                                              |===============================                                       |  44%  |                                                                              |===============================                                       |  45%  |                                                                              |================================                                      |  45%  |                                                                              |================================                                      |  46%  |                                                                              |=================================                                     |  46%  |                                                                              |=================================                                     |  47%  |                                                                              |=================================                                     |  48%  |                                                                              |==================================                                    |  48%  |                                                                              |==================================                                    |  49%  |                                                                              |===================================                                   |  49%  |                                                                              |===================================                                   |  50%  |                                                                              |===================================                                   |  51%  |                                                                              |====================================                                  |  51%  |                                                                              |====================================                                  |  52%  |                                                                              |=====================================                                 |  52%  |                                                                              |=====================================                                 |  53%  |                                                                              |=====================================                                 |  54%  |                                                                              |======================================                                |  54%  |                                                                              |======================================                                |  55%  |                                                                              |=======================================                               |  55%  |                                                                              |=======================================                               |  56%  |                                                                              |========================================                              |  56%  |                                                                              |========================================                              |  57%  |                                                                              |========================================                              |  58%  |                                                                              |=========================================                             |  58%  |                                                                              |=========================================                             |  59%  |                                                                              |==========================================                            |  59%  |                                                                              |==========================================                            |  60%  |                                                                              |==========================================                            |  61%  |                                                                              |===========================================                           |  61%  |                                                                              |===========================================                           |  62%  |                                                                              |============================================                          |  62%  |                                                                              |============================================                          |  63%  |                                                                              |============================================                          |  64%  |                                                                              |=============================================                         |  64%  |                                                                              |=============================================                         |  65%  |                                                                              |==============================================                        |  65%  |                                                                              |==============================================                        |  66%  |                                                                              |===============================================                       |  66%  |                                                                              |===============================================                       |  67%  |                                                                              |===============================================                       |  68%  |                                                                              |================================================                      |  68%  |                                                                              |================================================                      |  69%  |                                                                              |=================================================                     |  69%  |                                                                              |=================================================                     |  70%  |                                                                              |=================================================                     |  71%  |                                                                              |==================================================                    |  71%  |                                                                              |==================================================                    |  72%  |                                                                              |===================================================                   |  72%  |                                                                              |===================================================                   |  73%  |                                                                              |===================================================                   |  74%  |                                                                              |====================================================                  |  74%  |                                                                              |====================================================                  |  75%  |                                                                              |=====================================================                 |  75%  |                                                                              |=====================================================                 |  76%  |                                                                              |======================================================                |  76%  |                                                                              |======================================================                |  77%  |                                                                              |======================================================                |  78%  |                                                                              |=======================================================               |  78%  |                                                                              |=======================================================               |  79%  |                                                                              |========================================================              |  79%  |                                                                              |========================================================              |  80%  |                                                                              |========================================================              |  81%  |                                                                              |=========================================================             |  81%  |                                                                              |=========================================================             |  82%  |                                                                              |==========================================================            |  82%  |                                                                              |==========================================================            |  83%  |                                                                              |==========================================================            |  84%  |                                                                              |===========================================================           |  84%  |                                                                              |===========================================================           |  85%  |                                                                              |============================================================          |  85%  |                                                                              |============================================================          |  86%  |                                                                              |=============================================================         |  86%  |                                                                              |=============================================================         |  87%  |                                                                              |=============================================================         |  88%  |                                                                              |==============================================================        |  88%  |                                                                              |==============================================================        |  89%  |                                                                              |===============================================================       |  89%  |                                                                              |===============================================================       |  90%  |                                                                              |===============================================================       |  91%  |                                                                              |================================================================      |  91%  |                                                                              |================================================================      |  92%  |                                                                              |=================================================================     |  92%  |                                                                              |=================================================================     |  93%  |                                                                              |=================================================================     |  94%  |                                                                              |==================================================================    |  94%  |                                                                              |==================================================================    |  95%  |                                                                              |===================================================================   |  95%  |                                                                              |===================================================================   |  96%  |                                                                              |====================================================================  |  96%  |                                                                              |====================================================================  |  97%  |                                                                              |====================================================================  |  98%  |                                                                              |===================================================================== |  98%  |                                                                              |===================================================================== |  99%  |                                                                              |======================================================================|  99%  |                                                                              |======================================================================| 100%

# Run the SA and plot
set.seed(292)
plot_sa(f = f,
        x0 = c(-2, -2),
        T0 = 1,
        labs = c(-3, 3),
        g = function(x) {rnorm(length(x), mean = 0, sd = 0.3)},
               cooling = function(k, T0) {T0 * 0.99 ^ k},
        col = "red",
        max_k = 5000)
##   |                                                                              |                                                                      |   0%  |                                                                              |                                                                      |   1%  |                                                                              |=                                                                     |   1%  |                                                                              |=                                                                     |   2%  |                                                                              |==                                                                    |   2%  |                                                                              |==                                                                    |   3%  |                                                                              |==                                                                    |   4%  |                                                                              |===                                                                   |   4%  |                                                                              |===                                                                   |   5%  |                                                                              |====                                                                  |   5%  |                                                                              |====                                                                  |   6%  |                                                                              |=====                                                                 |   6%  |                                                                              |=====                                                                 |   7%  |                                                                              |=====                                                                 |   8%  |                                                                              |======                                                                |   8%  |                                                                              |======                                                                |   9%  |                                                                              |=======                                                               |   9%  |                                                                              |=======                                                               |  10%  |                                                                              |=======                                                               |  11%  |                                                                              |========                                                              |  11%  |                                                                              |========                                                              |  12%  |                                                                              |=========                                                             |  12%  |                                                                              |=========                                                             |  13%  |                                                                              |=========                                                             |  14%  |                                                                              |==========                                                            |  14%  |                                                                              |==========                                                            |  15%  |                                                                              |===========                                                           |  15%  |                                                                              |===========                                                           |  16%  |                                                                              |============                                                          |  16%  |                                                                              |============                                                          |  17%  |                                                                              |============                                                          |  18%  |                                                                              |=============                                                         |  18%  |                                                                              |=============                                                         |  19%  |                                                                              |==============                                                        |  19%  |                                                                              |==============                                                        |  20%  |                                                                              |==============                                                        |  21%  |                                                                              |===============                                                       |  21%  |                                                                              |===============                                                       |  22%  |                                                                              |================                                                      |  22%  |                                                                              |================                                                      |  23%  |                                                                              |================                                                      |  24%  |                                                                              |=================                                                     |  24%  |                                                                              |=================                                                     |  25%  |                                                                              |==================                                                    |  25%  |                                                                              |==================                                                    |  26%  |                                                                              |===================                                                   |  26%  |                                                                              |===================                                                   |  27%  |                                                                              |===================                                                   |  28%  |                                                                              |====================                                                  |  28%  |                                                                              |====================                                                  |  29%  |                                                                              |=====================                                                 |  29%  |                                                                              |=====================                                                 |  30%  |                                                                              |=====================                                                 |  31%  |                                                                              |======================                                                |  31%  |                                                                              |======================                                                |  32%  |                                                                              |=======================                                               |  32%  |                                                                              |=======================                                               |  33%  |                                                                              |=======================                                               |  34%  |                                                                              |========================                                              |  34%  |                                                                              |========================                                              |  35%  |                                                                              |=========================                                             |  35%  |                                                                              |=========================                                             |  36%  |                                                                              |==========================                                            |  36%  |                                                                              |==========================                                            |  37%  |                                                                              |==========================                                            |  38%  |                                                                              |===========================                                           |  38%  |                                                                              |===========================                                           |  39%  |                                                                              |============================                                          |  39%  |                                                                              |============================                                          |  40%  |                                                                              |============================                                          |  41%  |                                                                              |=============================                                         |  41%  |                                                                              |=============================                                         |  42%  |                                                                              |==============================                                        |  42%  |                                                                              |==============================                                        |  43%  |                                                                              |==============================                                        |  44%  |                                                                              |===============================                                       |  44%  |                                                                              |===============================                                       |  45%  |                                                                              |================================                                      |  45%  |                                                                              |================================                                      |  46%  |                                                                              |=================================                                     |  46%  |                                                                              |=================================                                     |  47%  |                                                                              |=================================                                     |  48%  |                                                                              |==================================                                    |  48%  |                                                                              |==================================                                    |  49%  |                                                                              |===================================                                   |  49%  |                                                                              |===================================                                   |  50%  |                                                                              |===================================                                   |  51%  |                                                                              |====================================                                  |  51%  |                                                                              |====================================                                  |  52%  |                                                                              |=====================================                                 |  52%  |                                                                              |=====================================                                 |  53%  |                                                                              |=====================================                                 |  54%  |                                                                              |======================================                                |  54%  |                                                                              |======================================                                |  55%  |                                                                              |=======================================                               |  55%  |                                                                              |=======================================                               |  56%  |                                                                              |========================================                              |  56%  |                                                                              |========================================                              |  57%  |                                                                              |========================================                              |  58%  |                                                                              |=========================================                             |  58%  |                                                                              |=========================================                             |  59%  |                                                                              |==========================================                            |  59%  |                                                                              |==========================================                            |  60%  |                                                                              |==========================================                            |  61%  |                                                                              |===========================================                           |  61%  |                                                                              |===========================================                           |  62%  |                                                                              |============================================                          |  62%  |                                                                              |============================================                          |  63%  |                                                                              |============================================                          |  64%  |                                                                              |=============================================                         |  64%  |                                                                              |=============================================                         |  65%  |                                                                              |==============================================                        |  65%  |                                                                              |==============================================                        |  66%  |                                                                              |===============================================                       |  66%  |                                                                              |===============================================                       |  67%  |                                                                              |===============================================                       |  68%  |                                                                              |================================================                      |  68%  |                                                                              |================================================                      |  69%  |                                                                              |=================================================                     |  69%  |                                                                              |=================================================                     |  70%  |                                                                              |=================================================                     |  71%  |                                                                              |==================================================                    |  71%  |                                                                              |==================================================                    |  72%  |                                                                              |===================================================                   |  72%  |                                                                              |===================================================                   |  73%  |                                                                              |===================================================                   |  74%  |                                                                              |====================================================                  |  74%  |                                                                              |====================================================                  |  75%  |                                                                              |=====================================================                 |  75%  |                                                                              |=====================================================                 |  76%  |                                                                              |======================================================                |  76%  |                                                                              |======================================================                |  77%  |                                                                              |======================================================                |  78%  |                                                                              |=======================================================               |  78%  |                                                                              |=======================================================               |  79%  |                                                                              |========================================================              |  79%  |                                                                              |========================================================              |  80%  |                                                                              |========================================================              |  81%  |                                                                              |=========================================================             |  81%  |                                                                              |=========================================================             |  82%  |                                                                              |==========================================================            |  82%  |                                                                              |==========================================================            |  83%  |                                                                              |==========================================================            |  84%  |                                                                              |===========================================================           |  84%  |                                                                              |===========================================================           |  85%  |                                                                              |============================================================          |  85%  |                                                                              |============================================================          |  86%  |                                                                              |=============================================================         |  86%  |                                                                              |=============================================================         |  87%  |                                                                              |=============================================================         |  88%  |                                                                              |==============================================================        |  88%  |                                                                              |==============================================================        |  89%  |                                                                              |===============================================================       |  89%  |                                                                              |===============================================================       |  90%  |                                                                              |===============================================================       |  91%  |                                                                              |================================================================      |  91%  |                                                                              |================================================================      |  92%  |                                                                              |=================================================================     |  92%  |                                                                              |=================================================================     |  93%  |                                                                              |=================================================================     |  94%  |                                                                              |==================================================================    |  94%  |                                                                              |==================================================================    |  95%  |                                                                              |===================================================================   |  95%  |                                                                              |===================================================================   |  96%  |                                                                              |====================================================================  |  96%  |                                                                              |====================================================================  |  97%  |                                                                              |====================================================================  |  98%  |                                                                              |===================================================================== |  98%  |                                                                              |===================================================================== |  99%  |                                                                              |======================================================================|  99%  |                                                                              |======================================================================| 100%

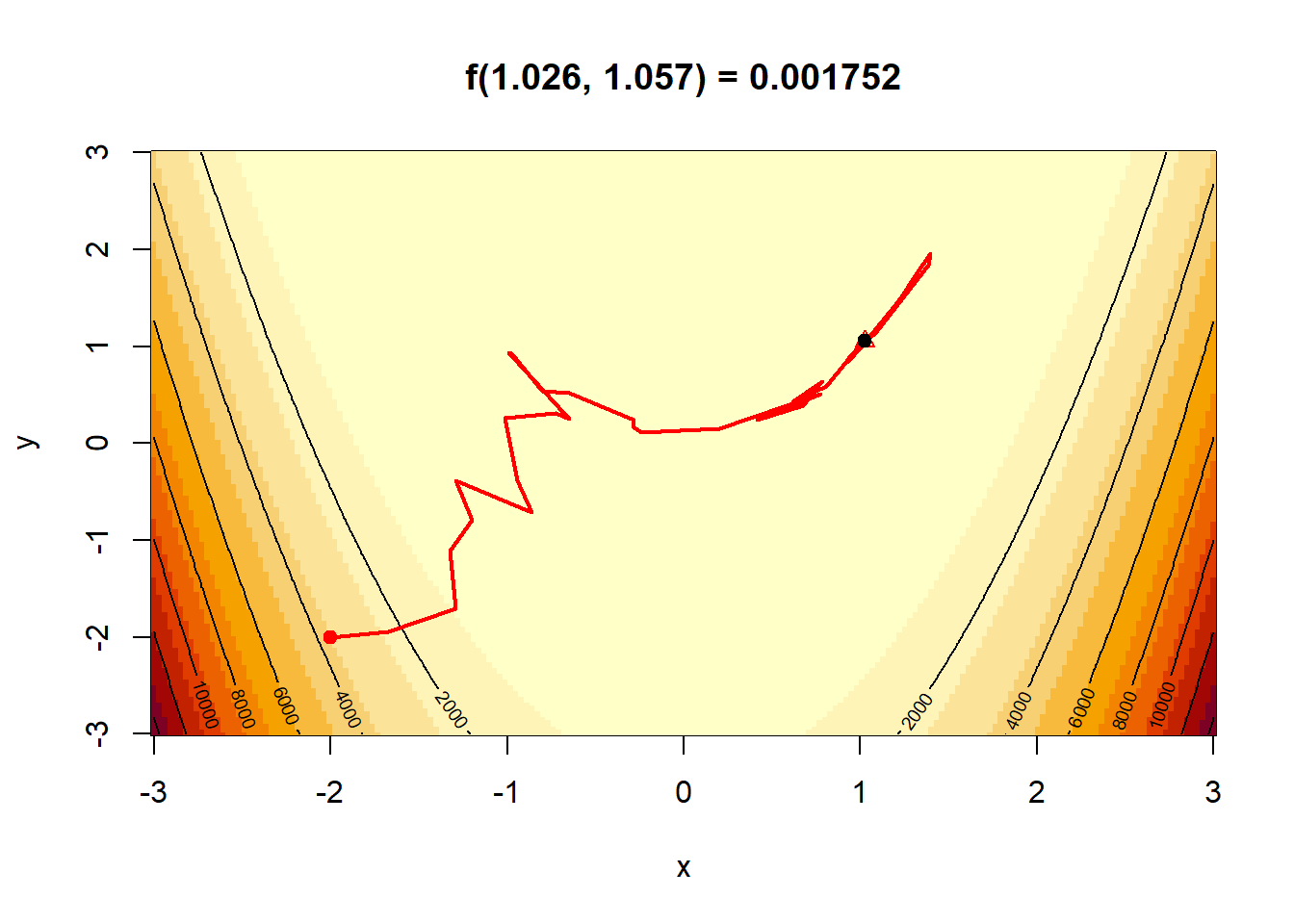
Παράδειγμα 4.11 Μεγιστοποιήστε τη συνάρτηση \[ f(x)=[\cos(50x)+\sin(20x)]^2, x\in[0,1], \] χρησιμοποιώντας τον αλγόριθμο simulated annealing.

Λύση:

f <- function(x) {
  x <- as.numeric(x)
  (cos(50 * x) + sin(20 * x)) ^ 2
}

x <- seq(-0, 1, length = 1000)
y <- f(x)

plot(x, y, type = "l")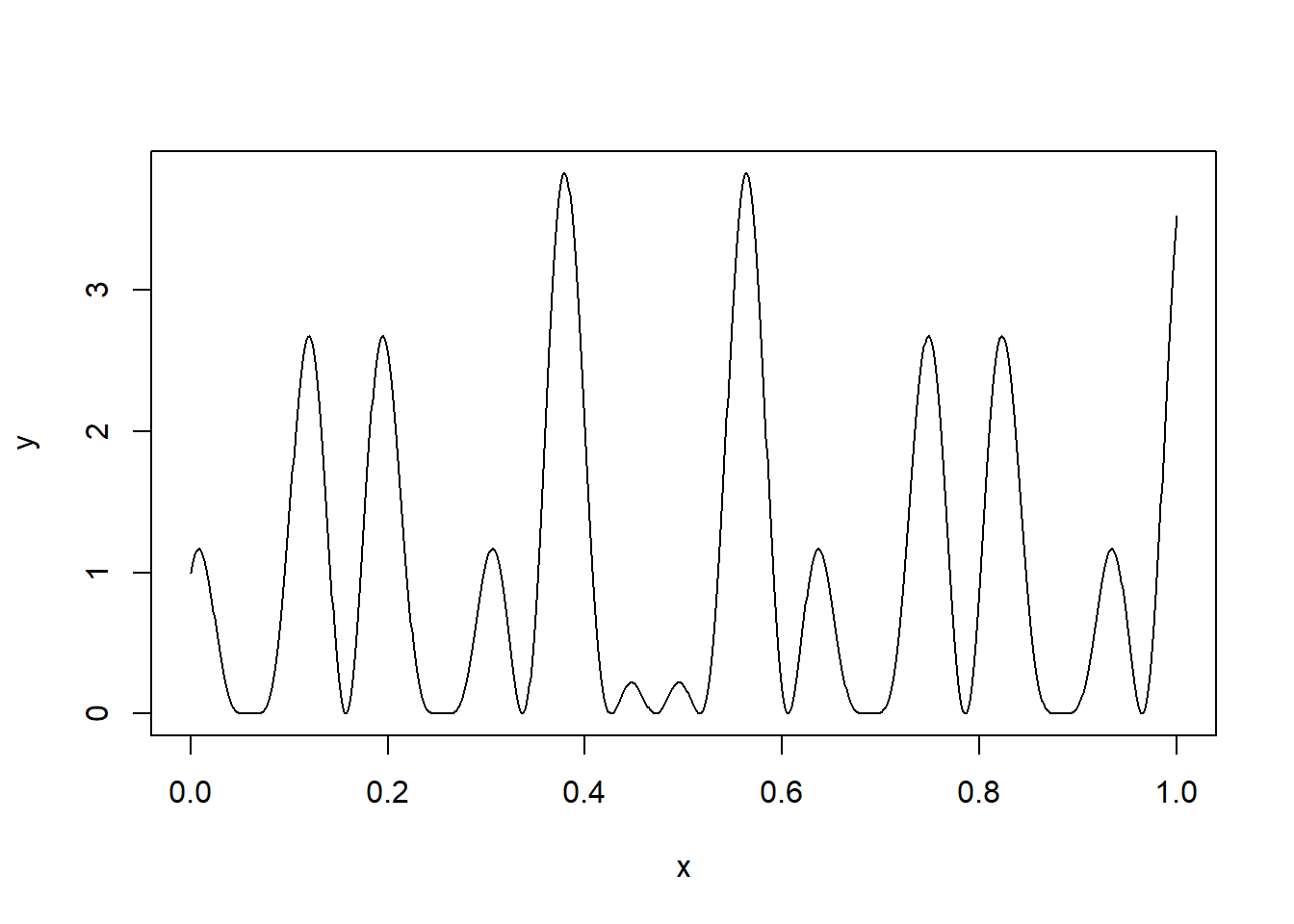

Εικόνα 4.15: Η συνάρτηση \(f\) στο (0, 1).

set.seed(123)
res <- sa(
  f = f,
  x0 = 0.5,
  T0 = 1,
  max_k = 5000,
  minimize = FALSE,
  show_progress = FALSE
)

res$x_best # estimated argmax
## [1] 1.007448
res$y_best # estimated max
## [1] 3.832544

4.6 Ο Αλγόριθμος EM

Ο αλγόριθμος Expectation-Maximization (EM) είναι ένας επαναληπτικός αλγόριθμος που μας επιτρέπει να προσεγγίσουμε την ε.μ.π. σε περιπτώσεις που στο εν λόγω στατιστικό μοντέλο υπεισέρχονται μη παρατηρήσιμες ή κρυμμένες μεταβλητές. Αυτό θα μπορούσε να συνδέεται άμεσα με τον τρόπο περιγραφής του μοντέλου ή να εισάγονται τέτοιες μεταβλητές ως τεχνική ομαλοποίησης της συνάρτησης πιθανοφάνειας του μοντέλου. Η χρήση του αλγορίθμου EM είναι περισσότερο ελκυστική σε προβλήματα που η συνάρτηση πιθανοφάνειας των πλήρων δεδομένων (με ενσωμάτωση των κρυμμένων μεταβλητών ως παρατηρήσιμων) οδηγεί σε ένα πολύ ευκολότερο πρόβλημα μεγιστοποίησης.

Έστω λοιπόν \(X\) ένα παρατηρήσιμο διάνυσμα, το οποίο εξαρτάται από κάποιο άλλο μη παρατηρήσιμο διάνυσμα \(Z\), και από μία παράμετρο \(\theta \in \Theta\) για την εκτίμηση της οποίας απαιτούνται παρατηρήσεις από τις μεταβλητές \(X\) και \(Z\). Καθώς το \(Z\) είναι μη παρατηρήσιμο, η \(L_{X,Z}(\theta)\) δε μπορεί να χρησιμοποιηθεί άμεσα για την εύρεση της ε.μ.π.. Η απευθείας μεγιστοποίηση της \(L_{X}(\theta)\) είναι αρκετά δύσκολη και τις περισσότερες φορές αδύνατη, άρα η ιδέα του αλγορίθμου EM είναι να αντικαταστήσει τη μεγιστοποίηση αυτή από μία ευκολότερη διαδικασία που να βασίζεται στην πιθανοφάνεια των πλήρων δεδομένων. Υπό κάποιες συνθήκες κανονικότητας, ο αλγόριθμος αυτός οδηγεί σε μία ακολουθία \(\theta^{(m)}\rightarrow \theta^\star\) που είναι ένα στάσιμο σημείο της \(l(\theta)=\log L_Y(\theta)\) και πολλές φορές το σημείο στο οποίο συγκλίνει είναι πράγματι η ΕΜΠ.

Συμβολίζοντας \(f(x, z|\theta)\) την από κοινού συνάρτηση πυκνότητας των \(x\) και \(z\), \(f(x|\theta)\) την περιθώρια συνάρτηση πυκνότητας των \(x\) και \(f(z| \theta, x)\) τη δεσμευμένη πυκνότητα των \(z\) δεδομένων των \(x\), έχουμε τη σχέση

\[\begin{equation*} f(z| \theta, x)=\frac{f(x, z|\theta)}{f(x|\theta)}, \ x\in S_x, z \in S_z. \end{equation*}\]

Βλέποντας τη σχέση αυτή ως συνάρτηση του \(\theta\) και λογαριθμίζοντας παίρνουμε

\[\begin{equation*} \log L(\theta|x) = \mathbf{E}_{\theta_0}\left[\log L^c (\theta|x, Z) \right] - \mathbf{E}_{\theta_0}\left[\log f(Z|\theta, x) \right], \end{equation*}\]

όπου η μέση τιμή είναι ως προς τη \(f(Z|\theta_0, x)\). Καθώς επιθυμούμε να μεγιστοποιήσουμε την \(L(\theta|x)\), μας ενδιαφέρει ο πρώτος όρος στο δεύτερο μέρος, \(\mathbf{E}_{\theta_0}\left[\log L^c (\theta|x, Z) \right]\). Θέτουμε

\[\begin{equation*} Q(\theta|\theta_0, x) = \mathbf{E}_{\theta_0}\left[\log L^c (\theta|x, Z) \right]. \end{equation*}\]

Ορισμός 4.3 Η \(Q\)-συνάρτηση που αντιστοιχεί στον αλγόριθμο EM, είναι η οικογένεια των συναρτήσεων \(\{Q(\cdot \ ; \theta')\}_{\theta'\in\Theta}\), που ορίζεται από τη σχέση \[\begin{equation*} Q(\theta ; \theta')=\int \log f(z,x ; \theta) f(z|x ; \theta') \lambda(dz) = E_{\theta'} \left[\ell_{x,Z}(\theta)| X=x \right]. \end{equation*}\]

1. \(\Theta \subset \mathbb{R}^{d_\theta}, d_\theta \geq 1\) είναι ανοικτό υποσύνολο,
2. \(\forall \theta \in \Theta\), η \(L_x(\theta)\) είναι θετική και πεπερασμένη,
3. \(\forall (\theta, \theta') \in \Theta\times\Theta, \int \lVert \nabla _\theta \log f(z|x ; \theta)\rVert\, f(z|x;\theta') \lambda(dz) = E_{\theta'}\left[ \lVert \nabla _\theta \log f(Z|x ; \theta)\lVert \, \mid x \right] < +\infty\).

Λήμμα 4.2 Έστω \[\begin{equation*} H(\theta ; \theta')= E_{\theta'} \big[ \underbrace{-\log f(Z|x ; \theta)}_{g(Z)}\mid x \big] =-\int \log f(z|x; \theta) \cdot f(z|x ; \theta') \lambda(dz) \end{equation*}\] Τότε \(Q(\theta ; \theta')=\ell_x(\theta) - H(\theta ; \theta')\).

Απόδειξη:

\[\begin{align*} f(x ; \theta) = \frac{f(z,x ; \theta)}{f(z|x ; \theta)}, \forall \text{εφικτό} \ z \end{align*}\]

Επομένως \[\begin{align*} f(x ; \theta) = \frac{f(Z,x ; \theta)}{f(Z|x ; \theta)}. \end{align*}\]

Άρα \[\begin{align*} Q(\theta ; \theta') &= E_{\theta'}\left[ \log f(Z, x ; \theta) \mid x \right] = E_{\theta'}\left[ \log f(x ; \theta) + \log f(Z | x ; \theta) \mid x \right] \\ &=\ell_x(\theta) - E_{\theta'}\left[ - \log f(Z | x ; \theta) \mid x \right] = \ell_x(\theta) - H(\theta ; \theta') \end{align*}\]

Πρόταση 4.2 Κάτω από τις υποθέσεις \((i)-(iii), \forall (\theta, \theta') \in \Theta \times \Theta\), έχουμε ότι: \[\begin{equation*} \ell_x(\theta) - \ell_x(\theta') \geq Q(\theta ; \theta') - Q(\theta' ; \theta') \end{equation*}\] Προφανώς, λοιπόν, αν \(\theta^\star = \arg\max_\theta Q(\theta ; \theta')\), τότε \(\ell_x(\theta^\star) \geq \ell_x(\theta')\), το οποίο δείχνει ότι σε κάθε επανάληψη του EM, έχουμε βελτίωση του \(\ell_x(\theta)\).

Απόδειξη:

Θέλουμε νδο: \[\begin{align*} \ell_x(\theta)-\ell_x(\theta') &\geq Q(\theta ; \theta') - Q(\theta' ; \theta') \\ \ell_x(\theta)- Q(\theta ; \theta') &\geq \ell_x(\theta') - Q(\theta' ; \theta') \\ H(\theta ; \theta') &\geq H(\theta' ; \theta') \\ H(\theta ; \theta') - H(\theta' ; \theta') &\geq 0 \end{align*}\]

Πρέπει νδο ισχύει \(H(\theta ; \theta') - H(\theta' ; \theta') \geq 0\). Όμως, \[\begin{align*} H(\theta ; \theta') &= E_{\theta'}\left[- \log f(Z |x ; \theta) \mid x \right] \\ H(\theta' ; \theta') &= E_{\theta'}\left[ -\log f(Z) \right], \text{όταν} Z \thicksim f(z)=f(z|x ; \theta') \end{align*}\]

Παίρνουμε τη διαφορά: \[\begin{align*} H(\theta ; \theta') - H(\theta' ; \theta') = E_{\theta'}\left[ -\log \frac{f(Z|x; \theta)}{f(Z|x; \theta')} \mid x \right] \text{(κυρτή συνάρτηση)} \end{align*}\]

Λόγω Jensen, \[\begin{align*} H(\theta ; \theta') - H(\theta' ; \theta') \geq -\log \left( E_{\theta'}\left[\frac{f(Z|x; \theta)}{f(Z|x; \theta')} \mid x \right] \right). \end{align*}\]

Όμως, \[\begin{align*} E_{\theta'}\left[\frac{f(Z|x; \theta)}{f(Z|x; \theta')} \mid x \right] = \int \frac{f(z|x; \theta)}{f(z|x; \theta')} \cdot f(z|x; \theta') \lambda(dz) = \int f(z|x; \theta) \lambda(dz) = 1 \end{align*}\]

Τελικά \[\begin{align*} H(\theta ; \theta') - H(\theta' ; \theta') \geq 0. \end{align*}\]

Ο αλγόριθμος EM κινείται αναδρομικά ως εξής:

1. Επιλέγουμε μία αρχική τιμή \(\theta_{0}\).

2. E-step: Υπολογίζουμε την \[\begin{equation*} Q\left(\theta|\theta_{m}, x\right) = \mathbf{E}_{\theta_{m}}\left[\log L^c (\theta|x, Z) \right], \end{equation*}\] όπου η μέση τιμή παίρνεται ως προς την \(f\left(z|\theta_{m}, x\right)\).

3. M-step: Μεγιστοποιούμε τη \(Q(\theta|\theta_{m}, x)\) στο \(\theta\) και παίρνουμε \[\begin{equation*} \theta_{m+1} = arg\max_{\theta\in\Theta} Q\left(\theta|\theta_{m}, x\right). \end{equation*}\]

4. Επαναλαμβάνουμε τα βήματα 2-3 μέχρι ο αλγόριθμος να συγκλίνει σε ένα σημείο, δηλαδή \(\theta_{m+1}=\theta_{m}\).

Παράδειγμα 4.12 Ας υποθέσουμε ότι έχουμε \(Y_1, Y_2, \dots, Y_m\) ανεξάρτητες και ισόνομες παρατηρήσεις από την κατανομή \(F\) με συνάρτηση πυκνότητας \(f(y-\theta)\) και ότι οι εναπομείνουσες \((n-m)\) παρατηρήσεις \(Y_{m+1}, Y_{m+2}, \dots, Y_n\) είναι censored με κατώφλι \(a\) (γνωρίζουμε δηλαδή ότι είναι \(\geq a\)). Τότε, η παρατηρούμενη πιθανοφάνεια είναι ίση με

\[\begin{equation*} L(\theta|y) = \left[1 - F(a-\theta)\right]^{n-m} \prod_{i=1}^m f(y_i-\theta). \end{equation*}\]

Μεγιστοποιήστε την πιθανοφάνειας χρησιμοποιώντας τον αλγόριθμο EM.

Λύση:

Αν είχαμε παρατηρήσει τα censored δεδομένα, έστω \(z_{m+1}, z_{m+2}, \dots, z_n\) με \(z_i\geq a\), θα μπορούσαμε να είχαμε την πλήρη πιθανοφάνεια

\[\begin{equation*} L^c (\theta|y,z) = \prod_{i=1}^m f(y_i-\theta) \prod_{i=m+1}^n f(z_i-\theta). \end{equation*}\]

Aν η κατανομή \(f(x-\theta)\) αντιστοιχεί στην κανονική κατανομή \(\mathcal{N}(\theta, 1)\), η πλήρης πιθανοφάνεια γράφεται

\[\begin{equation*} L^c (\theta|y,z) \propto \prod_{i=1}^m e^{-\frac{1}{2} (y_i-\theta)^2} \prod_{i=m+1}^n e^{-\frac{1}{2} (z_i-\theta)^2}, \end{equation*}\]

Παρατηρούμε ότι

\[\begin{equation*} L(\theta|y) = \mathbb{E}\left[L^c(\theta|y, Z)\right] = \int_{\mathcal{Z}}L^c(\theta|y, z) f(z|y,\theta) dz, \end{equation*}\]

όπου

\[\begin{equation*} f(z|y,\theta) = \prod_{i=m+1}^n f(z_i|y,\theta) = \prod_{i=m+1}^n \frac{f(z_i-\theta)}{[1-F(a-\theta)]}. \end{equation*}\]

επομένως

\[\begin{align*} Q(\theta|\theta_0, y) &= -\frac{1}{2} \sum_{i=1}^m (y_i-\theta)^2 -\frac{1}{2} \sum_{i=m+1}^n \mathbf{E}_{\theta_0} \left[(Z_i - \theta)^2 \right] \\ &= -\frac{1}{2} \sum_{i=1}^m (y_i-\theta)^2 -\frac{1}{2} \sum_{i=m+1}^n \mathbf{V}_{\theta_0}(Z_i-\theta) + \mathbf{E}_{\theta_0} \left[(Z_i - \theta) \right]^2 \end{align*}\]

όπου τα \(Z_i\) ακολουθούν κανονική κατανομή \(\mathcal{N}_a(\theta, 1)\) περικεκκομένη στο \(a\). Παραγωγίζοντας την \(Q(\theta|\theta_0, y)\) ως προς \(\theta\) και κάνοντας πράξεις βρίσκουμε το σημείο μεγίστου

\[\begin{equation*} \theta=\frac{m\overline{y} +(n-m)\mathbf{E}_{\theta_0}(Z_1)}{n}. \end{equation*}\]

Καθώς \[\begin{equation*} \mathbf{E}_{\theta}(Z_1) = \theta + \frac{\phi(a-\theta)}{1-\Phi(a-\theta)}, \end{equation*}\]

όπου τα \(\phi, \Phi\) συμβολίζουν τη σ.π.π. και σ.κ. της κανονικής κατανομής, ο αλγόριθμος EM παράγει την αναδρομική ακολουθία

\[\begin{equation*} \theta_{(j+1)} = \frac{m}{n} \overline{y} +\frac{n-m}{n} \left[\theta_{(j)} +\frac{\phi(a-\theta_{(j)})}{1-\Phi(a-\theta_{(j)})} \right]. \end{equation*}\]

Όπως μπορούμε να δούμε στην εικόνα 4.16, για \(\overline{y}=0, a=1, n=30, m=20\), ο αλγόριθμος συγκλίνει αρκετά γρήγορα.

repp <- 4
col <- c("blue", "red", "darkgreen", "purple")
n <- 30
m <- 20
ybar <- 0.32
a <- 1
like <- function(the) {
  dnorm(the, mean = ybar, sd = 1 / sqrt(m), log = T) + 
    (n - m) * pnorm(the - a, log = TRUE)
}
em <- function() {
  theta <- rnorm(1, mean = ybar)
  iter <- nonstop <- 1
  while (nonstop > 0) {
    theta <- c(theta, m * ybar / n + (n - m) * (theta[iter] + dnorm(a - theta[iter]) / pnorm(a - theta[iter])) / n)
    nonstop <- (abs(diff(theta[iter:(iter + 1)])) > 10 ^ (-4))
    iter <- iter + 1
  }
  theta
}
theta <- em()

for (t in 1:repp) {
  plot(theta, like(theta), type = "l", xlab = expression(theta[0]), col="white", 
       ylab = expression(l(theta[0])), lty = 2, xlim = c(-0.5, 1.8), ylim = c(-40, -10))
  curve(like, add = T, lwd = 4, col = "grey70")
  theta <- em()
  points(theta, like(theta), pch = 20, col = col[t])
  lines(theta, like(theta), lty = 2, col = col[t])
}

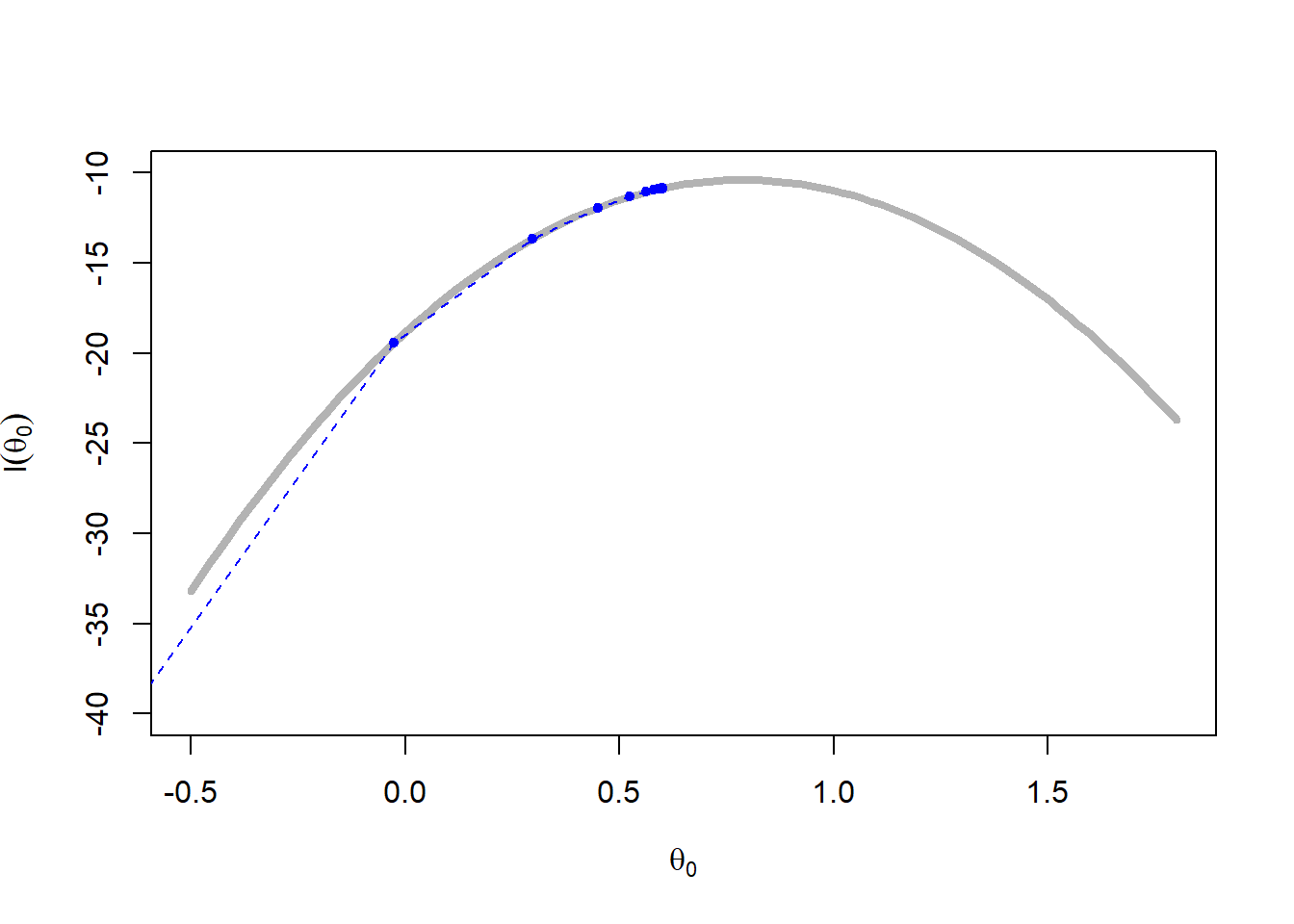
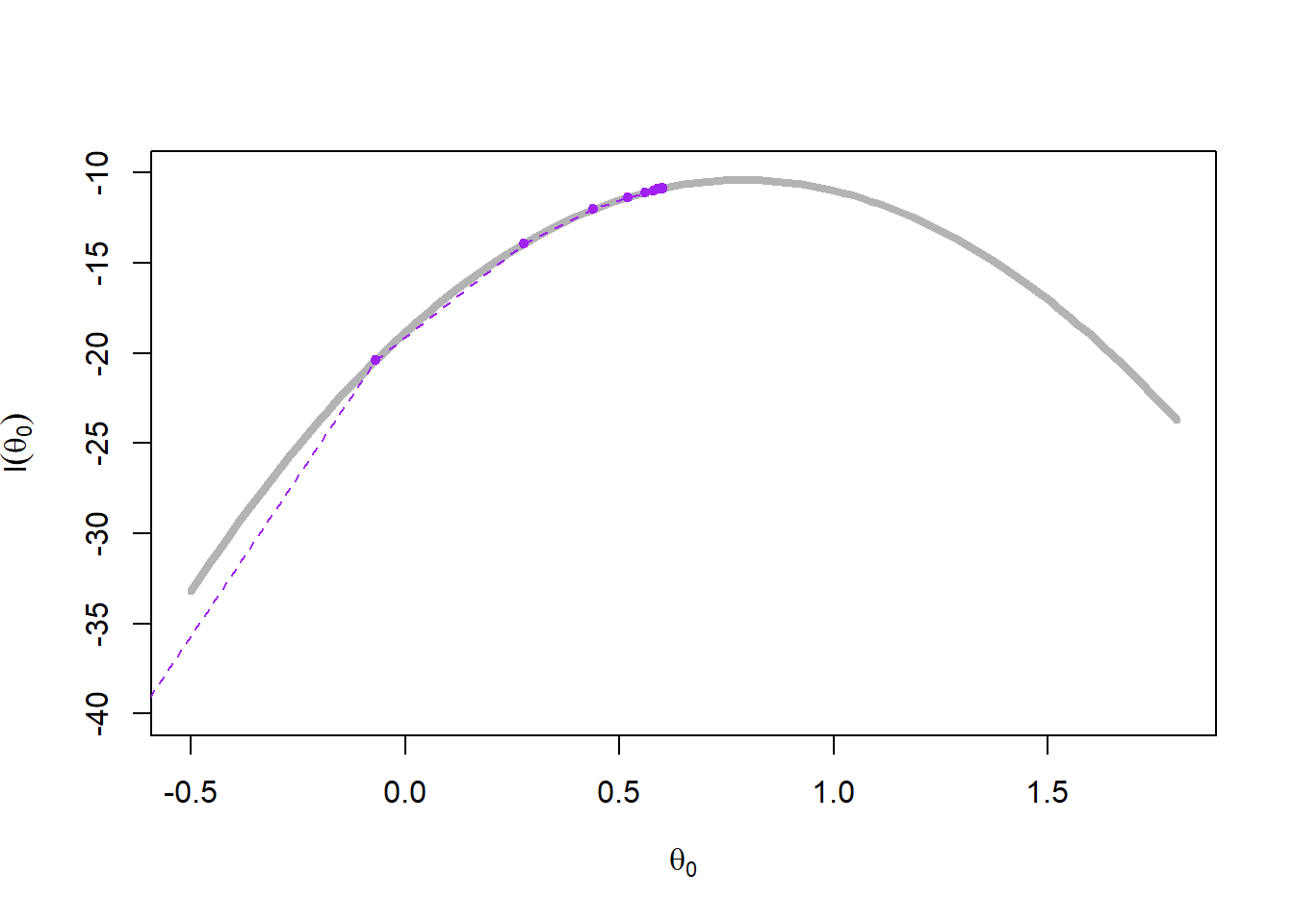
Εικόνα 4.16: Representation by 4 EM sequences started at random for the censored likelihood when the data is normal, \(\overline{y}=0, a=1, n=30, m=20\), on top of the true log-likelihood (grey curve).

Παράδειγμα 4.13 Στο παράδειγμα 4.4 είδαμε ένα δείγμα 400 παρατηρήσεων από μίξη κατανομών \(\mathcal{N}(1, 1)\) και \(\mathcal{N}(2.5, 1)\), με αντίστοιχες πιθανότητες \(1 / 4\) και \(3 / 4\) με πιθανοφάνεια

\[\begin{equation*} L(\mu_1, \mu_2) = \prod_{i=1}^n \left[\frac{1}{4} f(x_i;\mu_1) + \frac{3}{4} f(x_i;\mu_2)\right]. \end{equation*}\]

Σε αυτό το σημείο, εισάγουμε τις τ.μ. \(Z_i\sim Ber(1/4)\), έτσι ώστε \(X_i|Z_i=z\sim\mathcal{N}(\mu_z, 1)\). Γράψτε την πιθανοφάνεια στη μορφή \(\mathbf{E}\left[H(x,Z)\right]\) και υλοποιήστε τον αλγόριθμο EM για να βρείτε την ΕΜΠ.

Λύση:

Έχουμε:

\[\begin{equation*} H(x, z) = \prod_{i=1}^n f(x_i;\mu_{z_i}) \propto \prod_{i:z_i=1} \frac{1}{4} e^{-\frac{1}{2}(x_i-\mu_1)^2} \prod_{i:z_i=0} \frac{3}{4} e^{-\frac{1}{2}(x_i-\mu_2)^2} \end{equation*}\]

\[\begin{equation*} Q(\theta^{'}|\theta, x) = -\frac{1}{2} \sum_{i=1}^m \mathbf{E}_{\theta} \left[ Z_i (x_i-\mu_1)^2 +(1-Z_i)(x_i-\mu_2)^2 |x \right], \end{equation*}\]

όπου \(\theta=(\mu_1, \mu_2)\). Εκτελώντας το βήμα M του αλγορίθμου παίρνουμε τις λύσεις

\[\begin{equation*} \mu_1^{'} = \frac{\mathbf{E}_\theta \left[\sum_{i=1}^n Z_i x_i |x \right]}{\mathbf{E}_\theta \left[\sum_{i=1}^n Z_i |x \right]}, \quad \mu_2^{'} = \frac{\mathbf{E}_\theta \left[\sum_{i=1}^n (1-Z_i) x_i |x \right]}{\mathbf{E}_\theta \left[\sum_{i=1}^n (1-Z_i) |x \right]}. \end{equation*}\]

Καθώς έχουμε γνωστή μέση τιμή

\[\begin{equation*} \mathbf{E}_\theta \left[Z_i|x\right] = \frac{\phi(x_i-\mu_1)}{\phi(x_i-\mu_1)+3\phi(x_i-\mu_2)}, \end{equation*}\]

ο αλγόριθμος EM μπορεί εύκολα να υλοποιηθεί στο συγκεκριμένο πρόβλημα. Στην εικόνα 4.17 παρατηρούμε ότι από τις 6 ακολουθίες EM, δύο συγκλίνουν στο πραγματικό ολικό μέγιστο, δύο συγκλίνουν στο τοπικό, μη ολικό μέγιστο, και δύο συγκλίνουν στο σαγματικό σημείο της πιθανοφάνειας. Αξίζει να παρατηρήσουμε ότι στα αρχικά βήματα του αλγορίθμου η σύγκλιση είναι πολύ γρήγορη και μέσα σε 2-3 βήματα έχουμε φτάσει σε μία “μικρή” περιοχή γύρω από το σημείο σύγκλισης, ενώ στα επόμενα βήματα η σύγκλιση είναι σημαντικά πιο αργή. Αυτό το παράδειγμα κάνει εμφανή την ανάγκη να επαναλάβουμε τον αλγόριθμο αρκετές φορές, ξεκινώντας από τυχαία αρχικά σημεία, ώστε να εντοπίσουμε τα διαφορετικά ακρότατα της συνάρτησης που θέλουμε να βελτιστοποιήσουμε.

set.seed(1028)
da <- sample(rbind(rnorm(10 ^ 2), 2.5 + rnorm(3 * 10 ^ 2)))

# minus the log-likelihood function
like <- function(mu) {
  - sum(log((0.25 * dnorm(da - mu[1]) + 0.75 * dnorm(da - mu[2]))))
}

# log-likelihood surface
mu1 <- mu2 <- seq(-2, 5, le = 250)
lli <- matrix(0, ncol = 250, nrow = 250)

for (i in 1:250) {
  for (j in 1:250) {
    lli[i, j] <- like(c(mu1[i], mu2[j]))
  }
}

par(mar = c(4, 4, 1, 1))
image(mu1, mu2, -lli, xlab = expression(mu[1]), ylab = expression(mu[2]),
      col = hcl.colors(12, "YlOrRd", rev = FALSE))
contour(mu1, mu2, -lli, nle = 100, add = TRUE)

# sequence of NR maxima
starts <- matrix(c(1, 1, -1, -1, 4, -1, 4, 2.5, 1, 4, -1, 4.5), nrow = 2)
colours <- c("blue", "red", "black", "grey40", "green", "orange")

EMI <- function(start, x) {
  m1 <- start[1] ; m2 <- start[2]
  iter <- nonstop <- 1
  
  while (nonstop > 0) {
    a <- dnorm(x - m1[iter]) / (dnorm(x - m1[iter]) + 3 * dnorm(x - m2[iter])) 
    
    m1 <- c(m1, sum(x * a) / sum(a))
    m2 <- c(m2, sum(x * (1 - a)) / sum((1 - a)))
    
    nonstop <- (abs(diff(m1[iter:(iter + 1)])) > 10 ^ (-4)) | (abs(diff(m2[iter:(iter + 1)])) > 10 ^ (-4))
    iter <- iter + 1
  }
  cbind(m1, m2)
}

for (t in 1:6) {
  m <- EMI(starts[ , t], x = da)
  points(x = m[ , 1], y = m[ , 2], pch = 20, col = colours[t])
  lines(x = m[ , 1], y = m[ , 2], lty = 2, col = colours[t])
}

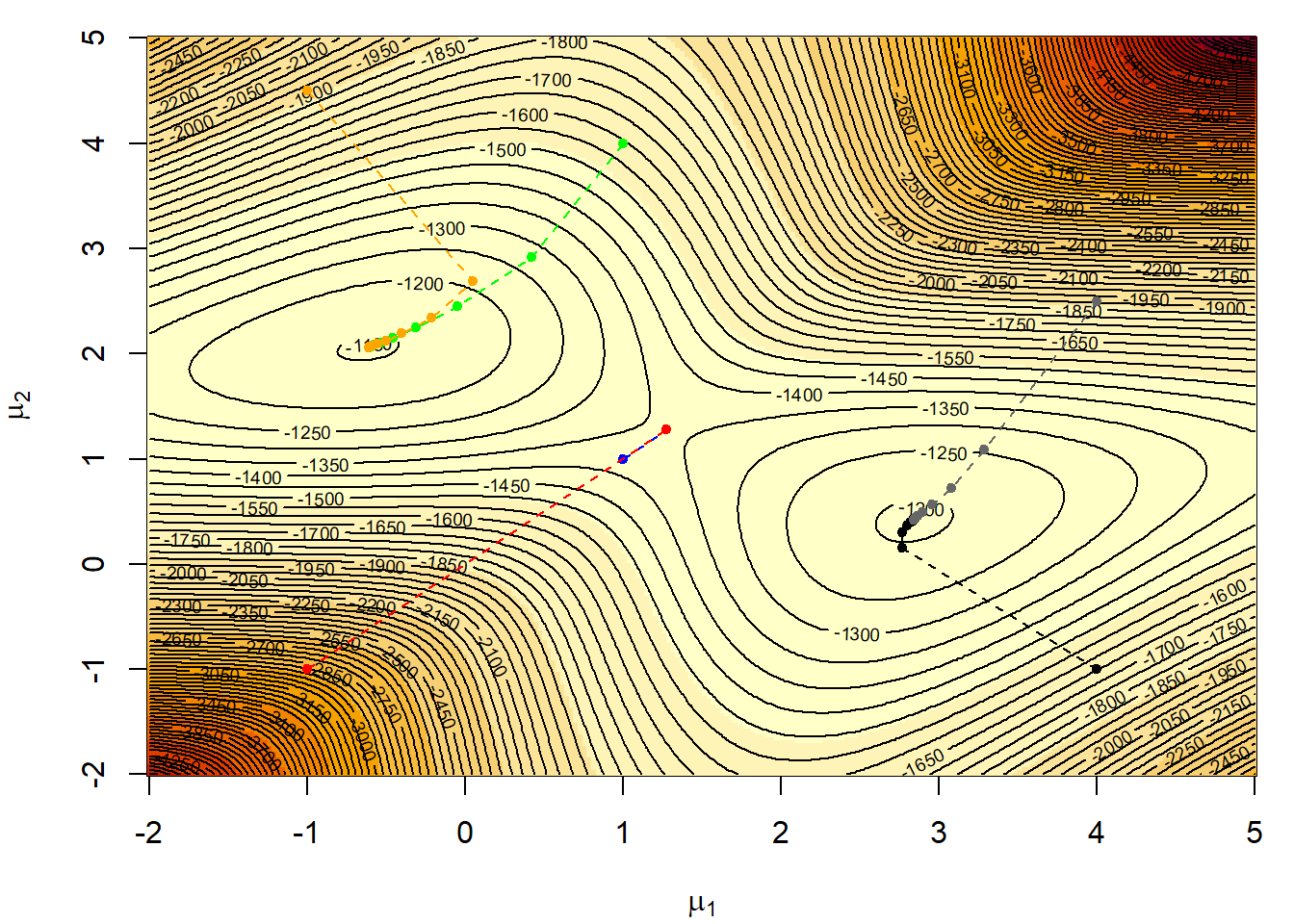
Εικόνα 4.17: Six EM sequences for a mixture likelihood ending in one of two modes depending on the starting point based on a sample of 400 observations from the normal mixture with \(\mu_1 = 0\) and \(\mu_2 = 2.5\)

4.6.1 Monte Carlo EM

Μία δυσκολία στην εφαρμογή του αλγορίθμου EM είναι ότι κάθε βήμα E απαιτεί τον υπολογισμό της μέσης τιμής της λογαριθμοπιθανοφάνειας, δηλαδή της \(Q(\theta|\theta_{m}, x)\). Πέρα από πολύ συγκεκριμένα παραδείγματα όπου η συνάρτηση \(Q\) γράφεται σε κλειστή μορφή, πρέπει να την εκτιμήσουμε. Καθώς η \(Q\) είναι μία μέση τιμή, είναι φυσικό να χρησιμοποιήσουμε μεθόδους Monte Carlo. Όπως είδαμε, μπορούμε να προσομοιώσουμε παρατηρήσεις \(Z_1, ..., Z_T\) από τη κατανομή \(f(z|x, \theta_{m})\) και να εκτιμήσουμε τη πλήρη λογαριθμοπιθανοφάνεια ως

\[\begin{equation*} Q(\theta|\theta_{m}, x) = \frac{1}{T} \sum_{i=1}^T \ell^c (\theta|x, z_i), \end{equation*}\]

μία μέθοδος που ονομάζεται Monte Carlo EM (Wei & Tanner, 1990). Σύμφωνα με τα παραπάνω, σε κάθε βήμα του αλγορίθμου πρέπει να προσομοιώνουμε ένα καινούριο δείγμα \(Z_i\) από την \(f(z|x, \theta_{m})\).

Παράδειγμα 4.14 Μία κλασική εφαρμογή του EM είναι στο ακόλουθο πρόβλημα βιολογίας (Dempster et al., 1977). Θεωρούμε παρατηρήσεις

\[\begin{equation*} (x_1, x_2, x_3, x_4)\sim\mathcal{M}\left(n ; p \right), \end{equation*}\]

με \[\begin{equation*} p = \left(\frac{1}{2} + \frac{\theta}{4}, \frac{1}{4} (1-\theta), \frac{1}{4} (1-\theta), \frac{\theta}{4}\right). \end{equation*}\]

Να εκτιμήσετε το \(\theta\).

Λύση:

Στο συγκεκριμένο πρόβλημα έχουμε μόλις μία παρατήρηση \(x = (x_1, \dots x_m)\) από την \(m\)-διάστατη πολυωνυμική κατανομή με διάνυσμα πιθανότητας \(p = (p_1, \dots, p_m)\). Η πιθανοφάνεια (που επειδή έχουμε μόλις μία παρατήρηση ταυτίζεται με τη συνάρτηση πυκνότητας) δίνεται από τον τύπο

\[\begin{equation*} L(p|x) = \prod_{j=1}^m p_j^{x_{j}}, \end{equation*}\]

και αντίστοιχα η λογαριθμοπιθανοφάνεια:

\[\begin{equation*} \ell(p|x) = \log p_j \sum_{i=1}^n x_{ij}. \end{equation*}\]

Στο συγκεκριμένο πρόβλημα,

\[\begin{equation*} f(x|\theta) = L(\theta|x) = \frac{1}{4^{x_1+x_2+x_3+x_4}} (2+\theta)^{x_1}\theta^{x_4} (1-\theta)^{x_2+x_3}. \end{equation*}\]

Η εκτίμηση του \(\theta\) γίνεται πολύ πιο εύκολα αν οι παρατηρήσεις \(x_1\) διαιρεθούν σε δύο τμήματα, \(x_1=z_1+z_2\), έτσι ώστε \((z_1, z_2, x_2, x_3, x_4)\sim\mathcal{M}\left(n ; p^\star \right)\) με

\[\begin{equation*} p^\star = \left(\frac{1}{2}, \frac{\theta}{4}, \frac{1}{4} (1-\theta), \frac{1}{4} (1-\theta), \frac{\theta}{4}\right). \end{equation*}\]

Η πλήρης πιθανοφάνεια γράφονται ως:

\[\begin{equation*} L^c(\theta|z, x) = \frac{1}{4^{x_1+x_2+x_3+x_4}} 2^{x_1-z_2}\theta^{z_2+x_4} (1-\theta)^{x_2+x_3}, \end{equation*}\]

και, αγνοώντας τις σταθερές ως προς \(\theta\),

\[\begin{equation*} L^c(\theta|z, x) \propto \theta^{z_2+x_4} (1-\theta)^{x_2+x_3}. \end{equation*}\]

Η λογαριθμοπιθανοφάνεια, αγνοώντας τις σταθερές ως προς \(\theta\), γράφεται

\[\begin{equation*} \ell^c(\theta|z, x) = (z_2+x_4)\log\theta +(x_2+x_3)\log(1-\theta). \end{equation*}\]

Για τον κλασικό EM:

Η αναμενόμενη τιμή της πλήρους λογαριθμοπιθανοφάνειας είναι

\[\begin{equation*} \mathbf{E}_{\theta_m}\left[\ell^c(\theta|Z, x)\right] = \mathbf{E}_{\theta_m}\left[ (Z_2 +x_4) \log \theta + (x_2 +x_3) \log (1-\theta) \right] \end{equation*}\]

Επομένως πρέπει να υπολογίσουμε την μέση τιμή της \(Z_2|\theta_m, x\). Θα υπολογίσουμε την κατανομή της:

\[\begin{equation*} f(z_2|\theta_m, x) \propto 2^{x_1-z_2}\theta_m^{z_2} \propto \left(\frac{2}{2+\theta_m}\right)^{x_1-z_2}\left(\frac{\theta_m}{2+\theta_m}\right)^{z_2}, \end{equation*}\]

επομένως \(z_2|\theta_m, x\sim Bin(x_1, \theta_m/(2+\theta_m) )\).

Επομένως:

\[\begin{equation*} \mathbf{E}_{\theta_m}\left[\ell^c(\theta|Z, x)\right] = \left[ \frac{\theta_m}{2+\theta_m}x_1 +x_4 \right] \log \theta + (x_2 + x_3) \log (1-\theta), \end{equation*}\]

η οποία εύκολα μεγιστοποιείται ως προς \(\theta\), με σημείο μεγίστου

\[\begin{equation*} \theta_{m+1} = \frac{ \frac{\theta_m x_1}{2+\theta_m+x_4} }{ \frac{\theta_m x_1}{2+\theta_m} +x_2 + x_3 + x_4 }. \end{equation*}\]

Για τον Monte-Carlo EM:

Αν δεν μπορούμε να υπολογίσουμε αναλυτικά την \(\mathbf{E}_{\theta_m}\left[\ell^c(\theta|Z_2, x)\right]\), πρέπει να κάνουμε προσομοιώσεις ώστε να την εκτιμήσουμε με Monte-Carlo. Αντικαθιστούμε λοιπόν την \(\mathbf{E}_{\theta_m}(Z_2)\) με τον εμπειρικό μέσο

\[\begin{equation*} \overline{z}_m = \frac{1}{m} \sum_{i=1}^m z_i, \end{equation*}\]

όπου τα \(z_i\) προσομοιώνονται από τη διωνυμική κατανομή \(Bin(x_1, \theta_m/(2+\theta_m) )\). Σε αυτή την περίπτωση θα είχαμε

\[\begin{equation*} \widehat{\theta}_{m+1} = \frac{ \overline{z}_m + x_4 }{ \overline{z}_m + x_2 + x_3 + x_4 }, \end{equation*}\]

η οποία συγκλίνει στη \(\theta_1\) καθώς το \(m\) πάει στο άπειρο.

Όπως είδαμε όμως, μία πιο σταθερή εκτίμηση βασίζεται στη δειγματοληψία σπουδαιότητας ώστε να μην απαιτείται η παραγωγή διαφορετικού δείγματος για κάθε τιμή της \(\theta_{m}\). Βασιζόμενοι στη σχέση των πυκνοτήτων

\[\begin{equation*} g(x|\theta)=\frac{f(x, z|\theta)}{k(z| \theta, x)}, \ x\in S_x, z \in S_z, \end{equation*}\]

παίρνουμε

\[\begin{equation*} \frac{f(x|\theta)}{f(x|\theta_{0})}=\frac{f(x, z|\theta)}{f(x, z|\theta_{0})} \frac{f(z| \theta_{0}, x)}{f(z| \theta, x)}, \ x\in S_x, z \in S_z. \end{equation*}\]

Παίρνοντας μέσες τιμές ως προς την κατανομή \(k(z|x, \theta)\), καταλήγουμε στη σχέση

\[\begin{equation*} \frac{f(x|\theta)}{f(x|\theta_{0})}=\mathbf{E}_{\theta} \left( \frac{f(x, z|\theta)}{f(x, z|\theta_{0})} \frac{f(z| \theta_{0}, x)}{f(z| \theta, x)}\right) =\mathbf{E}_{\theta_{0}} \left( \frac{f(x, z|\theta)}{f(x, z|\theta_{0})}\right) =\mathbf{E}_{\theta_{0}} \left( \frac{L^c(\theta|x, z)}{L^c(\theta_{0}|x, z)}\right), \end{equation*}\]

επομένως, αγνοώντας τον σταθερό ως προς το \(\theta\) όρο \(f(x|\theta_{0})\) βλέπουμε ότι για να μεγιστοποιήσουμε την πιθανοφάνεια \(L(\theta|x) = f(x|\theta)\) μπορούμε να χρησιμοποιήσουμε την Monte Carlo εκτιμήτρια

\[\begin{equation*} \frac{1}{T} \sum_{i=1}^T \frac{L^c(\theta|x, z_i)}{L^c(\theta_{0}|x, z_i)}. \end{equation*}\]

Η επιλογή της \(\theta_{0}\) είναι ιδιαίτερα σημαντική για να εξασφαλιστεί η πεπερασμένη διασπορά της εκτιμήτριας.