4 Εκτίμηση Monte Carlo

Οι μέθοδοι Monte Carlo αποτελούν μία σημαντική κατηγορία εντατικών υπολογιστικών μεθόδων της στατιστικής που έχουν ως βασικό στόχο την προσέγγιση πολύπλοκων ολοκληρωμάτων και την εύρεση βέλτιστων λύσεων σε προβλήματα βελτιστοποίησης με τη βοήθεια προσομοιώσεων. Σε αντίθεση με τη “ντετερμινιστική” αριθμητική επίλυση ενός προβλήματος, οι μέθοδοι Monte-Carlo επιλύουν στοχαστικά ένα πρόβλημα. Έτσι, αν ο αλγόριθμος επαναληφθεί κάτω από τις ίδιες αρχικές συνθήκες, με διαφορετικό σπόρο (seed) βέβαια, τότε το αποτέλεσμα θα είναι γενικά διαφορετικό.

Θα πρέπει να γίνει σαφές από την αρχή ότι σε πολλές τέτοιες περιπτώσεις μπορεί να υπάρχουν πολύ αποτελεσματικές μέθοδοι αριθμητικής ολοκλήρωσης που υπερτερούν της Monte Carlo ολοκλήρωσης. Γρήγορα όμως οι τελευταίες μπορούν να αποδειχθούν πιο αποτελεσματικές καθώς η διάσταση \(d\) αυξάνει. Μία συνάρτηση στην R που μπορεί να χρησιμοποιηθεί για υπολογισμό απλών ολοκληρωμάτων (\(d=1\)) είναι η integrate().

4.1 Ολοκλήρωση Monte Carlo

Στο κεφάλαιο αυτό εστιάζουμε στη χρήση των μεθόδων Monte Carlo στην προσέγγιση ολοκληρωμάτων. Ας υποθέσουμε λοιπόν ότι θέλουμε να υπολογίσουμε ένα ολοκλήρωμα της μορφής \(\int_Ag(x)dx\) κάποιας συνάρτησης \(g: A\rightarrow \mathbb{R}\), όπου \(A\subset \mathbb{R}^d\). Αν υποθέσουμε ότι \(\int_A |g(x)|dx<+\infty\) (δηλ. συγκλίνει απόλυτα), τότε

\[\begin{equation*} I=\int_Ag(x)dx = \int_A \frac{g(x)}{f(x)} \cdot f(x) dx = \int_{\mathbb{R}^d}h(x)f(x)dx, \end{equation*}\]

όπου η \(f(x)\) μπορεί να επιλεγεί ως σ.π.π. στον \(\mathbb{R}^d\) με στήριγμα το \(A\) και \(h(x)=g(x)/f(x)\). Έτσι λοιπόν, \(I=\mathbf{E}_f\left[h(X)\right]\), συμπεραίνοντας ότι το ζητούμενο ορισμένο ολοκλήρωμα γράφεται ως μία μέση τιμή μιας κατάλληλης συνάρτησης μιας τυχαίας μεταβλητής. Θα πρέπει να είναι σαφές από την αρχή ότι η αναπαράσταση του \(I\) στη μορφή αυτή δεν είναι μοναδική και έτσι αλλάζοντας τις \(h\) και \(f\) μπορούμε να οδηγηθούμε στην ίδια ολοκληρωτέα συνάρτηση \(h\cdot f\).

Η ανάλυση της αποδοτικότητας τέτοιων αναπαραστάσεων είναι ένα θέμα που θα μας απασχολήσει αργότερα. Ας ξεκινήσουμε με το πρόβλημα εκτίμησης του \(I\) στη μορφή αυτή. Είναι φανερό ότι αν μπορούμε να προσομοιώσουμε από την \(f\) χρησιμοποιώντας ένα (ψευδο)τυχαίο δείγμα \(X_1, X_2, ..., X_n\) από αυτήν την κατανομή θα έχουμε ότι ο δειγματικός μέσος

\[\begin{equation*} \overline{h}_n = \frac{1}{n}\sum_{j=1}^n h(X_j), \end{equation*}\]

αποτελεί μία αμερόληπτη εκτιμήτρια του \(I\).

Η μεγάλη υπολογιστική ισχύς που διαθέτουμε σήμερα μας δίνει τη δυνατότητα να παράγουμε εκατομμύρια παρατηρήσεις από μία κατανομή ενδιαφέροντος και έτσι τίθεται σε ισχύ η ασυμπτωτική θεωρία.

Συγκεκριμένα, αν \(\mathbf{E}_f|h(X)|<+\infty\), συνθήκη η οποία είναι αναγκαία για την ύπαρξη του ολοκληρώματος \(I\) που θέλουμε να υπολογίσουμε, τότε γνωρίζουμε ότι εφαρμόζεται ο Ισχυρός Νόμος των Μεγάλων Αριθμών (I.N.M.A.) και άρα,

\[\begin{equation*} \overline{h}_n \overset{a.s.}{\longrightarrow} \mathbf{E}_f\left[h(X)\right] = I, \quad n\rightarrow +\infty. \end{equation*}\]

Το παραπάνω αποτέλεσμα μας εξασφαλίζει ότι τυπικά (σχεδόν για κάθε πραγματοποίηση) θα έχουμε σύγκλιση της ακολουθίας \(\left(\overline{h}_n(\omega)\right)_n\) στην τιμή \(I\). Το ισχυρό αυτό αποτέλεσμα μας εξασφαλίζει ότι πρακτικά όποια προσομοίωση και να κάνουμε στον υπολογιστή, μπορούμε να βρεθούμε οσοδήποτε κοντά θέλουμε στο \(I\), χρησιμοποιώντας επαρκώς μεγάλο μέγεθος δείγματος.

Παράδειγμα 4.1 Εκτιμήστε το ολοκλήρωμα:

\[\begin{equation*} I = \int_{-\infty}^{+\infty} e^{-x^2/2} dx. \end{equation*}\]

Λύση:

Είναι γνωστό ότι \(I=\sqrt{2\pi}\), αφού το \(1/I\) αποτελεί τη σταθερά κανονικοποίησης της τυπικής κανονικής κατανομής. Έχουμε λοιπόν

\[\begin{equation*} I = \int_{-\infty}^{+\infty} \underbrace{\frac{2\,e^{-x^2/2}}{ e^{-|x|}}}_{h(x)} \cdot \underbrace{\frac{1}{2} e^{-|x|}}_{f(x)} dx = \mathbf{E}_f\left[h(X)\right], \end{equation*}\]

όπου \(f(x)\) είναι η σ.π.π. της διπλής εκθετικής (Laplace) και

\[\begin{equation*} h(x) = 2 e^{-\frac{x^2}{2}+|x|}, \ \forall x \in \mathbb{R}. \end{equation*}\]

Στο παρακάτω γράφημα μπορούμε να δούμε 4 προσομοιωμένα μονοπάτια της εξέλιξης του δειγματικού μέσου \(\overline{h}_{1,n}\), όταν η κατανομή πρότασης αντιστοιχεί στη διπλή εκθετική.

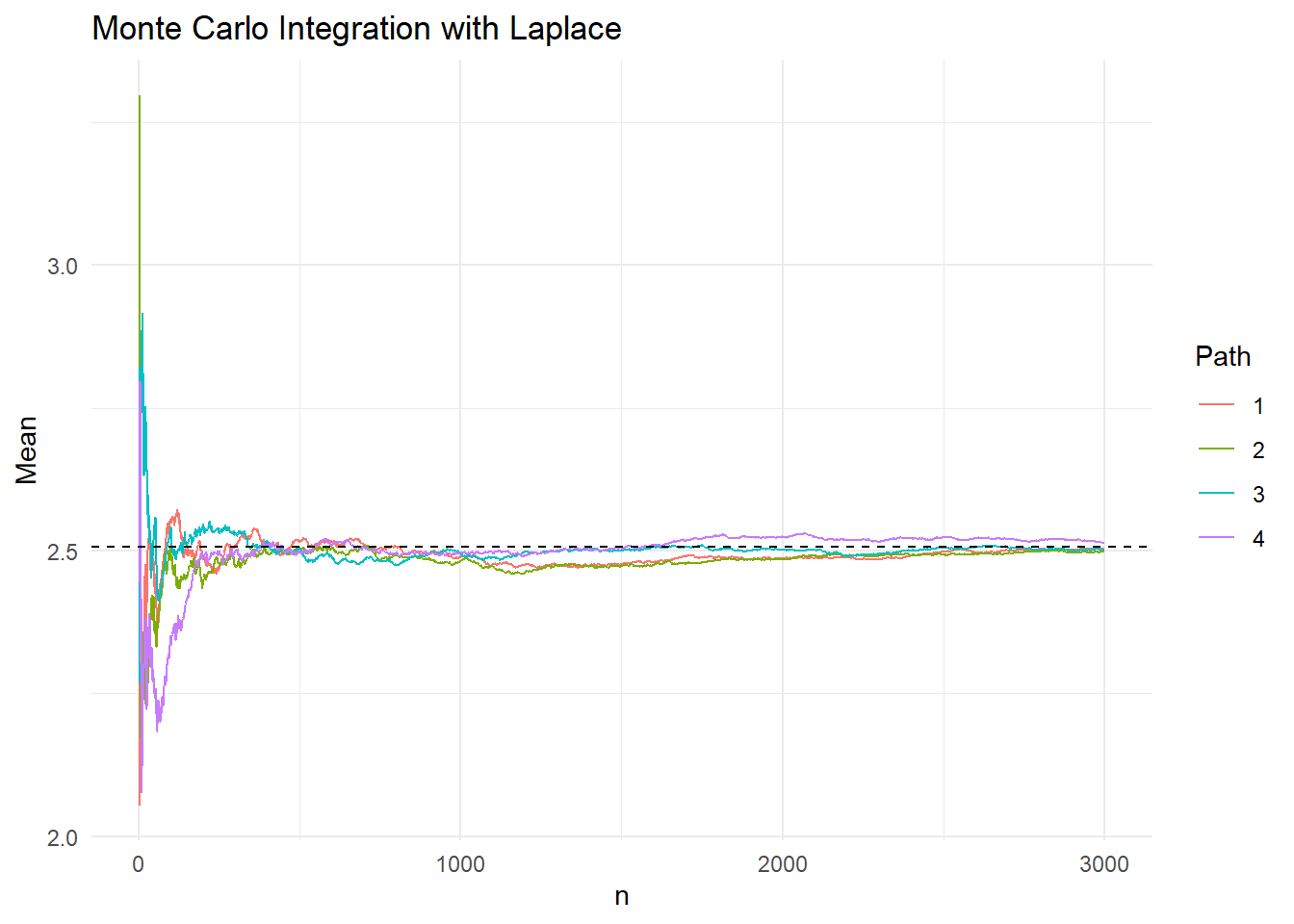
Η επιλογή \(f=f_1\) με \(f_1\) την σ.π.π. της διπλής εκθετικής είναι μία δυνατή από πολλές διαφορετικές επιλογές (προφανώς άπειρες). Ας δούμε μία διαφορετική επιλογή \(f=f_2\) με \(f_2\) τη σ.π.π. της τυπικής Cauchy. Με αυτήν την επιλογή της \(f\), έχουμε \(h_2=g/f_2\) και

\[\begin{equation*} I=\int_{-\infty}^{+\infty} \underbrace{e^{-x^2/2}}_{g(x)} dx = \int_{-\infty}^{+\infty} \underbrace{\pi (1+x^2) e^{-x^2/2}}_{g/f_2=h_2} \cdot \underbrace{\frac{1}{\pi(1+x^2)}}_{f_2} dx = \mathbf{E}_{f_2}\left[h_2(X)\right]. \end{equation*}\]

Στο παρακάτω γράφημα βλέπουμε 4 προσομοιωμένα μονοπάτια της εξέλιξης του δειγματικού μέσου \(\overline{h}_{2,n}\), όταν η κατανομή πρότασης αντιστοιχεί στην κατανομή Cauchy.

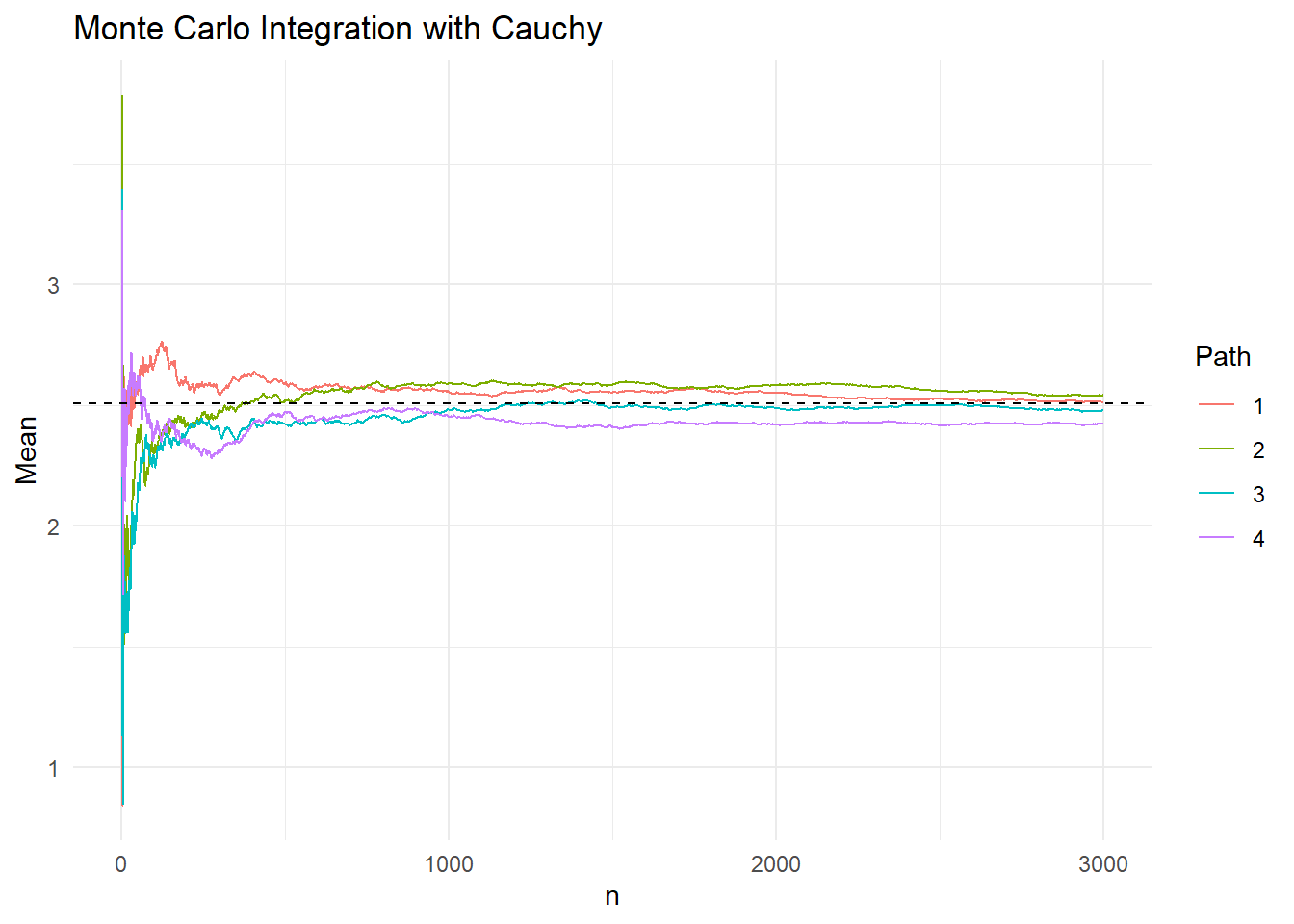
Αν και με τις δύο κατανομές πρότασης οι εκτιμήτριες που προκύπτουν είναι αμερόληπτες, μπορούμε εύκολα να παρατηρήσουμε ότι παρουσιάζουν διαφορετική μεταβλητότητα. Για να γίνει περισσότερο εμφανές, αντιπαραβάλλουμε τη συμπεριφορά των μονοπατιών σε ένα κοινό γράφημα

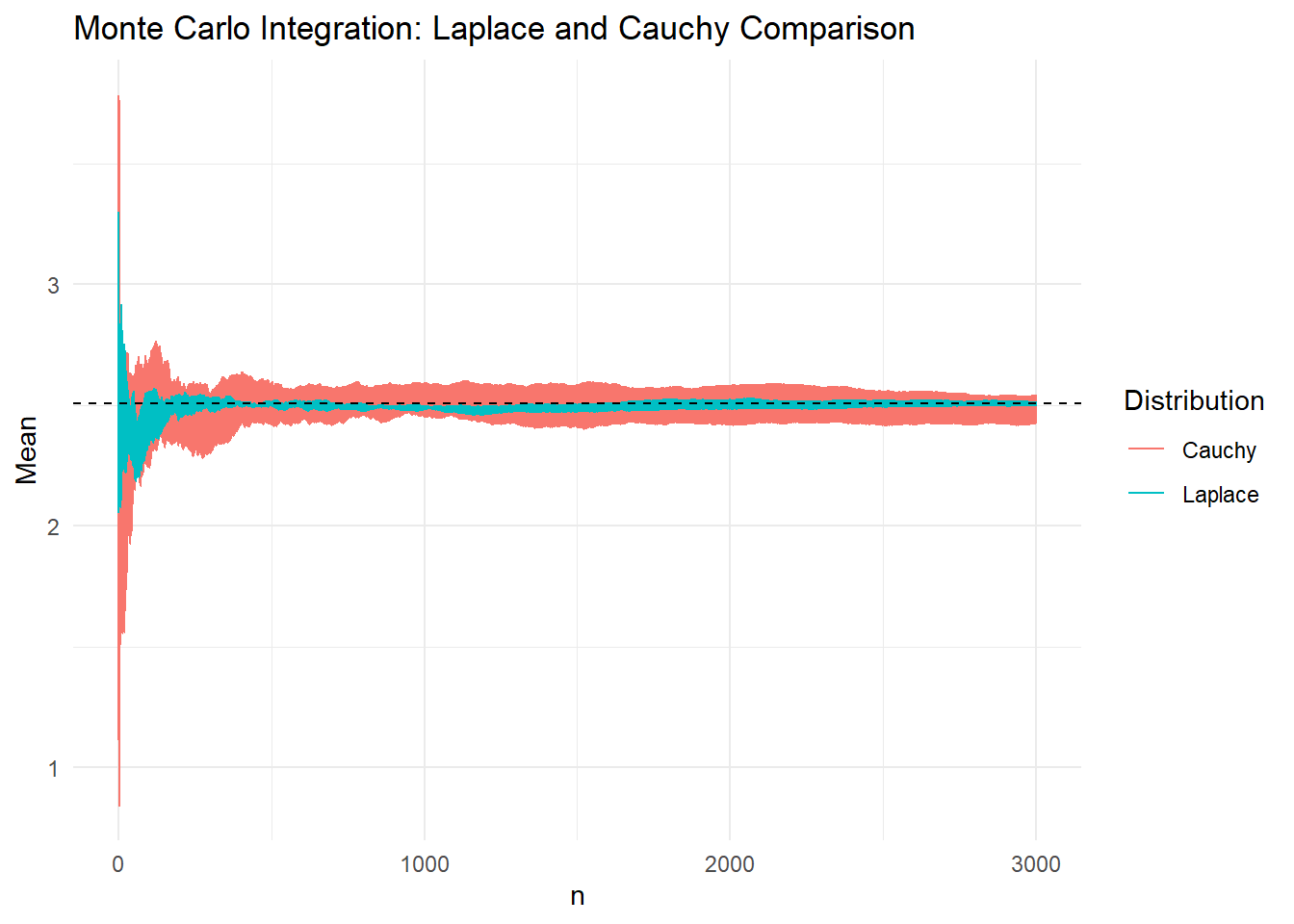
Στο παραπάνω γράφημα έχουν προσομοιωθεί 4 μονοπάτια από κάθε κατανομή και χρωματίζεται η περιοχή από την μικρότερη μέχρι την μεγαλύτερη τιμή των μονοπατιών σε κάθε βήμα \(n\). Είναι εμφανές ότι προσομοιώνοντας από τη Laplace επιτυγχάνουμε γρηγορότερη σύγκλιση στη σταθερά \(I\) απ’ ότι με την Cauchy.

Για να μπορέσουμε να συγκρίνουμε την απόδοση των δύο διαφορετικών τρόπων προσέγγισης χρειάζεται η σύγκριση των διασπορών τους. Ως αμερόληπτες εκτιμήτριες, εκείνη που θα έχει τη μικρότερη διασπορά, θα έχει και το μικρότερο μέσο τετραγωνικό σφάλμα. Σε κάποιες απλές περιπτώσεις, όπως εδώ, είναι δυνατός ο απ’ευθείας υπολογισμός της διασποράς. Σε κάποιες άλλες, που είναι η πλειοψηφία των περιπτώσεων σε πρακτικές εφαρμογές, είναι αναγκαία η εκτίμηση της διασποράς. Ας συγκρίνουμε πρώτα εδώ τις θεωρητικές τους διασπορές. Εφ’ όσον και οι δύο είναι αμερόληπτες εκτιμήτριες, η σύγκριση των διασπορών τους ανάγεται στη σύγκριση των ροπών δεύτερης τάξης.

\[\begin{align*} \mathbf{E}_{f_1}\left[h_1^2(X)\right] &= 4\int_{-\infty}^{+\infty} \left( e^{-x^2/2+|x|}\right)^2 \frac{1}{2} e^{-|x|} dx = 2 \int_{-\infty}^{+\infty} e^{-x^2+|x|} dx = 2 e^{1/4} \int_{-\infty}^{+\infty} e^{-x^2+|x|-1/4} dx \\ & = 2 e^{1/4} \int_{-\infty}^{+\infty} e^{-\frac{(\sqrt{2}|x|-1/\sqrt{2})^2}{2}} dx = 2 \sqrt{\pi} e^{1/4} \int_{-\infty}^{+\infty} \frac{\sqrt{2}}{\sqrt{2\pi}} e^{-\frac{(\sqrt{2}|x|-1/\sqrt{2})^2}{2}} dx \\ & = 2 \sqrt{\pi} e^{1/4} \left( \int_{-\infty}^{0} \frac{\sqrt{2}}{\sqrt{2\pi}} e^{-\frac{(\sqrt{2}x+1/\sqrt{2})^2}{2}} dx +\int_{0}^{+\infty} \frac{\sqrt{2}}{\sqrt{2\pi}} e^{-\frac{(\sqrt{2}x-1/\sqrt{2})^2}{2}} dx \right) \\ &= 2\sqrt{\pi} e^{1/4} \left( \int_{-\infty}^{1/\sqrt{2}} \frac{1}{\sqrt{2\pi}} e^{-y^2/2} dy + \int_{-1/\sqrt{2}}^{+\infty} \frac{1}{\sqrt{2\pi}} e^{-y^2/2} dy \right) \\ &= 2 \sqrt{\pi} e^{1/4} \left[ \Phi\left(1/\sqrt{2}\right) +1 -\Phi\left(-1/\sqrt{2}\right) \right] \\ &= 4 \sqrt{\pi} e^{1/4} \cdot \Phi\left(1/\sqrt{2}\right) \end{align*}\]

Από την άλλη μεριά,

\[\begin{align*} \mathbf{E}_{f_2}\left[h_2^2(X)\right] &= \int_{-\infty}^{+\infty} \pi^2 (1+x^2)^2 e^{-x^2} \frac{1}{\pi (1+x^2)} dx = \pi \int_{-\infty}^{+\infty} (1+x^2) e^{-x^2} dx \\ &= \pi \left( \int_{-\infty}^{+\infty} e^{-x^2} dx + \int_{-\infty}^{+\infty} x^2 e^{-x^2} dx \right) = \pi \left( \sqrt{\pi} + \sqrt{\pi} \underbrace{\int_{-\infty}^{+\infty} \frac{y^2}{\sqrt{2\pi}} e^{-y^2/2} dy}_{\mathbf{E}(Z^2)=1} \right) \\ &= 2\pi \sqrt{\pi}. \end{align*}\]

Η σύγκριση αυτή μας οδηγεί στο συμπέρασμα ότι \[\begin{equation*} \mathbf{E}_{f_1}\left[h_1^2(X)\right] \approx 6.92 < 11.14 \approx \mathbf{E}_{f_2}\left[h_2^2(X)\right] \end{equation*}\]

και συνεπώς \[\begin{equation*} \mathbf{V}_{f_1}\left[h_1(X)\right] \approx 0.64 < 4.85 \approx \mathbf{V}_{f_2}\left[h_2(X)\right] \end{equation*}\]

Όταν μία μέθοδος προσομοίωσης μας εξασφαλίζει μικρότερη διασπορά, τότε αυτό σημαίνει πρακτικά ότι θα χρειαζόμαστε μικρότερο πλήθος προσομοιώσεων για να εξασφαλίσουμε μία δεδομένη ακρίβεια και έτσι η μέθοδος αυτή είναι πιο αποδοτική. Τις περισσότερες φορές η διασπορά θα είναι άγνωστη και θα πρέπει να εκτιμηθεί από το ίδιο το δείγμα. Αν \(\overline{h}_n\) είναι ο δειγματικός μέσος, τότε

\[\begin{equation*} \sigma^2_{\overline{h}_n}=\mathbf{V}_f\left(\overline{h}_n\right) = \frac{\mathbf{V}_f\left[h(X)\right]}{n} = \frac{\sigma^2_h}{n}. \end{equation*}\]

Με την προϋπόθεση λοιπόν ότι η παραπάνω διασπορά είναι πεπερασμένη, μπορούμε να την εκτιμήσουμε με χρήση της δειγματικής διασποράς. Αν

\[\begin{equation*} \widehat{\sigma^2}_{h,n}=\frac{1}{n} \sum_{j=1}^n\left(h(X_j)-\overline{h}_n\right)^2, \end{equation*}\]

είναι η (μη αμερόληπτη) εκτιμήτρια της \(\mathbf{V}_f\left[h(X)\right]\), τότε η εκτιμήτρια της \(\mathbf{V}_f\left(\overline{h}_n\right)\) προκύπτει από τη σχέση

\[\begin{equation*} \widehat{\sigma^2}_{\overline{h}_n}=\frac{\widehat{\sigma^2}_{h,n}}{n}= \frac{1}{n^2} \sum_{j=1}^n\left(h(X_j)-\overline{h}_n\right)^2. \end{equation*}\]

Παρατηρούμε επίσης ότι

\[\begin{equation*} \widehat{\sigma^2}_{h,n} = \overline{h^{2}_{n}} - (\overline{h}_n)^2 \xrightarrow[n\rightarrow \infty]{a.s.}\mathbf{E}_{f}\left[h^2(X)\right] - \mathbf{E}_{f}^2\left[h(X)\right]=\mathbf{V}_f\left[h(X)\right], \end{equation*}\]

όπου χρησιμοποιήσαμε τον Ι.Ν.Μ.Α. για τις ακολουθίες \(\{h^2(X_j)\}\) και \(\{h(X_j)\}\), όπως επίσης και το θεώρημα συνεχούς απεικόνισης. Η (ισχυρή) συνέπεια της δειγματικής διασποράς μας επιτρέπει να εκτιμήσουμε την άγνωστη διασπορά \(\mathbf{V}_f\left[h(X)\right]\) και να κατασκευάσουμε ασυμπτωτικά διαστήματα εμπιστοσύνης για την τιμή του \(I\). Πράγματι, από το κλασικό κεντρικό οριακό θεώρημα έχουμε

\[\begin{equation*} \sqrt{n}\, \Big(\overline{h}_n - Ι \Big)\, \xrightarrow{d}\, N( 0, \sigma^2_h ) \end{equation*}\] ή ισοδύναμα \[\begin{equation*} \sqrt{n}\ \frac{\overline{h}_n - Ι }{\sigma_h}\, \xrightarrow{d}\, N( 0,1) \end{equation*}\]

Από το θεώρημα του Slutsky και το Θ.Σ.Α. προκύπτει ότι \[\begin{equation*} \sqrt{n}\ \frac{\overline{h}_n - Ι }{\widehat{\sigma}_{h,n}}\, \xrightarrow{d}\, N( 0,1), \end{equation*}\]

δίνοντας ασυμπτωτικά (1-α)-Δ.Ε. της μορφής \[\begin{equation*} \overline{h}_n \pm z_{a/2}\frac{\widehat{\sigma}_{h,n}}{\sqrt{n}} \end{equation*}\]

Παράδειγμα 4.2 Εκτιμήστε το ολοκλήρωμα της

\[\begin{equation*} h(x)=\left[\cos(50x)+\sin(20x)\right]^2, \end{equation*}\]

στο \(\left[ 0, 1 \right]\).

Λύση:

Μπορούμε να αναπαραστήσουμε το ολοκλήρωμα αυτό ως τη μέση τιμή μιας συνάρτησης μιας ομοιόμορφα κατανεμημένης τ.μ.. Με αυτόν τον τρόπο, μπορούμε να προσομοιώσουμε \(U_1, U_2, ..., U_n\) από την \(\mathcal{Unif}(0,1)\) και να εκτιμήσουμε το \(\int h(x) dx\) με το \(\sum h(U_i)/n\). Υλοποιούμε την προσομοίωση στην R και παρουσιάζουμε το γράφημα της h(x) και της σύγκλισης του δειγματικού μέσου.

h <- function(x){
  (cos(50 * x) + sin(20 * x)) ^ 2
}
par(mar = c(2, 2, 2, 1), mfrow = c(2, 1))
curve(h, xlab = "Function", ylab = "", lwd = 2)
H <- integrate(h, 0, 1); H
## 0.9652009 with absolute error < 1.9e-10

x <- h(runif(10 ^ 4))
estint <- cumsum(x) / (1:(10 ^ 4))
esterr <- sqrt(cumsum((x - estint) ^ 2))/(1:(10 ^ 4))

plot(estint, xlab = "Mean and error range", type = "l", lwd = 2,
     ylim = mean(x) + 20 * c(-esterr[10 ^ 4], esterr[10 ^ 4]), ylab = "") 
lines(estint + 1.96 * esterr, col = "gold", lwd = 2)
lines(estint - 1.96 * esterr, col = "gold", lwd = 2)
abline(a=H$value,b=0, col="red")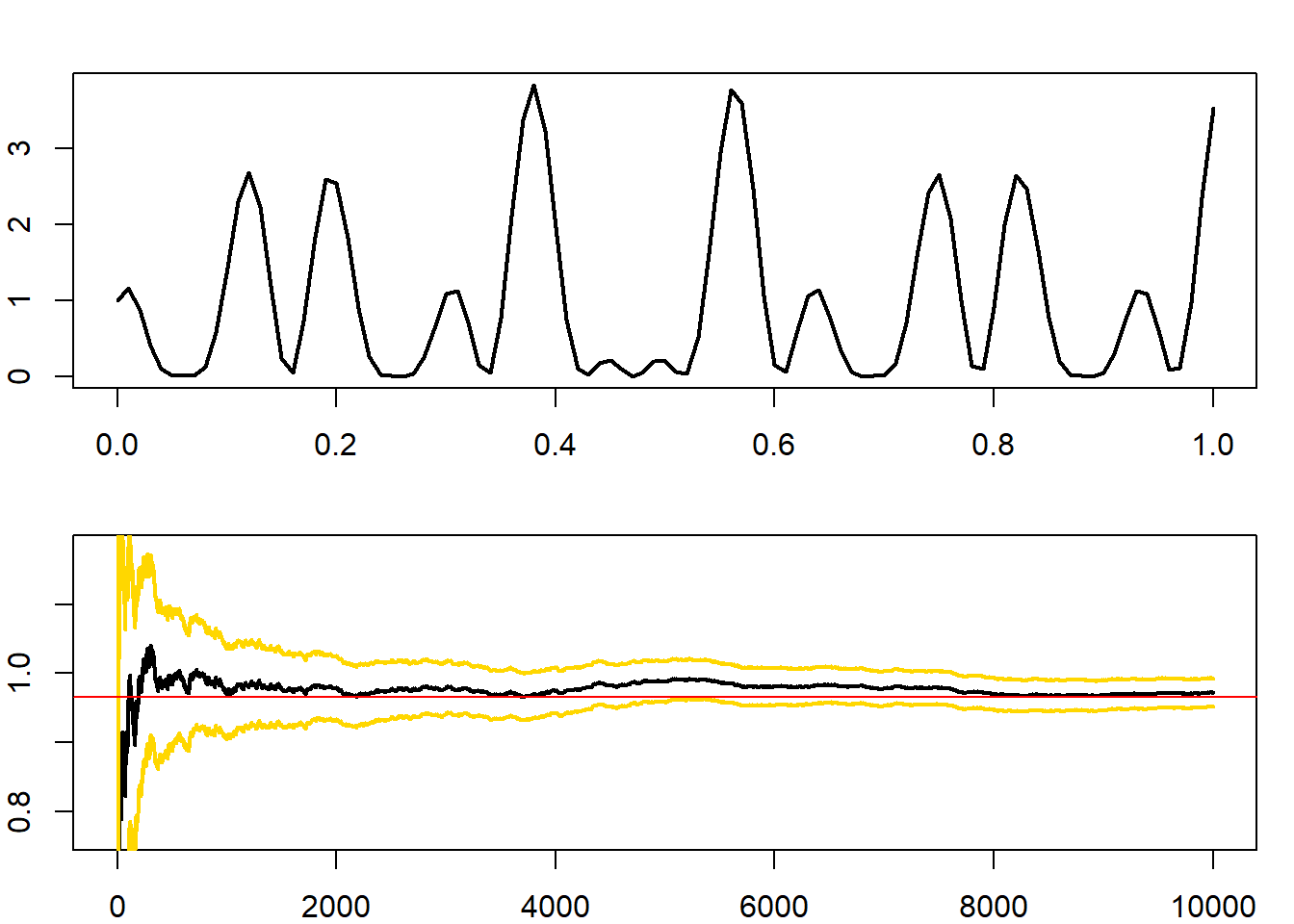

Σημειώνουμε ότι η λωρίδα εμπιστοσύνης που φαίνεται στο γράφημα δεν είναι μία ταυτόχρονη ασυμπτωτική \(95\%\) λωρίδα εμπιστοσύνης (simultaneous confidence band) αλλά μία σημειακή ασυμπτωτική (pointwise) \(95\%\) λωρίδα εμπιστοσύνης (δηλάδή υποδεικνύει το ασυμπτωτικό \(95\%\) διάστημα εμπιστοσύνης για κάθε μέγεθος δείγματος \(n\), εάν σταματούσαμε την προσομοίωση εκεί).

Παράδειγμα 4.3 Δοθέντος ενός δείγματος \((x_1, x_2, ..., x_n)\) από την κανονική \(\mathcal{N}(0,1)\), προσεγγίστε το

\[\begin{equation*} \Phi(t)=\int_{-\infty}^t \frac{1}{\sqrt{2\pi}} e^{-y^2/2} dy=\mathbf{P}(X\leq t)=\mathbf{E}\left[\mathbb{I}_{X\leq t}\right]. \end{equation*}\]

Λύση:

Επιλέγουμε ως εκτιμήτρια την

\[\begin{equation*} \widehat{\Phi}(t)=\frac{1}{n} \sum_{i=1}^n \mathbb{I}_{X_i\leq t}, \quad t\in \mathbb{R}. \end{equation*}\]

Η παραπάνω εκτιμήτρια είναι αμερόληπτη με (ακριβή) διασπορά \(\Phi(t)\left[1-\Phi(t)\right]/n\) (αφού οι \(\mathbb{I}_{Χ_i\leq t}\) είναι ανεξάρτητες Bernoulli με πιθανότητα επιτυχίας \(\Phi(t)\)).

x <- rnorm(10 ^ 8) # whole sample
bound <- qnorm(c(.5, .75, .8, .9, .95, .99, .999, .9999))
res <- matrix(0, ncol = 8, nrow = 7)
for (i in 2:8) { # lengthy loop!!
  for (j in 1:8) {
    res[i - 1, j] <- mean(x[1:(10 ^ i)] < bound[j])
  }
}
m <- matrix(as.numeric(format(res, digi = 4)), ncol = 8) 

Πίνακας 4.1: Εκτιμήσεις Monte Carlo

	0.0	0.67	0.84	1.28	1.65	2.32	3.09	3.72
100	0.4900	0.7600	0.8500	0.9000	0.9500	0.9900	1.0000	1.0000
1000	0.5030	0.7380	0.8000	0.8870	0.9420	0.9880	0.9990	1.0000
10.000	0.4911	0.7452	0.7987	0.9006	0.9514	0.9909	0.9988	1.0000
100.000	0.4987	0.7502	0.8009	0.9011	0.9513	0.9907	0.9990	0.9999
1.000.000	0.5003	0.7497	0.8000	0.9003	0.9500	0.9901	0.9990	0.9999
10.000.000	0.5002	0.7501	0.8000	0.9001	0.9501	0.9900	0.9990	0.9999
100.000.000	0.5000	0.7499	0.7999	0.9000	0.9500	0.9900	0.9990	0.9999

Για τιμές του \(t\) γύρω από το \(0\), η διασπορά είναι κατά προσέγγιση \(1/4n\), και για να επιτύχουμε ακρίβεια τεσσάρων δεκαδικών, χρειαζόμαστε \(2\cdot \sqrt{1/4n}\le 10^{-4}\) προσομοιώσεις, δηλαδή περίπου \(n=(10^4)^2=10^8\) προσομοιώσεις. Ο πίνακας δείχνει την εξέλιξη αυτής της προσέγγισης για αρκετές τιμές του \(t\) και δίνει μία εκτίμηση (με ακρίβεια 4 δεκαδικών ψηφίων) για 100 εκατομμύρια επαναλήψεις. Σημειώνουμε ότι καλύτερη (απόλυτη) ακρίβεια επιτυγχάνεται στις ουρές και ότι η συγκεκριμένη προσέγγιση μπορεί να υλοποιηθεί με πολύ πιο αποδοτικές μεθόδους.

Ενώ η χρήση των μεθόδων Monte Carlo ξεκίνησε ως μία διαδικασία προσεγγιστικής ολοκλήρωσης, μπορεί να χρησιμοποιηθεί για ποικίλους σκοπούς.

Παράδειγμα 4.4 Χρησιμοποιείστε το παράδειγμα 4.1 για να εκτιμήσετε το \(\pi\).

Λύση:

Έχουμε:

\[\begin{equation*} I=\sqrt{2\pi} \Rightarrow \pi = \frac{I^2}{2} = \phi(I). \end{equation*}\]

Είναι φανερό λοιπόν, ότι έχοντας εκτιμήσει το \(I\) με κάποια Monte Carlo εκτιμήτρια \(\widehat{I}_n\), τότε μπορούμε να πάρουμε άμεσα μία εκτιμήτρια για το \(\pi\) με τη μέθοδο της αντικατάστασης (plug-in). Συγκεκριμένα,

\[\begin{equation*} \widehat{\pi}_n=\phi(\widehat{I_n}) = \frac{\left(\widehat{I_n}\right)^2}{2}. \end{equation*}\]

Εφόσον η \(\widehat{I}_n\) είναι ισχυρά συνεπής εκτιμήτρια του \(I\) και η \(\phi\) είναι συνεχής, από το Θ.Σ.Α. έχουμε μία ισχυρά συνεπή εκτιμήτρια του \(\pi\) καθώς

\[\begin{equation*} \widehat{\pi}_n=\phi(\widehat{I_n}) \overset{a.s.}{\longrightarrow} \phi(I) = \pi, \end{equation*}\]

και από την ασυμπτωτική κανονικότητα της \(\widehat{I}_n\) και τη μέθοδο Δέλτα για τη διαφορίσιμη \(\phi\), έχουμε

\[\begin{equation*} \sqrt{n}\left(\widehat{\pi}_n-\pi\right)=\sqrt{n}\left(\phi(\widehat{I_n})-\phi(I)\right)\overset{d}{\longrightarrow} \mathcal{N}\left(0, \left(\phi'(I)\right)^2 \sigma_h^2\right) = \mathcal{N}\left(0, I^2 \sigma_h^2\right). \end{equation*}\]

Ο προσδιορισμός της ακρίβειας της εκτίμησης γίνεται ασυμπτωτικά, χρησιμοποιώντας plug-in εκτιμήτρια της τυπικής απόκλισης \(Ι\, \sigma_h\). Από τη σχέση

\[\begin{equation*} \sqrt{n}\, \frac{\widehat{\pi}_n-\pi}{\widehat{Ι_n}\widehat{\sigma}_{h,n}}\overset{d}{\longrightarrow} \mathcal{N}(0,1), \end{equation*}\]

προσδιορίζουμε το ασυμπτωτικό (1-α)-Δ.Ε. για το \(\pi\):

\[\begin{equation*} \widehat{\pi}_n \pm z_{a/2} \frac{\widehat{Ι_n}\widehat{\sigma}_{h,n}}{\sqrt{n}}. \end{equation*}\]

Στο παρακάτω γράφημα δείχνουμε μία πορεία εκτίμησης του \(\pi\), μαζί με την εξέλιξη των ασυμπτωτικών \(99\%\)-λωρίδων εμπιστοσύνης για το \(\pi\) όταν χρησιμοποιούμε \(10^5\) προσομοιώσεις από τη διπλή εκθετική. Η προσέγγιση του \(\pi\) είναι 3.1455051 και επομένως είναι σωστή σε 2 δεκαδικά ψηφία.

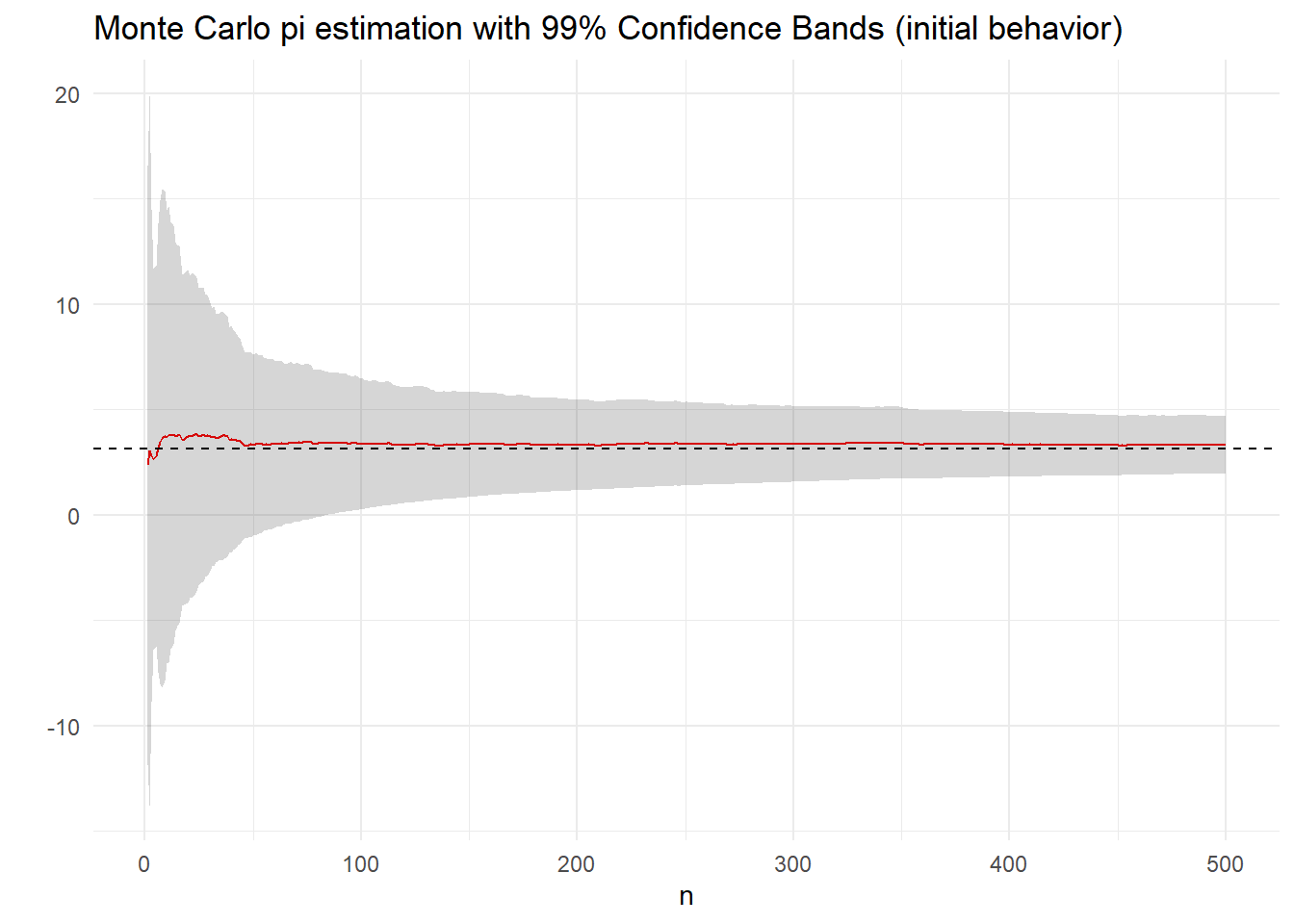
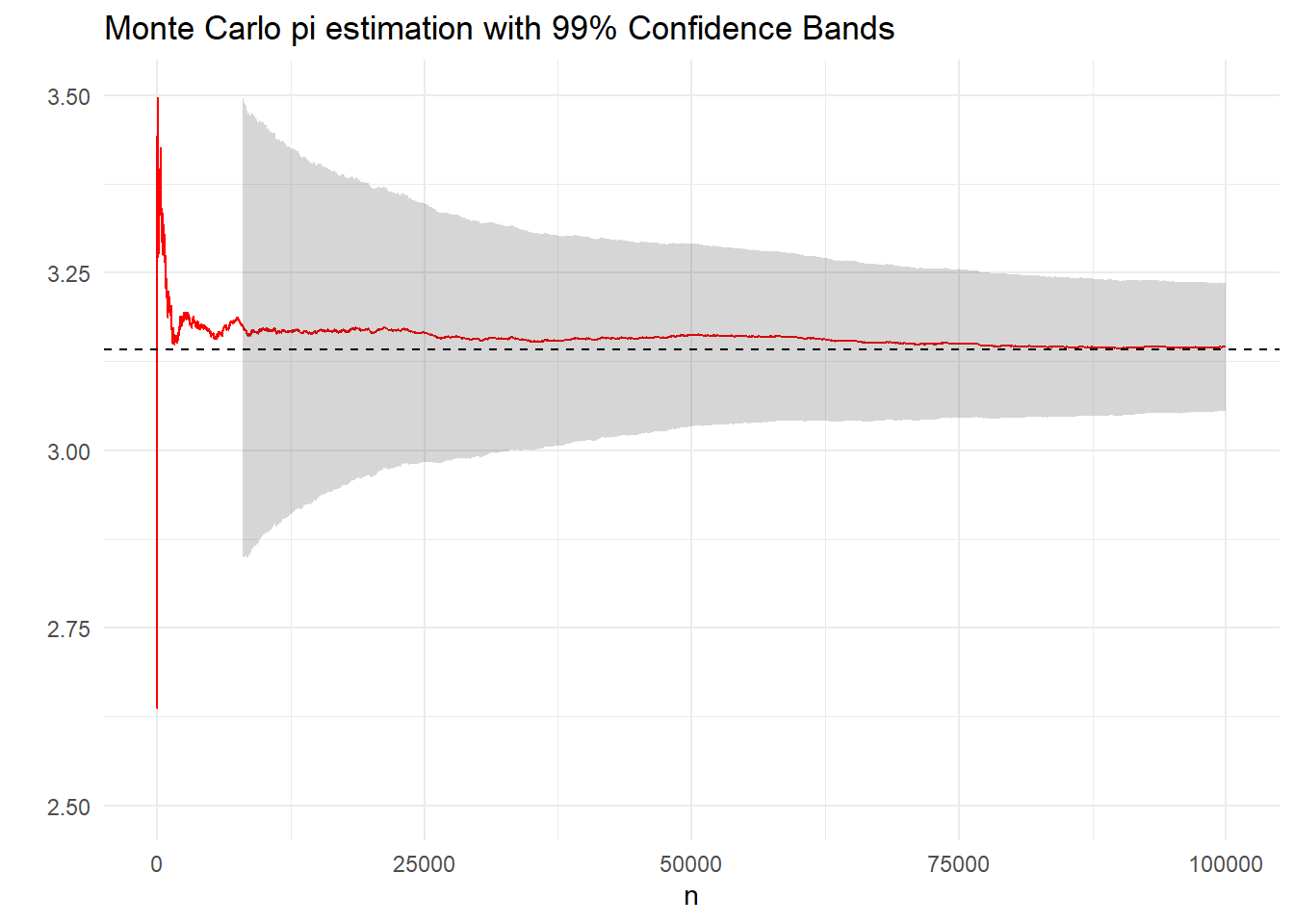
Αντίστοιχα μας ενδιαφέρει η ασυμπτωτική κατανομή της (μη αμερόληπτης) δειγματικής διασποράς \(\widehat{\sigma^2}_{h,n}=\frac{1}{n}\sum_{j=1}^n\left(h(X_j)-\overline{h}_n\right)^2\) της \(\mathbf{V}_f\left[ h(X) \right]\). Εκμεταλλευόμενοι το γεγονός ότι η παραπάνω έχει την ίδια ασυμπτωτική κατανομή με την \(\frac{1}{n}\sum_{j=1}^n\left(h(X_j)-Ι\right)^2\), για την οποία ισχύει \(\mathbf{E}_f\left[\left(h(X)-Ι\right)^2\right]=\sigma_h^2\) και \(\mathbf{V}_f\left[\left(h(X)-Ι\right)^2\right]=\mathbf{E}_f\left[\left(h(X)-Ι\right)^4\right]-\left(\mathbf{E}_f\left[h(X)-Ι\right]^2\right)^2=\mu_{4,h}-\sigma_h^4\), εφαρμόζεται άμεσα το (μονοδιάστατο) ΚΟΘ και παίρνουμε ότι

\[\begin{equation*} \sqrt{n}\left(\widehat{\sigma^2}_{h,n}-\sigma^2_h\right) \overset{d}{\longrightarrow} \mathcal{N}\left(0, \mu_{4,h}-\sigma_h^4 \right). \end{equation*}\]

Θα ήταν ενδιαφέρον να μελετήσουμε επίσης την από κοινού συμπεριφορά της εκτιμήτριας \(\widehat{I_n}\) και της εκτιμημένης διασποράς \(\widehat{\sigma^2}_{h,n}\). Προκειμένου να είμαστε σε θέση να τις μελετήσουμε, θα χρειαστούμε κάποια βασικά εργαλεία πολυδιάστατης στατιστικής, όπως επίσης και τον ορισμό και στοιχειώδεις ιδιότητες της πολυδιάστατης κανονικής.

Παράδειγμα 4.5 Εκτιμήστε το \(\pi\) κάνοντας τυχαία επιλογή σημείων εντός ενός τετραγώνου πλευράς 2 και μετρώντας το ποσοστό των σημείων που βρίσκονται εντός του εγγεγραμμένου του κύκλου (ακτίνας 1).

Λύση:

Αναμένουμε το ποσοστό των σημείων που πέφτουν μέσα στον κύκλο να είναι περίπου \[\begin{equation*} \lambda = \frac{\text{Εμβ}(K)}{\text{Εμβ}(T)}=\frac{\pi}{4}, \end{equation*}\]

όσο και ο λόγος των εμβαδών του κύκλου προς το τετράγωνο. H εκτίμηση \(\widehat{\pi}\) του \(\pi\) θα δίνεται τελικά από τη σχέση \(\widehat{\pi}=4\widehat{\lambda}\), όπου \(\widehat{\lambda}\) αντιστοιχεί στο ποσοστό των σημείων που βρίσκονται στο εσωτερικό του κύκλου. Ο παρακάτω αλγόριθμος υλοποιεί την εκτίμηση του \(\pi\).

set.seed(102)
N <- 1e4
radius <- 1
side <- 2 * radius
x <- runif(N, -radius, radius)
y <- runif(N, -radius, radius)

inside <- sqrt(x ^ 2 + y ^ 2) <= radius
percent <- sum(inside) / N
pi2 <- 4 * percent 
pi2
## [1] 3.1556
pi
## [1] 3.141593

Παρατηρούμε ότι όταν το μέγεθος του Monte-Carlo δείγματος είναι \(10^4\), τότε η ακρίβεια εκτίμησης του \(\pi\) είναι περίπου \(10^{-2}\). Μπορείτε να επαναλάβετε την εκτίμηση του \(\pi\) με διαφορετικούς σπόρους (είτε απλά να ξανατρέξετε πολλές φορές τον παραπάνω κώδικα, αγνοώντας την πρώτη γραμμή), ώστε να διαπιστώσετε ότι οι εκτιμήσεις διαφοροποιούνται. Αυτό είναι ένα βασικό χαρακτηριστικό των στοχαστικών αλγορίθμων. Το αποτέλεσμά τους αλλάζει κάθε φορά που επαναλαμβάνουμε το πείραμα. Για το λόγο αυτό, το αποτέλεσμα είναι τυχαία μεταβλητή.

Στο παρακάτω σχήμα απεικονίζεται γραφικά η παραγωγή τυχαίων σημείων. Όσα σημεία έχουν μπλε χρώμα ικανοποίησαν τη συνθήκη ότι η απόστασή τους από το κέντρο του κύκλου ήταν μικρότερη (ή ίση) από την ακτίνα, ενώ αντίθετα όσα έχουν κόκκινο χρώμα δεν ικανοποίησαν τη συνθήκη.

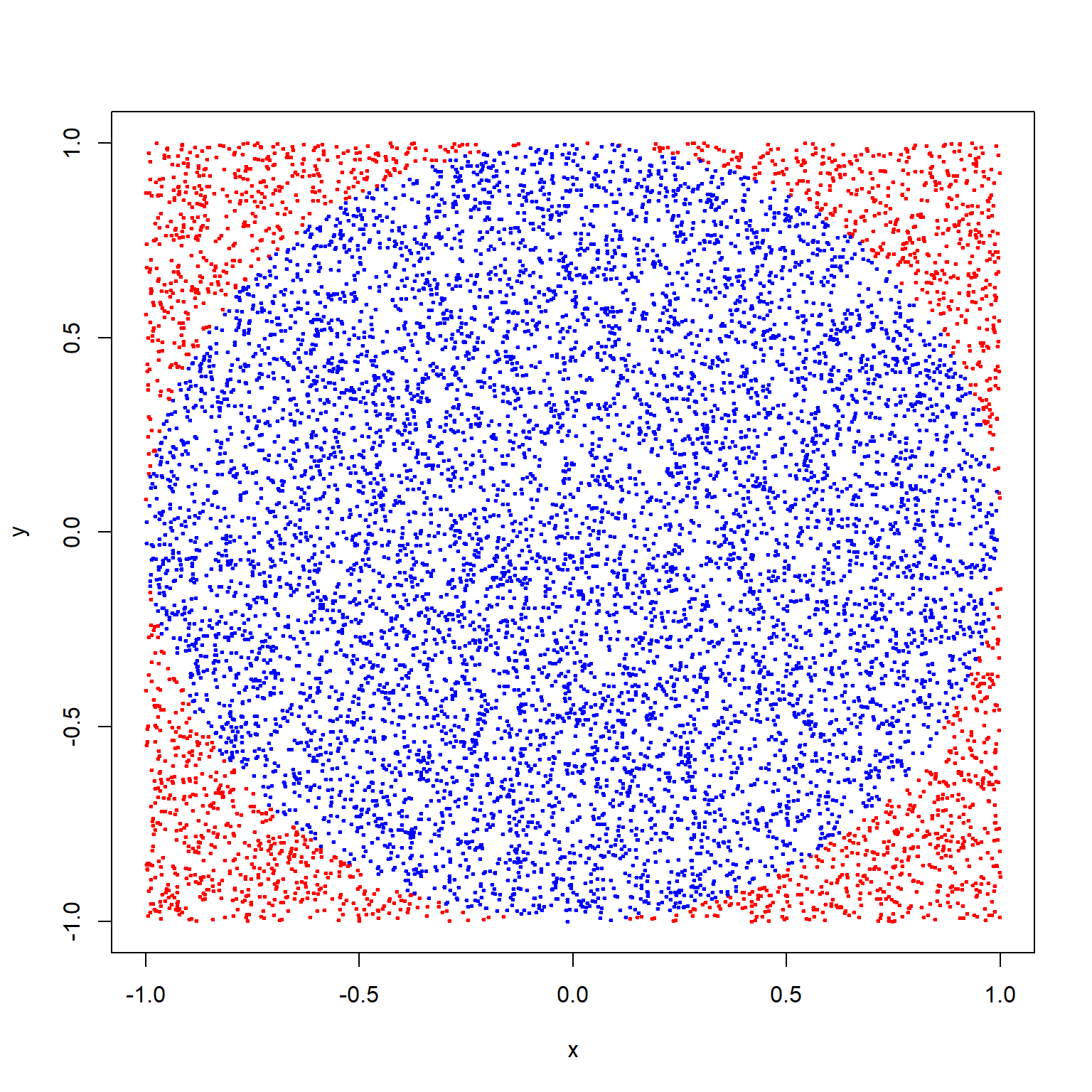
Για μία καλύτερη εκτίμηση του \(\pi\) θα χρειαστεί βέβαια να αυξήσουμε το μέγεθος του δείγματος.

N <- 1e6
x <- runif(N, -radius, radius)
y <- runif(N, -radius, radius)

inside <- sqrt(x ^ 2 + y ^ 2) <= radius
percent <- sum(inside) / N
area <- percent * side ^ 2
pi2 <- area / radius ^ 2
pi2
## [1] 3.13904
pi
## [1] 3.141593

Παρατηρούμε ότι όταν το μέγεθος του Monte-Carlo δείγματος είναι \(10^6\), τότε η ακρίβεια εκτίμησης του \(\pi\) είναι περίπου \(10^{-3}\). Θα μπορούσε να σκεφτεί λοιπόν κάποιος, αν συνδυάσει και το αποτέλεσμα για μέγεθος δείγματος \(10^4\), ότι όσο μεγαλώνει το μέγεθος του δείγματος, τόσο καλύτερα προσεγγίζουμε το \(\pi\) και μάλιστα για μέγεθος δείγματος \(N\), η ακρίβεια της εκτίμησης είναι κοντά στο \(1/\sqrt{N}\). Η πρώτη παρατήρηση θα αιτιολογηθεί αργότερα από τον Ισχυρό Νόμο των Μεγάλων Αριθμών και η δεύτερη από το Κεντρικό Οριακό Θεώρημα, που είναι τα σημαντικότερα αποτελέσματα της Θεωρίας Πιθανοτήτων.

Αυτό το σημείο χρειάζεται προσοχή, καθώς ναι μεν ο υπολογιστής μας δίνει τη δυνατότητα να προσομοιώνουμε ένα πολύ μεγάλο πλήθος αριθμών από μία κατανομή ενδιαφέροντος, αλλά η ακρίβεια με την οποία θέλουμε να εκτιμήσουμε μία ποσότητα παίζει ρόλο καθοριστικό για το αν η χρήση των υπολογιστικά εντατικών μεθόδων Monte-Carlo μπορεί να δώσει μία ικανοποιητική απάντηση στο πρόβλημα που μας απασχολεί. Είναι φανερό ότι για καλές προσεγγίσεις του \(\pi\), με αρκετά δεκαδικά ψηφία, η χρήση στοχαστικών αλγορίθμων δεν ενδείκνυται, αλλά παρ’όλα αυτά η προσέγγιση του \(\pi\) με Monte-Carlo παραμένει διδακτικά ενδιαφέρουσα.

Μπορούμε να επαναλάβουμε την εκτίμηση κάποιες φορές για να διαπιστώσουμε ακόμα μία φορά την “στοχαστικότητα” του αποτελέσματος.

Παράδειγμα 4.6 Βρείτε την από κοινού ασυμπτωτική κατανομή των \(\widehat{I}_n\) και \(\widehat{\sigma^2}_{h,n}\) του παραδείγματος (4.1).

Λύση:

Έχουμε:

\[\begin{equation*} \sqrt{n}\left[ \left(\widehat{I_n}, \widehat{\sigma}_{h,n}\right)^\top - \left( I, \sigma_h\right)^\top \right] \xrightarrow{d} \mathcal{N}_2(0, \Sigma_h'), \end{equation*}\]

όπου

\[\begin{equation*} \Sigma_h'=\sigma^2\begin{pmatrix} 1 & \lambda_h/2 \\ \lambda_h/2 & (\kappa_h-1)/4 \end{pmatrix}. \end{equation*}\]

Επομένως, για αρκετά μεγάλο \(n\) θα έχουμε

\[\begin{equation*} \left(\widehat{I_n}, \widehat{\sigma}_{h,n}\right)^\top \overset{d}{\approx} \mathcal{N}_2(\left( I, \sigma_h\right)^\top, \Sigma_h'/n). \end{equation*}\]

Έχοντας μία προσέγγιση της ασυμπτωτικής κατανομής των παραπάνω εκτιμητριών, μετά μπορούμε να βρούμε προσεγγιστικές κατανομές συναρτήσεών τους. Για παράδειγμα, μία προσέγγιση της κατανομής του ανώτερου και κατώτερου ορίου \(\widehat{I_n} \pm\frac{z_{a/2}}{\sqrt{n}} \widehat{\sigma}_{h,n}\) των \((1-a)-\)λωρίδων εμπιστοσύνης. Για το σκοπό αυτό εφαρμόζουμε το γραμμικό μετασχηματισμό για \(u=\left(1, \pm \frac{z_{a/2}}{\sqrt{n}}\right)^\top\) και παίρνουμε:

\[\begin{equation*} \widehat{I_n} \pm\frac{z_{a/2}}{\sqrt{n}} \widehat{\sigma}_{h,n} \overset{d}{\approx} \mathcal{N}\left(I\pm\frac{z_{a/2}}{\sqrt{n}} \sigma_h,\ \frac{\sigma_h^2}{n} \left(1\pm \frac{ z_{a/2}\lambda_h}{\sqrt{n}} +\frac{z^2_{a/2}(k_h-1)}{4n}\right)\right). \end{equation*}\]

Σε αυτό το πρόβλημα οι συντελεστές λοξότητας και κύρτωσης για την \(h_1(X)\) υπολογίζονται ακριβώς, αφού μπορούμε να βρούμε αναλυτικό τύπο για τις ροπές \(k-\)τάξης:

\[\begin{align*} \mathbf{E}_{f}\left[h_1^k(X)\right] &= \int_{-\infty}^{+\infty} 2^k e^{-\frac{k}{2}x^2 + k|x|} \frac{1}{2}e^{-|x|} dx = \int_{-\infty}^{+\infty} 2^{k-1} e^{-\frac{k}{2}x^2 + (k-1)|x|} dx = \int_{-\infty}^{+\infty} 2^{k-1} e^{-\frac{1}{2}\left(\sqrt{k}|x|-\frac{k-1}{\sqrt{k}}\right)^2 +\frac{(k-1)^2}{2k}} dx \\ &=2^{k-1} e^{\frac{(k-1)^2}{2k}} \int_{-\infty}^{+\infty}e^{-\frac{1}{2}\left(\sqrt{k}|x|-\frac{k-1}{\sqrt{k}}\right)^2} dx =2^{k-1} e^{\frac{(k-1)^2}{2k}} \int_{-\infty}^{0}e^{-\frac{1}{2}\left(\sqrt{k}x+\frac{k-1}{\sqrt{k}}\right)^2} + 2^{k-1} e^{\frac{(k-1)^2}{2k}} \int_{0}^{+\infty}e^{-\frac{1}{2}\left(\sqrt{k}x-\frac{k-1}{\sqrt{k}}\right)^2} dx \\ &=2^{k-1} e^{\frac{(k-1)^2}{2k}} \int_{-\frac{k-1}{\sqrt{k}}}^{+\infty} \frac{1}{\sqrt{k}} e^{-\frac{1}{2}y^2} dy +2^{k-1} e^{\frac{(k-1)^2}{2k}} \int_{-\infty}^{+\frac{k-1}{\sqrt{k}}} \frac{1}{\sqrt{k}} e^{-\frac{1}{2}y^2} dy =\frac{\sqrt{2\pi}}{\sqrt{k}}2^{k-1} e^{\frac{(k-1)^2}{2k}} \int_{-\frac{k-1}{\sqrt{k}}}^{+\infty} \frac{1}{\sqrt{2\pi}} e^{-\frac{1}{2}y^2} dy +\frac{\sqrt{2\pi}}{\sqrt{k}}2^{k-1} e^{\frac{(k-1)^2}{2k}} \int_{-\infty}^{+\frac{k-1}{\sqrt{k}}} \frac{1}{\sqrt{2\pi}} e^{-\frac{1}{2}y^2} dy \\ &=\frac{\sqrt{2\pi}}{\sqrt{k}}2^{k-1} e^{\frac{(k-1)^2}{2k}} \left(1-\Phi\left(-\frac{k-1}{\sqrt{k}}\right) \right) +\frac{\sqrt{2\pi}}{\sqrt{k}}2^{k-1} e^{\frac{(k-1)^2}{2k}}\Phi\left(\frac{k-1}{\sqrt{k}}\right) = \frac{\sqrt{2\pi}}{\sqrt{k}}2^{k-1} e^{\frac{(k-1)^2}{2k}} \cdot 2 \Phi\left(\frac{k-1}{\sqrt{k}}\right) \\ &=2^{k}\frac{\sqrt{2\pi}}{\sqrt{k}} e^{\frac{(k-1)^2}{2k}} \Phi\left(\frac{k-1}{\sqrt{k}}\right). \end{align*}\]

Αρχικά, επαληθεύουμε για \(k=1, 2\):

\[\begin{align*} \mathbf{E}_{f}\left[h_1(X)\right] &=\sqrt{2\pi} = I, \\ \mathbf{E}_{f}\left[h_1^2(X)\right] &=4\sqrt{\pi}e^{1/4} \Phi\left(\frac{1}{\sqrt{2}}\right). \end{align*}\]

Για \(k=3, 4\) έχουμε:

\[\begin{align*} \mathbf{E}_{f}\left[h_1^3(X)\right] &=8\frac{\sqrt{2\pi}}{\sqrt{3}}e \Phi\left(\frac{2}{\sqrt{3}}\right), \\ \mathbf{E}_{f}\left[h_1^4(X)\right] &=8\sqrt{2\pi}e^{9/8} \Phi\left(\frac{3}{2}\right). \end{align*}\]

Αφήνεται τώρα ως άσκηση ο υπολογισμός των \(\lambda_h\) και \(k_h\). Σε άλλες περιπτώσεις οι συντελεστές αυτοί πρέπει να εκτιμηθούν από το προσομοιωμένο δείγμα χρησιμοποιώντας τους αντίστοιχους δειγματικούς.

4.2 Δειγματοληψία Σπουδαιότητας

Ας υποθέσουμε ότι δε μπορούμε να προσομοιώσουμε από τη \(\mathcal{N}(0,1)\). Παρ’ όλα αυτά έχουμε τη δυνατότητα να προσομοιώνουμε από τη διπλή εκθετική. Το ερώτημα που τίθεται είναι κατά πόσον μπορούμε να φτάσουμε στο ίδιο αποτέλεσμα, δηλαδή μετά από ένα κατάλληλα μεγάλο μέγεθος δείγματος να μπορούμε να βρεθούμε οσοδήποτε κοντά θέλουμε στην κανονική κατανομή, και συγκεκριμένα στην σ.κ. \(\Phi\). Η πρώτη μας σκέψη θα ήταν ότι αν προσομοιώναμε από τη διπλή εκθετική, τότε χρησιμοποιώντας την εμπειρική συνάρτηση κατανομής της, θα μπορούσαμε να προσεγγίσουμε όσο καλά θέλουμε την \(F_L\), δηλαδή τη σ.κ. της \(Laplace(0,1)\) (δηλ. τη διπλή εκθετική) και όχι τη \(\Phi\). Με κάποιο τρόπο πρέπει να αντισταθμίσουμε ότι προσομοιώνουμε από διαφορετική κατανομή από αυτήν που ζητάμε. Παρατηρούμε ότι

\[\begin{equation*} \Phi(x) = \mathbf{E}_f\left[\mathbb{I}_{X\leq x}\right] = \mathbf{E}_g\left[\mathbb{I}_{X\leq x} \cdot \frac{f(X)}{g(X)}\right]. \end{equation*}\]

Προκειμένου λοιπόν να “στοχεύσουμε” με Monte Carlo στην \(\Phi\) θα μπορούσαμε να “προτείνουμε” από τη \(g\) και να αντισταθμίσουμε αυτή τη διαφορά εισάγοντας τη συνάρτηση “βάρους”

\[\begin{equation*} w(x)=\frac{f(x)}{g(x)}. \end{equation*}\]

Ο όρος importance function (συνάρτηση σπουδαιότητας) χρησιμοποιείται συχνά σε αυτό το πλαίσιο για τη \(g\) και ο όρος importance weight (βάρος σπουδαιότητας) για τη \(w=f/g\). Η ερμηνεία του βάρους σπουδαιότητας είναι αρκετά διαισθητική, αφού οι τιμές τις οποίες προσομοιώνει η \(g\) με μικρότερη (μεγαλύτερη) πυκνότητα από την \(f\) πρέπει να “ενισχυθούν” (“αποδυναμωθούν”) με μεγαλύτερο βάρος, έτσι ώστε τελικά ο “στόχος” να παραμένει στην \(f\). Γενικά, αυτό εκφράζεται ως

\[\begin{equation*} \mathbf{E}_f\left[h(X)\right] = \mathbf{E}_g\left[h(X) w(X)\right]. \end{equation*}\]

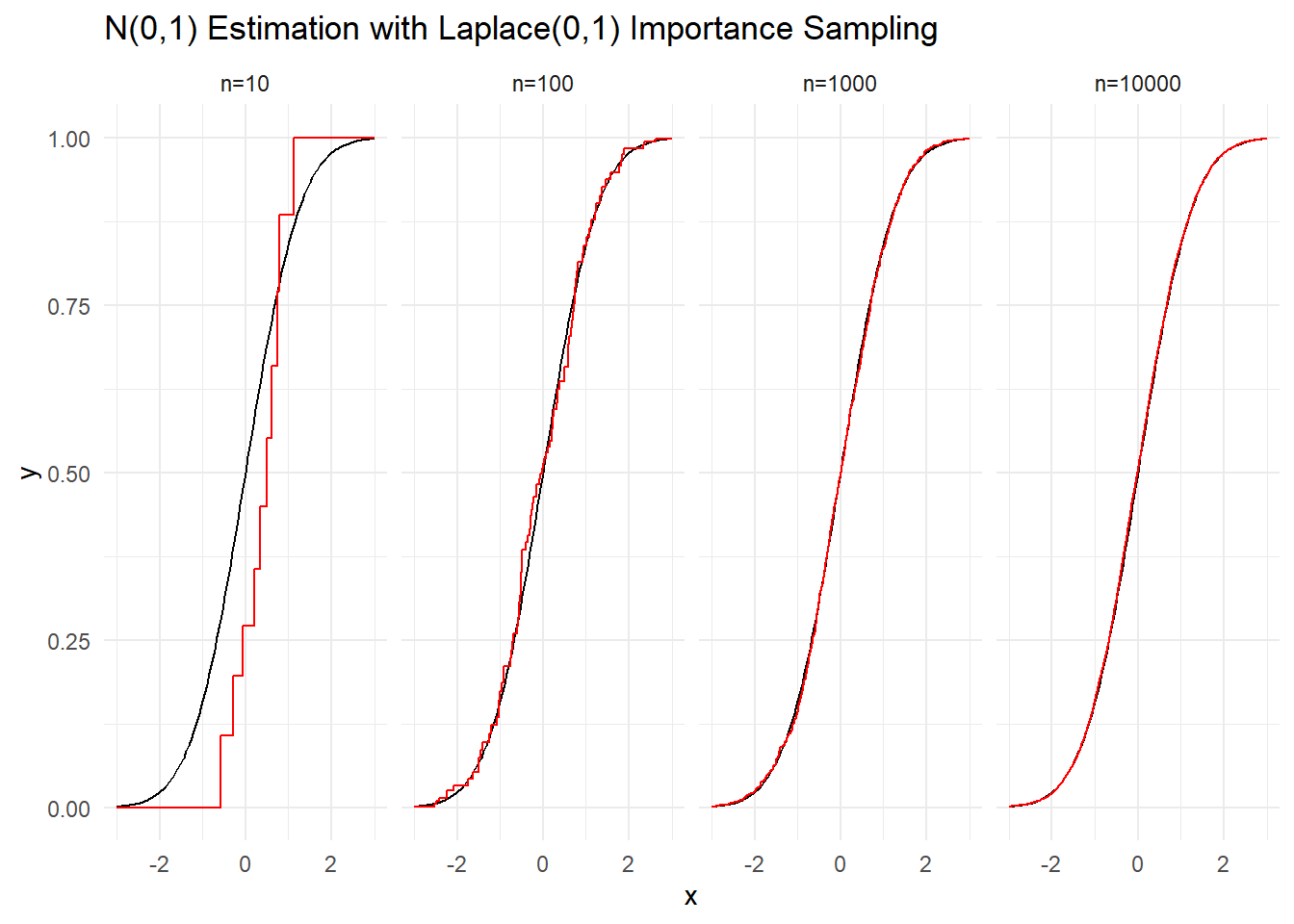
Παράδειγμα 4.7 Επαληθεύστε ότι με δειγματοληψία σπουδαιότητας από την \(Laplace(0,1)\) πετυχαίνουμε σύγκλιση στην \(\Phi\). Προσομοιώστε δείγματα μεγέθους \(n=10, 100, 1000\) και \(10000\).

Λύση:

# Importance weight
w <- function(s) {
  dnorm(s) / dlaplace(s)
}

# ecdf
Fn <- function(x, s) {
  sapply(x, FUN = function(x) { sum((s <= x) * w(s)) / sum(w(s)) })
}

Παράδειγμα 4.8 Εκτιμήστε την πιθανότητα \(\mathbf{P}(X>5)\) για \(X\sim \mathcal{N}(0,1)\).

Λύση:

Σύμφωνα με την R, η ζητούμενη πιθανότητα είναι \(p=2.8665\cdot 10^{-7}\). Σε αυτή την περίπτωση, η άμεση προσομοίωση από την \(\mathcal{N}(0,1)\) είναι ιδιαίτερα δύσκολη, αφού το ενδεχόμενο που θέλουμε να μελετήσουμε εμφανίζεται κατά μέσο όρο 1 φορά στις \(1/p=3488556\) παρατηρήσεις, δηλαδή θα χρειαστούμε περίπου 3.5 εκατομμύρια παρατηρήσεις για την εμφάνιση μίας παρατήρησης \(x_i>5\). Για τον λόγο αυτό, προτιμάμε να εκφράσουμε την πιθανότητα ως ολοκλήρωμα και να χρησιμοποιήσουμε Monte Carlo προσομοίωση.

\[\begin{equation*} \mathbf{P}(X>5) = \int_5^{+\infty} f(x) dx \overset{y=1/x}{=} \int_{1/5}^{0} f(1/y) \cdot \left(-\frac{1}{y^2}\right) dy = \int_0^{1/5} f(1/y) \frac{1}{y^2} dy. \end{equation*}\]

Σε αυτό το σημείο, μπορούμε να εκφράσουμε το ολοκλήρωμα ως μέση τιμή μιας τ.μ. \(Y\sim Unif(0, 1/5)\) με σ.π.π. \(g(y)=5\) στο διάστημα \((0, 1/5)\), και να πάρουμε

\[\begin{equation*} \int_0^{1/5} f(1/y) \frac{1}{y^2} dy = \int_0^{1/5} f(1/y) \frac{1}{5y^2} \cdot 5 dy = \int_0^{1/5} h(y)\cdot g(y) dy = \mathbf{E}_g\left[h(Y)\right)], \end{equation*}\]

όπου \(h(y)=f(1/y) \frac{1}{5y^2}\). Επομένως είμαστε έτοιμοι να προσομοιώσουμε από την \(Y\) και να λάβουμε την εκτίμησή μας καθώς και το εκτιμημένο τυπικό σφάλμα της εκτιμήτριας.

Στο παρακάτω γράφημα βλέπουμε την πορεία της εκτίμησης καθώς και την ασυμπτωτική σημειακή \(95\%\) λωρίδα εμπιστοσύνης για μέγεθος δείγματος \(n=10^5\). Η εκτίμηση που παίρνουμε είναι \(\widehat{p}_n=\) 2.9021 \(\cdot 10^{-7}\) με εκτιμημένο τυπικό σφάλμα \(\widehat{\sigma}_{\widehat{p}_n}=\) 0.0326\(\cdot 10^{-7}\).

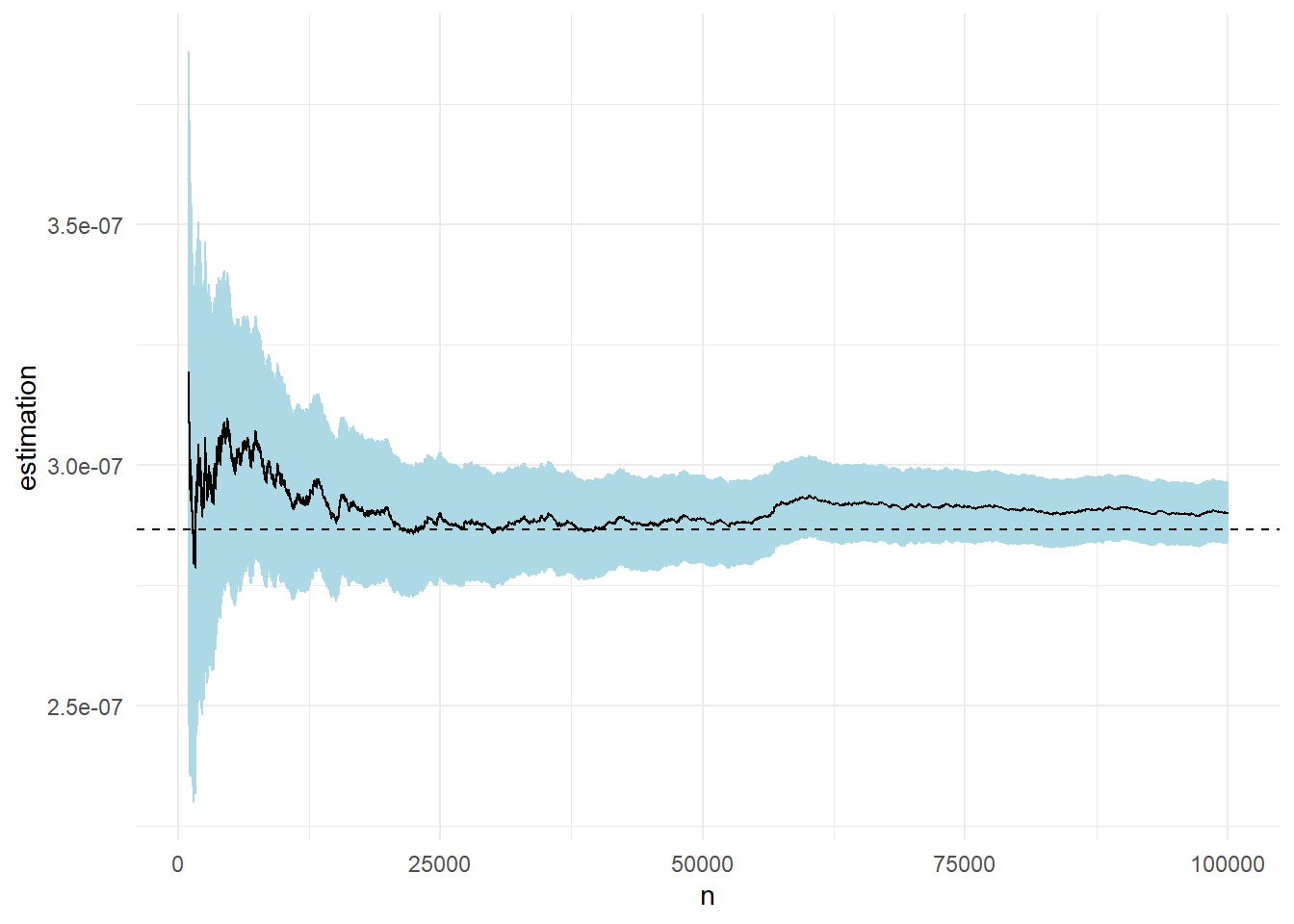
Παράδειγμα 4.9 Σε συνέχεια του Παραδείγματος 4.8, εκτιμήστε την πιθανότητα \(\mathbf{P}(X>5)\) όταν \(X\sim \mathcal{N}(0,1)\), αυτή τη φορά χρησιμοποιώντας δειγματοληψία σπουδαιότητας, με συνάρτηση σπουδαιότητας \(g\) από την περικεκκομένη εκθετική με παράμετρο 1 στο διάστημα \((5, +\infty)\).

Λύση:

Σημείωση: Έστω η τ.μ. \(Y\) που ακολουθεί μία συγκεκριμένη κατανομή. Η περικεκκομένη (truncated) κατανομή στο διάστημα \((a, \beta)\), το οποίο πρέπει να είναι υποσύνολο του στηρίγματος, όπου το \(a\) (αντίστοιχα, \(\beta\)) μπορεί να είναι και \(-\infty\) (αντίστοιχα, \(+\infty\)), χαρακτηρίζεται από την συνάρτηση κατανομής

\[\begin{equation*} F_{tr}(y) = \mathbf{P}\left(Y\leq y |Y\in (a, \beta)\right) = \frac{\int_a^y f(y) dy}{\int_a^\beta f(y) dy}, \ \ y\in (a, \beta). \end{equation*}\]

Ειδικά στην περίπτωση της εκθετικής κατανομής (που έχει την αμνήμονη ιδιότητα), έχουμε σημαντικές απλοποιήσεις. Έτσι, η περικεκκομένη εκθετική στο διάστημα \((a, +\infty)\) έχει συνάρτηση κατανομής

\[\begin{equation*} F_{tr}(y) = 1-e^{-\lambda(y-a)}\ \ y>a, \end{equation*}\]

και συνάρτηση πυκνότητας πιθανότητας

\[\begin{equation*} f(y) = \lambda e^{-\lambda (y-a)}, \ \ y>a. \end{equation*}\]

Τα παραπάνω υποδηλώνουν ότι αν \(Y\sim Exp(1)\), τότε η \((Y+a)\) ακολουθεί την περικεκκομένη εκθετική στο επιθυμητό διάστημα \((a, +\infty)\). Επομένως είναι ιδιαίτερα εύκολο να προσομοιώσουμε από την συγκεκριμένη κατανομή και να εφαρμόσουμε δειγματοληψία σπουδαιότητας. Έχουμε:

\[\begin{equation*} \mathbf{P}(X>5) = \mathbf{E}_f \left[\mathbb{I}_{\{X>5\}} \right] = \mathbf{E}_g \left[\mathbb{I}_{\{X>5\}} \cdot \frac{f(X)}{g(X)} \right] = \mathbf{E}_g \left[h(X) w(X) \right]=\mathbf{E}_g \left[w(X) \right], \end{equation*}\]

όπου \(h(x)=\mathbb{I}_{\{x>5\}}\) και \(w(x)=f(x)/g(x)\).

Στο παρακάτω γράφημα βλέπουμε την πορεία της εκτίμησης καθώς και την ασυμπτωτική σημειακή \(95\%\) λωρίδα εμπιστοσύνης για μέγεθος δείγματος \(n=10^5\). Η εκτίμηση που παίρνουμε είναι \(\widehat{p}_n=\) 2.869 \(\cdot 10^{-7}\) με εκτιμημένο τυπικό σφάλμα \(\widehat{s}_n=\) 0.0126\(\cdot 10^{-7}\).

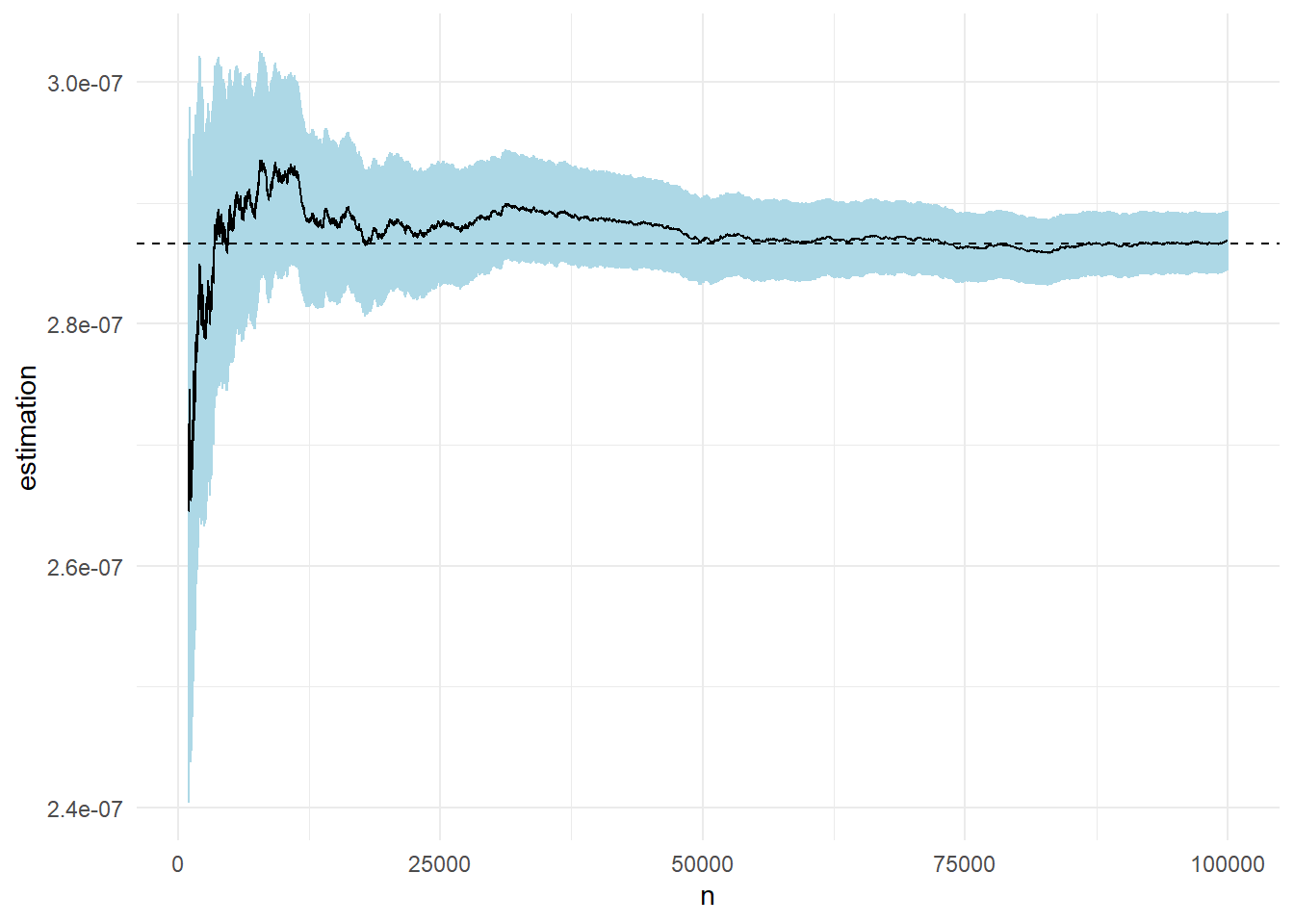
Παρατηρούμε ότι η σύγκλιση με αυτόν τον τρόπο είναι ταχύτερη σε σχέση με το προηγούμενο παράδειγμα, καθώς έχει μικρότερη ασυμπτωτική διασπορά, κάτι που φαίνεται και στα γραφήματα.

Παράδειγμα 4.10 Υπολογίστε την \(\mathbf{E}_f\left[h(X)\right]\), όπου \(f\) είναι η σ.π.π. της τυπικής κανονικής και \(h(x)=e^{-(x-3)^2/2}+e^{-(x-6)^2/2}\).

Λύση:

Η συγκεκριμένη μέση τιμή μπορεί να γραφεί σε κλειστή μορφή και να υπολογιστεί ως εξής:

\[\begin{align*} \mathbf{E}_f\left[h(X)\right] &= \int_{-\infty}^{+\infty} \left(e^{-(x-3)^2/2}+e^{-(x-6)^2/2}\right) \cdot \frac{1}{\sqrt{2\pi}} e^{-\frac{1}{2}x^2} dx \\ &= \int_{-\infty}^{+\infty} \frac{1}{\sqrt{2\pi}} e^{-\frac{1}{2}\left[ (x-3)^2 +x^2 \right]} dx + \int_{-\infty}^{+\infty} \frac{1}{\sqrt{2\pi}} e^{-\frac{1}{2}\left[ (x-6)^2 +x^2 \right]} dx \\ &=\int_{-\infty}^{+\infty}\frac{1}{\sqrt{2\pi}} e^{-\frac{1}{2} \cdot 2 \cdot \left[ (x-3/2)^2 +9/4\right]} dx + \int_{-\infty}^{+\infty}\frac{1}{\sqrt{2\pi}} e^{-\frac{1}{2} \cdot 2 \cdot \left[(x-3)^2 +9\right]} dx \\ &= \frac{e^{-9/4}}{\sqrt{2}} \int_{-\infty}^{+\infty} \frac{1}{\sqrt{\pi}} e^{-\frac{1}{2} \cdot 2 \cdot (x-3/2)^2} dx + \frac{e^{-9}}{\sqrt{2}} \int_{-\infty}^{+\infty} \frac{1}{\sqrt{\pi}} e^{-\frac{1}{2} \cdot 2 \cdot (x-3)^2} dx \\ &= \frac{e^{-9/4}}{\sqrt{2}} \int_{-\infty}^{+\infty} \underbrace{\frac{1}{\sqrt{2\pi \frac{1}{2}}} e^{-\frac{1}{2 \cdot \frac{1}{2}} \cdot (x-3/2)^2}}_{\mathcal{N}\left(\cdot \ ; \ \mu=3/2, \sigma^2=1/2\right)} dx + \frac{e^{-9}}{\sqrt{2}} \int_{-\infty}^{+\infty} \underbrace{\frac{1}{\sqrt{2\pi \frac{1}{2}}} e^{-\frac{1}{2 \cdot \frac{1}{2}} \cdot (x-3)^2}}_{\mathcal{N}\left(\cdot \ ; \ \mu=3, \sigma^2=1/2\right)} dx \\ &= \frac{e^{-9/4}+e^{-9}}{\sqrt{2}} \approx 0.0746 \end{align*}\]

Θέλουμε να εκτιμήσουμε την παραπάνω ποσότητα με ολοκλήρωση Monte Carlo προσομοιώνοντας από την \(\mathcal{N}(0,1)\) ένα δείγμα μεγέθους \(n=10^4\).

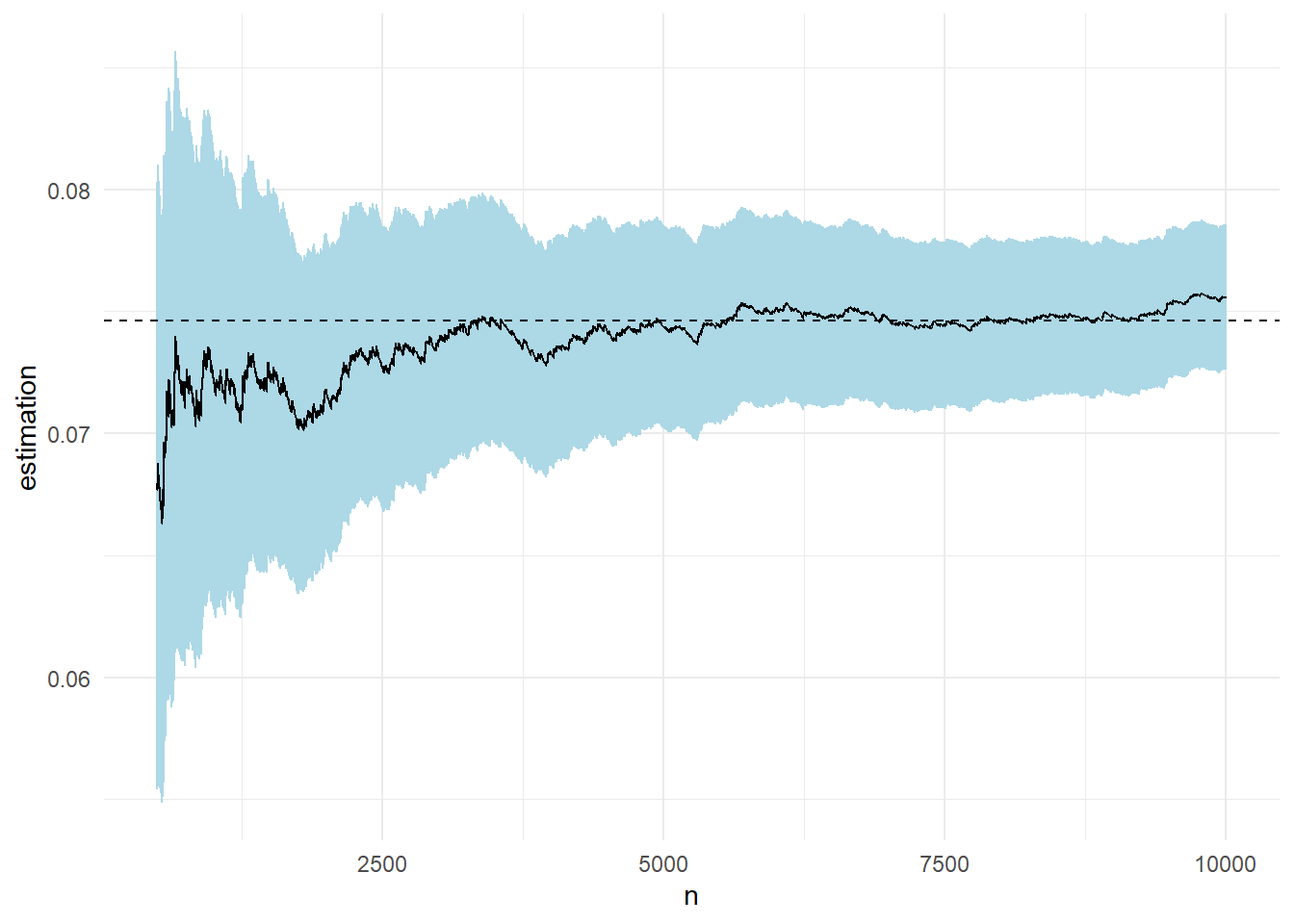
Θα προσπαθήσουμε τώρα να εκτιμήσουμε την ίδια ποσότητα με δειγματοληψία σπουδαιότητας, χρησιμοποιώντας ως συνάρτηση σπουδαιότητας \(g\) την σ.π.π. της \(Unif(-8, -1)\). Φυσικά, με το να επιλέξουμε μία \(g\) με στήριγμα υποσύνολο του στηρίγματος της \(h\times f\) εισάγουμε μεροληψία στην εκτίμησή μας. Αρχικά, παρατηρούμε ότι οι συναρτήσεις \(h, w\) είναι γνησίως αύξουσες στο διάστημα \((-8, -1)\), επομένως το ίδιο και η \(h\cdot w\).

h <- function(x) { 
  exp( - (x - 3) ^ 2 / 2) + exp( - (x - 6) ^ 2 / 2)
}
w <- function(x) { 
  dnorm(x) / dunif(x, min = -8, max = -1)
}

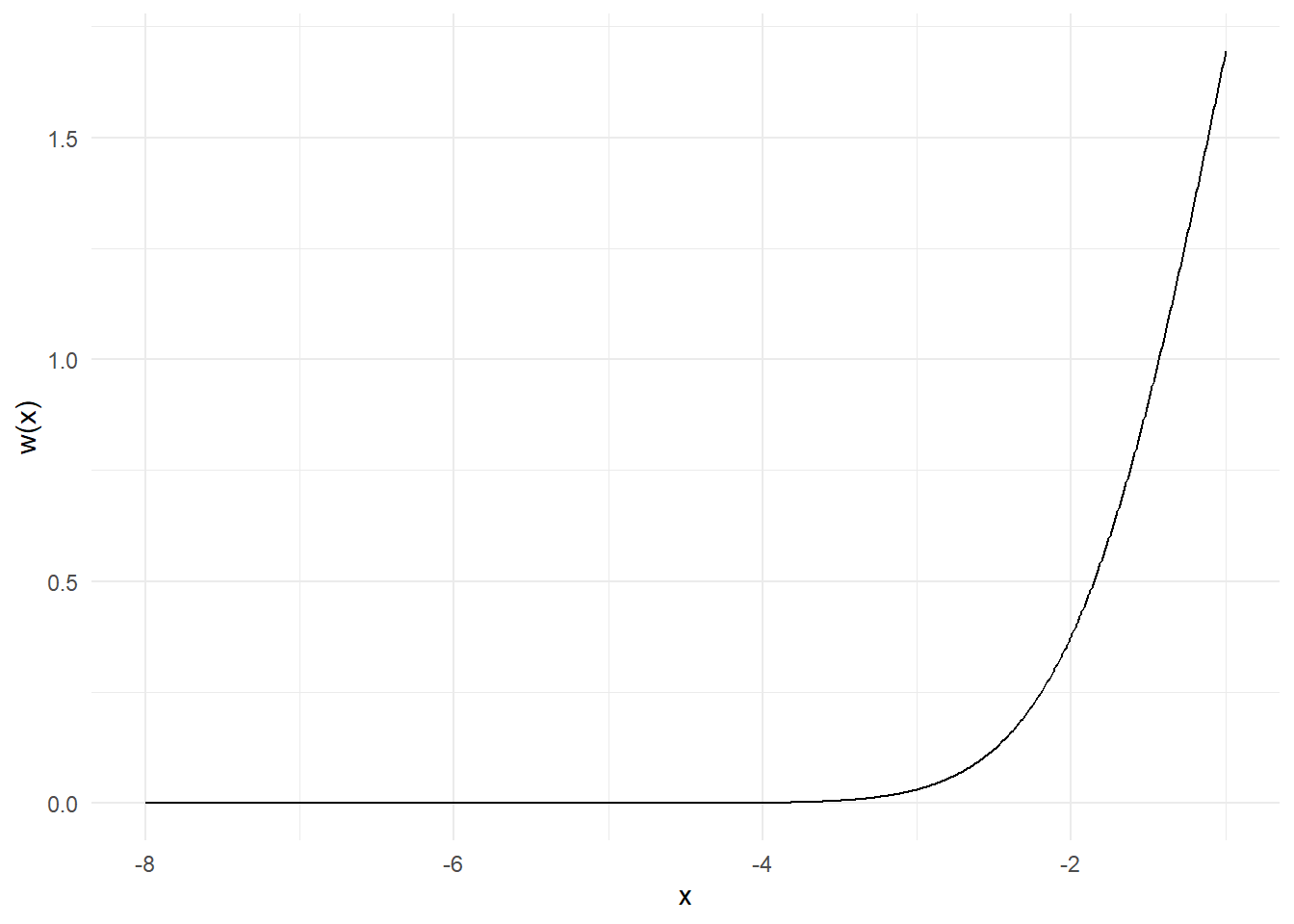
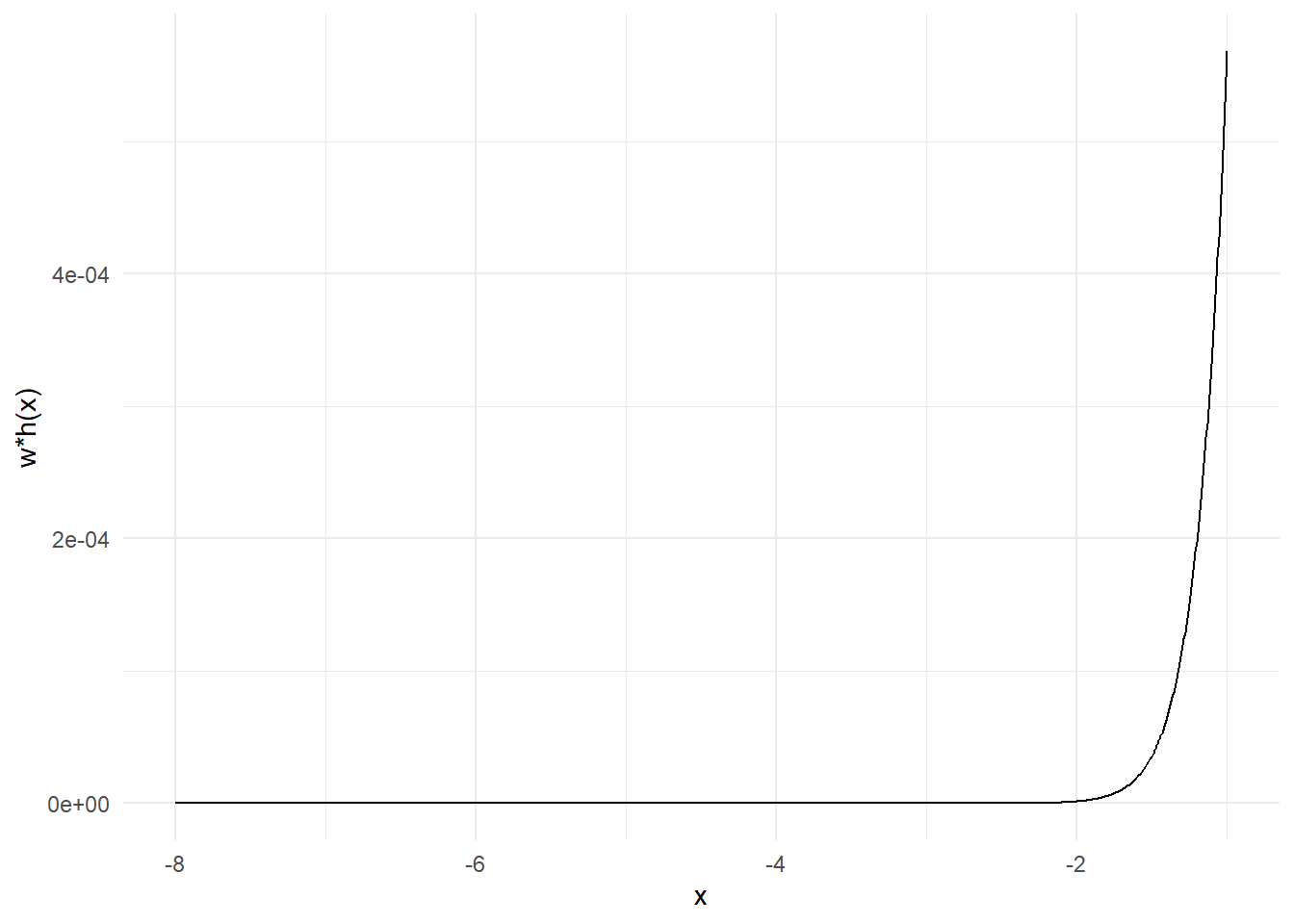
Παρατηρούμε πως υπάρχει πολύ μεγάλη διαφορά ανάμεσα στα βάρη που αντιστοιχούν στις τιμές του διαστήματος, κάτι που μπορεί να οδηγήσει σε πολύ μεγάλες αλλαγές στην εκτίμησή μας με την εισαγωγή μίας μόνο παρατήρησης. Ως παράδειγμα, έχουμε \(w(-6)=4.2531\cdot 10^{-8}\) και \(w(-2)=0.3779\), δηλαδή τα δύο βάρη έχουν λόγο \(\frac{w(-2)}{w(-6)}=8886111\).

Επιπλέον, για \(x \in [-8, -1]\), οι παρατηρήσεις \(h(x)\cdot w(x)\) θα παίρνουν τιμές στο διάστημα \([h(-8)\cdot w(-8), h(-1)\cdot w(-1)]=[1.8783\cdot 10^{-40}, 0.0005682]\), τη στιγμή που η υπό εκτίμηση ποσότητα υπολογίστηκε ίση με \(0.0746\), δηλαδή η πραγματική μέση τιμή βρίσκεται εκτός του στηρίγματος της εκτιμήτριας που κατασκευάσαμε.

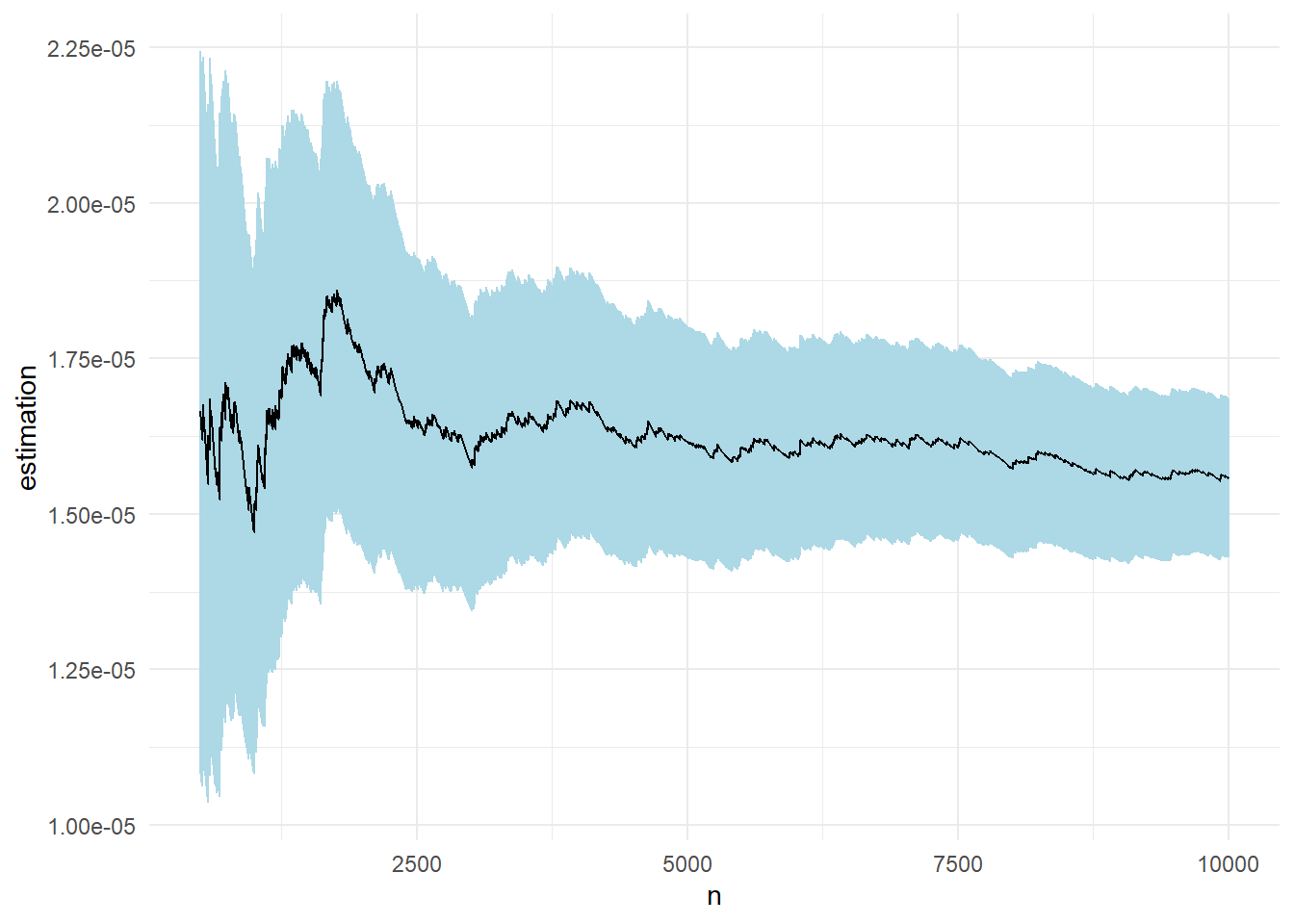
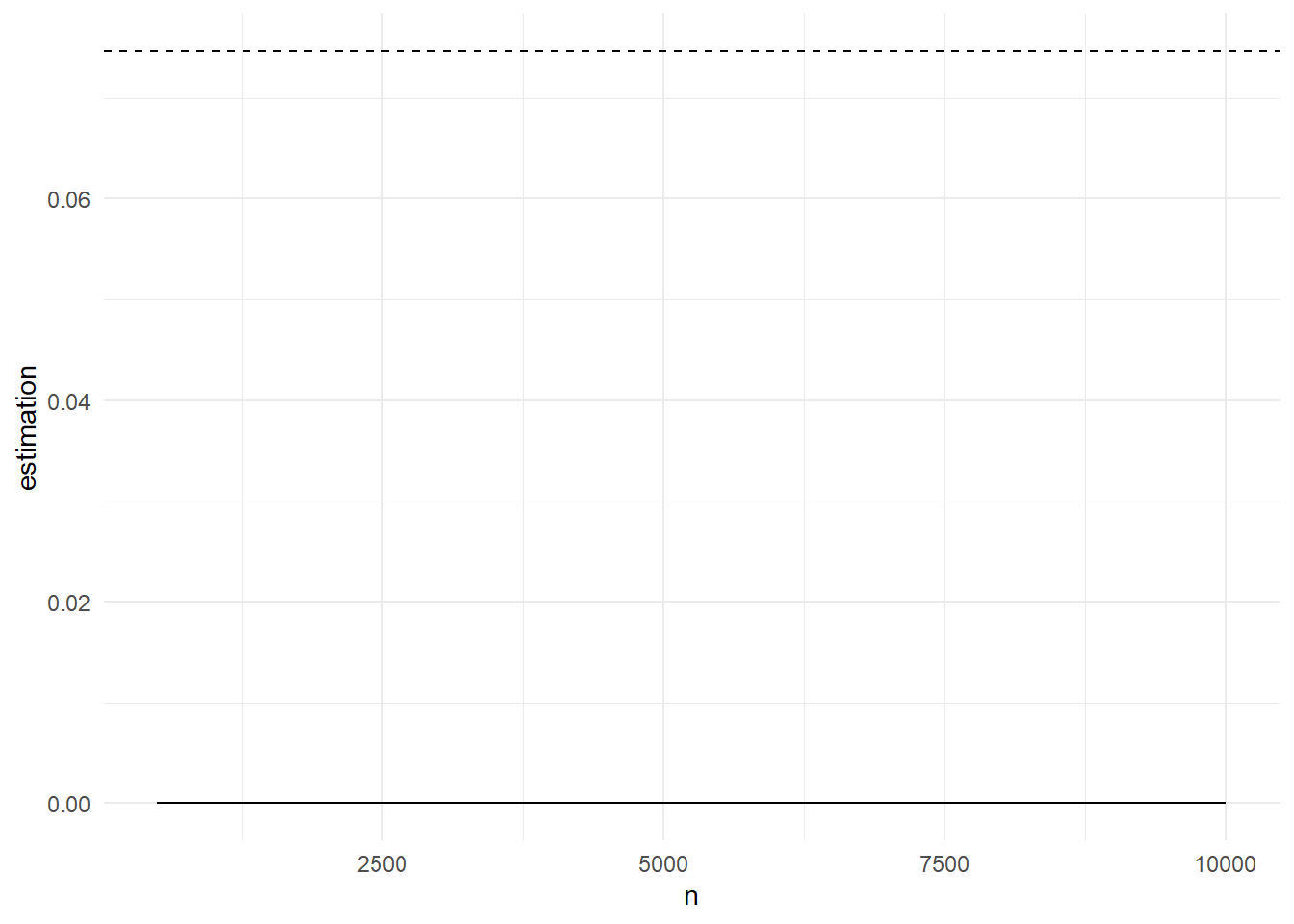
Η συγκεκριμένη δειγματοληψία σπουδαιότητας μας δίνει εκτίμηση \(\widehat{p}_n=\) 1.5576 \(\cdot 10^{-5}\) με εκτιμημένο τυπικό σφάλμα \(\widehat{s}_n=\) 0.0654\(\cdot 10^{-5}\) (σχήμα αριστερά). Η εκτίμηση αυτή πέφτει τόσο έξω από την πραγματική τιμή, που αν αναπαρασταθούν σε ένα κοινό γράφημα, η εκτίμησή μας δείχνει σχεδόν σταθερή στο 0.

Θα θέλαμε να τονίσουμε ότι η μέθοδος δειγματοληψίας σπουδαιότητας εφαρμόζεται και σε περιπτώσεις που οι σταθερές κανονικοποίησης είναι άγνωστες, κάτι το οποίο επεκτείνει κατά πολύ το πεδίο εφαρμογών της μεθόδου. Σε αυτές τις περιπτώσεις η εκτίμηση της μέσης τιμής μπορεί να δοθεί πάλι από τη σχέση

\[\begin{equation*} \frac{\sum_{i=1}^n w(X_i)h(X_i)}{\sum_{i=1}^n w(X_i)}, \end{equation*}\]

όπου η κανονικοποίηση ως προς το άθροισμα των βαρών απλοποιεί άγνωστες σταθερές. Εύκολα παρατηρούμε ότι

\[\begin{equation*} \frac{\sum_{i=1}^n w(X_i)h(X_i)}{\sum_{i=1}^n w(X_i)} = \frac{\sum_{i=1}^n w(X_i)h(X_i)/n}{\sum_{i=1}^n w(X_i)/n}\overset{a.s.}{\longrightarrow} \frac{\mathbf{E}_g\left[w(X)h(X)\right]}{\underbrace{\mathbf{E}_g\left[w(X)\right]}_{=1}} = \mathbf{E}_f\left[h(X)\right]. \end{equation*}\]

Στην περίπτωση που υπάρχει άγνωστη σταθερά κανονικοποίησης, τότε η παραπάνω σύγκλιση ισχύει πάλι, με μόνη διαφορά ότι

\[\begin{equation*} \frac{\mathbf{E}_g\left[w(X)h(X)\right]}{\mathbf{E}_g\left[w(X)\right]} = \frac{c\mathbf{E}_f\left[h(X)\right]}{c} \mathbf{E}_f\left[h(X)\right]. \end{equation*}\]

Χρησιμοποιώντας την παραπάνω σχέση, μπορούμε να εκτιμήσουμε τη σταθερά \(c\) μέσα από το \(\sum_{i=1}^n w(X_i)/n\).

Παράδειγμα 4.11 Ας μελετήσουμε μία εφαρμογή της δειγματοληψίας σπουδαιότητας στην Μπεϋζιανή Στατιστική. Αν \(x\) είναι μία παρατήρηση από την \(B(a, \beta)\), με σ.π.π.

\[\begin{equation*} f(x|α, \beta) = \frac{\Gamma(a+\beta)}{\Gamma(a)\Gamma(\beta)} x^{a-1} (1-x)^{\beta-1} \mathbb{I}_{[0,1]}(x), \end{equation*}\]

τότε υπάρχει μία οικογένεια συζυγών prior κατανομών για τα \((a, \beta)\) της μορφής

\[\begin{equation*} \pi(a, \beta) \propto \left\{\frac{\Gamma(a+\beta)}{\Gamma(a)\Gamma(\beta)}\right\}^\lambda x_0^{a} y_0^{\beta}, \end{equation*}\]

όπου \(\lambda, x_0, y_0\) είναι υπερπαράμετροι, οδηγώντας στην posterior κατανομή

\[\begin{equation*} \pi(a, \beta|x) \propto \left\{\frac{\Gamma(a+\beta)}{\Gamma(a)\Gamma(\beta)}\right\}^{\lambda+1} [xx_0]^{a} [(1-x)y_0]^{\beta}. \end{equation*}\]

Προσομοιώστε παρατηρήσεις από την \(\pi(a, \beta|x)\).

Λύση:

Αυτή η οικογένεια κατανομών είναι δύσχρηστη εξαιτίας της δυσκολίας των συναρτήσεων \(\Gamma\). Ως αποτέλεσμα, η άμεση προσομοίωση από την \(\pi(a, \beta|x)\) είναι αδύνατη.

Χρειαζόμαστε μία κατανομή \(g(a, \beta)\) η οποία θα λειτουργήσει ως συνάρτηση σπουδαιότητας. Κοιτώντας το γράφημα της \(\pi(a, \beta|x)\), για \(\lambda=1, x_0=y_0=0.5\) και \(x=0.6\), έχουμε:

f <- function(a, b){
  exp(2 * (lgamma(a + b) - lgamma(a) - lgamma(b)) + a * log(.3) + b * log(.2))
}

aa <- 1:150 # alpha grid for image
bb <- 1:100 # beta grid for image
post <- outer(aa, bb, f)

image(aa, bb, post, xlab = expression(alpha), ylab=" ")
contour(aa, bb, post, add = TRUE)

x <- matrix(rt(2 * 10 ^ 4, 3), ncol = 2) # T sample
E <- matrix(c(220, 190, 190, 180), ncol = 2) # Scale matrix
image(aa, bb, post, xlab = expression(alpha), ylab = " ")
y <- t(t(chol(E)) %*% t(x) + c(50, 45))
points(y, cex = .6, pch = 19)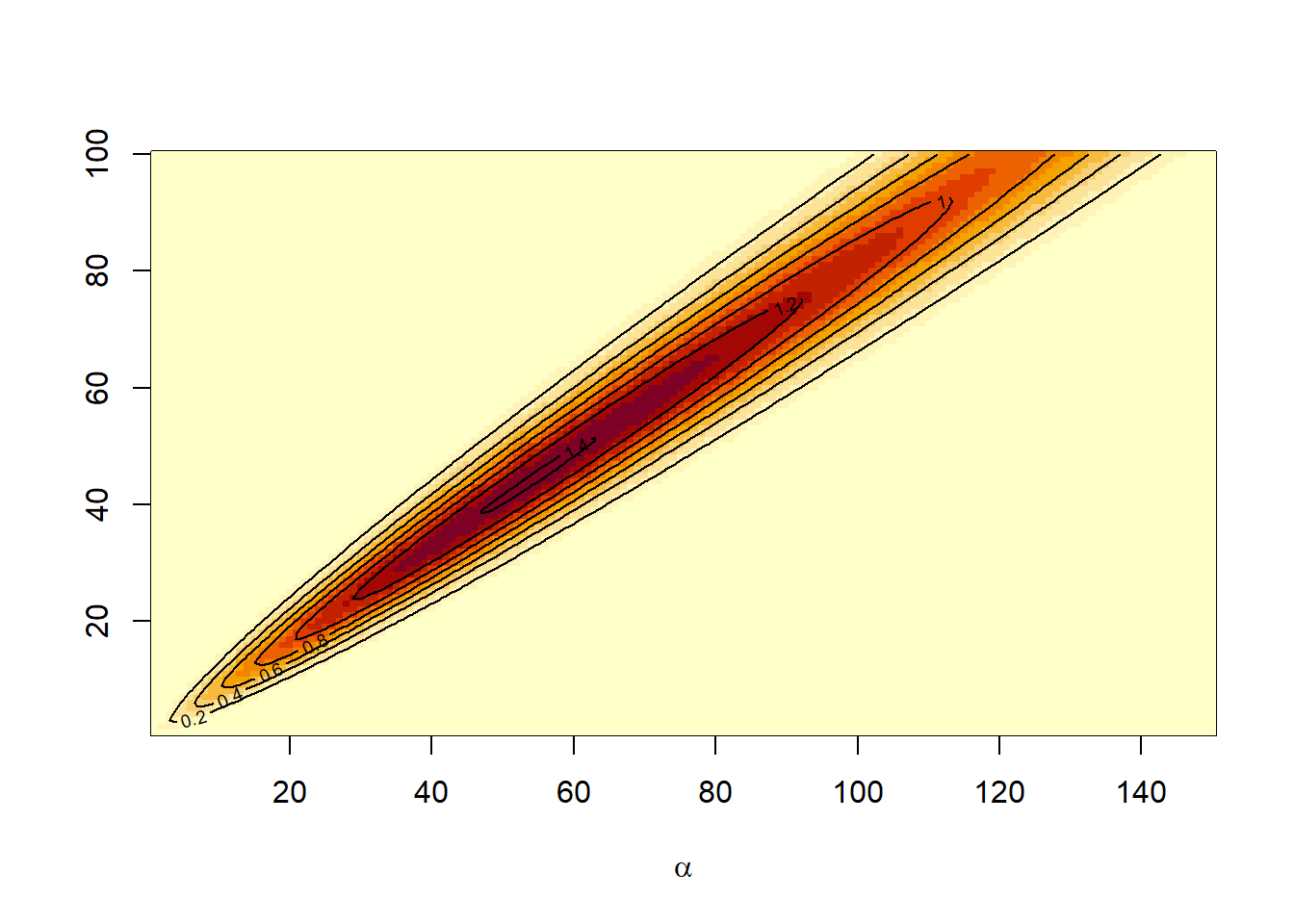

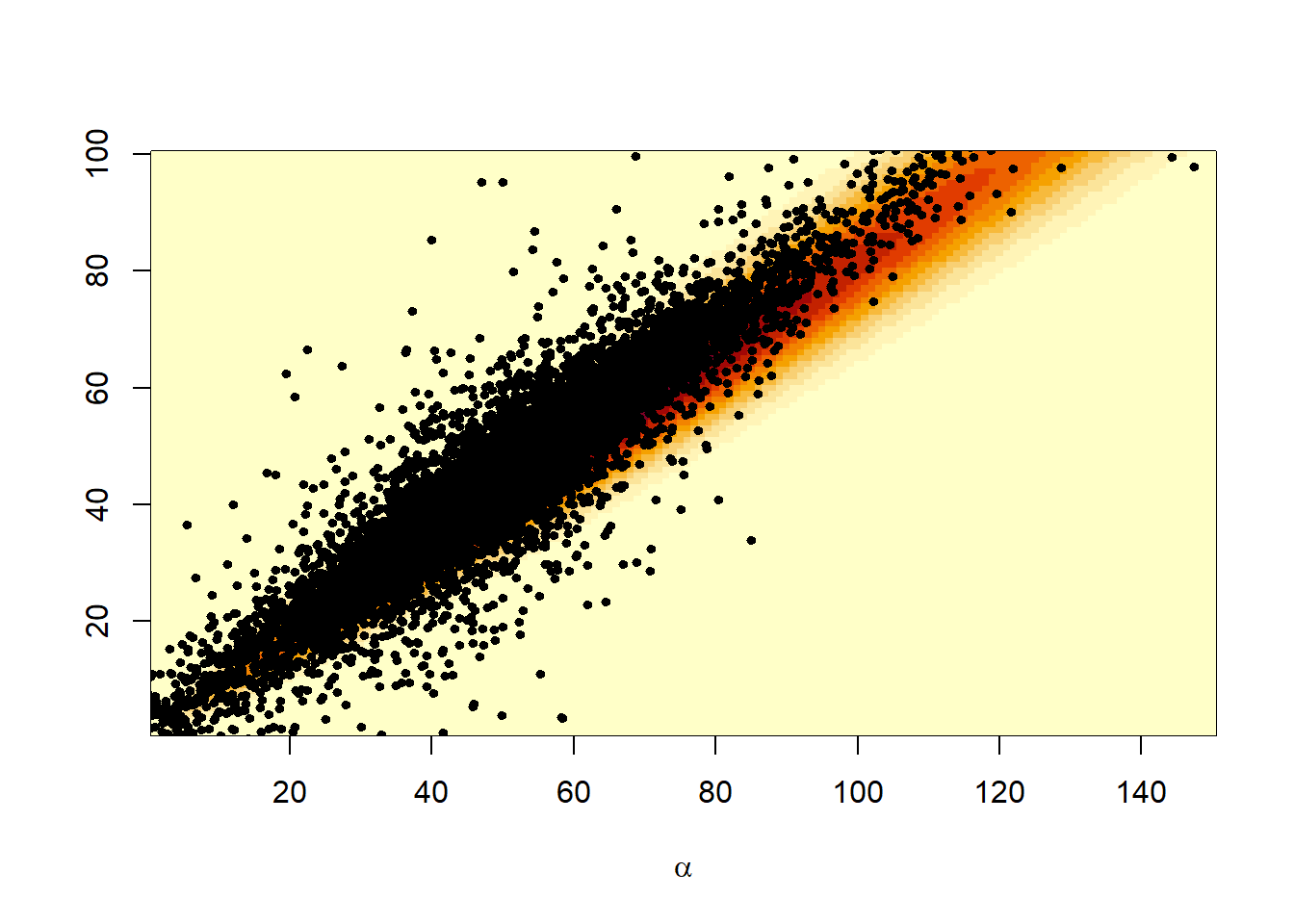
Εξετάζοντας το αριστερό γράφημα παρατηρούμε ότι μία κανονική ή Student’s \(t\) κατανομή ίσως είναι κατάλληλη για το ζεύγος \((a, \beta)\).

Υπενθυμίζουμε ότι μία τ.μ. \(X\sim t_n\) ανν μπορεί να αναπαρασταθεί στην μορφή

\[\begin{equation*} X = \frac{Z}{\sqrt{Q/n}}, \end{equation*}\]

όπου \(Z, Q\) ανεξάρτητες τ.μ. με \(Z\sim \mathcal{N}(0,1)\) και \(Q\sim\mathcal{X}^2_n\).

Υπάρχουν πολλοί διαφορετικοί τρόποι γενίκευσης της κατανομής Student. Περιγράφουμε έναν από αυτούς που χρησιμοποιείται συχνά.

Ορισμός 4.1 (Multivariate Student) Ένα τ.δ. \(X=(X_1, X_2, ..., X_d)\) ακολουθεί την πολυδιάστατη κατανομή Student \(\mathcal{T}_n(\mu, \Sigma)\) ανν μπορεί να αναπαρασταθεί στην μορφή

\[\begin{equation*} X = \mu +\frac{W}{\sqrt{Q/n}}, \end{equation*}\]

όπου \(W\sim \mathcal{N}_d(0,\Sigma)\), \(Q\sim\mathcal{X}^2_n\) και \(W, Q\) ανεξάρτητα.

Η συνάρτηση πυκνότητας πιθανότητας του \(X\) είναι

\[\begin{equation*} f(x) = \frac{\Gamma[(n+d)/2]}{\Gamma(n/2)n^{d/2}\pi^{d/2}|\Sigma|^{1/2}} \left[ 1 +\frac{1}{n} (x-\mu)^\top \Sigma^{-1} (x-\mu) \right]^{-(n+d)/2}. \end{equation*}\]

Επιλέγουμε την κατανομή \(\mathcal{T}_3(\mu, \Sigma)\) με \(\mu = (50, 45)^\top\) και \(\Sigma= \left(\begin{array}{cc} 220 & 190 \\ 190 & 180 \end{array} \right)\). Στο γράφημα δεξιά βλέπουμε ένα προσομοιωμένο δείγμα από την συγκεκριμένη κατανομή πάνω στην επιφάνεια της posterior κατανομής. Οι τιμές των \(\mu, \Sigma\) επιλέχθηκαν με trial-and-error, προκειμένου να ταιριάζουν στην posterior κατανομή.

Αν η ποσότητα που μας ενδιαφέρει είναι η περιθώρια πιθανοφάνεια (marginal likelihood),

\[\begin{equation*} m(x)=\int_{\mathbb{R}^2_+} f(x|a, \beta) \pi(a, \beta) da d\beta = \frac{\int_{\mathbb{R}^2_+}\left\{\frac{\Gamma(a+\beta)}{\Gamma(a)\Gamma(\beta)} \right\}^{\lambda+1} [xx_0]^a[(1-x)y_0]^\beta da d\beta}{x(1-x)\int_{\mathbb{R}^2_+}\left\{\frac{\Gamma(a+\beta)}{\Gamma(a)\Gamma(\beta)} \right\}^{\lambda} x_0^ay_0^\beta da d\beta}, \end{equation*}\]

χρειάζεται να προσεγγίσουμε και τα δύο ολοκληρώματα. Μπορούμε να χρησιμοποιήσουμε το δείγμα που προσομοιώσαμε από την παραπάνω κατανομή student και για τα δύο, αφού η επιλογή της κατανομής αυτής στέκει τόσο για την prior όσο και για την posterior. Η προσέγγισή μας είναι η

\[\begin{equation*} \widehat{m}(x) = \frac{\sum_{i=1}^n \left\{\frac{\Gamma(a_i+\beta_i)}{\Gamma(a_i)\Gamma(\beta_i)} \right\}^{\lambda+1} [xx_0]^{a_i} [(1-x)y_0]^{\beta_i} / g(a_i, \beta_i)}{\sum_{i=1}^n \left\{\frac{\Gamma(a_i+\beta_i)}{\Gamma(a_i)\Gamma(\beta_i)} \right\}^{\lambda} x_0^{a_i} y_0^{\beta_i} / g(a_i, \beta_i)}, \end{equation*}\]

όπου τα \((a_i, \beta_i)_{1\leq i \leq n}\) είναι ανεξάρτητες και ισόνομες παρατηρήσεις από την \(g\), μπορεί να πραγματοποιηθεί άμεσα στην R:

ine <- apply(y, 1, min)
y <- y[ine > 0, ]
x <- x[ine > 0, ]
normx <- sqrt(x[ , 1] ^ 2 + x[ , 2] ^ 2)

f <- function(a) {
  exp(2 * (lgamma(a[ , 1] + a[ , 2]) - lgamma(a[ , 1]) - lgamma(a[ , 2])) + a[ , 1] * log(.3) + a[ , 2] * log(.2))
}

h <- function(a) {
  exp(1 * (lgamma(a[ , 1] + a[ , 2]) - lgamma(a[ , 1]) - lgamma(a[ , 2])) + a[ , 1] * log(.5) + a[ , 2] * log(.5))
}

den <- dt(normx, 3)
m <- mean(f(y) / den) / mean(h(y) / den)
m
## [1] 0.244607

Η προσέγγιση της περιθώριας πιθανοφάνειας, βασισμένη σε αυτό το προσομοιωμένο δείγμα, είναι 0.2446. Ομοίως, οι posterior μέσες τιμές των παραμέτρων \(a\) και \(\beta\) εκτιμούνται ως

a <- mean(y[ , 1] * f(y) / den) / mean(h(y) / den)
b <- mean(y[ , 2] * f(y) / den) / mean(h(y) / den)
a ; b
## [1] 23.99874
## [1] 20.35882

4.2.1 Δειγματοληψία Σπουδαιότητας με Επαναδειγματοληψία

Στην προηγούμενη παράγραφο αναφέραμε ότι η δειγματοληψία σπουδαιότητας μπορεί να χρησιμοποιηθεί γενικότερα για την εναλλακτική προσέγγιση μίας κατανομής από κάποια άλλη με τη βοήθεια του σταθμισμένου δείγματος. Στην περίπτωση της εμπειρικής κατανομής, τα σταθμισμένα βάρη είναι ίσα για όλες τις παρατηρήσεις και έτσι αν κάνουμε επαναδειγματοληψία από τις παρατηρήσεις \((X_1, X_2, ..., X_n)\), η προκύπτουσα κατανομή παραμένει η ίδια. Θα μπορούσαμε λοιπόν να περιγράψουμε την επαναδειγματοληψία μέσω μίας τ.μ.

\[\begin{equation*} X_n^\star = \left\{ \begin{array}{ccc} X_1 & \text{με πιθ.} & 1/n \\ X_2 & \text{με πιθ.} & 1/n \\ \vdots & \vdots & \vdots \\ X_n & \text{με πιθ.} & 1/n \end{array} \right. . \end{equation*}\]

Στην περίπτωση του σταθμισμένου δείγματος, η επαναδειγματοληψία περιγράφεται μέσω μίας τ.μ.

\[\begin{equation*} X_n^\star = \left\{ \begin{array}{ccc} X_1 & \text{με πιθ.} & w_{1,n}(X_1) \\ X_2 & \text{με πιθ.} & w_{2,n}(X_2) \\ \vdots & \vdots & \vdots \\ X_n & \text{με πιθ.} & w_{n,n}(X_n) \end{array} \right. , \end{equation*}\]

όπου

\[\begin{equation*} w_{i,n}(X_i) = \frac{w(X_i)}{\sum_{j=1}^n w(X_j)}. \end{equation*}\]

Υπενθυμίζουμε ότι \(w(x)=f(x)/g(x)\).

Είναι σημαντικό να κατανοηθεί ότι με τη δειγματοληψία σπουδαιότητας από ένα σταθμισμένο δείγμα και την επακόλουθη δειγματοληψία, δεν έχουμε γενικά προσομοίωση ακριβώς από την \(f\), αλλά μόνο προσεγγιστικά. Η προσέγγιση αυτή γίνεται όλο και καλύτερη όσο μεγαλώνει το μέγεθος δείγματος. Επιπλέον, με την επαναδειγματοληψία το καινούριο δείγμα αντιστοιχεί σε δεσμευμένα ανεξάρτητες τ.μ. και όχι γενικά σε ανεξάρτητες τ.μ.. Αυτό μπορεί μπορεί να γίνει εμφανές με το παρακάτω απλό παράδειγμα.

Παράδειγμα 4.12 Προσομοιώστε παρατηρήσεις από την κατανομή \(Be(p)\) για κάποιο \(p \in (0, 1)\) χρησιμοποιώντας δειγματοληψία σπουδαιότητας με επαναδειγματοληψία, έχοντας ως συνάρτηση σπουδαιότητας την \(g\), την σ.π. της \(Be(1/2)\).

Λύση:

Τα βάρη \(w(X)\) παίρνουν την μορφή

\[\begin{equation*} w(X) = \frac{f(X)}{g(X)} = \frac{p^X(1-p)^{1-X}}{1/2} = 2p^X(1-p)^{1-X}, \end{equation*}\]

δηλαδή έχουμε \(w(1)=2p\) και \(w(0)=2(1-p)\). Θεωρούμε λοιπόν ότι έχουμε δύο παρατηρήσεις \(X_1, X_2\) από την \(Be(1/2)\). Τότε η \(X_2^\star\) έχει την μορφή

\[\begin{equation*} X_2^\star = \left\{ \begin{array}{ccc} X_1 & \text{με πιθ.} & w_{1,2}(X_1) \\ X_2 & \text{με πιθ.} & w_{2,2}(X_2) \end{array} \right. , \end{equation*}\]

όπου

\[\begin{equation*} w_{i,2}(X_i) = \frac{w(X_i)}{w(X_1)+w(X_2)}, \ i=1,2. \end{equation*}\]

Εύκολα προκύπτει ότι \[\begin{align*} X_1=1, X_2=1 &\Rightarrow w_{1,2}(X_1)=1/2,\ \ w_{2,2}(X_2)=1/2, \\ X_1=1, X_2=0 &\Rightarrow w_{1,2}(X_1)=p, \ \ \ \ w_{2,2}(X_2)=1-p, \\ X_1=0, X_2=1 &\Rightarrow w_{1,2}(X_1)=1-p, w_{2,2}(X_2)=p, \\ X_1=0, X_2=0 &\Rightarrow w_{1,2}(X_1)=1/2, \ \ w_{2,2}(X_2)=1/2. \end{align*}\]

Επομένως για την δεσμευμένη κατανομή της \(X_2^\star\), δεδομένων των \(X_1, X_2\), έχουμε

\[\begin{align*} \mathbf{P}(X_2^\star=1|X_1=1, X_2=1)&=1 \\ \mathbf{P}(X_2^\star=1|X_1=1, X_2=0)&=p \\ \mathbf{P}(X_2^\star=1|X_1=0, X_2=1)&=p \\ \mathbf{P}(X_2^\star=1|X_1=0, X_2=0)&=0 \end{align*}\]

Άμεσα συμπεραίνουμε τις συμπληρωματικές πιθανότητες των παραπάνω ενδεχομένων. Επομένως έχουμε ότι

\[\begin{align*} \mathbf{P}(X_2^\star=1)&=\sum_{i_1=0}^1\sum_{i_2=0}^1 \mathbf{P}(X_2^\star=1, X_1=i_1, X_2=i_2) =\sum_{i_1=0}^1\sum_{i_2=0}^1 \mathbf{P}(X_2^\star=1| X_1=i_1, X_2=i_2) \cdot \mathbf{P}(X_1=i_1, X_2=i_2) \\ &=\frac{1}{4} \sum_{i_1=0}^1\sum_{i_2=0}^1 \mathbf{P}(X_2^\star=1| X_1=i_1, X_2=i_2) = \frac{1}{4} \cdot (1 + p + p) = \frac{1+2p}{4}, \end{align*}\]

δηλαδή \(X_2^\star \sim Be(\frac{1+2p}{4})\). Επισημαίνουμε ότι για \(p\neq 1/2\), έχουμε \(\frac{1+2p}{4}\neq p\) δηλαδή η κατανομή που παίρνουμε διαφέρει από την επιθυμητή. Από αυτό παρατηρούμε ότι δεν μπορούμε γενικά με το σταθμισμένο δείγμα να πετύχουμε την ακριβή κατανομή. Επιπλέον, αν κάνουμε επαναδειγματοληψία και σχηματίσουμε δείγμα μεγέθους 2 από αυτή την κατανομή, παρατηρούμε ότι η από κοινού συνάρτηση πιθανότητας των δύο δεν αντιστοιχεί σε ανεξάρτητες Bernoulli. Πράγματι, ομοίως με παραπάνω προκύπτει ότι

\[\begin{align*} \mathbf{P}(X_2^{\star(1)}=1, X_2^{\star(2)}=1)&=\sum_{i_1=0}^1\sum_{i_2=0}^1 \mathbf{P}(X_2^{\star(1)}=1, X_2^{\star(2)}=1, X_1=i_1, X_2=i_2) \\ &= \sum_{i_1=0}^1\sum_{i_2=0}^1 \mathbf{P}(X_2^{\star(1)}=1, X_2^{\star(2)}=1 | X_1=i_1, X_2=i_2) \cdot \mathbf{P}(X_1=i_1, X_2=i_2) \\ &= \frac{1}{4} \sum_{i_1=0}^1\sum_{i_2=0}^1 \mathbf{P}(X_2^{\star(1)}=1, X_2^{\star(2)}=1 | X_1=i_1, X_2=i_2) \\ &=\frac{1}{4} (1\cdot 1 + p\cdot p +p\cdot p +0\cdot 0) = \frac{1+2p^2}{4}, \end{align*}\]

και όχι \(\left(\frac{1+2p}{4}\right)^2\) που θα είχαμε αν οι \(X_2^{\star(1)}, X_2^{\star(2)}\) ήταν ανεξάρτητες Bernoulli με παράμετρο \(\frac{1+2p}{4}\). Για λόγους πληρότητας παραθέτουμε ακόμη ότι

\[\begin{align*} \mathbf{P}(X_2^{\star(1)}=1, X_2^{\star(2)}=0)&= \frac{2p(1-p)}{4}, \\ \mathbf{P}(X_2^{\star(1)}=0, X_2^{\star(2)}=1)&= \frac{2p(1-p)}{4}, \\ \mathbf{P}(X_2^{\star(1)}=0, X_2^{\star(2)}=0)&= \frac{1+2(1-p)^2}{4}. \end{align*}\]

Φυσικά, η παραπάνω αδυναμία της επαναδειγματοληψίας δεν εμφανίζεται μόνο στις διακριτές κατανομές.

Παράδειγμα 4.13 Προσομοιώστε από την κατανομή \(\mathcal{N}(1,1)\) χρησιμοποιώντας δειγματοληψία σπουδαιότητας με επαναδειγματοληψία, έχοντας ως συνάρτηση σπουδαιότητας την \(g\), την σ.π.π. της \(\mathcal{N}(0,1)\).

Λύση:

Σε αυτή την περίπτωση, τα βάρη σπουδαιότητας παίρνουν την μορφή:

\[\begin{equation*} w(X)=\frac{f(X)}{g(X)} = \frac{1/\sqrt{2\pi}e^{-\frac{1}{2}(X-1)^2}}{1/\sqrt{2\pi}e^{-\frac{1}{2}X^2}}=e^{-\frac{1}{2}\left[(X-1)^2-X^2\right]}=e^{-\frac{1}{2}(-2X+1)}. \end{equation*}\]

Θεωρούμε λοιπόν ότι έχουμε δύο παρατηρήσεις \(X_1, X_2\) από την \(\mathcal{N}(0,1)\). Τότε η \(X_2^\star\) έχει την μορφή

\[\begin{equation*} X_2^\star = \left\{ \begin{array}{ccc} X_1 & \text{με πιθ.} & w_{1,2}(X_1) \\ X_2 & \text{με πιθ.} & w_{2,2}(X_2) \end{array} \right. , \end{equation*}\]

όπου

\[\begin{equation*} w_{i,2}(X_i) = \frac{w(X_i)}{w(X_1)+w(X_2)}, \ i=1,2. \end{equation*}\]

Θέλουμε να δούμε μέσα από προσομοίωση την κατανομή της \(X_2^\star\). Για τον λόγο αυτό, προσομοιώνουμε δύο παρατηρήσεις από την \(\mathcal{N}(0,1)\) και χρησιμοποιώντας δειγματοληψία σπουδαιότητας, επιλέγουμε μία παρατήρηση για την \(X_2^\star\). Επαναλαμβάνουμε αυτή τη διαδικασία \(n=10^4\) φορές και δημιουργούμε το ιστόγραμμα.

Το δείγμα μας έχει δειγματικό μέσο 0.3628, αρκετά μακριά από το επιθυμητό \(1\). Επαναλαμβάνουμε την διαδικασία, αυτή τη φορά όμως προσομοιώνουμε \(100\) παρατηρήσεις \(X_1, X_2, ..., X_{100}\) για κάθε πραγματοποίηση της \(X_{100}^\star\).

Πράγματι, αυτή τη φορά το δείγμα μας έχει δειγματικό μέσο 0.9797, αρκετά κοντά στο \(1\).

Συνεχίζοντας το παράδειγμα, η εγκυρότητα των προσεγγίσεων της περιθώριας πιθανοφάνειας μπορεί να ελεγχθεί γραφικά ως εξής:

weit <- (f(y) / den) / mean(h(y) / den)
image(aa, bb, post, xlab = expression(alpha), ylab = expression(beta))
points(y[sample(1:length(weit), 10 ^ 3, replace = TRUE, prob = weit), ], cex = .6, pch = 19)
boxplot(weit, ylab = "importance weight")
plot(cumsum(weit) / (1:length(weit)), type = "l", xlab = "simulations", ylab = "marginal likelihood")

boot <- matrix(0, ncol = length(weit), nrow = 500)
for (t in 1:500)
  boot[t, ] <- cumsum(sample(weit)) / (1:length(weit))
uppa <- apply(boot, 2, quantile, .95)
lowa <- apply(boot, 2, quantile, .05)
polygon(c(1:length(weit), length(weit):1), c(uppa, rev(lowa)), col = "gold")
lines(cumsum(weit) / (1:length(weit)), lwd = 2)
plot(cumsum(weit) ^ 2 / cumsum(weit ^ 2), type = "l", xlab = "simulations", ylab = "Effective sample size", lwd = 2)

Το γράφημα πάνω αριστερά δείχνει ότι το σταθμισμένο δείγμα με τα βάρη σπουδαιότητας \(\pi(a_i, \beta_i|x)/g(a_i, \beta_i)\) παράγει μία δίκαιη εικόνα ενός δείγματος από την \(\pi(a, \beta|x)\). Οι επανεκλεγμένες παρατηρήσεις δεν συγκεντρώνονται σε λίγα σημεία, αντίθετα καλύπτουν με υψηλή πυκνότητα την ορθή περιοχή της κατανομής στόχου. Το γράφημα πάνω δεξιά δίνει μία απεικόνιση της έκτασης των βαρών σπουδαιότητας. Παρότι υπάρχουν προσομοιωμένες παρατηρήσεις με πολύ μεγαλύτερα βάρη από άλλες, οι διαφορές τους δεν είναι τόσο μεγάλες ώστε να υποδηλώσουν εκφυλισμό της μεθόδου. Για παράδειγμα, το σημείο με το μεγαλύτερο βάρος αντιπροσωπεύει μόλις το \(1\%\) του συνολικού δείγματος. Το γράφημα κάτω αριστερά αναπαριστά την σύγκλιση της εκτιμήτριας \(\widehat{m}(x)\) καθώς το \(n\) αυξάνει. Η χρωματισμένη λωρίδα που παρουσιάζεται έχει δημιουργηθεί με bootstrap και μιμείται την λωρίδα εμπιστοσύνης. Η καμπύλη κάτω δεξιά αναπαριστά την αποδοτικότητα της δειγματοληψίας σπουδαιότητας ως προς το αποτελεσματικό μέγεθος δείγματος (effective sample size),

\[\begin{equation*} \frac{\left\{\sum_{i=1}^n \pi(a_i, \beta_i|x)/g(a_i, \beta_i) \right\}^2}{\sum_{i=1}^n \left\{\pi(a_i, \beta_i|x)/g(a_i, \beta_i)\right\}^2}, \end{equation*}\]

το οποίο θα ήταν ίσο με \(n\), αν τα \((a_i, \beta_i)\) είχαν παραχθεί από την posterior. Το συγκεκριμένο γράφημα δείχνει απόδοσης περίπου \(6\%\).

Παρατήρηση:.

1. Ο τρόπος αυτός κανονικοποίησης των βαρών γίνεται έτσι ώστε να αποτελούν συνάρτηση πιθανότητας.

2. Υπολογίζοντας την μέση τιμή \[\begin{equation*} \mathbf{E}_g\left[\sum_{i=1}^n w(X_j)\right] = \sum_{i=1}^n \mathbf{E}_g\left[w(X_j)\right] = n \cdot \mathbf{E}_g\left[w(X_1)\right] = n \int_{-\infty}^{+\infty} \frac{f(x)}{g(x)} \cdot g(x) dx = n \int_{-\infty}^{+\infty} f(x) dx = n, \end{equation*}\] παρατηρούμε ότι συμπίπτει με το συνολικό μέγεθος του δείγματος. Αυτό είναι το καλύτερο που μπορούμε να εξασφαλίσουμε, αφού βέβαια οι πραγματοποιήσεις τους δεν αθροίζουν γενικά στο \(n\).

3. Η επαναδειγματοληψία μας επιτρέπει να φτιάξουμε ένα καινούριο δείγμα από μία κατανομή που προσεγγίζει την \(f\) για μεγάλο μέγεθος δείγματος. Παρ’ όλα αυτά εισάγεται μία μεροληψία μέσα από τη διαδικασία της κανονικοποίησης. Όταν το μέγεθος του δείγματος γίνει αρκετά μεγάλο, τότε η αμεροληψία γίνεται αμελητέα. Επομένως μπορούμε να χρησιμοποιήσουμε την πολυωνυμική κατανομή για να εξάγουμε τιμές από αυτήν.

Ας υποθέσουμε ότι έχουμε σχηματίσει ένα σταθμισμένο δείγμα \(\{(X_i,w(X_i))\}_{i=1}^{n}\) με στόχο να παράγουμε από την \(f\). Όπως αναφέραμε ήδη η επαναδειγματοληψία μας δίνει τη δυνατότητα προσέγγισης της \(f\), σχηματίζοντας ένα καινούριο δείγμα \(\{X_n^{*(i)}\}_{i=1}^{R}\) από τα \(\{X_i\}_{i=1}^{n}\). Ο τρόπος επιλογής του δείγματος γίνεται με \(R\) ανεξάρτητες κατηγορικές δοκιμές, όπου κάθε παρατήρηση \(X_i\) επιλέγεται με πιθανότητα ανάλογη του βάρους της \(w(X_i)\). Ο τρόπος αυτός επαναδειγματοληψίας μπορεί να περιγραφεί με τη βοήθεια ενός τυχαίου διανύσματος \(Ν=(Ν_1,\ldots,N_n)\sim \mathcal{M}_{n}(R,w_{1,n},\ldots,w_{n,n})\), όπου θέτουμε για συντομία \(w_{i,n}\) το κανονικοποιημένο βάρος πιθανότητας που αντιστοιχεί στην επιλογή της παρατήρησης \(X_i\) που έχει προκύψει από το αρχικό δείγμα μεγέθους \(n\).

4.2.2 Επιλογή συνάρτησης σημαντικότητας

Η ευελιξία της δειγματοληψίας σπουδαιότητας είναι μεγάλη, αλλά ένα μειονέκτημα που μπορεί να προκύψει συνδέεται με μία κακή επιλογή της συνάρτησης σπουδαιότητας \(g\). Παρότι η επιλογή της βέλτιστης \(g\) αποτελεί θεωρητική άσκηση (βλ. Rubinstein, 1981, ή Robert and Casella, 2004, Θεώρημα 3.12), μπορούμε να αξιολογήσουμε τη συνάρτηση σπουδαιότητας μελετώντας τη διασπορά της παραγόμενης εκτιμήτριας. Πράγματι, γνωρίζουμε ότι

\[\begin{equation*} \frac{1}{n}\sum_{j=1}^n \frac{f(X_j)}{g(X_j)}h(X_j)\rightarrow \mathbf{E}_f\left[h(X)\right], \end{equation*}\]

όταν η μέση τιμή υπάρχει, η διασπορά αυτής της εκτιμήτριας είναι πεπερασμένη μόνο όταν η μέση τιμή

\[\begin{equation*} \mathbf{E}_g\left[h^2(X)\frac{f^2(X)}{g^2(X)}\right]=\mathbf{E}_f\left[h^2(X)\frac{f(X)}{g(X)}\right]=\int_\mathcal{X}h^2(x)\frac{f^2(x)}{g(x)}dx, \end{equation*}\]

είναι πεπερασμένη. Επισημαίνουμε εδώ ότι η χρήση συναρτήσεων σπουδαιότητας \(g\) με ουρές ελαφρύτερες από εκείνες της \(f\) δεν είναι απαγορευτική, αλλά οδηγεί σε μη φραγμένους λόγους \(f/g\), που με τη σειρά τους οδηγούν σε εκτιμήτριες άπειρης διασποράς.

Παράδειγμα 4.14 Εφαρμόστε δειγματοληψία σπουδαιότητας με στόχο την προσομοίωση από την κατανομή Cauchy \(\mathcal{C}(0,1)\), χρησιμοποιώντας ως συνάρτηση σπουδαιότητας την κανονική \(\mathcal{N}(0,1)\).

Λύση:

Σε αυτή την περίπτωση, ο λόγος

\[\begin{equation*} \frac{f(x)}{g(x)}\propto \frac{e^{\frac{x^2}{2}}}{1+x^2} \end{equation*}\]

εκρήγνυται, δίνοντας πολύ μεγάλα βάρη σπουδαιότητας για σχετικά υψηλές τιμές του \(x\). Τρέχοντας τον κώδικα

set.seed(10)
x <- rnorm(10 ^ 6)
wein <- dcauchy(x) / dnorm(x)
boxplot(wein / sum(wein))
plot(cumsum(wein * (x > 2) * (x < 6)) / cumsum(wein), type = "l")
abline(a = pcauchy(6) - pcauchy(2), b = 0, col = "sienna")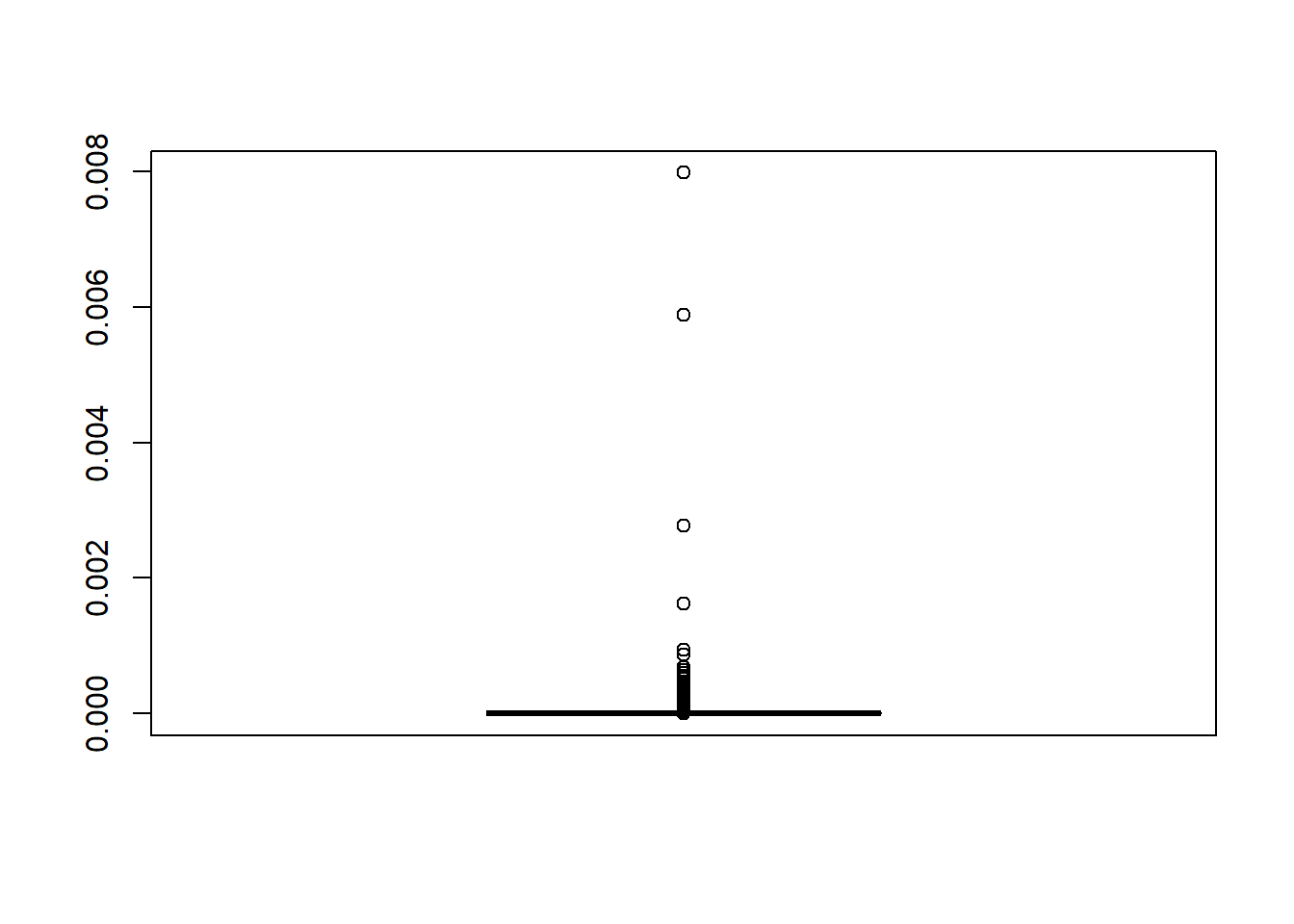

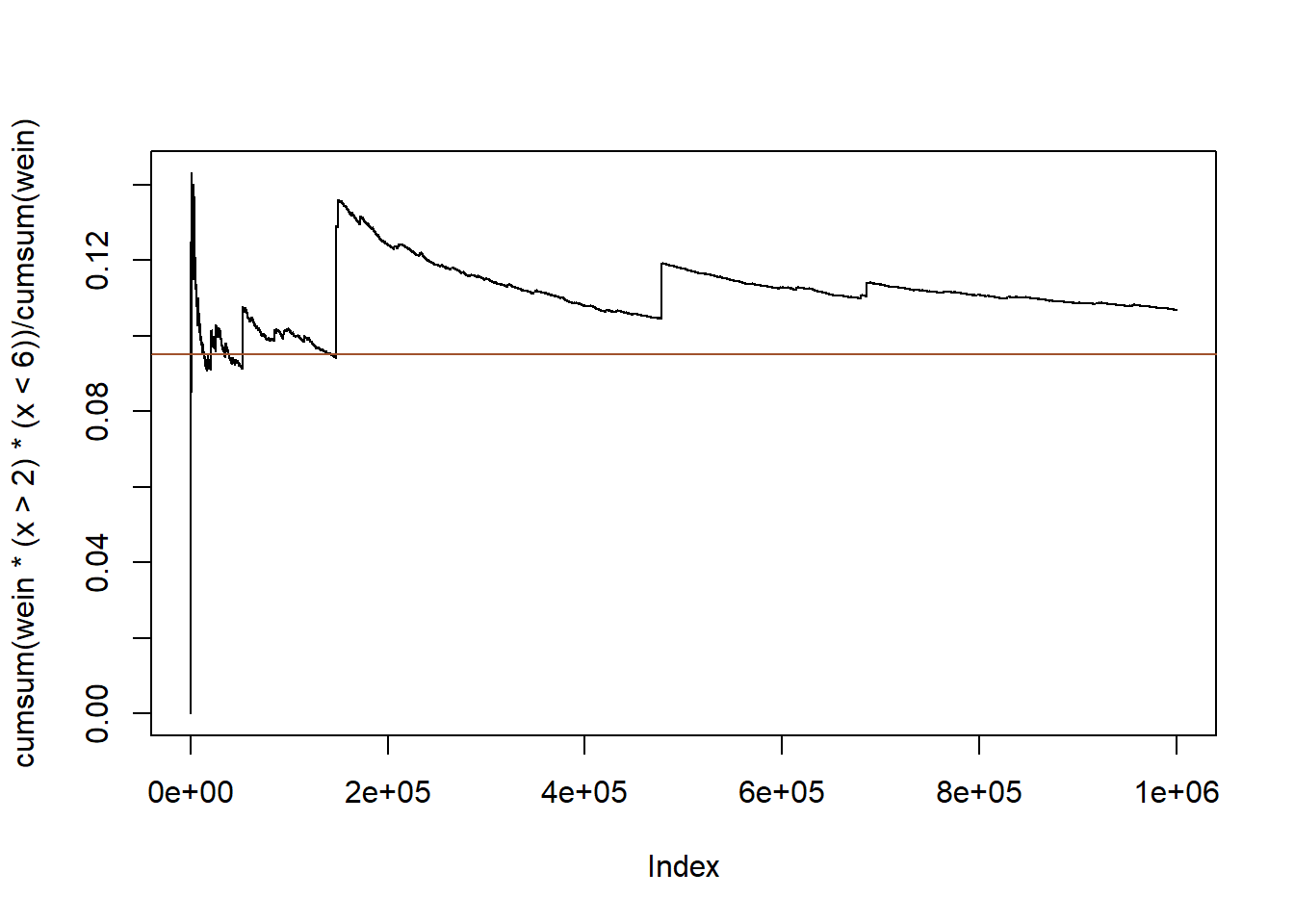
παρατηρούμε ότι ο δειγματικός μέσος εμφανίζει μεγάλα άλματα, ακόμα και για μεγάλες τιμές του \(n\). Τα άλματα αυτά παρατηρούνται σε τιμές για τις οποίες το \(exp(x^2/2)/(1+x^2)\) είναι μεγάλο, δηλαδή το \(x\) είναι μεγάλο. Ο λόγος πίσω από αυτό το φαινόμενο είναι πως τέτοιες τιμές σπανίζουν στην κανονική κατανομή (περισσότερο απ’ ότι στην Cauchy), κάτι που διορθώνουν λαμβάνοντας μεγάλες τιμές στα βάρη τους. Φυσικά, είναι αδύνατο να εμπιστευτούμε τα αποτελέσματα αυτής της προσομοίωσης, καθώς οι λίγες τιμές με μεγάλα βάρη καθιστούν τα βάρη των υπολοίπων αμελητέα.

4.3 Μέθοδοι Ελέγχου Σύγκλισης

4.3.1 Αποτίμηση της Μεταβλητότητας

Είναι σημαντικό να κατανοήσουμε πως υπάρχει ένας απλός και άμεσος τρόπος να αξιολογήσουμε τη μεταβλητότητα μιας ακολουθίας εκτιμήσεων Monte Carlo, και αυτός είναι να προσομοιώσουμε αρκετές ανεξάρτητες ακολουθίες. Η μέθοδος αυτή, παρότι θεωρητικά απλή, είναι ιδιαίτερα χρονοβόρα και υπολογιστικά απαιτητική. Αυτό είναι κάτι που θα συναντάμε συχνά στην προσομοίωση Monte Carlo, ότι δηλαδή η πολυπλοκότητα εκτίμησης της μεταβλητότητας μίας εκτιμήτριας είναι μεγαλύτερη από τη μελέτη της σημειακής της συμπεριφοράς.

Παράδειγμα 4.15 Επαναλάβετε την εκτίμηση του Παραδείγματος 4.2, προσομοιώνοντας πολλά ανεξάρτητα δείγματα, κάθε ένα μεγέθους \(10^4\) και δημιουργήστε ένα \(95\%\) διάστημα εμπιστοσύνης (Δ.Ε.).

Λύση:

Υπενθυμίζουμε ότι εκτιμήσαμε το ολοκλήρωμα της

\[\begin{equation*} h(x)=\left[\cos(50x)+\sin(20x)\right]^2, \end{equation*}\]

στο \(\left[ 0, 1 \right]\). Προσομοιώνουμε πολλά δείγματα, με τα οποία βρίσκουμε τα δειγματικά ποσοστημόρια \(q_{0.025}\) και \(q_{0.975}\) και κατασκευάζουμε ένα εμπειρικό \(95\%\) Δ.Ε. \((q_{0.025}, q_{0.975})\) μέσα στο οποίο συγκεντρώνονται το \(95\%\) των τιμών \(\{\overline{h}_n^{(i)}\}_{i=1}^{M}\) της εκτιμήτριας \(\overline{h(X)}_n\).

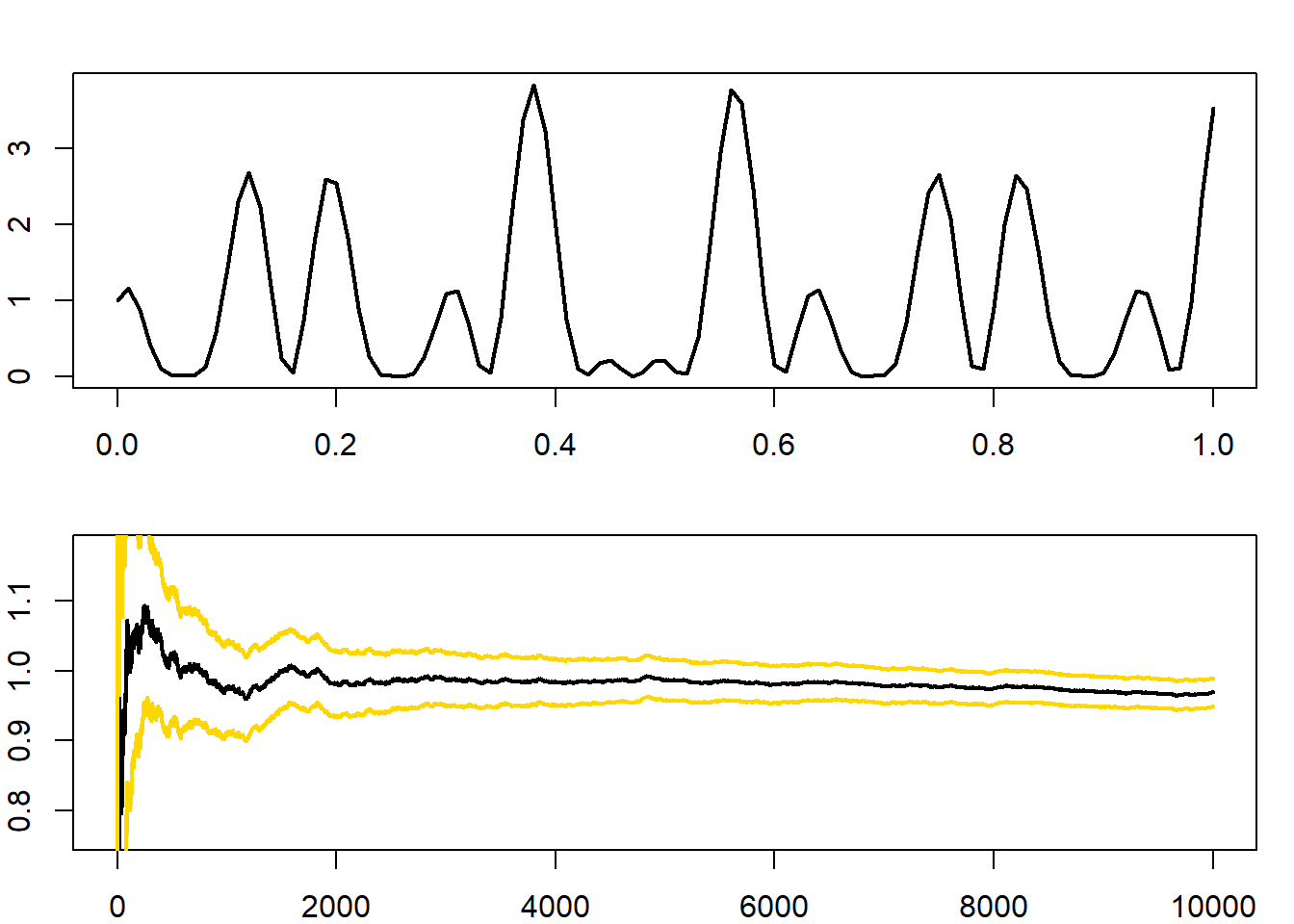
Εικόνα 4.1: (Πάνω) Γράφημα της h. (Κάτω) Monte Carlo εκτίμηση του ολοκληρώματος, μαζί με 95% Δ.Ε. βασισμένα στην ασυμπτωτική κανονικότητα.

Αξίζει ιδιαίτερη προσοχή στη διαφορά ανάμεσα στο παραπάνω Δ.Ε., το οποίο δημιουργείται από ένα μεγάλο αριθμό ανεξάρτητων προσομοιωμένων δειγμάτων και στηρίζεται στην εμπειρική κατανομή του δειγματικού μέσου \(\overline{h(X)}_n\), για κάθε \(n\), και στο ασυμπτωτικό \(95\%\) διάστημα εμπιστοσύνης, το οποίο δημιουργείται από ένα μοναδικό προσομοιωμένο δείγμα και στηρίζεται στην ασυμπτωτική κανονικότητα του δειγματικού μέσου \(\overline{h(X)}_n\), καθώς \(n\rightarrow +\infty\). Το τελευταίο διάστημα επηρεάζεται από τη μεταβλητότητα του ενός δείγματος από το οποίο κατασκευάστηκε.

Προσομοιώνουμε \(10^4\) μονοπάτια και συγκρίνουμε το ασυμπτωτικό \(95\%\) διάστημα εμπιστοσύνης στο πρώτο προσομοιωμένο μονοπάτι \(\left(\overline{h(X_{n,1})}-z_{0.025}\frac{\widehat{\sigma}}{\sqrt{n}}, \overline{h(X_{n,1})}+z_{0.025}\frac{\widehat{\sigma}}{\sqrt{n}}\right)\) με τα διαστήματα που δημιουργούνται από 200 και \(10^4\) ανεξάρτητα δείγματα, όπως περιγράφηκε παραπάνω.

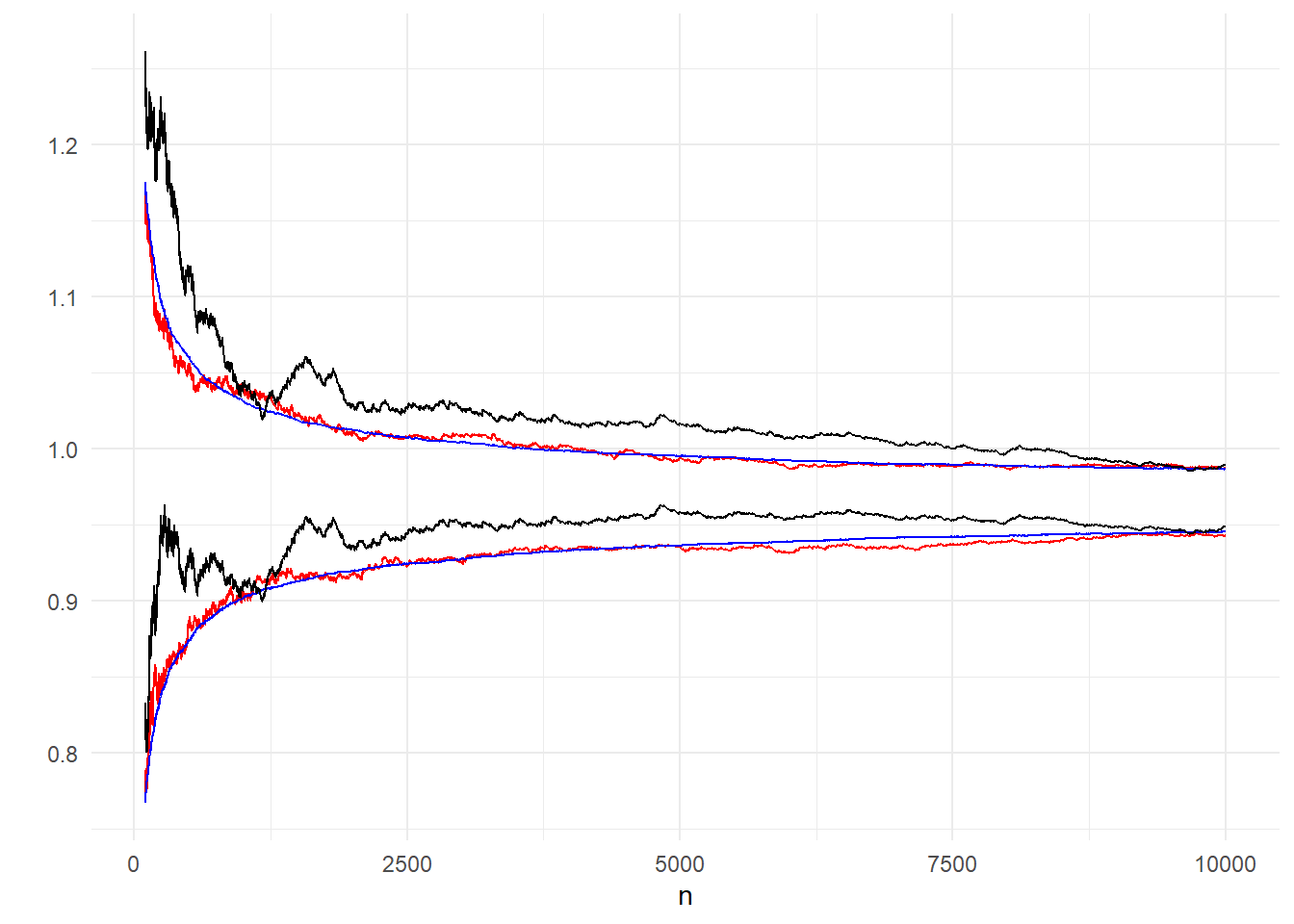
Εικόνα 4.2: Comparison of the 95% inter-quantile range from 200 (red), 10000 (blue) independent paths and 95% confidence interval from one path, based on asymptotic normality (black).

Στην εικόνα 4.2 φαίνεται μία αισθητή διαφορά ανάμεσα στο ασυμπτωτικό διάστημα εμπιστοσύνης, το οποίο είναι επηρεασμένο από τα σφάλματα του πρώτου μονοπατιού, με τα άλλα δύο που δημιουργήθηκαν από ανεξάρτητα μονοπάτια, οδηγώντας σε μικρότερο σφάλμα. Καθώς το μέγεθος \(n\) αυξάνεται, το διάστημα που παράγεται από 200 ανεξάρτητα μονοπάτια έρχεται πολύ κοντά στο διάστημα των \(10^4\) ανεξάρτητων μονοπατιών και αποτελεί μία καλή προσέγγιση.

Στο παραπάνω παράδειγμα συγκρίναμε το διάστημα \((q_{0.025}, q_{0.975})\) που προκύπτει από μία μη παραμετρική εκτίμηση 200 μονοπατιών με το παραμετρικό διάστημα ενός μόνο μονοπατιού. Εναλλακτικά, μπορούμε να κατασκευάσουμε ένα παραμετρικό διάστημα χρησιμοποιώντας και τα 200 μονοπάτια, αφού γνωρίζουμε πως καθώς το μέγεθος του δείγματος \(n\) αυξάνει, η κατανομή του Monte Carlo σφάλματος συγκλίνει στην κανονική. Συγκεκριμένα, για ένα σταθερό \(n\) παίρνουμε τον δειγματικό μέσο των \(s\) μονοπατιών \(Y_n=\frac{1}{s}\sum_{j=1}^s X_{n,j}\) και χρησιμοποιούμε την ασυμπτωτική κανονικότητα του δειγματικού μέσου \(\overline{Y_{n}}\) για να πάρουμε το διάστημα \(\left(\overline{Y_{n}}-z_{0.025}\frac{\widehat{\sigma}}{\sqrt{n}}, \overline{Y_{n}}+z_{0.025}\frac{\widehat{\sigma}}{\sqrt{n}}\right)\).

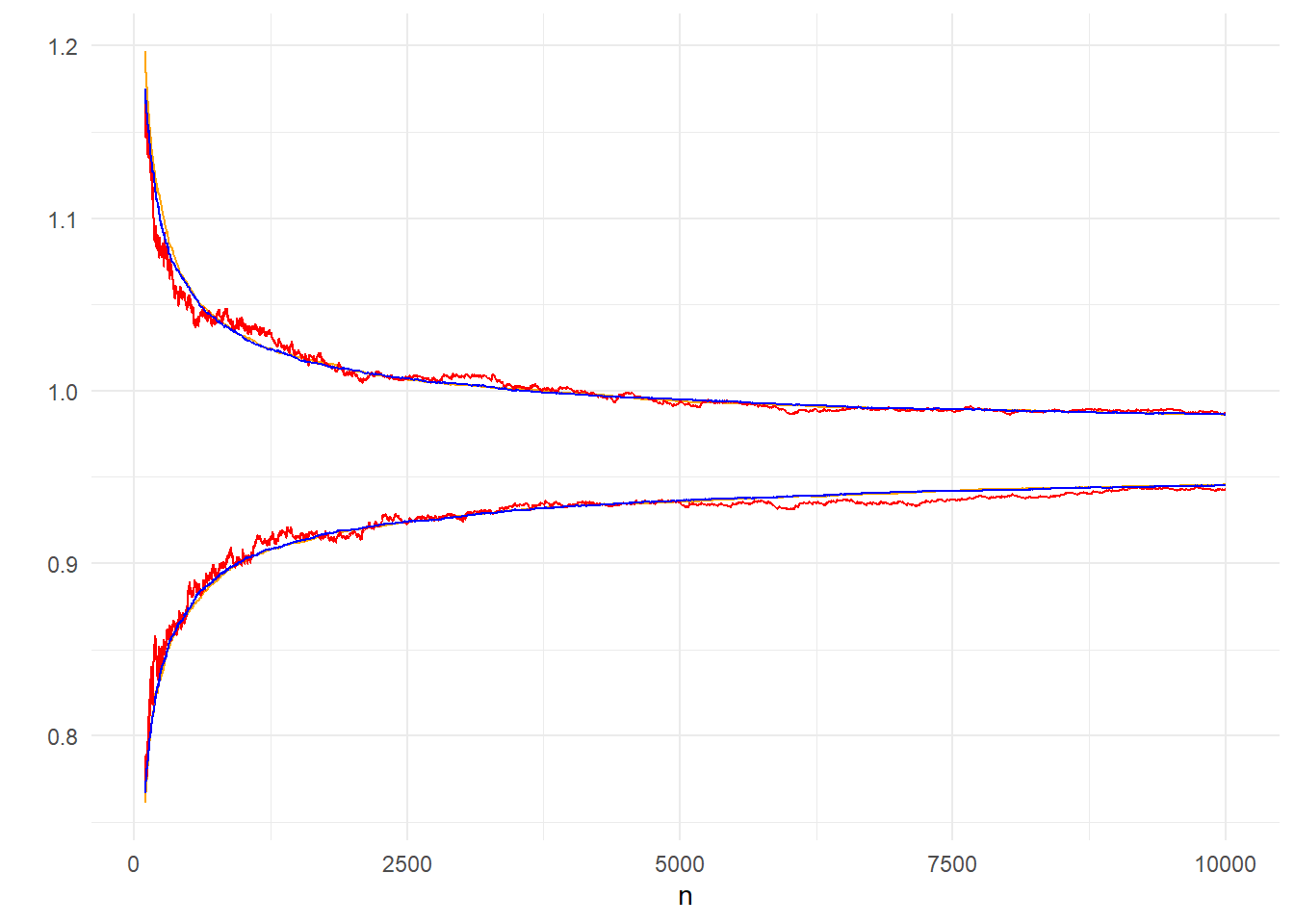
Εικόνα 4.3: Comparison of 95% CI of 200 paths (orange) based on asymptotic normality and 95% inter-quantile range of 200 (red) and 10000 (blue) paths.

Στην εικόνα 4.3 είναι εμφανές πως η ποιότητα της παραμετρικής εκτίμησης είναι καλύτερη, ήδη από μικρά \(n\). Επομένως, αν έχουμε 200 μονοπάτια, προτιμούμε την παραμετρική προσέγγιση από την μη-παραμετρική. Αυτό οφείλεται στην καλή προσέγγιση της κανονικής κατανομής από μικρά \(n\), κάτι που μπορεί να ελεγχθεί και με ένα έλεγχο κανονικότητας.

Μία διαφορετική μέθοδος εκτίμησης της μεταβλητότητας, χρησιμοποιώντας μόλις μία προσομοιωμένη ακολουθία, είναι το bootstrap, το οποίο εφαρμόζει επαναδειγματοληψία σε ένα ήδη υπάρχον δείγμα για να δημιουργήσει τον επιθυμητό αριθμό ακολουθιών. Έτσι, μπορούμε να παράγουμε μόλις ένα μονοπάτι και από αυτό να δημιουργήσουμε με Bootstrap τα 200 μονοπάτια που θέλουμε για τον υπολογισμό των δειγματικών ποσοστημορίων.

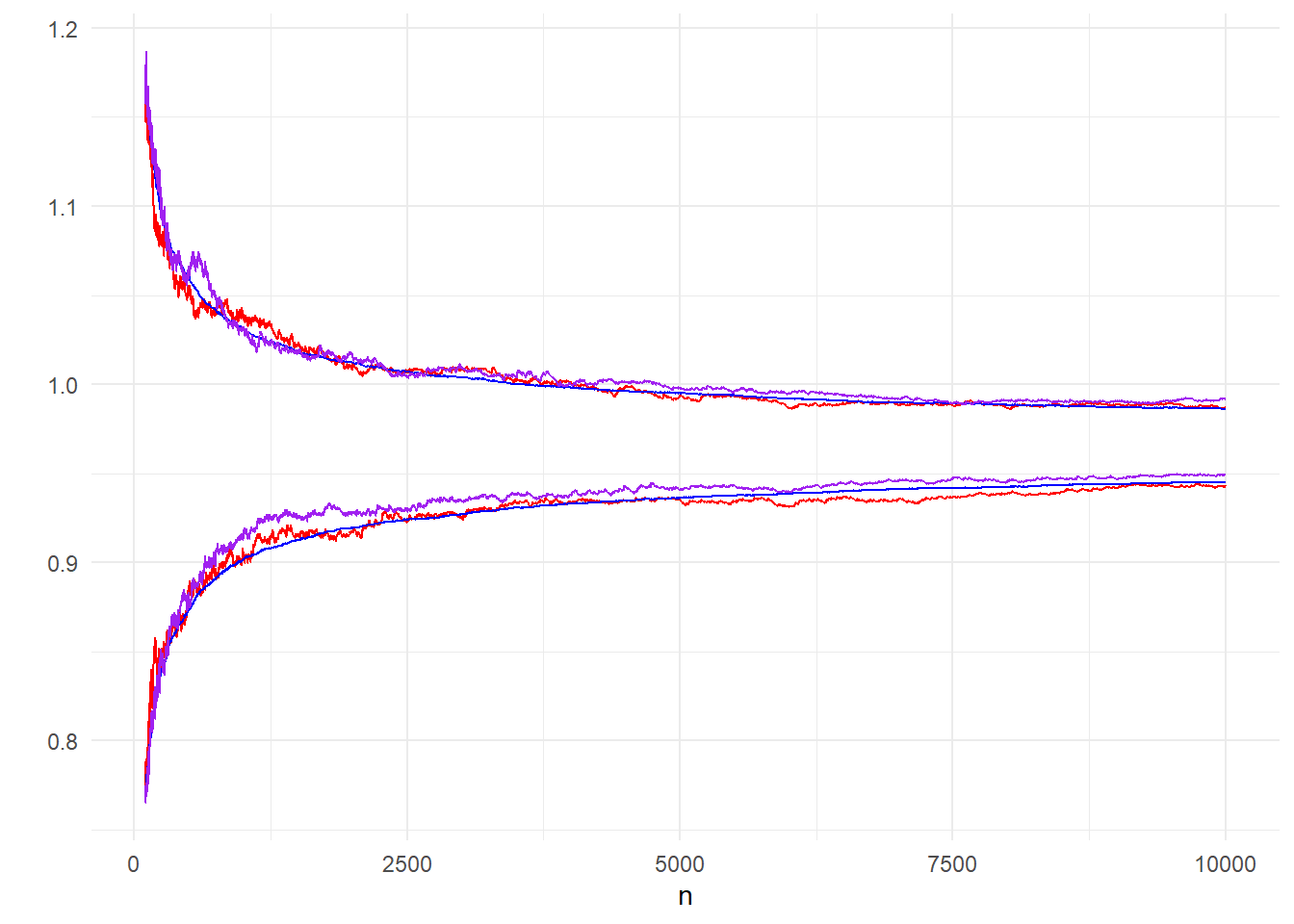
Εικόνα 4.4: Comparison of 95% inter-quantile ranges made from 200 bootstrap paths (purple), 200 (red) and 10000 (blue) independent paths.

Στην εικόνα 4.4 γίνεται φανερό ότι το bootstrap μας οδηγεί σε αντίστοιχα αποτελέσματα με αυτά που πήραμε με τα ανεξάρτητα μονοπάτια Monte Carlo και επομένως θα λέγαμε ότι είναι προτιμητέο.

Επιπλέον, με τα Bootstrap μονοπάτια μπορούμε να δημιουργήσουμε παραμετρικά διαστήματα εμπιστοσύνης στηριζόμενοι στην ασυμπτωτική κανονικότητα της εκτιμήτριας, ακριβώς όπως πριν. Έτσι αναπαράγουμε την εικόνα 4.3 με τα αντίστοιχα Bootstrap μονοπάτια, αντιπαραβάλοντας τα διαφορετικά διαστήματα εμπιστοσύνης που παίρνουμε μέσω Bootstrap, από μόλις ένα προσομοιωμένο μονοπάτι.

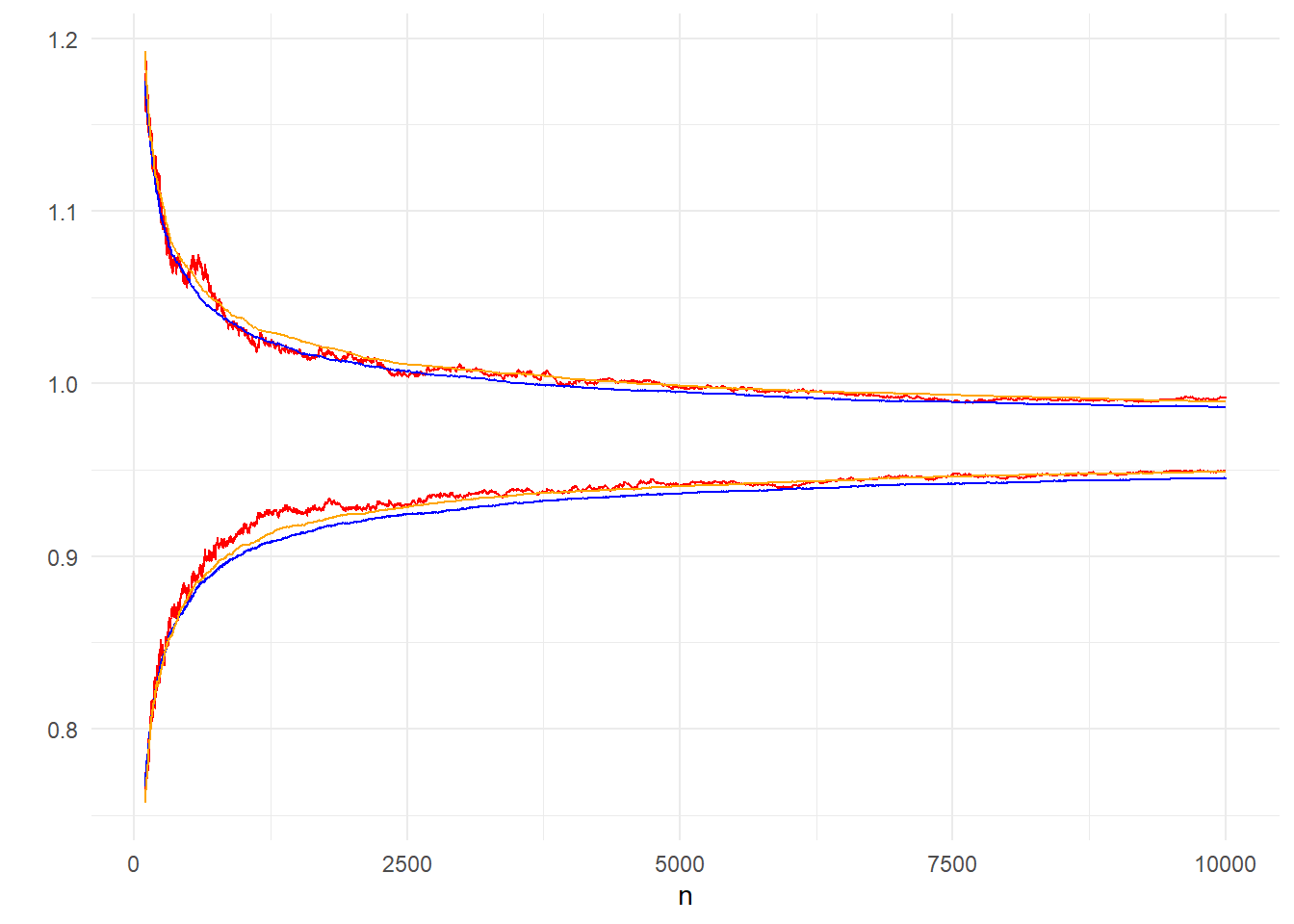
Εικόνα 4.5: Comparison of 95% CI (orange), 95% inter-quantile range (red) from 200 bootstrap paths and inter-quantile range from 10000 (blue) independent paths.

Η εικόνα 4.5 των διαστημάτων από 200 Bootstrap μονοπάτια μας οδηγεί σε τελείως ανάλογα συμπεράσματα με την 4.4 των διαστημάτων από 200 ανεξάρτητα μονοπάτια, με το παραμετρικό διάστημα εμπιστοσύνης να επιτυγχάνει πολύ καλές προσεγγίσεις ήδη από μικρά \(n\).

Στο παράδειγμα αυτό δεν είναι εμφανής ο λόγος για τον οποίο κάποιος θα προτιμούσε το bootstrap αντί της προσομοίωσης παράλληλων αλυσίδων, διότι το υπολογιστικό κόστος είναι συγκρίσιμο. Παρ’ όλα αυτά, σε πιο πολύπλοκα προβλήματα, η δημιουργία παράλληλων αλυσίδων μπορεί να είναι υπολογιστικά πολύ πιο ακριβή από την επαναδειγματοληψία ενός υπάρχοντος δείγματος.

4.3.2 Ασυμπτωτική Διασπορά Εκτιμητριών Σπουδαιότητας

Παράδειγμα 4.16 Θεωρούμε μία τ.μ. \(X\sim \mathcal{N}(\theta,1)\), με prior \(\theta\sim\mathcal{C}(0,1)\), καθώς και μία παρατήρηση \(x=2.5\).

Σε αυτή την περίπτωση έχουμε posterior πυκνότητα

\[\begin{equation*} f(\theta|x)=\frac{\frac{1}{1+\theta^2} e^{-(x-\theta)^2/2}}{\int_{-\infty}^{+\infty} \frac{1}{1+\theta^2} e^{-(x-\theta)^2/2}d\theta}, \end{equation*}\]

δηλαδή posterior μέση τιμή

\[\begin{equation*} \delta(x)=\frac{\int_{-\infty}^{+\infty} \frac{\theta}{1+\theta^2} e^{-(x-\theta)^2/2} d\theta}{\int_{-\infty}^{+\infty} \frac{1}{1+\theta^2} e^{-(x-\theta)^2/2} d\theta}. \end{equation*}\]

Επομένως, μία προσέγγιση του \(\delta(x)\) βασισμένη στην προσομοίωση ανεξάρτητων και ισόνομων \(\theta_1, \theta_2, \dots, \theta_n \sim\mathcal{N}(x,1)\) είναι η

\[\begin{equation*} \widehat{\delta}(x)=\frac{\sum_{i=1}^{n} \frac{\theta_i}{1+\theta_i^2}}{\sum_{i=1}^{n} \frac{1}{1+\theta_i^2}}, \end{equation*}\]

αφού και τα δύο αθροίσματα συγκλίνουν. Η εκτιμήτρια αυτή μπορεί να ερμηνευθεί ως μία κανονικοποιημένη προσέγγιση επαναδειγματοληψίας σπουδαιότητας με την κανονική σ.π.π. ως συνάρτηση σπουδαιότητας και λόγο \(1/(1+\theta^2)\). Σημειώνουμε εδώ ότι η εκτιμήτρια \(\widehat{\delta}(x)\) είναι λόγος εκτιμητριών και γενικά η διασπορά ενός λόγου δεν είναι ο λόγος των διασπορών. Το πρόβλημα αυτό συναντάται συχνά στην Μπεϋζιανή Στατιστική.

Θεωρούμε λοιπόν την εκτιμήτρια

\[\begin{equation*} \widehat{\delta}(x)=\frac{\sum_{i=1}^{n} w_ih(x_i)}{\sum_{i=1}^{n} w_i}, \end{equation*}\]

όπου \(x_i\) οι πραγματοποιήσεις των τυχαίων μεταβλητών \(X_i\) από την υποψήφια πυκνότητα \(g\). Επιπλέον, τα \(w_i\) είναι οι πραγματοποιήσεις των τυχαίων μεταβλητών \(W_i\) για τις οποίες ισχύει \(\mathbf{E}\left[W_i|x_i=x\right]=k f(x)/g(x)\), όπου \(k\) μία αυθαίρετη σταθερά (η οποία εμπεριέχει τις πιθανώς άγνωστες σταθερές των \(f,g\)). Συμβολίζουμε

\[\begin{equation*} S_{h,n}=\sum W_i h(X_i), \ \ S_{1,n}=\sum_{i=1}^n W_i. \end{equation*}\]

Σημειώνουμε εδώ πως δεν έχουμε υποθέσει ανεξαρτησία ανάμεσα στις \(X_i\), σε αντίθεση με την δειγματοληψία σπουδαιότητας. Τότε, η ασυμπτωτική διασπορά της \(\delta_{h,n}\) είναι (Liu 1996, Robert & Casella 2002 Chapter 4)

\[\begin{equation*} \mathbf{V}\left(\delta_{h,n}\right) = \frac{1}{n^2k^2}\left[ \mathbf{V}\left(S_{h,n}\right) -2\mathbf{E}_f[h] Cov(S_{h,n}, S_{1,n}) +\mathbf{E}_f[h]^2 \mathbf{V}\left(S_{1,n}\right) \right]. \end{equation*}\]

Μπορούμε να συμπεράνουμε ότι, αν οι \(X_i\) είναι ανεξάρτητες και ισόνομες, μία αδρή εκτίμηση της διασποράς της \(\delta_{h,n}\) είναι

\[\begin{equation*} \mathbf{V}\left(\delta_{h,n}\right) \approx \frac{1}{n} \mathbf{V}_f\left(h(X)\right) \left[1+\mathbf{V}_g\left(W\right) \right]. \end{equation*}\]

Η παραπάνω προσέγγιση είναι έγκυρη μόνο για την κανονικοποιημένη μορφή των βαρών \(w_i\), καθώς διαφορετικά εξαρτάται από την άγνωστη σταθερά \(k\). Η εκτίμηση Monte Carlo που παίρνουμε είναι

\[\begin{equation*} \frac{\sum_{i=1}^n w_i \left(h(x_i)-\delta_{h,n}\right)^2}{n \sum_{i=1}^n w_i} \cdot \left[ 1+\frac{n \widehat{\mathbf{V}}(W)}{\left(\sum_{i=1}^n w_i\right)^2}\right]. \end{equation*}\]

Η παραπάνω έκφραση δεν αποτελεί μια καλή προσέγγιση της διασποράς, αφού όπως είναι φανερό είναι πάντοτε μεγαλύτερη από την \(\mathbf{V}_f\left(h(X)\right)\), την διασπορά ενός ανεξάρτητου και ισόνομου δείγματος μεγέθους \(n\).

Παράδειγμα 4.17 Εάν προσομοιώσουμε ένα δείγμα από την \(\mathcal{N}(x,1)\), η προσέγγιση της διασποράς που δόθηκε μπορεί να χρησιμοποιηθεί για να αξιολογήσουμε την μεταβλητότητα της εκτίμησής μας, αλλά και πάλι, η ασυμπτωτική φύση αυτών των προσεγγίσεων πρέπει να ληφθεί υπ’ όψιν.

Αν πάρουμε 500 ακολουθίες των εκτιμητριών των \(\delta (x)\) μπορούμε να βρούμε το \(95\%\) ποσοστημοριακό εύρος (γκρι λωρίδα) και να το αντιπαραβάλουμε με το \(95\%\) ασυμπτωτικό διάστημα εμπιστοσύνης βασισμένο σε μία ακολουθία χρησιμοποιώντας τη συνήθη εκτίμηση διασποράς (μαύρες γραμμές) καθώς και το αντίστοιχο δ.ε. με την διόρθωση βαρών (καφέ γραμμές).

Μπορούμε να επαναλάβουμε την διαδικασία, αυτή τη φορά προσομοιώνοντας τα \(\theta_i\) από την prior \(\mathcal{C}(0,1)\) και χρησιμοποιώντας την εκτιμήτρια της επαναδειγματοληψίας σπουδαιότητας

\[\begin{equation*} \tilde{\delta}_{h,n} = \frac{\sum_{i=1}^n \theta_i e^{-\frac{1}{2}(x-\theta_i)^2}}{\sum_{i=1}^n e^{-\frac{1}{2}(x-\theta_i)^2}}. \end{equation*}\]

4.3.3 Αποτελεσματικό Μέγεθος Δείγματος

Η αναπαράσταση

\[\begin{equation*} \frac{\sum_{i=1}^n w_i \left(h(x_i)-\delta_{h,n}\right)^2}{n \sum_{i=1}^n w_i} \cdot \left[ 1+ \frac{n \widehat{\mathbf{V}}(W)}{\left(\sum_{i=1}^n w_i\right)^2}\right]. \end{equation*}\]

που προτάθηκε για την προσέγγιση της διασποράς της εκτιμήτριας που προκύπτει από τη δειγματοληψία σπουδαιότητας μας οδηγεί σε ένα αναγκαίο εργαλείο αξιολόγησης της απόδοσης των συναρτήσεων σπουδαιότητας. Για την \(\widehat{\mathbf{V}}(W)\) ισχύει

\[\begin{equation*} \widehat{\mathbf{V}}(W) = \frac{1}{n} \sum_{i=1}^n w_i^2 - \frac{1}{n^2} \left( \sum_{i=1}^n w_i \right)^2, \end{equation*}\]

επομένως

\[\begin{equation*} 1+\widehat{\mathbf{V}}_g(W) = \frac{n \sum_{i=1}^n w_i^2}{\left( \sum_{i=1}^n w_i \right)^2}. \end{equation*}\]

Συμβολίζοντας τα κανονικοποιημένα βάρη \(w_{i,n} = w_i/\sum_{j=1}^n w_j\), ορίζουμε το αποτελεσματικό μέγεθος δείγματος ως

\[\begin{equation*} ESS_n = \frac{1}{\sum_{i=1}^n w_{i,n}^2}. \end{equation*}\]

Το αποτελεσματικό μέγεθος δείγματος είναι χρήσιμο στην αξιολόγηση της επιβάρυνσης της διασποράς εξαιτίας των βαρών σπουδαιότητας, κάτι που παράλληλα μας δίνει μια αξιολόγηση για της συνάρτησης σπουδαιότητας. Για ένα δείγμα με ίσα βάρη, έχουμε \(ESS_n=n\), ενώ για ένα εκφυλισμένο δείγμα με όλα τα βάρη ίσα με 0 εκτός από ένα, έχουμε \(ESS_n=1\). Επομένως, το αποτελεσματικό μέγεθος δείγματος αντιστοιχεί το δείγμα σπουδαιότητας με το μέγεθος ενός ισοδύναμου δείγματος ανεξάρτητων και ισόνομων παρατηρήσεων.

Ένα ακόμα μέτρο αξιολόγησης παρέχεται από την perplexity \(e^{PP}/n\), όπου

\[\begin{equation*} PP_n = -\sum_{i=1}^n w_{i,n} \log(w_{i,n}), \end{equation*}\]

είναι η εντροπία των κανονικοποιημένων βαρών σπουδαιότητας. (Το εργαλείο αυτό χρησιμοποιείται κυρίως στην θεωρία πληροφόρησης και την αναγνώριση λόγου, βλ Jelinek 1999). Το perplexity παρέχει μία εκτίμηση της \(e^{D_{KL}(f,g)}\), όπου

\[\begin{equation*} D_{KL}(f,g) = \int \log\left\{\frac{f(x)}{g(x)}\right\} f(x) dx, \end{equation*}\]

είναι η απόκλιση Kullback-Leibler ανάμεσα στην συνάρτηση-στόχο \(f\) και την συνάρτηση σπουδαιότητας \(g\). Επομένως, όσο πιο κοντά βρίσκεται το perplexity στο 1, τόσο πιο κατάλληλη η συνάρτηση σπουδαιότητας.

Παράδειγμα 4.18 Συγκρίνετε το αποτελεσματικό μέγεθος δείγματος για τις προσομοιώσεις από κανονική και Cauchy των προηγούμενων παραδειγμάτων.

Λύση:

Για τα αποτελεσματικά μεγέθη δειγμάτων (αριστερά) και για τα perplexity (δεξιά) της κανονικής (κόκκινο) και της Cauchy (μπλε), έχουμε:

Όπως είναι φανερό, η προσομοίωση βασισμένη στην κανονική είναι περίπου διπλά αποδοτική από την προσομοίωση που βασίστηκε στην Cauchy.

4.4 Rao-Blackwellization

Θεώρημα 4.1 (Rao-Blackwell) Έστω ένα τυχαίο δείγμα \(X\) και μία εκτιμήτρια \(\delta(X)\). Αν \(Y\) μία επαρκής στατιστική συνάρτηση, τότε

\[\begin{equation*} \mathbf{V}\left(\mathbf{E}\left(\delta(X)|Y\right)\right) \leq \mathbf{V}\left(\delta(X)\right). \end{equation*}\]

Το θεώρημα Rao-Blackwell δείχνει ότι δεσμεύοντας μία εκτιμήτρια ως προς μία επαρκή στατιστική συνάρτηση οδηγεί σε εκτιμήτριες με μικρότερη ίση διασπορά. Αυτό το θεώρημα μας οδηγεί άμεσα σε μία τεχνική μείωσης της διασποράς των Monte Carlo εκτιμητριών χρησιμοποιώντας δέσμευση. Η τεχνική αυτή ονομάζεται Rao-Blackwellization, παρότι στο πλαίσιο του Monte Carlo η δέσμευση δεν γίνεται πάντα ως προς επαρκείς στατιστικές συναρτήσεις. Η βασική ιδέα είναι ότι χρησιμοποιώντας δεσμευμένη μέση τιμή (η οποία μπορεί να υπολογιστεί) οδηγούμαστε εκτιμήσεις μικρότερης μεταβλητότητας, χωρίς να επηρεάζεται η αμεροληψία των εκτιμήσεων αυτών.

Πιο αυστηρά, αν \(\delta(X)\) είναι μία εκτιμήτρια της ποσότητας \(m=\mathbf{E}_f\left(h(X)\right)\) και η \(X\) μπορεί να προσομοιωθεί με την από κοινού κατανομή \(f^\star(x,y)\) η οποία ικανοποιεί η σχέση

\[\begin{equation*} f(x)=\int f^\star (x,y) dy, \end{equation*}\]

τότε η νέα εκτιμήτρια \(\delta^\star (Y) = \mathbf{E}\left(\delta(X)|Y\right)\) κυριαρχεί της \(\delta\) ως προς τη διασπορά, ενώ η μεροληψία παραμένει η ίδια. Φυσικά, αυτό το αποτέλεσμα είναι ιδιαίτερα χρήσιμο όταν η \(\delta^\star (Y)\) μπορεί να υπολογιστεί αναλυτικά.

Παράδειγμα 4.19 Υπολογίστε τη μέση τιμή της \(h(X)=e^{-X^2}\), όπου \(X\sim\mathcal{T}_n(\mu, \sigma^2)\).

Λύση:

Αρχικά ας μελετήσουμε την κατανομή αυτή. Γνωρίζουμε ότι η κατανομή Student \(t_n\) κατασκευάζεται από τον λόγο μίας τυπικής κανονικής προς την ρίζα μίας \(\mathcal{X}^2_n\), διαιρεμένη με τους βαθμούς ελευθερίας της, δηλαδή:

\[\begin{equation*} T=\frac{Z}{\sqrt{Q}/n}, \ Z\sim\mathcal{N}(0,1), Q\sim\mathcal{X}^2_n. \end{equation*}\]

Η οικογένεια των κανονικών κατανομών μπορεί να βασιστεί στην τυπική κατανομή χρησιμοποιώντας μετασχηματισμούς θέσης-κλίμακας, δηλαδή

\[\begin{equation*} Z\sim N(0,1) \Rightarrow X=\mu+\sigma Z \sim\mathcal{N}(\mu,\sigma^2). \end{equation*}\]

Ανάλογα, κάνοντας μετασχηματισμό θέσης κλίμακας στην \(Τ~t_n\) που κατασκευάσαμε παραπάνω, έχουμε

\[\begin{equation*} T=\frac{Z}{\sqrt{Q}/n}\sim t_n \Rightarrow X=\mu+\sigma T= \mu+\sigma \frac{Z}{\sqrt{Q}/n} \sim\mathcal{T}_n(\mu, \sigma^2). \end{equation*}\]

Ορίζουμε την τ.μ. \(Y=Q/n\) και παρατηρούμε ότι

\[\begin{equation*} X|Y=y = \mu +\frac{\sigma}{\sqrt{y}}Z \sim \mathcal{N}\left(\mu, \frac{\sigma^2}{y}\right). \end{equation*}\]

Επομένως μπορούμε να υπολογίσουμε την από κοινού συνάρτηση πυκνότητας των \(X, Y\) δεσμεύοντας ως προς \(Y\) (Dikey’s Decomposition),

\[\begin{equation*} f_{X,Y}^\star (x,y) = f_{X|Y} (x|y) \cdot f_Y(y) = \frac{\sqrt{y}}{\sqrt{2\pi\sigma^2}} e^{-\frac{y}{2\sigma^2}(x-\mu)^2} \cdot \frac{(n/2)^{n/2}}{\Gamma(n/2)} y^{n/2 - 1} e^{-yn/2}. \end{equation*}\]

Η εφαρμογή του παραπάνω στην R είναι άμεση

Nsim <- 10 ^ 4 ; nu <- 5 ; mu <- 3 ; sigma <- 0.5
y <- sqrt(rchisq(Nsim, df = nu) / nu)
x <- rnorm(Nsim, mu, sigma / y)

Ο παραπάνω κώδικας προσομοιώνει ζευγάρια τ.μ. \((X_i, Y_i), i=1,2, \ldots, n\). Στηριζόμενοι μόνο στις παρατηρήσεις της \(X\), εκτιμούμε την \(\mathbf{E}_f\left(h(X)\right)\) ως

\[\begin{equation*} \delta_n = \frac{1}{n} \sum_{j=1}^n e^{-X_j^2}. \end{equation*}\]

Η εκτίμηση αυτή μπορεί να βελτιωθεί χρησιμοποιώντας Rao-Blackwellization

\[\begin{equation*} \delta_n^\star = \frac{1}{n} \sum_{j=1}^n \mathbf{E}\left(e^{-X_j^2} | Y_j\right), \end{equation*}\]

όπου η \(\mathbf{E}\left(e^{-X^2} | Y\right)\) υπολογίζεται αναλυτικά

\[\begin{align*} \mathbf{E}\left(e^{-X^2} | Y=y\right) &= \int_{-\infty}^{+\infty} e^{-x^2} \frac{\sqrt{y}}{\sqrt{2\pi \sigma^2}} e^{-\frac{y}{2\sigma^2}(x-mu)^2} dx = \int_{-\infty}^+{+\infty} \frac{\sqrt{y}}{\sqrt{2\pi \sigma^2}} e^{(-\frac{y}{2\sigma^2}-1)x^2+\frac{y}{2\sigma^2}2x\mu-\frac{y}{2\sigma^2}\mu^2} dx \\ &=\ldots=\frac{\sqrt{y}}{\sqrt{2\pi \sigma^2}} e^{-\frac{y}{2\sigma^2}\mu^2+\frac{(y\mu)^2}{2\sigma^2(y+2\sigma^2)}} \int_{-\infty}^{+\infty} e^{-\frac{y+2\sigma^2}{2\sigma^2}(x-\frac{y\mu}{y+2\sigma^2})^2}dx = \frac{\sqrt{y}}{\sqrt{2\pi \sigma^2}} e^{-\frac{y}{2\sigma^2}\mu^2+\frac{(y\mu)^2}{2\sigma^2(y+2\sigma^2)}}\cdot \sqrt{2\pi \frac{\sigma^2}{y+2\sigma^2}} \\ &= \ldots = \frac{1}{\sqrt{\frac{2\sigma^2}{y}+1}} e^{-\frac{\mu^2}{\frac{2\sigma^2}{y}+1}}. \end{align*}\]

Επομένως έχουμε την εκτιμήτρια

\[\begin{equation*} \delta_n^\star = \frac{1}{n}\sum_{j=1}^n \mathbf{E}\left(e^{-X^2}|Y_j\right) = \frac{1}{n}\sum_{j=1}^n \frac{1}{\sqrt{\frac{2\sigma^2}{Y_j}+1}} e^{-\frac{\mu^2}{\frac{2\sigma^2}{Y_j}+1}}, \end{equation*}\]

η οποία υπολογίζεται αναλυτικά.

d1 <- cumsum(exp( - x ^ 2)) / (1:Nsim)
d2 <- cumsum(exp(- mu ^ 2 / (1 + 2 * (sigma / y) ^ 2)) / sqrt(1 + 2 * (sigma / y) ^ 2)) / (1:Nsim)

Στην εικάνα 4.6 γίνεται σύγκριση των εκτιμητριών των δύο εκτιμητριών \(\delta_n, \delta_n^\star\) για τις τιμές \(n=5, \mu=3, \sigma=0.5\). Είναι εμφανής η μείωση της μεταβλητότητας που επιτεύχθηκε με τη μέθοδο Rao-Blackwellization. Εκτιμώντας τις διασπορές τους έχουμε \(\widehat{\mathbf{V}(\delta_n)}=0.00279\) και \(\widehat{\mathbf{V}(\delta_n^\star)}=0.00022\), δηλαδή επιτύχαμε μείωση της διασποράς περίπου στο 1/10 της αρχικής.

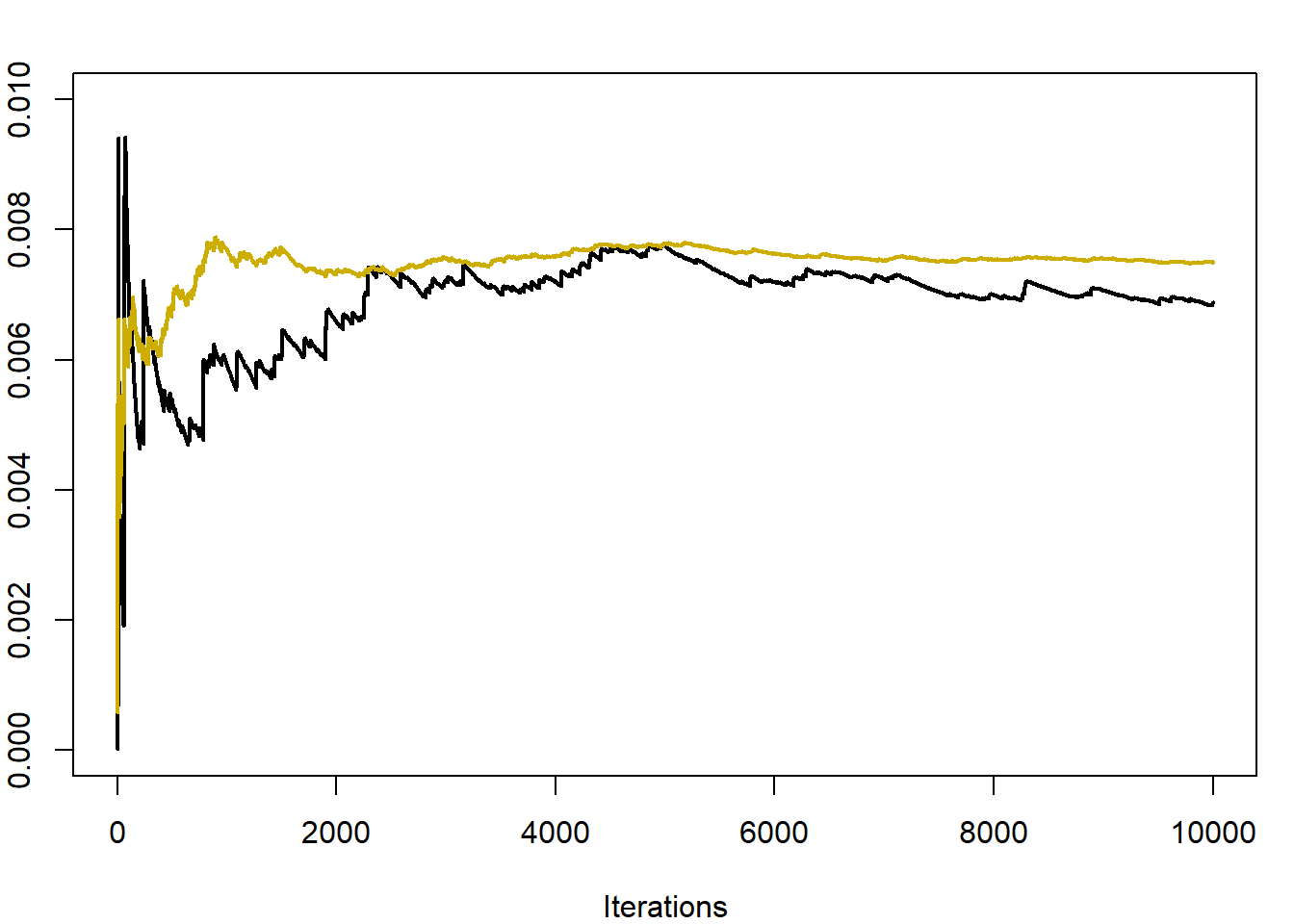
Εικόνα 4.6: Convergence of the estimators \(\delta_n\) (darker) and \(\delta_n^\star\) (lighter), for \(n=5, \mu=3, \sigma=0.5\).

Παράδειγμα 4.20 Έστω ένας αλγόριθμος αποδοχής-απόρριψης στον οποίο έχουμε πυκνότητα-στόχο την \(f\) και υποψήφια πυκνότητα την \(g\).

1. Δείξτε ότι το δείγμα \((X_1, X_2, ..., X_n)\) μπορεί να περιγραφεί πλήρως από ένα τυχαίο δείγμα \((U_1, U_2, ..., U_N)\) από την \(Unif(0,1)\), και ένα τυχαίο δείγμα \((Y_1, Y_2, ..., Y_N)\) από την κατανομή με σ.π.π. τη \(g\). Με \(N\) συμβολίζουμε την τ.μ. του πλήθος παρατηρήσεων που πρέπει να προσομοιωθούν μέχρι να υπάρξουν \(n\) αποδεκτές παρατηρήσεις.

2. Συμπεράνετε ότι η εκτιμήτρια της \(\mathbf{E}\left(h(X)\right)\) που βασίζεται στο παραπάνω δείγμα \((X_1, X_2, ..., X_n)\) μπορεί να γραφτεί ως

\[\begin{equation*} \delta_1 = \frac{1}{n} \sum_{i=1}^n h(X_i) = \frac{1}{n} \sum_{j=1}^N h(Y_j) 1_ {U_j\leq w_j}, \end{equation*}\] όπου \(w_j=f(Y_j)/Mg(Y_j)\).

Λύση:

Ας θυμηθούμε κάποια βασικά στοιχεία του αλγορίθμου αποδοχής-απόρριψης. Για να προσομοιώσουμε την παρατήρηση \(X_i\), προσομοιώνουμε τις \(Y_{i,1}\) και \(U_{i,1}\). Αν \(U_{i,1}\leq f(Y_{i,1})/Mg(Y_{i,1})\), τότε δεχόμαστε την υποψήφια παρατήρηση και έχουμε \(X_i=Y_{i,1}\), ενώ διαφορετικά προσομοιώνουμε τις \(Y_{i,2}\) και \(U_{i,2}\) και επαναλαμβάνουμε τη διαδικασία. Αυτό οδηγεί σε ένα τυχαίο πλήθος \(N_i\) προσομοιώσεων, μέχρι να έχουμε την πρώτη αποδοχή, ενώ σε κάθε επανάληψη έχουμε πιθανότητα αποδοχής \(p=1/M\). Επομένως, το \(N_i\) ακολουθεί γεωμετρική κατανομή με παράμετρο \(p\), δηλαδή \(N_i~Geo(p)\). Τα παραπάνω μας οδηγούν στη σχέση:

\[\begin{equation*} X_i = \sum_{j=1}^{N_i} Y_j 1_{U_j\leq w_j}, \ i=1, 2, \dots, n. \end{equation*}\]

Η παραπάνω διαδικασία πρέπει να επαναληφθεί συνολικά \(N=N_1 +N_2 +... +N_n\) φορές εώς ότου έχουμε συνολικά \(n\) αποδεκτές παρατηρήσεις (όπου \(N_i, N_j\) ανεξάρτητα για \(i\neq j\)). Επομένως, το συνολικό πλήθος επαναλήψεων είναι μία τ.μ. που ακολουθεί αρνητική διωνυμική, δηλ. \(N~NegBin(n,p)\). Η εκτιμήτριά μας επομένως μπορεί να περιγραφεί ως

\[\begin{equation*} \delta_1 = \frac{1}{n} \sum_{i=1}^n h(X_i) = \frac{1}{n} \sum_{i=1}^n \sum_{j=1}^ {N_i} h(Y_{i,j}) 1_{U_{i,j}\leq w_{i,j}}, \end{equation*}\]

το οποίο με αλλαγή αρίθμησης των δεικτών \((i,j)\) γίνεται

\[\begin{equation*} \delta_1 = \frac{1}{n} \sum_{i=1}^n h(X_i) = \frac{1}{n} \sum_{j=1}^N h(Y_j) 1_ {U_j\leq w_j}. \end{equation*}\]

Το Rao-Blackwellization βρίσκει μία ακόμα εφαρμογή στα πλαίσια της αμυντικής δειγματοληψίας (defensive sampling, Hesterberg, 1995), μία παραλλαγή της δειγματοληψίας σπουδαιότητας. Έχουμε δει πως όταν προσομοιώνουμε με δειγματοληψία σπουδαιότητας από μία σ.π.π. \(f\) χρησιμοποιώντας τη σ.π.π. \(g\), οι ουρές της \(g\) πρέπει να είναι βαρύτερες από εκείνες της \(f\), προκειμένου η εκτιμήτρια που θα προκύψει να έχει πεπερασμένη διασπορά. Καθώς αυτό μπορεί να είναι δύσκολο, μία γενική τεχνική που συχνά επιστρατεύεται είναι αυτή της αμυντικής δειγματοληψίας η οποία στην θέση της \(g\) χρησιμοποιεί τη μίξη

\[\begin{equation*} pg(x) + (1-p) \ell(x), \ 0<p<1, \end{equation*}\]

όπου η \(\ell\) είναι μία πυκνότητα με βαριές ουρές (όπως η Cauchy ή η Pareto) και το \(p\) είναι κοντά στη μονάδα. Από τεχνική σκοπιά, εάν μπορούμε να προσομοιώσουμε από τις \(g, \ell\), μπορούμε εύκολα να προσομοιώσουμε από την μίξη τους προσομοιώνοντας μία παρατήρηση από την \(Bin(n, p)\) η οποία θα κρίνει πόσες παρατηρήσεις θα προέρχονται από την \(g\) και πόσες από την \(\ell\).

mix <- function(n = 1, p = 0.5) {
    m <- rbinom(1, size, pro = p)  # simg and siml simulate from
    c(simg(m), siml(n - m)) # g and l, respectively.
}

Αξίζει προσοχή το γεγονός πως τα βάρη σπουδαιότητας είναι ίσα με

\[\begin{equation*} w_i(x_i) = \frac{f(x_i)}{pg(x_i) + (1-p) \ell(x_i)}, \ i=1, 2, \dots, n, \end{equation*}\]

ανεξάρτητα από το αν η παρατήρηση \(x_i\) προσομοιώθηκε από την \(g\) ή την \(\ell\). Η εισαγωγή της τυχαιότητας στο πλήθος των παρατηρήσεων που προέρχονται από κάθε πυκνότητα επιβαρύνει την μεταβλητότητα της εκτίμησής μας. Γι’ αυτό, μπορούμε να επιλέξουμε από τις \(n\) παρατηρήσεις οι \(x_1, x_2, \dots, x_{pn}\) να προέρχονται από την \(g\) και οι \(y_1, y_2, \dots, y_{(1-p)n}\) από την \(\ell\) (υποθέτοντας ότι το \(pn\) είναι ακέραιος). Κάτι τέτοιο οδηγεί στην εκτιμήτρια

\[\begin{equation*} \frac{1}{n}\sum_{i=1}^{pn} h(x_i) \frac{f(x_i)}{pg(x_i)+(1-p)\ell(x_i)} + \frac{1}{n}\sum_{i=1}^{(1-p)n} h(y_i) \frac{f(y_i)}{pg(y_i)+(1-p)\ell(y_i)}, \end{equation*}\]

η οποία είναι αμερόληπτη. Επομένως, προσομοιώνοντας ένα σταθερό αριθμό παρατηρήσεων από κάθε κατανομή εξαλείφει την μεταβλητότητα που εισήγαγε η διωνυμική κατανομή.

Παράδειγμα 4.21 Έστω \(f\) η πυκνότητα της κατανομής \(\mathcal{T}_n\). Εκτιμήστε την ποσότητα \(\mathbf{E}\left(h(X)\right)\), όπου \(h(x)=\sqrt{x/(1-x)}\).

Λύση:

Εάν προσπαθήσουμε να κάνουμε δειγματοληψία σπουδαιότητας με συνάρτηση σπουδαιότητας \(g: g(1)<+\infty\), η εκτίμηση που θα προκύψει θα έχει άπειρη διασπορά. Συγκεκριμένα, η εκτίμηση του ολοκληρώματος

\[\begin{equation*} \int_1^{+\infty} \sqrt{\frac{x}{x-1}}t_2(x) dx = \int_1^{+\infty} \sqrt{\frac{x}{x-1}} \frac{\Gamma(3/2)/\sqrt{2\pi}}{(1+x^2/2)^{3/2}} dx, \end{equation*}\]

δεν μπορεί να γίνει άμεσα, αφού η συνάρτηση \(h(x)=\sqrt{1/(x-1)}\) δεν είναι δύο φορές ολοκληρώσιμη και επομένως αν προσομοιώσουμε από την κατανομή \(\mathcal{T}_2\) θα προκύψει μία εκτιμήτρια του ολοκληρώματος με άπειρη διασπορά. Για τον λόγο αυτό, θα χρησιμοποιήσουμε μία μίξη της σ.π.π. της \(\mathcal{T}_2\) με μία \(\ell\). Προκειμένου η \(h^2(x)f(x)/\ell(x)\) να είναι ολοκληρώσιμη, η \(\ell\) πρέπει να αποκλίνει καθώς το \(x\) τείνει στο 1 (όπως και η \(h(x)\)) και να φθίνει πιο γρήγορα από το \(x^5\) όταν το \(x\) τείνει στο άπειρο. Με βάση τα παραπάνω, η

\[\begin{equation*} \ell(x) \propto \frac{1}{\sqrt{x-1}} \frac{1}{x^{3/2}} 1_{x>1}, \end{equation*}\]

είναι μία αποδεκτή πυκνότητα. Παρατηρούμε ότι

\[\begin{equation*} \int_1^y \frac{1}{\sqrt{x-1}x^{3/2}} dx = \int_0^{y-1} \frac{1}{\sqrt{w}(w+1)^{3/2}} dw = \int_0^{\sqrt{y-1}} \frac{2}{(u^2+1)^{3/2}} du = \int_0^{\sqrt{2(y-1)}} \frac{2}{(1+t^2/2)^{3/2}} dt. \end{equation*}\]

Από αυτό συμπεραίνουμε ότι η \(\ell(x)\) είναι η πυκνότητα μίας \(1+T^2/2\), όπου \(T\sim\mathcal{T}_3\), δηλαδή

\[\begin{equation*} \ell(x) = \frac{\sqrt{2}\Gamma(3/2)/\sqrt{2\pi}}{\sqrt{x-1}x^{3/2}} 1_{(1, +\infty)}(x). \end{equation*}\]

Παρατηρήστε πως οι προσομοιώσεις που είναι μικρότερες της μονάδας στην αμυντική δειγματοληψία παίρνουν ένα βάρος ίσο με \(1/0.95\), αφού \(\ell(x)=0\) για \(x\leq 1\). Η σύγκριση της αμυντικής δειγματοληψίας με την δειγματοληψία σπουδαιότητας μπορεί να γίνει προσθέτοντας ένα μικρό δείγμα από την \(\ell\) στο αρχικό δείγμα από την \(g\). Συγκρίνοντας τις δύο εκτιμήτριες, είναι εμφανές ότι η αμυντική δειγματοληψία λύνει το πρόβλημα της διασποράς (Εικόνα 4.7).

h <- function(x){
  (x > 1) / sqrt(abs(x - 1))
}

sam1 <- rt(.95 * 10 ^ 4, df = 2)
sam2 <- 1 + .5 * rt(.05 * 10 ^ 4, df = 2) ^ 2
sam <- sample(c(sam1, sam2), .95 * 10 ^ 4)
weit <- dt(sam, df = 2) / (0.95 * dt(sam, df = 2) + .05 * (sam > 0) * dt(sqrt(2 * abs(sam - 1)), df = 2) * sqrt(2) / sqrt(abs(sam - 1)))
plot(cumsum(h(sam1)) / (1:length(sam1)), ty = "l", xlab = "Iterations", ylab = "", lwd = 2)
lines(cumsum(weit * h(sam)) / 1:length(sam1), col = "blue", lwd = 2)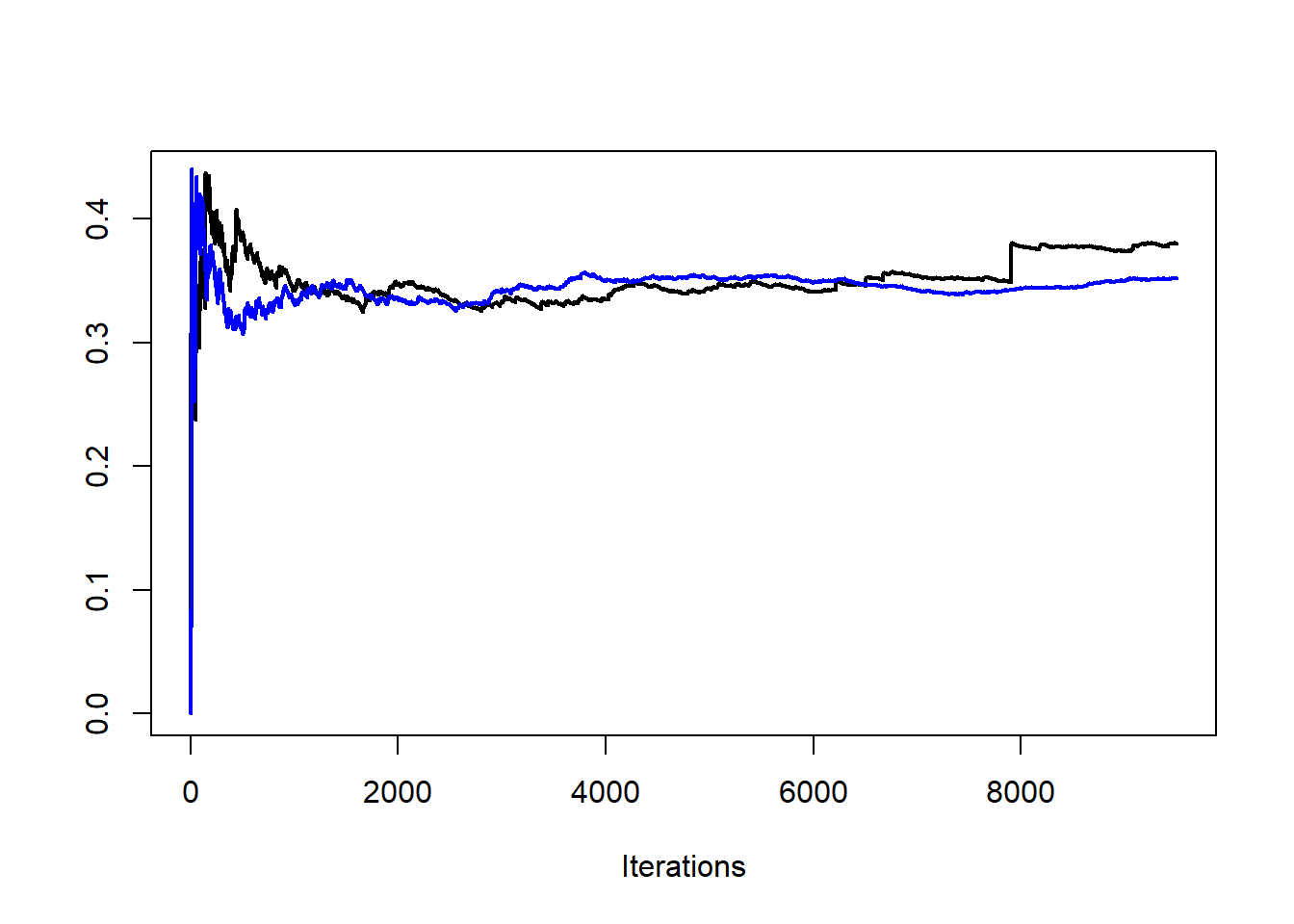

Εικόνα 4.7: Convergence of two estimators based on a sample from \(\mathcal{T}_2\) (black) and a defensive version (blue).

Υποθέτουμε τώρα ότι θέλουμε να προσομοιώσουμε από μία μίξη κατανομών \(g(x)=pg_1(x)+(1-p)g_2(x)\), όπου το \(p\) είναι γνωστό, με την προσθήκη μίας βοηθητικής, δίτιμης τ.μ. \(Y\). Έτσι, αν η εκτιμήτρια σπουδαιότητας είναι η

\[\begin{equation*} \delta_n = \frac{1}{n} \sum_{i=1}^n h(X_i) \left\{ \frac{f(X_i)}{g_1(X_i)} 1_{Y_i=1} + \frac{f(X_i)}{g_2(X_i)} 1_{Y_i=2}\right\}, \end{equation*}\]

τότε η βελτιωμένη εκδοχή της είναι η

\[\begin{align*} \delta_n^\star &= \frac{1}{n} \sum_{i=1}^n h(X_i) \mathbf{E}\left( \frac{f(X_i)}{g_{Υ_i}(X_i)} | X_i \right) = \frac{1}{n} \sum_{i=1}^n h(X_i) f(X_i) \mathbf{E}\left( \frac{1}{g_{Υ_i}(X_i)} | X_i \right) \\ &= \frac{1}{n} \sum_{i=1}^n h(X_i)f(X_i) \left[\mathbf{P}(Y_i=1|X_i) \frac{1}{g_1(X_i)} + \mathbf{P}(Y_i=2|X_i) \frac{1}{g_2(X_i)} \right] \\ &= \frac{1}{n} \sum_{i=1}^n h(X_i)f(X_i) \left[\frac{f(X_i|Y_i=1)\mathbf{P}(Y_i=1)}{f(X_i)} \frac{1}{g_1(X_i)} + \frac{f(X_i|Y_i=2)\mathbf{P}(Y_i=2)}{f(X_i)} \frac{1}{g_2(X_i)} \right] \\ &=\frac{1}{n} \sum_{i=1}^n h(X_i)f(X_i) \left[\frac{pg_1(X_i)}{pg_1(X_i)+(1-p)g_2(X_i)} \frac{1}{g_1(X_i)} + \frac{(1-p)g_2(X_i)}{pg_1(X_i)+(1-p)g_2(X_i)} \frac{1}{g_2(X_i)} \right] \\ &=\frac{1}{n} \sum_{i=1}^n h(X_i)f(X_i) \frac{1}{pg_1(X_i)+(1-p)g_2(X_i)} = \frac{1}{n} \sum_{i=1}^n h(X_i)\frac{f(X_i) }{pg_1(X_i)+(1-p)g_2(X_i)} \end{align*}\]

Σε αυτό το σημείο αξίζει να σημειώσουμε ότι δέσμευση ως προς το πλήθος των παρατηρήσεων που προέρχονται από κάθε κατανομή που είδαμε στο προηγούμενο παράδειγμα, δεν αποτελεί Rao-Blackwellization, παρότι οδηγεί σε μία αμερόληπτη εκτιμήτια με μικρότερη διασπορά από εκείνη που στηρίζεται στην διωνυμική \(Bin(n,p)\) για το μοίρασμα των παρατηρήσεων στις \(g_1\) και \(g_2\).

4.5 Μέθοδοι Επιτάχυνσης Σύγκλισης

Θα μελετήσουμε μερικές μεθόδους επιτάχυνσης σύγκλισης, οι οποίες λειτουργούν ανεξάρτητα από τις ιδιαίτερες συνθήκες μίας προσομοίωσης και επομένως μπορούν (και συνιστάται) να χρησιμοποιούνται.

4.5.1 Συσχετισμένες Παρατηρήσεις

Παρότι το γενικό πλαίσιο των Monte Carlo προσομοιώσεων στηρίζεται σε τυχαία δείγματα (παρατηρήσεις από ανεξάρτητες και ισόνομες τ.μ.), μπορεί να είναι ιδιαίτερα επιθυμητό να προσομοιώσουμε δείγματα από αρνητικά ή θετικά συσχετισμένες τ.μ., καθώς αυτό μπορεί να οδηγήσει σε μείωση της διασποράς της προκύπτουσας εκτιμήτριας. Ας μελετήσουμε ένα τέτοιο πλαίσιο.

Έστω δύο ποσότητες \(m_1, m_2\),

\[\begin{equation*} m_1=\int g_1(x)f_1(x)dx, m_2=\int g_2(x)f_2(x)dx, \end{equation*}\]

και οι αντίστοιχες εκτιμήτριες \(\delta_1, \delta_2\), οι οποίες είναι ανεξάρτητες μεταξύ τους. Ενδιαφερόμαστε να εκτιμήσουμε την διαφορά \(m_2-m_1\). Εάν χρησιμοποιήσουμε ως εκτιμήτρια την \(\delta=\delta_2-\delta_1\), παρατηρούμε ότι η διασπορά της είναι

\[\begin{equation*} \mathbf{V}(\delta)=\mathbf{V}(\delta_2-\delta_1)=\mathbf{V}(\delta_2)+\mathbf{V}(\delta_1), \end{equation*}\]

λόγω της ανεξαρτησίας των \(\delta_1, \delta_2\). Η διασπορά αυτή είναι πιθανώς πολύ μεγάλη για να υποστηρίξει μία ακριβή εκτίμηση της διαφοράς \(m_2-m_1\), ιδιαίτερα οι δύο αυτές ποσότητες είναι σχεδόν ίσες. Εάν οι \(\delta_1, \delta_2\) είναι θετικά συσχετισμένες, τότε η διασπορά της \(\delta\) είναι

\[\begin{equation*} \mathbf{V}(\delta)=\mathbf{V}(\delta_2-\delta_1)=\mathbf{V}(\delta_2)+\mathbf{V}(\delta_1)-2Cov(\delta_1, \delta_2), \end{equation*}\]

έχει δηλαδή μειωθεί κατά \(2Cov(\delta_1, \delta_2)\). Γενικότερα, στο πλαίσιο της στατιστικής συμπερασματολογίας, μία εκτιμήτρια \(\delta\) της παραμέτρου \(\theta\) αξιολογείται μέσω του ρίσκου \(R(\delta, \theta)=\mathbf{E}\left(L(\delta, \theta)\right)\), όπου \(L(\delta, \theta)\) μία συνάρτηση σφάλματος (π.χ. τετραγωνικό σφάλμα \(L(\delta, \theta)=(\delta-\theta)^2\)). Επομένως η σύγκριση δύο εκτιμητριών \(\delta_1, \delta_2\) μίας παραμέτρου \(\theta\) ανάγεται στην σύγκριση των ρίσκων \(R(\delta_1, \theta), R(\delta_2, \theta)\) και συγκεκριμένα στη διαφορά τους. Όμως, το ρίσκο είναι μία μέση τιμή, η οποία συχνά δεν μπορεί να υπολογιστεί αναλυτικά. Αν προσομοιώσουμε λοιπόν από την \(f(\cdot|\theta)\) δύο τυχαία δείγματα \(X_1, X_2, \dots, X_n\) και \(Y_1, Y_2, \dots, Y_n\), ανεξάρτητα μεταξύ τους, παίρνουμε τις εκτιμήσεις

\[\begin{equation*} \widehat{R}(\delta_1, \theta) = \frac{1}{n} \sum_{i=1}^n L\left( \delta_1 (X_i), \theta \right), \widehat{R}(\delta_2, \theta) = \frac{1}{n} \sum_{i=1}^n L\left( \delta_2 (Y_i), \theta \right). \end{equation*}\]

Επομένως εκτιμάμε την διαφορά \(R(\delta_2, \theta)-R(\delta_1, \theta)\) με την διαφορά \(\widehat{R}(\delta_2, \theta)-\widehat{R}(\delta_1, \theta)\), οπότε θετική συσχέτιση ανάμεσα στις ποσότητες \(L(\delta_1(X_i), \theta)\) και \(L(\delta_2(Y_i), \theta)\) οδηγεί σε μικρότερη διασπορά της εκτιμήτριας.