2 Εισαγωγή στην R

2.1 Εισαγωγή στον Προγραμματισμό

Σε αυτή την ενότητα θα κάνουμε μία βασική εισαγωγή στην R. Η ενότητα χωρίζεται σε δύο υποενότητες. Στην πρώτη θα κατεβάσουμε την R και το RStudio και θα εξοικειωθούμε με το περιβάλλον τους. Στη δεύτερη θα γράψουμε τις πρώτες μας γραμμές κώδικα, και θα συζητήσουμε κάποιες βασικές αρχές του προγραμματισμού.

2.1.1 Το περιβάλλον της R και του RStudio

Για να εγκαταστήσετε την R και το RStudio, παρακολουθήστε τα σχετικά βίντεο του μαθήματος.

2.1.2 Σχόλια και Κώδικας

Κάθε γραμμή που ξεκινάει με δίεση θεωρείται σχόλιο. Αυτό σημαίνει πως η R θα το αγνοήσει. Τα σχόλια είναι πολύ σημαντικά για να εξηγούμε στους συναδέλφους μας τι ακριβώς κάνει ο κώδικας που γράφουμε.

Κάθε γραμμή που δεν ξεκινά με είναι κώδικας. Για να ζητήσουμε από τη R να εκτελέσει μία γραμμή κώδικα, τοποθετούμε τον κέρσορα στη γραμμή (κάνουμε κλικ πάνω της), και μετά πατάμε Ctrl + Enter (το Ctrl είναι το πλήκτρο στην κάτω αριστερή γωνία).

2.1.3 Αντικείμενα

Όπως και στα μαθηματικά, στον προγραμματισμό βολεύουν πολύ οι μεταβλητές. Η R μπορεί να “θυμάται” όποια μεταβλητή της δώσουμε και να εκτελεί εντολές με αυτήν. Για να δώσουμε μία τιμή σε μία μεταβλητή, χρησιμοποιούμε το σύμβολο <- (μπορεί να χρησιμοποιηθεί και το = αλλά καλό είναι να αποφεύγεται).

# Ορίζουμε μία νέα μεταβλητή
x <- 1

Για να μας πει η R την τιμή της x, αρκεί να της το ζητήσουμε.

x
## [1] 1

Στο παραπάνω παράδειγμα, το x ονομάζεται “όνομα” ή “μεταβλητή” (name και variable αντίστοιχα), και το 1 ονομάζεται “αντικείμενο” ή “τιμή” (object και value αντίστοιχα).

Πώς λειτουργεί αυτό;

Κάθε υπολογιστής έχει μία μνήμη (Random Access Memory - RAM) στην οποία μπορεί να αποθηκεύει προσωρινά πληροφορίες, σαν μία “αποθήκη” στην οποία μπορεί να καταχωρεί κιβώτια για μετέπειτα χρήση. Όταν εκτελούμε την εντολή x <- 1 η R ψάχνει μία ελεύθερη θέση στη μνήμη του υπολογιστή ώστε να καταχωρίσει την τιμή 1, και της δίνει το όνομα x. Στην πραγματικότητα, το μόνο που κρατάει το x σαν πληροφορία είναι η θέση στην οποία έχει αποθηκευτεί το 1. Έτσι, όταν ζητάμε το x, η R κοιτάει τη διεύθυνση μνήμης που αυτό κρατάει, και εκεί βρίσκει την τιμή 1. Στον προγραμματισμό, αυτό συχνά ονομάζεται “δέσιμο ενός ονόματος σε μία τιμή” (binding a name to a value).

Μπορούμε να αλλάξουμε την τιμή του x;

Ναι. Γράφοντας x <- 2 ζητάμε από την R να ψάξει μία άλλη ελεύθερη θέση μνήμης για να καταχωρίσει τη νέα τιμή (το 2), και να δώσει στο x τη διεύθυνση της νέας θέσης. Παρότι το 1 υπάρχει ακόμα στην παλιά του θέση, το x πλέον έχει τη διεύθυνση που βρίσκεται το 2. Δεν έχουμε πια πρόσβαση στο 1.

x <- 2
x
## [1] 2

Μπορούμε να διαγράψουμε ένα αντικείμενο με τη συνάρτηση rm() η οποία παίρνει το όνομά της από τη λέξη [r]e[m]ove.

rm(x)
x
## Error: object 'x' not found

Στην πραγματικότητα δε διαγράψαμε το αντικείμενο. Οι τιμές 1 και 2 βρίσκονται ακόμα στην ίδια θέση μνήμης που ήταν και πριν. Όμως, το x δεν είναι πια “δεμένο” με καμία θέση, δεν έχουμε δηλαδή τις διευθύνσεις στις οποίες έχουν καταχωρηθεί τα αντικείμενα 1 και 2. Στην παρομοίωση της αποθήκης, είναι σα να πετάξαμε το χαρτάκι στο οποίο σημειώσαμε πού βρίσκονται τα κιβώτια 1 και 2. Η διαγραφή των αντικειμένων θα γίνει αργότερα, από τον ρακοσυλλέκτη (Garbage Collector) της R, ο οποίος ανά τακτά χρονικά διαστήματα διαγράφει αντικείμενα που δε χρησιμοποιούνται πια, προκειμένου να ελευθερώσει μνήμη στον υπολογιστή.

2.1.4 Ονοματοδοσία

Το όνομα ενός αντικειμένου δεν είναι απαραίτητα ένα μόνο γράμμα. Μπορεί να είναι μία λέξη ή και ολόκληρη φράση. Εάν θέλουμε να χωρίσουμε τις λέξεις μεταξύ τους, μπορούμε να χρησιμοποιήσουμε το σύμβολο _ (“κάτω παύλα”).

x1 <- 5
x2 <- 3

year <- 2000
last_year <- 1999

Το όνομα ενός αντικειμένου πρέπει να είναι σύντομο και καθαρό. Τα δύο παρακάτω ονόματα δε βολεύουν στη συγγραφή κώδικα. Το πρώτο έχει πολύ μεγάλο όνομα, ενώ το δεύτερο δεν είναι ξεκάθαρο τι αφορά.

year_of_new_millenium <- 2000
yonm <- 2000

Προσοχή, το όνομα ενός αντικειμένου διαφοροποιεί τα μικρά από τα κεφαλαία γράμματα (case sensitive). Η συνήθης σύμβαση στον προγραμματισμό ζητά όλα τα ονόματα να γράφονται με μικρά γράμματα (lowercase), Τα κεφαλαία (uppercase) χρησιμοποιούνται σε συγκεκριμένες περιστάσεις που συναντάμε σε βαθύτερα επίπεδα προγραμματισμού.

x1 <- 5
X1
## Error: object 'X1' not found

x2 <- 4

name <- 1
Name
## Error: object 'Name' not found

Προσοχή, το όνομα ενός αντικειμένου δε μπορεί να είναι φράση με “κενό” ανάμεσα στις λέξεις, ή να ξεκινάει με σύμβολο / νούμερο.

new year <- 2001
_year <- 2001
1year <- 2001
## Error in parse(text = input): <text>:1:5: unexpected symbol
## 1: new year
##         ^

Τέλος, υπάρχουν κάποιες δεσμευμένες λέξεις που απαγορεύεται να χρησιμοποιηθούν ως ονόματα. Όλες αυτές οι λέξεις είναι εντολές που θα μελετήσουμε στην πορεία.

if <- 4
for <- 10
while <- 1
## Error in parse(text = input): <text>:1:4: unexpected assignment
## 1: if <-
##        ^

2.2 Διανύσματα και Πίνακες

Στον προγραμματισμό και ιδιαίτερα στη στατιστική, δεν λειτουργούμε με μεμονωμένα στοιχεία, αλλά με σύνθετες δομές: το διάνυσμα (vector), τον δισδιάστατο πίνακα (matrix), και το πλαίσιο δεδομένων (data frame).

2.2.1 Διανύσματα

Είναι σημαντικό να είμαστε ακριβείς στην ορολογία που χρησιμοποιούμε. Τα διανύσματα (vectors), χωρίζονται σε δύο κατηγορίες: τα ατομικά (atomic vectors) και τις λίστες (lists). Η ενότητα αυτή αφορά τα ατομικά διανύσματα, ενώ οι λίστες θα μελετηθούν στην επόμενη ενότητα, όπου θα γίνει αντιληπτή και η διαφορά τους.

Μπορούμε να φτιάξουμε ένα διάνυσμα με τη συνάρτηση c() που παίρνει το όνομά της από τη λέξη [c]oncatenate.

x <- c(2, 4, 6, -8)
y <- c(3, -5, 7, 11)
z <- c(1, -1)

x
## [1]  2  4  6 -8
y
## [1]  3 -5  7 11
z
## [1]  1 -1

animals <- c("dog", "cat")
animals
## [1] "dog" "cat"

Η συνάρτηση length() μας επιστρέφει το μήκος ενός διανύσματος, το πλήθος δηλαδή των στοιχείων του.

length(x)
## [1] 4
length(animals)
## [1] 2

Τα ατομικά διανύσματα είναι η βασική δομή με την οποία δουλεύει η R. Στην πραγματικότητα, ένα “απλό” αντικείμενο όπως το 1 ή το “dog” για την R είναι ένα διάνυσμα μήκους 1.

a <- 5
length(a)
## [1] 1

Μπορούμε να χρησιμοποιήσουμε την c() για να ενώσουμε διανύσματα.

a <- c(x, y)
a
## [1]  2  4  6 -8  3 -5  7 11

Μπορούμε να κάνουμε πράξεις με διανύσματα αριθμητικού τύπου (double). Η R εκτελεί όλες τις πράξεις κατά στοιχείο (element-wise). Συγκεκριμένα:

1. Μία πράξη που περιλαμβάνει διανύσματα ίσου μήκους γίνεται κατά στοιχείο.

x
## [1]  2  4  6 -8
y
## [1]  3 -5  7 11
x + y
## [1]  5 -1 13  3
x * y
## [1]   6 -20  42 -88

2. Μία πράξη που περιλαμβάνει διανύσματα μη ίσου μήκους ανακυκλώνει το μικρό διάνυσμα.

x
## [1]  2  4  6 -8
z
## [1]  1 -1
x + z
## [1]  3  3  7 -9

3. Μία πράξη που περιλαμβάνει αριθμό και διάνυσμα, ενεργεί όπως το 2, ανακυκλώνοντας τον αριθμό για όλο το διάνυσμα.

x + 2
## [1]  4  6  8 -6
3 * x
## [1]   6  12  18 -24
1 / x
## [1]  0.5000000  0.2500000  0.1666667 -0.1250000
x ^ 2
## [1]  4 16 36 64

Ιδιαίτερη προσοχή χρειάζεται ο πολλαπλασιασμός διανυσμάτων. Το x * y εκτελεί πολλαπλασιασμό κατά στοιχείο, ο οποίος διαφέρει από τον πολλαπλασιασμό διανυσμάτων στα μαθηματικά (εσωτερικό γινόμενο). Για το εσωτερικό γινόμενο χρησιμοποιούμε το σύμβολο x %*% y.

x
## [1]  2  4  6 -8
y
## [1]  3 -5  7 11
x * y
## [1]   6 -20  42 -88
x %*% y
##      [,1]
## [1,]  -60

Σε αρκετές περιπτώσεις θέλουμε να δημιουργήσουμε μία ακολουθία μεγάλου μήκους, κάτι που δύσκολα γίνεται με την c(). Μπορούμε να δημιουργήσουμε αριθμητικές ακολουθίες που αυξάνουν κατά 1 με την άνω και κάτω τελεία.

a <- 1:20
a
##  [1]  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20
b <- 15:1
b
##  [1] 15 14 13 12 11 10  9  8  7  6  5  4  3  2  1

Μπορούμε να κατασκευάσουμε οποιαδήποτε αριθμητική ακολουθία με τη συνάρτηση seq(), η οποία παίρνει τα παρακάτω ορίσματα μέσα στις παρενθέσεις της: from: ο αρχικός όρος to: ο τελικός όρος by: το βήμα της ακολουθίας length: το μήκος της ακολουθίας Προσοχή, μόνο ένα από τα by, length μπορούμε να επιλέξουμε.

seq(from = 0, to = 10, by = 0.5)
##  [1]  0.0  0.5  1.0  1.5  2.0  2.5  3.0  3.5  4.0  4.5  5.0  5.5  6.0  6.5  7.0
## [16]  7.5  8.0  8.5  9.0  9.5 10.0
seq(from = 0, to = 5, length = 30)
##  [1] 0.0000000 0.1724138 0.3448276 0.5172414 0.6896552 0.8620690 1.0344828
##  [8] 1.2068966 1.3793103 1.5517241 1.7241379 1.8965517 2.0689655 2.2413793
## [15] 2.4137931 2.5862069 2.7586207 2.9310345 3.1034483 3.2758621 3.4482759
## [22] 3.6206897 3.7931034 3.9655172 4.1379310 4.3103448 4.4827586 4.6551724
## [29] 4.8275862 5.0000000

Τέλος, η συνάρτηση rep() (από τη λέξη [rep]licate) μπορεί να επαναλάβει ένα διάνυσμα της επιλογής μας. Παίρνει τα παρακάτω ορίσματα μέσα στις παρενθέσεις της: x: το διάνυσμα που θα επαναληφθεί times: η επανάληψη ολόκληρου του διανύσματος each: η επανάληψη κάθε στοιχείου μέσα στο διάνυσμα

rep(0, times = 10)
##  [1] 0 0 0 0 0 0 0 0 0 0
rep(c(1, 2, 3), times = 3)
## [1] 1 2 3 1 2 3 1 2 3
rep(c(1, 2, 3), each = 3)
## [1] 1 1 1 2 2 2 3 3 3
rep(c(1, 2, 3), each = 3, times = 2)
##  [1] 1 1 1 2 2 2 3 3 3 1 1 1 2 2 2 3 3 3

Παρακάτω παρουσιάζονται μερικές χρήσιμες συναρτήσεις στη διαχείριση διανυσμάτων.

x
## [1]  2  4  6 -8
sum(x)      # Άθροισμα
## [1] 4
length(x)   # Μήκος
## [1] 4
mean(x)     # Δειγματικός Μέσος (Μέσος Όρος)
## [1] 1
sort(x)     # Διάταξη του x κατά αύξουσα σειρά
## [1] -8  2  4  6

Μπορούμε να κρατήσουμε ένα τμήμα διανύσματος βάζοντας αγκύλες αμέσως μετά το διάνυσμα. Μέσα στις αγκύλες, δηλώνουμε τις θέσεις που θέλουμε να κρατήσουμε. Η μέθοδος αυτή ονομάζεται indexing.

x
## [1]  2  4  6 -8
x[3]         # το 3ο στοιχείο του x
## [1] 6
x[c(1, 3)]   # το 1ο και το 3ο στοιχείο του x
## [1] 2 6
x[-c(2, 3)]  # όλα εκτός από το 2ο και το 3ο στοιχείο του x
## [1]  2 -8
x[x < 3]     # τα στοιχεία του x που είναι μικρότερα από 3
## [1]  2 -8

Αν θέλουμε να εντοπίσουμε τις θέσεις των στοιχείων που ικανοποιούν μία λογική συνθήκη, χρησιμοποιούμε τη συνάρτηση which().

x
## [1]  2  4  6 -8
x[x < 3]      # τα στοιχεία του x που είναι μικρότερα από 3
## [1]  2 -8
which(x < 3)  # οι θέσεις των στοιχείων αυτών
## [1] 1 4

Μπορούμε να κάνουμε indexing σε διανύσματα οποιουδήποτε τύπου.

animals[1]
## [1] "dog"
animals[-1]
## [1] "cat"

2.2.2 Πίνακες

Μία επέκταση των διανυσμάτων είναι οι δισδιάστατοι πίνακες (matrices). Υπάρχουν οι ακόλουθοι τρόποι για να κατασκευάσουμε έναν πίνακα:

1: Με τη συνάρτηση rbind() που ενώνει δύο διανύσματα ή πίνακες κατά γραμμή (r από το [r]ow).

m1 <- rbind(c(1, 2, 3), c(4, 5, 6))
m1
##      [,1] [,2] [,3]
## [1,]    1    2    3
## [2,]    4    5    6

2: Με τη συνάρτηση cbind() που ενώνει δύο διανύσματα ή πίνακες κατά στήλη (c από το [c]olumn).

m2 <- cbind(c(1, 2, 3), c(4, 5, 6))
m2
##      [,1] [,2]
## [1,]    1    4
## [2,]    2    5
## [3,]    3    6

3: Με τη συνάρτηση matrix() που δέχεται ένα μεγάλο διάνυσμα και το χωρίζει σε στήλες και γραμμές.

m3 <- matrix(1:6, nrow = 2, ncol = 3)
m3
##      [,1] [,2] [,3]
## [1,]    1    3    5
## [2,]    2    4    6

Η matrix() γεμίζει τον πίνακα κατά στήλες. Εάν θέλουμε να γεμίσουμε τον πίνακα κατά γραμμές, προσθέτουμε το όρισμα byrow = TRUE.

m4 <- matrix(1:6, nrow = 2, ncol = 3, byrow = TRUE)
m4
##      [,1] [,2] [,3]
## [1,]    1    2    3
## [2,]    4    5    6
class(m4)
## [1] "matrix" "array"

2.2.3 Πλαισία Δεδομένων

Τα πλαίσια δεδομένων (data frames) είναι λίστες ορθογώνιας δομής, παρόμοια με τους πίνακες. Σε αντίθεση όμως με τους πίνακες, κάθε στήλη του data.frame μπορεί να κρατάει διαφορετικό τύπο δεδομένων. Είναι η κύρια δομή που χρησιμοποιείται στην στατιστική για τα σετ δεδομένων.

Μπορούμε να δημιουργήσουμε ένα πλαίσιο δεδομένων με τη συνάρτηση data.frame()

df <- data.frame(names = letters[1:10], numbers = 1:10)
df
##    names numbers
## 1      a       1
## 2      b       2
## 3      c       3
## 4      d       4
## 5      e       5
## 6      f       6
## 7      g       7
## 8      h       8
## 9      i       9
## 10     j      10

Εάν έχουμε ήδη φτιάξει ένα data.frame, μπορούμε να προσθέσουμε στοιχεία όπως και στις λίστες.

df$logi <- rep(c(TRUE, FALSE), 5)
df
##    names numbers  logi
## 1      a       1  TRUE
## 2      b       2 FALSE
## 3      c       3  TRUE
## 4      d       4 FALSE
## 5      e       5  TRUE
## 6      f       6 FALSE
## 7      g       7  TRUE
## 8      h       8 FALSE
## 9      i       9  TRUE
## 10     j      10 FALSE

Η class() μας επιστρέφει το όνομα της κλάσης, data.frame. Η typeof() όμως μας πληροφορεί ότι τα data.frame στον πυρήνα τους είναι λίστες.

typeof(df)
## [1] "list"
class(df)
## [1] "data.frame"

Σχετικά με την ονοματοδοσία, κλασικά ονόματα για data.frames είναι το df και το dat, αλλά όχι το data, καθώς αυτό είναι μία συνάρτηση στην R την οποία θα δούμε στην πορεία.

Οι παρακάτω συναρτήσεις μας βοηθούν να δούμε τα δεδομένα.

View(df)   # Άνοιγμα σε νέο παράθυρο
head(df)   # Πρώτες 6 γραμμές
tail(df)   # Τελευταίες 6 γραμμές

Μπορούμε να δούμε τα ονόματα των γραμμών και των στηλών με τις rownames() και colnames(). Μπορούμε ακόμη να αλλάξουμε τα ονόματά τους. Προσοχή, στις λίστες χρησιμοποιούσαμε τη συνάρτηση names(), η οποία εδώ αντιστοιχεί στην colnames().

names(df)
## [1] "names"   "numbers" "logi"
colnames(df)
## [1] "names"   "numbers" "logi"
rownames(df)
##  [1] "1"  "2"  "3"  "4"  "5"  "6"  "7"  "8"  "9"  "10"

rownames(df) <- c(paste0("A", 1:10))
head(df)
##    names numbers  logi
## A1     a       1  TRUE
## A2     b       2 FALSE
## A3     c       3  TRUE
## A4     d       4 FALSE
## A5     e       5  TRUE
## A6     f       6 FALSE

Μπορούμε να δούμε το πλήθος των γραμμών και των στηλών με τις συναρτήσεις ncol() και nrow().

ncol(df)
## [1] 3
nrow(df)
## [1] 10

2.3 Έλεγχος Ροής Κώδικα

Σε αυτή την ενότητα θα μελετήσουμε τους βρόγχους, εντολές που μας επιτρέπουν να ελέγχουμε τη ροή του κώδικα.

2.3.1 if

Η δομή if - else if - else, χρησιμοποιείται για να μοντελοποιήσει διαδικασίες επιλογής.

Ας δούμε ένα παράδειγμα: Παίζουμε ένα παιχνίδι. Εάν κερδίσουμε, το σκορ μας αυξάνεται κατά 2. Διαφορετικά, μένει σταθερό. Αυτό μπορεί να μοντελοποιηθεί ως εξής:

score <- 15
win <- FALSE

if (win) {
  score <- score + 2 # Η γραμμή αυτή εκτελείται μόνο όταν το win είναι TRUE.
}

score
## [1] 15

Ας κάνουμε το παράδειγμα λίγο πιο σύνθετο: Παίζουμε ένα παιχνίδι. Εάν κερδίσουμε, το σκορ μας αυξάνεται κατά 2, ενώ εάν χάσουμε, μειώνεται κατά 2. Αυτό μπορεί να μοντελοποιηθεί ως εξής:

score <- 7
win <- FALSE

if (win) {
  score <- score + 2 # Η γραμμή αυτή εκτελείται μόνο όταν το win είναι TRUE.
} else {
  score <- score - 2 # Η γραμμή αυτή εκτελείται μόνο όταν το win είναι FALSE.
}

score
## [1] 5

Η δομή μπορεί να αναπτυχθεί σε περισσότερα από δύο σκέλη, με τη προσθήκη ενδιάμεσων ελέγχων else if.

Ας κάνουμε το παράδειγμα ακόμα πιο σύνθετο: Παίζουμε ένα παιχνίδι. Εάν κερδίσουμε, το σκορ μας αυξάνεται κατά 2, ενώ εάν χάσουμε, μειώνεται κατά 2. Σε περίπτωση ισοπαλίας, εάν παίζουμε στο γήπεδο A το σκορ μας αυξάνεται κατά 1, ενώ αν παίζουμε στο γήπεδo Β μειώνεται κατά 1. Αυτό μπορεί να μοντελοποιηθεί ως εξής:

score <- 7
result <- "draw"
field <- "A"

if (result == "win") {
  score <- score + 2
} else if (result == "draw" && field == "A"){
  score <- score + 1
} else if (result == "draw" && field == "B") {
  score <- score - 1
} else {
  score <- score - 2
}

score
## [1] 8

Δεν υπάρχει περιορισμός στο πλήθος των else if που μπορούμε να έχουμε.

2.3.2 for

Η δομή επανάληψης for χρησιμοποιείται για να επαναλάβουμε ένα τμήμα κώδικα συγκεκριμένο αριθμό επαναλήψεων. Ας δούμε ένα παράδειγμα:

x <- c(3, 7, -2, 4, 9)
y <- rep(0, times = 5)
y
## [1] 0 0 0 0 0

for (i in 1:5) {
  y[i] <- x[i] + i + 2
}
y
## [1]  6 11  3 10 16

Εάν δε γνωρίζουμε εκ των προτέρων τον αριθμό των επαναλήψεων που θέλουμε να κάνουμε, μπορούμε να χρησιμοποιήσουμε τη συνάρτηση seq_along().

x <- c(3, 7, -2, 4, 9)
y <- rep(0, times = 5)
y
## [1] 0 0 0 0 0

seq_along(x)
## [1] 1 2 3 4 5

for (i in seq_along(x)) {
  y[i] <- x[i] + i + 2
}
y
## [1]  6 11  3 10 16

Μπορούμε να χρησιμοποιήσουμε τη συνάρτηση print για να εκτυπώνουμε μηνύματα σε κάθε επανάληψη.

for (i in seq_along(x)) {
  print(i)
  y[i] <- x[i] + i + 2
}
## [1] 1
## [1] 2
## [1] 3
## [1] 4
## [1] 5
y
## [1]  6 11  3 10 16

Το διάνυσμα από το οποίο παίρνουμε τις τιμές κάθε επανάληψης μπορεί να περιέχει ό,τι τιμές θέλουμε. Δεν χρειάζεται να είναι συνεχόμενες, ούτε καν να είναι αριθμοί.

numbers <- c("18", "2039", "5")

for (num in numbers) {
  print(paste0("My favorite number is ", num, "."))
}
## [1] "My favorite number is 18."
## [1] "My favorite number is 2039."
## [1] "My favorite number is 5."

Μπορούμε να έχουμε ένα for μέσα σε ένα άλλο. Σε αυτή την περίπτωση τα for ονομάζονται “εμφωλιασμένα” (nested for loops).

A <- matrix(0, nrow = 3, ncol = 4) # πίνακας 3x4
A
##      [,1] [,2] [,3] [,4]
## [1,]    0    0    0    0
## [2,]    0    0    0    0
## [3,]    0    0    0    0
nrow(A) ; ncol(A)
## [1] 3
## [1] 4

for (i in 1:nrow(A)) {
  for (j in 1:ncol(A)) {
    print(c(i, j))
    A[i, j] <- i + j
  }
}
## [1] 1 1
## [1] 1 2
## [1] 1 3
## [1] 1 4
## [1] 2 1
## [1] 2 2
## [1] 2 3
## [1] 2 4
## [1] 3 1
## [1] 3 2
## [1] 3 3
## [1] 3 4
A
##      [,1] [,2] [,3] [,4]
## [1,]    2    3    4    5
## [2,]    3    4    5    6
## [3,]    4    5    6    7

2.4 Συναρτήσεις και Πακέτα

2.4.1 Δημιουργία Συναρτήσεων

Οι γλώσσες προγραμματισμού μας επιτρέπουν να δημιουργήσουμε τις δικές μας συναρτήσεις. Μία συνάρτηση αποτελείται από τα ακόλουθα στοιχεία: - Όνομα: Το όνομα της συνάρτησης με την οποία την καλούμε. - Ορίσματα: Τα αντικείμενα που γράφουμε μέσα στις παρενθέσεις της συνάρτησης. - Σώμα: Ο κώδικας που εκτελεί η συνάρτηση χρησιμοποιώντας τα ορίσματα.

Ας εξετάσουμε ένα παράδειγμα: Η παρακάτω συνάρτηση δέχεται δύο ορίσματα (x, y) και επιστρέφει τη διαφορά τους.

dif <- function(x, y) {
  x - y
}

dif(5, 3)
## [1] 2

Η R δέχεται τα ορίσματα μέσα στις παρενθέσεις της είτε με τη σειρά, είτε με βάση το όνομά τους. Θα μπορούσαμε δηλαδή να γράψουμε το παρακάτω:

dif(5, 3)
## [1] 2
dif(x = 5, y = 3)
## [1] 2
dif(y = 3, x = 5)
## [1] 2

Η συνάρτηση που δημιουργήσαμε δέχεται ακριβώς δύο ορίσματα. Επομένως οι παρακάτω κλήσεις της συνάρτησης θα προκαλέσουν error.

dif(2)
## Error in dif(2): argument "y" is missing, with no default
dif(1, 2, 5)
## Error in dif(1, 2, 5): unused argument (5)

2.4.2 Εγκατάσταση Πακέτων

Παρότι η R διαθέτει ένα μεγάλο αριθμό συναρτήσεων, είναι σχεδιασμένη ώστε οι προγραμματιστές να έχουν τη δυνατότητα να δημιουργούν επιπρόσθετα πακέτα, τα οποία οι χρήστες της R μπορούν να εγκαταστήσουν και να χρησιμοποιήσουν κατάλληλα.

Υπάρχουν δύο βήματα προτού μπορούμε να χρησιμοποιήσουμε μία συνάρτηση ενός πακέτου:

1. Εγκατάσταση του πακέτου.
2. Φόρτωση του πακέτου.

Ως παράδειγμα, επιλέγουμε το πακέτο ggplot2, που χρησιμοποιείται για τη δημιουργία γραφημάτων.

“Εγκατάσταση” (installation) ενός πακέτου σημαίνει να αποκτήσουμε το λογισμικό στο μηχάνημα το οποίο βρισκόμαστε, και συνήθως υπονοεί το “κατέβασμα” του κώδικα από το διαδίκτυο. Είναι μία διαδικασία που χρειάζεται να γίνει μόλις μία φορά ανά μηχάνημα. Από εκεί και πέρα, το λογισμικό υπάρχει στον υπολογιστή μας. Μπορούμε να εγκαταστήσουμε το πακέτο ggplot2 ως εξής:

install.packages("ggplot2")

Τα πακέτα κατεβαίνουν από το Comprehensive R Archive Network (CRAN), απ’ όπου κατεβάσαμε και την R. Υπάρχουν χιλιάδες πακέτα διαθέσιμα προς κατέβασμα.

Η R δεν “φορτώνει” (load) όλα τα πακέτα που έχουμε εγκαταστήσει. Κάτι τέτοιο θα είχε ως αποτέλεσμα να αυξήσει σημαντικά τον αριθμό των εργαλείων που διαθέτει και επομένως να αργεί να “εντοπίσει” εκείνο που της ζητάμε. Επομένως, πρέπει να ζητήσουμε με ξεχωριστή εντολή να φορτώσει ένα πακέτο. Μπορούμε να φορτώσουμε το πακέτο ggplot2 ως εξής:

library(ggplot2)

Η library() πρέπει να τρέχει κάθε φορά που ανοίγουμε την R, αφού εκείνη θα φορτώσει μόνο τα βασικά της πακέτα. Παρατηρήστε ότι τα πακέτα base και utils είναι προεγκατεστημένα και πάντοτε φορτωμένα (έτοιμα προς χρήση).

Μπορούμε να χρησιμοποιήσουμε τη συνάρτηση search() για να δούμε όλα τα φορτωμένα πακέτα, ή την detach() για να ξεφορτώσουμε κάποιο πακέτο.

search()
detach(package:ggplot2)
search()

2.4.3 Αναζήτηση στο Διαδίκτυο

Προκειμένου να διαβάσουμε τη σελίδα βοηθείας μίας συνάρτησης, πρέπει πρώτα να γνωρίζουμε την ύπαρξή της. Συχνά λοιπόν καλούμαστε να αναζητήσουμε μία λύση στο πρόβλημά μας online. Αυτό μπορεί να γίνει με τους ακόλουθους τρόπους:

1. Αναζήτηση σε μία μηχανή αναζήτησης (Google, Bing, DuckDuckGo κ.ά.): Η πρώτη λύση είναι να πληκτρολογίσουμε μία ερώτηση ή κάποιες λέξεις-κλειδιά σε μία μηχανή αναζήτησης. Εάν υπάρχει συνάρτηση που να λύνει το πρόβλημά μας, είναι πολύ πιθανό τα πρώτα αποτελέσματα να είναι μία online έκδοση της σελίδας βοηθείας της συνάρτησης. Είναι επίσης πολύ πιθανό να συναντήσουμε κάποιον άλλο χρήστη που έθεσε το ίδιο ή παραπλήσιο ερώτημα σε ένα online forum, όπως είναι το StackOverflow.

2. Αναζήτηση σε ένα AI ChatBot (Perplexity, ChatGPT κ.ά.): Μία εναλλακτική προσέγγιση είναι να θέσουμε το ερώτημα σε ένα AI ChatBot, το οποίο θα προσπαθήσει να καταλάβει το ερώτημά μας και να μας δώσει μία λύση, είτε με μία έτοιμη συνάρτηση, είτε κατασκευάζοντας μία το ίδιο. Αυτό το βήμα χρειάζεται ιδιαίτερη προσοχή: Οι απαντήσεις που έχουν παραχθεί από τεχνητή νοημοσύνη (Artificial Intelligence - AI) πολλές φορές περιέχουν λάθη ή είναι ανακριβείς. Για το λόγο αυτό, συστήνουμε τη χρήση ChatBot τα οποία δίνουν αναφορές για τις πηγές με βάση τις οποίες συνέθεσαν την απάντησή τους.

3. Δημοσίευση ερώτησης σε online forum (StackOverflow κ.ά.): Εάν οι παραπάνω ενέργειες προβούν άκαρπες, μπορούμε πάντα να θέσουμε μία ερώτηση σε κάποιον εξειδικευμένο χρήστη. Το StackOverflow είναι ένα forum στο οποίο μπορούμε να θέσουμε δημόσια μία ερώτηση, και οι άλλοι χρήστες έχουν τη δυνατότητα να σχολιάσουν και να γράψουν δημόσια κάποια λύση. Είναι σημαντικό να τονιστεί ότι η λειτουργία του forum είναι εθελοντική.

2.5 Στατιστική και Διαχείριση Δεδομένων

Έχοντας μάθει κάποιες βασικές λειτουργίες της R, είμαστε έτοιμοι να κάνουμε μία εισαγωγή στη στατιστική και τη διαχείριση δεδομένων.

2.5.1 Αρχεία .RData

Ας υποθέσουμε ότι έχουμε τα παρακάτω αντικείμενα:

x <- matrix(1:20, nrow = 4, ncol = 5)
rownames(x) <- paste0("A", 1:4)
colnames(x) <- paste0("B", 1:5)
x
##    B1 B2 B3 B4 B5
## A1  1  5  9 13 17
## A2  2  6 10 14 18
## A3  3  7 11 15 19
## A4  4  8 12 16 20

y <- letters[1:4]

z <- 7L

Τα δεδομένα αυτά θα χαθούν μόλις κλείσουμε την R.

Μπορούμε να χρησιμοποιήσουμε τη συνάρτηση save() για να αποθηκεύσουμε τα δεδομένα μας. Η R θα δημιουργήσει ένα αρχείο με την κατάληξη .RData με το οποίο μπορούμε να φορτώσουμε ξανά τα δεδομένα, χρησιμοποιώντας τη συνάρτηση load().

save(x, y, file = "my_variables.RData")
rm(list = ls()) Διαγραφή
load("my_variables.RData")

Η συνάρτηση save.image() αποθηκεύει όλα τα αντικείμενα του global environment.

save.image("my_variables2.RData")
rm(list = ls())
load("my_variables2.RData")

Η ερώτηση που κάνει από προεπιλογή η R όταν κλείνουμε το πρόγραμμα, είναι εάν θέλουμε να αποθηκεύσουμε τα αντικείμενα του workspace, δηλαδή, εάν θέλουμε να τρέξουμε τη συνάρτηση save.image() όπως παραπάνω.

2.5.2 Αρχεία .csv

Οι συναρτήσεις write.csv() και read.csv() της R αποθηκεύουν και διαβάζουν αντίστοιχα αρχεία μορφής .csv

Ο τύπος αρχείου .csv είναι ίσως ο πιο διαδεδομένος τύπος αποθήκευσης δεδομένων στην στατιστική. Όλα τα προγράμματα στατιστικής μπορούν εύκολα να διαβάσουν αυτό τον τύπο αρχείου, ή να αποθηκεύσουν δεδομένα σε αυτόν τον τύπο.

write.csv(x, file = "mymatrix.csv")
rm(list = ls())
x <- read.csv("mymatrix.csv")
class(x)

Διαβάστε τις σελίδες βοηθείας για να βρείτε επιπρόσθετες λειτουργίες των παραπάνω συναρτήσεων.

2.5.3 Προσομοίωση

Η R έχει προγραμματισμένη μία συνάρτηση προσομοίωσης παρατηρήσεων από τις περισσότερες γνωστές κατανομές. Το όνομα των συναρτήσεων αυτών ξεκινά με το γράμμα r (από το random, τυχαίο), ακολουθούμενο από το όνομα της κατανομής. Θα συνεχίσουμε το παράδειγμα της Poisson και της Normal.

?rnorm
?rpois

Προσομοιώνουμε ένα δείγμα μεγέθους n = 10000 από τη N(0, 4).

n <- 1000
x <- rnorm(n, mean = 0, sd = 2)
x
##    [1] -1.608663200 -2.113051308 -2.070791568 -2.371120707 -1.000879023
##    [6] -1.049977414 -0.604865913  0.943936265 -0.496767898  2.518636059
##   [11]  0.701841928  1.726637092 -0.957822618 -2.376958437 -0.537132747
##   [16] -0.160442111 -0.246471371 -0.198879611 -1.669507957  3.715559086
##   [21] -0.996794039 -2.540109216 -1.873887425  1.066878485 -3.233526211
##   [26] -0.634113279 -0.839527351 -0.361711649  1.603622423 -1.507835809
##   [31]  0.355549398  0.416685698  1.606274450 -3.190162973  3.199167314
##   [36]  0.998541266  0.735228191 -0.821060324  1.854700838  1.729032158
##   [41]  1.444304573  0.542531107  0.628216291  1.511047497 -0.378319281
##   [46]  0.754485371 -0.816465890 -0.532184218  0.172530314 -0.397025394
##   [51]  1.122175461  0.894344926 -0.535087758 -0.627768045 -1.221595049
##   [56]  0.232637142 -1.608230027 -0.401251339  0.677993953  0.676442732
##   [61] -1.418458837  1.045937761 -0.707290567 -1.556157523  1.594606456
##   [66] -1.810903046 -1.922070950 -0.514671686  0.821672756 -0.790080393
##   [71]  2.164088485  0.104719301  2.509840709  0.044144116  2.224677720
##   [76] -0.716409841  3.866207915 -0.225184513  1.664060450  1.963127016
##   [81]  2.082172959 -0.111694666  0.351434194 -1.821852474 -3.065267410
##   [86]  2.087646315  2.534275447 -1.491484825 -0.429241880 -2.881663475
##   [91]  2.072924583  0.373084603 -0.032705987 -2.244319866  2.436635247
##   [96] -0.418840226  0.621789297 -0.210558096  2.192497200 -0.497877393
##  [101] -1.009022561  2.589971813  0.305170295 -0.623148748 -2.140400819
##  [106]  1.139716911 -0.978911356  0.501529219 -0.522425724  0.523064602
##  [111]  2.862157941  0.792169672 -0.950369425  3.577265479 -0.102219874
##  [116] -1.478917002  4.158730517  0.753345581 -4.578975507  2.369653589
##  [121]  0.610853805  1.289259164  2.327453745  1.870668352  0.195965625
##  [126]  1.536470700  2.216539416 -0.770859928  0.806114440 -0.554917583
##  [131]  1.114627030 -0.393306941 -0.163865273  1.324692722 -0.732293278
##  [136]  1.190448860 -1.631210994 -1.813612066 -2.847213690  0.700606658
##  [141]  0.316075147 -4.145540523  1.643211496 -1.185772810 -1.959548045
##  [146]  0.324082476  1.213818058 -1.320422240 -1.000044662 -0.992877325
##  [151] -3.788525627 -1.019584602 -1.555259455  1.472917989  2.714807119
##  [156]  0.027759065 -3.009447837  1.786053924 -0.862583486  0.844447376
##  [161] -0.679727278 -0.996204153 -2.060262202  1.500071879 -1.177594368
##  [166]  2.712971978  1.282901371  2.223402388 -1.770810764 -2.077882640
##  [171]  1.972315452 -1.397365947 -1.692257352 -0.839746873  0.549040932
##  [176]  3.575176058  2.172075315 -2.105331378  0.574839842  2.212343702
##  [181] -1.305327398  1.651215603  1.499906838  0.460304662  3.396834511
##  [186]  0.631712741 -3.748221150  1.212589459  1.758036887 -2.186203920
##  [191] -0.474909460 -0.983276934  1.232569324 -0.492857569  1.847247793
##  [196] -1.446295874  1.268955089  2.662569639  1.861938967  3.217144191
##  [201] -0.514734846 -1.251974090 -0.610305678 -0.334973733  1.992171805
##  [206]  2.371803479 -1.779352373  0.080619804 -1.282870910  0.165625440
##  [211]  4.693262217 -0.558774119 -5.541165928  0.307354281 -0.572402231
##  [216]  0.621508237 -0.809881498 -0.322239877  1.387969145  2.540294047
##  [221]  1.531428332 -1.930903725 -5.570220577 -0.160731274  2.497209697
##  [226] -0.334780019 -2.385010000 -2.116757951  0.031907051 -0.599760960
##  [231] -3.087158191  1.416341091 -2.640798326  0.918331910  0.485528729
##  [236]  2.202753199 -0.073877116 -1.218396251 -0.721288325  1.244749140
##  [241] -1.660829190  0.829199636  0.233515371 -3.615260266 -1.950635694
##  [246] -0.130621148  0.694160751 -2.158415116  0.656779053 -1.090270273
##  [251]  0.986738089  2.956161493 -0.871370191 -0.491065871 -2.569133943
##  [256] -2.279361099  2.596072964 -1.469238891  0.523324706 -0.511343624
##  [261] -0.648942278  2.324037169  0.621095470  2.274635297  1.250641616
##  [266] -1.109719773 -2.967349185 -0.831402800 -0.418593911  1.386791530
##  [271]  2.958840330 -1.665711670  2.144962842  3.279665419 -3.551441882
##  [276]  0.539287628 -1.275188140 -0.371106553 -0.256346955 -2.183456890
##  [281] -1.383780197  1.021415813  0.286381477 -2.705895926 -1.387009645
##  [286]  1.389214782  2.006969959 -4.608155240  0.578562224  1.335841003
##  [291] -3.080422441  1.023995509 -0.988599575 -0.439727844  1.079398240
##  [296]  2.481787924  0.387534122  2.242572373  1.648425824  1.667488761
##  [301] -0.695995943  0.528380877  1.729247720  4.405792840 -2.924668582
##  [306]  0.825741481 -1.421362559 -2.447261884 -0.621458030  2.245408679
##  [311]  2.146010124  1.705864080 -0.558006207 -2.423006079  2.037884651
##  [316]  1.083082297  0.234339933  2.858539665  0.573983212 -3.922835391
##  [321] -2.200018564 -1.333239881 -0.921150697 -1.278954573 -2.134345669
##  [326]  5.742168157 -1.159423965 -1.626164536 -1.442526796  0.361468826
##  [331] -2.635541666  1.818264279  0.475406676  2.268841829 -1.469627507
##  [336]  3.064521941  4.367775324  0.995499691  1.599907612 -0.942627457
##  [341]  1.879063259 -3.130049628  3.001429153  1.934538561 -2.344857555
##  [346] -0.448935813  0.125750573  2.639564921  0.719823045 -3.824513709
##  [351] -0.472621764  1.445804555 -0.354782862  5.254524706 -0.690668657
##  [356] -2.051369494  0.254158611 -0.414818299 -1.874859996  1.384936109
##  [361] -1.537111065  1.942643689  3.012766298 -1.213089049 -0.198222136
##  [366]  1.759418458 -0.784510611 -2.668487678 -3.492909228  2.771087641
##  [371]  0.600415398 -0.142971207  1.882793399  0.399260842 -0.535378820
##  [376] -2.355547984 -0.745487670 -5.515007353  1.669454165  2.541868587
##  [381] -3.142303880  0.767089590 -0.766845927 -1.487983074  0.086760285
##  [386]  1.004848218  1.786899267  1.048356571 -0.088156548  0.134320470
##  [391] -1.980973394 -2.899339590  0.892022392  1.357424822 -0.090623406
##  [396] -2.949873741  0.662316117 -3.726197788  1.279705453 -1.047784558
##  [401] -0.994033576 -0.779088296 -0.155710293 -1.810098625  0.328880735
##  [406] -0.231894401 -0.696420137 -0.579984191 -2.278129867 -0.008744951
##  [411]  1.808416051  0.165428905  1.356279966  0.031020326 -2.433235801
##  [416] -0.874742139  1.653177111  1.935365030 -0.740148412  2.733346091
##  [421] -1.030293390  0.002680912  0.440408055 -0.272721650 -3.494196619
##  [426] -0.329277777  5.195195447 -1.010127715  0.503587736 -1.607655091
##  [431] -1.089167428 -2.458797796  2.369544183 -2.823446446 -0.089802150
##  [436] -1.043628647 -1.537782983 -4.349820759 -2.055682077 -0.190179689
##  [441]  0.402580881 -2.032739680  1.795121386 -0.517729998  1.808909631
##  [446] -2.482738490 -2.046750508 -0.081969345 -0.860339506  2.711767378
##  [451]  2.126750646  3.333937832 -1.392924586 -4.460122228 -2.946191791
##  [456] -1.576136800  0.566265619  0.603829998  3.256793329 -0.207137648
##  [461]  0.705000189  1.815855753  2.682721684 -0.655812939  2.809048908
##  [466]  2.330516162  2.442045954 -0.145594125 -2.138745254 -1.275973671
##  [471] -1.895657514  0.278059870  1.777582785  3.094938856  0.313268101
##  [476]  4.295405466 -0.280164959 -0.385961474  0.670623687 -3.199144692
##  [481]  1.313928082  1.278610408  3.002425239 -1.742793208  2.569970012
##  [486]  1.058622079 -1.782419094 -1.832890475 -2.214515321  0.368012660
##  [491]  1.576015786 -1.366047027 -1.377347632 -2.038077675  2.557902756
##  [496] -1.099394618 -1.144617049 -1.408176264  2.318231945  0.440641523
##  [501]  1.410221318 -1.253737510 -0.646059332  0.719298270 -1.871326734
##  [506] -2.005405932 -0.189226184  3.935343885 -2.148700780  0.299018053
##  [511]  2.958530220 -2.204580368 -2.400261510 -0.904305953 -5.645593688
##  [516] -1.922327681 -2.893157884 -0.174167143 -0.556801256 -0.445163675
##  [521] -0.404162818 -0.743922072  0.522666928  3.644976018 -0.546380708
##  [526]  0.780602470  1.693715643  0.126408771 -0.554694071  1.628580013
##  [531]  3.685478959  1.693075226 -0.690138514 -1.366679946 -2.242209078
##  [536] -0.055974304  2.811016798 -3.570628787  1.966093895 -2.840795427
##  [541]  3.063194295 -0.672752134  0.876924149 -0.658587710 -3.252967957
##  [546] -0.348252461  2.134897584  1.478825813  0.332890122  2.830860322
##  [551] -2.577595166 -1.124123204  2.357177696 -0.078762644  0.636108147
##  [556]  0.158106908 -2.698648762  2.791740951 -0.392405427 -0.388142403
##  [561] -1.527260401  0.309022069  3.088052481  0.521111435  0.803226499
##  [566] -2.094767257 -0.157714443  0.279801913  0.364159778  0.690123706
##  [571] -0.201720538  2.348078040  1.118615948  0.132227661  2.148670902
##  [576] -2.011917645  0.164624828 -0.125080092  1.444695290  0.690678181
##  [581]  0.061885807  1.445507157  1.149512976  2.328261285 -1.127271432
##  [586]  0.831627463 -1.856936694 -2.869788581 -2.822699245 -0.264446484
##  [591] -3.456353678 -0.077928185  1.079751402  1.243354975  0.730086984
##  [596] -1.180979367 -0.295804622 -2.033731545  0.651016941  1.609001138
##  [601]  1.757422970 -2.517022151 -0.521441016 -1.952711846 -1.147412729
##  [606]  0.033500381  1.084445325  0.069029919  1.154508094  1.230798708
##  [611] -1.519172432  0.804576407  0.855100380 -3.837344271 -0.111761427
##  [616] -2.004306903 -2.719644042  2.146049801 -0.355906517 -0.536166531
##  [621]  2.311295959 -3.775309901 -2.187894783  4.701024033  0.266537504
##  [626]  0.256957826  2.253275731  0.401495666 -0.196075480  1.647213206
##  [631]  1.588804096  1.064092186 -0.129514607  0.949300335  0.750046927
##  [636] -0.745688118  1.633661187  0.719733476 -1.630802940  3.379581325
##  [641] -1.245897124 -0.071214098  0.687672701  1.106915473  2.338731902
##  [646] -1.592752472  1.048431265 -0.302973566  0.635853048  1.736638441
##  [651] -0.802417175  3.527116543  0.721503131  3.251731575  0.155861039
##  [656] -0.476749952 -0.801610838  0.250243676 -0.747217477  0.186880804
##  [661] -2.042238248  0.665535964 -0.160398151  0.340438501 -0.449603891
##  [666] -0.820028628  0.463068078  0.947388129 -2.266354468  0.635921964
##  [671]  3.101833843 -0.557491517  1.394948360  1.736080669  1.196287852
##  [676] -1.217445844 -2.458003203 -2.753189788 -0.286937528 -3.252036142
##  [681]  1.763922018  2.567514923 -2.461914348 -4.207198316 -5.122509499
##  [686] -0.039492250 -0.073627741  1.257824690 -0.136447057 -1.784103281
##  [691] -2.577697846 -0.078345296  0.960776095  0.654160473  4.670237044
##  [696]  4.457871230 -0.266927857 -1.991284910 -0.682615870  1.427734548
##  [701]  3.772214195 -0.857941088  1.142344246 -2.366566855  2.608721291
##  [706] -1.542738008 -1.436646851 -1.345326285 -2.150203144 -1.974391418
##  [711]  0.281718945 -1.525986594 -1.324345579  2.197382662 -0.508392840
##  [716]  2.017140181  0.144148982 -3.107565574 -3.481064217  0.814166924
##  [721]  1.690729164 -3.738542700 -1.732392879  0.234925564  0.260497342
##  [726]  0.914584700  1.404840595  0.577221914  1.785176869 -0.938587748
##  [731]  4.054223763  0.396367840  2.355423054 -0.952333642 -0.211745077
##  [736]  1.491533189 -1.831750849 -0.177203439 -0.758173594 -0.435935478
##  [741] -0.069627064 -2.686444838 -4.425401919  0.464057457 -0.137247764
##  [746] -0.805023655  0.089190378 -1.780823411 -1.010858039  3.411340990
##  [751] -2.009967808 -1.762530184  1.172704610 -0.457219361 -1.446064072
##  [756]  3.097233855  2.443400945 -0.779117351  2.944015688  0.932136893
##  [761]  0.137728190 -1.261510153 -0.629365772 -0.251351119  1.864499325
##  [766]  0.484861907  0.145439713 -3.932435998  0.102072479 -1.736529642
##  [771] -1.213137857  0.700751521 -0.456433295  0.795638855  0.916250822
##  [776]  0.199225900  2.333567836  0.049778253 -0.687289474 -1.306476209
##  [781]  1.883927102  1.093356064 -0.740070707 -3.456286954  3.328700909
##  [786]  1.503601605  3.412373535  1.550849696  3.828955929 -2.979015744
##  [791]  2.120678273 -2.788746016 -3.397674229  1.054955666  2.926444780
##  [796] -2.103227584 -1.133581789  0.157960270  0.957664049  1.106777673
##  [801]  1.879515415  3.704529898  1.980985983 -2.217819070  0.165443376
##  [806] -0.665129819  0.669932735  0.477414698 -0.964448456 -1.651693697
##  [811] -3.150523666 -0.129913514 -2.861875157  1.282687567 -1.577558726
##  [816]  3.070608295 -0.104451695 -2.281820056 -0.081835188  1.883856577
##  [821] -0.781807172  1.610226644  0.683444512 -0.954718793 -0.499688598
##  [826]  0.398135725 -1.903482121 -4.038512281  1.501506406  0.871617551
##  [831] -1.348671116  0.822004556  2.416740018 -1.838725322  1.582896929
##  [836] -0.415845148  1.093626385 -0.739044479 -0.907720269 -8.605562873
##  [841] -1.600682179 -0.522400362 -2.696409224 -1.612454959 -3.975588976
##  [846] -1.878014457  2.094111305  1.692495857  0.748403551 -0.767218620
##  [851]  0.453564064  1.089624311  1.015367540 -3.904017158 -1.376319332
##  [856] -0.559770187 -1.071409069  0.726753637  0.580304223 -0.620852930
##  [861] -1.036449523 -2.483219418 -0.880844981 -1.280740350  1.745203622
##  [866] -1.729314613 -0.448816787 -1.423587955  2.226805291 -0.270107753
##  [871]  1.583468941 -0.676647903  1.695560761  0.763602741  0.800330003
##  [876]  2.274342523  0.839463306  0.029439471  0.226363467  0.371212009
##  [881]  1.116464018 -0.157291540  1.496172160 -0.698223037  1.892995713
##  [886]  3.212561798 -1.078037392 -0.261993253  2.071186897  1.535003333
##  [891] -1.521122131 -0.021855153 -0.309484887  2.685037262 -2.085327259
##  [896]  2.424267942 -2.450124723  1.183794731  3.459828798  1.699712625
##  [901] -1.427293823 -1.691671911  1.376932992  2.529070002  1.001046591
##  [906] -0.666571181 -1.229461506 -3.904454769  0.038707264  1.231356369
##  [911]  0.480963608  1.563068816 -1.229158142  2.198672367  0.282817722
##  [916]  2.412425223  2.931156996 -0.286451776  2.693653199 -0.140297950
##  [921] -1.528960888  0.360092681 -0.020141413  0.895232892  2.255030009
##  [926]  0.677928339 -2.437764262  2.222720012  0.870991873  1.545294995
##  [931] -1.594019302  0.688074048  2.329361969  1.113441197 -1.647039784
##  [936] -0.011213829 -1.200217245  0.137783113 -2.419314555 -1.079444168
##  [941]  0.840292904 -1.672846547  0.111177388  0.240352473 -3.105321614
##  [946] -1.284350393 -1.551010473 -0.850990321 -0.383235274  0.877039305
##  [951]  0.630363487 -1.215373531 -2.760020863  1.633297098 -0.259596168
##  [956] -0.741103268  2.454640652 -3.386687562  4.276545243 -1.618089407
##  [961]  0.495535301  3.704884281  0.517315179  3.532572687 -2.582330876
##  [966]  1.477229631  0.028555904 -0.327170914  5.078037003 -0.065863210
##  [971]  0.143033902  1.117652726  0.431130633  0.898409372  1.382075458
##  [976] -1.438581610  2.812596659 -1.970113781  0.153910910 -1.514188241
##  [981]  3.803305432 -2.601150307 -1.679181193 -3.213274052 -1.852839518
##  [986]  1.892515120  0.361059193  2.177505253 -4.644239803 -2.472734362
##  [991]  3.331875954 -1.498520393 -2.207901084  3.502763004 -1.407179788
##  [996] -0.092338036  0.301561410 -1.016012329 -3.453220752 -0.790852446

Προσομοιώνουμε ένα δείγμα μεγέθους n = 10000 από την Poisson(4).

x <- rpois(n, lambda = 4)
x
##    [1]  1  2  6  7  6  0  4  2  3  5  3  4  2  1  4  0  5  0  5  5  2  1  7  6
##   [25]  6  2  2  2  5  4  4  3  6  2  2  1  6  2  6  5  1  4  3  2  5  3  3  3
##   [49]  0  5  3  6  3  2  0  4  3  4  2  9  3  3  4  8  2  4  3 10  0  1  4  3
##   [73]  1  6  4  3  8  6  2  2  5  8  1  6  4  2  7  3  5  2  6  8  3  4  3  6
##   [97]  5  5  7  5  3  2  3  6  5  7  6  0  6  4  3  5  5  5  2  3  1  4  1  1
##  [121]  3  5  3  6  1  1  5  9  2  3  2  2  8  6  5  1  4  5  5  1  2  2  7  4
##  [145]  3  4  5  7  2  6  5  3  2  5  1  4  6  7  5  7  3  1  4  3  1  2  7  3
##  [169]  7  0  4  2  8  5  7  4  6  7  5  5  4  5  4  4  4  1  7  4  6  3  2  4
##  [193]  2  5  5  3  3  2  4  4  3  4  2  5  3  3  4  6 10  5  1  1  4  7  4  3
##  [217]  0  5  3  2  5  8  5  3  1  0  1  2  3  5  1  3  8  3  4  9  6  4  3  8
##  [241]  5  3  6  1  1  0  3  2  3  0  3  4  5  4  3  6  7  3  5  3  1  1  1  6
##  [265]  5  4  5  4  5  1  3  0  6  5  1  5  3  5  2  3  7  3  4  7  6  3  3  3
##  [289]  4  5  3  6  7  3  2  6  8  3  5  6  4  1  4  7  6  3  5  4  6  6  2  3
##  [313]  5  4  5  3  8  5  2  7  5  3  0  1  5  4  3  4  2  6  6  4  3  4  3  4
##  [337]  3  4  4  4  7  2  3  7  4  5  5  4  4  4  2  3  2  4  4  4  5  2  1  3
##  [361]  4  2  5  5  8  4  4  1  3  2  5  0  2  1  5  5  6  7  4  2  2  3  5  3
##  [385]  5  5  4  3  2  5  6  3  1  6  3  2  3  4  3  6  2  4  1  5  5  4  3  3
##  [409]  3  4  7  5  0  4  5  8  6  4  3  3  5  4  4  2  9  4  2  6  2  2  6  4
##  [433]  2  4  6  3  6  4  9  9  2  3  1  4  6  4  6  4  2  3  5  5  2  7  2  2
##  [457]  3  2  7  4  7  6  9  2  4  3  4  2  1  5  4  3  3  3  2  4  6  8  0  1
##  [481]  1  4  8  3  4  3  4  9  7  2  5  3  6  4  3  1  1  6  6  2  5  3  5  3
##  [505]  2  4  6  4  5  7  3  3  3  7  3  3  5  0  2  3  8  6  2  5  3  3  0  5
##  [529]  4  5  6  5  4  5  2  5  1  0  3  3  1  3  4  5  1  3  3  5  9  8  2  3
##  [553]  4  2  3  3  5  3  3  2  1  6  5  5  9  4  3  3  3  4  2  6  3  3  5  2
##  [577]  9  2  5  5  5  3  5  2  2  5  3  2  2  4  6  4  3  7  3  2  3  6  3  4
##  [601]  6  4  5  3  2  2  2  4  7  2  6  2  3  1  2  6  2  8  3  3 12  8  4  5
##  [625]  1  5  2  9  4  4  5  4  2  4  4  5  3  4  5  3  4  3  2  3  7  3  9  5
##  [649]  3  4  6  3  6  4  6  4  8 10  3  3  2  4  4  5  2  3  4  4  1  3  4  1
##  [673]  2  7  5  4  6  3  2  3  6  0  5  8  5  3  9  4  2  5  9  5  3  4  4  5
##  [697]  4  2  2  8  4  5  2  2  2  2  2  3  4  6  6  3  4  7  6  5  6  3  2  3
##  [721]  5  3  2  5  3  5  6  3  5  2  2  2  7  3  2  6  3  2  2  3  1  0  4  4
##  [745]  3  4  2  5  3  4  1  2  4  1  2  7  5  5  2  6  3  0  2  0  8  4  5  5
##  [769]  7  5  1  3  5  2  5  3  3  2  4  1  3  5  2  5  4  2  2  5  5  3  3  3
##  [793]  4  3  4  5  4  4  2  3  2  4  3  3  1  1  3  4  3  4  4  1  3  6  5  3
##  [817]  4  7  7  3  3  1  3  3  2  1  8  4  4  4  3  3  4  5  6  4  3  7  3  3
##  [841]  6  3  5  1  5  8  0  6  3  0  4  4  4  3  3  1  1  1  2  4  1  4  5  2
##  [865]  4  8  6  7  4  7  6  4  4  1  8  5  3  7  2  4  4  6  3  2  3  3  2  3
##  [889]  7  6  7  4  2  3  2  4  8  2  8  4  5  3  5  4  1  6  3  2  5  8  1  3
##  [913]  1  8  7  2  4  9  6  6  7 10  4  5  4  4  0  3  3  4  6  6  4  2  4  4
##  [937]  0  2  2  4  7  6  6  4  5  9  4  8  3  6  2  3  3  3  4  5  6  4  1  6
##  [961]  4  9  4  4  6  5  7  2  5  6  6  4  4  0  7  3  3  6  5  3  3  1  5  5
##  [985]  7  1  3  5  2  2  7  4  5  3  5  3  5  2  5  7

Οι παρακάτω εντολές αποτελούν παραδείγματα προσομοίωσης από γνωστές κατανομές.

x1 <- rbeta(n, shape1 = 2, shape2 = 4)  # Βήτα
x2 <- rgamma(n, shape = 3, rate = 5)    # Γάμμα
x3 <- runif(n, min = 0, max = 10)       # Ομοιόμορφη
x4 <- rexp(n, rate = 3)                 # Εκθετική
x5 <- rnorm(n, mean = -2, sd = 3)       # Κανονική
x6 <- rbinom(n, size = 10, prob = 0.7)  # Διωνυμική
x7 <- rpois(n, lambda = 3)              # Poisson

2.5.4 Η συνάρτηση plot

Ξεκινάμε με τη δημιουργία των δεδομένων τα οποία θέλουμε να παρουσιάσουμε.

set.seed(1929)
x <- rnorm(n = 100, mean = 5, sd = 1)
y <- x + rnorm(n = 100, mean = 1, sd = 0.5)
df <- data.frame(x, y)

Η βασική συνάρτηση δημιουργίας γραφημάτων είναι η plot(), η οποία σαν αρχικό τύπο γραφήματος έχει το σημειόγραμμα.

plot(y)

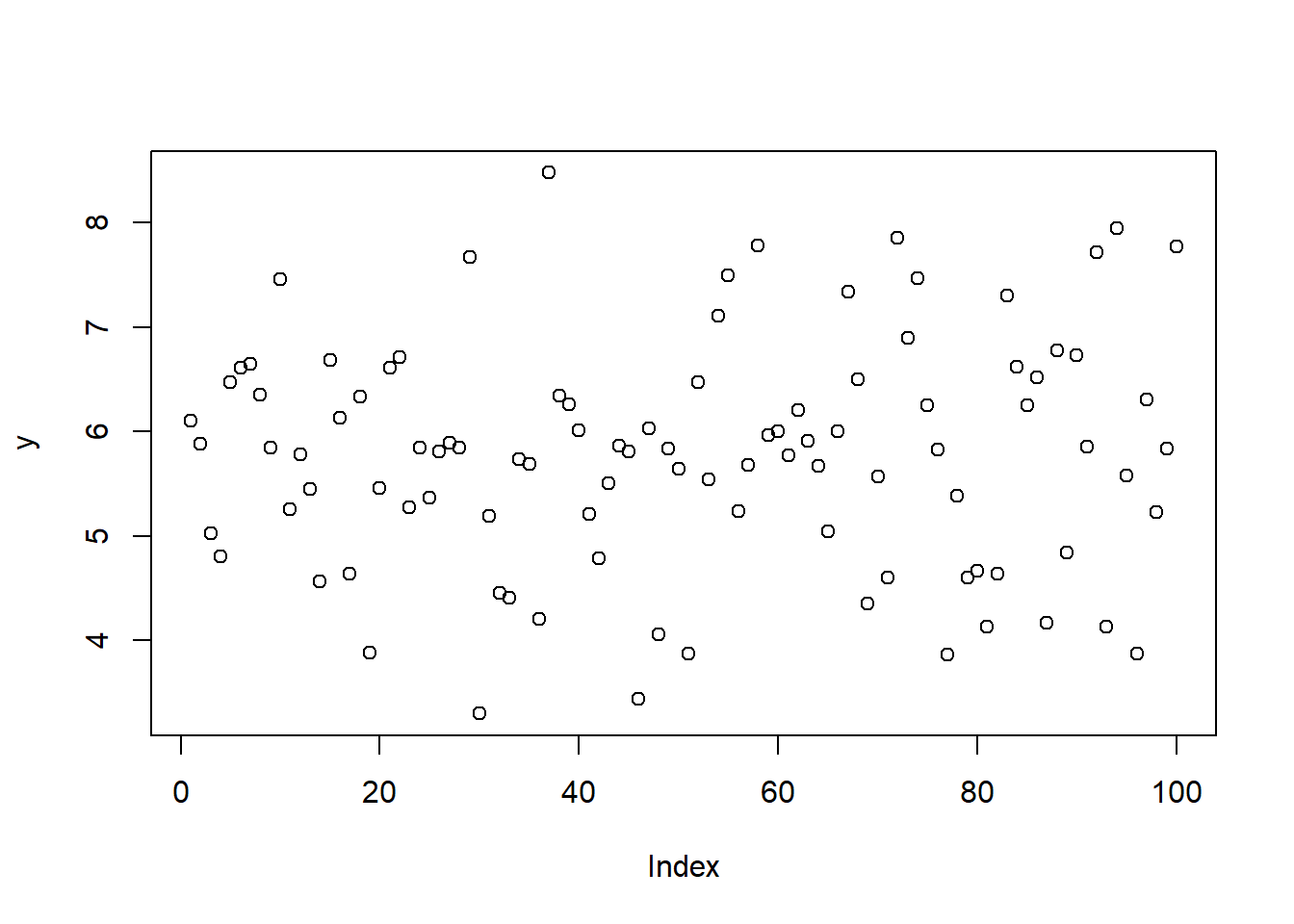
Η παράμετρος pch χρησιμοποιείται για να αλλάξει το σχήμα των σημείων. Μπορεί να πάρει τις τιμές pch = 1, 2, ..., 25.

plot(y, pch = 20)

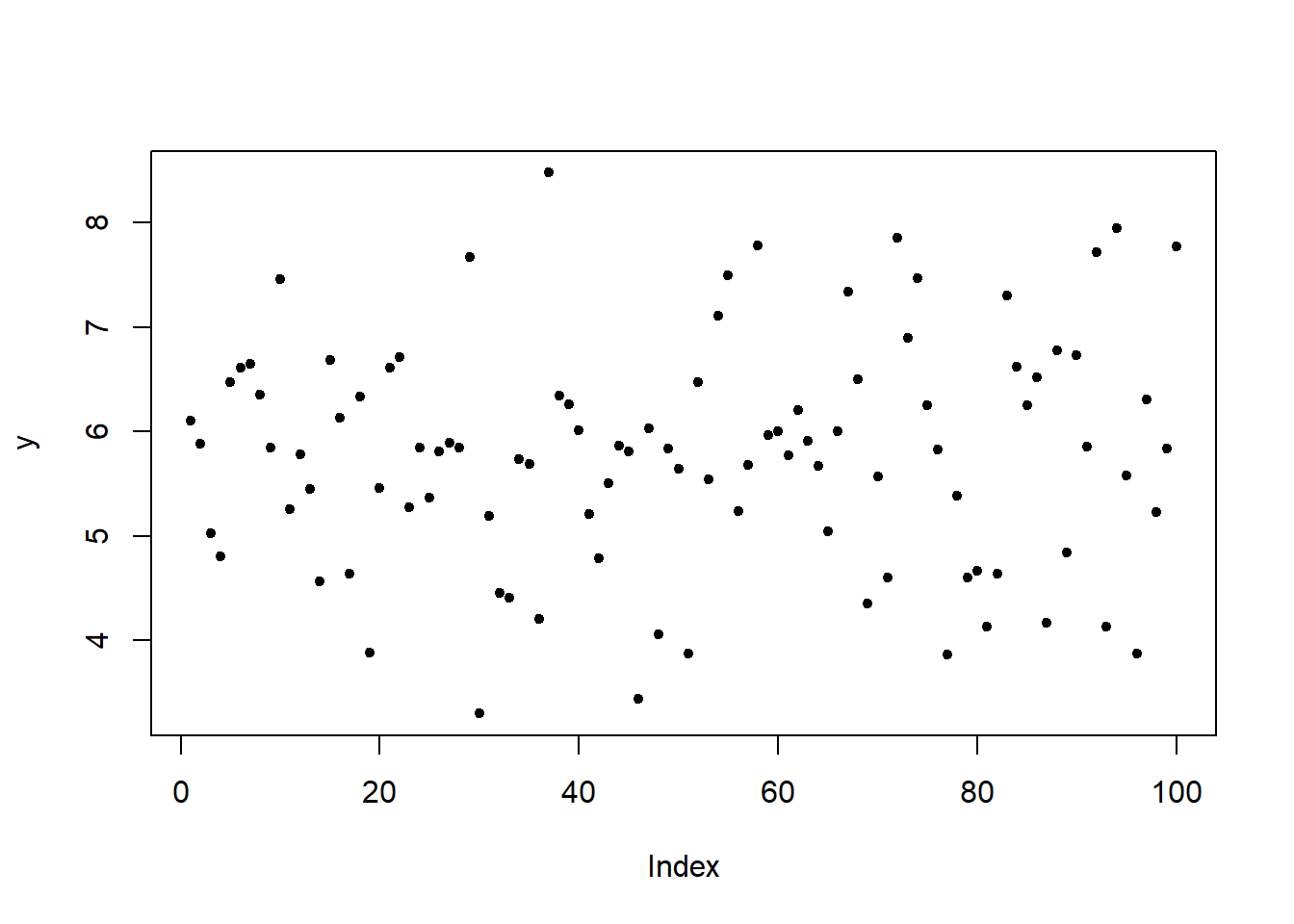
Η plot μπορεί να δημιουργήσει και άλλους τύπους γραφημάτων πέρα από το σημειόγραμμα, αλλάζοντας το όρισμα type:

plot(y, type = "p") # points (σημεία)
plot(y, type = "l") # lines (γραμμές)
plot(y, type = "b") # both (και τα δύο - πρώτος τρόπος)
plot(y, type = "o") # overplotted (και τα δύο - δεύτερος τρόπος)
plot(y, type = "h") # histogram (ιστόγραμμα)
plot(y, type = "s") # steps (βήματα)

Η παράμετρος lty καθορίζει τον τύπο της γραμμής. Παίρνει τις τιμές lty = 1, 2, ..., 6.

plot(y, type = "l", lty = 2)

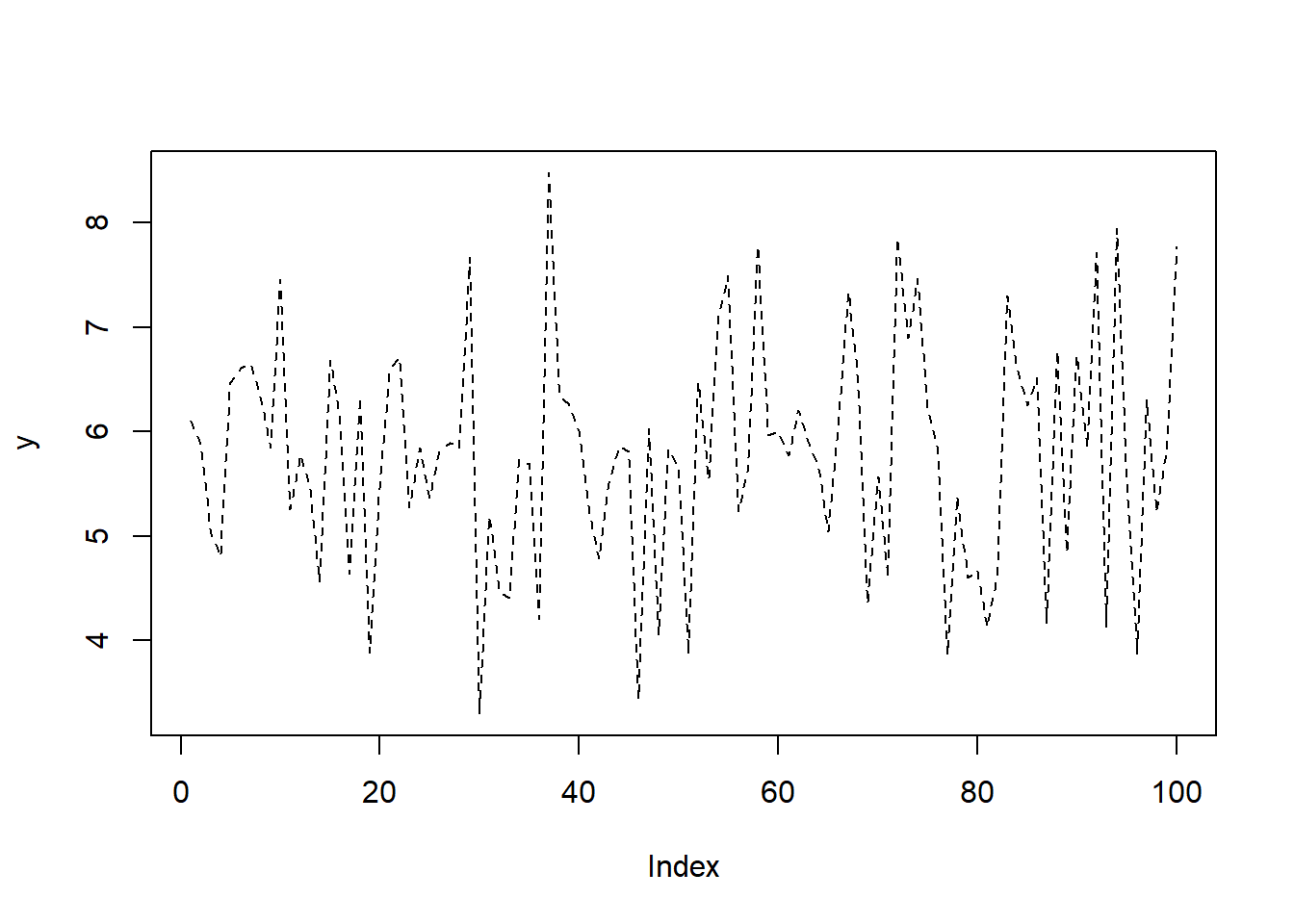
Η παράμετρος lwd καθορίζει το πάχος της γραμμής.

plot(y, type = "l", lwd = 2)

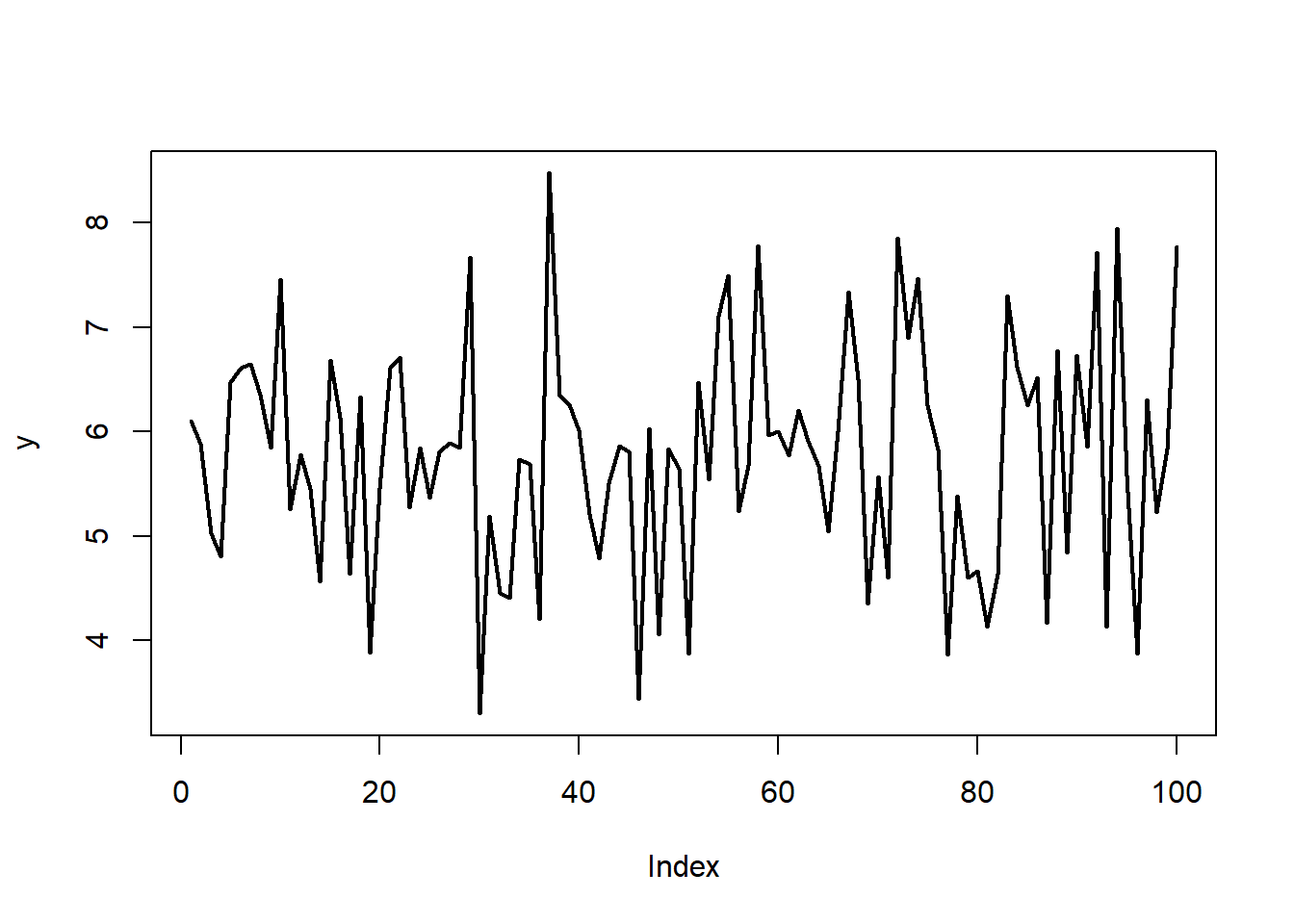
Μπορούμε να προσθέσουμε ένα γράφημα πάνω σε ένα άλλο με τις συναρτήσεις points() και lines().

plot(y, pch = 1)
points(x, pch = 2)

plot(y, lty = 1, type = "l")
lines(x, lty = 2)

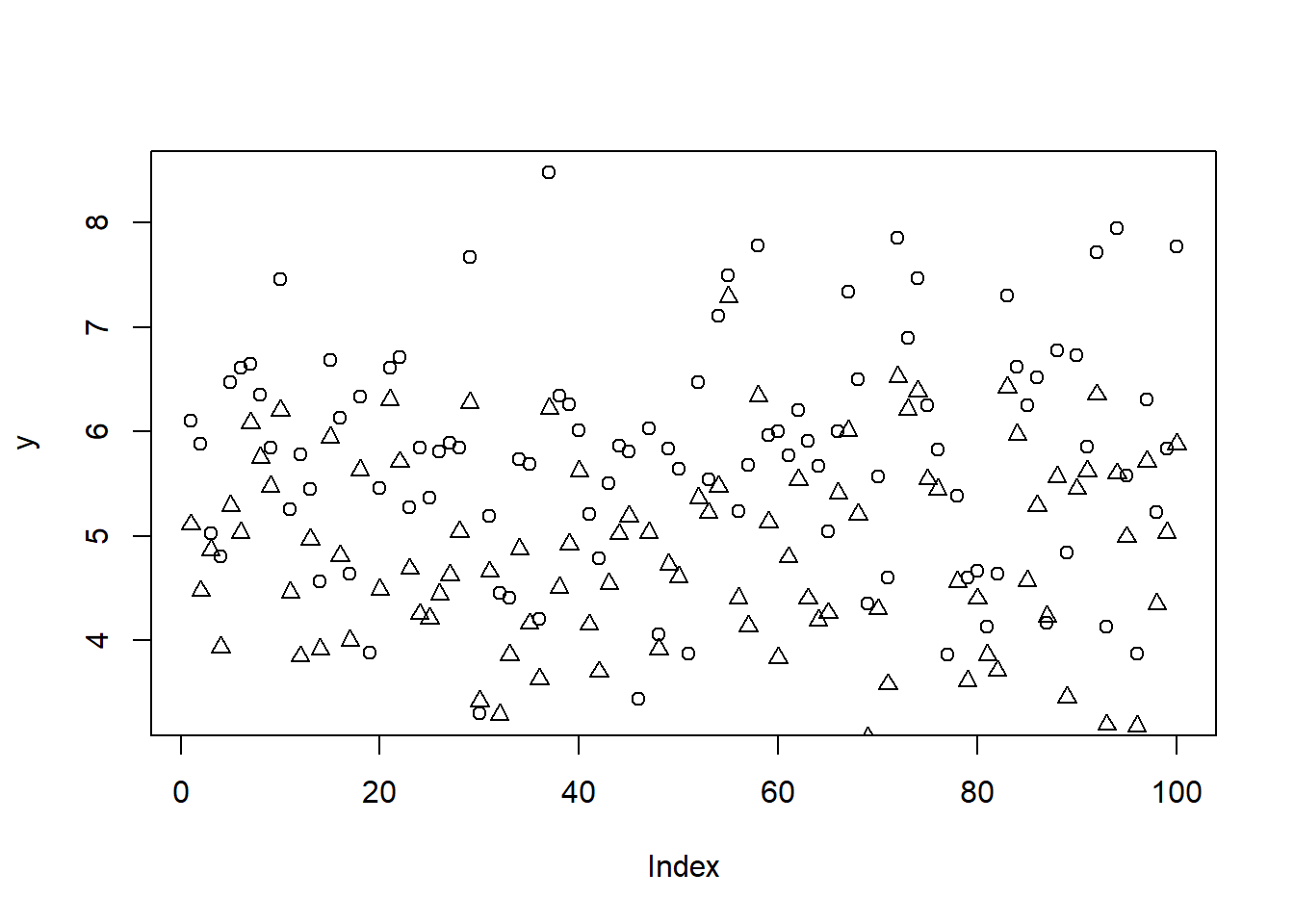
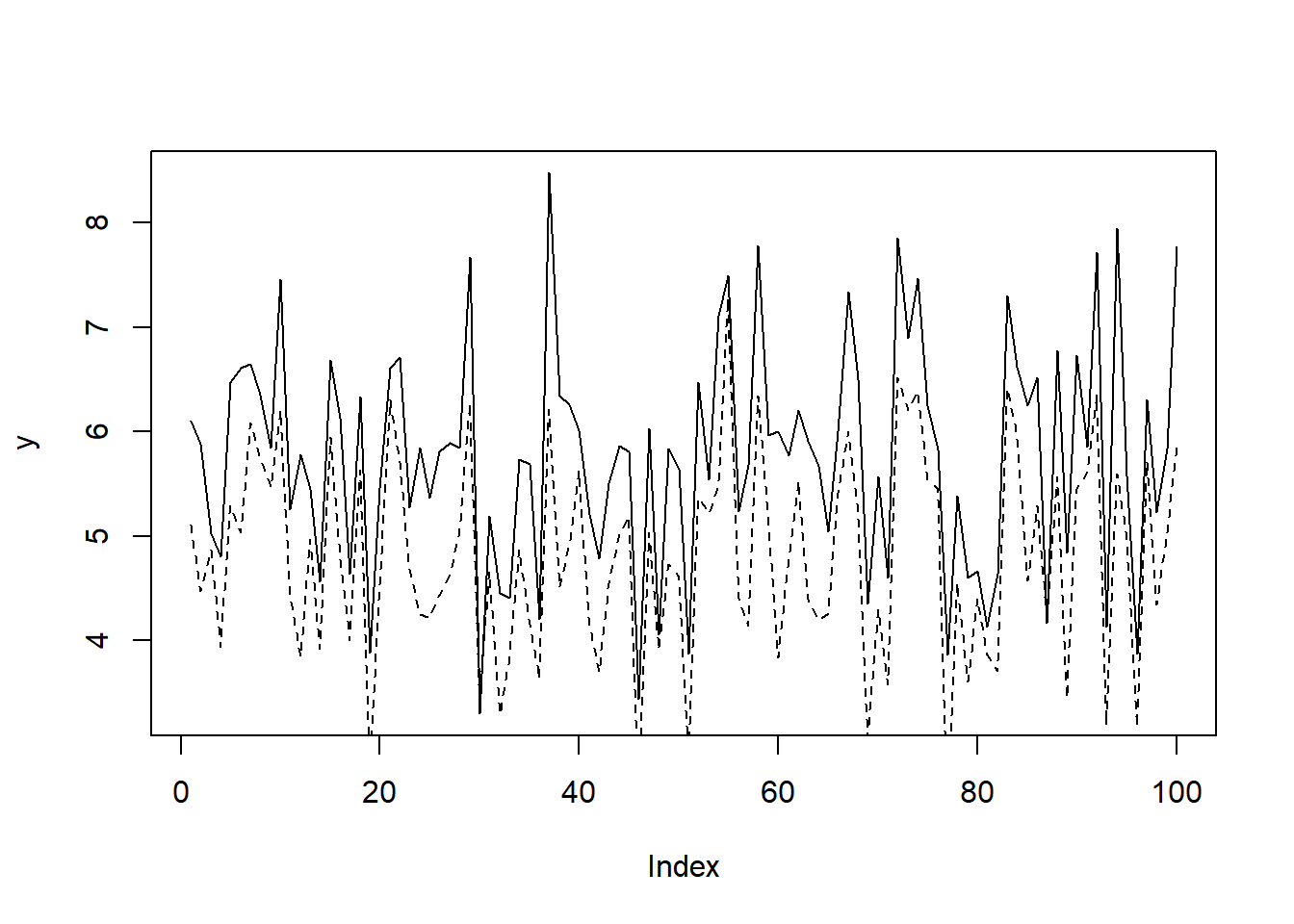
Η R μπορεί να δημιουργήσει γραφήματα με μία ή δύο μεταβλητές. Αν εισάγουμε ένα διάνυσμα, αυτό ανατίθεται στον άξονα y, και ο άξονας x παίρνει τις τιμές 1 έως n (το μήκος του διανύσματος). Εάν εισάγουμε δύο διανύσματα, κάθε ένα ανατίθεται σε έναν άξονα.

plot(x = x, y = y)

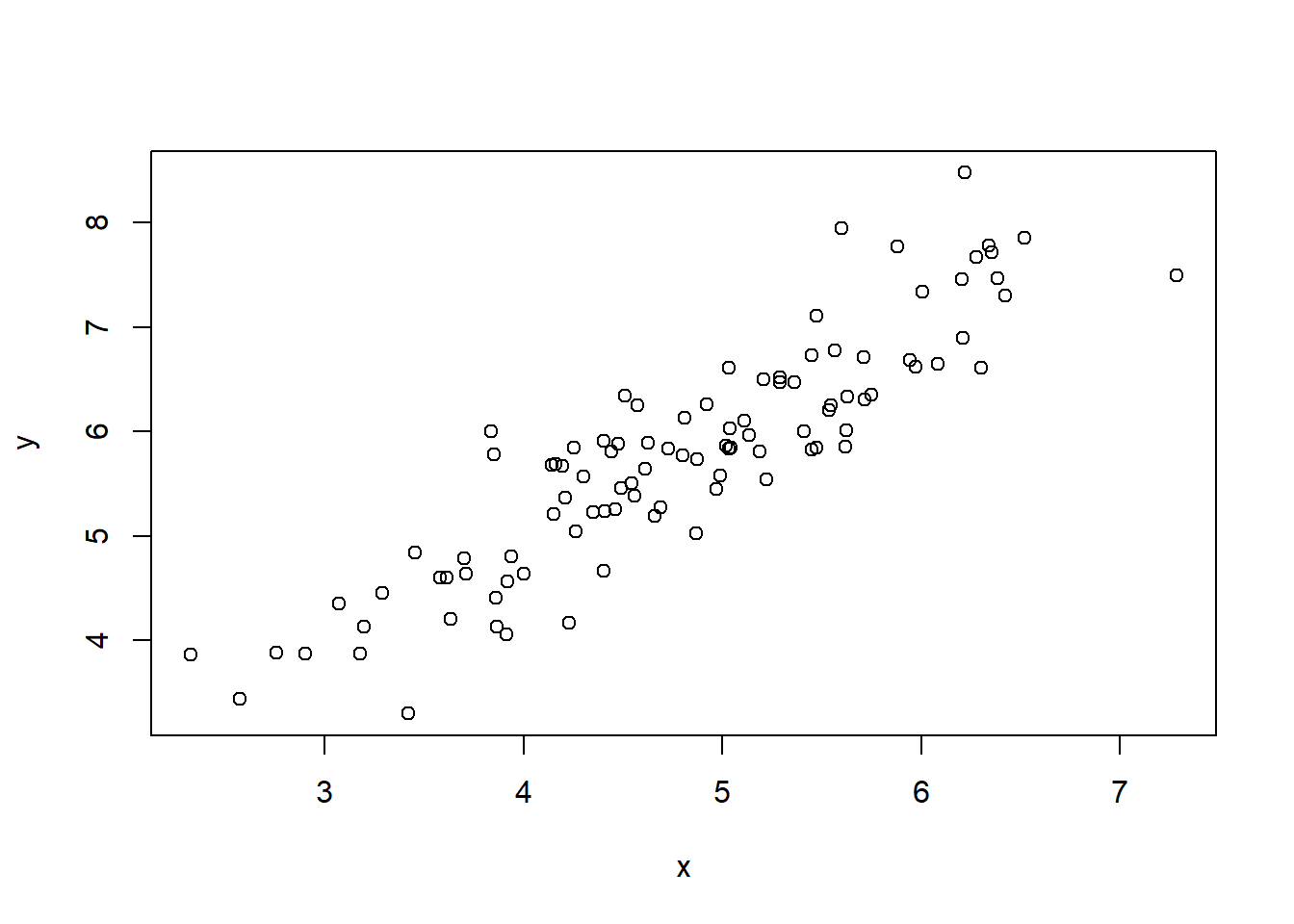
Η plot() δέχεται ένα μεγάλο αριθμό ορισμάτων τα οποία διαμορφώνουν το γράφημα.

?plot