The NM-BANGLE Model
1. Overview
2.1. Cosmic Rays recorded at ground level
2.2. Primary Solar Cosmic Rays at the boundary of the atmosphere
2.3. The role of the Earth's magnetic field
3. An application of the NM-BANGLE Model
4. References
The NM-BANGLE model (Plainaki et al., 2006) is a new cosmic ray model which couples primary solar cosmic rays (SCR) at the top of the Earth's atmosphere with the secondary ones detected at ground level by neutron monitors (NMs) during Ground Level Enhancements (GLEs). This model calculates the evolution of several GLE parameters such as the SCR spectrum and anisotropy as well as the particle flux distribution, revealing crucial information on the SCR particle propagation and distribution. As an input the NM-BANGLE model uses cosmic ray GLE data from NM stations widely distributed around the world. The total output of the NM-BANGLE model is a multi-dimensional GLE picture that gives an important contribution to understanding the physics of solar cosmic ray particles under extreme solar conditions.
The SCR intensity distribution observed at the Earth depends on the source site, acceleration mechanism, coronal transport and the ejection profile as well as on the transport of accelerated particles through the interplanetary magnetic field (IMF). The problem of determining the variations in the SCR distribution outside the magnetosphere using the NM observations presents considerable difficulties. To solve this problem one requires adequate assumptions about the form of the SCR intensity distribution as well as knowledge of particle trajectories in the magnetosphere and the atmospheric interactions that create the secondary particles observed by ground based stations.
2.1 Cosmic Rays recorded at ground level
Possible time variation of the intensity of any cosmic ray component of type (e.g. total neutron counting rate, muon component on the ground and underground at different depths, electron-photon component), observed at a specific cut-off rigidity, at some certain level in the atmosphere at some moment can be determined on the basis of the Coupling Function Method (Dorman, 1963; 2004; Belov et al., 2005):
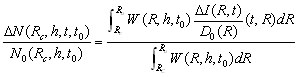 (1)
(1)
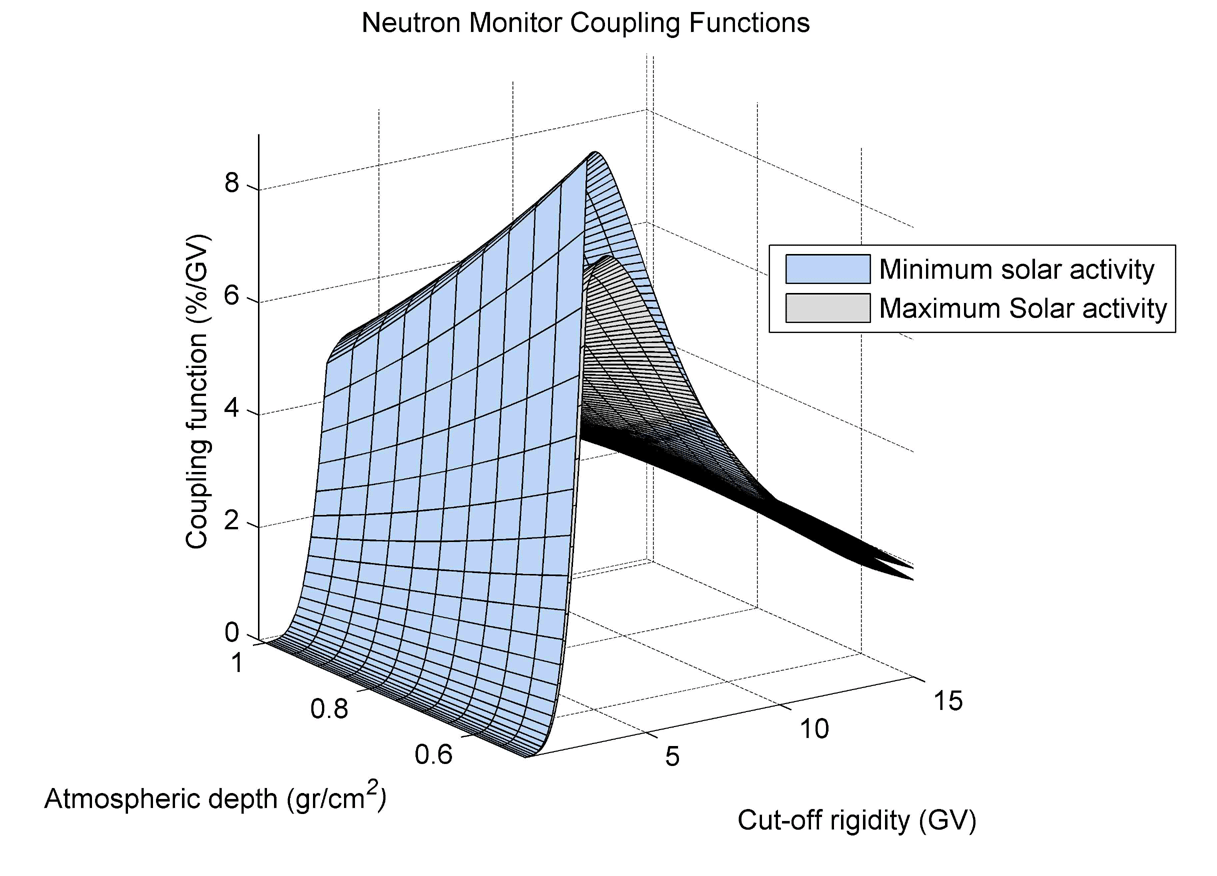
where W(R,h,to) is the coupling function between secondary CR of type i and primary CR arriving at the top of the atmosphere, firstly introduced by Dorman (1957) and ΔI is the differential rigidity spectrum of solar cosmic rays at the top of the atmosphere and Do (R)is the background of the galactic cosmic ray variation, recorded at ground level.. The rigidity dependent coupling functions can be calculated after parameterization of the results of Dorman and Yanke (1981) using an altitude dependent Dorman function (Clem and Dorman, 2000) and a special power-law form in the low kinetic energy range (Belov and Struminsky ,1997). These functions have been used many times in the study of galactic cosmic ray variations and GLEs (Belov et al., 1994; Belov and Eroshenko, 1996; Belov et al., 2005), mainly for the NM64 neutron monitors. However, as it was shown in Clem and Dorman (2000), the difference between coupling coefficients of IGY and NM64 neutron monitors is not significant. A graphical presentation of the neutron monitor coupling functions is presented in Fig.1.
Fig.1 : Neutron Monitor Coupling Functions (from Plainaki et al., 2006)
2.2. Primary Solar Cosmic Rays at the boundary of the atmosphere
Solar cosmic rays arriving at the vicinity of the Earth after a burst of solar activity have in general an anisotropic spatial distribution. The primary solar cosmic ray differential spectrum is a function of the particle energy (or rigidity) distribution as well as some anisotropic function which reflects the angular dependence of the solar cosmic ray flux coming from a certain asymptotic direction.
The anisotropy function represents the distribution of solar cosmic ray particles at the top of the atmosphere during a GLE, revealing information on the way these particles propagated in the interplanetary magnetic field and finally arrived at the vicinity of the Earth. Its exact form is a crucial point in every GLE analysis, since it characterizes in the most significant way the anisotropic GLE model thatís being applied. Therefore its choice is a GLE-specific task depending essentially on the special observational characteristics of the GLE under analysis.
It is important to notice that during extremely intense GLEs (e.g. GLE-05 in February 1956, GLE-69 in January 2005) the anisotropy function seems to have a common form reflecting a narrow-beam like relativistic solar particle arrival (Belov et al., 2005; Plainaki et al., 2006). Especially in the case of GLE-69, the choice of the anisotropy function was made as to describe beam-like solar particle arrival leading to reliable results for the evolution other GLE-parameters, consistent with the satellite observations (Plainaki et al., 2006).
2.3. The role of the Earth's magnetic field
Cosmic ray particles arriving at the vicinity of the Earth propagate inside the magnetosphere and finally access low-altitude satellites or ground level neutron monitors, if their energy is sufficiently high. The main tool for studying the details of the cosmic-ray particle transport is a numerical back-tracing of the protons trajectory in a magnetospheric field model. The asymptotic directions of viewing for a significant number of neutron monitors stations widely distributed around the globe covering a wide range of longitudes and rigidities can be evaluated using a magnetospheric field model. The NM-BANGLE model uses the Tsyganenko 1989 magnetospheric field model (Tsyganenko, 1989).
3. An application of the NM-BANGLE Model
Five-minute data from 41 NM stations, widely distributed around the Earth were incorporated to apply the NM-BANGLE model to the extreme case of GLE-69 (Fig.2), that took place on 20 January 2005. The optimization problem was solved on the basis of the Levenberg-Marquardt non-linear optimization algorithm (Levenberg, 1944; Marquardt, 1963). The beginning of the event is very difficult to model due to the extremely anisotropic direction of propagation of the solar particles and due to the big differences (1-2 orders of magnitude) in the counting rates recorded between different neutron monitors. However, the results of the above described model based on the Levenberg-Marquardt algorithm proved to be relatively reliable especially for the initial phase of the event.
Fig.2 : The GLE-69 (from Plainaki et al., 2006)
In summary, the results from a physical point of view consider the following areas (for a detailed analysis see Plainaki et al, 2006)
SCR spectrum
According to the results of the modeling the primary SCR rigidity spectrum outside the magnetosphere appears hard enough during the initial phase of the event implying that on 20 January 2005 there had been quite significant fluxes of higher energy solar particles. In the second 5min-interval the spectrum became significantly softer while during the third one it hardened. This behavior is quite unexpected taking into consideration the fact that before the maximum event the proton spectrum is usually harder than on the maximum itself.
Integral Fluxes
The behavior of the mean integral fluxes of the lower energy solar cosmic ray particles (for energies greater than 100 MeV and 300 MeV) on 20 January 2005 was calculated by extrapolation on the basis of the NM-BANGLE model. This is due to the fact that no NM can record CR particles with energy ≲500 MeV (or R≲1GV). At this point it should be clarified that the results in this energy range were derived upon the assumption that spectral index is independent on energy. The time of maximum flux seems to depend on the energy of the solar particles. Although the mean integral flux was obtained by extrapolation on the basis of the model there is a good agreement with the satellite observations being of the same order of magnitude.
Anisotropic particle distribution
The angular distribution of the primary solar cosmic ray flux, in the beginning, has a narrow beam-like form, centered around specific locations. As time evolves the distribution of the anisotropy function spreads. Such an evolution of the anisotropy function gives an explanation to the big differences in the counting rates recorded by NM stations located at different longitudes around the globe. In the beginning of the event only the stations with asymptotic cones falling into this narrow beam of energetic particles recorded significant enhancements (e.g. South Pole, McMurdo, Terre Adelie). Later, the particle beam widens and the energetic particles can be sensed by more neutron monitors since the anisotropy function distribution covers an extended range of longitudes and latitudes.
4. References
Belov, A. V. and A.B. Struminsky (1997), Neutron monitor sensitivity to primary protons below 3 GeV derived from data of ground level events, Proc. Int. Conf. Cosmic Rays 25th, 1, 201.
Belov A.V., E.A. Eroshenko and M.A. Livshits (1994), The Energy Spectra of the Accelerated Particles Near the Earth and in the Source in 15 June 1991 Enhancement. Proc. Eighth Int. Symp. on Solar Terrestrial Physics, Sendai, Japan, 26.
Belov, A., E. Eroshenko, H. Mavromichalaki, C. Plainaki and V. Yanke (2005), Solar cosmic rays during the extremely high ground level enhancement of February 23, 1956, Anal. Geophys. 23, 1.
Clem J. and L. I. Dorman (2000), Neutron monitor response functions. Space Sci. Rev., 93, 1, 335.
Dorman, L. I. (1963), Progress in Elementary Particle and Cosmic Ray Physics, J. G. Wilson and S.A. Wouthuysen (ed), North-Holland Publ. Co., Amsterdam.
Dorman, L.I. (2004), Cosmic Rays in the Earthís atmosphere and underground, Kluwer Academic Publishers, The Netherlands
Dorman, L.I. and V. Yanke (1981), The Coupling Functions of NM-64 Neutron Supermonitor, Proc. Int. Conf. Cosmic Rays 17th, 4, 326.
Plainaki, C., A. Belov, E. Eroshenko, H. Mavromichalaki and V. Yanke (2006), Modeling ground level enhancements : The event of 20 January 2005, J. Geophys. Res., in press.
Tsyganenko, N.A. (1989), A magnetospheric magnetic field model with the warped tail current sheet, Planet. Space Sci., 37, 5.