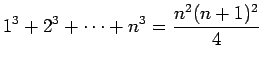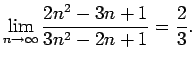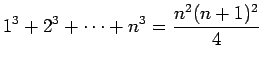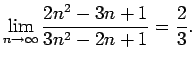Next: About this document ...
Προόδος Σύνολα και Αριθμοί
30 Νοεμβρίου 2003
- Να αποδείξετε με επαγωγή ότι για κάθε φυσικό
αριθμό ισχύει
- Να υπολογιστούν οι δέκατες ρίζες του μιγαδικού
αριθμού
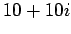 .
.
- Δίνονται οι ακολουθίες πραγματικών αριθμών
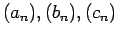 για τις οποίες ισχύει η
ανισότητα
και επίσης είναι γνωστό ότι οι ακολουθίες
για τις οποίες ισχύει η
ανισότητα
και επίσης είναι γνωστό ότι οι ακολουθίες
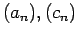 συγκλίνουν στον αριθμό
συγκλίνουν στον αριθμό
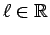 .
Αποδείξτε ότι και η
.
Αποδείξτε ότι και η 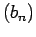 συγκλίνει στο
συγκλίνει στο 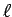 .
.
- Να υπολογιστεί με την βοήθεια του ορισμού ότι:
Διάρκεια διαγωνίσματος 2 ώρες
Καλή Επιτυχία
Aristides Kontogeorgis
2003-12-08