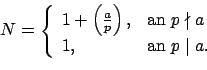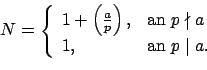Next: About this document ...
Ασκήσεις Θ. Αριθμών
6 Φυλλάδιο
Παράδοση Τετάρτη 11 Ιανουαρίου
- Αν ισχύει
να αποδειχτεί ότι ισχύει
- Αν ισχύει
τότε θα ισχύει
- Αν για ένα πρώτο αριθμό
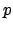 ισχύει
ισχύει
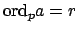
και
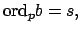
και επιπλέον ισχύει 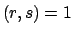 , να αποδειχτεί ότι θα
ισχύει
, να αποδειχτεί ότι θα
ισχύει
- Αν
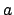 είναι μία αρχική ρίζα modulo
είναι μία αρχική ρίζα modulo 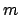 ,
τότε
,
τότε 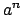 είναι αρχική ρίζα modulo
είναι αρχική ρίζα modulo 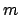 ,
αν ισχύει
,
αν ισχύει
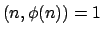 .
.
- Αν
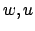 είναι δύο αρχικές ρίζες modulo
είναι δύο αρχικές ρίζες modulo 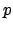 ,
όπου
,
όπου 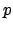 πρώτος αριθμός, να αποδειχτεί ότι ισχύει
πρώτος αριθμός, να αποδειχτεί ότι ισχύει
- Να αποδειχτεί ότι το πλήθος των λύσεων
της ισοδυναμίας
όπου
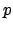 περιττός πρώτος αριθμός είναι
περιττός πρώτος αριθμός είναι
Aristides Kontogeorgis
2005-12-15