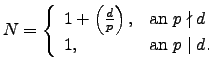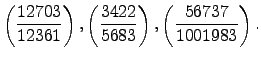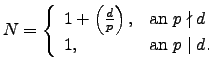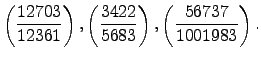Next: About this document ...
Ασκήσεις Θ. Αριθμών
5 Φυλλάδιο
Παράδοση Τετάρτη 14 Δεκεμβρίου
- Δίνεται η ισοδυναμία
όπου
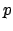 περιττός πρώτος και
περιττός πρώτος και
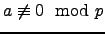 . Αν
. Αν
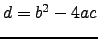 είναι η διακρίνουσα του τριωνύμου
είναι η διακρίνουσα του τριωνύμου
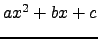 να αποδειχτεί ότι το
πλήθος λύσεων αυτής είναι
να αποδειχτεί ότι το
πλήθος λύσεων αυτής είναι
- Να υπολογιστούν τα παρακάτω σύμβολα του Legendre
- Να εξεταστεί αν έχει λύση η ισοδυναμία:
- Για ποιούς πρώτους ο
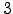 είναι τετραγωνικό υπόλοιπο
είναι τετραγωνικό υπόλοιπο  .
.
- Για ποιούς πρώτους ο
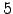 είναι τετραγωνικό υπόλοιπο
είναι τετραγωνικό υπόλοιπο  .
.
Aristides Kontogeorgis
2005-12-08