Next: About this document ...
Ασκήσεις Θ. Αριθμών
4 Φυλλάδιο
Παράδοση Πέμπτη 1 Δεκεμβρίου
- Αν για τον ακέραιο αριθμό
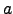 και για τον φυσικό αριθμό
και για τον φυσικό αριθμό 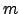 ισχύει
ισχύει
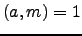 και
και 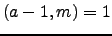 , να αποδειχτεί ότι ισχύει
, να αποδειχτεί ότι ισχύει
- Να αποδειχτεί ότι ισχύει
- Να αποδειχτεί ότι η ισοδυναμία
έχει μοναδική λύση την
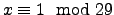 .
.
- Να λυθούν οι ισοδυναμίες:
- Αν
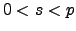 όπου
όπου 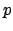 πρώτος αριθμός να αποδειχτεί ότι ισχύει
πρώτος αριθμός να αποδειχτεί ότι ισχύει
- Να λυθεί το σύστημα
Aristides Kontogeorgis
2005-11-24