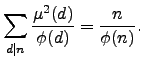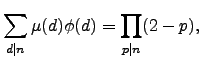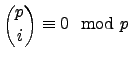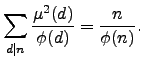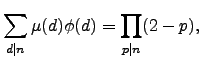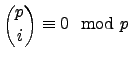Next: About this document ...
Ασκήσεις Θ. Αριθμών
3 Φυλλάδιο
Παράδοση Τετάρτη 16 Νοεμβρίου
- Αν
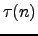 παριστάνει το πλήθος των φυσικών διαιρετών του
παριστάνει το πλήθος των φυσικών διαιρετών του
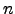 να αποδειχτεί ότι η συνάρτηση
να αποδειχτεί ότι η συνάρτηση
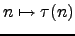 , είναι
αριθμητική πολλαπλασιαστική.
, είναι
αριθμητική πολλαπλασιαστική.
- Να αποδειχτεί ότι για κάθε φυσικό αριθμό
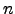
- Να αποδειχτεί ότι για κάθε φυσικό αριθμό
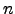 ισχύει
όπου το
ισχύει
όπου το 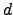 διατρέχει τους φυσικούς διαιρέτες του
διατρέχει τους φυσικούς διαιρέτες του 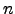 , και το
, και το 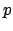 τους πρώτους διαιρέτες του
τους πρώτους διαιρέτες του 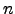 .
.
- Nα βρεθεί το πλήθος και το άθροισμα των φυσικών
διαιρετών του
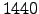 .
.
- Αν
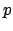 πρώτος, δείξτε ότι
για κάθε
πρώτος, δείξτε ότι
για κάθε 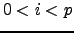 . Αποδείξτε στην συνέχεια
Το παραπάνω για ευνόητους λόγους αποκαλείται ((το όνειρο του πρωτοετούς)).
. Αποδείξτε στην συνέχεια
Το παραπάνω για ευνόητους λόγους αποκαλείται ((το όνειρο του πρωτοετούς)).
- Nα αποδειχτεί ότι για κάθε ακέραιο αριθμό
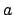 ισχύει
Επίσης να αποδειχτεί ότι για κάθε ακέραιο αριθμό
ισχύει
Επίσης να αποδειχτεί ότι για κάθε ακέραιο αριθμό 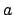 ισχύει
ισχύει
- Αν
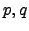 είναι πρώτοι αριθμοί, διαφορετικοί μεταξύ τους,
να αποδειχτεί ότι
είναι πρώτοι αριθμοί, διαφορετικοί μεταξύ τους,
να αποδειχτεί ότι
Aristeides Kontogeorgis
2005-11-09