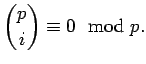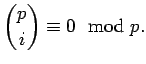Next: About this document ...
Εξέταση Θεωρίας Αριθμών
17 Σεπτεμβρίου 2003
- Να αποδειχτεί ότι το γινόμενο τεσάρων διαδοχικών αριθμών
διαιρείται με το
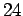 .
.
- Αν ο
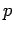 είναι πρώτος δείξτε ότι
Αποδείξτε στην συνέχεια ότι
Γιατί το
είναι πρώτος δείξτε ότι
Αποδείξτε στην συνέχεια ότι
Γιατί το
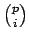 είναι ακέραιος?
είναι ακέραιος?
- Να βρεθεί ο μέγιστος κοινός διαιρέτης των αριθμών
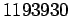 και
και 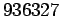 και να γραφεί σαν ακέραιος γραμμικός συνδιασμός των
αριθμών αυτών.
και να γραφεί σαν ακέραιος γραμμικός συνδιασμός των
αριθμών αυτών.
- Να λυθεί το σύστημα
- Να οριστεί πότε μια συνάρτηση
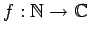 θα λέγεται αριθμητική πολλαπλασιαστική.
Να οριστεί η συνάρτηση
θα λέγεται αριθμητική πολλαπλασιαστική.
Να οριστεί η συνάρτηση 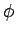 του Euler
και να αποδειχτεί ότι είναι αριθμητική πολλαπλασιαστική.
Αποδείξτε ότι
του Euler
και να αποδειχτεί ότι είναι αριθμητική πολλαπλασιαστική.
Αποδείξτε ότι
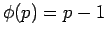
και
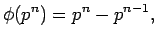
για 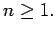
- Να αποδειχτεί ότι ο
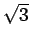 είναι άρρητος.
είναι άρρητος.
- Να εξεταστεί αν έχει λύσεις η ισοδυναμία
Δίνεται ότι ο αριθμός
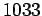 είναι πρώτος.
είναι πρώτος.
Καλή Επιτυχία
Aristides Kontogeorgis
2003-09-18