


Next: About this document ...
Εξέταση Θεωρίας Αριθμών
27 Ιανουαρίου 2003
- Για
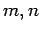 ακεραίους
ακεραίους 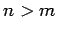 , oρίζεται το
, oρίζεται το
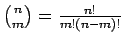 .
Δείξτε ότι το
.
Δείξτε ότι το
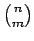 είναι ακέραιος.
είναι ακέραιος.
- Nα υπολογίσετε τον μέγιστο κοινό διαιρέτη των αριθμών
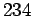 και
και 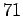 και να
εφράσετε σαν γραμμικό συνδιασμός αυτών. Στην συνέχεια να λυθεί η
και η
και να
εφράσετε σαν γραμμικό συνδιασμός αυτών. Στην συνέχεια να λυθεί η
και η
- Nα βρεθούν οι αριθμοί
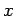 που όταν διαιρεθούν με το
που όταν διαιρεθούν με το 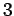 αφήνουν υπόλοιπο
αφήνουν υπόλοιπο 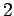 ,
όταν διαιρεθούν με το
,
όταν διαιρεθούν με το 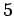 αφήνουν υπόλοιπο
αφήνουν υπόλοιπο 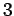 και όταν διαιρεθούν με το
και όταν διαιρεθούν με το 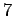 αφήνουν υπόλοιπο
αφήνουν υπόλοιπο 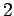 .
.
- Να οριστεί η συνάρτηση
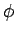 του Euler. Να δείξετε ότι είναι
πολλαπλασιαστική και ότι
του Euler. Να δείξετε ότι είναι
πολλαπλασιαστική και ότι
- Να διατυπώσετε το ((μικρό)) θεώρημα του Fermat.
Aν
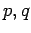 είναι πρώτοι αριθμοί, διαφορετικοί μεταξύ τους, να αποδειχτεί ότι
είναι πρώτοι αριθμοί, διαφορετικοί μεταξύ τους, να αποδειχτεί ότι
- Να οριστεί η τάξη ενός αριθμού modulo
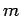 . Να οριστεί η
πρωταρχική ρίζα modulo
. Να οριστεί η
πρωταρχική ρίζα modulo 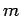 , και ο δείκτης ενός αριθμού ως προς
μια πρωταρχική ρίζα.
Αν
, και ο δείκτης ενός αριθμού ως προς
μια πρωταρχική ρίζα.
Αν 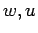 είναι δύο αρχικές ρίζες modulo
είναι δύο αρχικές ρίζες modulo 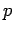 ,
όπου
,
όπου 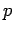 πρώτος αριθμός, να αποδειχτεί ότι ισχύει
πρώτος αριθμός, να αποδειχτεί ότι ισχύει
- Nα εξετάσετε αν η ισοδυναμία
έχει λύσεις. Δίνεται ότι ο αριθμός
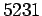 είναι πρώτος.
είναι πρώτος.
Καλή Επιτυχία
Aristides Kontogeorgis
2003-09-18