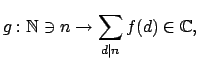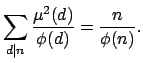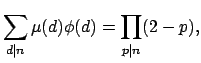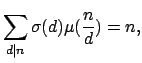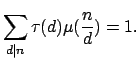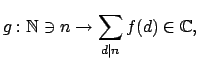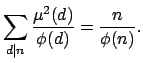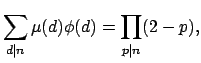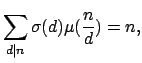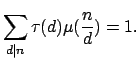Next: About this document ...
Ασκήσεις Θ. Αριθμών
4 Φυλλάδιο
Παράδοση Παρασκευή 15 Νοεμβρίου
- Αν
 παριστάνει το πλήθος των φυσικών διαιρετών του
παριστάνει το πλήθος των φυσικών διαιρετών του
 να αποδειχτεί ότι η συνάρτηση
να αποδειχτεί ότι η συνάρτηση
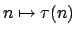 , είναι
αριθμητική πολλαπλασιαστική.
, είναι
αριθμητική πολλαπλασιαστική.
- Αν η συνάρτηση
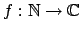 είναι
πολλαπλασιαστική αριθμητική να αποδειχτεί ότι και η
είναι πολλαπλασιαστική αριθμητική.
είναι
πολλαπλασιαστική αριθμητική να αποδειχτεί ότι και η
είναι πολλαπλασιαστική αριθμητική.
- Να αποδειχτεί ότι για κάθε φυσικό αριθμό
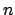
- Να αποδειχτεί ότι για κάθε φυσικό αριθμό
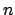 ισχύει
όπου το
ισχύει
όπου το 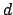 διατρέχει τους φυσικούς διαιρέτες του
διατρέχει τους φυσικούς διαιρέτες του 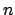 , και το
, και το 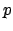 τους πρώτους διαιρέτες του
τους πρώτους διαιρέτες του 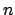 .
.
- Nα βρεθεί το πλήθος και το άθροισμα των φυσικών
διαιρετών του
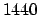 .
.
- An
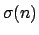 συμβολίζει το άθροισμα των φυσικών διαιρετών
του
συμβολίζει το άθροισμα των φυσικών διαιρετών
του 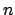 και
και 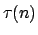 το πλήθος των φυσικών διαιρετών του
το πλήθος των φυσικών διαιρετών του 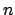 να αποδειχτεί ότι
και
να αποδειχτεί ότι
και
- Αν
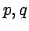 είναι πρώτοι αριθμοί, διαφορετικοί μεταξύ τους,
να αποδειχτεί ότι
είναι πρώτοι αριθμοί, διαφορετικοί μεταξύ τους,
να αποδειχτεί ότι
Aristides Kontogeorgis
2002-11-08