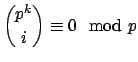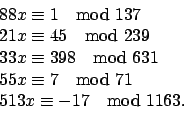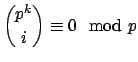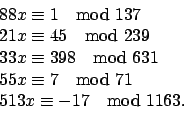Next: About this document ...
Ασκήσεις Θ. Αριθμών
3 Φυλλάδιο
Παράδοση Τετάρτη 6 Νοεμβρίου
- Δύο πρώτοι αριθμοί
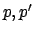 θα λέγονται δίδυμοι αν η διαφορά τους
είναι
θα λέγονται δίδυμοι αν η διαφορά τους
είναι 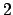 , Βρείτε το πλήθος των διδύμων πρώτων που είναι μικρότεροι από
, Βρείτε το πλήθος των διδύμων πρώτων που είναι μικρότεροι από
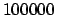 .
.
- Nα δείξετε ότι το
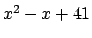 για
για
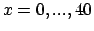 είναι πρώτος. Ομοίως
να δείξετε ότι τι
είναι πρώτος. Ομοίως
να δείξετε ότι τι
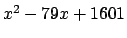 για
για
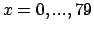 είναι πρώτος.
είναι πρώτος.
- Να υπολογιστούν οι πρώτοι αριθμοί του Fermat,
δηλαδή πρώτοι αριθμοί της μορφής
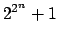 για
για 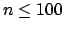 .
.
- Αν
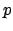 πρώτος, δείξτε ότι
για κάθε
πρώτος, δείξτε ότι
για κάθε 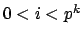 . Αποδείξτε στην συνέχεια
Το παραπάνω για ευνόητους λόγους αποκαλείται ((το όνειρο του πρωτοετούς)).
. Αποδείξτε στην συνέχεια
Το παραπάνω για ευνόητους λόγους αποκαλείται ((το όνειρο του πρωτοετούς)).
- Nα αποδειχτεί ότι για κάθε ακέραιο αριθμό
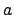 ισχύει
Επίσης να αποδειχτεί ότι για κάθε ακέραιο αριθμό
ισχύει
Επίσης να αποδειχτεί ότι για κάθε ακέραιο αριθμό 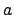 ισχύει
ισχύει
- Nα λυθούν οι γραμμικές ισοδυναμίες
Να πάτε στην διευθύνση
http://eloris.samos.aegean.gr/mailman/listinfo/numth
και να γίνετε μέλη της δημόσιας λίστας συζήτησης σχετικά
με το μάθημα.
Aristides Kontogeorgis
2002-10-30