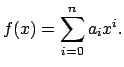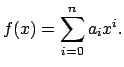Next: About this document ...
Ασκήσεις Θ. Αριθμών
1 Φυλλάδιο
Παράδοση Παρασκευή 11 Οκτωβρίου
- Θεωρούμε το πολυώνυμο με συντελεστές από το
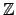 της μορφής
Δείξτε ότι αν το
της μορφής
Δείξτε ότι αν το 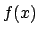 έχει ρητή ρίζα
έχει ρητή ρίζα 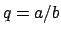 τότε το
τότε το
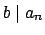 και το
και το
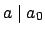 . Να δείξετε ότι οι αριθμοί
. Να δείξετε ότι οι αριθμοί
![$ \sqrt[13]{3}$](img7.png) ,
,
![$ \sqrt[3]{5}$](img8.png) ,
δεν είναι ρητοί. Είναι σωστό ότι το άθροισμα δύο άρρητων είναι άρρητος?
,
δεν είναι ρητοί. Είναι σωστό ότι το άθροισμα δύο άρρητων είναι άρρητος?
- Να αποδειχτεί ότι ο αριθμός
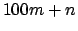 διαιρείται δια του
διαιρείται δια του 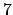 , αν ο
αριθμός
, αν ο
αριθμός 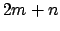 διαιρείται δια του
διαιρείται δια του 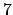 .
.
- Να αποδειχτεί ότι ένας αριθμός διαιρείται δια του
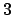 ή του
ή του 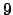 ,
αν το άθροισμα των ψηφίων του διαιρείται δια του
,
αν το άθροισμα των ψηφίων του διαιρείται δια του 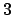 ή του
ή του 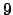 ,
αντίστοιχα.
,
αντίστοιχα.
- Να αποδειχτεί ότι ο αριθμός
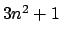 ,
,
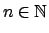 , δεν
μπορεί να είναι το τετράγωνο ενός φυσικού αριθμού.
, δεν
μπορεί να είναι το τετράγωνο ενός φυσικού αριθμού.
- Αν για τους φυσικούς αριθμούς
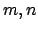 ισχύει
ισχύει 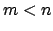 να αποδειχτεί
ότι
να αποδειχτεί
ότι
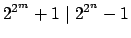 .
.
- Να αποδειχτεί ότι για κάθε φυσικό αριθμό
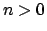 ισχύει
ισχύει
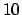 δεν διαιρεί το
δεν διαιρεί το 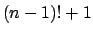 .
.
Aristides Kontogeorgis
2002-10-25