Next: About this document ...
Ασκήσεις Θ. Ομάδων
1 Φυλλάδιο
Παράδoση Παρασκευή 22 Φεβρουαρίου
- Να δείξετε ότι το σύνολο
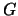 των
των 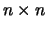 πινάκων
με ορίζουσα διαφορετική του μηδενός αποτελεί ομάδα με
πράξη τον πολ/σμό πινάκων. Να δείξετε ότι το υποσύνολο
πινάκων
με ορίζουσα διαφορετική του μηδενός αποτελεί ομάδα με
πράξη τον πολ/σμό πινάκων. Να δείξετε ότι το υποσύνολο
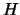 του
του 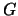 που αποτελείτε από τους
που αποτελείτε από τους 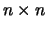 πίνακες
με ορίζουσα
πίνακες
με ορίζουσα 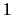 αποτελεί υποομάδα του
αποτελεί υποομάδα του 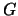 .
.
- Αν
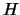 ,
, 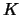 είναι υποομάδες της ομάδας
είναι υποομάδες της ομάδας 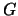 , η τομή τους
είναι υποομάδα της
, η τομή τους
είναι υποομάδα της 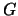 ? Η ένωση τους είναι υποομάδα της
? Η ένωση τους είναι υποομάδα της 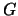 ?
?
- Καθορίστε αν είναι ομάδες οι παρακάτω
- Αν σε μία ομάδα
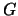 ισχύει
ισχύει
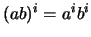 για τρείς διαδοχικούς
ακαίρεους
για τρείς διαδοχικούς
ακαίρεους 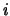 , αποδείξτε ότι η
, αποδείξτε ότι η 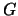 είναι αβελιανή.
είναι αβελιανή.
- Δείξτε ότι μία ομάδα με δύο ή τρία στοιχεία είναι αβελιανή.
- Να δείξετε ότι το σύνολο των πινακών
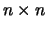 με συντελεστές πραγματικούς,
για τους οποίους ισχύει:
αποτελεί ομάδα με πράξη τον πολ/σμό πινάκων.
με συντελεστές πραγματικούς,
για τους οποίους ισχύει:
αποτελεί ομάδα με πράξη τον πολ/σμό πινάκων.
- Είναι οι ομάδες που ορίστηκαν στις ασκήσεις (1) και (6) αβελιανές?
Aristides Kontogeorgis
2002-03-03
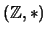 όπου
όπου 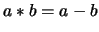
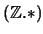 όπου
όπου