


Next: About this document ...
Εξέταση Γραμμικής Άλγεβρας Ι
Παρασκευή 18 Ιανουαρίου 2002
truecm
- Έστω
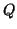 διανυσματικός χώρος και
διανυσματικός χώρος και
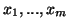 ιδιοδιανύσματα
της γραμμικής συνάρτησης
ιδιοδιανύσματα
της γραμμικής συνάρτησης
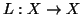 , που αντιστοιχούν σε
διαφορετικές ανά δύο
ιδιοτιμές
, που αντιστοιχούν σε
διαφορετικές ανά δύο
ιδιοτιμές
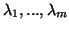 .
Nα δείξετε ότι τα
.
Nα δείξετε ότι τα
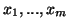 είναι γραμμικά ανεξάρτητα.
είναι γραμμικά ανεξάρτητα.
- Να δείξετε ότι όμοιοι πίνακες έχουν το ίδιο
χαρακτηριστικό πολυώνυμο. Nα δώσετε παράδειγμα πινάκων
με ίδιο χαρακτηριστικό πολυώνυμο που να μην είναι όμοιοι.
- Δίνεται η γραμμική απεικόνιση
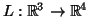 με
πίνακα
Nα υπολογίσετε βάσεις για τον πυρήνα και την εικόνα της
με
πίνακα
Nα υπολογίσετε βάσεις για τον πυρήνα και την εικόνα της 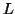 .
.
- Να βρείτε όλες τις λύσεις του συστήματος:
- Ένας πίνακας
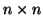 θα λέγεται αντισυμμετρικός αν και μόνο
αν
θα λέγεται αντισυμμετρικός αν και μόνο
αν 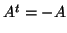 . Να δείξετε ότι για
. Να δείξετε ότι για 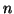 περιττό κάθε αντισυμμετρικός πίνακας
δεν είναι αντιστρέψιμος.
περιττό κάθε αντισυμμετρικός πίνακας
δεν είναι αντιστρέψιμος.
- Βρείτε μια ορθοκανονική βάση του υποχώρου του
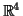 που
παράγεται από τα
που
παράγεται από τα
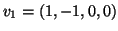 ,
,
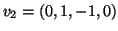 ,
,
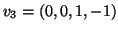 .
.
- Είναι ο πίνακας
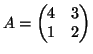 διαγωνοποιήσιμος? Αν ναι, να τον γράψετε σε διαγώνια μορφή.
διαγωνοποιήσιμος? Αν ναι, να τον γράψετε σε διαγώνια μορφή.
- Θεωρούμε δύο ακολουθίες
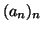 και
και 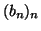 που ορίζονται ως εξής:
που ορίζονται ως εξής:
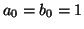 ,
,
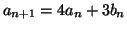 ,
,
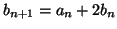 . Nα υπολογίσετε
τα
. Nα υπολογίσετε
τα 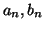 συναρτήσει του
συναρτήσει του 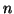 .
.
- Θεωρήστε τον γραμμικό χώρο
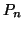 των πολυωνύμων βαθμού
των πολυωνύμων βαθμού 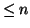 με
συντελεστές πραγματικούς. Θεωρήστε την βάση
με
συντελεστές πραγματικούς. Θεωρήστε την βάση
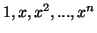 του
του 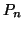 . Να δείξετε ότι η συνάρτηση
. Να δείξετε ότι η συνάρτηση
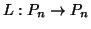 που στέλνει το πολυώνυμο
που στέλνει το πολυώνυμο 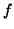 στην
παράγωγο του είναι γραμμική. Αφού υπολογίσετε τον πίνακα της
στην
παράγωγο του είναι γραμμική. Αφού υπολογίσετε τον πίνακα της 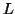 ως προς
την παραπάνω βάση, να υπολογίσετε τις ιδιοτιμές και τους ιδιόχωρους
κάθε ιδιοτιμής. Για ποιους φυσικούς
ως προς
την παραπάνω βάση, να υπολογίσετε τις ιδιοτιμές και τους ιδιόχωρους
κάθε ιδιοτιμής. Για ποιους φυσικούς 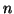 είναι ο πίνακας της
είναι ο πίνακας της
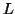 διαγωνοποιήσιμος?
διαγωνοποιήσιμος?
truecm
Καλή επιτυχία
Kontogiwrghs Aristeidhs
2002-01-18
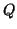 διανυσματικός χώρος και
διανυσματικός χώρος και
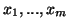 ιδιοδιανύσματα
της γραμμικής συνάρτησης
ιδιοδιανύσματα
της γραμμικής συνάρτησης
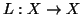 , που αντιστοιχούν σε
διαφορετικές ανά δύο
ιδιοτιμές
, που αντιστοιχούν σε
διαφορετικές ανά δύο
ιδιοτιμές
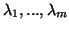 .
Nα δείξετε ότι τα
.
Nα δείξετε ότι τα
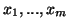 είναι γραμμικά ανεξάρτητα.
είναι γραμμικά ανεξάρτητα.
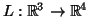 με
πίνακα
Nα υπολογίσετε βάσεις για τον πυρήνα και την εικόνα της
με
πίνακα
Nα υπολογίσετε βάσεις για τον πυρήνα και την εικόνα της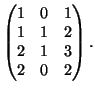
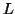 .
.
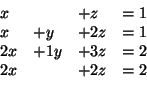
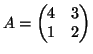 διαγωνοποιήσιμος? Αν ναι, να τον γράψετε σε διαγώνια μορφή.
διαγωνοποιήσιμος? Αν ναι, να τον γράψετε σε διαγώνια μορφή.
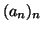 και
και 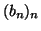 που ορίζονται ως εξής:
που ορίζονται ως εξής:
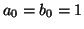 ,
,
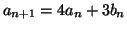 ,
,
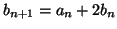 . Nα υπολογίσετε
τα
. Nα υπολογίσετε
τα 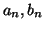 συναρτήσει του
συναρτήσει του 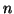 .
.