Next: About this document ...
Πρόοδος Γραμμικής Άλγεβρας Ι
Κυριακή 18 Νοεμβρίου 2001
- Έστω
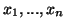 διανύσματα εντός του
διανύσματα εντός του 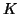 -διανυσματικού χώρου
-διανυσματικού χώρου 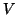 .
Δείξτε ότι τα
.
Δείξτε ότι τα
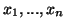 είναι γραμμικά εξαρτημένα αν και μόνο
αν ένα από αυτά μπορεί να γραφτεί σαν γραμμικός συνδιασμός των
υπολοίπων.
είναι γραμμικά εξαρτημένα αν και μόνο
αν ένα από αυτά μπορεί να γραφτεί σαν γραμμικός συνδιασμός των
υπολοίπων.
- Έστω
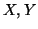 διανυσματικοί χώροι και
διανυσματικοί χώροι και
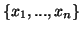 βάση του
βάση του 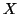 .
Θεωρούμε την γραμμική συνάρτηση
.
Θεωρούμε την γραμμική συνάρτηση
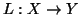 .
Ορίζουμε τα
.
Ορίζουμε τα
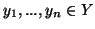 σαν
σαν
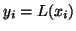 .
Δείξτε ότι αν η
.
Δείξτε ότι αν η 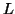 είναι 1-1 τότε τα
είναι 1-1 τότε τα
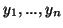 είναι γραμμικά
ανεξάρτητα. Εξηγήστε τι μπορεί να συμβεί αν η
είναι γραμμικά
ανεξάρτητα. Εξηγήστε τι μπορεί να συμβεί αν η 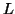 δεν είναι 1-1,
δίνοντας κατάληλο παράδειγμα.
δεν είναι 1-1,
δίνοντας κατάληλο παράδειγμα.
- Θεωρούμε τον χώρο
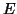 των πολυωνύμων βαθμού μικρότερου ή ίσου του
των πολυωνύμων βαθμού μικρότερου ή ίσου του 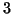 .
Να δείξετε ότι τα πολυώνυμα
.
Να δείξετε ότι τα πολυώνυμα
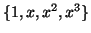 αποτελούν βάση του
αποτελούν βάση του 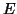 .
Στην συνέχεια να δείξετε ότι η συνάρτηση
.
Στην συνέχεια να δείξετε ότι η συνάρτηση
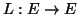 , η
οποία στέλνει το
, η
οποία στέλνει το 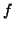 στην παράγωγο του είναι γραμμική συνάρτηση.
Να γράψετε τον πίνακα της ως προς την παραπάνω βάση να υπολογίσετε
μια βάση για τον πυρήνα και την εικόνα της.
στην παράγωγο του είναι γραμμική συνάρτηση.
Να γράψετε τον πίνακα της ως προς την παραπάνω βάση να υπολογίσετε
μια βάση για τον πυρήνα και την εικόνα της.
- Έστω
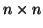 πίνακας
πίνακας 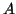 , ο οποίος γράφεται στην μορφή
, ο οποίος γράφεται στην μορφή
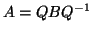 ,
όπου
,
όπου 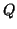 αντιστρέψιμος
αντιστρέψιμος 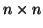 πίνακας. Να εκφράσετε τις δυνάμεις του
πίνακας. Να εκφράσετε τις δυνάμεις του
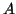 συναρτήσει των δυνάμεων του
συναρτήσει των δυνάμεων του 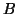 .
.
- Να υπολογίσετε τους
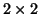 πίνακες
πίνακες 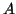 τέτοιους ώστε
για όλους τους
τέτοιους ώστε
για όλους τους 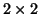 πίνακες
πίνακες 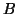 .
.
- Δίνεται ο πίνακας
ο οποίος ορίζει γραμμική απεικόνιση από το
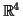 στο
στο
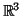 .
Να κατασκευαστεί μία βάση για τον πυρήνα και την εικόνα της
παραπάνω γραμμικής απεικόνισης.
Να θεωρήσετε την γραμμική απεικόνιση από τον
.
Να κατασκευαστεί μία βάση για τον πυρήνα και την εικόνα της
παραπάνω γραμμικής απεικόνισης.
Να θεωρήσετε την γραμμική απεικόνιση από τον
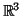 στον
στον
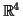 που ορίζεται από τον ανάστροφο πίνακα και να
υπολογίσετε μια βάση για τον πυρήνα και την εικόνα αυτής.
που ορίζεται από τον ανάστροφο πίνακα και να
υπολογίσετε μια βάση για τον πυρήνα και την εικόνα αυτής.
Καλή επιτυχία
Kontogiwrghs Aristeidhs
2001-11-18
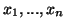 διανύσματα εντός του
διανύσματα εντός του 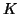 -διανυσματικού χώρου
-διανυσματικού χώρου 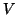 .
Δείξτε ότι τα
.
Δείξτε ότι τα
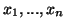 είναι γραμμικά εξαρτημένα αν και μόνο
αν ένα από αυτά μπορεί να γραφτεί σαν γραμμικός συνδιασμός των
υπολοίπων.
είναι γραμμικά εξαρτημένα αν και μόνο
αν ένα από αυτά μπορεί να γραφτεί σαν γραμμικός συνδιασμός των
υπολοίπων.
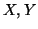 διανυσματικοί χώροι και
διανυσματικοί χώροι και
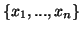 βάση του
βάση του 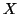 .
Θεωρούμε την γραμμική συνάρτηση
.
Θεωρούμε την γραμμική συνάρτηση
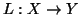 .
Ορίζουμε τα
.
Ορίζουμε τα
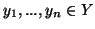 σαν
σαν
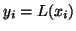 .
Δείξτε ότι αν η
.
Δείξτε ότι αν η 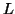 είναι 1-1 τότε τα
είναι 1-1 τότε τα
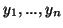 είναι γραμμικά
ανεξάρτητα. Εξηγήστε τι μπορεί να συμβεί αν η
είναι γραμμικά
ανεξάρτητα. Εξηγήστε τι μπορεί να συμβεί αν η 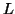 δεν είναι 1-1,
δίνοντας κατάληλο παράδειγμα.
δεν είναι 1-1,
δίνοντας κατάληλο παράδειγμα.