


Next: About this document ...
Ασκήσεις Γραμμικής Άλγεβρας, Φυλ. 9
Παράδοση 3/12/01
- Καθορίστε όλα τα εσωτερικά γινόμενα επί ενός
πραγματικού διανυσματικού χώρου διάστασης 2.
- Αποδείξτε ότι επί ενός πραγματικού διανυσματικού
χώρου
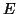 διαστάσεως 1 η γωνία δεν εξαρτάται από το εσωτερικό
γινόμενο.
διαστάσεως 1 η γωνία δεν εξαρτάται από το εσωτερικό
γινόμενο.
- Έστω
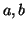 με
με 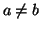 δύο δεδομένα διανύσματα ενός διανυσματικού
χώρου
δύο δεδομένα διανύσματα ενός διανυσματικού
χώρου 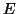 επί του
επί του
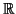 , ο οποίος είναι εφοδιασμένος με ένα εσωτερικό
γινόμενο.
Αποδείξτε ότι κάθε
, ο οποίος είναι εφοδιασμένος με ένα εσωτερικό
γινόμενο.
Αποδείξτε ότι κάθε 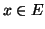 τέτοιο ώστε
τέτοιο ώστε
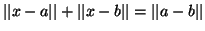 γράφεται
γράφεται
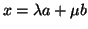 με
με
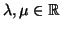 και
και
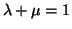 .
.
- Θεωρούμε επί του διανυσματικού χώρου
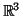 εφοδιασμένου με την
κανονική βάση, το κανονικό εσωτερικό γινόμενο
εφοδιασμένου με την
κανονική βάση, το κανονικό εσωτερικό γινόμενο
- Επαληθεύστε ότι τα δανύσματα
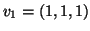 ,
,
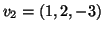 ,
,
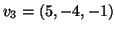 είναι ανά δύο ορθογώνια. Συμπεράνετε μια
ορθοκανονική βάση του
είναι ανά δύο ορθογώνια. Συμπεράνετε μια
ορθοκανονική βάση του
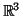 .
.
- Καθορίστε τα μοναδιαία διανύσματα (δηλαδή αυτά με μήκος 1)
τα οποία είναι ταυτόχρονα ορθογώνια με τα δύο διανύσματα
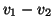 και
και 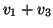 .
.
- Καθορίστε τα διανύσματα τα οποία είναι ορθογώνια με
το
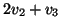 και ταυτόχρονα ανήκουν σε ένα διανυσματικό υπόχωρο
που γεννάται από τα
και ταυτόχρονα ανήκουν σε ένα διανυσματικό υπόχωρο
που γεννάται από τα 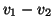 και
και 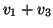 .
.
- Έστω ο διανυσματικός χώρος των πολυωνύμων
Αποδείξτε ότι η απεικόνιση
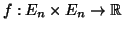 ορισμένη ως εξής:
είναι ένα εσωτερικό γινόμενο.
ορισμένη ως εξής:
είναι ένα εσωτερικό γινόμενο.
- Ένας πίνακας
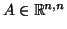 λέγεται ορθογώνιος αν
λέγεται ορθογώνιος αν
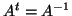 .
.
- Δείξτε ότι οι ορθογώνιοι πίνακες τάξεως
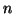 σχηματίζουν
μια ομάδα για τον πολλαπλασιασμό των πινάκων.
σχηματίζουν
μια ομάδα για τον πολλαπλασιασμό των πινάκων.
- Ο ανάστροφος ενός ορθογωνίου πίνακα είναι ορθογώνιος.
- Οι στήλες (και οι γραμμές)
ενός ορθογωνίου πίνακα σχηματίζουν μία ορθοκανονική βάση.
- O πίνακας περάσματος από μία ορθοκανονική βάση σε μία άλλη
ορθοκανονική βάση είναι ορθογώνιος.
Kontogiwrghs Aristeidhs
2001-11-26
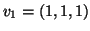 ,
,
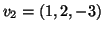 ,
,
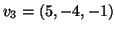 είναι ανά δύο ορθογώνια. Συμπεράνετε μια
ορθοκανονική βάση του
είναι ανά δύο ορθογώνια. Συμπεράνετε μια
ορθοκανονική βάση του
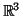 .
.
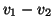 και
και 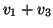 .
.
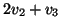 και ταυτόχρονα ανήκουν σε ένα διανυσματικό υπόχωρο
που γεννάται από τα
και ταυτόχρονα ανήκουν σε ένα διανυσματικό υπόχωρο
που γεννάται από τα 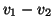 και
και 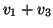 .
.
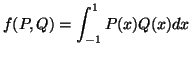
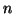 σχηματίζουν
μια ομάδα για τον πολλαπλασιασμό των πινάκων.
σχηματίζουν
μια ομάδα για τον πολλαπλασιασμό των πινάκων.