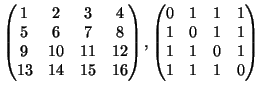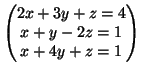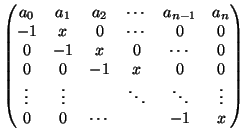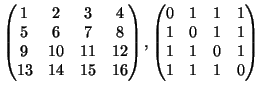Next: About this document ...
Ασκήσεις Γραμμικής Άλγεβρας, Φυλ. 8
Παράδοση 19/11/01
- Αποδείξτε ότι το σύστημα:
έχει ακριβώς μία λύση.
- Nα υπολογίσετε την ορίζουσα του πίνακα:
- Έστω
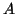 αντισυμμετρικός πίνακας
αντισυμμετρικός πίνακας 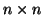 ,
δηλαδή
,
δηλαδή 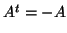 . Να δείξετε ότι αν ο
. Να δείξετε ότι αν ο 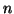 είναι
περιττός, τότε
είναι
περιττός, τότε 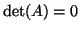 .
.
- Έστω
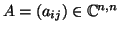 . Θέτουμε
. Θέτουμε
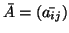 (μιγαδική συζηγία).
Δείξτε ότι
(μιγαδική συζηγία).
Δείξτε ότι
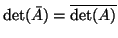 . Δείξτε ότι οι
πίνακες με
. Δείξτε ότι οι
πίνακες με
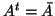 έχουν πραγματική ορίζουσα.
έχουν πραγματική ορίζουσα.
- Έστω
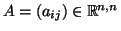 .
Για κάθε
.
Για κάθε
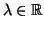 θεωρούμε την
συνάρτηση
θεωρούμε την
συνάρτηση
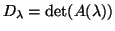 , όπου
, όπου
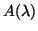 είναι ο πίνακας
είναι ο πίνακας
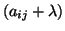 .
.
- Δείξτε ότι η απεικόνιση
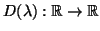 ,
είναι πολυονυμική συνάρτηση βαθμού 1 ή 0.
,
είναι πολυονυμική συνάρτηση βαθμού 1 ή 0.
- Υποθέτουμε ότι τα
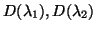 είναι
γνωστά για δύο τιμές
είναι
γνωστά για δύο τιμές
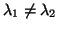 . Υπολογίστε
το
. Υπολογίστε
το
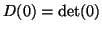 .
.
- Έστω
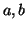 δύο διαφορετικά στοιχεία του
δύο διαφορετικά στοιχεία του
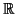 .
Υπολογίστε την ορίζουσα του πίνακα
.
Υπολογίστε την ορίζουσα του πίνακα
- Να υπολογίστουν οι ορίζουσες των πινάκων
Kontogiwrghs Aristeidhs
2001-11-19
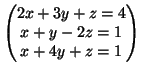
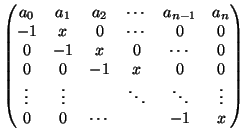
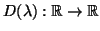 ,
είναι πολυονυμική συνάρτηση βαθμού 1 ή 0.
,
είναι πολυονυμική συνάρτηση βαθμού 1 ή 0.
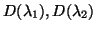 είναι
γνωστά για δύο τιμές
είναι
γνωστά για δύο τιμές
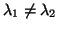 . Υπολογίστε
το
. Υπολογίστε
το
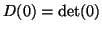 .
.
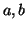 δύο διαφορετικά στοιχεία του
δύο διαφορετικά στοιχεία του
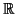 .
Υπολογίστε την ορίζουσα του πίνακα
.
Υπολογίστε την ορίζουσα του πίνακα