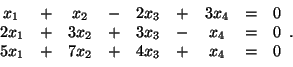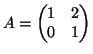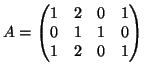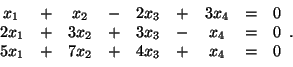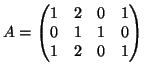Next: About this document ...
Ασκήσεις Γραμμικής Άλγεβρας, Φυλ. 7
Δοκιμαστική Πρόοδος
- Έστω
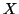 ένας διανυσματικός χώρος και
ένας διανυσματικός χώρος και 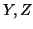 υπόχωροι του
υπόχωροι του 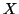 με
με
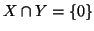 . Να δείξετε ότι ισχύει
. Να δείξετε ότι ισχύει
- Να βρεθούν οι λύσεις του παρακάτω συστήματος
- Να υπολογιστούν οι δυνάμεις
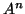 για τον πίνακα
για τον πίνακα
- Έστω
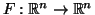 αντιστρέψιμη γραμμική
απεικόνιση. Δείξτε ότι αν
αντιστρέψιμη γραμμική
απεικόνιση. Δείξτε ότι αν 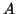 είναι ο πίνακας που αντιστοιχεί
στην
είναι ο πίνακας που αντιστοιχεί
στην 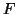 τότε ο
τότε ο 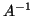 είναι ο πίνακας που αντιστοιχεί στην
αντίστροφη της
είναι ο πίνακας που αντιστοιχεί στην
αντίστροφη της 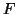 .
.
- Ένας πίνακας
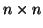 θα λέγεται αντισυμμετρικός αν
θα λέγεται αντισυμμετρικός αν 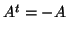 .
Δείξτε ότι οι αντισυμμετρικοί πίνακες έχουν μηδενικά στην διαγώνιο.
Δείξτε ότι οι αντισυμμετρικοί πίνακες αποτελούν διανυσματικό χώρο,
γράψτε μια βάση και υπολογίστε την διάσταση του χώρου
των αντισυμμετρικών πινάκων.
.
Δείξτε ότι οι αντισυμμετρικοί πίνακες έχουν μηδενικά στην διαγώνιο.
Δείξτε ότι οι αντισυμμετρικοί πίνακες αποτελούν διανυσματικό χώρο,
γράψτε μια βάση και υπολογίστε την διάσταση του χώρου
των αντισυμμετρικών πινάκων.
- Θεωρήστε τον σύνολο
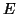 των πολυωνύμων βαθμού μικρότερου ή ίσου με 4 με
πραγματικούς συντελεστές. Δείξτε ότι το παραπάνω σύνολο αποτελεί
διανυσματικό χώρο και γράψτε μία βάση. Θεωρήστε την συνάρτηση
των πολυωνύμων βαθμού μικρότερου ή ίσου με 4 με
πραγματικούς συντελεστές. Δείξτε ότι το παραπάνω σύνολο αποτελεί
διανυσματικό χώρο και γράψτε μία βάση. Θεωρήστε την συνάρτηση
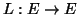 η οποία στέλνει το πολυώνυμο
η οποία στέλνει το πολυώνυμο 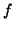 στο
πολυώνυμο
στο
πολυώνυμο
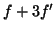 , όπου με
, όπου με 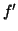 συμβολίζουμε την
παράγωγο του
συμβολίζουμε την
παράγωγο του 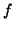 . Δείξτε ότι η
. Δείξτε ότι η 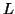 είναι γραμμική
και υπολογίστε τον πίνακα της ως προς την βάση που γράψατε παραπάνω.
είναι γραμμική
και υπολογίστε τον πίνακα της ως προς την βάση που γράψατε παραπάνω.
- Δίνεται ο πίνακας
ο οποίος ορίζει γραμμική απεικόνιση από το
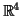 στο
στο
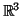 .
Να κατασκευαστεί μία βάση για τον πυρήνα και την εικόνα της
παραπάνω γραμμικής απεικόνισης.
.
Να κατασκευαστεί μία βάση για τον πυρήνα και την εικόνα της
παραπάνω γραμμικής απεικόνισης.
Αποδείξεις που πρέπει να γνωρίζετε
2.2.4, 2.2.6, 2.3.1,
3.1.2, 3.1.3, 3.2.2 (σελ. 33), 3.3.2 (σελ. 34)
Kontogiwrghs Aristeidhs
2001-11-12