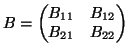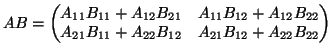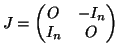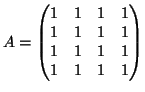Next: About this document ...
Ασκήσεις Γραμμικής Άλγεβρας, Φυλ. 6
Παράδoση: 12/11/2001
- Έστω
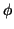 η απεικόνιση από τον
η απεικόνιση από τον
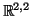 στον
στον
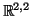 η οποία στον
πίνακα
η οποία στον
πίνακα
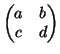 αντιστοιχεί τον πίνακα
αντιστοιχεί τον πίνακα
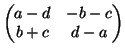 .
Δείξτε ότι είναι γραμμική απεικόνιση.
Γράψτε μία βάση του
.
Δείξτε ότι είναι γραμμική απεικόνιση.
Γράψτε μία βάση του
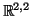 και υπολογίστε τον πίνακα
της παραπάνω συνάρτησης ως προς αυτή την βάση.
Βρείτε βάσεις του
και υπολογίστε τον πίνακα
της παραπάνω συνάρτησης ως προς αυτή την βάση.
Βρείτε βάσεις του
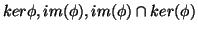 .
.
- Αποδείξτε ότι το σύνολο
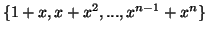 είναι μία βάση του
διανυσματικού χώρου
είναι μία βάση του
διανυσματικού χώρου 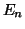 των πολυωνύμων με πραγματικούς συντελεστές
με βαθμό μικρότερο του
των πολυωνύμων με πραγματικούς συντελεστές
με βαθμό μικρότερο του 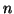 .
Έστω
.
Έστω 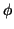 η γραμμική απεικόνιση από τον
η γραμμική απεικόνιση από τον 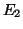 στον
στον 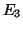 που καθορίζεται από την σχέση
Καθoρίστε τον πίνακα της
που καθορίζεται από την σχέση
Καθoρίστε τον πίνακα της 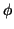 ως προς τις βάσεις
ως προς τις βάσεις
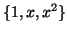 και
και
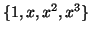 και τον πίνακα
ως προς τις βάσεις
και τον πίνακα
ως προς τις βάσεις
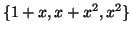 και
και
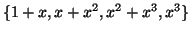 .
.
- Θεωρούμε δυο πίνακες
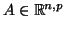 και
και
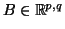 τους
οποίους γράφουμε στην μορφή
τους
οποίους γράφουμε στην μορφή
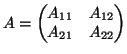
και
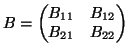
όπου
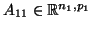 ,
,
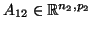 ,
,
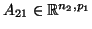 ,
,
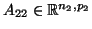 με
με 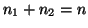 και
και 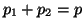 και
και
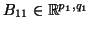 ,
,
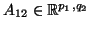 ,
,
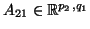 ,
,
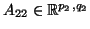 με
με 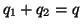 .
Aποδείξτε ότι
Παράδειγμα: Aν ο
.
Aποδείξτε ότι
Παράδειγμα: Aν ο 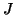 είναι ο τετραγωνικός πίνακας
είναι ο τετραγωνικός πίνακας
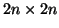 όπου τα
όπου τα 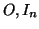 είναι οι τετραγωνικοί πίνακες
είναι οι τετραγωνικοί πίνακες 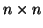 ,
υπολογίστε τον
,
υπολογίστε τον 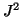 .
.
- Θεωρούμε τον πίνακα
Δείξτε ότι ο πίνακας
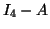 , όπου ο
, όπου ο 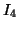 είναι ο ταυτοτικός
είναι ο ταυτοτικός 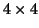 πίνακας, δέχεται αντίστροφο πίνακα της μορφής
πίνακας, δέχεται αντίστροφο πίνακα της μορφής 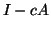 .
.
- Έστω
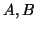 πίνακες
πίνακες 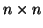 .
Δείξτε ότι αν
.
Δείξτε ότι αν 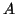 αντιστρέψιμος και
αντιστρέψιμος και 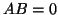 τότε
τότε
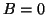 και αν
και αν 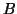 αντιστρέψιμος και
αντιστρέψιμος και 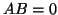 τότε
τότε 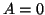 .
Εξ αυτού συμπεράνετε ότι αν
.
Εξ αυτού συμπεράνετε ότι αν 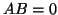 ή
ή 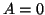 ή
ή 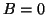 ή
ή 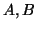 μη αντιστρέψιμοι.
Έστω
μη αντιστρέψιμοι.
Έστω 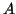 τέτοιος ώστε
τέτοιος ώστε 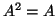 . Δείξτε ότι αν ο
. Δείξτε ότι αν ο 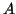 είναι
αντιστρέψιμος τότε ο
είναι
αντιστρέψιμος τότε ο 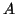 είναι ο ταυτοτικός.
είναι ο ταυτοτικός.
- Ένας πίνακας θα λέγεται συμμετρικός αν
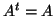 .
Δείξτε ότι οι συμετρικοί
.
Δείξτε ότι οι συμετρικοί 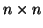 αποτελούν υπόχωρο του
συνόλου των
αποτελούν υπόχωρο του
συνόλου των 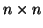 πινάκων.
Βρείτε μία βάση του χωρου των συμμετρικών πινάκων και υπολογίστε
την διάσταση του.
πινάκων.
Βρείτε μία βάση του χωρου των συμμετρικών πινάκων και υπολογίστε
την διάσταση του.
Kontogiwrghs Aristeidhs
2001-11-05
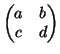 αντιστοιχεί τον πίνακα
αντιστοιχεί τον πίνακα
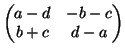 .
Δείξτε ότι είναι γραμμική απεικόνιση.
Γράψτε μία βάση του
.
Δείξτε ότι είναι γραμμική απεικόνιση.
Γράψτε μία βάση του
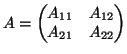 και
και 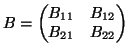
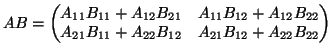
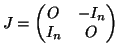
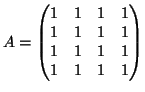
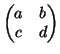 αντιστοιχεί τον πίνακα
αντιστοιχεί τον πίνακα
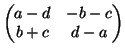 .
Δείξτε ότι είναι γραμμική απεικόνιση.
Γράψτε μία βάση του
.
Δείξτε ότι είναι γραμμική απεικόνιση.
Γράψτε μία βάση του
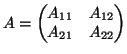 και
και