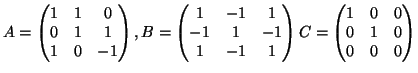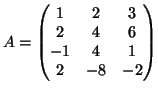Next: About this document ...
Ασκήσεις Γραμμικής Άλγεβρας, Φυλ. 5
Παράδoση: 5/11/2001
- Θεωρούμε τους διαν. χώρους
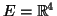 και
και
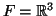 και την
συνάρτηση
και την
συνάρτηση
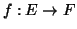 η οποία στέλνει το
η οποία στέλνει το
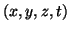 του
του 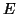 στο
στο
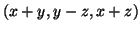 του
του 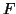 .
Να δειχτεί ότι είναι γραμμική. Δώστε μια βάση του
πυρήνα και της εικόνας. Ποιά είναι η τάξη της συνάρτησης?
.
Να δειχτεί ότι είναι γραμμική. Δώστε μια βάση του
πυρήνα και της εικόνας. Ποιά είναι η τάξη της συνάρτησης?
- Έστω
![$ E=\mathbb{R}[x]$](img8.gif) ο χώρος των πολυωνύμων με πραγματικούς
συντελεστές και η απεικόνιση
ο χώρος των πολυωνύμων με πραγματικούς
συντελεστές και η απεικόνιση
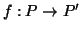 του
του
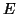 στο
στο 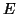 . Να δειχτεί ότι η
. Να δειχτεί ότι η 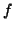 είναι γραμμική και
να υπολογίσετε τον πυρήνα και την εικόνα της.
είναι γραμμική και
να υπολογίσετε τον πυρήνα και την εικόνα της.
- Θεωρούμε το ευθή άθροισμα
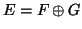 δύο διανυσματικών χώρων και
δύο διανυσματικών χώρων και
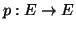 την συνάρτηση που ορίζεται στο τυχαίο
την συνάρτηση που ορίζεται στο τυχαίο 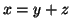 ,
,
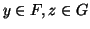 ως
ως 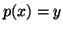 (προβολή στον πρώτο χώρο).
Αποδείξτε ότι η
(προβολή στον πρώτο χώρο).
Αποδείξτε ότι η 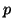 είναι γραμμική συνάρτηση τέτοια ώστε
είναι γραμμική συνάρτηση τέτοια ώστε
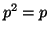 . Καθορίστε τους
. Καθορίστε τους 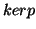 και
και 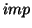 .
Θεωρήστε βάσεις
.
Θεωρήστε βάσεις
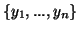 του
του 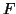 και
και
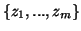 .
Γράψτε μια βάση του
.
Γράψτε μια βάση του 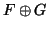 και εκφράστε την
και εκφράστε την 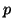 ως προς την
βάση αυτή.
ως προς την
βάση αυτή.
- Θεωρήστε
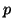 μία γραμμική συνάρτηση
μία γραμμική συνάρτηση
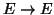 , τέτοια ώστε
, τέτοια ώστε
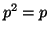 . Nα δείξεται ότι ο πυρήνας και η εικόνα της
. Nα δείξεται ότι ο πυρήνας και η εικόνα της 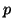 είναι
συμπληρωματικοί υπόχωροι του
είναι
συμπληρωματικοί υπόχωροι του 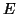 .
.
- Επαληθεύστε ότι το σύνολο των
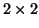 πινάκων με συντελεστές από το
πινάκων με συντελεστές από το
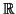 της μορφής
της μορφής
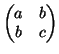 είναι υπόχωρος του διαν. χώρου των
είναι υπόχωρος του διαν. χώρου των 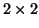 πινάκων.
Βρείτε μία βάση του.
πινάκων.
Βρείτε μία βάση του.
- Θεωρήστε τους
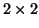 πίνακες
Να υπολογιστούν οι πίνακες
πίνακες
Να υπολογιστούν οι πίνακες
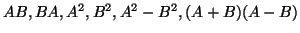 .
.
- Θεωρούμε τους πίνακες
Υπολογίστε τους
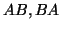 . Nα βρεθεί μη μηδενικός πίνακας
. Nα βρεθεί μη μηδενικός πίνακας 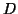 τέτοιος ώστε
τέτοιος ώστε 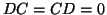 .
.
- Έστω
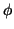 η γραμμική απεικόνιση από τον
η γραμμική απεικόνιση από τον
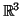 στον
στον
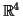 ορισμένη από τον πίνακα
όταν στον
ορισμένη από τον πίνακα
όταν στον
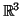 και στον
και στον
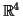 θεωρήσουμε τις κανονικές βάσεις.
Βρέστε βάσεις του πυρήνα και της εικόνας.
Θεωρήστε τον ανάστροφο του πίνακα
θεωρήσουμε τις κανονικές βάσεις.
Βρέστε βάσεις του πυρήνα και της εικόνας.
Θεωρήστε τον ανάστροφο του πίνακα 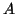 . Αυτός ορίζει γραμμική
απεικόνιση
. Αυτός ορίζει γραμμική
απεικόνιση
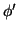 από τον
από τον
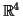 στον
στον
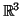 . Βρέστε βάση του πυρήνα και της εικόνας της
. Βρέστε βάση του πυρήνα και της εικόνας της
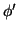 .
.
Kontogiwrghs Aristeidhs
2001-10-29
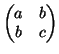 είναι υπόχωρος του διαν. χώρου των
είναι υπόχωρος του διαν. χώρου των 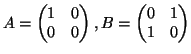
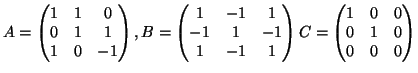
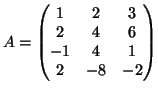
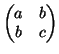 είναι υπόχωρος του διαν. χώρου των
είναι υπόχωρος του διαν. χώρου των