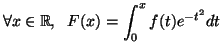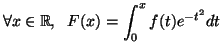Next: About this document ...
Ασκήσεις Γραμμικής Άλγεβρας, Φυλ. 4
Παράδoση: 29/10/2001
- Έστω
![$ E_n=\{P\in \mathbb{C}[x]: P=0$](img1.gif) ή
ή 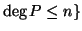 .
Έστω
.
Έστω 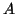 στοιχείο βαθμού
στοιχείο βαθμού 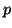 του
του
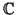 -διανυσματικού χώρου
-διανυσματικού χώρου
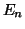 . Θεωρούμε το σύνολο
. Θεωρούμε το σύνολο 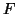 των
στοιχείων του
των
στοιχείων του 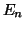 που διαιρούνται με το
που διαιρούνται με το 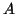 και
και
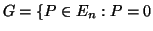 ή
ή 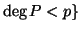 .
Να δείξετε ότι οι
.
Να δείξετε ότι οι 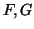 είναι συμπληρωματικοί
υπόχωροι του
είναι συμπληρωματικοί
υπόχωροι του 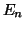 . Ποιές είναι οι διαστάσεις αυτών
των υποχώρων?
. Ποιές είναι οι διαστάσεις αυτών
των υποχώρων?
- Μέσα στον χώρο
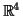 θεωρούμε τα διανύσματα
θεωρούμε τα διανύσματα
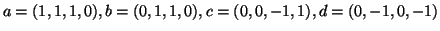 .
Είναι τα
.
Είναι τα 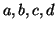 γραμ. ανεξάρτητα? Από αυτά
βρέστε το μέγιστο σύνολο γραμμικά ανεξαρτήτων διανυσμάτων
και συμπληρώστε το σε μία βάση του
γραμ. ανεξάρτητα? Από αυτά
βρέστε το μέγιστο σύνολο γραμμικά ανεξαρτήτων διανυσμάτων
και συμπληρώστε το σε μία βάση του
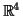 , χρησιμοποιόντας
τα διανύσματα της κανονικής βάσης
, χρησιμοποιόντας
τα διανύσματα της κανονικής βάσης
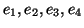 .
.
- Θεωρούμε τον διανυσματικό χώρο
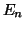 της πρώτης
άσκησης. Δείξτε ότι αν
της πρώτης
άσκησης. Δείξτε ότι αν 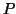 πολυώνυμο βαθμού
πολυώνυμο βαθμού 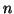 ,
τότε οι πρώτες
,
τότε οι πρώτες 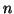 παράγωγοι
παράγωγοι
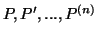 είναι βάση του
είναι βάση του
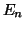 .
Αν
.
Αν
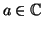 , να υπολογίσετε την γραφή του πολυωνύμου
, να υπολογίσετε την γραφή του πολυωνύμου
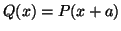 ως προς την παραπάνω βάση.
ως προς την παραπάνω βάση.
- Ονομάζουμε πολυώνυμα του Tchebychev τα πολυώνυμα
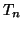 ,
,
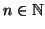 τέτοια ώστε
Αποδείξτε την επαγωγική σχέση
Συμπεράνετε ότι τα
τέτοια ώστε
Αποδείξτε την επαγωγική σχέση
Συμπεράνετε ότι τα 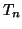 είναι πολυώνυμα βαθμού
είναι πολυώνυμα βαθμού 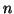 .
Να δείξετετε ότι το σύνολο
.
Να δείξετετε ότι το σύνολο
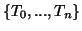 είναι μία βάση
του διανυσματικού χώρου των πολυωνύμων
είναι μία βάση
του διανυσματικού χώρου των πολυωνύμων
![$ \mathbb{R}[x]$](img28.gif) με βαθμό
το πολύ
με βαθμό
το πολύ 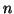 .
.
- Εξετάστε ποιές από τις παρακάτω συναρτήσεις από τον
διανυσματικό χώρο
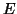 στον διανυσματικό χώρο
στον διανυσματικό χώρο 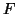 είναι
γραμμικές και στην συνέχεια υπολογίσετε για αυτές τον πυρήνα και
την εικόνα τους.
είναι
γραμμικές και στην συνέχεια υπολογίσετε για αυτές τον πυρήνα και
την εικόνα τους.
-
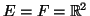 .
.
- Έστω
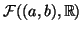 o χώρος των πραγματικών συναρτήσεων
από το
o χώρος των πραγματικών συναρτήσεων
από το 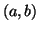 στο
στο
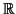 .
.
- Θεωρούμε τον χώρο των συνεχών συναρτήσεων επί του
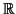 .
Σημειώνουμε με
.
Σημειώνουμε με 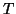 την απεικόνιση η οποία σε κάθε συνάρτηση
την απεικόνιση η οποία σε κάθε συνάρτηση
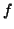 του
του 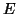 στέλνει την συνάρτηση
στέλνει την συνάρτηση 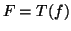 , ορισμένη από την σχέση
Να δείξετε ότι η
, ορισμένη από την σχέση
Να δείξετε ότι η 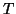 είναι γραμμική συνάρτηση. Είναι 1-1?
Είναι επί?
είναι γραμμική συνάρτηση. Είναι 1-1?
Είναι επί?
- Έστω
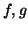 γραμμικές συναρτήσεις
γραμμικές συναρτήσεις
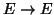 τέτοιες ώστε
τέτοιες ώστε
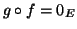 ,
, 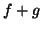 είναι 1-1 και επί.
Να δείξετε ότι
είναι 1-1 και επί.
Να δείξετε ότι
- Έστω
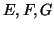 τρείς διανυσματικοί χώροι και
τρείς διανυσματικοί χώροι και
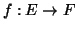 ,
,
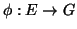 , με
, με
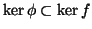 .
Να δείξετε ότι υπάρχει γραμμική συνάρτηση
.
Να δείξετε ότι υπάρχει γραμμική συνάρτηση
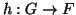 , τέτοια ώστε
, τέτοια ώστε
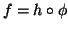 .
.
Kontogiwrghs Aristeidhs
2001-10-23
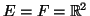 .
.
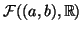 o χώρος των πραγματικών συναρτήσεων
από το
o χώρος των πραγματικών συναρτήσεων
από το 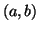 στο
στο
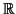 .
.
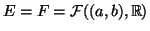 ,
,
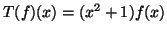 .
.
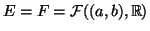 ,
, 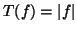 .
.