


Next: About this document ...
Ασκήσεις Γραμμικής Άλγεβρας, Φυλ. 3
Παράδoση: 22/10/2001
- Να δείξετε ότι τα διανύσματα,
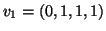 ,
,
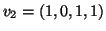 ,
,
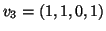 ,
,
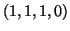 , σχηματίζουν μία βάση του
, σχηματίζουν μία βάση του
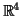 . Να εκφραστούν τα διανύσματα
. Να εκφραστούν τα διανύσματα
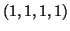 και
και 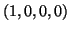 σαν γραμμικοί συνδιασμοί της βάσης
σαν γραμμικοί συνδιασμοί της βάσης
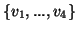 .
.
- Δείξτε ότι το σώμα
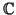 θεωρούμενο ως διανυσματικός χώρος επί του
θεωρούμενο ως διανυσματικός χώρος επί του
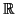 , είναι διάστασης 2. Πως πρέπει να εκλέξουμε το
, είναι διάστασης 2. Πως πρέπει να εκλέξουμε το 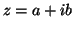 , ώστε
τα
, ώστε
τα 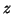 και
και 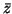 να σχηματίζουν βάση του
να σχηματίζουν βάση του
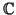 ?
Υπολογίστε τις συντεταγμένες του μιγαδικού αριθμού
?
Υπολογίστε τις συντεταγμένες του μιγαδικού αριθμού 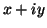 ως προς
την βάση
ως προς
την βάση
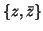
- Έστω
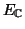 διανυσματικός χώρος επί του
διανυσματικός χώρος επί του
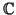 . Να δείξετε ότι μπορούμε να
εφοδιάσουμε τον
. Να δείξετε ότι μπορούμε να
εφοδιάσουμε τον
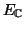 με την δομή διανυσματικού χώρου
με την δομή διανυσματικού χώρου
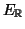 υπέρ το
υπέρ το
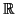 .
Αν ο
.
Αν ο
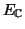 είναι πεπερασμένης διάστασης, να δείξετε ότι και ο
είναι πεπερασμένης διάστασης, να δείξετε ότι και ο
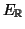 είναι
πεπερασμένης διάστασης και μάλιστα ισχύει:
είναι
πεπερασμένης διάστασης και μάλιστα ισχύει:
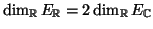 .
.
- Έστω
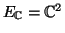 . Να ορίσετε τον
. Να ορίσετε τον
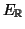 . Να δείξετε ότι ο
. Να δείξετε ότι ο
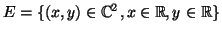 , είναι υπόχωρος του
, είναι υπόχωρος του
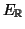 αλλά όχι του
αλλά όχι του
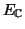 .
.
- Σε ένα δ.χ.
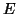 διάστασης 4 επί του σώματος
διάστασης 4 επί του σώματος
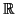 , αναφερόμενοι στην
βάση
, αναφερόμενοι στην
βάση
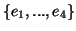 , θεωρούμε τα διανύσματα:
Να καθορίσετε τους πραγματικούς αριθμούς
, θεωρούμε τα διανύσματα:
Να καθορίσετε τους πραγματικούς αριθμούς 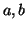 , έτσι ώστε τα
, έτσι ώστε τα
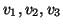 να είναι γραμμικά ανεξάρτητα. Ποια σχέση υπάρχει τότε
μεταξύ των
να είναι γραμμικά ανεξάρτητα. Ποια σχέση υπάρχει τότε
μεταξύ των
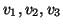 .
Ποιά είναι η διάσταση του υπόχωρου
.
Ποιά είναι η διάσταση του υπόχωρου 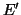 που παράγεται από τα
που παράγεται από τα
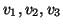 ? Δώστε μια βάση.
? Δώστε μια βάση.
- Έστω
![$ E=\{f:[0,1] \rightarrow \mathbb{R}, f$](img30.gif) συνεχής
συνεχής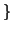 , o διανυσματικός
χώρος των συνεχών συναρτήσεων στο
, o διανυσματικός
χώρος των συνεχών συναρτήσεων στο ![$ [0,1]$](img32.gif) . Έστω
. Έστω 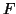 το σύνολο των
συναρτήσεων που είναι σταθερές στο
το σύνολο των
συναρτήσεων που είναι σταθερές στο ![$ [0,1]$](img32.gif) , και έστω
, και έστω
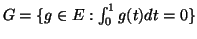 . Να δείξετε ότι
. Να δείξετε ότι
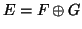 .
.
- Έστω
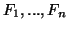 υπόχωροι του δ.χ.
υπόχωροι του δ.χ. 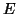 .
Να οριστούν
.
Να οριστούν
- Το
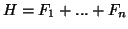
- Το ευθή άθροισμα
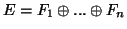 .
.
Nα αποδείξετε την ισοδυναμία των παρακάτω προτάσεων
Αποδείξτε ότι
Αποδείξτε ότι το αντίστροφο δεν είναι σωστό.
- Έστω
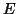 ένας
ένας 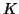 -διανυσματικός χώρος διαστάσεως
-διανυσματικός χώρος διαστάσεως 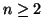 . Έστω
. Έστω
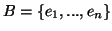 μία βάση του
μία βάση του 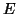 . Τα σύνολα
. Τα σύνολα
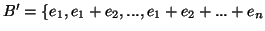 και
και
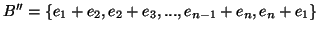 είναι
βάσεις του
είναι
βάσεις του 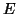 ? Το σύνολο
? Το σύνολο
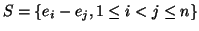 ,
παράγει το
,
παράγει το 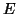 ?
?
Kontogiwrghs Aristeidhs
2001-10-15
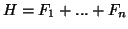
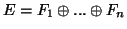 .
.
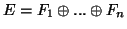
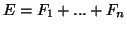 και για κάθε
και για κάθε
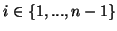 ,
,
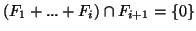 .
.