


Next: About this document ...
Ασκήσεις Γραμμικής Άλγεβρας, Φυλ. 2
Παράδoση: 12/10/2001
- Εστω
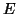 δ.χ. επί του σώματος
δ.χ. επί του σώματος 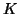 και
και 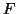 μη κενό υποσύνολο του
μη κενό υποσύνολο του 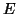 .
Αποδείξτε ότι το
.
Αποδείξτε ότι το 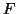 είναι υπόχωρος του
είναι υπόχωρος του 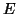 τότε και μόνο τότε αν
τότε και μόνο τότε αν
- Αποδείξτε ότι η τομή δυο διανυσματικών υποχώρων
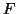 ,
, 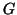 του διανυσματικού
χώρου
του διανυσματικού
χώρου 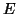 είναι διανυσματικός υπόχωρος του
είναι διανυσματικός υπόχωρος του 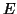 . Έστω
. Έστω
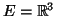 ,
,
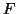 παράγεται από τα
παράγεται από τα 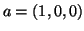 και
και 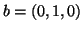 ενώ
ενώ 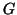 παράγεται από τα
παράγεται από τα
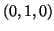 και
και 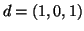 . Βρέστε τον
. Βρέστε τον 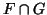 .
.
Αποδείξτε ότι 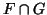 είναι διανυσματικός υπόχωρος του
είναι διανυσματικός υπόχωρος του 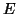 αν και μόνο
αν
αν και μόνο
αν
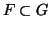 ή
ή
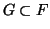 . Είναι δυνατόν η ένωση δύο γνήσιων υπόχωρων
του
. Είναι δυνατόν η ένωση δύο γνήσιων υπόχωρων
του 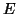 να ταυτίζεται με τον
να ταυτίζεται με τον 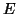 ?
?
- Έστω
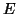 ένας διανυσματικός χώρος,
ένας διανυσματικός χώρος, 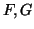 υπόχωροι του
υπόχωροι του 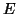 . Σημειώνουμε με
. Σημειώνουμε με
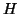 το σύνολο
το σύνολο
- Αποδείξτε ότι ο
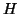 είναι υπόχωρος του
είναι υπόχωρος του 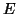 τον οποίο θα συμβολίζουμε με
τον οποίο θα συμβολίζουμε με
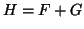 .
.
- Αποδείξτε ότι
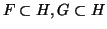 και ότι αν
και ότι αν 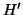 είναι υπόχωρος
τέτοιος ώστε
είναι υπόχωρος
τέτοιος ώστε
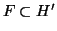 και
και
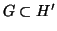 , τότε
, τότε
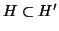 .
.
- Αποδείξτε ότι
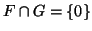 αν και μόνο αν κάθε
αν και μόνο αν κάθε 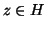 γράφεται
κατά μοναδικό τρόπο ως
γράφεται
κατά μοναδικό τρόπο ως 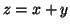 με
με
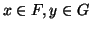 .
.
- Επαληθεύσετε ότι το σώμα
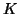 είναι ένας διανυσματικός χώρος επί του
ευατού του, το οποίο θα σημειώνουμε με
είναι ένας διανυσματικός χώρος επί του
ευατού του, το οποίο θα σημειώνουμε με 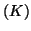 .
.
Δείξτε ότι οι μοναδικοί διανυσματικοί υπόχωροι του 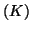 , είναι το
, είναι το 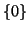 και το
και το 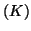 .
.
Έστω 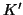 γνήσιο υπόσωμα του
γνήσιο υπόσωμα του 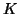
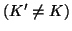 . Είναι το
. Είναι το
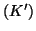 διανυσματικός υπόχωρος του
διανυσματικός υπόχωρος του 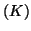 ? Δείξτε ότι το
? Δείξτε ότι το
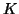 είναι ένας διανυσματικός χώρος επί του
είναι ένας διανυσματικός χώρος επί του 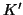 .
Εφαρμόστε το στο
.
Εφαρμόστε το στο
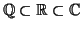 .
.
- Στον
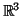 , αποδείξτε ότι τα διανύσματα
, αποδείξτε ότι τα διανύσματα
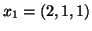 ,
,
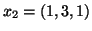 και
και
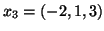 είναι γραμμικώς ανεξάρτητα
είναι γραμμικώς ανεξάρτητα
- Στον
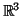 , αποδείξτε ότι τα διανύσματα
, αποδείξτε ότι τα διανύσματα
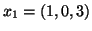 ,
,
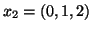 ,
,
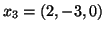 είναι γραμμικώς εξαρτημένα.
είναι γραμμικώς εξαρτημένα.
- Θεωρόντας το σώμα
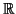 σαν διανυσματικό χώρο επί του σώματος
σαν διανυσματικό χώρο επί του σώματος
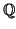 των
ρητών αριθμών αποδείξτε ότι οι αριθμοί
των
ρητών αριθμών αποδείξτε ότι οι αριθμοί
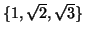 είναι ανά δύο γραμμικώς ανεξάρτητοι. Αποδείξτε ότι
οι
είναι ανά δύο γραμμικώς ανεξάρτητοι. Αποδείξτε ότι
οι
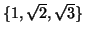 είναι γραμμικώς ανεξάρτητοι.
είναι γραμμικώς ανεξάρτητοι.
- Αποδείξτε ότι μέσα στον διανυσματικό χώρο
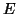 των συναρτήσεων
των συναρτήσεων
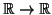 ,
τα στοιχεία
,
τα στοιχεία
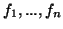 , όπου
, όπου
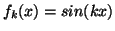 είναι γραμμικώς ανεξάρτητα.
είναι γραμμικώς ανεξάρτητα.
- Στον χώρο
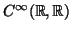 θέτουμε
θέτουμε
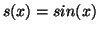 . Μελετήσατε την
ανεξαρτησία της οικογένειας
. Μελετήσατε την
ανεξαρτησία της οικογένειας
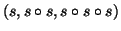 .
.
Να γραφτείτε στην δημόσια λίστα μυνημάτων στην διεύθηνση
http:\\poseidon.math.uoc.gr\mailman\listinfo\gral
Εκεί θα δοθούν υποδείξεις σχετικές με την λύση των ασκήσεων.
Kontogiwrghs Aristeidhs
2001-10-05
![]() είναι διανυσματικός υπόχωρος του
είναι διανυσματικός υπόχωρος του ![]() αν και μόνο
αν
αν και μόνο
αν
![]() ή
ή
![]() . Είναι δυνατόν η ένωση δύο γνήσιων υπόχωρων
του
. Είναι δυνατόν η ένωση δύο γνήσιων υπόχωρων
του ![]() να ταυτίζεται με τον
να ταυτίζεται με τον ![]() ?
?
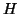 είναι υπόχωρος του
είναι υπόχωρος του 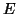 τον οποίο θα συμβολίζουμε με
τον οποίο θα συμβολίζουμε με
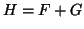 .
.
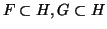 και ότι αν
και ότι αν 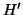 είναι υπόχωρος
τέτοιος ώστε
είναι υπόχωρος
τέτοιος ώστε
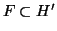 και
και
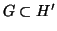 , τότε
, τότε
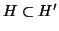 .
.
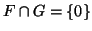 αν και μόνο αν κάθε
αν και μόνο αν κάθε 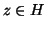 γράφεται
κατά μοναδικό τρόπο ως
γράφεται
κατά μοναδικό τρόπο ως 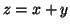 με
με
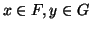 .
.
![]() , είναι το
, είναι το ![]() και το
και το ![]() .
.
![]() γνήσιο υπόσωμα του
γνήσιο υπόσωμα του ![]()
![]() . Είναι το
. Είναι το
![]() διανυσματικός υπόχωρος του
διανυσματικός υπόχωρος του ![]() ? Δείξτε ότι το
? Δείξτε ότι το
![]() είναι ένας διανυσματικός χώρος επί του
είναι ένας διανυσματικός χώρος επί του ![]() .
Εφαρμόστε το στο
.
Εφαρμόστε το στο
![]() .
.