Next: About this document ...
Ασκήσεις Γραμμικής Άλγεβρας, Φυλ. 11
Παράδοση 17/12/01
- Nα βρείτε το χαρακτηριστικό πολυώνυμο και τις ιδιοτιμές
του πίνακα:
- Βρείτε τις ιδιοτιμές και μια βάση για καθέναν από τους ιδιόχωρους του
πίνακα
- Έστω
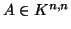 και
και 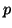 το χαρακτηριστικό πολυώνυμο του
το χαρακτηριστικό πολυώνυμο του 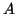 .
Αν
.
Αν
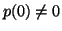 να υπολογίσετε το χαρακτηριστικό πολυώνυμο του
να υπολογίσετε το χαρακτηριστικό πολυώνυμο του
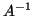 . Αποδείξτε ότι
. Αποδείξτε ότι 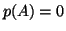 . Έστω
. Έστω
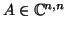 και
έστω ότι υπάρχει
και
έστω ότι υπάρχει 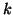 για τον οποίο
για τον οποίο 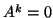 . Δείξτε ότι ένας
τέτοιος πίνακας δέχεται μόνο την μηδανική ιδιοτιμή. Δείξτε ότι
. Δείξτε ότι ένας
τέτοιος πίνακας δέχεται μόνο την μηδανική ιδιοτιμή. Δείξτε ότι
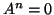 .
.
- O πίνακας
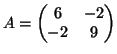 είναι διαγωνοποιήσημος?
Θεωρούμε δύο ακολουθίες
είναι διαγωνοποιήσημος?
Θεωρούμε δύο ακολουθίες 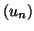 και
και 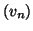 που ορίζονται
αναδρομικά ως εξής:
που ορίζονται
αναδρομικά ως εξής:
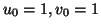
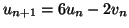 ,
,
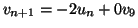 .
Υπολογίστε τα
.
Υπολογίστε τα 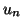 και
και 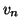 συναρτήσει του
συναρτήσει του 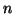 .
.
- Είναι (για
 σταθερό) ο πίνακας
σταθερό) ο πίνακας
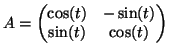 διαγωνοποιήσιμος στο
διαγωνοποιήσιμος στο
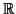 ?
Ποια είναι η γεωμετρική ερμηνεία της γραμμικής
απεικόνισης
?
Ποια είναι η γεωμετρική ερμηνεία της γραμμικής
απεικόνισης
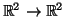 που ορίζεται
από αυτόν τον πίνακα?
Να γράψετε τον
που ορίζεται
από αυτόν τον πίνακα?
Να γράψετε τον 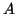 σε διαγώνια μορφή στο σώμα
σε διαγώνια μορφή στο σώμα
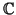 .
.
- (ΙΚΥ 1995)
Έστω
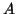 διαγωνοποιήσιμος πίνακας
διαγωνοποιήσιμος πίνακας 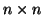 ,
, 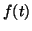 αναλυτική συνάρτηση, δηλαδή η
αναλυτική συνάρτηση, δηλαδή η 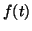 δέχεται ανάπτυγμα σε
δυναμοσειρά
Δείξτε ότι υπάρχει αντιστρέψιμος πίνακας
δέχεται ανάπτυγμα σε
δυναμοσειρά
Δείξτε ότι υπάρχει αντιστρέψιμος πίνακας
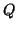 και διαγώνιος πίνακας
και διαγώνιος πίνακας
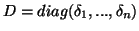 έτσι ώστε
έτσι ώστε
- Έστω
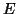 o διανυσματικός χώρος των πολυωνύμων βαθμού το πολύ
o διανυσματικός χώρος των πολυωνύμων βαθμού το πολύ 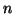 .
Θεωρήστε την γραμμική απεικόνιση
.
Θεωρήστε την γραμμική απεικόνιση 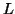 που ορίζει η παράγωγος.
Να βρεθούν οι ιδιοτιμές της και μία βάση για κάθε ιδιόχωρο.
Μπορεί να γραφεί η
που ορίζει η παράγωγος.
Να βρεθούν οι ιδιοτιμές της και μία βάση για κάθε ιδιόχωρο.
Μπορεί να γραφεί η 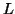 σε διαγώνια μορφή?
σε διαγώνια μορφή?
Kontogiwrghs Aristeidhs
2001-12-09
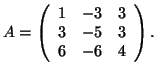

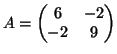 είναι διαγωνοποιήσημος?
Θεωρούμε δύο ακολουθίες
είναι διαγωνοποιήσημος?
Θεωρούμε δύο ακολουθίες 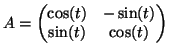 διαγωνοποιήσιμος στο
διαγωνοποιήσιμος στο
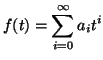
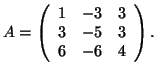

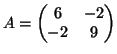 είναι διαγωνοποιήσημος?
Θεωρούμε δύο ακολουθίες
είναι διαγωνοποιήσημος?
Θεωρούμε δύο ακολουθίες 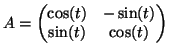 διαγωνοποιήσιμος στο
διαγωνοποιήσιμος στο