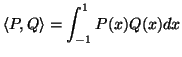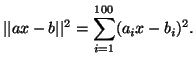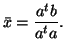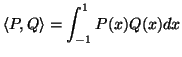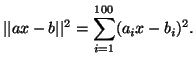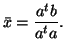Next: About this document ...
Ασκήσεις Γραμμικής Άλγεβρας, Φυλ. 10
Παράδοση 10/12/01
- Mέσα στον
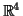 εφοδιασμένο με το κανονικό
εσωτερικό γινόμενο, θεωρούμε τον διανυσματικό υπόχωρο
εφοδιασμένο με το κανονικό
εσωτερικό γινόμενο, θεωρούμε τον διανυσματικό υπόχωρο
 που γεννάτε από τα
που γεννάτε από τα
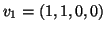 ,
,
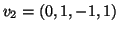 .
Kαθορίστε μία ορθοκανονική βάση του χώρου
.
Kαθορίστε μία ορθοκανονική βάση του χώρου
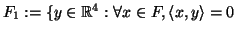 και συμπληρώστε την σε μία ορθοκανονική βάση του
και συμπληρώστε την σε μία ορθοκανονική βάση του
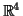 .
.
- Θεωρούμε τον χώρο
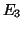 των πολυωνύμων βαθμού μικρότερου ή ίσου
του
των πολυωνύμων βαθμού μικρότερου ή ίσου
του 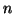 , μαζί με το εσωτερικό γινόμενο:
Μία βάση του
, μαζί με το εσωτερικό γινόμενο:
Μία βάση του 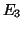 είναι τα
είναι τα
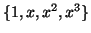 . Nα βρείτε μία
ορθοκανονική βάση του
. Nα βρείτε μία
ορθοκανονική βάση του 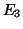 αποτελούμενη από τέσσερα πολυώνυμα
διαφόρων βαθμών και της οποίας το πρώτο στοιχείο να είναι το
σταθερό πολυώνυμο. Να υπολογίσετε το πολυώνυμο
αποτελούμενη από τέσσερα πολυώνυμα
διαφόρων βαθμών και της οποίας το πρώτο στοιχείο να είναι το
σταθερό πολυώνυμο. Να υπολογίσετε το πολυώνυμο
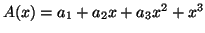 , έτσι ώστε το
ολοκλήρωμα
, έτσι ώστε το
ολοκλήρωμα
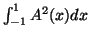 να είναι ελάχιστο.
να είναι ελάχιστο.
- Θεωρούμε τον διανυσματικού χώρο
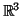 εφοδιασμένο με την
κανονική βάση και το κανονικό εσωτερικό γινόμενο.
Δείξτε ότι τα διανύσματα
εφοδιασμένο με την
κανονική βάση και το κανονικό εσωτερικό γινόμενο.
Δείξτε ότι τα διανύσματα
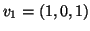 ,
,
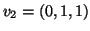 ,
,
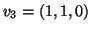 σχηματίζουν μία βάση και υπολογίστε μία ορθοκανονική
βάση της οποίας το πρώτο διάνυσμα να είναι της μορφής
σχηματίζουν μία βάση και υπολογίστε μία ορθοκανονική
βάση της οποίας το πρώτο διάνυσμα να είναι της μορφής
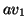 .
.
- Έστω
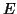 διανυσματικός χώρος και
διανυσματικός χώρος και 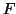 γνήσιος υπόχωρος. Ορίζουμε
το ορθογώνιο συμπλήρωμα
γνήσιος υπόχωρος. Ορίζουμε
το ορθογώνιο συμπλήρωμα  του
του 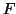 ως τον διανυσματικό
υπόχωρο
ως τον διανυσματικό
υπόχωρο
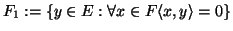 .
Δείξτε ότι
.
Δείξτε ότι
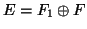 .
.
- Ένας μηχανικός πέρνει πειραματικές μετρήσεις, με σφάλματα,
και καταλήγει ένα σύνολο γραμμικών εξισώσεων της μορφής
Είναι απίθανο όλες οι μετρήσεις που έχει κάνει να είναι
ακριβείς όποτε το παραπάνω σύστημα δεν έχει λύση.
Για να υπολογίσουμε την «καλύτερη» λύση εργαζόμαστε ως
εξής: Ελαχιστοποιούμε τα σφάλματα, ελαχιστοποιόντας το
Δείξτε ότι η ελάχιστη τιμή του σφάλματος επιτυγχάνεται στο
- Θεωρήστε το σύνολο των παραγωγισίμων συναρτήσεων
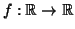 για οι οποίες ταυτίζονται με την παράγωγο
τους, δηλαδή
για οι οποίες ταυτίζονται με την παράγωγο
τους, δηλαδή
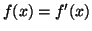 . Δείξτε ότι αποτελούν διανυσμάτικό
χώρο. Αποδείξτε ότι κάθε τέτοια συνάρτηση είναι της μορφής
. Δείξτε ότι αποτελούν διανυσμάτικό
χώρο. Αποδείξτε ότι κάθε τέτοια συνάρτηση είναι της μορφής
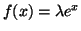 .
.
Kontogiwrghs Aristeidhs
2001-12-03