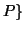Next: About this document ...
Ασκήσεις Γραμμικής Άλγεβρας, Φυλ. 1
Παράδoση: 5/10/2001
- Έστω
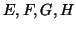 σύνολα και έστω οι απεικονίσεις
Δείξτε ότι
σύνολα και έστω οι απεικονίσεις
Δείξτε ότι 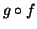 και
και
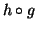 είναι 1-1 και επί αν
και μόνο αν οι
είναι 1-1 και επί αν
και μόνο αν οι 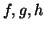 είναι 1-1 και επί
είναι 1-1 και επί
- Έστω
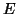 , ένα μη κενό σύνολο εφοδιασμένο με την πράξη
, ένα μη κενό σύνολο εφοδιασμένο με την πράξη  ,
προσεταιριστική και τέτοια ώστε για κάθε
,
προσεταιριστική και τέτοια ώστε για κάθε 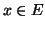 , οι
απεικονίσεις,
, οι
απεικονίσεις, 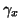 και
και 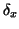 , ορισμένες ως
εξής
, ορισμένες ως
εξής
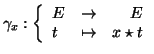
και
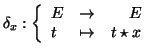
να είναι επί. Να δείξετε ότι η 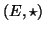 είναι ομάδα
είναι ομάδα
- Έστω
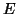 ένα μη κενό σύνολο και
ένα μη κενό σύνολο και 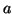 ένα στοιχείο του
ένα στοιχείο του 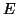 . Να δείξετε ότι το σύνολο των 1-1 και επί
απεικονίσεων του
. Να δείξετε ότι το σύνολο των 1-1 και επί
απεικονίσεων του 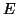 επί του εαυτού του, οι οποίες αφήνουν το
επί του εαυτού του, οι οποίες αφήνουν το 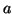 , αμετάβλητο, σχηματίζουν ομάδα
με πράξη την σύνθεση των απεικονίσεων.
, αμετάβλητο, σχηματίζουν ομάδα
με πράξη την σύνθεση των απεικονίσεων.
- Θεωρούμε το σύνολο
Δείξτε ότι
- Για κάθε
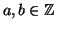 ,
,
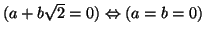
- Αποδείξτε ότι το
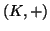 , είναι προσθετική ομάδα.
, είναι προσθετική ομάδα.
- Αποδείξτε ότι το γινόμενο δύο στοιχείων του
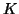 ανήκει στο
ανήκει στο 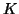 .
.
- Έστω η συνάρτηση
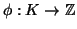 , η οποία στέλνει το
, η οποία στέλνει το
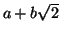 στο
στο
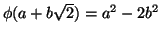 . Αποδείξτε ότι
. Αποδείξτε ότι
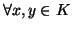 ,
,
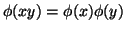 .
.
- Δείξτε ότι το σύνολο των στοιχειών του
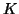 για τα οποία ισχύει
για τα οποία ισχύει
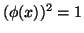 ,
αποτελούν ομάδα με πράξη τον πολ/σμο.
,
αποτελούν ομάδα με πράξη τον πολ/σμο.
- Είναι το
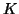 σώμα με πράξεις την συνήθη πρόσθεση και πολλ/σμό?
σώμα με πράξεις την συνήθη πρόσθεση και πολλ/σμό?
- Να κατασκευάσετε ένα σώμα με
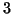 στοιχεία. Υπάρχει σώμα με τέσσερα στοιχεία?
στοιχεία. Υπάρχει σώμα με τέσσερα στοιχεία?
- Στο σύνολο
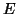 των διατεταγμένων ζευγών από πραγματικούς αριθμούς, θέτουμε
Οι παραπάνω πράξεις, ορίζουν διανυσματικό χώρο επί του σώματος των πραγματικών αριθμών?
των διατεταγμένων ζευγών από πραγματικούς αριθμούς, θέτουμε
Οι παραπάνω πράξεις, ορίζουν διανυσματικό χώρο επί του σώματος των πραγματικών αριθμών?
- Καθορίστε μεταξύ των παρακάτω συνόλων, αυτά τα οποία είναι διανυσματικοί χώροι επί του
σώματος των πραγματικών αριθμών:
-
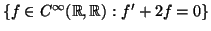 , με
, με
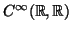 συμβολίζουμε τις απειροδιαφορίσιμες
συναρτήσεις από το
συμβολίζουμε τις απειροδιαφορίσιμες
συναρτήσεις από το
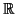 στο
στο
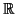 .
.
-
![$ \{f \in C([a,b],\mathbb{R}): \int_a^bf(t)dt=0 \}$](img33.gif) ,
,
![$ C([a,b],\mathbb{R})$](img34.gif) συμβολίζει τις συνεχείς συναρτήσεις από το
συμβολίζει τις συνεχείς συναρτήσεις από το ![$ [a,b]$](img35.gif) στο
στο
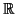 .
.
-
![$ \{P \in \mathbb{R}[x]: deg(P) \geq 4\}$](img36.gif)
-
![$ \{P \in \mathbb{R}[x]: P^\prime$](img37.gif) διαιρεί το
διαιρεί το 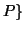
Kontogiwrghs Aristeidhs
2001-10-05
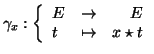 και
και 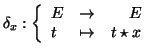
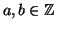 ,
,
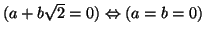
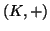 , είναι προσθετική ομάδα.
, είναι προσθετική ομάδα.
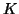 ανήκει στο
ανήκει στο 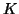 .
.
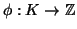 , η οποία στέλνει το
, η οποία στέλνει το
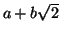 στο
στο
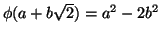 . Αποδείξτε ότι
. Αποδείξτε ότι
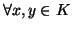 ,
,
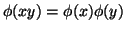 .
.
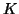 για τα οποία ισχύει
για τα οποία ισχύει
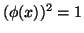 ,
αποτελούν ομάδα με πράξη τον πολ/σμο.
,
αποτελούν ομάδα με πράξη τον πολ/σμο.
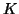 σώμα με πράξεις την συνήθη πρόσθεση και πολλ/σμό?
σώμα με πράξεις την συνήθη πρόσθεση και πολλ/σμό?
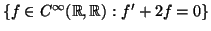 , με
, με
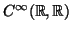 συμβολίζουμε τις απειροδιαφορίσιμες
συναρτήσεις από το
συμβολίζουμε τις απειροδιαφορίσιμες
συναρτήσεις από το
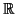 στο
στο
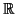 .
.
![$ \{f \in C([a,b],\mathbb{R}): \int_a^bf(t)dt=0 \}$](img33.gif) ,
,
![$ C([a,b],\mathbb{R})$](img34.gif) συμβολίζει τις συνεχείς συναρτήσεις από το
συμβολίζει τις συνεχείς συναρτήσεις από το ![$ [a,b]$](img35.gif) στο
στο
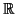 .
.
![$ \{P \in \mathbb{R}[x]: deg(P) \geq 4\}$](img36.gif)
![$ \{P \in \mathbb{R}[x]: P^\prime$](img37.gif) διαιρεί το
διαιρεί το