Next: About this document ...
Ασκήσεις Ελλειπτικών Καμπύλων
2 Φυλλάδιο
Παράδοση Παρασκευή 26 Μαρτίου
- Θεωρούμε ένα ομογενές πολυώνυμο
![$ f(x,y,z) \in k[x,y,z]$](img1.png) ,
βαθμού
,
βαθμού 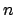 .
Αποδείξτε ότι
Δείξτε ότι στην περίπτωση ομογενών πολυωνύμων, το
να ελέγξουμε αν ένα σημείο
.
Αποδείξτε ότι
Δείξτε ότι στην περίπτωση ομογενών πολυωνύμων, το
να ελέγξουμε αν ένα σημείο
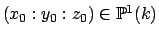 ,
είναι η όχι ιδιόμορφο αρκεί να κυτάξουμε μόνο τις
μερικές παραγώγους του.
,
είναι η όχι ιδιόμορφο αρκεί να κυτάξουμε μόνο τις
μερικές παραγώγους του.
- Θεωρήστε την ελλιπτική καμπύλη στην ((μακρά)) μορφή του Weierstrass,
Διατυπώστε τον ορίσμο της χαρακτηριστικής ενός σώματος.
Αποδείξτε ότι αν η χαρακτηριστική του σώματος
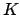 είναι
διαφορετική του
είναι
διαφορετική του 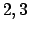 , τότε ο μετασχηματισμός
όπου
, τότε ο μετασχηματισμός
όπου
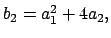 φέρνει την ελλειπτική καμπύλη στην μορφή
για κάποια κατάλληλα
φέρνει την ελλειπτική καμπύλη στην μορφή
για κάποια κατάλληλα 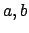 .
.
- Έστω
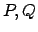 διαφορετικά ρητά σημεία της
διαφορετικά ρητά σημεία της 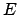 με συντεταγμένες
με συντεταγμένες
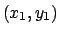 και
και 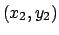 αντίστοιχα. Αποδείξτε ότι το
σημείο
αντίστοιχα. Αποδείξτε ότι το
σημείο 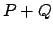 αν
αν
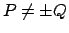 έχει συντεταγμένες
έχει συντεταγμένες 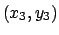 που δίνονται από τον τύπο:
όπου
που δίνονται από τον τύπο:
όπου
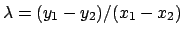 και
και
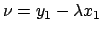 .
.
- Να χρησιμοποιήσετε ένα πρόγραμμα όπως το Maple,
Mathematica προκειμένου να σχεδιάσετε
τις γραφικές παραστάσεις των
καμπύλων:
- Θεωρήστε την ελλειπτική καμπύλη που ορίζεται από την
σαν υποσύνολο του
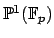 ,
όπου
,
όπου 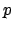 πρώτος αριθμός και
πρώτος αριθμός και
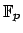 είναι το
σώμα με
είναι το
σώμα με 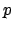 στοιχεία. Αποδείξτε ότι
η ελλειπτική καμπύλη έχει πεπερασμένα το πλήθος
στοιχεία. Θεωρήστε το σύμβολο του
Legendre
στοιχεία. Αποδείξτε ότι
η ελλειπτική καμπύλη έχει πεπερασμένα το πλήθος
στοιχεία. Θεωρήστε το σύμβολο του
Legendre
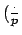 , και
απόδειξτε ότι το πλήθος των σημείων της
ελλειπτικής καμπύλης δίνεται από τον τύπο
, και
απόδειξτε ότι το πλήθος των σημείων της
ελλειπτικής καμπύλης δίνεται από τον τύπο
Aristides Kontogeorgis
2004-03-22