


Next: About this document ...
Ασκήσεις Ελλειπτικών Καμπύλων
1 Φυλλάδιο
Παράδοση Παρασκευή 12 Μαρτίου
- Θεωρούμε τις επίπεδες αλγεβρικές καμπύλες που δίνονται από τις
παρακάτω εξισώσεις:
-
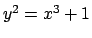 .
.
-
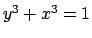 .
.
-
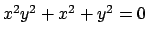 .
.
-
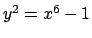 .
.
-
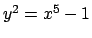 .
.
-
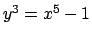 .
.
-
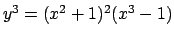 .
.
-
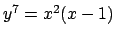 .
.
-
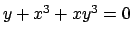 .
.
Να δειχτεί ότι οι αφινικές καμπύλες (1a),(1b),(1d),(1e),(1)
και (1j), είναι ομαλές. Να δειχτεί ότι οι καμπύλες (1g),(1h)
είναι ιδιόμορφες και να βρεθούν τα σημεία στα οποία είναι ιδιόμορφες.
- Θεωρούμε την επίπεδη καμπύλη
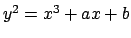 . Να αποδειχτεί ότι είναι
μη ιδιόμορφη αν και μόνο αν
. Να αποδειχτεί ότι είναι
μη ιδιόμορφη αν και μόνο αν
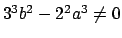 . Στην περίπτωση
που είναι ιδιόμορφη να υπολογιστούν τα ιδιόμορφα σημεία.
. Στην περίπτωση
που είναι ιδιόμορφη να υπολογιστούν τα ιδιόμορφα σημεία.
- Σε κάθε μία από τις περιπτώσεις της πρώτης άσκησης να υπολογιστούν
ομογενή πολυώνυμα τα οποία να δίνουν προβολικές καμπύλες των οποίων
ο περιορισμός στο αφινικό επίπεδο
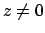 να δίνει τις αρχικές αφινικές
καμπύλες. Να υπολογιστούν οι τομές των καμπύλων με την επ' άπειρο
ευθεία
να δίνει τις αρχικές αφινικές
καμπύλες. Να υπολογιστούν οι τομές των καμπύλων με την επ' άπειρο
ευθεία 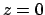 .
.
Aristides Kontogeorgis
2004-03-01