


Next: About this document ...
Ασκήσεις Αναλυτικής Γεωμετρίας
1 Φυλλάδιο
Παράδοση Δευτέρα 30 Οκτωβρίου
- Να δείξετε ότι τα παρακάτω διανύσματα του χώρου είναι γραμμικά ανεξάρτητα.
-
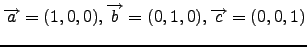
-
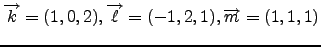
- Να δείξετε ότι τα διανύσματα
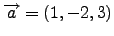 και
και
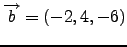 είναι συγραμμικά.
είναι συγραμμικά.
- Δίνονται τα διανύσματα
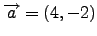 και
και
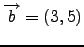 . Να γράψετε το διάνυσμα
. Να γράψετε το διάνυσμα
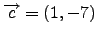 ως γραμμικό συνδιασμό των
ως γραμμικό συνδιασμό των
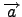 και
και
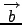 .
.
- Θεωρούμε τα διανύσματα
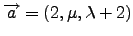 και
και
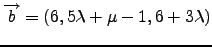 .
Να προσδιορίσετε τα
.
Να προσδιορίσετε τα
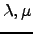 ώστε τα διανύσματα
ώστε τα διανύσματα
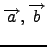 να είναι παράλληλα.
να είναι παράλληλα.
- Να δείξετε ότι τα διανύσματα
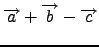 ,
,
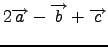 ,
,
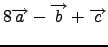 είναι συνεπίπεδα.
είναι συνεπίπεδα.
- Να δείξετε ότι τα σημεία
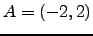 ,
, 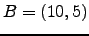 ,
, 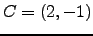 ,
, 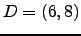 είναι κορυφές παραλληλογράμμου.
Στην συνέχεια να υπολογίσετε τα μήκη των πλευρών του.
είναι κορυφές παραλληλογράμμου.
Στην συνέχεια να υπολογίσετε τα μήκη των πλευρών του.
- Να υπολογισετε τη γωνία των διανυσμάτων
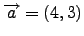 και
και
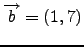 καθώς και των
καθώς και των
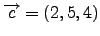 και
και
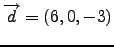 .
.
- Να υπολογιστεί η τιμή του πραγματικού αριθμού
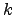 ώστε τα διανύσματα
ώστε τα διανύσματα
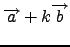 και
και
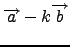 να είναι κάθετα μεταξύ τους, αν γνωρίζουμε ότι
να είναι κάθετα μεταξύ τους, αν γνωρίζουμε ότι
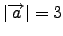 και
και
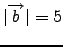 και ότι
και ότι
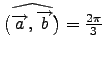 .
.
- Να υπολογιστεί το εσωτερικό και το εξωτερικό γινόμενο των διανυσμάτων
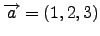 και
και
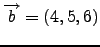 .
.
Aristides Kontogeorgis
2006-10-22
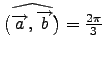 .
.
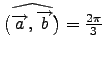 .
.