Next: About this document ...
Τελική εξέταση Άλγεβρας
24 Ιουνίου 2004
- Να οριστεί η ομάδα μεταθέσεων
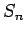 .
Ποιά είναι η τάξη της και γιατί. Πότε μία μετάθεση
είναι άρτια? Να οριστεί η ομάδα των αρτίων μεταθέσεων
.
Ποιά είναι η τάξη της και γιατί. Πότε μία μετάθεση
είναι άρτια? Να οριστεί η ομάδα των αρτίων μεταθέσεων 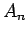 .
Ποιά είναι η τάξη της
.
Ποιά είναι η τάξη της 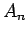 και γιατί?
Να αποδειχτεί ότι η
και γιατί?
Να αποδειχτεί ότι η 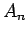 είναι κανονική υπομάδα της
είναι κανονική υπομάδα της 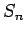 .
Δίνονται οι μεταθέσεις
.
Δίνονται οι μεταθέσεις
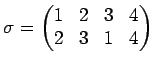
και
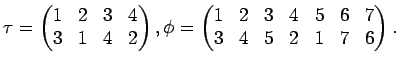
Να υπολογιστεί το
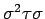 . Να γραφεί το
. Να γραφεί το
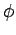 σαν γινόμενο ξένων κύκλων.
σαν γινόμενο ξένων κύκλων.
- Πότε μία ομάδα είναι κυκλική? Να αποδειχτεί ότι κάθε
υποομάδα κυκλικής ομάδας είναι κυκλική.
- Αν
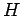 είναι κανονική υποομάδα της
είναι κανονική υποομάδα της 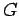 και
και ![$ m=[G:H]$](img9.png) ,
να αποδειχτεί ότι
,
να αποδειχτεί ότι 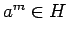 για κάθε
για κάθε 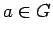 .
.
- Να αποδειχτεί ότι κάθε ομάδα με τάξη πρώτο είναι κυκλική.
- Να δoθεί ο ορισμός της ακεραίας περιοχής. Να δoθούν παραδείγματα
δακτυλίων που είναι ακέραιες περιοχές και δακτυλιών που δεν
είναι.
- Έστω
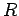 αντιμεταθετικός δακτύλιος με μονάδα. Να δειχτεί ότι ο
αντιμεταθετικός δακτύλιος με μονάδα. Να δειχτεί ότι ο
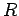 είναι σώμα αν και μόνο αν τα μοναδικά του ιδεώδη είναι τα
τετριμμένα.
είναι σώμα αν και μόνο αν τα μοναδικά του ιδεώδη είναι τα
τετριμμένα.
- Να αποδειχτεί ότι κάθε ιδεώδες του
![$ \mathbb{R}[x]$](img13.png) είναι κύριο.
είναι κύριο.
- Δίνεται ο δακτύλιος
![$ \mathbb{Z}[i]$](img14.png) των ακεραίων του Gauß:
Να υπολογιστεί η ομάδα των μονάδων του.
των ακεραίων του Gauß:
Να υπολογιστεί η ομάδα των μονάδων του.
- Ποιά από τα παρακάτω πολυώνυμα είναι ανάγωγα στο
![$ \mathbb{Q}[x]$](img16.png) ?
?
Να απαντήσετε σε ακριβώς 8 θέματα
Διάρκεια διαγωνίσματος 2 ώρες και 45 λεπτά
Καλή Επιτυχία
Aristides Kontogeorgis
2004-06-29
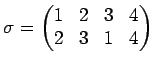 και
και 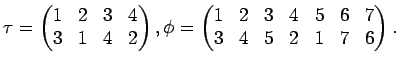
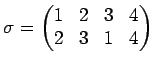 και
και