


Next: About this document ...
Προόδος Άλγεβρας
7 Μαϊου 2004
- Να δείξετε ότι αν σε μια ομάδα κάθε στοιχείο έχει τάξη δύο, τότε
η ομάδα είναι αβελιανή.
- Να δείξετε ότι ο πυρήνας ενός ομομορφισμού
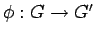 ,
είναι κανονική υποομάδα της ομάδας
,
είναι κανονική υποομάδα της ομάδας 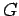 .
.
- Nα δείξετε ότι αν η
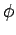 είναι ομομορφισμός ομάδων, τότε η
είναι ομομορφισμός ομάδων, τότε η 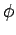 είναι
1-1 αν και μόνο αν ο πυρήνας της
είναι
1-1 αν και μόνο αν ο πυρήνας της 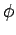 είναι η τετριμένη υποομάδα, δηλαδή
είναι η τετριμένη υποομάδα, δηλαδή
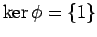 .
.
- Να υπολογιστούν όλες οι δυνατές αβελιανές υποομάδες με τάξη
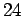 .
.
- Έστω
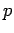 πρώτος. Να δικαιολογήσετε γιατί οι ομάδες
πρώτος. Να δικαιολογήσετε γιατί οι ομάδες
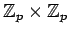 και
και
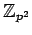 δεν είναι ισόμορφες.
δεν είναι ισόμορφες.
- Nα αποδείξετε ότι αν
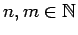 και
και 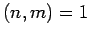 , τότε
οι ομάδες
, τότε
οι ομάδες
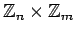 και
και
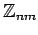 είναι ισόμορφες.
είναι ισόμορφες.
- Αν
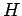 υποομάδα της
υποομάδα της 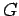 , και
, και 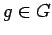 , να αποδείξετε ότι το σύνολο
είναι υποομάδα της
, να αποδείξετε ότι το σύνολο
είναι υποομάδα της 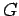 . Aν επιπλέον η
. Aν επιπλέον η 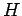 , έχει τάξη
, έχει τάξη 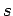 , να δείξετε
ότι και η ομάδα
, να δείξετε
ότι και η ομάδα
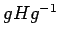 έχει τάξη
έχει τάξη 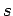 . Nα δείξετε ότι η τομή όλων
των υποομάδων της
. Nα δείξετε ότι η τομή όλων
των υποομάδων της 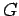 με τάξη
με τάξη 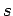 , είναι κανονική υποομάδα της
, είναι κανονική υποομάδα της 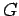 .
.
Διάρκεια διαγωνίσματος 2 ώρες
Καλή Επιτυχία
Aristides Kontogeorgis
2004-05-13