Θεωρούμε το απλό μαθηματικό εκκρεμές. Η Λαγκρανζιανή του συνάρτηση
έχει τη μορφή ![]() . Αν θεωρήσουμε ότι το σημείο ανάρτησης
εκτελεί κατακόρυφη κίνηση
. Αν θεωρήσουμε ότι το σημείο ανάρτησης
εκτελεί κατακόρυφη κίνηση ![]() τότε η Λαγκρανζιανή θα πάρει
τη μορφή
τότε η Λαγκρανζιανή θα πάρει
τη μορφή ![]() όπου οι παραπάνω όροι οφείλονται στην αλλαγή
της κινητικής και δυναμικής ενέργειας του ταλαντωτή λόγω
της
όπου οι παραπάνω όροι οφείλονται στην αλλαγή
της κινητικής και δυναμικής ενέργειας του ταλαντωτή λόγω
της ![]() . Η Λαγκρανζιανή αυτή έχει όρους που είναι σταθερές
ή συναρτήσεις του χρόνου οι οποίες μπορούν να παραληφθούν γιατί δεν επηρεάζουν την εξίσωση της
κίνησης. Άρα έχουμε την Λαγκρανζιανή
. Η Λαγκρανζιανή αυτή έχει όρους που είναι σταθερές
ή συναρτήσεις του χρόνου οι οποίες μπορούν να παραληφθούν γιατί δεν επηρεάζουν την εξίσωση της
κίνησης. Άρα έχουμε την Λαγκρανζιανή ![]() . Η Λαγκρανζιανή
αυτή μπορεί να μετασχηματιστεί με ένα μετασχηματισμό
βαθμίδας
. Η Λαγκρανζιανή
αυτή μπορεί να μετασχηματιστεί με ένα μετασχηματισμό
βαθμίδας ![]() ,
όπου
,
όπου ![]() , και να πάρει τη
μορφή
, και να πάρει τη
μορφή ![]() . Η συζυγής ορμή δίνεται από τη
σχέση
. Η συζυγής ορμή δίνεται από τη
σχέση ![]() . Άρα η Χαμιλτονιανή συνάρτηση θα
είναι
. Άρα η Χαμιλτονιανή συνάρτηση θα
είναι ![]()
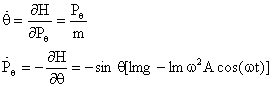 .
.
Θεωρούμε τις
παραμέτρους ![]()
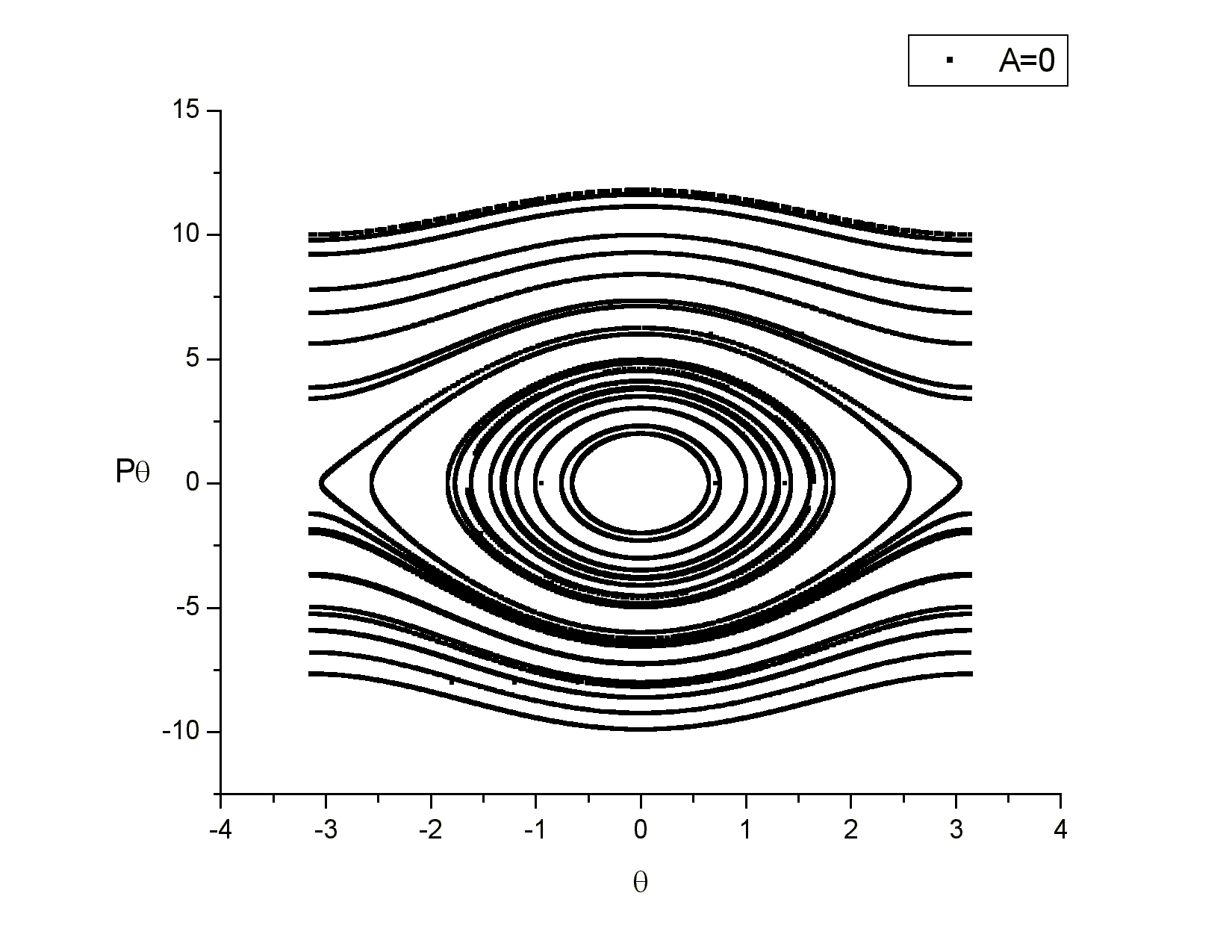
που είναι ο χώρος των φάσεων για το απλό εκκρεμές.
Παρατηρούμε ότι υπάρχουν νησίδες με κανονικές τροχιές, όπως η κεντρική περιοχή ή οι τέσσερις περιοχές που είναι συμμετρικά κατανεμημένες γύρω από την κεντρική περιοχή, καθώς και χαοτικές περιοχές, όπως η περιοχή που περιβάλει την κεντρική νησίδα κανονικότητας.
Θεωρούμε δύο αρχικές συνθήκες στην χαοτική περιοχή που έχουν πολύ μικρή απόσταση. Έστω η αρχική
συνθήκη ![]() και μια δεύτερη αρχική συνθήκη που να απέχει από
την πρώτη
και μια δεύτερη αρχική συνθήκη που να απέχει από
την πρώτη ![]() . Η εξέλιξη της απόστασης των δύο σημείων με τον
χρόνο είναι
. Η εξέλιξη της απόστασης των δύο σημείων με τον
χρόνο είναι ![]() όπου το λ είναι ο εκθέτης Lyapunov.
όπου το λ είναι ο εκθέτης Lyapunov.
Ολοκληρώνουμε το σύστημα για τις δύο αρχικές συνθήκες και υπολογίζουμε την απόσταση των δύο τροχιών σε κάθε χρονική στιγμή. Με τις αποστάσεις αυτές φτιάχνουμε το παρακάτω διάγραμμα :
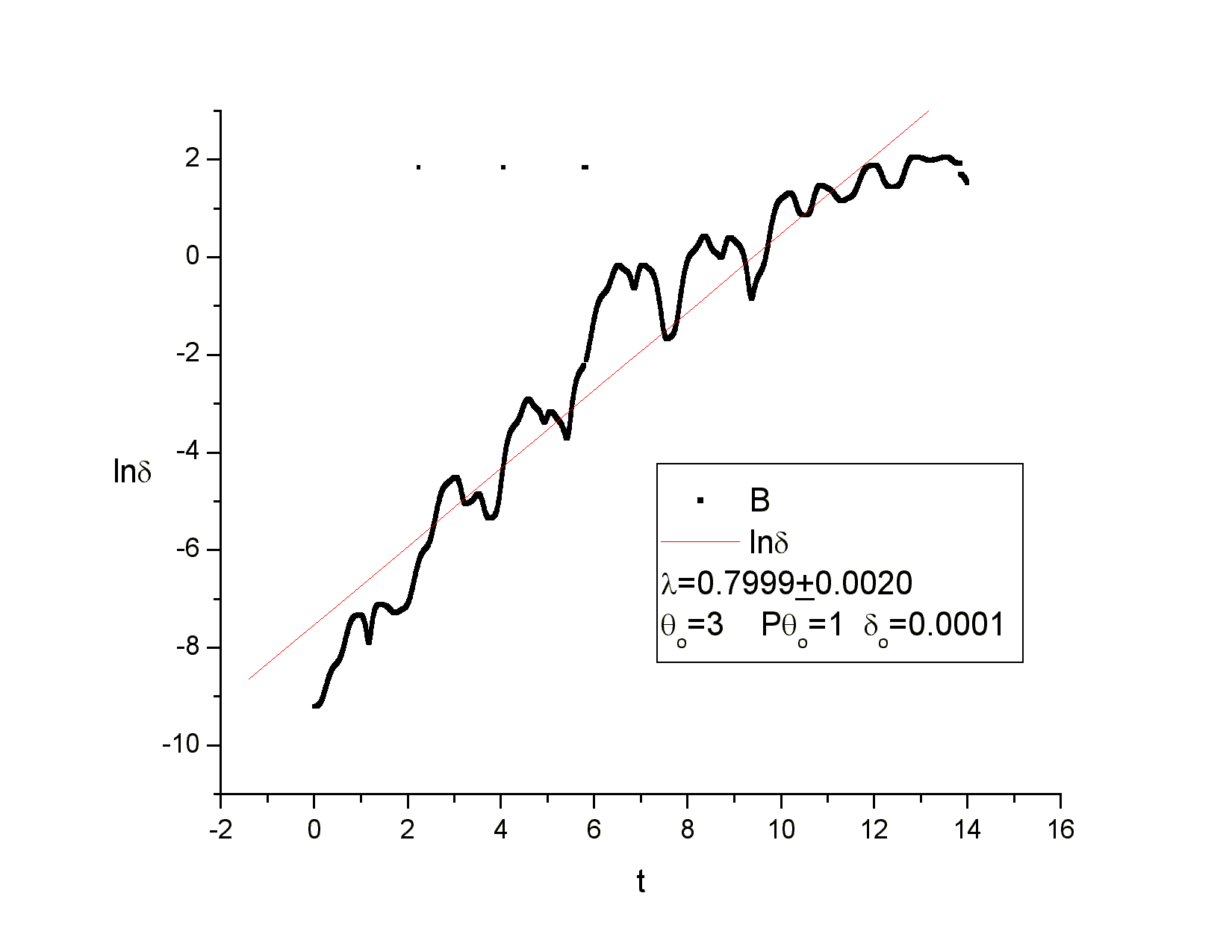
Από το γράφημα υπολογίζουμε την ευθεία ελαχίστων τετραγώνων η κλίση
της οποίας είναι ο εκθέτης Lyapunov. Άρα έχουμε ότι στη χαοτική περιοχή που περιβάλει την κεντρική
νησίδα ο εκθέτης Lyapunov είναι ![]()
Με τον ίδιο τρόπο υπολογίζουμε τον Lyapunov σε μια νησίδα
κανονικότητας. Έτσι για την αρχική συνθήκη ![]() και για μια
δεύτερη που απέχει
και για μια
δεύτερη που απέχει ![]() έχουμε :
έχουμε :
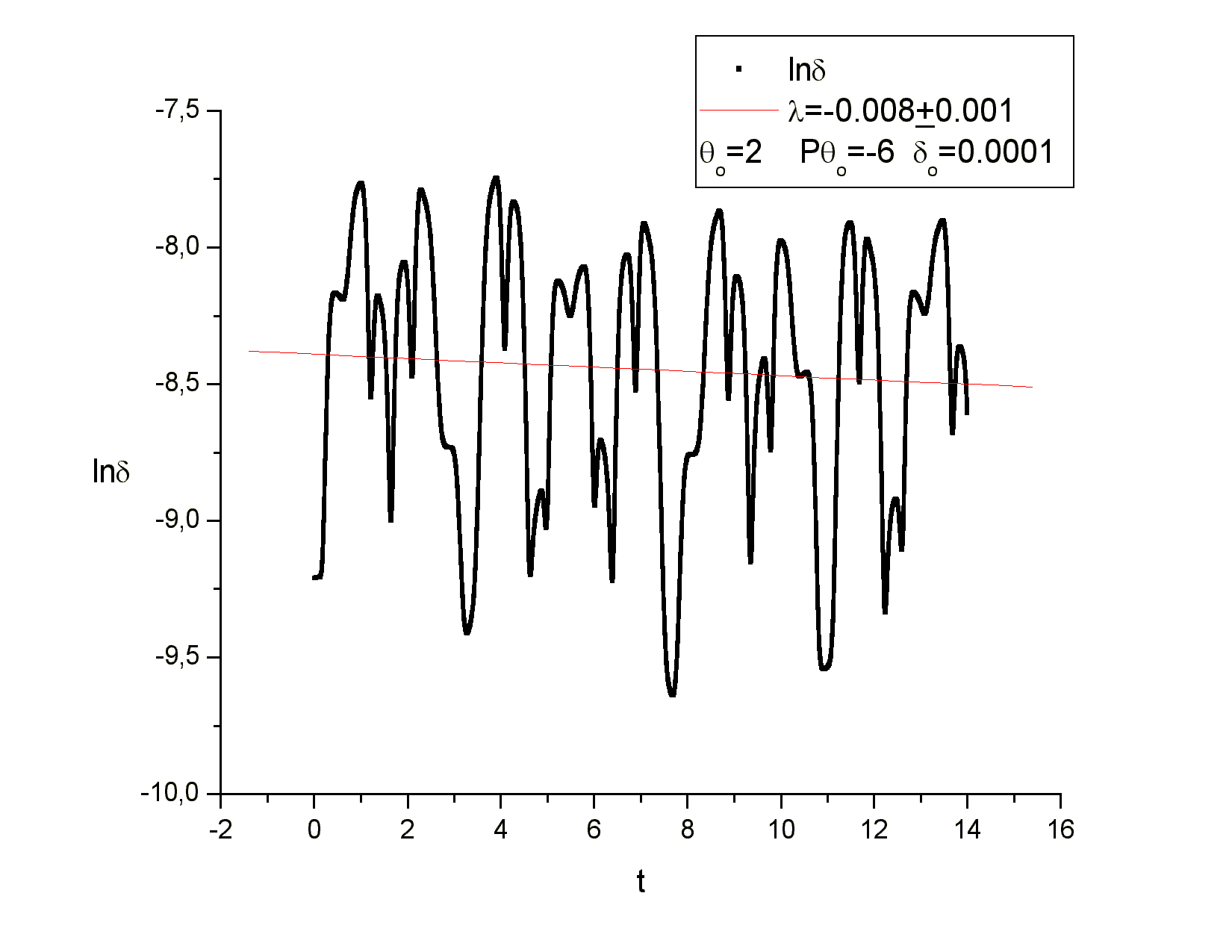
Από το γράφημα υπολογίζουμε
ότι ο εκθέτης Lyapunov είναι ![]() .
.
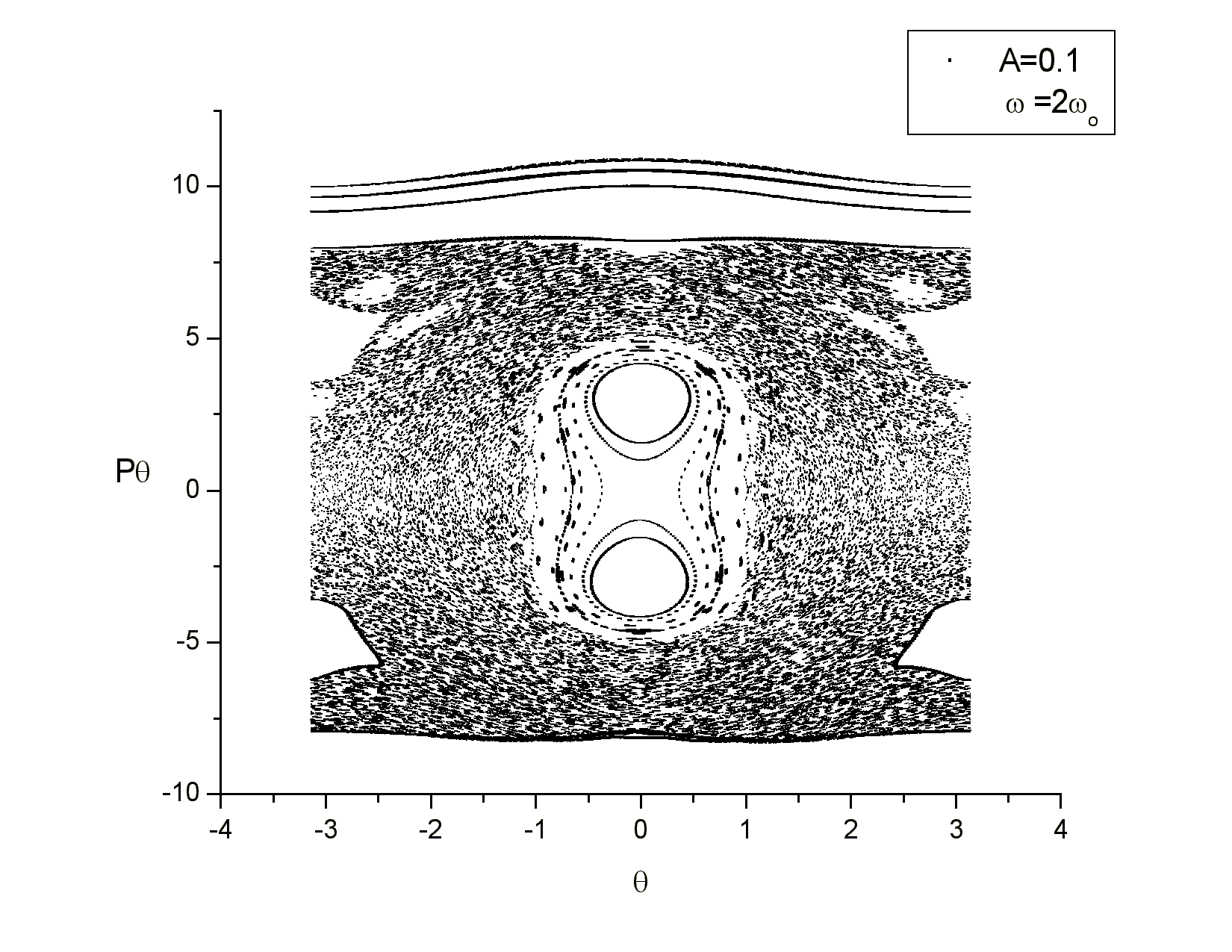
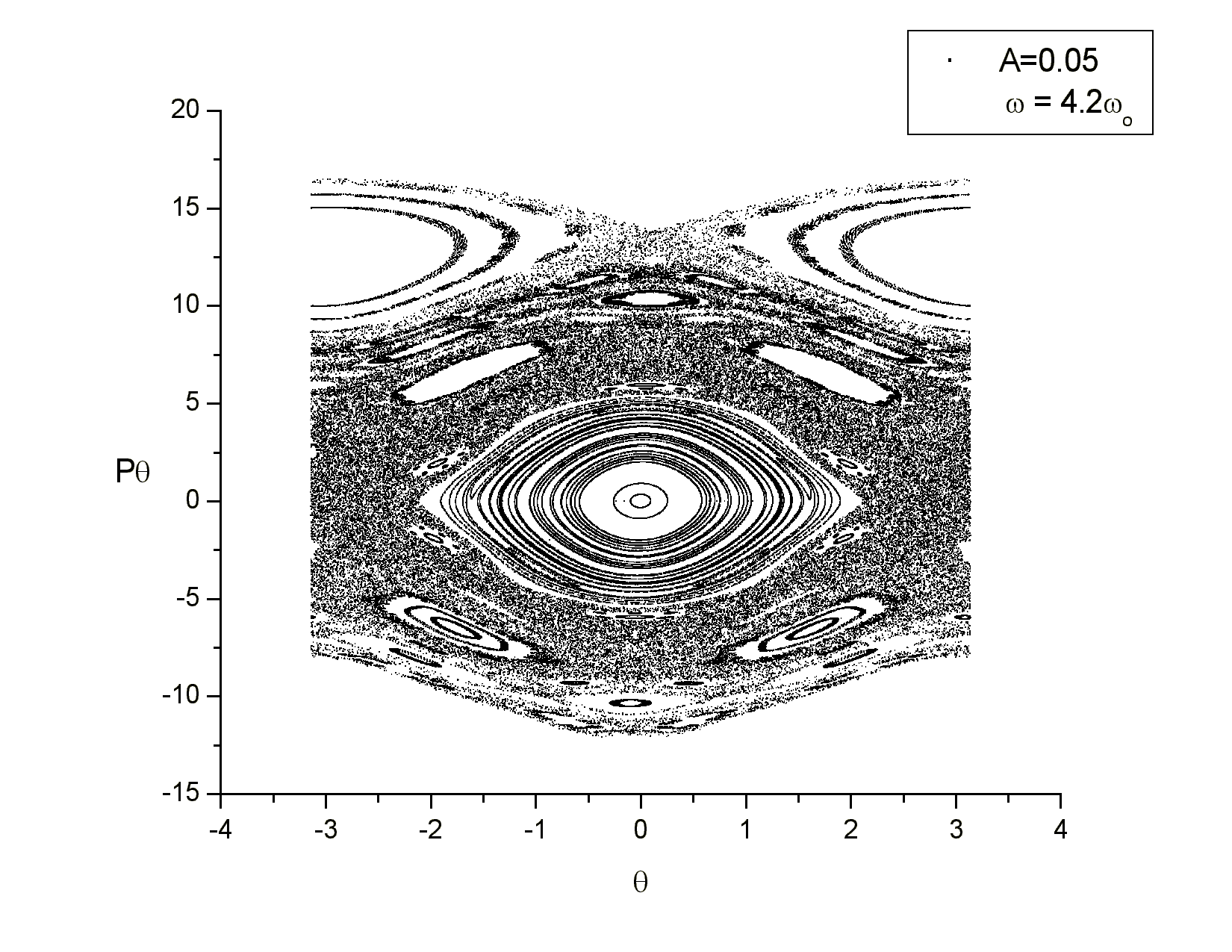
Από την απεικόνιση
περιόδου βλέπουμε ότι έχουμε περιοχές περιοδικών τροχιών στο κέντρο του διαγράμματος καθώς και
χαοτικές περιοχές. Επίσης αυτό που παρατηρούμε είναι ότι για αυτή τη συχνότητα έχουμε ότι το σημείο
(0,0) έχει αλλάξει ευστάθεια και από ευσταθές έχει γίνει ασταθές. Αυτό το περιμέναμε γιατί από τη
μελέτη του συστήματος ![]() , το οποίο είναι η γραμμικοποίηση
του προβλήματος που έχουμε για μικρές γωνίες, έχουμε συμπεράνει ότι υπάρχουν τιμές της συχνότητας
της διαταραχής για τις οποίες έχουμε αλλαγή της ευστάθειας.
, το οποίο είναι η γραμμικοποίηση
του προβλήματος που έχουμε για μικρές γωνίες, έχουμε συμπεράνει ότι υπάρχουν τιμές της συχνότητας
της διαταραχής για τις οποίες έχουμε αλλαγή της ευστάθειας.
και ολοκληρώνουμε το σύστημα και έχουμε την απεικόνιση περιόδου
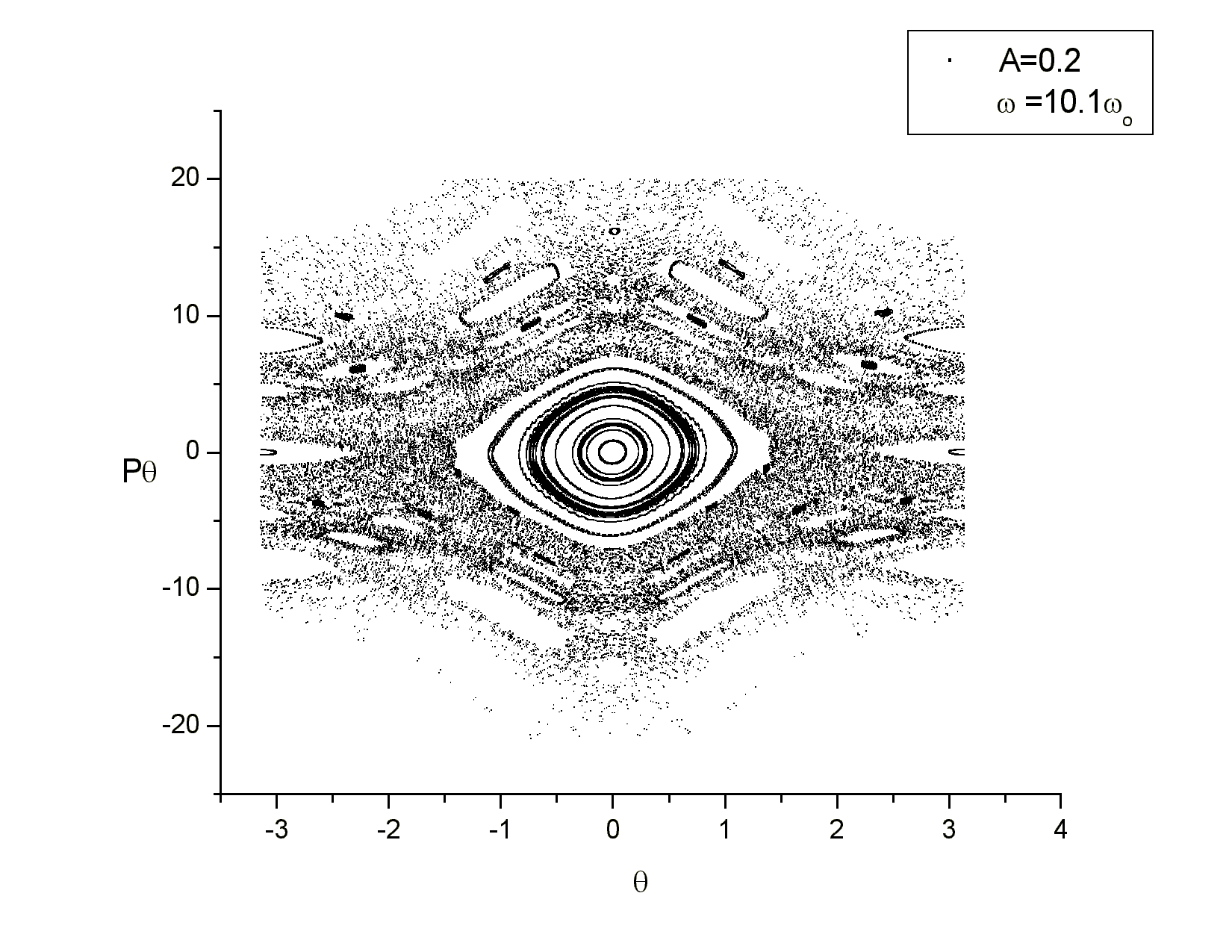
Από την απεικόνιση περιόδου βλέπουμε ότι το σημείο (0,0) ξανά έγινε ευσταθές. Επίσης βλέπουμε ότι ο αριθμός των νησίδων έχει αυξηθεί και υπάρχει φυσικά και η εκτεταμένη χαοτική περιοχή που περιβάλει τις νησίδες.
Για να εκτιμήσουμε τον εκθέτη Lyapunov κάνουμε ότι κάναμε και στην προηγούμενη περίπτωση και έχουμε το γράφημα :
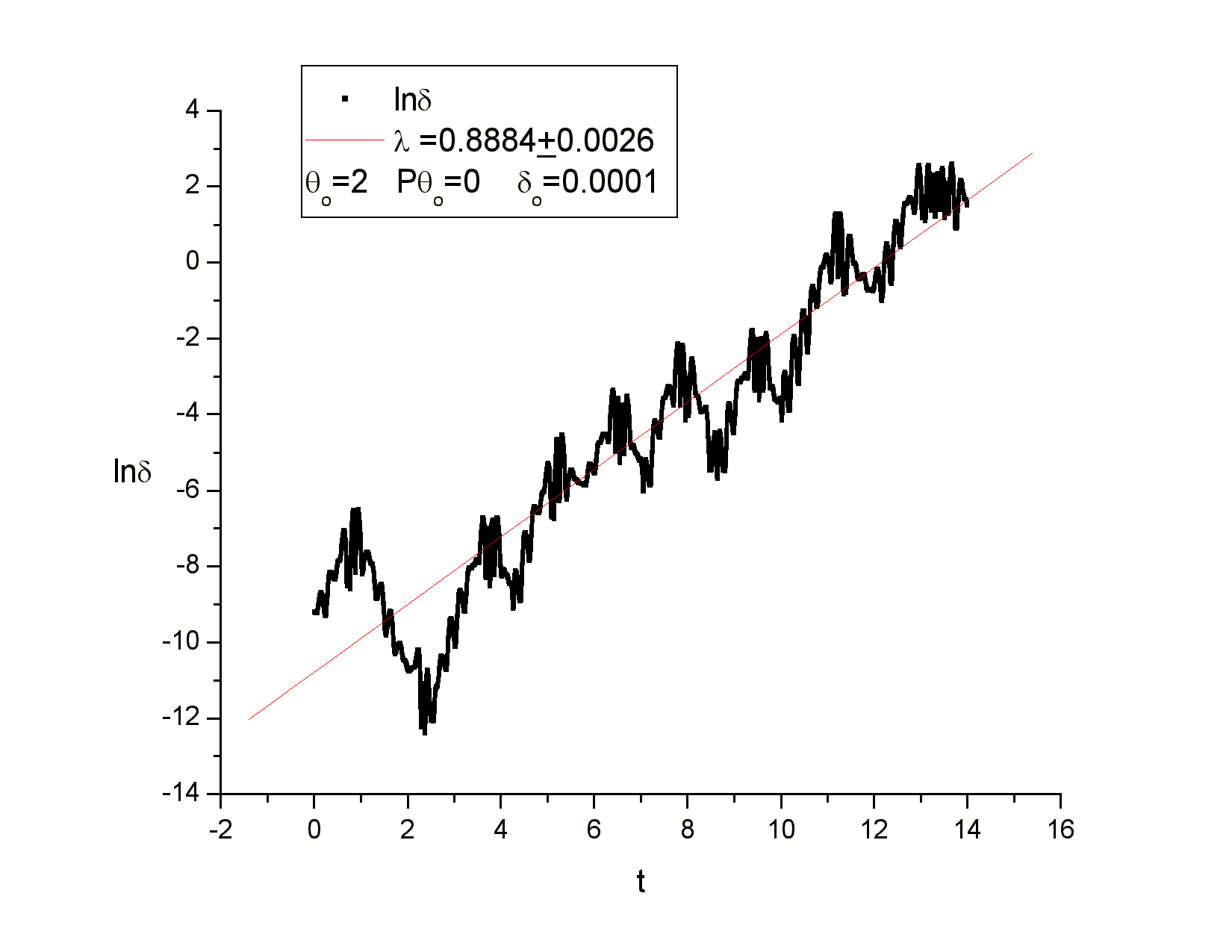
Ο εκθέτης Lyapunov
είναι ![]() . και είναι λίγο μεγαλύτερος από αυτόν τον οποίο
υπολογίσαμε στην περίπτωση 2.
. και είναι λίγο μεγαλύτερος από αυτόν τον οποίο
υπολογίσαμε στην περίπτωση 2.