Off[General :: "spell1"]

This is some matterial that could be a helpfull companion to the paper,
"An all-purpose metric for the exterior of any kind of rotating neutron star", by G. Pappas and T. A. Apostolatos.

Multipole Moments for the two-soliton

multipoleOrder = 6 ;

P3 = (z - M - I a) (z + I b) - k ;

Q3 = (z + M - I a) (z + I b) - k ;

Ε3 = P3/Q3 ;

ξ3 = z (1 - Ε3)/(1 + Ε3) ;

z = 1/x ;

multipoleseriesTwoSoliton = Simplify[Series[ξ3, {x, 0, multipoleOrder}]] ;

FullSimplify[CoefficientList[multipoleseriesTwoSoliton, x]]//MatrixForm

Metric functions for the two-soliton

The metric functions can be expressed using the following quantities:

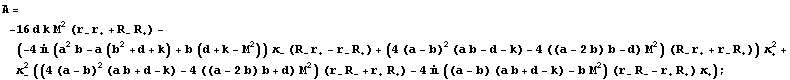
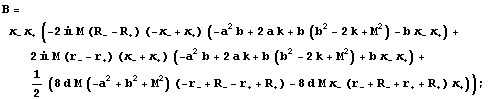
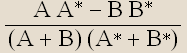From A and B we define the Ernst potential:  E(ρ,z)=(A - B)/(A + B), and the metric function: f(ρ,z)=(A A^* - B B^*)/((A + B) (A^* + B^*)).

Using L and E we also define the metric function: ω(ρ,z)=i([(A + B) L^* - (A^* + B^*) E] -[(A^* + B^*) L - (A + B) E^*])/(2 (A A^* - B B^*)).

Ko = 16 d κ_ -^2 κ_ +^2 ;

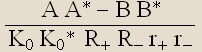And from K_0 we define the metric function: e^(2 γ(ρ, z))=(A A^* - B B^*)/(K_0 K_0^*   R_ + R_ - r_ + r_ -).

Metric functions for the Manko et al.

The metric functions of Manko et al. (Manko V. S., Mielke E. W., Sanabria-Gòmez J. D., 2000, Phys. Rev. D, 61, 081501) with parameters M, a and, b expressed in Weyl-Papapetrou coordinates.

δ = (-M^2 b^2)/(M^2 - (a - b)^2) ;

d = 1/4 (M^2 - (a - b)^2) ;

kk = (d + δ)^(1/2) ;

{x->1/(2 kk) (((kk + z)^2 + ρ^2)^(1/2) + ((kk - z)^2 + ρ^2)^(1/2)), y->1/(2 kk) (((kk + z)^2 + ρ^2)^(1/2) - ((kk - z)^2 + ρ^2)^(1/2))} ;

fM = EM/DM ;

ωM = -(1 - y^2) FM/EM/.{x->1/(2 kk) (((kk + z)^2 + ρ^2)^(1/2) + ((kk - z)^2 + ρ^2)^(1/2)), y->1/(2 kk) (((kk + z)^2 + ρ^2)^(1/2) - ((kk - z)^2 + ρ^2)^(1/2))} ;

Mgtt3[ρ_, z_] = -fM ;

Mgtφ3[ρ_, z_] = fM ωM ;

Mgφφ3[ρ_, z_] = -fM ωM^2 + ρ^2 fM^(-1) ;

Mgzz3[ρ_, z_] = fM^(-1) Exp2γM ;

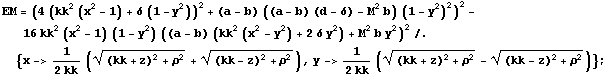
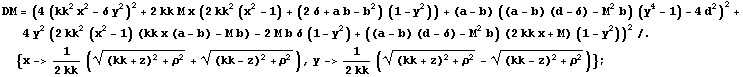
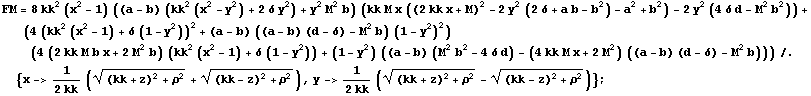
Hartle-Thorne metric

Hartle - Thorne  from Berti et al.,  2005, MNRAS, 358, 923
  (with a change in sign of g_tφ term so as to correspond to a rotation parameter defined as j=J/M^2).

Am1 = (15 r (r - 2 Mm) (1 - 3 u^2))/(16 Mm^2) Log[r/(r - 2 Mm)] ;

Am2 = (15 (r^2 - 2 Mm^2) (3 u^2 - 1))/(16 Mm^2) Log[r/(r - 2 Mm)] ;

L1 = 80 Mm^6 + 8 Mm^4 r^2 + 10 Mm^3 r^3 + 20 Mm^2 r^4 - 45 Mm r^5 + 15 r^6 ;

p1 = (8 Mm r^4 (r - 2 Mm))^(-1) ;

W1 = (r - Mm) (16 Mm^5 + 8 Mm^4 r - 10 Mm^2 r^3 - 30 Mm r^4 + 15 r^5) + u^2 (48 Mm^6 - 8 Mm^5 r - 24 Mm^4 r^2 - 30 Mm^3 r^3 - 60 Mm^2 r^4 + 135 Mm r^5 - 45 r^6) ;

Fm1[Mm_, r_, u_] = -p1 W1 + Am1 ;

Fm2[Mm_, r_, u_] = 5 r^3 p1 (3 u^2 - 1) (r - Mm) (2 Mm^2 + 6 Mm r - 3 r^2) - Am1 ;

Gm1[Mm_, r_, u_] = p1 ((L1 - 72 Mm^5 r) - 3 u^2 (L1 - 56 Mm^5 r)) - Am1 ;

Hm1[Mm_, r_, u_] = Am2 + (8 Mm r^4)^(-1) (1 - 3 u^2) (16 Mm^5 + 8 Mm^4 r - 10 Mm^2 r^3 + 15 Mm r^4 + 15 r^5) ;

Hm2[Mm_, r_, u_] = -Am2 + (8 Mm r)^(-1) 5 (1 - 3 u^2) (2 Mm^2 - 3 Mm r - 3 r^2) ;

gttHT[Mm_, jj_, q_, r_, u_] = -(1 - 2 Mm/r) (1 + jj^2 Fm1[Mm, r, u] - q Fm2[Mm, r, u]) ;

grrHT[Mm_, jj_, q_, r_, u_] = (1 - 2 Mm/r)^(-1) (1 + jj^2 Gm1[Mm, r, u] + q Fm2[Mm, r, u]) ;

gθθHT[Mm_, jj_, q_, r_, u_] = r^2 (1 + jj^2 Hm1[Mm, r, u] - q Hm2[Mm, r, u]) ;

gφφHT[Mm_, jj_, q_, r_, u_] = r^2 (1 + jj^2 Hm1[Mm, r, u] - q Hm2[Mm, r, u]) (1 - u^2) ;

gtφHT[Mm_, jj_, r_, u_] = -2 Mm^2/r jj (1 - u^2) ;

Using the expressions presented in, Fintan D . Ryan, Phys . Rev . D 52, 5707–5718 (1995), to calculate the moments of the Hartle - Thorne spacetime .

gtt = gttHT[M, j, q, r, u] ;

gφφ = gφφHT[M, j, q, r, u] ;

gtφ = gtφHT[M, j, r, u] ;

Series[gtt, {r, ∞, 4}]

Simplify[Series[gφφ/(r^2 (1 - u^2)), {r, ∞, 4}]]

Simplify[Series[gtφ, {r, ∞, 4}]]

-1 + (2 M)/r + (-M^3 q + 3 M^3 q u^2) (1/r)^3 + (-M^4 q + 2 j^2 M^4 u^2 + 3 M^4 q u^2) (1/r)^4 + O[1/r]^5

1 + M^3 q (-1 + 3 u^2) (1/r)^3 + 1/2 M^4 (j^2 + 5 q) (-1 + 3 u^2) (1/r)^4 + O[1/r]^5

(2 j M^2 (-1 + u^2))/r + O[1/r]^5

Ω = (-D[gtφ, r] + (D[gtφ, r]^2 - D[gtt, r] D[gφφ, r])^(1/2))/D[gφφ, r] ;

FullSimplify[Series[(M Ω)^(1/3)//.{r→M/x^2, u→0}, {x, 0, 13}]]

Xpar = Simplify[InverseSeries[%]/.{x→U}]

Em = (-gtt - gtφ Ω)/(-gtt - 2 gtφ Ω - gφφ Ω^2)^(1/2) ;

Eseries = Simplify[Series[Normal[Series[Em//.{r→M/x^2, u→0}, {x, 0, 12}]]//.{x→Xpar}, {U, 0, 12}]]

Series[-U/3 D[Normal[Eseries], U], {U, 0, 12}]

Comparing this expression with the on in eq . (17) in, Fintan D . Ryan, Phys . Rev . D 52, 5707–5718 (1995), one sees that j = J/M^2 and q = Q/M^3 .

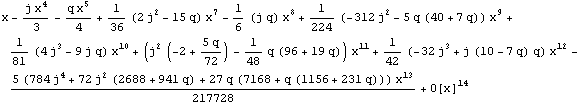
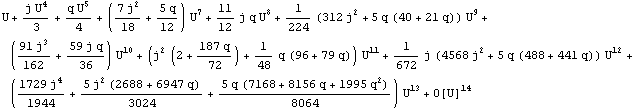
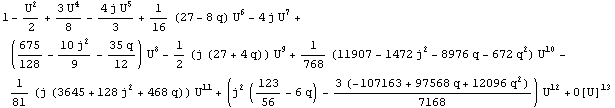
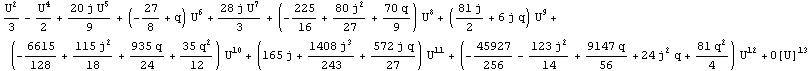
Created by Mathematica  (September 27, 2012) Valid XHTML 1.1!