reading the numerical data and calculating everything in Weyl-Papapetrou coordinates
In[23]:=
![]()
![]()
![]()
![]()
![]()
![]()
Out[26]=
![]()
Out[28]=
![]()
Out[29]=
![]()
In[112]:=
![]()
In[1042]:=
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()


![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()

![]()

![]()




![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()




Out[1053]=
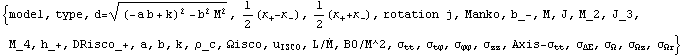
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Out[1105]=
![]()
Out[1106]=
![]()
Out[1107]=
![]()
![]()
![]()
| Created by Mathematica (September 26, 2012) |