Phone: 30 210 7274 536

akoutsel@chem.uoa.gr

Research Interests

The dynamic and kinetic phenomena of systems out of equilibrium have entered a new phase due to advances in selective monitor experimental techniques. Systems that interest us involve chemical solutions constrained away from equilibrium and ions moving in fluids under the action of external fields. Such systems undergo rotational, vibrational and electronic excitation and relaxation, as well as, chemical transformations that vary from those that appear close to equilibrium. The new experimental observations require the development of theoretical tools that treat few-body interactions sampled with statistics of microscopic properties that emerge far from equilibrium. Especially, the excitation of internal molecular degrees requires the use of quantum methods for their description, though at low temperatures even the translational motion requires a similar treatment. In addition, the statistical distribution of microscopic properties has to be calculated accurately depending on microscopic interactions and macroscopic constraints. We use stochastic theory for the description of dense reactive systems [1] and kinetic theory calculations for the transport of ions in low density fluids [2]. Complex molecular systems, such as many atom complexes, nanoparticles and oligopeptides, are more easily amenable to study through molecular dynamic (MD) simulation. In this case we have developed MD methods that efficiently reproduce the experimental transport and relaxation data of the ions in fluids, from low to intermediate density, and for the whole experimental electric field range [3].

[1] "Steady State Thermodynamics for Homogeneous Chemical Systems" A. D. Koutselos, J. Chem. Phys. 101, 10866, (1994).

[2] a) "Third Order Transport Properties of Ions in Electrostatic Fields", A. D. Koutselos, J. Chem. Phys. 110, 3256, (1999).

[3] a) "Transport and dynamic properties of O₂⁺ (X²Π_g) in Kr under the action of an electrostatic field: Single or multiple potential energy surface treatment", A. D. Koutselos, J. Chem. Phys. 134, 194301 (2011).

b) "Mixed quantum-classical molecular dynamics simulation of vibrational relaxation of ions in an electrostatic field", A. D. Koutselos, J. Chem. Phys. 125, 244304 (2006).

c) "Molecular dynamics simulation of ion transport in moderately dense gases in an electrostatic field", G. Balla and A. D. Koutselos, J. Chem. Phys. 119, 11374 (2003).

d) "Transport properties of diatomic ions in moderately dense gases in an electrostatic field", A. D. Koutselos and J. Samios, Pure Appl. Chem. 76, 223 (2004).

Research Work of recent Graduate Students:

Maria Anagnostopoulou

The experimental measurements of the mobility of ions at very low temperature noble gases have shown an unexpected deep that has not been explained fully so far. We study this system through a nonequilibrium molecular dynamics method with the use of an effective cooling technique. This system requires a quantum treatment for the translational motion, which is implemented here through a semi-classical variational solution of the Schrödinger equation based on a trial bosonic wave function that is constructed from single particle wave packets.

Iraklis Litinas

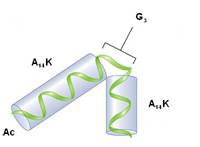
The motion of peptide ions (Ac-A₁₄KG₃A₁₄K+2H⁺ in a noble gas) in drift tube measurements presents an abrupt change at high temperature that is speculated to be due to the variation of the ion-neutral collision cross section. If such a change is due to a temporary unfolding of the oligopeptide at high temperature then it should show up in the accumulation of energy of the bending mode involved in the peptide transformation. This system is a prototype for the study of peptide transformations in ion mobility spectrometry and its transport properties are reproduced here through an MD simulation method that treats molecular translation, rotation and bending motion explicitly through a model interaction potential [4].

[4] a) "Molecular Dynamics Simulation for the Dynamics and Kinetics of Folding Peptides in the Gas Phase", I. Litinas and A. Koutselos. J. Phys. Chem. A. 119, 12935 (2015).

b) "Structure Distribution of Gaseous Ions in Strong Electrostatic Fields", I. Litinas and A. Koutselos. J. Phys. Chem. A. 123, 5683 (2019).