...δεν είναι συνέχεια του μαθήματος
Πραγματική Ανάλυση! Το περιεχόμενο του μαθήματος είναι:
Σειρές
Fourier και Ολοκλήρωμα Lebesgue
Σύντομη Περιγραφή:
Ο J. Fourier (1768-1830) πίστευε ότι κάθε 2π-περιοδική συνάρτηση f μπορεί να «αναπαρασταθεί» με μια «τριγωνομετρική σειρά» της μορφής
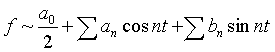
την «σειρά Fourier της f». Πίστευε δηλαδή ότι κάθε περιοδική συνάρτηση αποτελεί «συνδυασμό» των «καθαρών» ημιτονοειδών συναρτήσεων. Χρησιμοποίησε αυτές τις «αναπαραστάσεις» για την επίλυση διαφορικών εξισώσεων (με μερικές παραγώγους) που περιέγραφαν φυσικά φαινόμενα. Από την αρχή τέθηκαν ερωτήματα σχετικά με την σύγκλιση των σειρών αυτών. Για την απάντηση τέτοιων ερωτημάτων χρειάστηκε να αναπτυχθούν πολλά από τα εργαλεία της Μαθηματικής Ανάλυσης, και κυρίως να διευκρινισθεί η ίδια η έννοια της συνάρτησης. Ταυτόχρονα όμως οι σειρές Fourier αποτέλεσαν και αποτελούν απαραίτητο εργαλείο για τις εφαρμογές των Μαθηματικών στις Επιστήμες και την Τεχνολογία.
-
Ποιές συναρτήσεις f έχουν σειρά Fourier και πώς "αναλύεται" μια συνάρτηση σε σειρά Fourier (φασματική ανάλυση); Αν ξέρουμε τους συντελεστές της σειράς Fourier της f, μπορούμε να "συνθέσουμε" την f (φασματική σύνθεση);
-
Συγκλίνει η σειρά Fourier της f , και αν ναι, με ποια έννοια (σημειακή, ομοιόμορφη, μέση τετραγωνική σύγκλιση);
-
Είναι κάθε (συγκλίνουσα) τριγωνομετρική σειρά η σειρά Fourier κάποιας συνάρτησης; Είναι μοναδική αυτή η συνάρτηση, αν υπάρχει;
Επειδή οι συντελεστές υπολογίζονται μέσω ολοκληρωμάτων, όπως:
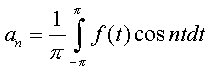
θα χρειαστεί να επανεξετάσουμε την έννοια του ολοκληρώματος. Θα διαπιστώσουμε ότι το ολοκλήρωμα Riemann δεν αρκεί για να αντιμετωπίσει τα προβλήματα, και θα οδηγηθούμε έτσι σε μια ιδιαίτερα γόνιμη γενίκευσή του, το ολοκλήρωμα Lebesgue
Η βασική ιδέα για τον ορισμό του ολοκληρώματος αυτού μπορεί να περιγραφεί με τον ακόλουθο τρόπο:
Στο ολοκλήρωμα
Riemann διαμερίζει κανείς το πεδίο ορισμού μιας συνάρτησης f και δημιουργεί τα
μερικά αθροίσματα 
, όπου
Δti είναι το μήκος του αντίστοιχου υποδιαστήματος. Έτσι, αν η συμπεριφορά
της f σε μικρά υποδιαστήματα του πεδίου ορισμού της είναι αρκετά ακατάστατη, η
συνάρτηση δεν θα είναι ολοκληρώσιμη κατά Riemann. Κλασσικό παράδειγμα αποτελεί η
συνάρτηση Dirichlet, που είναι 0 στους άρρητους και 1 στους ρητούς (του [0,1]).
Στο ολοκλήρωμα
Lebesgue αντίθετα διαμερίζουμε το σύνολο τιμών της f σε υποδιαστήματα I1,
I2 ,In και θεωρούμε μερικά αθροίσματα της μορφής 
, όπου τώρα 
, και μ(Ai) το «μήκος» του Ai. Έτσι αν
οι αντίστροφες εικόνες Ai έχουν «μήκος», μπορεί κανείς να εξετάσει τη σύγκλιση
των μερικών αθροισμάτων.
Το ολοκλήρωμα Lebesgue έχει δύο βασικά πλεονεκτήματα:
1) Επιτρέπει την ολοκλήρωση πολύ γενικότερων συναρτήσεων από ότι το ολοκλήρωμα Riemann.
2) Συμπεριφέρεται πολύ καλύτερα από το ολοκλήρωμα Riemann ως προς οριακές διαδικασίες.
Θα ασχοληθούμε με τον προσεκτικό ορισμό του ολοκληρώματος αυτού, για συναρτήσεις μιας πραγματικής μεταβλητής, με τα βασικά θεωρήματα σύγκλισης, και με τις βασικές εφαρμογές του στις σειρές Fourier.
Προαπαιτούμενες γνώσεις
Απειροστικός Λογισμός μιάς πραγματικής μεταβλητής, κυρίως ολοκλήρωμα Riemann και σειρές.
Ακολουθίες και σειρές συναρτήσεων: σημειακή και ομοιόμορφη σύγκλιση.
(Θα υπάρξει μια σύντομη υπενθύμιση του ολοκληρώματος Riemann και των βασικών αποτελεσμάτων για σειρές συναρτήσεων.)
Ώρες διδασκαλίας: Δευτέρα 3-5, Αίθουσα Γ21
Τρίτη 13-14, Αίθουσα Γ31
Έναρξη: Δευτέρα 7 Φεβρουαρίου
Είμαι στη διάθεση των φοιτητών για περισσότερες πληροφορίες
